0 引 言
随着现代遥感技术的飞速发展，通过卫星观测获取的数据量不断增大，从而使对地数传的难度增加。在频谱资源有限的情况下，极化复用可以提高有限频带数传系统的数据传输率［1］。但实际上，在信号传输过程中，容易受到传输信道的非理想特性、雨衰、天线的隔离度等因素的影响，使得电磁波的极化方向发生偏转，产生交叉极化干扰［2］。天线隔离度固定时，可以采用极化标定方法进行标校，消除系统极化隔离度的影响［3］。但是对于相控阵天线，波束扫描过程中交叉极化耦合的参数不断变化，极化标效无法实现，需要采用交叉极化干扰对消技术（Cross-polarization Interference Canceller，XPIC），抑制两路信号之间的相互干扰。
目前国内外对于XPIC 的研究，主要集中在解调前对消和解调后对消这两种方案。接收机先解调再进行对消，需要两路极化信号的载波同步、符号同步，再进行对消。在强交叉极化干扰下，若载波环和符号同步环无法锁定，则后续对消无法进行，使接收机不能正常工作［4］。解调前对消不需要载波、符号同步等处理，在强干扰下具有较大优势。文献［4］介绍了一种基于判决的LMS 检后盲自适应XPIC 算法，该方法需要两个极化信号同步，以保证对消性能。文献［5］提出一种基于采样样本的相关对消技术，无须进行载波、符号同步和符号判决等处理，但运算量较大。
独立分量分析（ICA）方法是一种混合信号的盲源分离算法，本质是利用源信号的非高斯和独立性［6］。如果分量是独立的，则该方法可以将独立分量从混合信号中分离出来。由于传输的两路源信号之间相关性很小，基本满足统计独立要求。因此，该方法应用于交叉极化干扰抵消，可以将源信号从混合信号中分离出来。本文提出一种基于ICA 的交叉极化干扰抑制算法，不需要信号的先验信息和信号同步、符号判决等处理，即可实现信号干扰抵消。仿真结果表明，该算法可以有效地消除交叉极化干扰，解决极化复用模式下的交叉极化干扰问题。
1 交叉极化干扰分析
双极化频率复用方式，是在同一频率上以两种正交的极化方式传输两路独立信号，可以使传输容量加倍，提高频谱利用率。然而采用极化复用技术容易受到传输信道的非理想特性、雨衰［7］、天线的隔离度等影响，使原本极化状态相互正交的两路信号相互耦合，引起交叉极化干扰，降低信号的信噪比。极化复用可以是水平H 和垂直V 线性极化复用，也可以是左旋和右旋圆极化复用。以线极化传输复用为例，如图1所示。
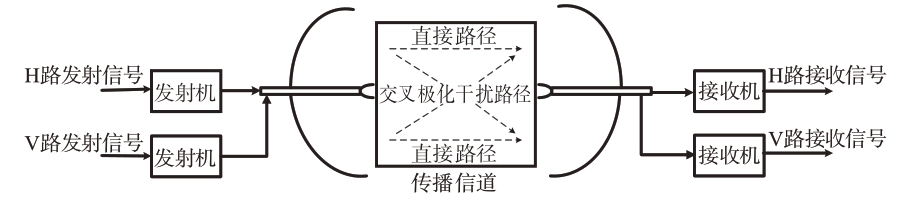
图1 极化复用通信系统
由于收发天线均是双极化模式工作，极化隔离度有限，因此，进入接收机之前的两路信号呈现相互对称性的极化干扰。交叉极化干扰传输模型如图2所示。
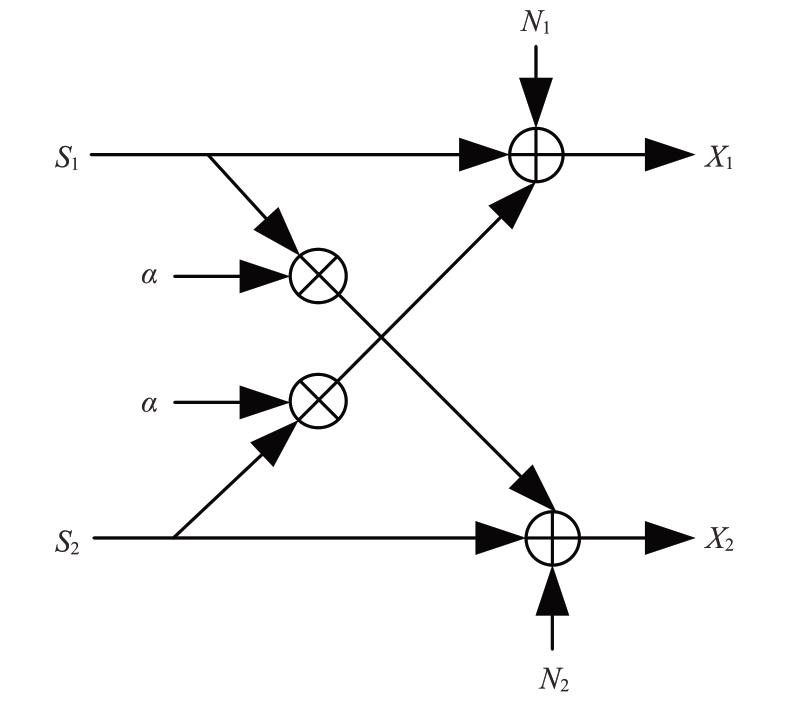
图2 交叉极化干扰传输模型
交叉极化干扰用交叉极化隔离度（Cross Polarization Discrimination，XPD）来表示，定义为本极化方向的信号与泄露到交叉极化方向的信号功率之比［8］。
其中XPD 的值越小，交叉极化干扰越大。根据收发天线的极化隔离性能，以及无线传输信道等影响因素，XPD取值在5～40 dB［4］。
根据图2，在接收端对交叉极化干扰进行建模，如下：
接收到的两路信号可表示为
式中：S1，S2 为极化发射天线发射的两路信号；X1，X2 为通信系统接收到的经极化干扰的两路信号；N1，N2为高斯白噪声；α为交叉极化干扰，包含交叉极化增益和两种极化通道之间相位差这两部分的干扰；S1，S2，X1，X2，α均为复数。
2 盲分离线性瞬时混合模型
在线性瞬时混合模型中，源信号是线性组合的，且混合是瞬态的，混合模型可表示为
式中：X=(x1,x2,…,xm)T 为观测信号矢量；S=(s1,s2,…,sn)T 为未知源信号矢量，由n 个相互独立成分组成；A 为M×N 维未知混合矩阵；N=(n1,n2,…,nm)T为加性噪声，在该模型中噪声项的分布是未知的，仅被视为一个干扰因素，为了简化模型，这里忽略了噪声项。
分解过程如下式所示：
式中，W为分离矩阵，此时WA近似为一个单位阵，使得分离出的Y为源信号的估计。
盲源分离在源信号S 和混合矩阵A 未知的情况下，仅通过观测信号X 估计出源信号。该过程分为未知信号混合和盲分离两部分，盲源分离模型框图如图3所示。
图3 盲源分离模型框图
将交叉极化干扰传输模型对应于盲信号分离中线性瞬时模型M=2 的情况，且发射机发射的两路信号S1、S2是独立、非高斯的，满足盲分离可解的条件，因此可以通过相关分离算法对源信号进行估计。本文考虑的是混合信号数量与源信号数量相等，即M=N时的正定盲源分离问题［9］。
3 CMA算法
LMS 算法是目前常用的XPIC 算法，需要发送一段训练序列来调节滤波器的抽头系数。该序列并无实际通信含义，会消耗一定的信道资源，降低频谱利用率。CMA 算法无需训练序列，核心思想是利用源信号的模值统计信息，代替发送信号的训练序列来构造代价函数。
CMA算法的基本公式如下：
代价函数：
误差函数：
抽头权向量的迭代公式：
滤波器的输出：
其中，R2=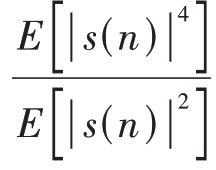
，s(n)为源信号，x(n)为观测信号，μ为步长参数。
4 盲分离交叉极化干扰抑制算法
ICA 的许多目标函数中，峭度是最常用的统计量，其绝对值被广泛用作ICA和相关领域的非高斯性度量，主要原因在于其计算和理论上的简单性，对有限采样的鲁棒性［10］。本节算法使用峭度函数绝对值作为目标函数，通过最佳步长的高效计算技术进行优化，提取非零峭度的独立分量即源信号。
假设观测信号为x，这里不用进行预白化处理，仅需要去中心化，即减去均值向量，使其均值为零，解混合信号为y=wTx，峭度公式为
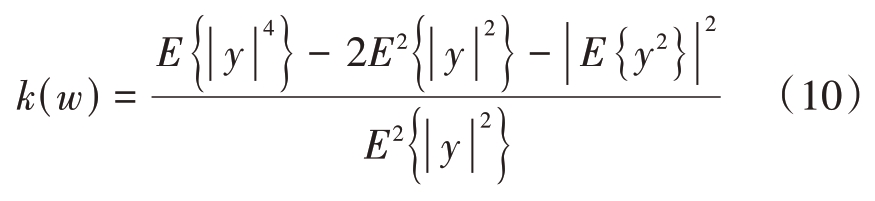
进行精确线性搜索［10］优化：
搜索方向g 通常是梯度，g=∇wκ(w)，由以下公式给出：
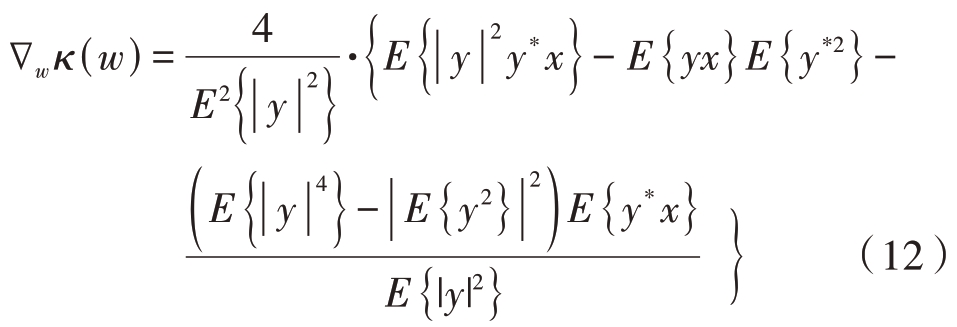
精确线性搜索通常计算复杂度高且存在诸多限制条件，然而可以通过最优步长算法将归一化峭度表示成μ的多项式或有理函数，然后计算低次多项式的根，找到梯度迭代的最优步长μopt。
在wi(n)+μg 处的峭度表示为关于μ 的函数，并用有理分式表示：
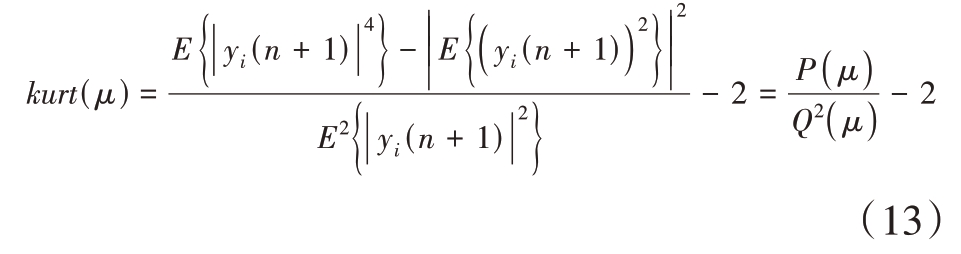
式中yi(n+1)=yi(n)+μgHx(n)；yi(n)=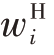
(n)x(n)；
将P(μ)、Q(μ)表示为μ的多项式：
令a=yi2(n)，b=(gHx(n))2，c=yi(n)gHx(n)，d=Re(yi(n)(gHx(n))*)，则P(μ)、Q(μ)中的参数可表示为
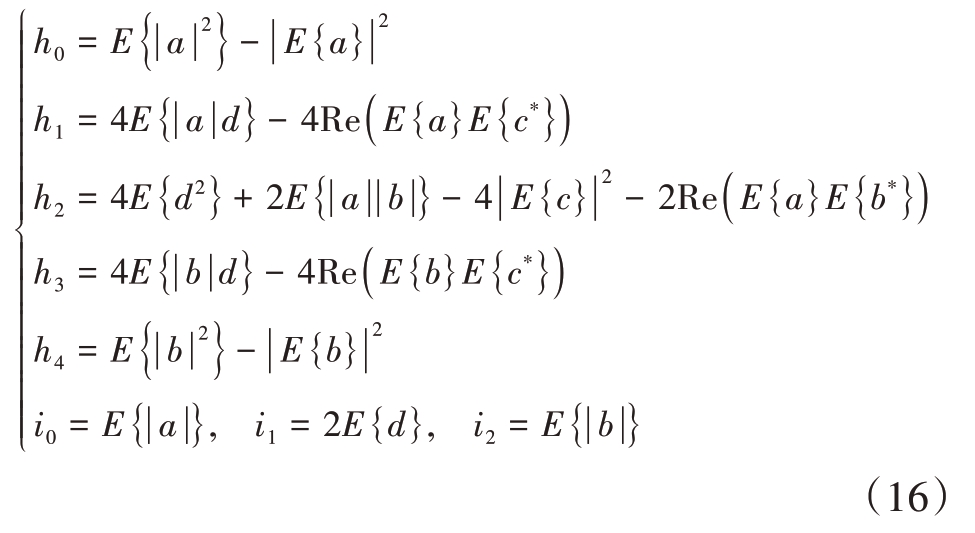
通过峭度最大化找到独立分量，需使kurt(wi(n)+μg)关于μ的导数为零，将归一化峭度转化为方程：
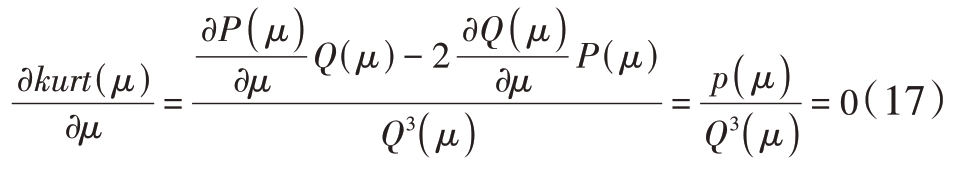
则最优步长多项式可表示为
通过式（14）～（17），可以得到p(μ)的系数:
a0=-2h0i1+h1i0，a1=-4h0i2- h1i1+2h2i0，a2=-3h1i2+3h3i0，a3=-2h2i2+h3i1+4h4i0，a4=-h3i2+2h4i1。
具体步骤归纳如下:
1）计算最优步长多项式的系数。最优步长多项式如下式所示：
系数{a}4k=0可以很容易地在每次迭代时，从观测信号和当前的w、g中获得。
2）提取最优步长多项式的根
3）在搜索方向上选择使峭度函数绝对值最大的根：
4）更新，wi(n+1)=wi(n)+μoptg。
5）归一化，wi(n+1)=
6）若未收敛则返回步骤1），当|1-|wH(n)·w（n+1)| |＜ε时算法停止，ε是具有统计意义的小常数。
未采用预白化的算法，需要用线性回归方法归一化观测信号。将估计出的第i 路源信号，通过X ←(X-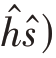
)的方式缩小。源信号的方向可以通过最小均方误差（MMSE）计算得到，即
5 算法仿真分析
本节对盲分离交叉极化干扰抑制算法和恒模（CMA）算法的分离性能进行仿真分析，采用信干噪比（SINR）来衡量信号分离效果。SINR 越大，分离效果越好。
仿真中，信号均采用QPSK 调制，数据长度为5 000 个符号，α 的相位取某个随机固定值，盲分离算法终止参数设为ε=1×10-10，CMA 算法的步长参数设为μ=0.002。
首先仿真高信噪比下（SNR=30 dB），XPD=5 dB 时，算法迭代过程中分离信号的SINR 如图4所示。
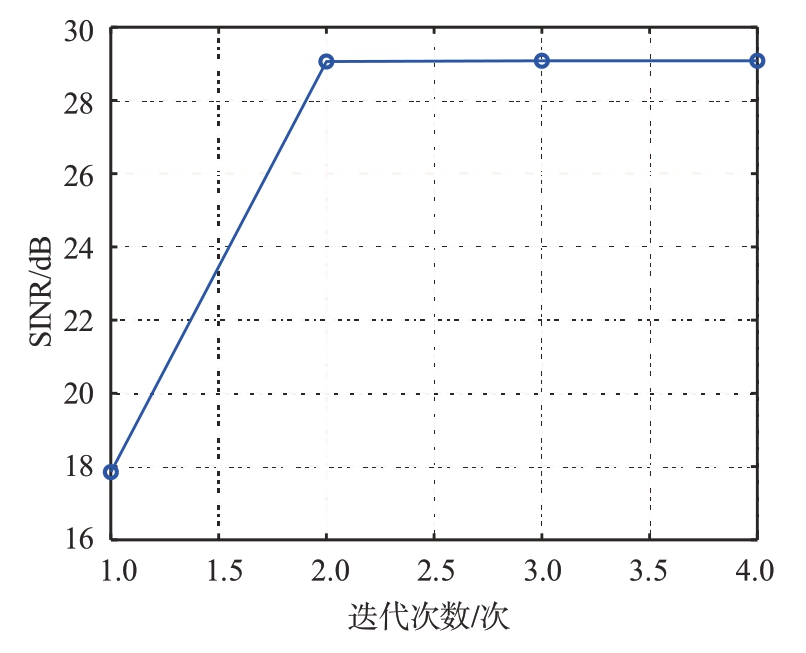
图4 迭代过程中SINR变化情况
该算法单次迭代计算量高，但在每次迭代的搜索方案上更加有效，迭代次数较少。
5.1 隔离度的影响
SNR=30 dB 时，仿真XPD 变化的情况，信干噪比改善程度如图5所示。
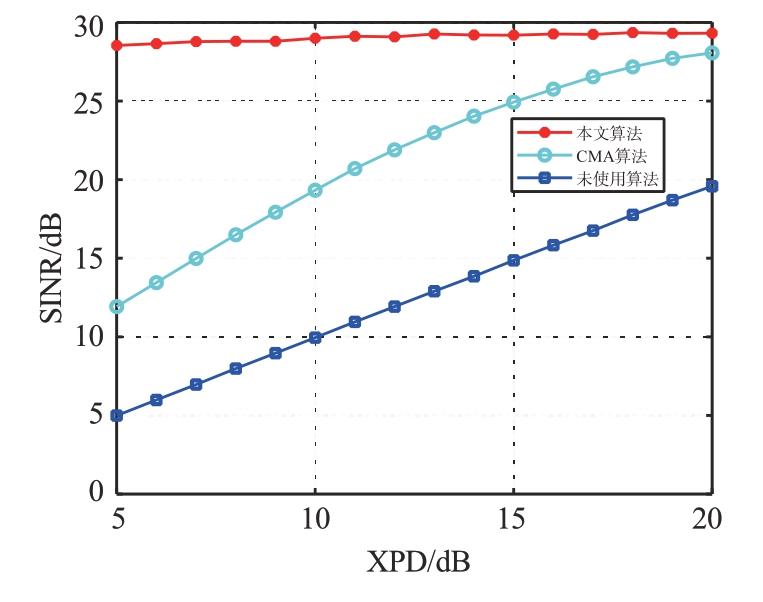
图5 信干噪比改善程度SNR=30 dB
SNR=10 dB 时，仿真XPD 变化的情况，信干噪比改善程度如图6所示。
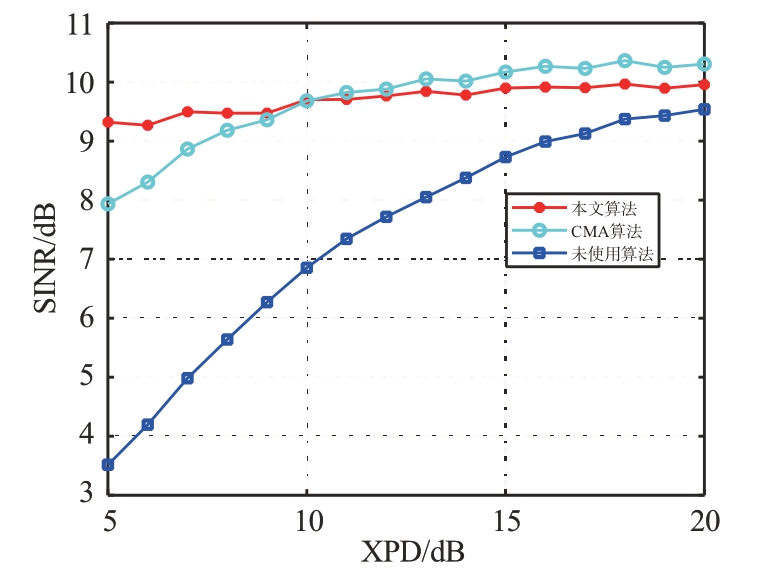
图6 信干噪比改善程度SNR=10 dB
从图5、图6可以看出，固定信噪比时，随着隔离度的变化，盲分离算法的分离性能比较稳定，且交叉极化干扰越严重（XPD 数值越小），该算法的干扰抑制效果越明显。在高信噪比情况下，盲分离算法的性能明显优于CMA算法。低信噪比情况下，CMA 算法在隔离度为5～10 dB 之间的性能欠佳，通过盲分离算法处理后的SINR 明显高于处理前的SINR，算法仍有较好的干扰抑制效果。
仿真SNR=10 dB，XPD 从5 dB 增加到20 dB时，使用盲分离交叉极化干扰抑制算法后的XPD。每个实验点重复200 次，对结果取平均，如图7所示。
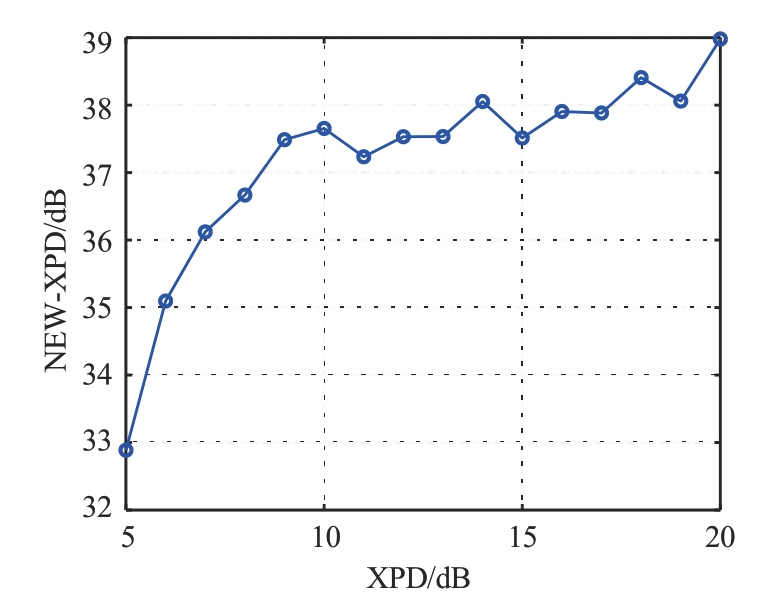
图7 使用盲分离算法前后的XPD对比
仿真结果表明，经盲分离算法处理后，XPD 改善效果明显。交叉极化干扰越小，交叉极化改善度越小。
5.2 信噪比的影响
XPD=10 dB 时，仿真SNR 变化的情况，信干噪比改善程度如图8所示。
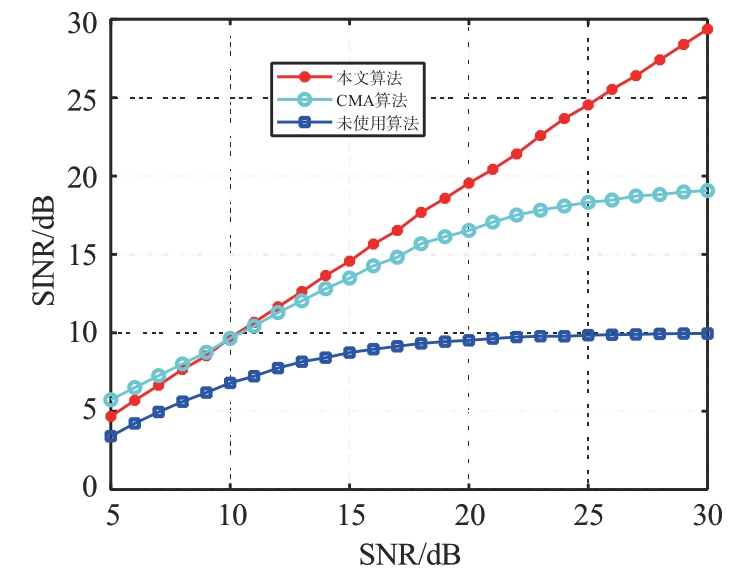
图8 信干噪比改善程度XPD=10 dB
仿真结果表明，盲分离算法在信噪比为10～30 dB之间的性能优于CMA 算法。CMA 算法对噪声较为敏感，进一步影响了信号的分离性能。隔离度固定时，盲分离算法的分离性能随信噪比趋势变化，随着信噪比增加，信号的分离性能逐渐提高，从而获得更高的信干噪比增益。
5.3 数据长度的影响
仿真中，信噪比和隔离度均取10 dB，数据长度从100 个符号增加到3 500 个符号，间隔100 个符号，使用盲分离算法和CMA 算法进行干扰对消得到的结果如图9所示。
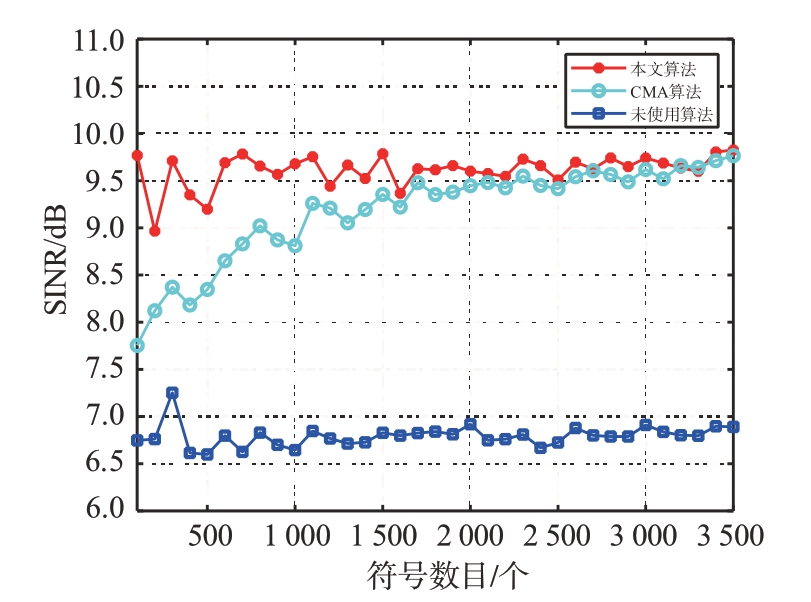
图9 两种算法随符号数目变化的性能比较
从图9可以看出，在低信噪比、隔离度下，随着符号数目的增加，本文算法性能优于CMA算法，尤其在符号数目小于1 500 时，本文算法具有明显的优势。
5.4 估计信号的EVM分析
QPSK调制体制下，SNR=10 dB，XPD=10 dB时，对盲分离算法处理前后的信号星座图进行仿真，并用误差向量幅度（Error Vector Magnitude,EVM）衡量估计信号的误差，EVM 越小，信号质量越好［11］，如图10所示。
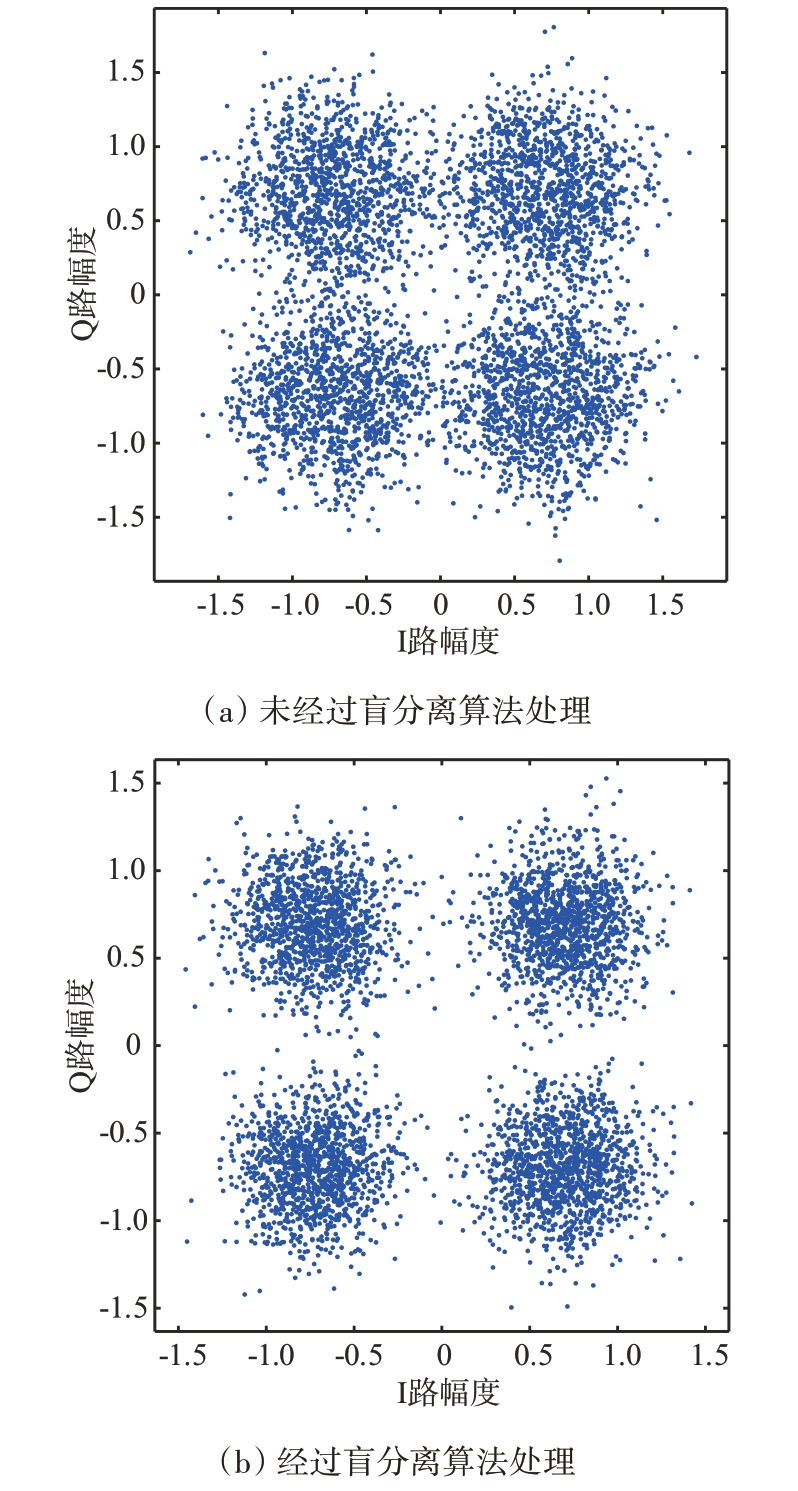
图10 盲分离算法处理前后的对比
从图10可以看出，交叉极化干扰抑制作用明显，星座图的收敛效果较好。计算图10（a）中观测信号的EVM 为-6.8 dB，图10（b）中估计信号的EVM 为-9.7 dB，经本文算法处理后，EVM 改善了约2.9 dB。仿真结果表明，在低信噪比、隔离度下，本文提出的盲分离交叉极化干扰抑制算法仍可以有效地抑制交叉极化干扰。
6 结束语
针对极化复用技术引入交叉极化干扰导致信号信干比下降的问题，本文将盲源分离算法应用到交叉极化干扰传输模型中，进行干扰抑制。与传统的CMA 算法对比，盲分离算法无需信号先验信息，即可从混合信号中提取源信号。仿真结果表明，本文算法的分离鲁棒性好，可以有效地抑制交叉极化干扰，改善极化复用系统的信干比。相比于应用广泛的FastICA 算法，本文算法不需要预白化处理，计算复杂度更低，对于盲分离算法应用在交叉极化干扰抵消领域具有一定的参考价值。下一步可以将本文算法与传统XPIC 算法结合，进一步提升交叉极化干扰对消性能，并且对盲分离算法进行改进，降低算法复杂度。
［1］郑生华，李景峰，张洪涛.对地观测卫星相控阵数传系统参数设计［C］∥第二届高分辨率对地观测学术年会论文集，北京：中国宇航学会，2013：1-6.
［2］操礼长，谢学东，王志超.交叉极化干扰对消的研究及仿真［J］.无线电工程，2021，51（3）:212-216.
［3］翟计全，马林，杨文军.全极化雷达极化标校技术研究［J］.电波科学学报，2019，34（6）:806-813.
［4］王宇舟，王春蓉，陈颖.基于LMS 的检后盲自适应XPIC算法仿真［J］.通信技术，2018，51（7）:1516-1521.
［5］王宇舟，钟瑜，刘金山.一种高速卫星通信交叉极化干扰对消技术仿真［J］.通信技术，2014，47（2）:141-144.
［6］DONG Jiacheng,ZHOU Wenhai.Research on the Improved FastICA Blind Signal Separation Algorithm［C］∥2020 IEEE 20th International Conference on Communication Technology,Nanning,China:IEEE,2020：1231-1236.
［7］朱胜利.极化对消算法的进一步研究［J］.通信技术，2020，53（12）:2908-2914.
［8］KIM B,KIM D.An Enhanced Dual-polarized Transmission System with 4D-TCM 8PSK Modulation and XPIC［C］∥2020 International Conference on Information and Communication Technology Convergence,Jeju Island,Korea:IEEE,2020：806-808.
［9］肖瑛，马艺伟，黄小青.盲源分离不确定性问题研究综述［J］.大连民族大学学报，2021，23（5）:446-453.
［10］ZARZOSO V,COMON P.Robust Independent Component Analysis by Iterative Maximization of the Kurtosis Contrast with Algebraic Optimal Step Size［J］.IEEE Trans on Neural Networks,2010,21（2）:248-261.
［11］王小燕.QPSK 信号的相干光检测的EVM 值分析［J］.兰州文理学院学报（自然科学版），2021，35（2）:60-64.
