0 引 言
在自适应雷达信号处理中，干扰协方差矩阵（Interference Covariance Matrix，ICM）估计是一个长期存在的基本问题［1-2］。传统的样本协方差矩阵（Sample Covariance Matrix，SCM）估计方法，依赖于均匀环境下不少于两倍系统自由度（Degrees of Freedom，DOF）的独立同分布（Independent and Identically Distributed，IID）训练样本。然而，在真实场景中雷达所处的环境通常是非均匀的，以至于仅能获得较为有限的训练数据来估计待检测单元（Cell Under Test，CUT）的ICM，这会导致估计精度下降，从而影响干扰抑制性能［3］。因此，如何在小样本情况下准确估计协方差矩阵成为当前面临的一个严峻挑战。
针对上述问题，一类有效的策略是利用雷达场景中的先验知识提高ICM 的估计精度，其中结构化ICM 估计方法被证实是一种可行的解决方案［4-5］。利用ICM 的结构信息（比如Persymmetric,Toeplitz 结构等），可以减少协方差矩阵的DOF，从而降低对样本数量的依赖性。根据这一处理范式，国内外学者依据不同的协方差模型，提出了多种结构化估计方法［6-13］。文献［7-9］利用协方差矩阵的Persymmetric 结构增加了可用训练数据，并将其引入广义似然比（Generalized Likelihood Ratio，GLR）检测器中，提高了非结构化算法的检测性能。但上述算法只考虑了矩阵结构信息，当结构模型不匹配时可能会导致性能下降。文献［11］联合了Toeplitz 结构信息与杂波环境知识（比如合成孔径雷达图像、数字高程模型、地理地形图等），将Toeplitz结构引入知识辅助（Knowledge Aided，KA）色加载矩阵中，提高了算法性能。但该算法依赖于先验协方差矩阵的准确程度，当先验杂波知识失配时会带来较大的误差损失。文献［12］从几何角度研究了Toeplitz 协方差矩阵估计问题，证明了当训练数据较少时，几何方法能够获得优越的性能。文献［14-19］利用额外的约束条件，如正定、低秩和条件数上限等，以控制所得自适应算法的数值稳定性，从而提高了估计精度。
本文遵循几何范式，提出了基于Persymmetric和Toeplitz 结构的两种协方差矩阵估计算法。首先，假设协方差矩阵具有上述结构特性，运用这些特性信息对训练数据进行处理，进而推导生成了两种结构样本协方差矩阵（Structured Sample Covariance Matrices，SSCMs）。然后，根据ICM 与相对应SSCMs的最小化欧氏距离建立目标函数，并施加正定和条件数约束。通过该极小化问题的转化，最终求得闭式的协方差矩阵估计。在分析阶段，我们使用两种场景（空域和多普勒处理）下的输出信干噪比（Signal-to-Interference-plus-Noise Ratio，SINR）评估了所提出算法的性能。实验结果表明，本文所提算法相比于其他同类算法具有更优性能。
1 信号模型与结构信息
1.1 信号模型
首先将训练样本x1,…,xK 建模为N 维、循环对称和零均值的随机向量，具有相同的协方差结构
式中，E[·]表示期望，(·)H表示共轭转置，≻表示广义矩阵不等式，M 表示ICM，K 为样本总数。xk ∈ℂN×1的第n个元素表示为xn(k)，则xk定义为
式中，(·)T表示转置。ICM可以具体表示为
式中，Mc 表示色干扰矩阵，σ2n 表示噪声功率，IN 为N×N维的单位矩阵。
为了使滤波器输出信号中的SINR 最大化，将最优权矢量定义为［3］
式中，s∈ℂN×1 为目标的导向矢量，其表达式取决于具体应用场景和雷达配置。在传统方法中，待估计的协方差矩阵M由SCM所代替
1.2 结构信息
1.2.1 Persymmetric结构
在雷达系统中，如果采用阵列中心为相位中心，那么ICM 具有Persymmetric 结构，满足以下等式［6,8］：
式中(·)*表示共轭，JN为N×N维的置换矩阵，即
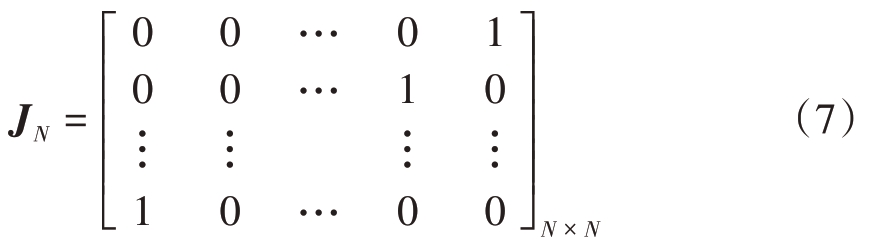
此外，信号导向矢量s也满足Persymmetric特性：
1.2.2 Toeplitz结构
与1.2.1 节相似，线性阵列与均匀发射脉冲雷达的干扰回波满足Toeplitz 结构，即协方差矩阵M沿平行主对角线的每一对角线上的元素都是相同的，此时的ICM可以表示为［6］
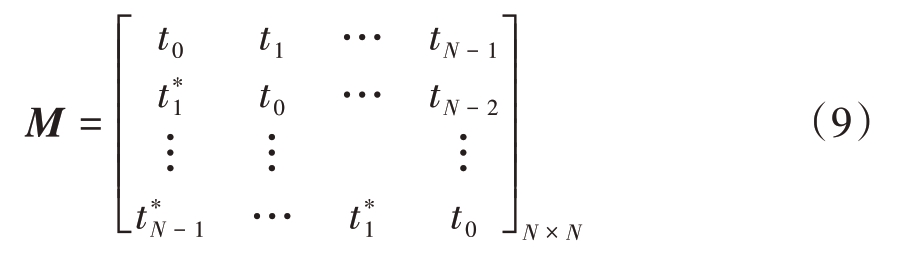
可以看出M 是由第一行的N 个元素所构成，我们将其定义为tl,l=0,…,N-1，表示第一行的第l个元素。
2 结构化协方差矩阵估计
基于Persymmetric 和Toeplitz 结构特性，下文构造了两种SSCMs，并在特定约束集下分别利用它们与ICM 的最小化欧氏距离（也称为Frobenius 距离）建立优化问题，从而提出了两种估计算法，即Persymmetric 协方差矩阵估计（Persymmetric Covariance Matrix Estimation,P-CME）算法和Toeplitz 协方差矩阵估计（Toeplitz Covariance Matrix Estimation,T-CME）算法。
2.1 Persymmetric结构协方差矩阵估计
基于Persymmetric 结构的协方差矩阵估计算法可分为两步：
第一步，根据协方差矩阵的Persymmetric 特性，将第k个训练样本处理为［8］
式中，
是通过分解训练数据获得的独立样本向量。此时协方差矩阵可以表示为
且E[xokxHek]=0。因此，由训练样本估计的Persymmetric SSCM 为
第二步，由于本文提出的框架依赖于正定矩阵空间中欧式距离的使用，所考虑的矩阵是正定的。因此，必须利用先验信息得出正定性。为了实现这个目标，我们假设已知噪声的功率下限σ2（σ2n ≥σ2，且为了不失一般性，设置σ2=0 dB）［14,19］。此外，同时考虑了在条件数上限约束下最小化M与
的Frobenius距离，由此可得优化问题
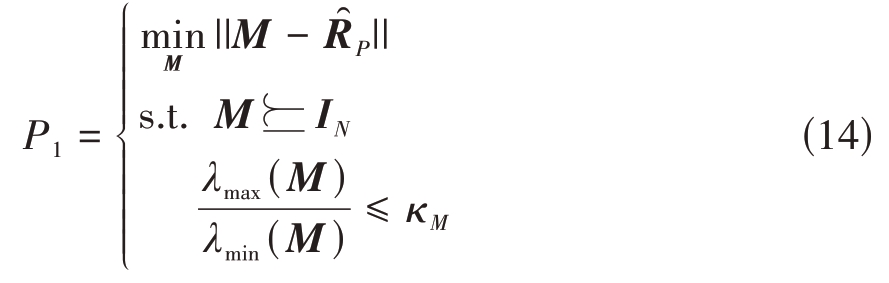
式中，||·||表示Frobenius 范数，λmax(·)和λmin(·)表示矩阵最大和最小特征值，κM ≥1为协方差矩阵条件数的上限，可以使用关于实际雷达电磁环境的先验信息或根据基于观测的自适应框架来指定［12］。
接下来，我们用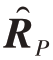
=UP ΛPUHP 表示
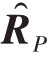的谱分解，其中ΛP=diag([d1,d2,…,dN])T，diag(·)表示对角阵，d1 ≥d2 ≥… ≥dN 是按递减顺序排列的 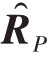的特征值，UP是一个酉矩阵，其列包含相应的特征向量。问题P1的最优解为
式中，Λ★=diag([λ★1,λ★2,…,λ★N])T 为以下优化问题的最优解：
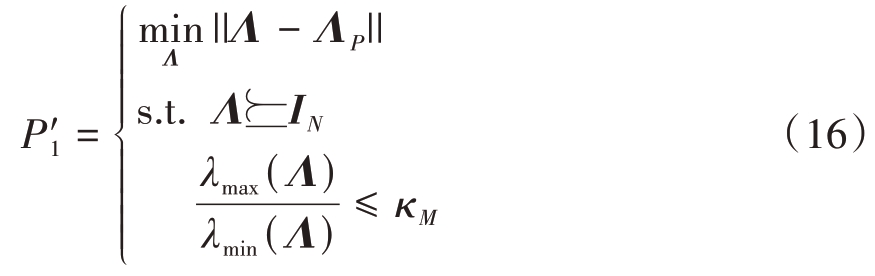
式中，Λ=diag([λ1,λ2,…,λN])T，λ1 ≥λ2 ≥… ≥λN为M 的特征值。为了求解式（16）中的优化问题，我们引入辅助变量u ＞0，并将问题P＇1 进一步等价为
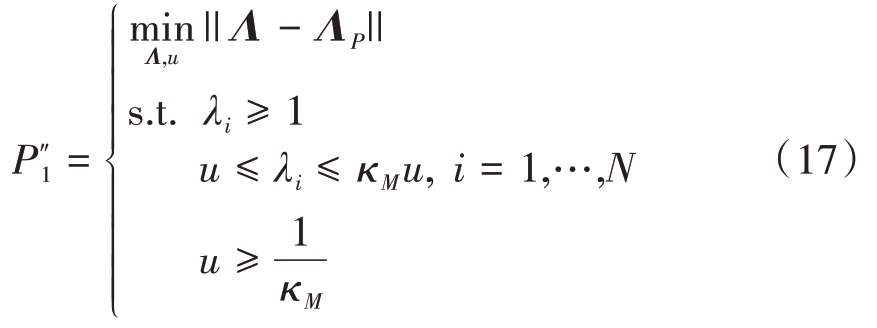
由此可得式（17）的最优解为
式中，λ★(u)=[λ1(u),λ2(u),…,λN(u)]T，λi(u)=min(κMu,max(di,max(1,u))),i=1,…,N。此外，μ★为u的最优值，可以利用文献［14］中的结果以闭式解表示。
2.2 Toeplitz结构协方差矩阵估计
现在我们考虑第二种情况，即协方差矩阵M是Toeplitz 结构的。利用Toeplitz 特性和训练样本将tl估计为［6］
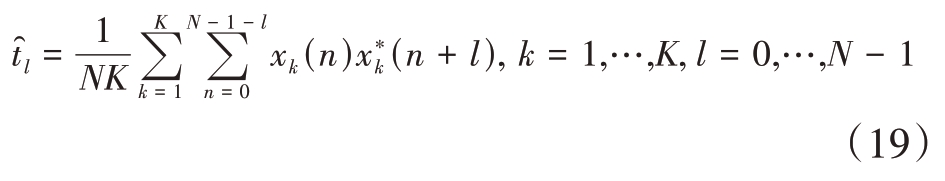
基于估计序列，我们可以构造出M 的Toeplitz SSCM 估计（用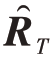
表示）。相似地，通过利用在特定约束集下最小化M 与
的Frobenius 距离建立优化问题，即
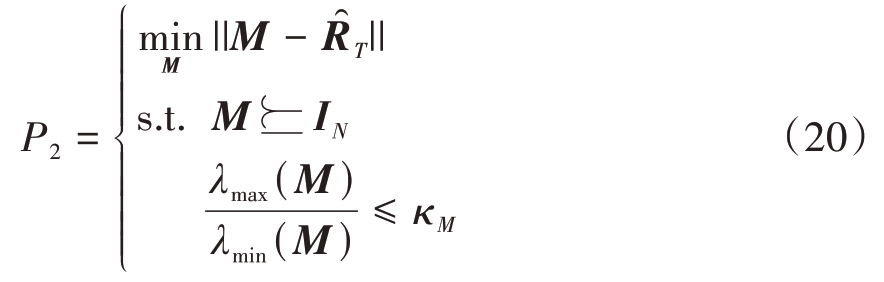
由于优化问题P1 和P2 结构的内在一致性，故可用P1的求解方法获得P2的最优解。
综上所述，本文所提出算法的整体流程如下：
步骤1 根据雷达系统中阵列和脉冲序列先验知识，判断ICM 的结构特性（即Persymmetric 或Toeplitz 结构。下述步骤以ICM 满足Persymmetric结构进行描述）。
步骤2 运用协方差矩阵的Persymmetric 结构特性并结合训练数据集{x1,…,xK}，生成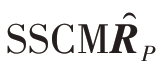
。
步骤3 通过利用M 与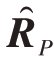
的最小化欧氏距离构造目标函数||M-
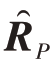||，并遵守M 
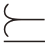IN 和λmax(M) λmin(M) ≤κM 约束条件，以此建立优化问题P1。
步骤4 求解问题P1，其最优解M★=UP Λ★UHP为估计的协方差矩阵。
步骤5 依据w★=M★-1s 获得估计的滤波器自适应权矢量。
3 仿真及分析
本节考虑了两种典型的雷达信号处理方案：宽带干扰机干扰接收数据的空域处理和杂波干扰回波的多普勒处理［12］。利用SINR 评估了所提出算法的性能，并与现有的一些同类算法进行比较。滤波器的输出SINR（由200 次蒙特卡洛实验得到）定义为
式中，|·|表示复数的模，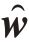
=
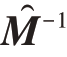s(x)为w 的自适应估计向量
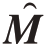为M 的估计量。此外，考虑到实际雷达场景，目标状态x 可以是波达角θ，也可以是归一化多普勒频率v。最后，假设κM=λmax(M)/λmin(M)来进行两种场景下的模拟实验［14］。
3.1 空域处理
在此场景下，假定雷达系统配置了一个由N=16 个单元组成的均匀线阵。天线之间的距离为d=λ0/2，其中λ0 为波长。假设总干扰由宽带干扰机干扰和噪声组成，则ICM 可以表示为M=Ms+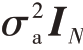
，其中σ2a 是噪声的实际功率水平，Ms 是与J 个干扰机相关的协方差矩阵，即
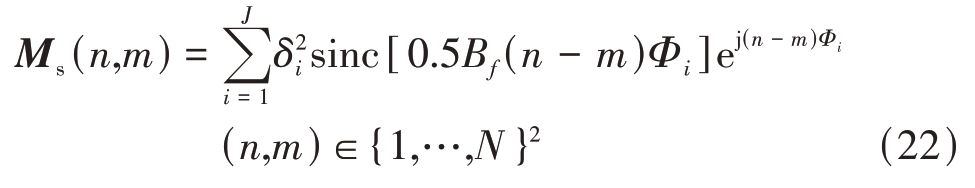
式中，Bf=B/f0表示相对带宽，B为所需信号的瞬时带宽，以及f0=c/λ0，c 为光速。此外，δ2i 表示第i 个干扰机的功率，Φi=2πd(sin θi) λ0 表示干扰机相对于天线相位中心的相位角，θi 为干扰机的偏离角。那么，在这种情况下产生的导向矢量为s(θ)=[1,ejπ sin(θ),…,ejπ sin(θ)(N-1)]T。
图1展示了在高斯训练数据下，不同算法SINR 与θ 的对应关系。仿真设置σ2a=0 dB，干扰机数量J=2，且拥有相同的功率δ2i=20 dB，i=1,2，相位分别为θ1=-30°和θ2=30°，两个相对带宽Bf=0.3。图1（a）与图1（b）分别将样本数目设为8 和16，并将训练样本建模为IID、循环对称和零均值的高斯随机向量。图1将所提算法与文献中其他算法的性能进行了比较，分别是：基于Frobenius 范数的估计（Frobenius Norm based Estimator,FNE）和基于谱范数的估计（Spectral Norm based Estimator,SNE）［14］、约束极大似然估计（Constrained Maximum Likelihood estimator,CML）［16］、快速极大似然估计（Fast Maximum Likelihood estimator,FML）［17］、Oracle 近似收缩估计（Oracle Approximating Shrinkage estimator,OAS）［18］、秩约束极大似然估计（Rank-Constrained Maximum Likelihood estimator,RCML）［19］、Toeplitz 结构约束估计（Toeplitz-Structured Estimator，TSE）［12］以及SCM 算法。由图1可得，所提算法在SINR 方面都能优于同类算法，尤其是在小样本（K=8）情况下的优化效果更为突出。这是因为所提出的算法不仅利用了协方差矩阵的结构信息，并同时考虑了矩阵的正定特性和条件数约束。这相当于将估计的协方差矩阵强制约束为趋近于真实协方差矩阵条件的良好特性，使得未知参数的不确定区域减小，以提高估计精度。
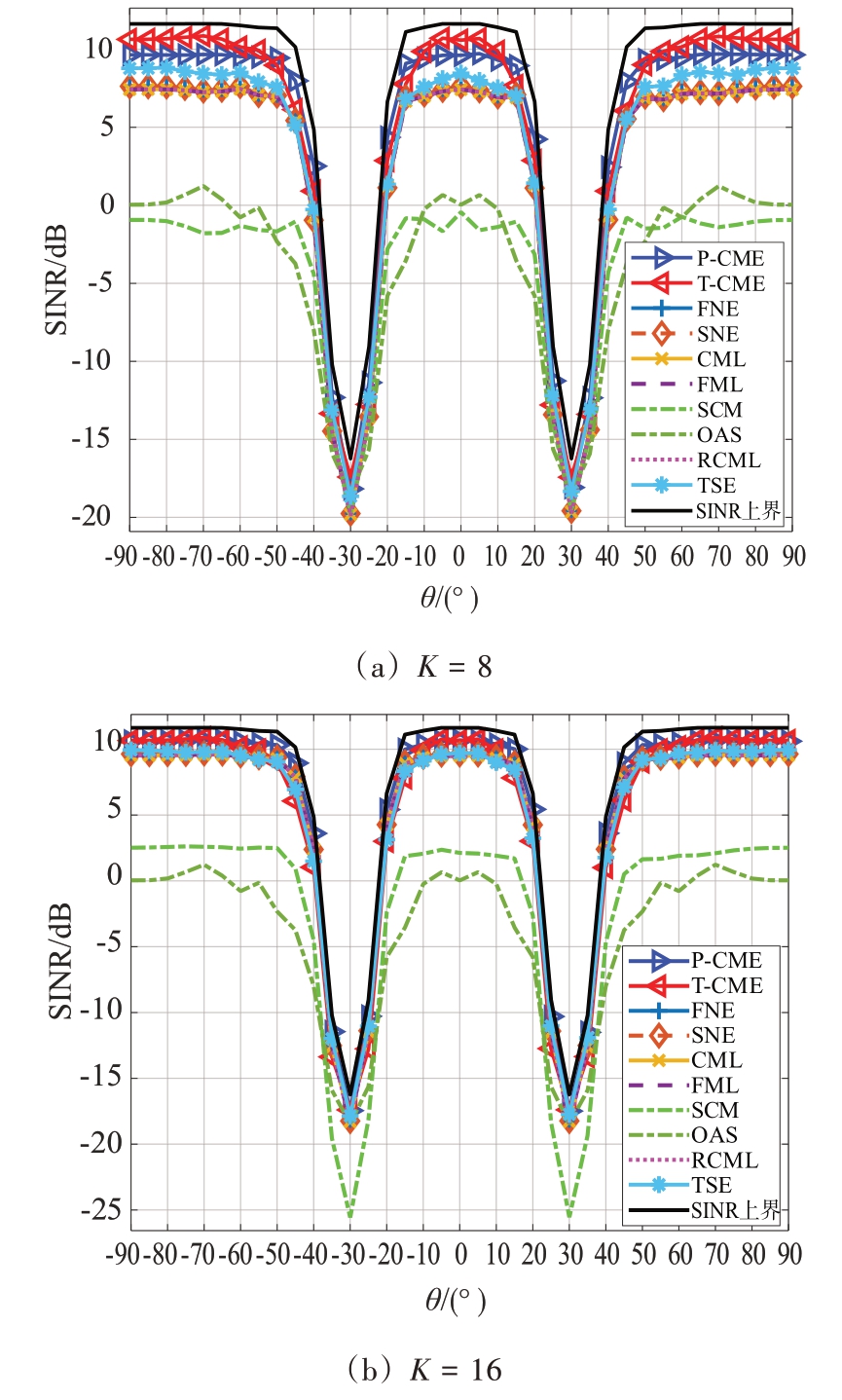
图1 高斯训练数据下SINR与θ的对应关系
图2展示了在非高斯训练数据下，不同算法SINR与θ的对应关系。此时的训练样本建模为
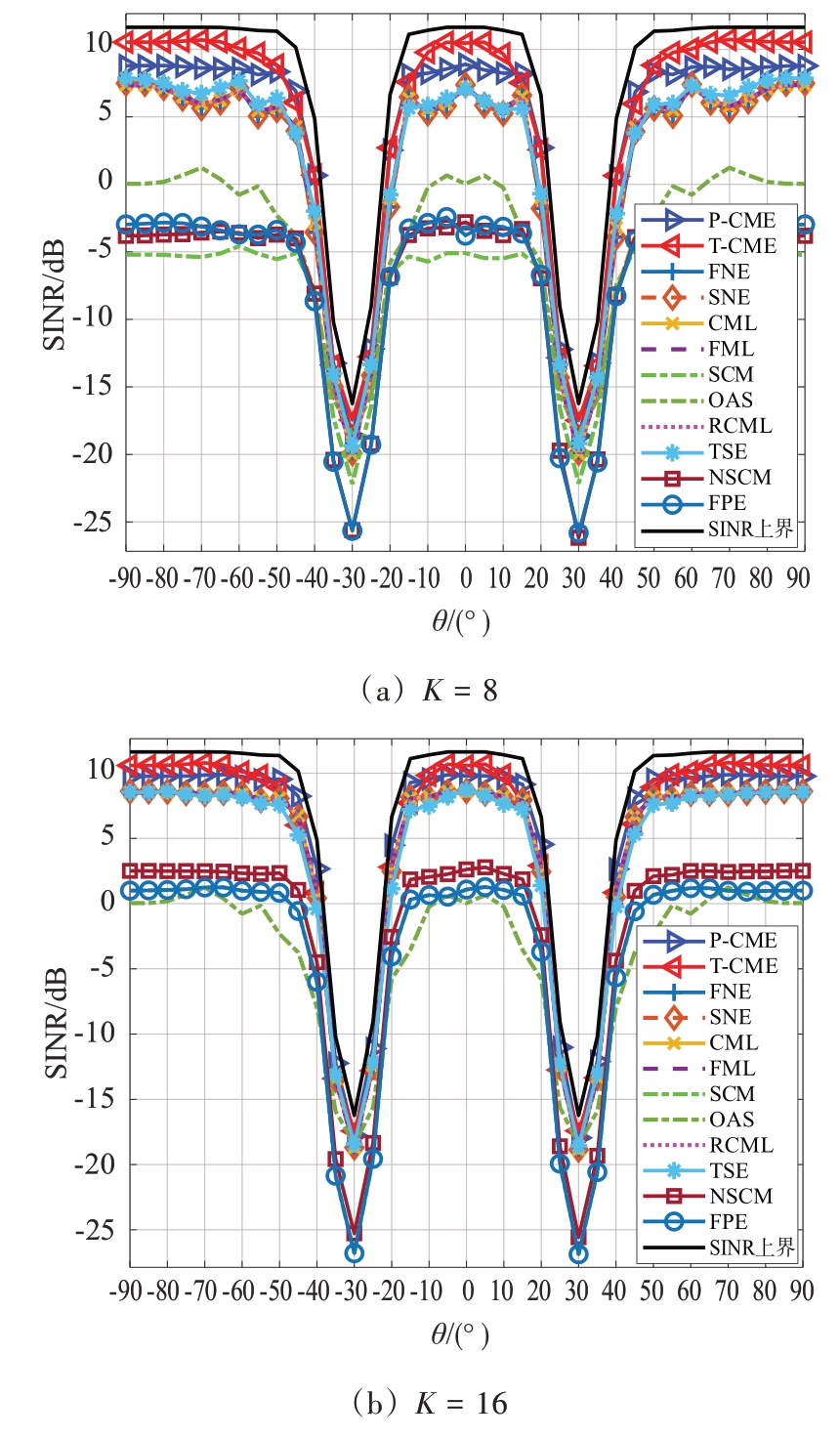
图2 非高斯训练数据下SINR与θ的对应关系
式中，nk ～CN(0,σ2a IN)和rk ～CN(0,Ms)表示独立的随机向量，τk ～Γ(0.5,2)为随机变量。为了进行比较，除了图1所对比的算法之外，还考虑了两种用于复合高斯杂波的算法，即归一化样本协方差矩阵（Normalized Sample Covariance Matrix，NSCM）算法［20］和不动点估计（Fixed-Point Estimator,FPE）算法［21］。由图2可以看出，所提出的算法在复合高斯情况下的性能仍优于所对比算法。此外，相较于高斯训练数据情况，所提算法比同类算法的SINR 增益更高，这表明所提算法在训练数据偏离高斯模型的情况下具有较强的稳健性。
3.2 多普勒处理
仿真设置了一个以固定脉冲重复时间（Pulse Repetition Time,PRT）发射N=16个相干脉冲序列的雷达系统。在该场景中，x 指的是目标的归一化多普勒频率v=[-1/2,1/2]，导向矢量s(v)=[1,ej2πv,…,ej2πv(N-1)]T。假定雷达是在由海上和地面杂波组成的双模杂波中工作，则ICM 可以表示为M=Mt+σ2a IN，其中Mt为
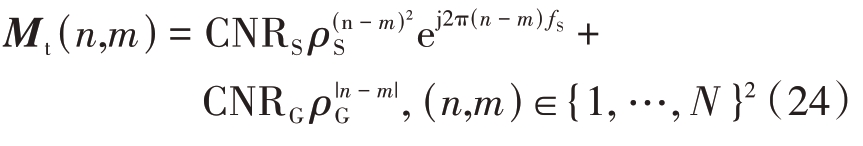
式中，fS 表示海杂波的归一化多普勒频率，CNRS 和CNRG 分别表示海杂波和地杂波的功率，ρS 和ρG 分别为海杂波和地杂波的相关系数。
图3展示了在高斯训练数据下，不同算法（与图1中相同）SINR 与v的对应关系。仿真设置σ2a=10 dB，CNRS=10 dB，CNRG=25 dB，ρS=0.8，ρG=0.95，fS=0.2。训练数据满足高斯分布，且样本数目和上一场景设置相同。观察曲线可知，在所考虑的情况下，所提出的T-CME 算法在SINR 方面均优于对比算法，但P-CME 算法的SINR 略低于TSE算法。然而值得注意的是，Toeplitz 结构为Persymmetric 结构的一个子集［6］，当ICM 仅满足Persymmetric 结构而非Toeplitz 结构时，T-CME 和TSE 算法将不再适用，而本文所提P-CME 算法则优于其他同类算法。
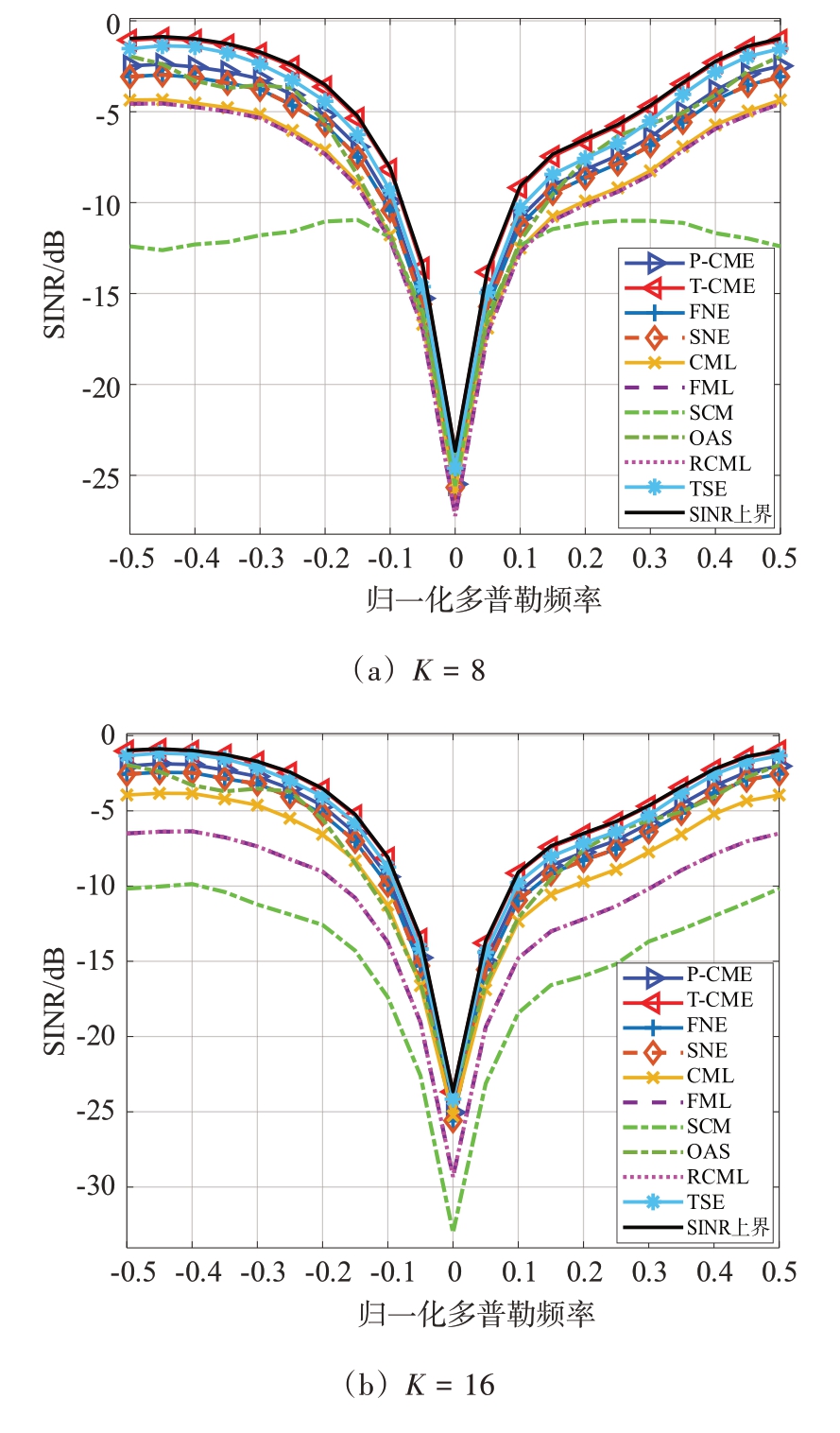
图3 高斯训练数据下SINR与v的对应关系
3.3 实测数据验证
本小节，我们利用实测数据进行算法验证。该实测数据来自于2021年海军航空大学在烟台第一海水浴场进行的雷达对海探测数据集20210106155330_01_staring.mat，海杂波数据具体说明可详见文献［22-23］。该雷达系统以固定PRT发射相干脉冲序列进行对海探测实验。
我们选取第700 个距离单元作为CUT，使用两侧临近距离单元数据作为训练数据进行实验。图4展示了脉冲数N=16 时，实测数据下不同算法SINR 与v的对应关系。由图4可知，使用实测数据的T-CME 算法同样优于同类算法，而P-CME 的SINR 略低于TSE 算法，实测数据仿真结果和模拟数据结果保持一致。
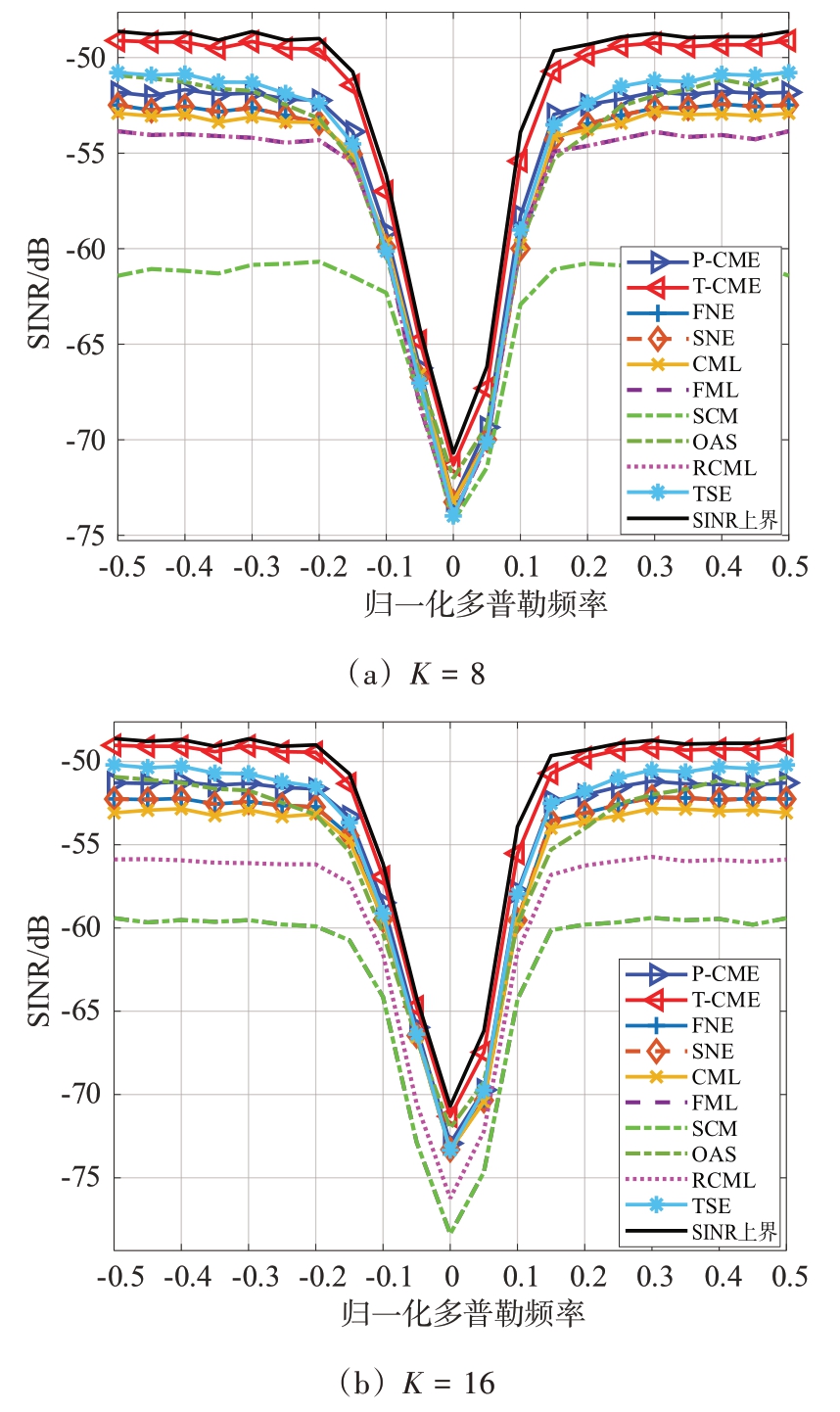
图4 实测数据下SINR与v的对应关系
3.4 复杂度分析及运行时间对比
计算复杂度是衡量算法运行效率的重要指标，本文所提算法的计算量主要集中在构造SSCMs、谱分解及求解u 的过程中，通过分析可得出两种算法生成SSCMs 和进行谱分解的复杂度为O(N2K+N3+N2)，而u 则利用了MATLAB 中一维优化函数fminbnd 进行求解，故所提两种算法最终的计算复杂度约为O(N2K+N3+N2)。
表1给出了200 次蒙特卡洛实验下不同算法的平均运行时间（计算机处理器为Intel Core i5-7200U@2.5 GHz，内存为8 GB），由表1可知，在相同仿真条件（采用高斯训练数据的空域处理）下，本文所提算法与其他结构化方法运行时间处于同一数量级，且远远小于迭代型方法。
表1 算法运行时间对比结果（N=16）
算法P-CME T-CME FNE SNE CML FML OAS RCML TSE时间/s K=8 10-4 10-4 10-4 10-5 10-5 10-4 10-5 10-4 10-2 K=16 10-4 10-4 10-4 10-4 10-4 10-4 10-5 10-4 10-2
3.5 适用性及工程实现分析
本文考虑到在雷达系统中，若线性阵列与脉冲序列满足对称或均匀间隔，则产生的ICM 为Persymmetric 或Toeplitz 结构，且合理的利用结构信息可提高协方差矩阵估计精度。此外，通过上文对算法SINR 和运行时间的对比分析，可得出TCME 算法要优于P-CME 算法。因此，在确定ICM具有Toeplitz 结构的性质时，优先使用T-CME 算法。而当ICM 仅满足Persymmetric 结构时，即可使用P-CME算法。
对于工程实现方面的问题，通过在两种场景下不同算法性能及运行时间的比较，可以看出所提算法不仅拥有更优的干扰抑制能力且计算复杂度较低，从而有利于信号的实时处理，适合工程应用。并且，在实际应用中获取的训练数据无论是否服从高斯分布，所提算法都能够有效地提高雷达干扰抑制性能。
4 结束语
遵循几何范式，本文提出了两种雷达自适应信号处理中结构化ICM 估计算法。首先利用结构先验知识并结合训练数据，构建了两种SSCMs，然后在特定（正定矩阵空间和条件数上限）约束下通过SSCMs 与ICM 之间的最小化欧氏距离建立优化问题并进行求解。所建立的优化问题等同于在Frobenius 范数下将两种SSCMs 投影到具有实际相关性的约束集中，以减少估计问题的DOF。在两种场景下的仿真结果表明了所提出的算法具有良好的干扰抑制性能。
［1］TANG Bo，LIU Jun，HUANG Zhongrui，et al.Adaptive Target Detection in Gaussian Clutter Edges［J］.IEEE Trans on Aerospace and Electronic Systems，2020，56（2）:1662-1673.
［2］TANG Mengjiao，RONG Yao，DE MAIO A，et al.Adaptive Radar Detection in Gaussian Disturbance with Structured Covariance Matrix via Invariance Theory［J］.IEEE Trans on Signal Processing，2019，67（21）:5671-5685.
［3］WARD J.Space-Time Adaptive Processing for Airborne Radar［C］//1995 International Conference on Acoustics,Speech,and Signal Processing，Detroit，MI，USA: IEEE，1995:2809-2812.
［4］SUN Guohao，LI Ming，TONG Jun，et al.Structured Clutter Covariance Matrix Estimation for Airborne MIMO Radar with Limited Training Data［J］.IEEE Geoscience and Remote Sensing Letters，2020，19:1-5.
［5］LI Jianbo，AUBRY A，DE MAIO A，et al.An EL Approach for Similarity Parameter Selection in KA Covariance Matrix Estimation［J］.IEEE Signal Processing Letters，2019，26（8）:1217-1221.
［6］LIU Jun，HAN Jinwang，ZHANG Zijing，et al.Target Detection Exploiting Covariance Matrix Structures in MIMO Radar［J］.Signal Processing，2019，154:174-181.
［7］LIU Jun，ZHOU Wuyang，ZAIMBASHI A，et al.Persymmetric Adaptive Array Detection of Spread Spectrum Signals［J］.IEEE Trans on Information Theory，2020，66（12）:7828-7834.
［8］CAI L，WANG H.A Persymmetric Multiband GLR Algorithm［J］.IEEE Trans on Aerospace and Electronic Systems，1992，28（3）:806-816.
［9］LIU Jun，LIU Weijian，HAO Chengpeng，et al.Persymmetric Subspace Detectors with Multiple Observations in Homogeneous Environments［J］.IEEE Trans on Aerospace and Electronic Systems，2020，56（4）:3276-3284.
［10］孙国皓.基于协方差矩阵结构特征的机载雷达空时处理［D］.成都:电子科技大学，2019.
［11］KANG Naixin，SHANG Zheran，DU Qinglei.Knowledge-Aided Structured Covariance Matrix Estimator Applied for Radar Sensor Signal Detection［J］.Sensors，2019，19（3）:664.
［12］DU Xiaolin，AUBRY A，DE MAIO A，et al.Toeplitz Structured Covariance Matrix Estimation for Radar Applications［J］.IEEE Signal Processing Letters，2020，27:595-599.
［13］李明，孙国皓，何子述.基于截断核范数正则化的协方差矩阵估计［J］.雷达科学与技术，2020，18（6）:633-639.
［14］AUBRY A，DE MAIO A，PALLOTTA L.A Geometric Approach to Covariance Matrix Estimation and its Applications to Radar Problems［J］.IEEE Trans on Signal Processing，2018，66（4）:907-922.
［15］CUI Guolong，LI Na，PALLOTTA L，et al.Geometric Barycenters for Covariance Estimation in Compound-Gaussian Clutter［J］.IET Radar,Sonar & Navigation，2017，11（3）:404-409.
［16］AUBRY A，DE MAIO A，PALLOTTA L，et al.Maximum Likelihood Estimation of A Structured Covariance Matrix with A Condition Number Constraint［J］.IEEE Trans on Signal Processing，2012，60（6）:3004-3021.
［17］STEINER M，GERLACH K.Fast Converging Adaptive Processor or A Structured Covariance Matrix［J］.IEEE Trans on Aerospace and Electronic Systems，2000，36（4）:1115-1126.
［18］CHEN Y，WIESEL A，ELDAR Y C，et al.Shrinkage Algorithms for MMSE Covariance Estimation［J］.IEEE Trans on Signal Processing，2010，58（10）:5016-5029.
［19］KANG B，MONGA V，RANGASWAMY M.Rank-Constrained Maximum Likelihood Estimation of Structured Covariance Matrices［J］.IEEE Trans on Aerospace and Electronic Systems，2014，50（1）:501-515.
［20］GINI F.Performance Analysis of Two Structured Covariance Matrix Estimators in Compound-Gaussian Clutter［J］.Signal Processing,2000，80（2）:365-371.
［21］PASCAL F，CHITOUR Y，OVARLEZ J P，et al.Covariance Structure Maximum-Likelihood Estimates in Compound Gaussian Noise:Existence and Algorithm Analysis［J］.IEEE Trans on Signal Processing，2007，56（1）:34-48.
［22］刘宁波，丁昊，黄勇，等.X波段雷达对海探测试验与数据获取年度进展［J］.雷达学报，2021，10（1）:173-182.
［23］刘宁波，董云龙，王国庆，等.X波段雷达对海探测试验与数据获取［J］.雷达学报，2019，8（5）:656-667.
