0 引 言
随着无人机的广泛应用，商业级无人机由于造价低廉，且能携带爆炸物、危险物、高分辨率摄像头等，对军港、机场、核电站等要地的安全带来严峻挑战［1-3］。面对日益严峻的无人机威胁，反无人机技术及系统逐步成为研究和发展热点［4-8］。在反无人机系统中，雷达作为核心传感器，具有作用距离远、覆盖范围大、全天时全天候工作等优点。无人机飞行高度低、速度慢、RCS小，是一种典型的“低慢小”目标。由于目标高度低，雷达波束下视，地物回波从波束主瓣进入，杂波很强，而目标RCS小，目标回波微弱，所以雷达探测“低慢小”目标，将面临强杂波环境中的弱目标检测问题［9］。
为实现弱目标探测，脉冲多普勒（PD）雷达一般通过脉冲压缩和FFT 处理来提高目标信噪比，并且在多普勒维实现目标和杂波分离。同时，为了压低距离维和多普勒维副瓣，在脉冲压缩和FFT处理时需进行适当的加权［10］。加权将会导致杂波在多普勒维的主瓣展宽，使杂波能量泄漏到邻近的几个多普勒通道，从而淹没慢速弱目标。为避免杂波多普勒维主瓣的影响，可对杂波进行对消，将其从回波信号中消除。传统脉冲体制雷达一般通过动目标显示（MTI）［11］技术来对消杂波，但是MTI 在多普勒维的凹口较宽，在对消杂波的同时，对慢速目标也有较大的衰减，从而降低了系统对慢速目标的检测能力。
最小均方（Least-Mean-Square,LMS）类算法［12］以其实现简单、性能稳定成为自适应信号处理中的一种重要算法，已广泛应用于外辐射源雷达（连续波体制）杂波对消领域［13-14］，具有计算复杂度低、多普勒维凹口窄的特点。该类算法通过自适应估计分布在各距离单元上的杂波复幅度，然后重构杂波、将其从回波中减去，实现杂波对消。但LMS算法采用逐点更新权向量，只适用于连续波雷达，不能直接用于PD 雷达。因为连续波雷达回波的各个采样点均包含所有距离单元的杂波，滤波器权值在各采样点之间保持不变，而脉冲体制雷达发射脉冲很窄，每个采样点仅包含部分距离单元的杂波，滤波器权值在采样点之间将发生剧烈变化，所以直接采用LMS 算法，滤波器将难以收敛，无法有效对消杂波。
针对脉冲体制雷达杂波对消，本文对LMS 算法进行了改进，提出了频域脉冲LMS（Frequencydomain Pulse LMS，FPLMS）算法。一、逐脉冲更新权向量。由于每个接收脉冲均包含了所有距离单元的杂波，滤波器权值在脉冲间保持不变，所以FPLMS 算法采用逐脉冲更新权向量。二、频域实现。将算法中的矩阵乘法运算转化为相关运算，通过频域FFT 实现，降低了算法的计算量。仿真结果表明，FPLMS 算法能够有效对消杂波，消除杂波主瓣对目标检测的影响，适用于“低慢小”探测雷达的杂波对消。
1 信号模型
假设“低慢小”探测雷达为脉冲体制，发射线性调频信号，其复数形式为
式中，t 为时间变量，T 为脉冲宽度，κ 为调频率，rect(t)为矩形函数，定义为
对发射信号进行离散采样有
式中，Ts为采样率，N为发射脉冲采样点数，NTs=T。
雷达接收的回波信号包括杂波、目标回波和噪声。第k 个发射脉冲的回波信号离散采样后的复数形式为
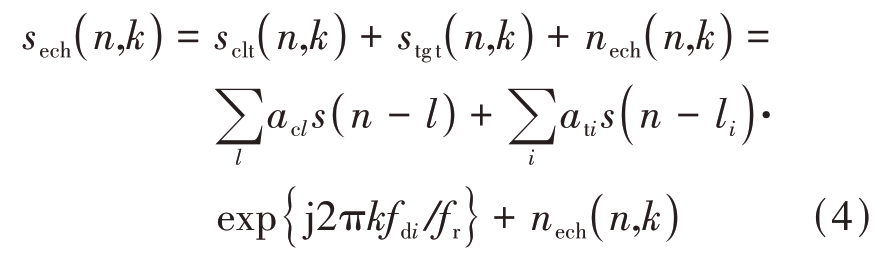
式中:sclt(n,k)，stgt(n,k)，nech(n,k)分别表示第k 个发射脉冲对应的杂波、目标回波、噪声；acl表示第l个距离单元的杂波复幅度；ati，li，fdi 分别为第i 个目标的复幅度、距离单元、多普勒频率；fr为重频。
由式（4）可以看出，杂波信号可表示为发射信号时延副本的线性组合。若能估计出各个距离单元上杂波的复幅度，则可重构出杂波信号，将其从回波信号中滤除。
2 基于FPLMS算法的杂波对消
2.1 LMS算法存在的问题
LMS 算法可以自适应估计杂波的复幅度，实现杂波对消。但是，对于脉冲体制雷达，由于发射信号为脉冲形式，杂波在不同采样点的分量不同，滤波器系数也在采样点间变化。
例如，杂波在n0采样点值为
采用LMS 算法进行杂波幅度估计，滤波器系数应为ac,n0-N2+1…ac,n0+N2。
而杂波在n0+1采样点的值为
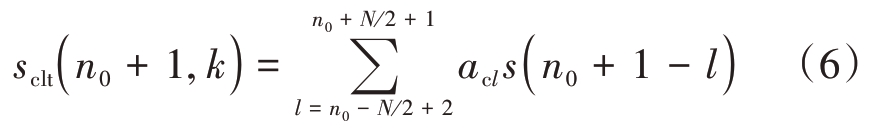
滤波器系数应为ac,n0-N2+2…ac,n0+N2+1，与n0采样点的滤波器系数不同。
由于滤波器系数一直变化、难以收敛，所以LMS算法无法有效对消脉冲体制雷达杂波。
2.2 PLMS算法原理
从另一角度来看，杂波在脉冲间的组成分量相同，均为所有距离单元的杂波的线性组合。例如，第k个脉冲的杂波信号矢量为
式中，sl=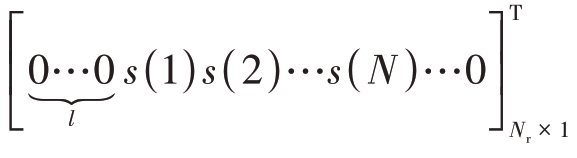
为发射脉冲矢量时延l 个距离单元后的信号，sclt(k)=
滤波器系数为ac0,ac1…ac,Nr-N+1，与脉冲编号k无关，在脉冲间保持不变。
所以，针对脉冲体制雷达的特点，本文对LMS算法进行了改进，提出了脉冲LMS（PLMS）算法，在脉冲间进行权向量更新，来对消杂波。
PLMS算法的原理框图如图1所示。
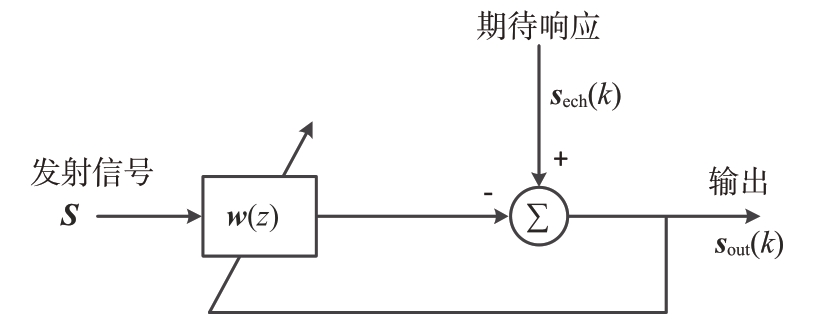
图1 PLMS算法原理框图
发射信号及其时延副本构成了输入矩阵S:
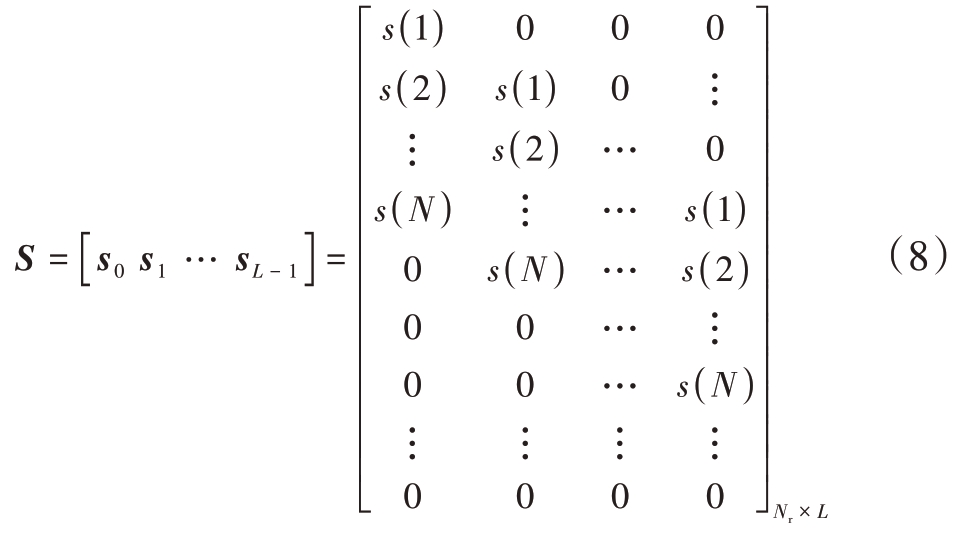
式中Nr为回波信号的采样点数，L为滤波器阶数。
对于第k 个脉冲，将矩阵S 与滤波器权向量w(k)相乘，得到杂波信号的估计，然后将其从期待响应（回波信号）中减去，得到k个脉冲的对消输出信号，也称作估计误差，表示为
式中，sech(k)=
为第k 个脉冲的回波信号，w(k)=[w0(k)w1(k)…wL-1(k)]T，wl(k)表示滤波器对第l个距离单元杂波复幅度的估计。
根据LMS算法原理，权向量的更新公式为
式中，μ为滤波器步长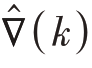
为梯度估计。
梯度估计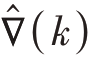
可由估计误差的平方和对wH(k)求偏导得到，即
将式（11）代入式（10），权向量的更新公式变为
以上为PLMS 算法的推导过程，现将其总结如表1所示。
表1 PLMS算法总结
输入数据：s()n=发射信号sech()n,k=回波信号参数：L=滤波器阶数μ=步长初始化：w()0=0数据准备：sl=■■■■■■■T︸0…0s()1 s()2 … s()N …0■■■l Nr×1 S=[]s0 s1 … sL-1对消过程：对k=0,1,2…，计算sech()Nr,kT k=■■■■sech()1,k sech()2,k … sech()sout()k=sech()k- Sw()k（对消输出结果）w()k+1=w()k+μSHsout()k（权向量更新）
2.3 FPLMS算法
PLMS 算法直接实现，计算量较大，主要的计算量在Sw(k)和SHsout(k)，而这两项均可看成是信号的相关处理，可以利用快速傅里叶变换在频域实现，因此本文进一步提出了频域脉冲LMS（FPLMS）算法。
令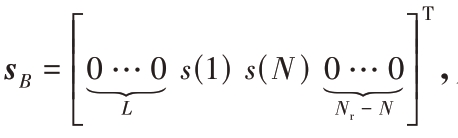
则
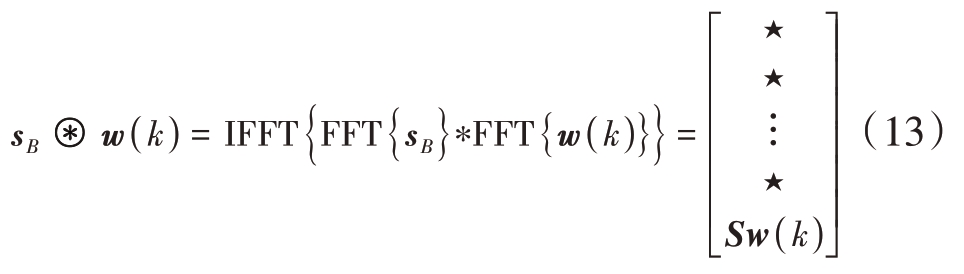
式中，⊛表示圆周卷积，★表示圆周卷积得到的无效值。取sB ⊛w(k)得后
个值得到Sw(k)，利用式（9）即可计算出对消输出信号sout(k)。
令
则s*B 圆周反褶后与u(k) 的圆周卷积为
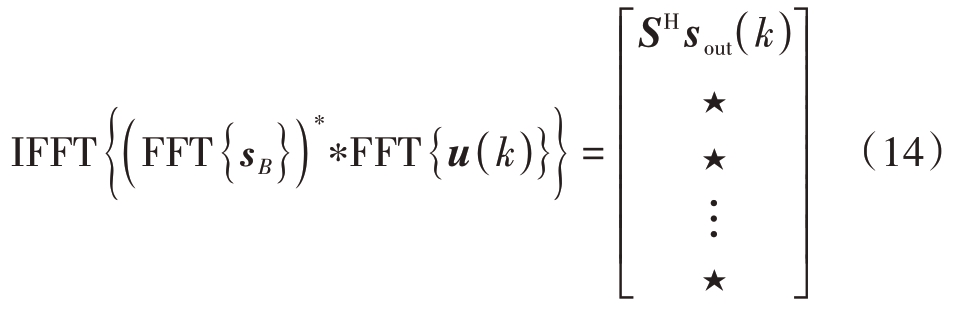
取式（14）前L 个值得到SHsout(k)，利用式（12）即可实现权向量的更新。
根据以上分析，FPLMS算法流程如图2所示。
图2 FPLMS算法流程图
3 仿真试验
3.1 仿真参数
本文通过仿真实验来验证算法性能。雷达发射线性调频信号，系统参数如表2所示。根据系统参数，进行回波信号仿真。回波信号包括杂波、噪声和目标回波信号。杂波由静止地物反射产生，分布在整个探测距离内，幅度随距离而衰减（由雷达方程确定），杂噪比设为40 dB。为分析系统对慢速目标的探测能力，目标速度设为1 m/s，具体参数如表3所示。
表2 系统参数
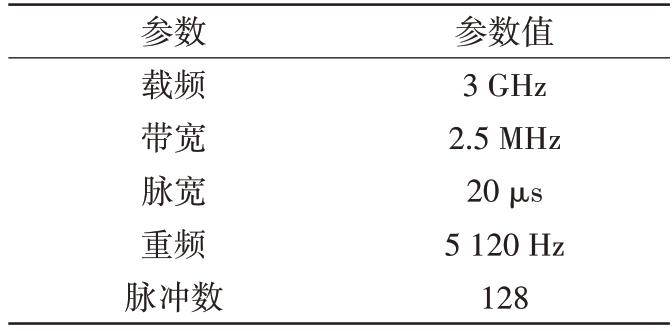
参数载频带宽脉宽重频脉冲数参数值3 GHz 2.5 MHz 20 μs 5 120 Hz 128
表3 目标参数
参数距离速度信噪比参数值3 km 1.5 m/s-10 dB
仿真得到的回波信号如图3所示，其中不同的颜色表示不同发射脉冲的回波信号。
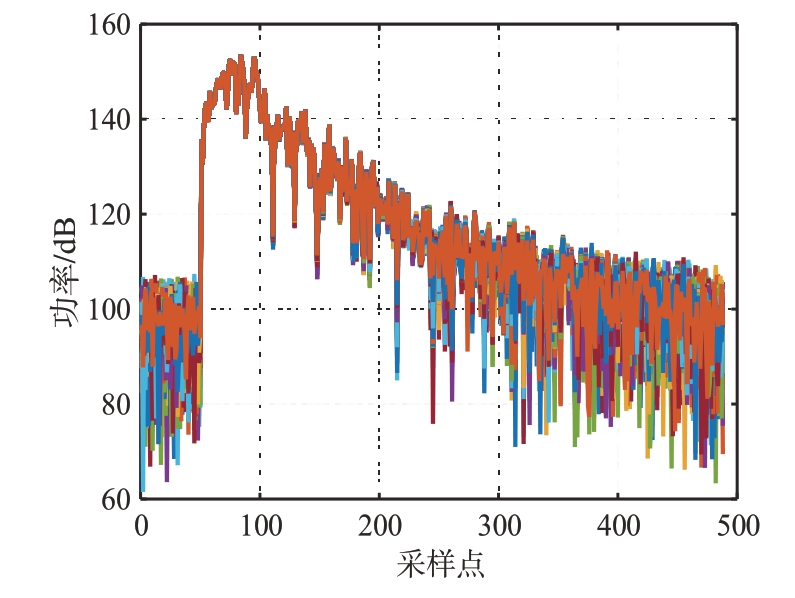
图3 回波信号时域波形
对回波信号进行脉冲压缩和FFT 处理。为抑制距离维和多普勒维旁瓣，脉冲压缩采用40 dB 的泰勒权，FFT 采用70 dB 的泰勒权，处理结果如图4所示。可以看出，由于杂波主瓣展宽，速度小于5 m/s的目标都将淹没在杂波中，无法检测。
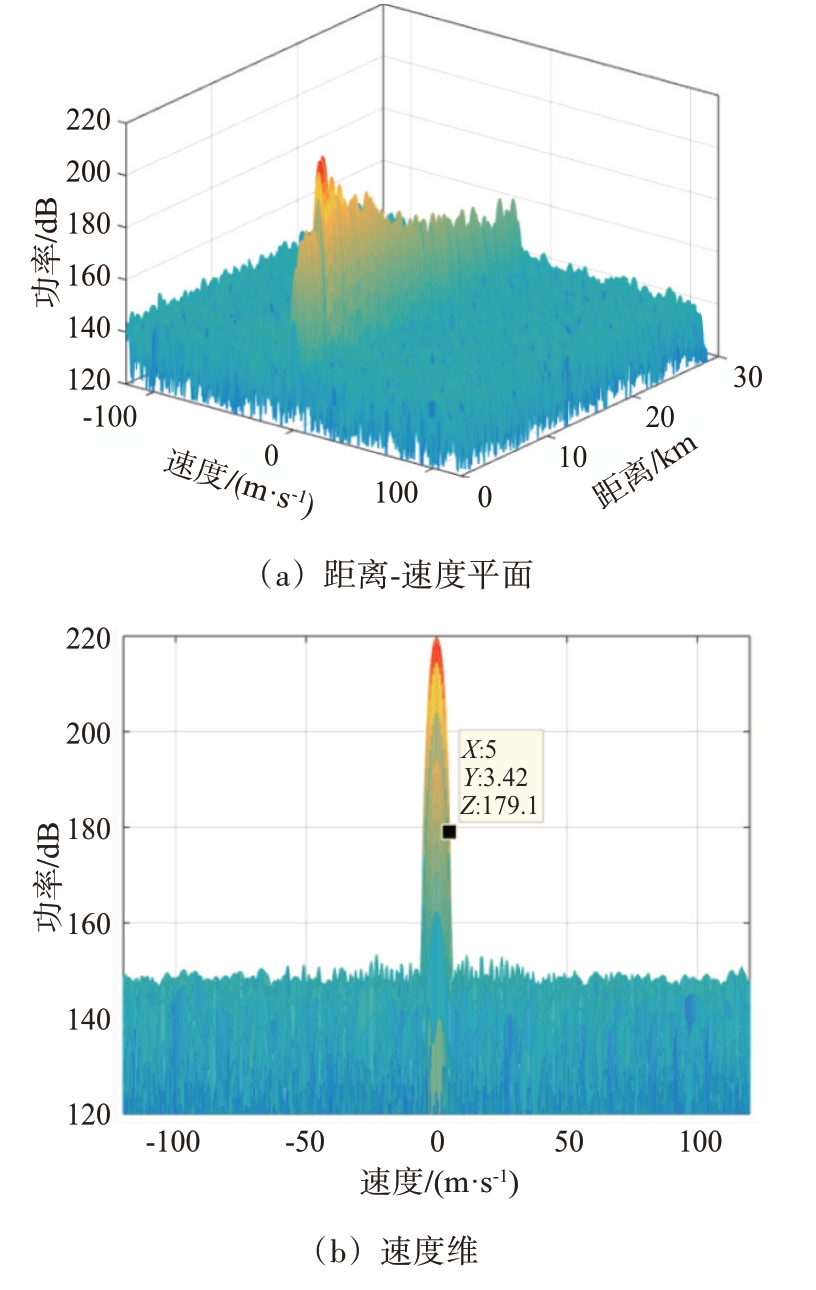
图4 回波信号处理结果
若要检测目标，需要对杂波进行对消，进而消除杂波主瓣。理想的对消结果是将杂波完全对消，只保留噪声和目标回波。对理想对消结果进行脉冲压缩和FFT 处理，结果如图5所示。处理之后，目标的峰值为165.2 dB，噪声基底为139.7 dB，目标信噪比为25.5 dB。后续对消算法将与理想对消结果进行比较，来评价其性能。
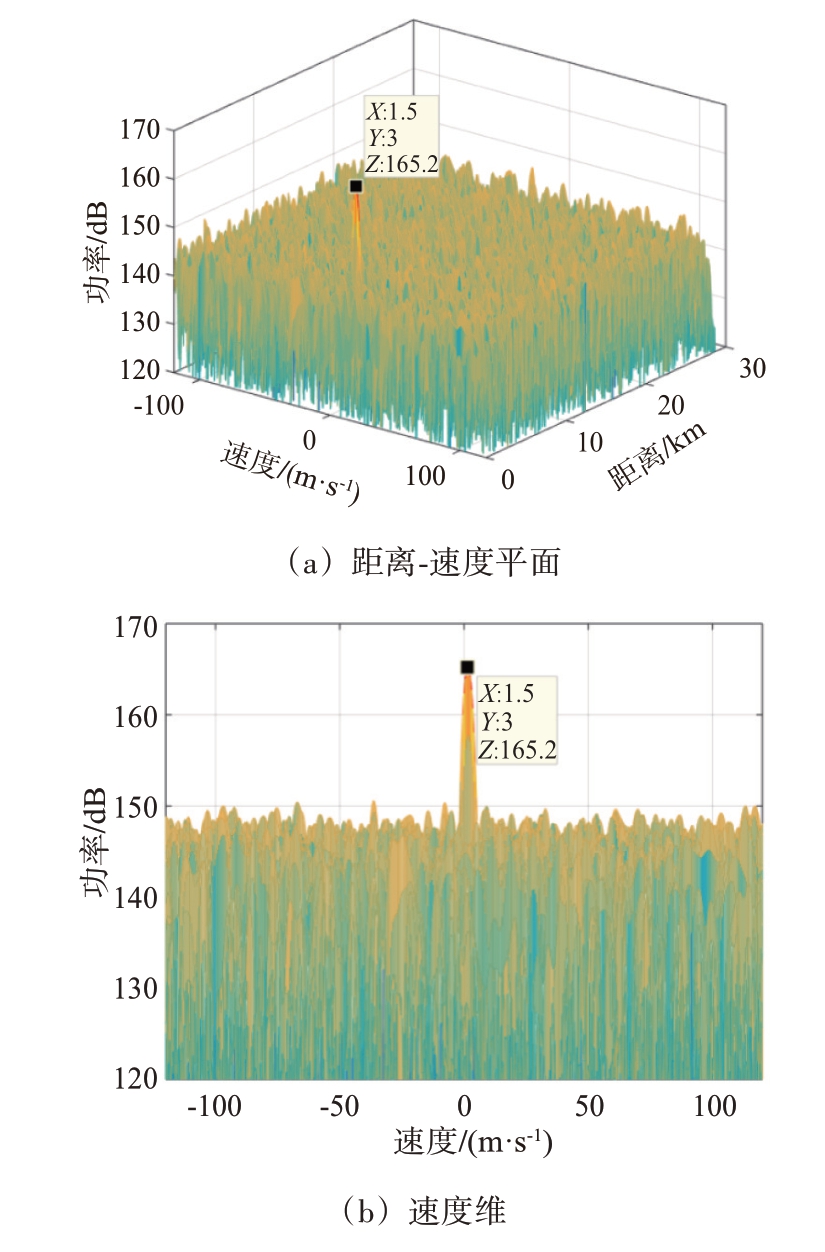
图5 理想对消输出信号处理结果
3.2 杂波对消
1）MTI对消
对回波信号采用三脉冲MTI 对消，对消结果如图6所示。可以看出，MTI 对消在零速附近形成了很深的凹口，杂波得到了充分的抑制。但是由于凹口较宽，慢速目标也被对消了。所以，MTI 对消不适合慢速目标探测场景。
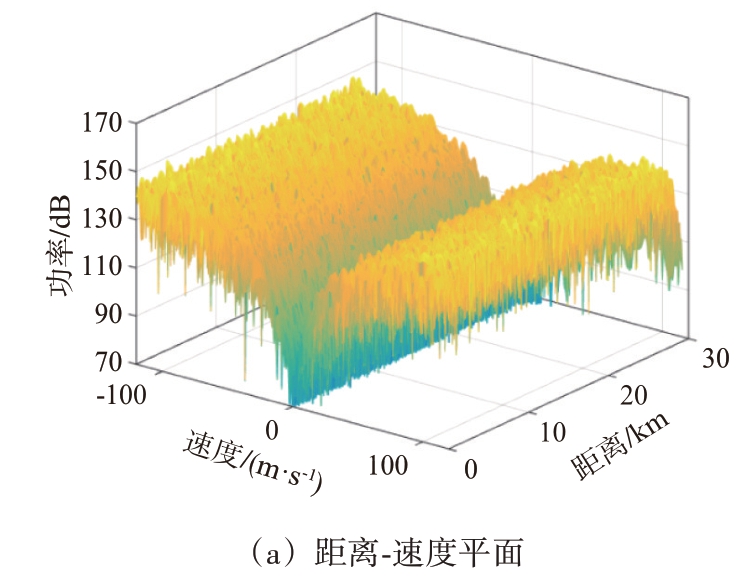
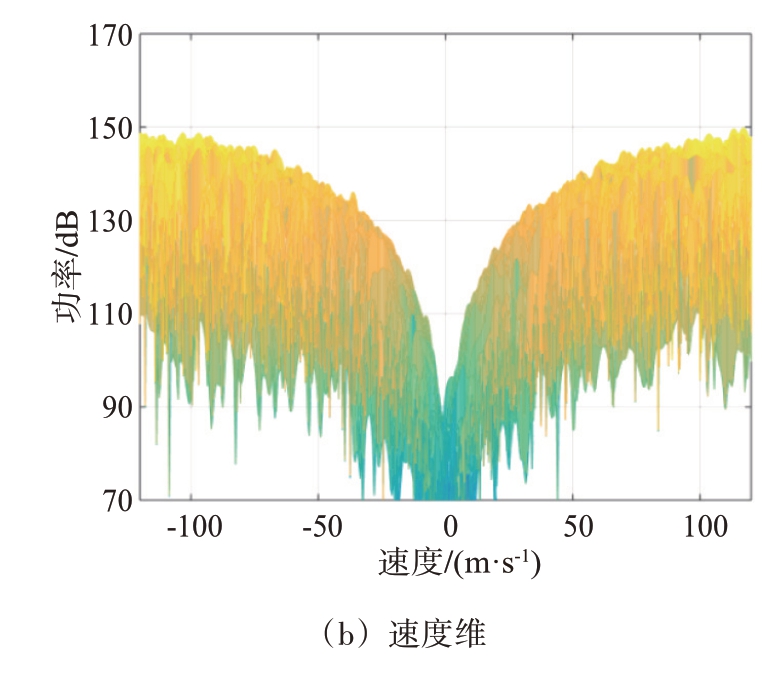
图6 MTI对消输出信号处理结果
2）FPLMS对消
对回波信号采用FPLMS 算法进行对消。FPLMS 算法的滤波器阶数设为500（与信号长度相同）。步长对FPLMS 算法的性能影响较大。步长越小，滤波器凹口越窄，对慢速目标的衰减越小，目标探测性能越好。但是，步长太小，滤波器系数难以收敛，杂波剩余较大，影响目标探测。所以，为保证杂波充分对消，且对目标衰减较小，本文采用3 次重复对消、先大步长后小步长的对消策略。第一次采用大步长对消，步长取5×10-3，滤波器系数初始值设为零，通过对消得到收敛的滤波器系数；第二次对消，步长取5×10-4，以第一次对消得到的滤波器系数为初始值；第三次对消，步长取5×10-5，以第二次对消得到的滤波器系数为初始值。
FPLMS算法的对消输出结果如图7所示。可以看出，相比回波信号，对消输出信号功率大幅衰减，与理想对消输出相近，说明杂波得到了有效的对消。
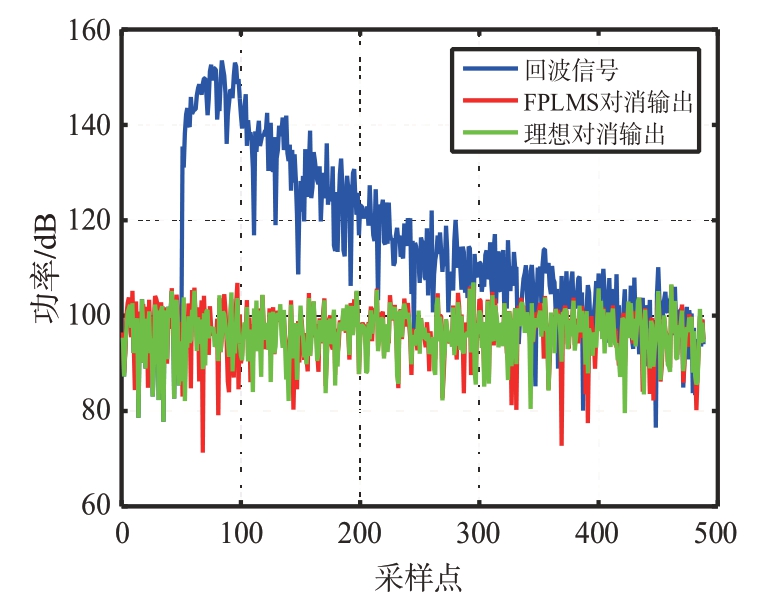
图7 FPLMS对消输出结果
对对消输出信号进行脉冲压缩和FFT 处理，结果如图8所示。可以看出，对消之后杂波谱消失，而目标清晰可见。其中，目标的峰值为164.6 dB，噪声基底为139.8 dB，目标信噪比为24.8 dB。与理想对消相比，目标信噪比仅损失0.7 dB。
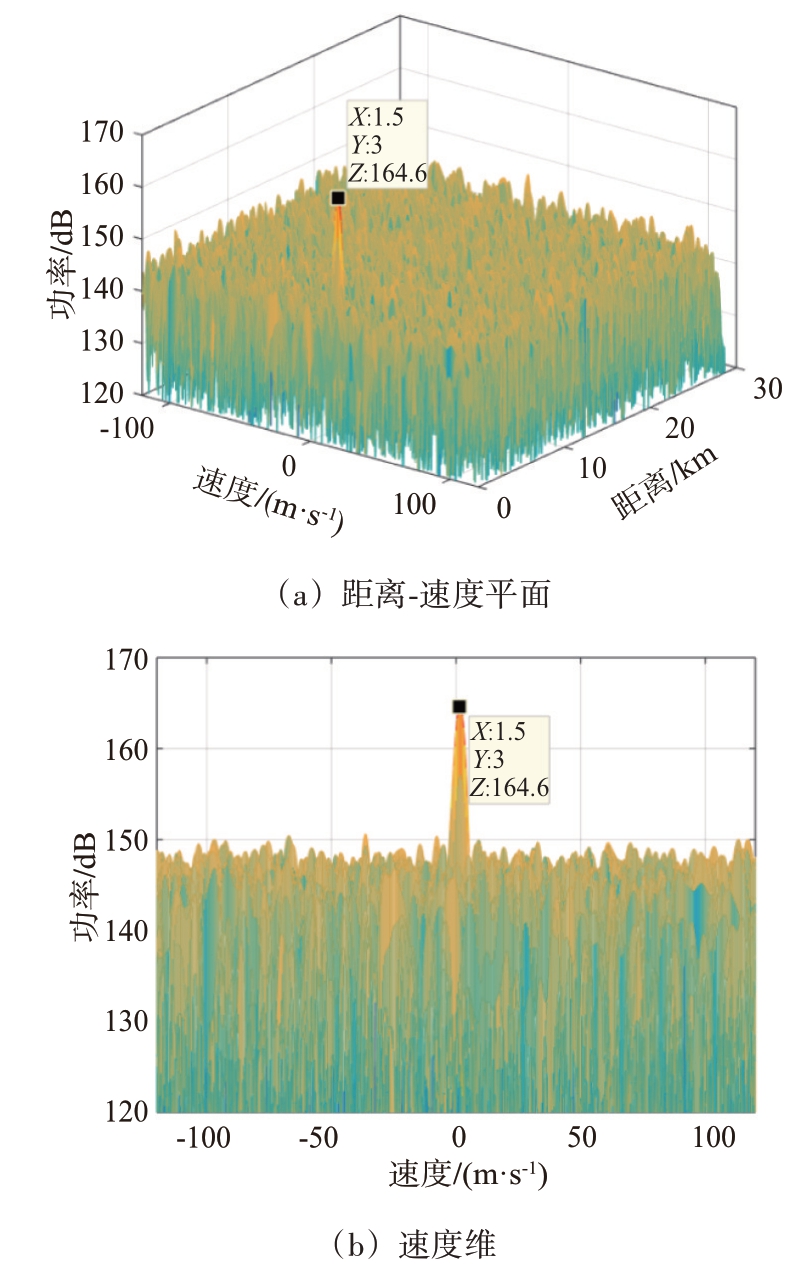
图8 FPLMS对消输出信号处理结果
以上结果说明：FPLMS 算法能够对杂波进行有效对消，消除杂波主瓣展宽对目标检测的影响，且对慢速目标的对消损失较小。
3.3 滤波器凹口
不论是MTI 对消，还是FPLMS 对消，均可以看成是一种滤波器，对不同速度的目标有不同的信噪比损失。为评价FPLMS 滤波器的性能，对3.1节中仿真的回波，将其目标速度从-10 m/s 到10 m/s，以0.5 m/s 为间隔进行遍历，然后利用FPLMS 算法进行对消，经过脉冲压缩和FFT 处理之后，与理想对消输出信号进行对比。目标信噪比损失随速度的变化曲线如图9蓝线所示。作为对比，对同样的数据也采用MTI 进行对消，并计算目标信噪比损失，见图9红线。
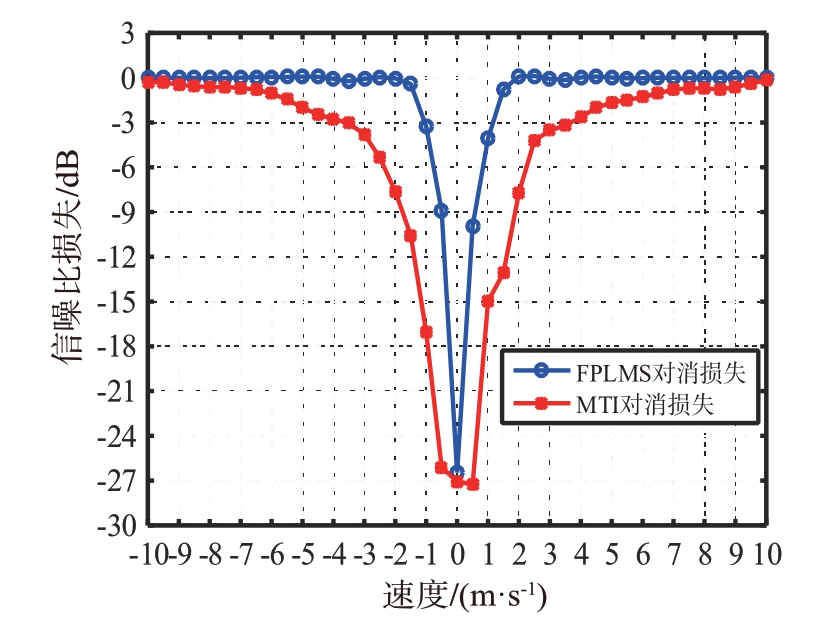
图9 FPLMS滤波器凹口
由图9可以看出，FPLMS滤波器的3 dB宽度约为1.2 m/s（0.6倍速度分辨率，速度分辨率为2 m/s），目标速度在2 m/s（1 倍速度分辨率）时信噪比损失已接近于0；而MTI 滤波器的3 dB 宽度约为3.5 m/s（1.7 倍速度分辨率），目标速度在10 m/s（5 倍速度分辨率）时信噪比损失才接近于0。FPLMS 滤波器的凹口宽度约为MTI 的1/3，且对高于1 倍速度分辨率的目标SNR损失接近于0。
以上结果表明：FPLMS 算法具有很窄的滤波器凹口，在充分对消杂波的前提下，对慢速目标的影响很小，适用于“低慢小”探测雷达的杂波对消。
4 结束语
本文针对“低慢小”探测雷达杂波多普勒维主瓣淹没慢速弱目标问题，提出了FPLMS 算法。该算法能够有效对消杂波，且具有滤波器凹口窄、对目标影响小的优点，提高了强杂波环境下“低慢小”探测雷达的慢速弱目标探测能力。本文算法也可用于其他脉冲体制雷达的杂波对消。
FPLMS 算法在模型上假设杂波信号是发射信号的线性组合，通过重构杂波来实现对消。因此，在使用时需要已知真实的发射信号。若采用理论发射信号，则由于相关性的降低，难以达到预期的对消性能。所以，采用FPLMS 算法进行杂波对消时，系统需要预留一路发射信号采集通道。
［1］王宁.沿海城市反无人机蜂群袭扰研究［J］.中国军转民，2022（19）:75-77.
［2］蒋冬婷，范长军，雍其润，等.面向重点区域安防的无人机探测与反制技术研究［J］.应用科学学报，2022，40（1）:167-178.
［3］郭彬，孙可.从民用机场角度谈民用无人机的管控［J］.民航管理，2022（8）:85-91.
［4］王书恒.国外反无人机系统的发展动态和未来趋势［J］.军事文摘，2022（3）:43-47.
［5］孙昭，何广军，李广剑.美军反无人机技术研究［J］.飞航导弹，2021（11）:12-18.
［6］薛猛，周学文，孔维亮.反无人机系统研究现状及关键技术分析［J］.飞航导弹，2021（5）:52-56.
［7］付鑫，赵然，梁延峰，等.反无人机蜂群技术发展综述［J］.中国电子科学研究院学报，2022，17（5）:421-428.
［8］吴浩，徐婧，李刚.无人机探测与反制技术发展现状及建议［J］.飞航导弹，2020（9）:89-95.
［9］张少峰.低慢小目标雷达探测技术研究［J］.现代导航，2017，8（6）:436-440.
［10］ALABASTER C.脉冲多普勒雷达——原理、技术与应用［M］.张伟，刘洪亮，译.北京:电子工业出版社，2016.
［11］陈伯孝.现代雷达系统分析与设计［M］.西安：西安电子科技大学出版社，2012.
［12］HAYKIN S.自适应滤波器原理［M］.北京：电子工业出版社,2003.
［13］许德刚，朱子平，洪一.自适应滤波在无源探测中对杂波抑制的应用［J］.系统工程与电子技术，2006，28（2）:202-204.
［14］杨鹏程，吕晓德，刘宇，等.基于波束域分块RDLMS 的机载外辐射源雷达杂波对消算法［J］.电子与信息学报，2017，39（4）:960-967.
