0 引 言
海杂波的定义是海表面对雷达发射电磁波的后向散射回波,海面慢速小目标检测所面临的主要困难就在于海杂波的存在[1-2]。作为对海探测雷达的背景,海杂波特性高度复杂,在高分辨率雷达体制下,海杂波的非平稳、非均匀和非高斯特性更加明显,整个探测场景内的海杂波特性不再相同,很难达到经典CFAR 方法和自适应类检测方法所要求的独立同分布的前提条件。
为实现稳健的海杂波中目标检测,需要对整个探测场景的背景信息进行精细化动态辨识,进而将探测场景划分为多个子场景,针对不同的子场景,采用与之匹配的目标检测方法进行探测,从而提高整体的目标检测性能[3-5]。海况等级的高低(本文将3级以下海况看作低海况,3级及以上海况看作高海况)作为雷达对海上目标检测的重要背景信息,很大程度地影响着探测场景的划分和检测器的选择,故采用一种灵活、快速和准确的方法识别对海探测雷达的高/低海况背景信息,在对海探测雷达的目标精细化探测中具有重要意义。本文海况等级采用有效波高进行划分,对应道格拉斯海况等级标准[6]。气象浮标和海洋天气预报等能够用于获取高/低海况信息,但存在实时性和灵活性差的问题。基于对海雷达回波,已有研究主要采用一种海态反演的方法,获取所需要的浪高、浪向、表面径向流速、风向和风速等信息。其大致流程是将回波信号或雷达图像反演为海浪谱和方向谱,进而通过相应关系公式计算所需背景信息参数,该方法获取背景信息的精度高、种类多,但对雷达工作参数和工作方式要求严格,且对回波数据量要求高,无法应用于一般的对海探测雷达系统[7-9]。
特征检测方法将雷达目标检测问题转化为分类问题解决,极大简化了目标检测问题的复杂度[10]。鉴于此,本文采用杂波分类方法解决高/低海况的辨识问题。针对雷达杂波分类的研究最早开始于1991年,Haykin 等人训练了一个神经网络,对空中监视雷达的杂波进行分类[11];文献[12]提出了一种利用反射率、幅度统计和时间相关性对陆海杂波分类的方法;为解决工作于扫描模式雷达分辨单元级的陆海分割问题,Shui 等人提出了对两帧脉冲的平均幅度、多普勒偏移和初始相位保持不变的度量,来表征两帧脉冲之间的相似性,并在此基础上提出了一种基于K 近邻算法的分类器[13]。就目前研究而言,很少有人采用杂波分类方法,对高/低海况信息进行识别,只有文献[14]采用了CNN 的方法对高/低海况识别问题进行了初步探索,但由于其采用的数据预处理方法较为单一,无法稳定地突出高/低海况海杂波的差异,导致使用的相干脉冲数均达到400 以上,不能满足雷达工作于扫描模式的需求。本文在对海杂波序列进行时频变换和频域变换预处理的基础上,提出三种能够稳定区分高/低海况海杂波的特征,以此实现对高/低海况海杂波的分类,获取所需要的高/低海况信息。
本文首先在对实测海杂波数据进行时频特性和频域特性分析的基础上,提出两种时频谱特征和一种多普勒功率谱特征用于区分高/低海况海杂波,并使用实测数据对每种特征的适用条件和区分效果进行测试;其次,基于支持向量机(Support Vector Machine,SVM)和所提三种特征,构建了一种三特征联合的高/低海况分类器;最后,使用实测数据集对所提分类器性能进行测试。
1 特征提取
1.1 实测数据简介
本文实验所使用的雷达实测数据均来自于海军航空大学“雷达对海探测数据共享计划”数据集(2020年第1 期)。该数据集主要包括不同海况等级下的海杂波和目标回波数据,数据采集时,雷达主要工作于凝视模式,极化方式为HH 极化,距离向采样率为60 MHz,雷达架高80 m,PRF 为1.6 kHz[15-16],更详细介绍如表1所示,每个数据编号包含2 至3 组数据,本文采用序号代替相应数据编号对数据进行引用。
表1 “雷达对海探测数据共享计划”数据介绍
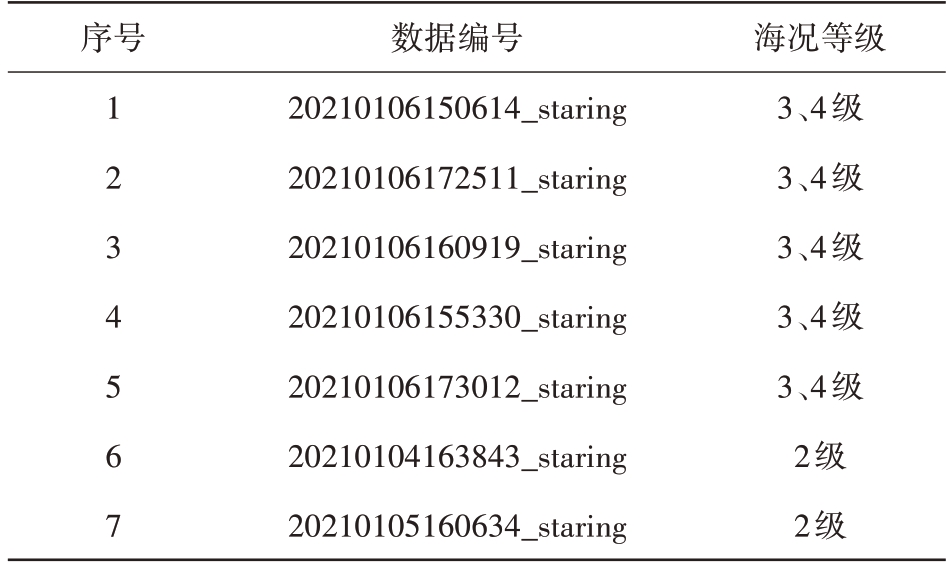
序号1234567数据编号20210106150614_staring 20210106172511_staring 20210106160919_staring 20210106155330_staring 20210106173012_staring 20210104163843_staring 20210105160634_staring海况等级3、4级3、4级3、4级3、4级3、4级2级2级
1.2 两种时频谱特征提取
将海杂波建模为非平稳随机过程,对其进行时频特性分析,才能发现其本质特征。常见的时频变换工具有短时傅里叶变换(Short-Time Fourier Transform,STFT)、维格纳-威尔分布(Wigner-Ville Distribution,WVD)、平滑伪WVD(Smoothed Pseudo WVD,SPWVD)等,它们各有其优缺点,为避免交叉项影响和提升计算速度,本文选择STFT 作为时频变换工具。事实上,其他时频分析工具也可应用于本文所提方法。假设对海探测雷达在某方位上发射多个相参脉冲,某距离单元上接收到长度为N 的海杂波序列,即r(n)=c(n), n=1,2,…,N。较小范围内,其周围距离单元的海况等级可看作是同等水平的,其周围距离单元接收到的回波脉冲可表示为
式中S 表示周围距离单元数目。对该距离单元的海杂波进行STFT,得到时频谱STFT(t,f|r)。对长度为1 024的实测海杂波序列进行STFT,取长度为127的海明窗为时间窗,频率点数设为512,典型结果如图1所示,可知仅进行时频变换的预处理,并不能稳定反映高/低海况海杂波的差异。通过STFT,可将海杂波序列由时域上的一维随机过程转换成时频域上的二维随机过程,本文将此随机过程的均值函数和标准差函数表示为μ(t,f) 和σ(t,f),分别表征了海杂波在时频域(t,f)点处的平均功率水平及其波动程度[17]。事实上,μ(t,f) 和σ(t,f)都是未知的,需要通过海杂波单元周围距离单元数据估计它们,计算公式如下:
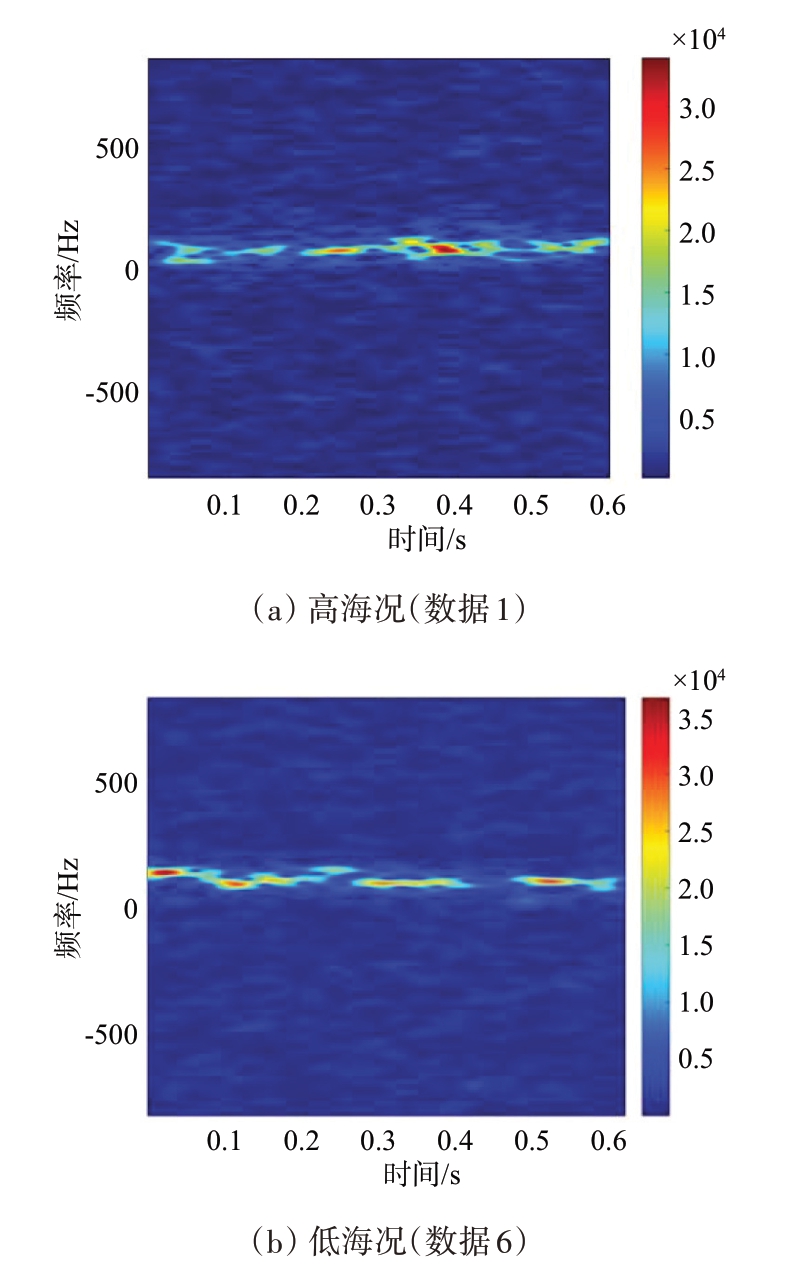
图1 典型海杂波时频谱
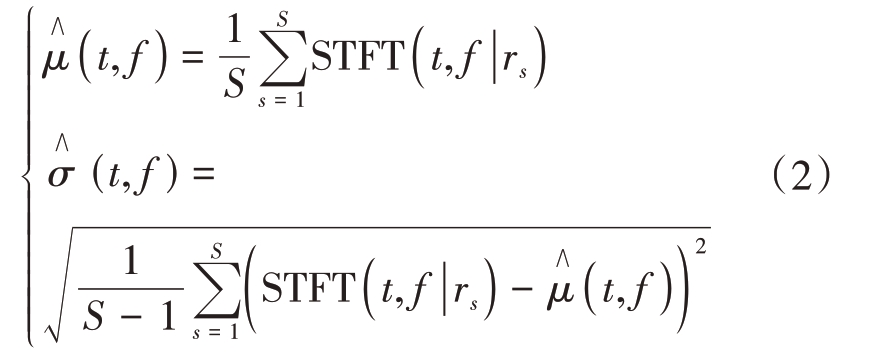
μ(t,f)和σ(t,f)均能够更加稳定、突出地反映高/低海况海杂波在时频域的差异,实测数据分析结果如图2和图3所示,STFT参数与上文相同。本文使用文献[17]提出的脊累积量(Ridge Integration,RI)来量化这一差异。μ(t,f) 和σ(t,f)的脊定义如下:
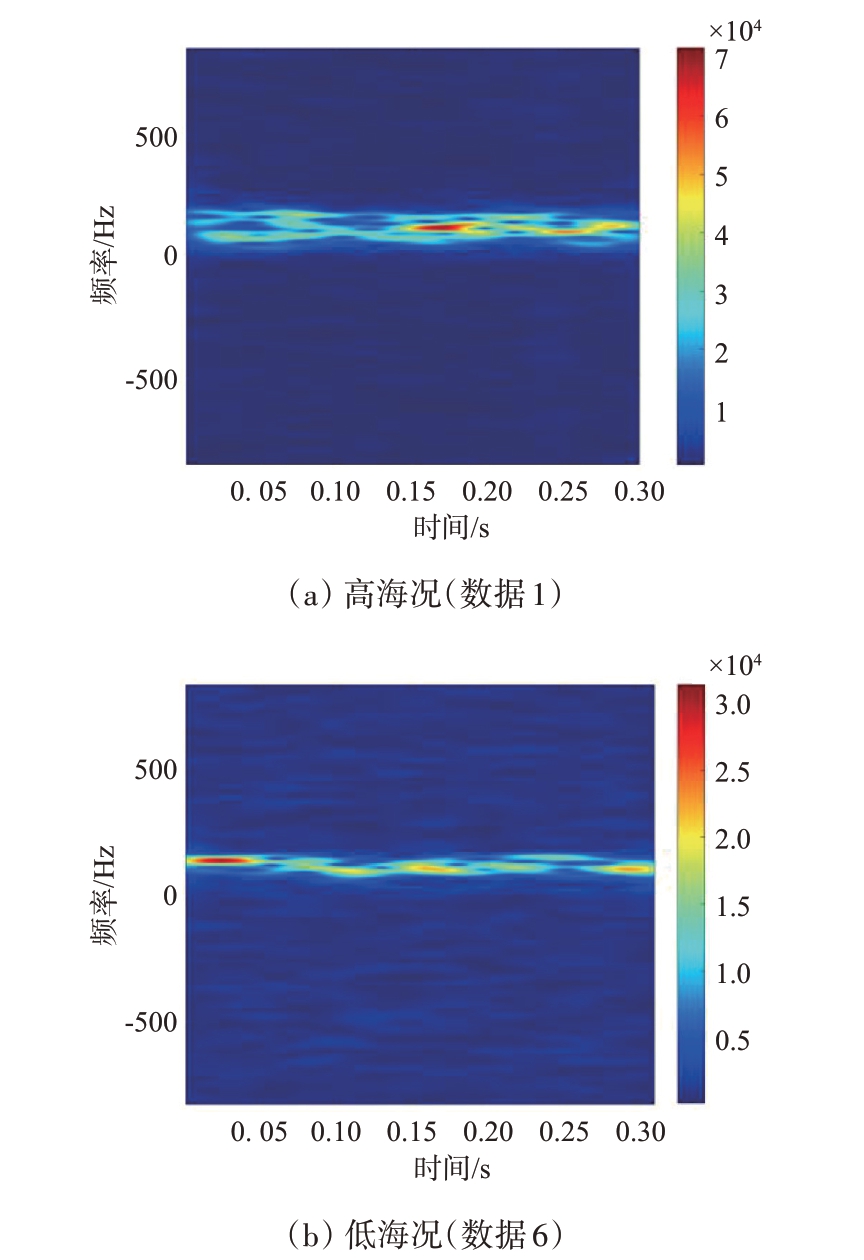
图2 典型海杂波时频谱的均值函数
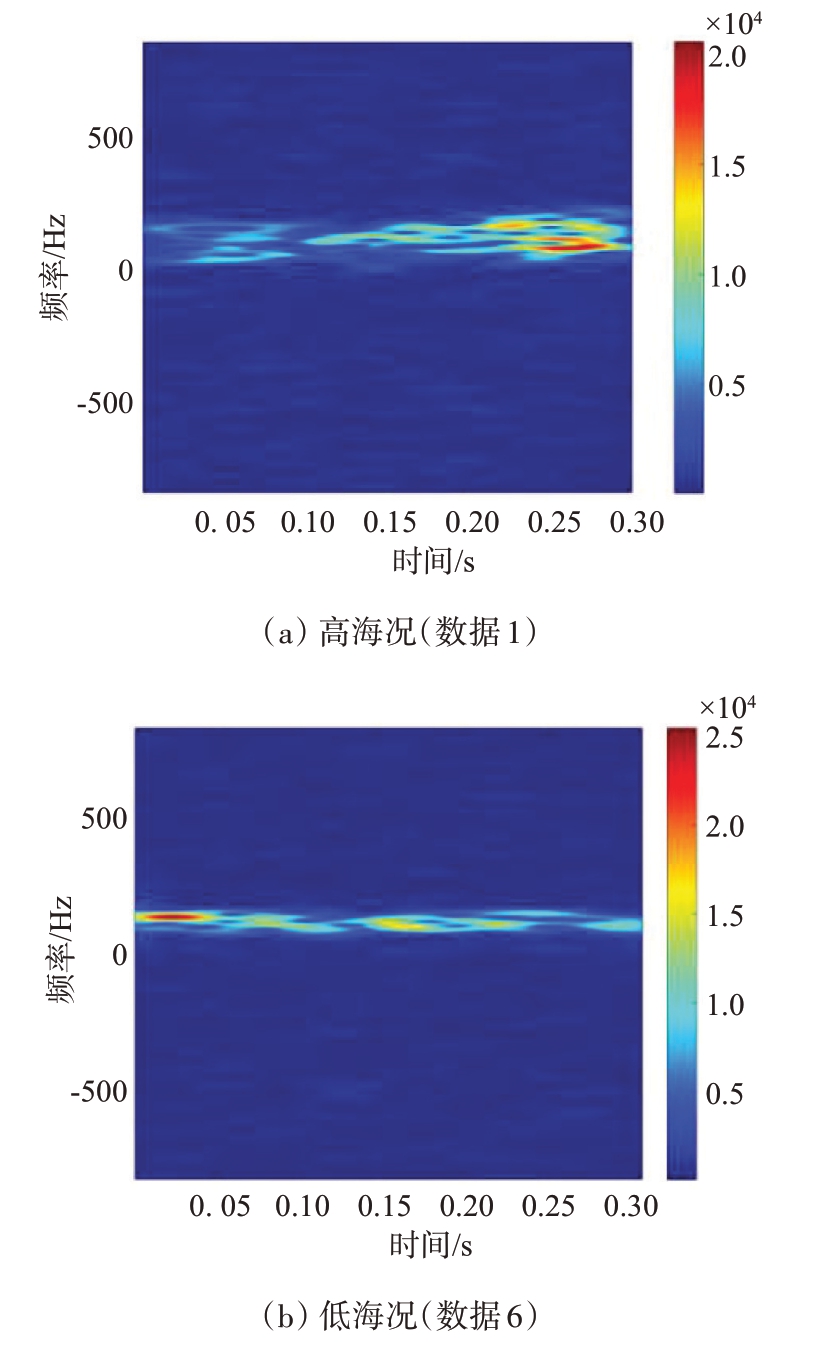
图3 典型海杂波时频谱的标准差函数
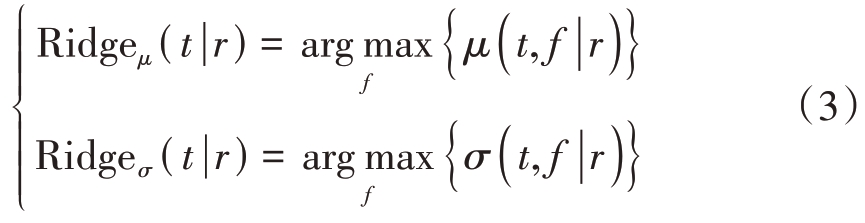
它表示由μ(t,f)或σ(t,f)的每个时间切片t 上的最大值组成的集合。均值函数的脊累积量(Ridge Integration of Mean Function,RIMF)和标准差函数的脊累积量(Ridge Integration of Standard Deviation function,RISD)即为所有脊点值的求和,定义如下:
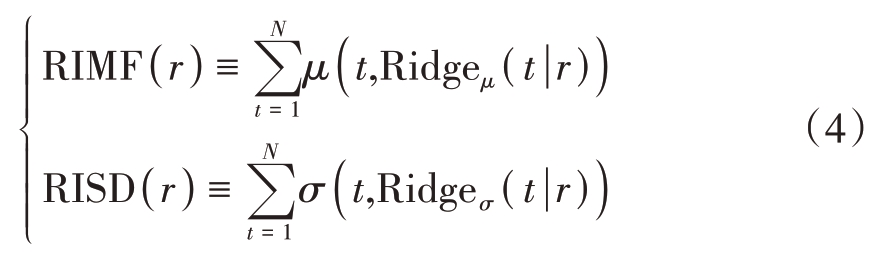
由RIMF 和RISD 的定义可知,二者本质上表征了海杂波的某种最大功率水平及其最大波动程度,因此高海况海杂波的RIMF、RISD 应当大于低海况海杂波。事实上,其统计分布特点与海杂波距离单元对应的实际径向距离关系密切。数据1和数据6 所提取两种特征的距离向分布如图4所示,可知,随着径向距离的增加,RIMF与RISD都存在减小的趋势;同一距离段上,海况等级大致相同的海杂波,RIMF、RISD 均相近,高海况海杂波的RIMF与RISD基本都大于低海况,且在全部数据集上均有类似现象。使用实测数据集验证所提特征的有效性,64 个脉冲计算一次RIMF 与RISD,取长度为31 的海明窗作为STFT 的时间窗;将径向距离为1.3 km 至3.8 km 的海杂波数据分成三段,统计不同距离段上高/低海况海杂波RIMF 和RISD 的分布差异,典型结果如图5所示。可知,不同距离段上,高/低海况海杂波的RIMF 和RISD 分布差异都比较明显,使用64个脉冲时,这两种特征仍能够很好地区分高/低海况海杂波。
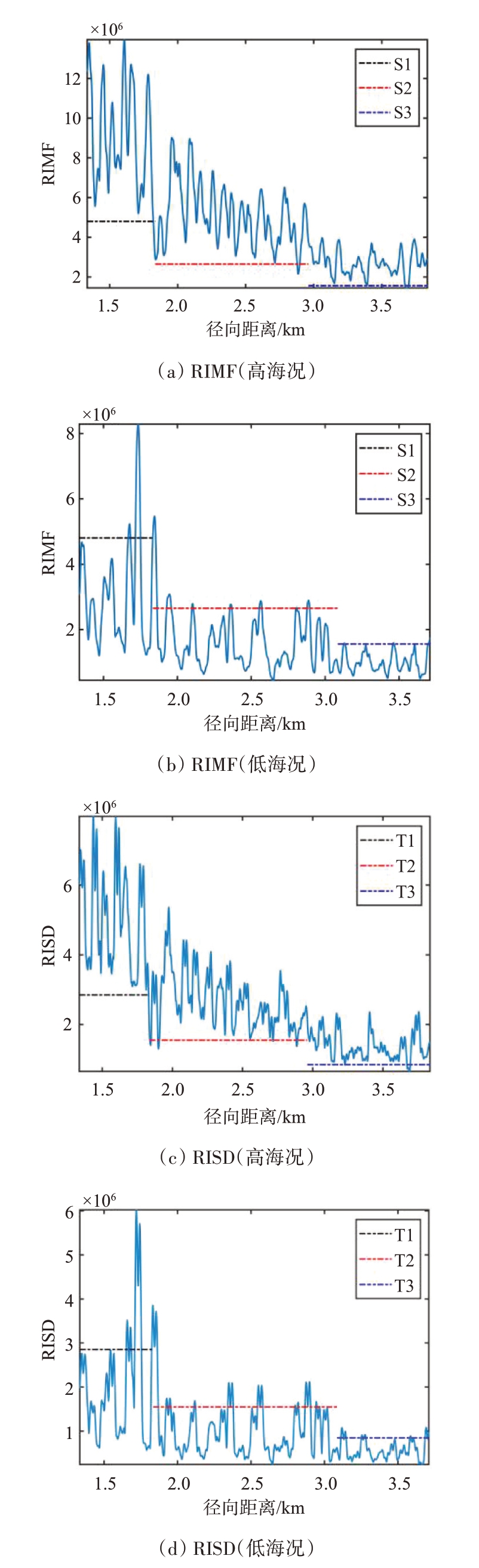
图4 RIMF和RISD的距离向分布
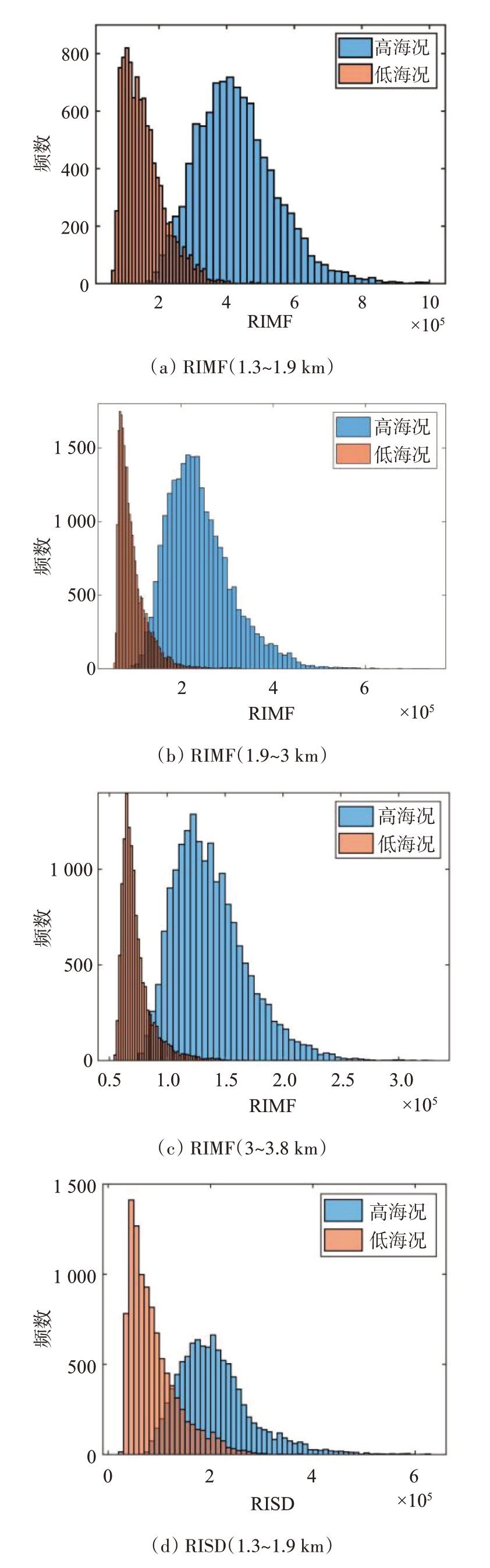
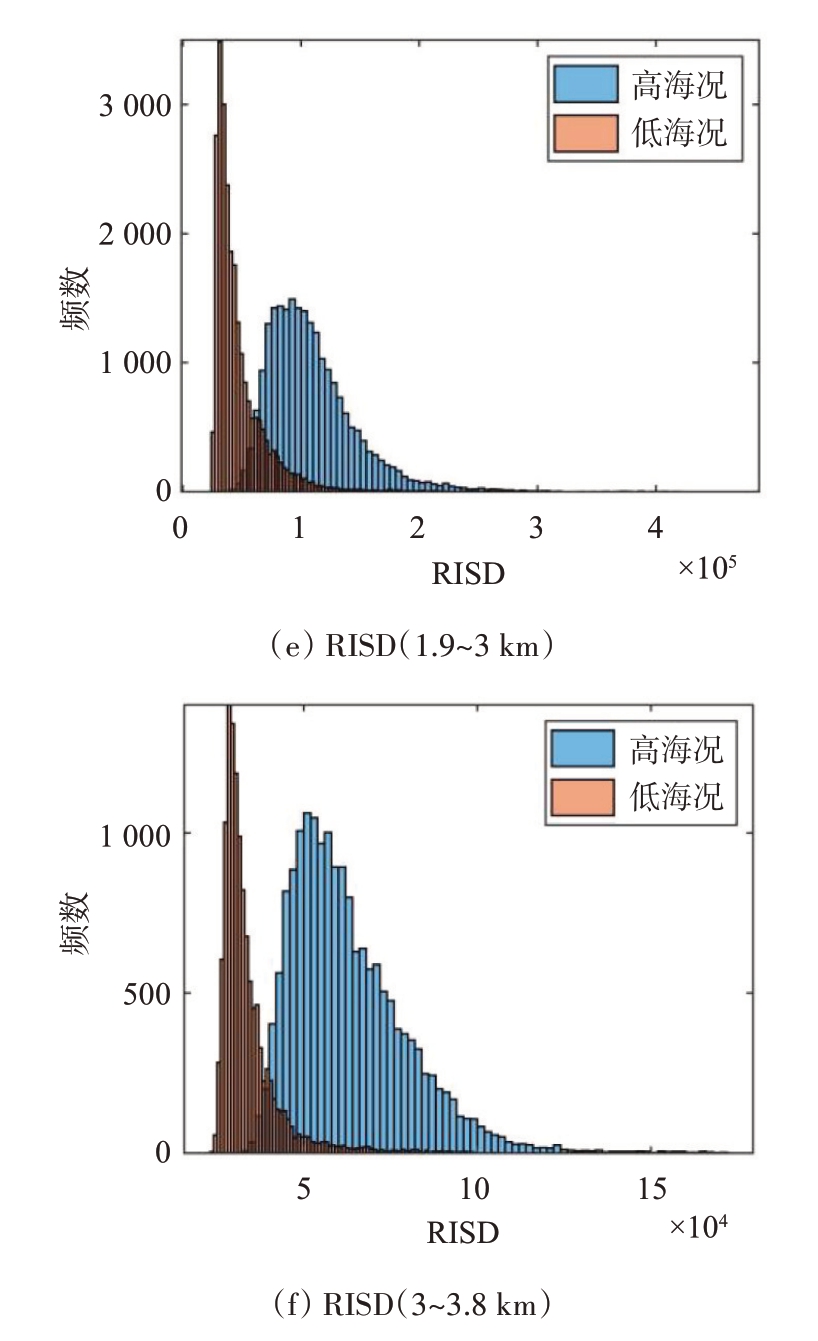
图5 RIMF和RISD统计分布
1.3 一种多普勒谱特征提取
高/低海况海杂波在多普勒谱上也存在较大差异,采用AR 模型法估计长度为256 的海杂波序列的功率谱,模型阶数设为8,结果如图6所示。可知,高海况海杂波多普勒谱的杂波主瓣谱宽(3 dB谱宽)和杂噪比(Clutter-Noise Ratio,CNR)一般大于低海况。事实上,单独使用谱宽或CNR 来区分高/低海况海杂波并不能取得稳定的结果。鉴于此,本文综合谱宽和CNR 两种特征,提出一种新的多普勒谱特征,即区域峰值功率与噪声均值功率比(Ratio of Regional Peak Power to Noise Mean Power,RPNM)来表征高/低海况海杂波在多普勒功率谱上的差异,RPNM定义如下:
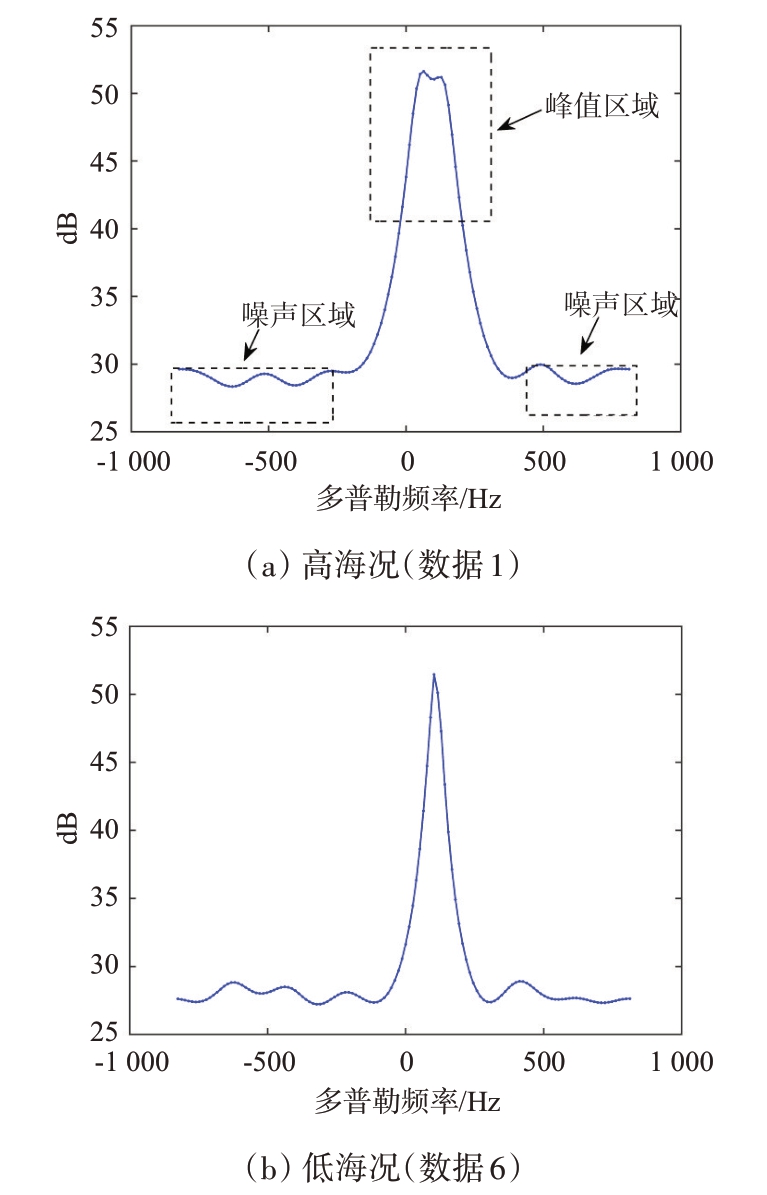
图6 典型海杂波的多普勒功率谱

X1(p),p=1,2,…,P 为功率谱的峰值区域,其位置可通过功率谱峰值所在位置确定,峰值区域大小P通过高海况海杂波多普勒功率谱的3 dB 谱宽来确定;X2(k),k=1,2,…,K 为功率谱的噪声区域,其范围大致是高海况海杂波功率谱的3 倍峰值区域之外的部分。需要注意的是,为减小多普勒功率谱的方差,可使用AR 模型对功率谱进行估计;为提升特征的稳定性和有效性,需联合使用待测海杂波序列周围几个距离单元的数据求取平均功率谱,再使用式(5)计算RPNM。
RPNM 本质上综合了谱宽和CNR 的特点,故高海况海杂波的RPNM 应当大于低海况,事实上,RPNM 的分布特点也与海杂波距离单元对应的实际径向距离关系密切。数据1 和数据6 所提取RPNM 的距离向分布如图7所示,可知,随着径向距离的增加,RPNM 存在减小趋势;同一距离段上,海况等级大致相同的海杂波,RPNM 相近,高海况海杂波的RPNM 基本都大于低海况,且在全部数据集上均有类似现象。使用实测数据集验证所提特征的有效性,64 个脉冲计算一次RPNM,典型结果如图8所示。可知,在不同距离段上,高/低海况海杂波的RPNM 分布差异明显,使用64 个相参脉冲时,所提特征仍能够很好地区分高/低海况。
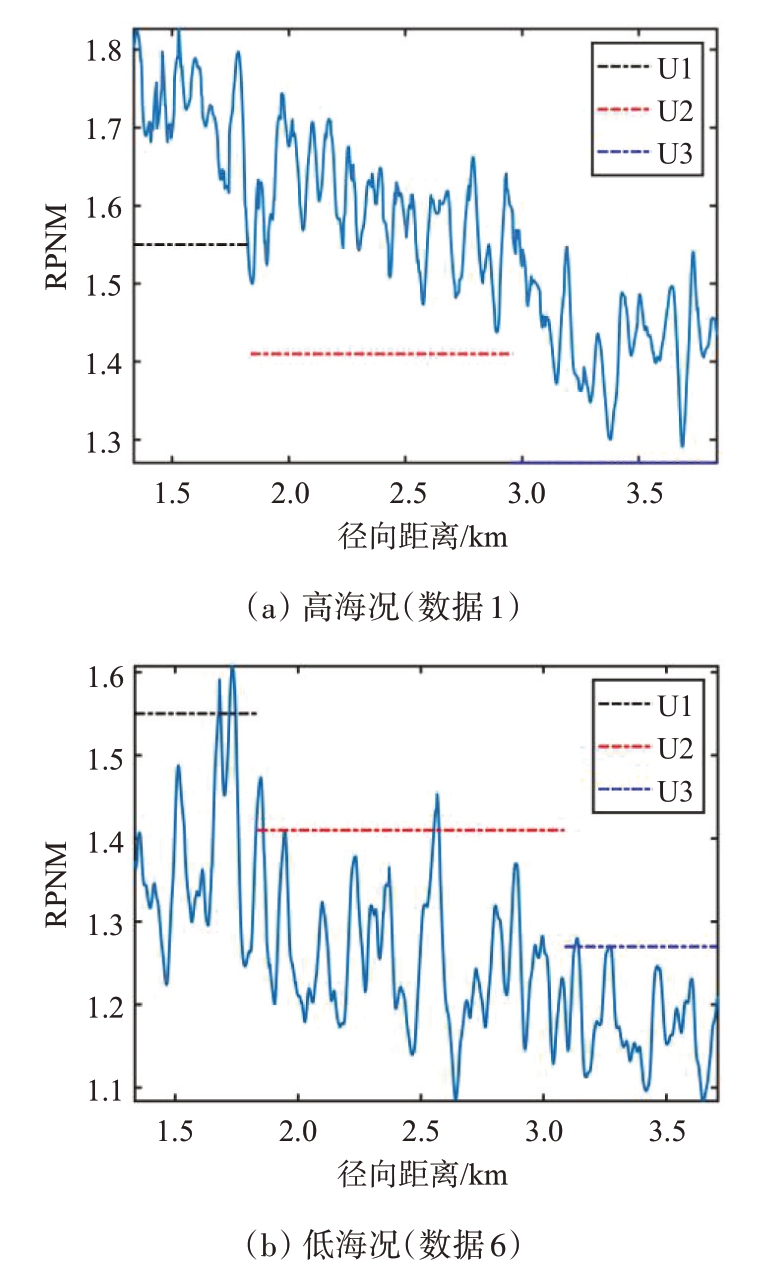
图7 RPNM的距离向分布
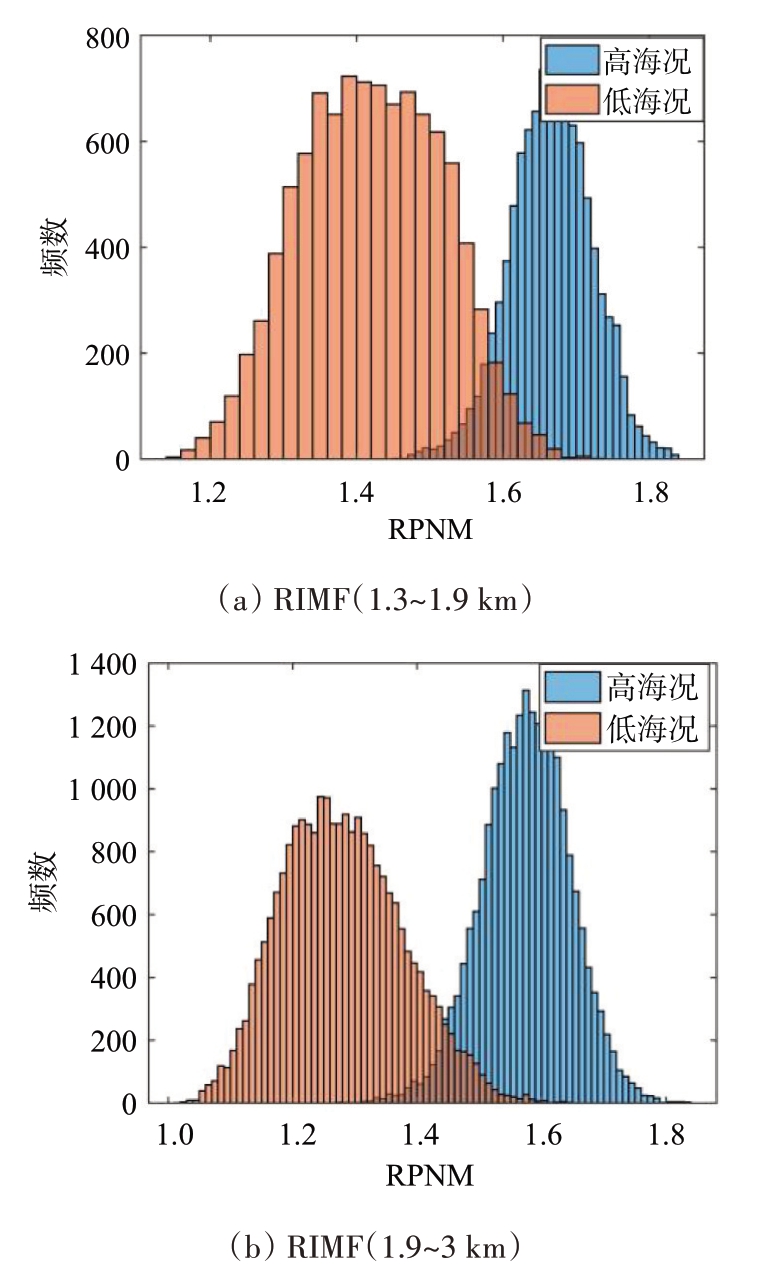
图8 RPNM的统计分布
2 三特征分类器构建
将海杂波的高/低海况辨识问题看作模式识别问题,从海杂波数据中提取RIMF、RISD 和RPNM,将高/低海况海杂波由高度重合的时域观测空间变换到三特征组成的特征空间,在特征空间中完成海杂波的分类。SVM 作为一种广泛应用于模式识别问题的机器学习分类器,能够在少量训练样本的情形下实现中高维向量的二分类,且训练得到的分类器具有较高的泛化能力,故本文基于SVM,构建能够实现高/低海况海杂波分类的三特征联合分类器。
从海杂波中提取三种特征,构成所需要的特征样本,对于训练集中的样本i,本文构造了一个由时频谱的RIMF(fi,1)、RISD(fi,2)和多普勒谱的RPNM(fi,3)有序组成的三维特征向量Fi,即
并且使用yi ∈{+1,-1},标记高海况海杂波(+1)和低海况海杂波(-1)的类别,故样本容量为M 的训练集为{(Fi,yi),i= 1,2,…, M}。事实上,高/低海况海杂波的特征向量在构造的特征空间中并不一定是线性可分,甚至可能是本质上的线性不可分,如图9所示,图中三特征均归一化处理。SVM采用广义线性化的方法解决本质上线性不可分的问题,即通过引入核函数将低维特征空间中的非线性可分问题转换成一个高维特征空间中的线性分类问题,同时核函数的引入也避免了维度转换带来的计算量的骤增[18]。常用的核函数有高斯核函数、径向基核函数、线性核函数和多项式核函数等,核函数的一般表达式如下:
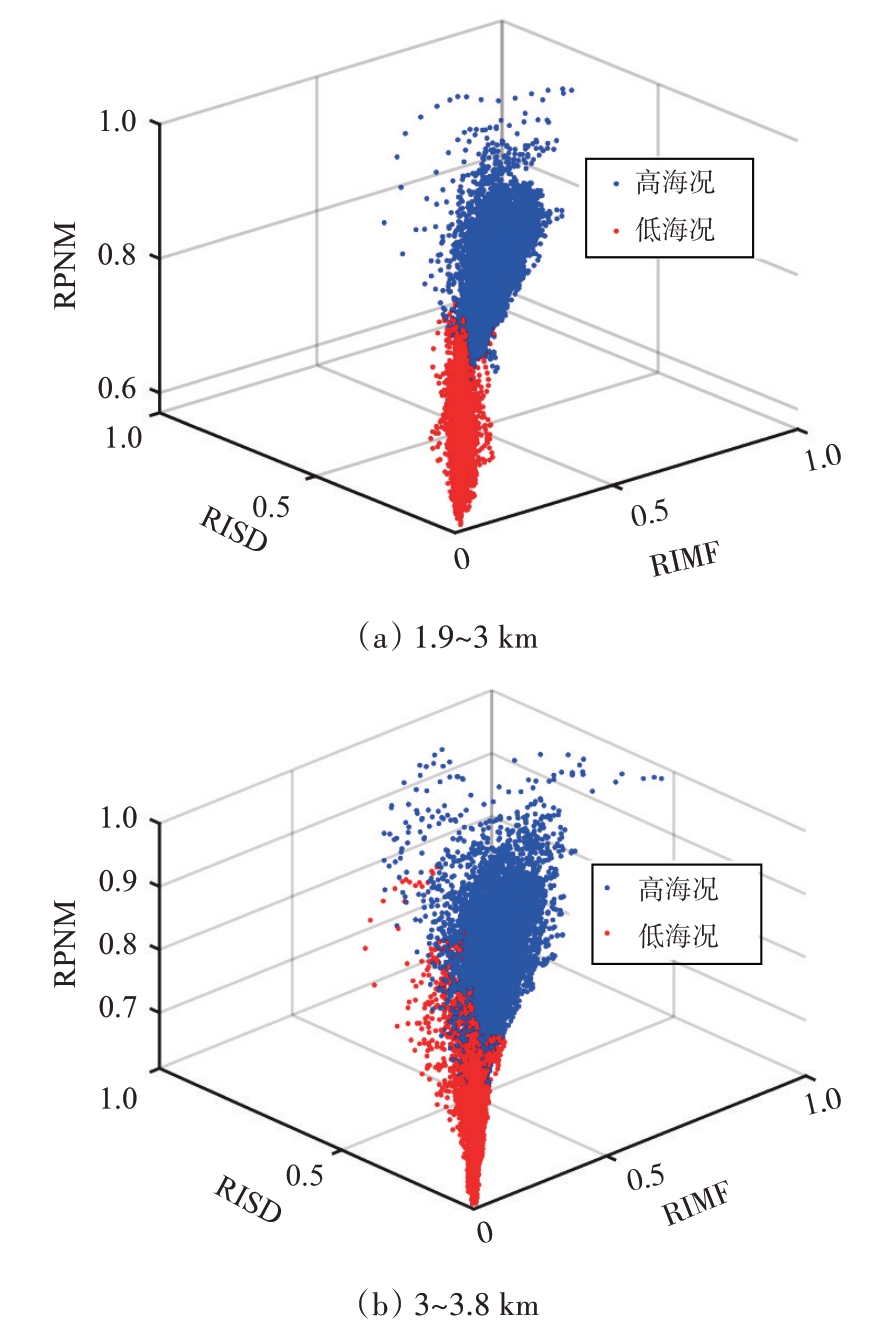
图9 海杂波在三维特征空间中分布
式中Φ(F1)和Φ(F2)分别表示特征向量F1和F2在高维特征空间的映射。映射到高维特征空间之后,问题的关键转换成求解线性SVM 的超平面,即ωTF+b=0,其中权向量ω 和截距b 都是未知参数,可通过求解式(8)中的最优化问题来解决。
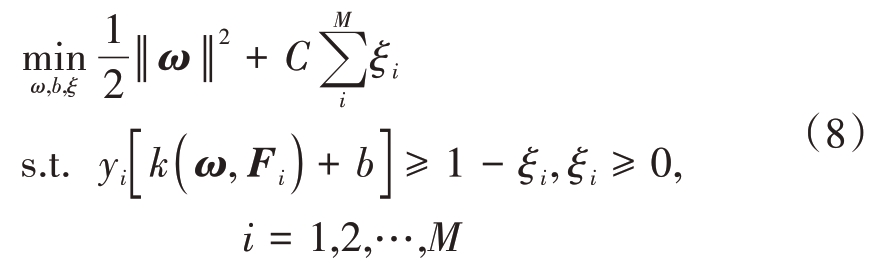
ξi 为松弛变量,是未知变量,用于将分类间隔转化成软间隔;C 为惩罚因子,取值大于0,表示对分类器中异常点存在的容忍程度。该最优化问题可以通过构造拉格朗日函数,并将其转化成对偶问题,借助序列最小优化算法来求解[19-20]。得到用于分类的超平面ωTF+b=0 之后,对于输入的特征向量Fj,可以通过以下原则确定其类别:
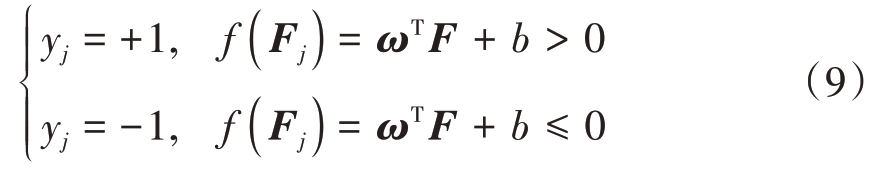
式中f(Fj)=ωTF+b 即为训练得到的判决函数。至此,本文基于非线性SVM,构造了一种三特征联合分类器,该分类器可以对高/低海况海杂波进行分辨单元级分类。由于本文所提三种特征与待测海杂波序列所在实际径向距离关系密切,故在实际分类过程中,需要在不同距离段上分别训练不同的分类器,再进行分类,每个距离段的经验长度大致在0.8~1 km之间。
3 分类器性能分析
使用“雷达对海探测数据共享计划”数据集测试所提分类器性能。考虑到基于学习的分类器需要较多的训练样本,但高/低海况海杂波在三特征空间中区分较为明显,同时为缩短训练时间,将训练集和测试集按照1∶3的比例划分。将海杂波数据按照径向距离划分成多个距离段,在不同距离段上分别训练不同的分类器。本文实验只使用1.3 km 至3.8 km范围内的海杂波数据,并将其分成三段。
提取时频谱的RIMF、RISD 时,使用64 个脉冲计算STFT,取长度为31 的海明窗作为时间窗,参考距离单元数设为16 个,以求取均值函数和标准差函数。提取多普勒功率谱的RPNM 时,使用64个脉冲,通过阶数为8 的AR 模型估计功率谱,参考单元数设为16 个,以求取平均功率谱。事实上,参考单元数决定了分类器的实际空间分辨率;使用脉冲数一定时,分类器的空间分辨率与准确度成反比;准确度一定时,分类器的空间分辨率与使用脉冲数成反比。测试结果如表2所示,其中交叉验证准确度为10 折交叉验证准确度,表征分类器的泛化能力。可知,无论使用哪种核函数,分类器泛化能力基本相同;分类器对1.9~3 km 距离段海杂波的分类效果最佳;线性核函数分类器性能最稳定,在各距离段上,对高/低海况的分类准确度均能达到92%以上;三种核函数分类器,对高/低海况的平均分类准确度均保持在93.5%左右。
表2 三特征分类器测试结果
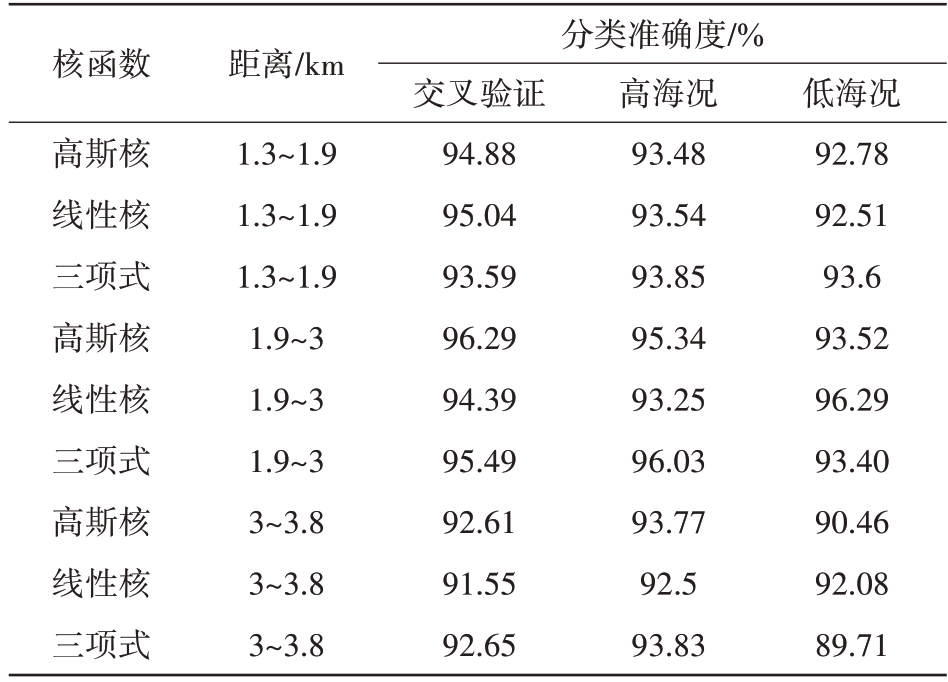
核函数高斯核线性核三项式高斯核线性核三项式高斯核线性核三项式距离/km 1.3~1.9 1.3~1.9 1.3~1.9 1.9~3 1.9~3 1.9~3 3~3.8 3~3.8 3~3.8分类准确度/%交叉验证94.88 95.04 93.59 96.29 94.39 95.49 92.61 91.55 92.65高海况93.48 93.54 93.85 95.34 93.25 96.03 93.77 92.5 93.83低海况92.78 92.51 93.6 93.52 96.29 93.40 90.46 92.08 89.71
改变分类器使用的特征类别,且使用高斯核函数,其他实验条件与上文所述相同,分类器测试结果如表3所示。可知,就单个特征而言,RPNM效果最佳,分类准确度保持在83%以上;其次是RIMF,准确度保持在80%以上。对比表2和表3可知,相较于单特征,三特征的联合使用明显提高了分类器的泛化能力;三特征分类器对于高/低海况海杂波均可实现较为准确分类,且性能稳定,这是由于多特征的使用,提升了海杂波信息利用的维度,包含有更多的信息量。
表3 分类器的其他测试结果
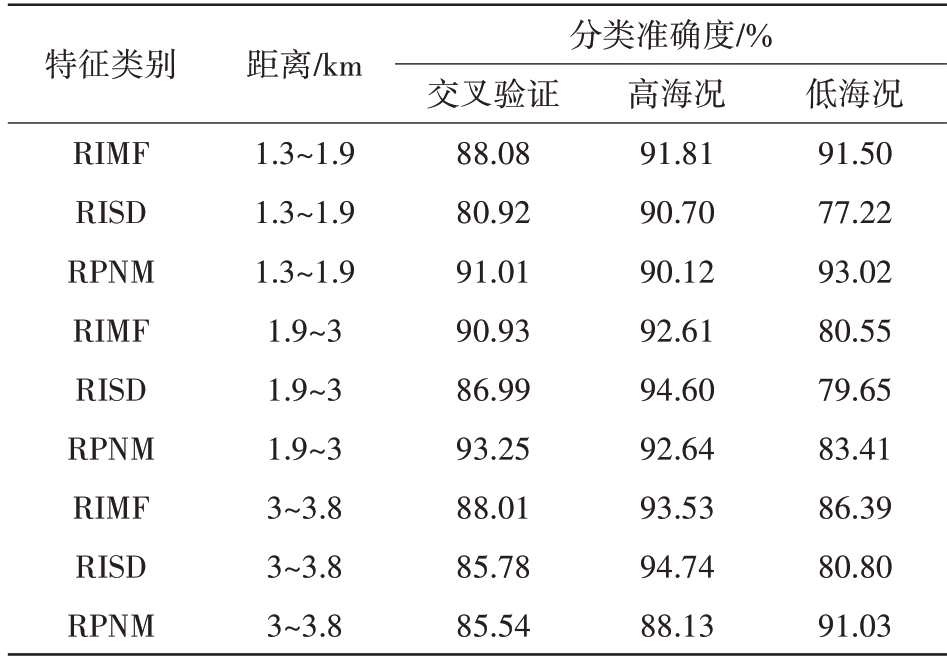
特征类别距离/km 分类准确度/%RIMF RISD RPNM RIMF RISD RPNM RIMF RISD RPNM 1.3~1.9 1.3~1.9 1.3~1.9 1.9~3 1.9~3 1.9~3 3~3.8 3~3.8 3~3.8交叉验证88.08 80.92 91.01 90.93 86.99 93.25 88.01 85.78 85.54高海况91.81 90.70 90.12 92.61 94.60 92.64 93.53 94.74 88.13低海况91.50 77.22 93.02 80.55 79.65 83.41 86.39 80.80 91.03
为进一步验证所提方法的有效性,本文与文献[14]所提CNN 的分类方法,及文献[20]所提原始三特征检测器进行了对比。实验过程中,CNN分类方法使用脉冲数分别设为64、144和256,训练集和测试集按照1∶3的比例划分,文献[21]检测器的判决区域通过低海况海杂波特征样本训练凸包得到,其他实验条件保持不变,实验结果如图10和图11所示。可知,使用64 个脉冲时,CNN 分类方法的平均准确度为92%左右;文献[21]检测器对低海况的平均分类准确度可达85%,对高海况的平均分类准确度为60%左右,这两种方法性能均不如本文所提三特征联合分类器。
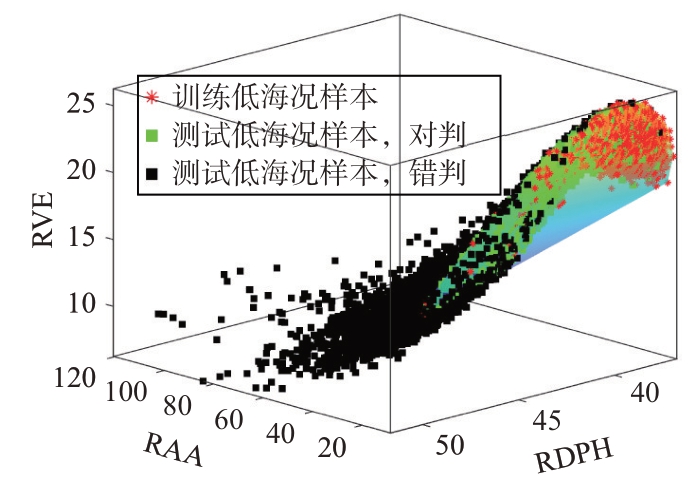
图10 文献[21]检测器的分类结果
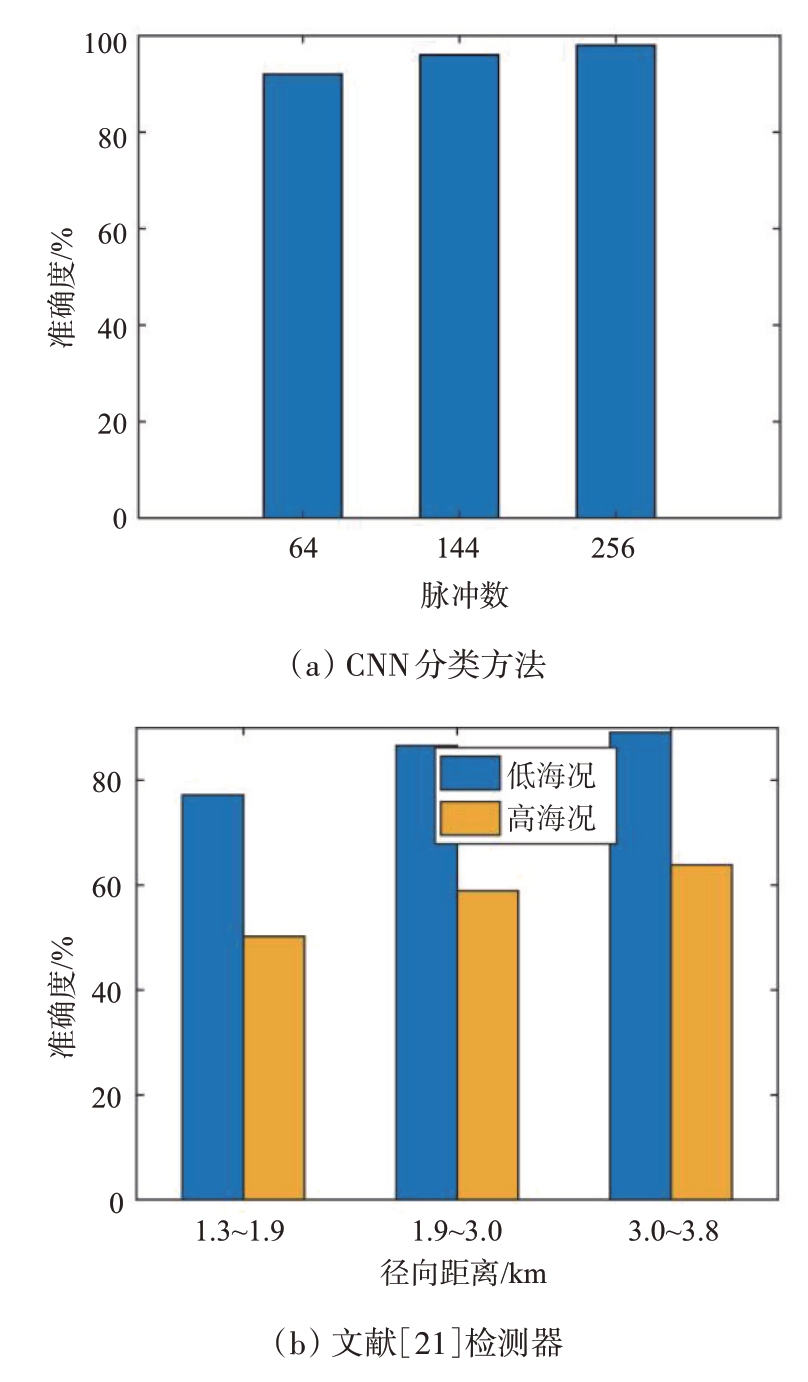
图11 对比实验的分类准确度
4 结束语
本文采用海杂波分类的思想,实现对海探测雷达高/低海况背景信息的灵活、快速和准确辨识。通过对实测海杂波数据的时频特性和频域特性进行分析,本文提出了时频谱的RIMF、RISD 和多普勒谱的RPNM 三种能够稳定、准确区分高/低海况海杂波的特征,并在此基础上构造了一种三特征联合高/低海况分类器。实测数据集测试结果表明,相较于单特征分类器,三特征的使用明显提高了分类器的泛化能力;相较于CNN 的分类方法和文献[21]检测器,本文所提三特征联合分类器性能更佳,使用64 个相干脉冲,即可实现高/低海况的准确辨识,能够满足对海探测雷达工作于扫描模式的需求。事实上,由于海况等级不随时间快速变化,所以对海况等级判断所需脉冲数的约束可以不用那么严格,在实际使用过程中可以按秒级时间量级输出结果即可。
[1]CORRETJA V,MESLOT V,KEMKEMIAN S,et al.Statistical Analysis on Sea Clutter Doppler Properties in X-Band for Low Grazing Angles[C]//2017 IEEE Radar Conference,New York:IEEE,2017:1046-1051.
[2]时艳玲,刘子鹏,张学良,等.基于EMD 能量占比的海面漂浮小目标特征检测[J].系统工程与电子技术,2021,43(2):300-310.
[3]RIEDL M,POTTER L C.Knowledge-Aided Bayesian Space-Time Adaptive Processing[J].IEEE Trans on Aerospace and Electronic Systems,2018,54(4):1850-1861.
[4]WANG Y,XIA W,HE Z.CFAR Knowledge-Aided Radar Detection with Heterogeneous Samples[J].IEEE Signal Processing Letters,2017,24(5):693-697.
[5]周明,马亮,王宁,等.面向海面目标检测的陆海分离和海面分区算法研究[J].雷达学报,2019,8(3):366-372.
[6]马令琪,杨家轩,简俊.恶劣天气和恶劣海况的学术含义分析[J].中国航海,2021,44(1):14-20.
[7]XIE T,PERRIE W,HE Y J,et al.Ocean Surface Wave Measurements from Fully Polarimetric SAR Imagery[J].Science China(Earth Sciences),2015,58(10):1849-1861.
[8]李艳.超高频雷达海洋表面流及风向反演算法研究[D].武汉:武汉大学,2017.
[9]范林刚.微波多普勒雷达海浪反演关键技术研究[D].武汉:武汉大学,2013.
[10]许述文,白晓惠,郭子薰,等.海杂波背景下雷达目标特征检测方法的现状与展望[J].雷达学报,2020,9(4):684-714.
[11]HAYKIN S,DENG C.Classification of Radar Clutter Using Neural Networks[J].IEEE Trans on Neural Networks,1991,2(6):589-600.
[12]SARIKAYA T B,SOYSAL G,EFE M,et al.Sea-Land Classification Using Radar Clutter Statistics for Shore-Based Surveillance Radars[C]// International Conference on Radar Systems,New York:IEEE,2017:1-4.
[13]SHUI P L,XIA X Y,ZHANG Y S.Sea-Land Segmentation in Maritime Surveillance Radars via K-Nearest Neighbor Classifier[J].IEEE Trans on Aerospace and Electronic Systems,2020,56(5):3854-3867.
[14]徐雅楠,刘宁波,丁昊,等.利用CNN 的海上目标探测背景分类方法[J].电子学报,2019,47(12):2505-2514.
[15]刘宁波,丁昊,黄勇,等.X波段雷达对海探测试验与数据获取年度进展[J].雷达学报,2021,10(1):173-182.
[16]刘宁波,董云龙,王国庆,等.X 波段雷达对海探测试验与数据获取[J].雷达学报,2019,8(5):656-667.
[17]SHI S,SHUI P.Sea-Surface Floating Small Target Detection by One-Class Classifier in Time-Frequency Feature Space[J].IEEE Trans on Geoscience and Remote Sensing,2018,56(11):6395-6411.
[18]LI Y,XIE P,TANG Z,et al.SVM-Based Sea-Surface Small Target Detection: A False-Alarm-Rate-Controllable Approach[J].IEEE Geoscience and Remote Sensing Letters,2019,16(8):1225-1229.
[19]YANG Y,WANG J,YANG Y.Exploiting Rotation Invariance with SVM Classifier for Microcalcification Detection[C]//2012 9th IEEE International Symposium on Biomedical Imaging(ISBI),New York:IEEE,2012:590-593.
[20]ISLAM T,RICO-RAMIREZ M A,HAN D,et al.Artificial Intelligence Techniques for Clutter Identification with Polarimetric Radar Signatures[J].Atmospheric Research,2012(109-110):95-113.
[21]SHUI P L,LI D C,XU S W.Tri-Feature-Based Detection of Floating Small Targets in Sea Clutter[J].IEEE Trans on AerospaceandElectronicSystems,2014,50(2):1416-1430.
