0 引 言
空间目标探测是利用各种探测装备对航天器进入空间、在空间运行及离开空间的过程进行探测和跟踪，对目标的轨道变化情况进行观测，对观测数据进行综合处理、分析，在此基础上进行空间目标编目，以掌握空间态势，并向军事和民用航天活动提供空间目标的信息支援等。目前我国已建设了多部地基雷达系统、地基望远镜和天基系统。其中，地基雷达系统因其监视范围大，同时跟踪目标多，肩负着新目标发现、编目维持、空间事件监视等太空态势实时感知任务［1-6］。在进行此类任务时，需要为雷达提供目标的实时精密指示，包括目标的轨道、姿态和特征，引导我方系统精确打击目标。因此，实时性、精确性是实现太空态势实时感知任务的核心要求。
然而，随着巨型星座的不断发射入网，太空环境日益拥挤，新发射目标以及碰撞/解体等太空事件产生的碎片等敏感目标，在一定程度上造成定轨精度下降并影响编目的稳定性，给完成目标跟踪及编目管理任务带来新的挑战。此外，监视装备体制不一、探测精度各异，需要更高效地利用多源探测数据，提高数据精度和数据利用率，支撑高精度轨道预报。总之，如何实现多源探测数据的实时处理，实时提供高精度目标指示，有效支撑太空任务，成为当前面临的最紧迫问题。
通常，空间目标精密轨道计算方法包括批处理法和序贯处理法［7-10］。批处理法主要是利用空间目标监视网探测的大量观测数据，以轨道初值为基础，应用最小二乘法获得轨道改进，确定精确的历元状态矢量。文献［11］采用批处理法实现了空间目标精密定轨；文献［12］采用基于天地基观测数据的联合定轨策略，可以较好地解决轨道确定中的亏秩问题。文献［13］论述了批处理精密定轨的数据处理流程和定轨算法，并采用实测数据对处理流程和算法进行验证。然而，上述方法属于事后处理，对于低轨目标往往需要积累三天及以上的测量数据才能实现高精度定轨，难以满足太空态势实时感知任务的时效要求。
序贯处理［14-18］主要是利用滤波方法递推改进状态矢量，实时性较强。文献［15］讨论了如何已知消除观测异常对滤波的影响。文献［16］讨论了GEO 目标实时导航问题。文献［17］比较了三种不同的滤波算法在估算空间目标参数中的应用。文献［19］采用联合EKF 和EKPF 方法解决了空间目标的实时位姿滤波问题。但是，上述的空间目标跟踪滤波算法仅支持单弧段，除单弧段滤波精度无法达到应用要求外，还难以解决空间目标观测过程中的多装备、多弧段的滤波协方差传播问题。
为此，本文提出了基于高精度空间目标轨道模型和空间目标轨道预报误差协方差传播理论的不敏卡尔曼滤波（UKF）方法。利用高精度轨道模型在进行滤波计算的同时还需定量分析初始状态误差和模型误差传播情况，计算误差协方差传播趋势。采用这种方法，随着多部装备接力探测以及多弧段探测数据的积累，可以逐步提高实时定轨精度。
本文以单/多雷达探测数据为例，详细介绍了多装备数据融合并进行UKF 实时滤波定轨的方法。文中采用Monte-Carlo 仿真数据验证，该方法可以快速收敛，实时性高，稳定性好，积累三圈数据后位置精度即可达百米级，速度精度可达分米级。
1 高精度实时目标指示算法
高精度实时目标指示算法采用基于高精度空间目标轨道模型和空间目标轨道预报误差协方差传播理论的不敏卡尔曼（UKF）滤波。首先，建立精确的空间目标力学模型，摄动力包括50 阶地球引力场、海潮、大气阻力、固体潮、极移、太阳光压、太阳引力、月球引力；接着，对多雷达数据进行UKF滤波。滤波首点无需星历等先验信息，可根据稳定跟踪后的前两点数据求出首点坐标，再针对各装备采用对应的测量误差，遇到跨弧段问题，则计算轨道预报误差的协方差，解决跨弧段时误差协方差不匹配易发散的问题。
1.1 力学模型
传统的单弧段滤波通常采用J2 空间目标轨道模型，但J2 模型精度较差，仅支持分钟级轨道跟踪。在实际观察中，相邻圈次弧段间隔约2 h，采用J2 模型预报位置误差可达公里级，间隔时间越长，误差越大。以低轨激光测距卫星Envisat 的轨道预报为例，分别采用精密轨道模型和J2模型预报1天轨道，并与精密星历对比计算预报的位置误差。如图1所示，预报1 天后，精密轨道模型的预报误差约80 m，而J2 模型的预报误差达到约9 km。采用J2 模型在进行跨弧段跟踪滤波时由于预报误差较大可能导致滤波失败，为了确保滤波精度需要高精度空间目标轨道模型。
图1 J2模型与精密模型预报1天位置误差图
空间目标在运行过程中受到大量摄动因素的影响［7］，如地球引力、日月引力、大气阻尼、地球粘弹性体潮汐等，运动规律异常复杂。这些摄动力归为两类：保守力和非保守力。保守力包括地球中心引力、地球非球形引力、日月等三体引力、地球固体潮和海潮等，它们的大小只与空间目标的位置有关，与目标的速度及表面特征无关，因此，可以使用“位函数”的形式进行描述。非保守力包括大气阻力、太阳光压和地球辐射压等，非保守力不仅与目标的位置相关，还与其速度、几何形状以及表面特性存在密切关系，不能使用“位函数”来表达，只能使用力模型的微分形式来表示。
在惯性系统中，空间目标的动力学方程可写为
式中，a0 为地球引力引起的加速度，aε 为除地球引力加速度外其他摄动加速度之和，即
其中aNS 为地球非球型摄动加速度，aSL为日月引力加速度，aA 为大气阻力引力摄动加速度，aS 为太阳光压摄动加速度，aTD 为潮汐力摄动加速度，aSD 为固体潮摄动加速度。通常，对于低轨目标而言，只需要考虑大气阻力即可；对于高轨目标则只需考虑太阳光压即可。
本文采用的力学模型和参数见表1。
表1 力学模型和参数表
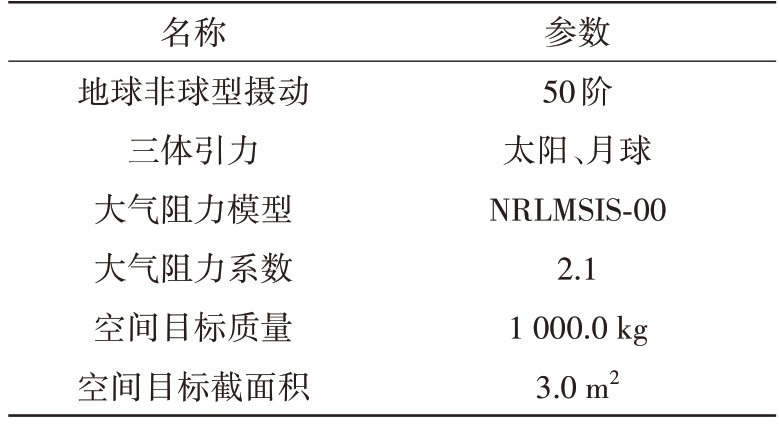
名称地球非球型摄动三体引力大气阻力模型大气阻力系数空间目标质量空间目标截面积参数50阶太阳、月球NRLMSIS-00 2.1 1 000.0 kg 3.0 m2
1.2 不敏卡尔曼滤波（UKF）与轨道预报误差协方差传播
结合空间目标运动非线性的特点，以及各雷达装备的跟踪特性，实时定轨采用不敏卡尔曼滤波法（UKF）。UKF引入具有统计学特性的采样点，利用不敏变换对状态和误差协方差进行估计和更新，可以克服EKF 难以解决的非线性因子问题。UKF 经非线性系统传递后，后验均值与方差均能精确到二阶。
其中相应的状态更新协方差为
通常，同一观测弧段中相邻点间隔时间通常为秒级，协方差可以采用式（3）；而相邻圈次弧段间隔约2 h，协方差已扩散，采用式（3）计算的协方差易导致滤波收敛变慢甚至发散。因此，在处理跨弧段问题时不能简单地使用式（1），需要进一步考虑误差协方差传播。
空间目标轨道预报误差由两部分组成［19-20］：初始误差和模型误差。初始历元时刻的目标状态矢量可以通过对各类测量数据（雷达、光学、GPS 等）处理后根据轨道确定算法获得。由于测量数据有误差，这一状态矢量必然带有误差，即初始状态误差。在进行轨道预报时，初始误差会随着轨道模型的外推而发散，其传播特性和趋势因轨道类型的不同而不同。轨道均值和协方差的预报，可以得到一个误差管道，轨道真值以很高的概率在此管道之内。
其中，轨道协方差定义了一个沿均值轨道状态分布的等概率密度的6维超椭球（考虑位置和速度）或3 维椭球（仅考虑位置），且随时间的外推而发散。初始协方差矩阵可表述为
式中：B为误差方程矩阵；W为观测值权阵，为对角矩阵；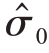
为验后观测标准差，即为
为定轨观测值残差；n 为参与定轨解算观测值个数；t为待估计参数的个数。
而基于线性模型的轨道误差传播表达为
式中，Φ(t,t0)表示初始历元t0 时刻状态的微小变化所导致的其后历元t 时刻状态的变化。实验中，Φ(t,t0)通过数值轨道理论，利用Cowell 积分器并顾及作用在碎片上的所有摄动力计算得到。
2 仿真实验
2.1 仿真场景
采用激光测距卫星Envisat 的精密轨道数据模拟空间目标探测弧段。Envisat 为近圆轨道，其近地点高度764 km，远地点高度766 km。共设置3部地基雷达，雷达参数如表2所示。
表2 装备测量误差表
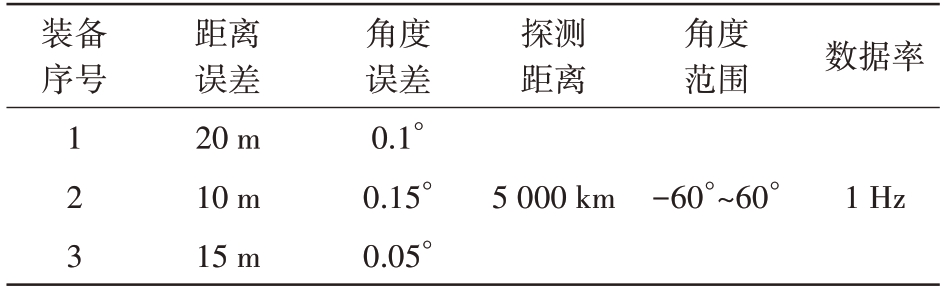
装备序号探测距离角度范围数据率123距离误差20 m 10 m 15 m角度误差0.1°0.15°0.05°5 000 km-60°～60°1 Hz
仿真共设置3个不同场景，如图2和表3所示。
表3 仿真场景表
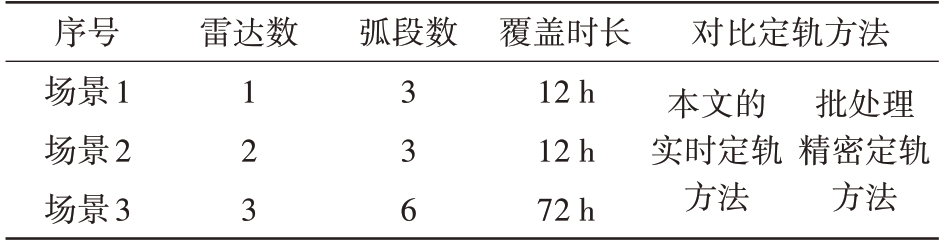
序号场景1场景2场景3雷达数弧段数123 336覆盖时长12 h 12 h 72 h对比定轨方法本文的实时定轨方法批处理精密定轨方法
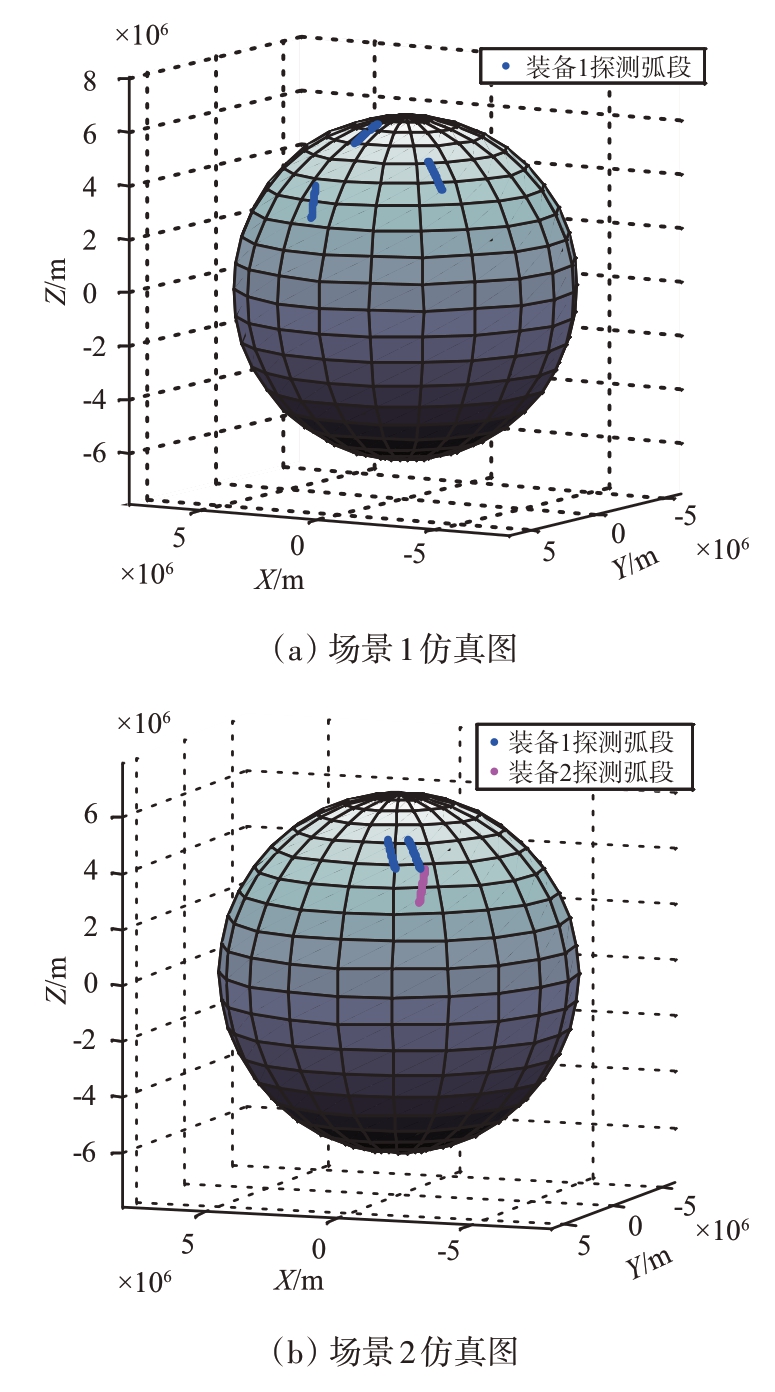
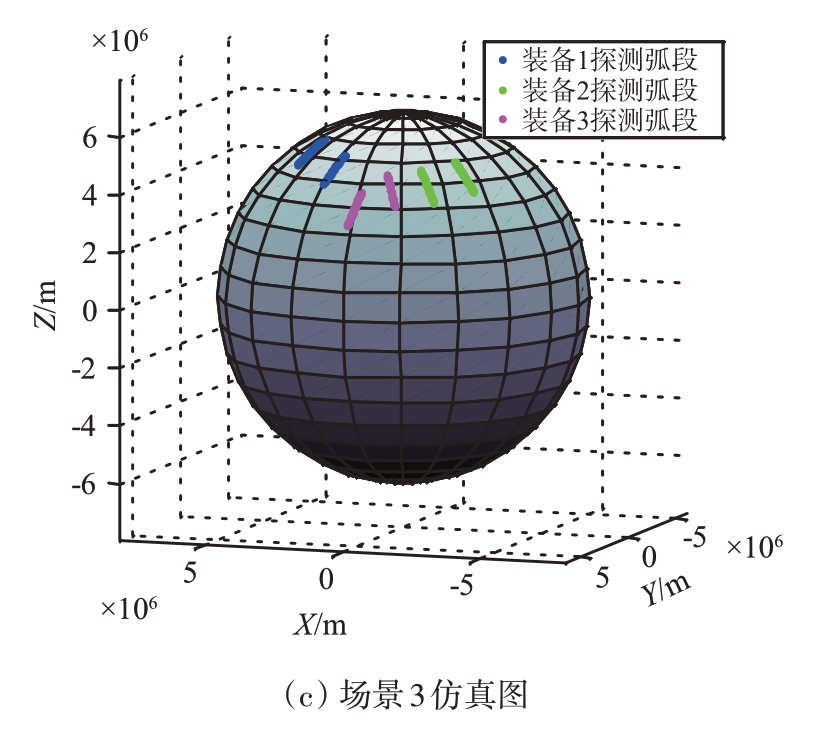
图2 装备仿真探测轨迹图
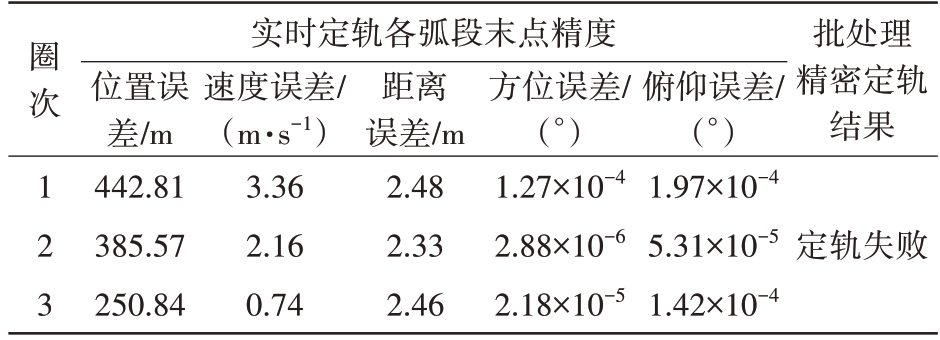
试验中，采用100次Monte-Carlo模拟产生随机数作为随机误差。实时定轨完成后再分别统计各滤波结果的位置、速度的均方根误差，如式（6）:
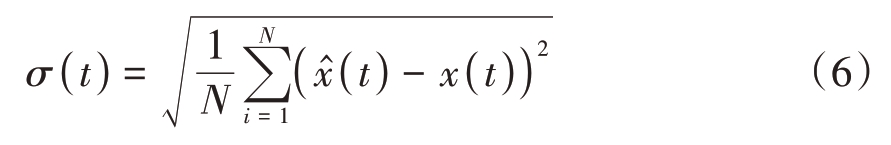
式中，N为总试验次数。
2.2 仿真结果分析
分别统计3个仿真场景的实时定轨结果。
（a）场景1
场景1 为1 部装备在12 h 内探测同一目标获得3 个弧段的实时定轨统计结果，如图3所示。实时定轨很快收敛，且随着圈次的累积，定轨精度不断提升。如表4所示，经过1 圈实时定轨，距离误差可达到2.48 m，方位和俯仰误差均小于0.0001°；3 圈实时定轨后，距离误差均方差达到2.46 m，角度均方差小于1×10-4，位置均方差250.84 m，速度均方差0.74 m/s。且跨弧段跟踪时，实时定轨依然保持收敛。
表4 场景1两种定轨方法结果对比表
圈次123实时定轨各弧段末点精度位置误差/m 442.81 385.57 250.84速度误差/（m·s-1）3.36 2.16 0.74距离误差/m 2.48 2.33 2.46方位误差/（°）1.27×10-4 2.88×10-6 2.18×10-5俯仰误差/（°）1.97×10-4 5.31×10-5 1.42×10-4批处理精密定轨结果定轨失败
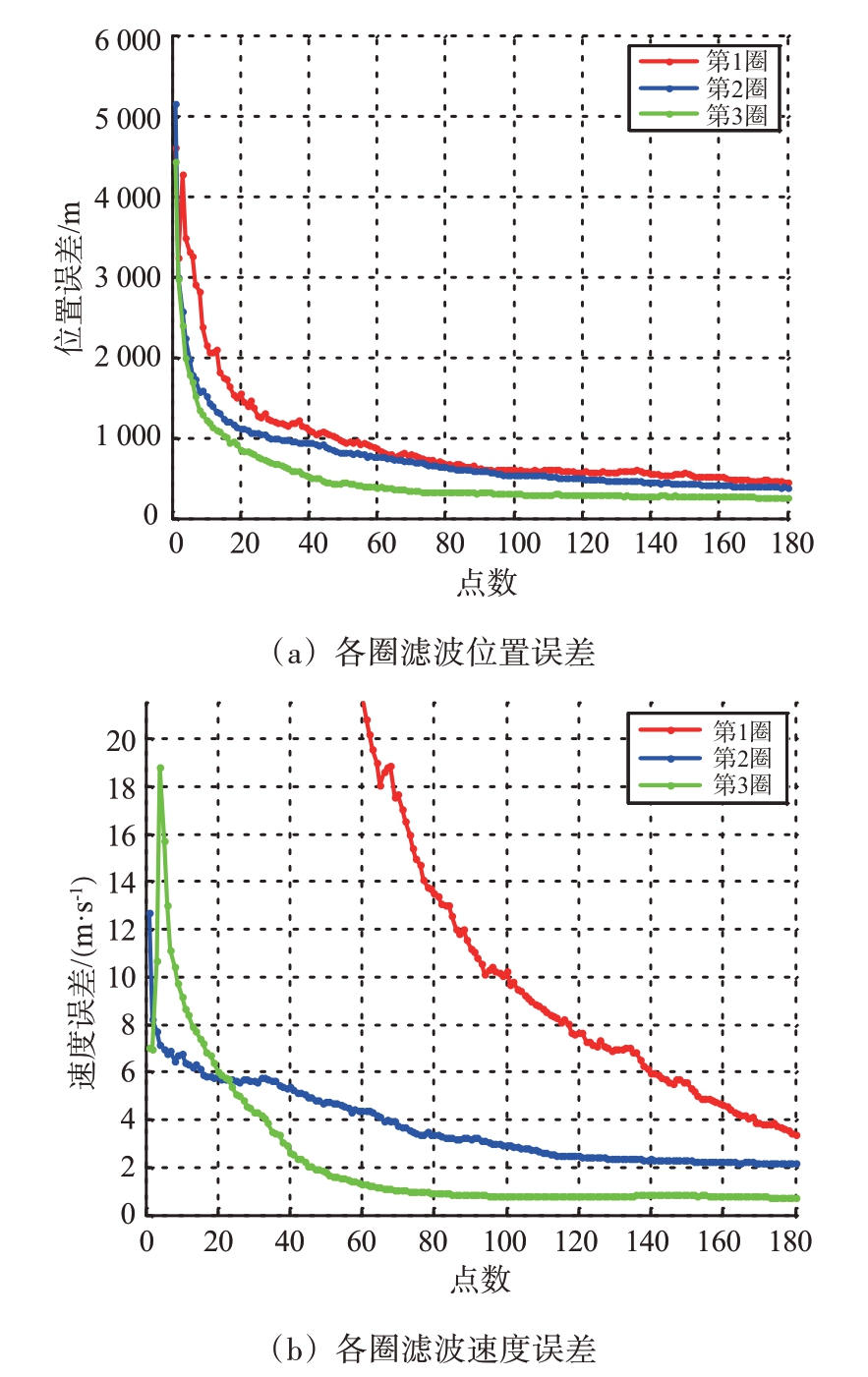
图3 场景1实时定轨各圈收敛图
相应地，对场景1 进行批处理定轨，但由于弧段仅有3条，且分布在12 h以内，批处理定轨失败，难以支持高精度实时目标指示任务。
（b）场景2
场景2 为2 部装备在12 h 内探测同一目标获得3 个弧段的实时定轨统计结果，结果如图4和表5所示。第1 圈结束时，实时定轨距离误差已收敛至2.82 m，角度误差皆小于10-4，且随着圈次的累积，实时定轨精度不断提升。经过3 圈的计算，距离误差均方差已经达到2.39 m，角度均方差小于0.5×10-4，位置均方差283.47 m，速度均方差1.50 m/s。且跨弧段跟踪时，实时定轨依然保持收敛。相应地，采用同样的初轨和探测弧段进行批处理定轨，但由于弧段仅有3条，且分布在12 h以内，批处理精密定轨失败，难以支持高精度实时目标指示任务。
表5 场景2两种定轨方法结果对比表
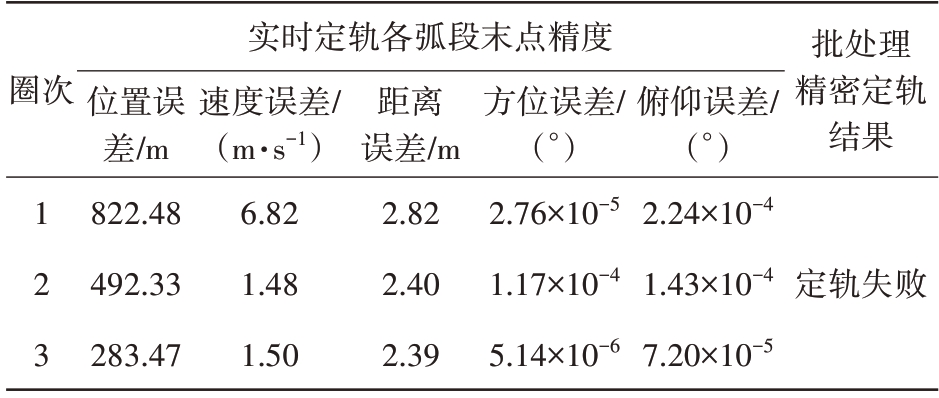
实时定轨各弧段末点精度圈次批处理精密定轨结果123位置误差/m 822.48 492.33 283.47速度误差/（m·s-1）6.82 1.48 1.50距离误差/m 2.82 2.40 2.39方位误差/（°）2.76×10-5 1.17×10-4 5.14×10-6俯仰误差/（°）2.24×10-4 1.43×10-4 7.20×10-5定轨失败
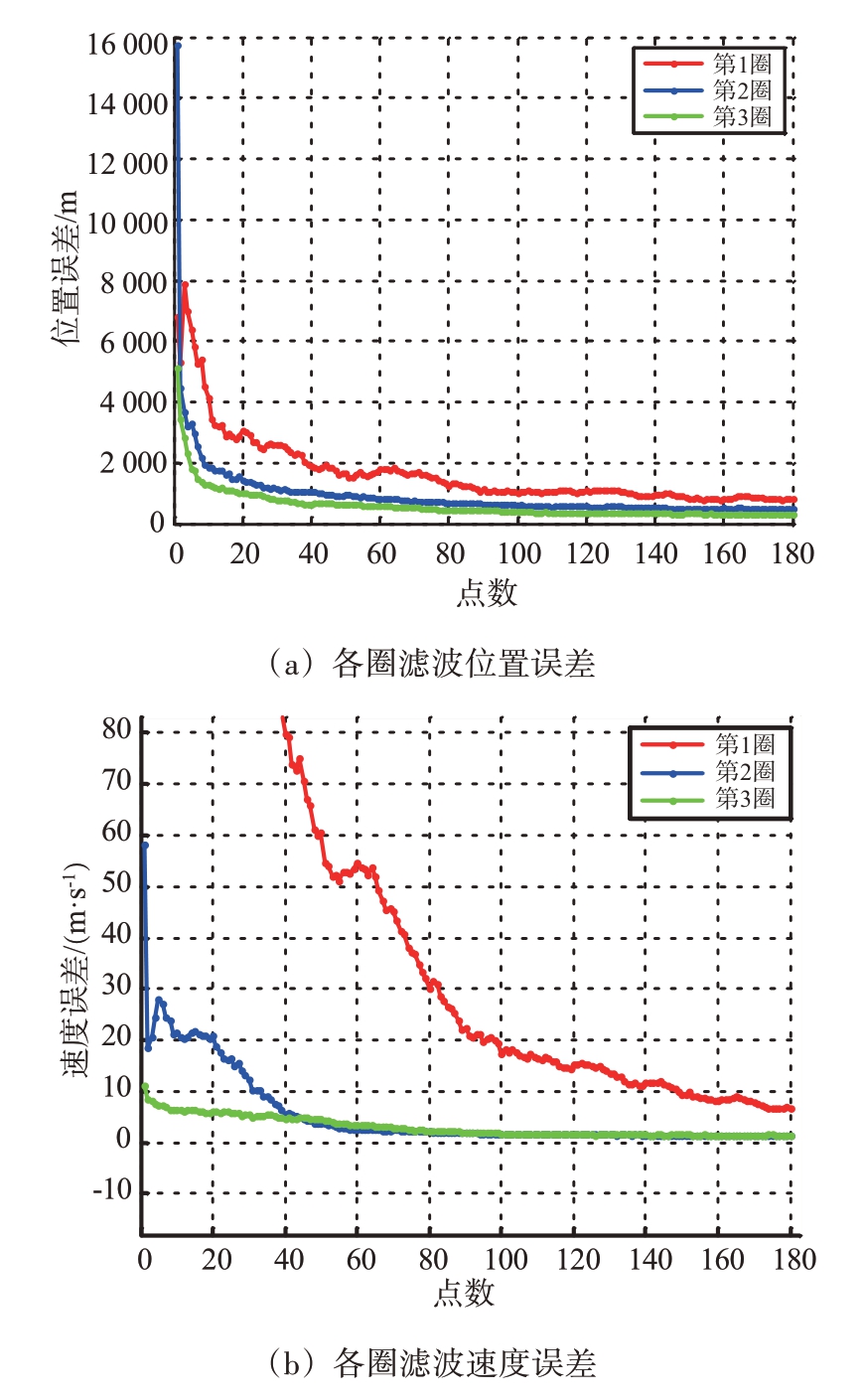
图4 场景2实时定轨各圈收敛图
（c）场景3
下面讨论3 部装备连续3 天观测同一目标，共6 个弧段，每天一升一降的情况。采用实时定轨技术，其定轨结果如图5所示。各圈次末点收敛统计结果如表6所示，第1 圈结束时，距离误差已达到3.09 m，角度误差皆小于10-4，且随着圈次的累积，滤波精度不断提升。经过6圈的滤波，距离滤波均方差已经达到2.10 m，角度均方差小于10-5，位置均方差96.38 m，速度均方差0.49 m/s。且跨弧段跟踪时，滤波依然保持收敛。
表6 场景3实时定轨各弧段末点精度
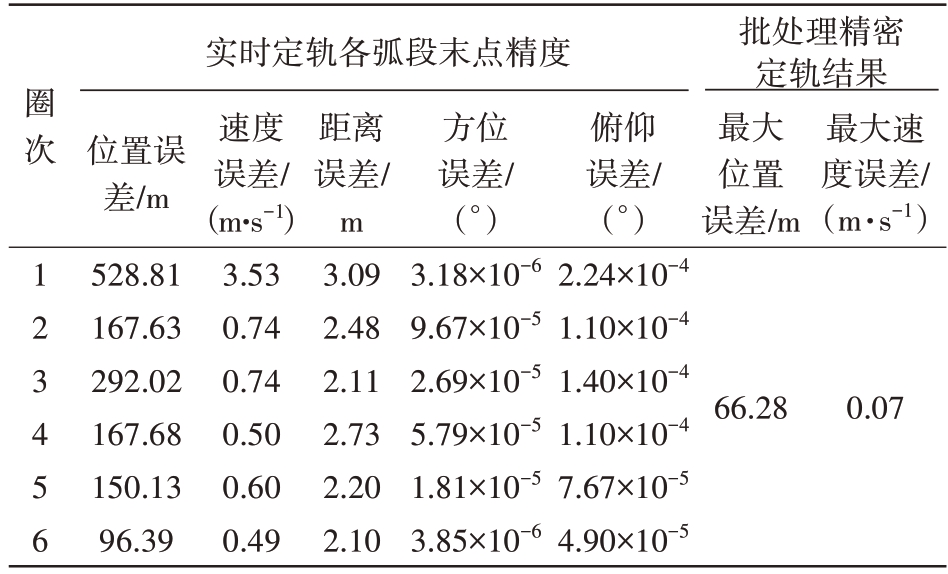
实时定轨各弧段末点精度圈次123456批处理精密定轨结果位置误差/m 528.81 167.63 292.02 167.68 150.13 96.39速度误差/（m·s-1）3.53 0.74 0.74 0.50 0.60 0.49距离误差/m 3.09 2.48 2.11 2.73 2.20 2.10方位误差/（°）3.18×10-6 9.67×10-5 2.69×10-5 5.79×10-5 1.81×10-5 3.85×10-6俯仰误差/（°）2.24×10-4 1.10×10-4 1.40×10-4 1.10×10-4 7.67×10-5 4.90×10-5最大位置误差/m最大速度误差/（m·s-1）66.28 0.07
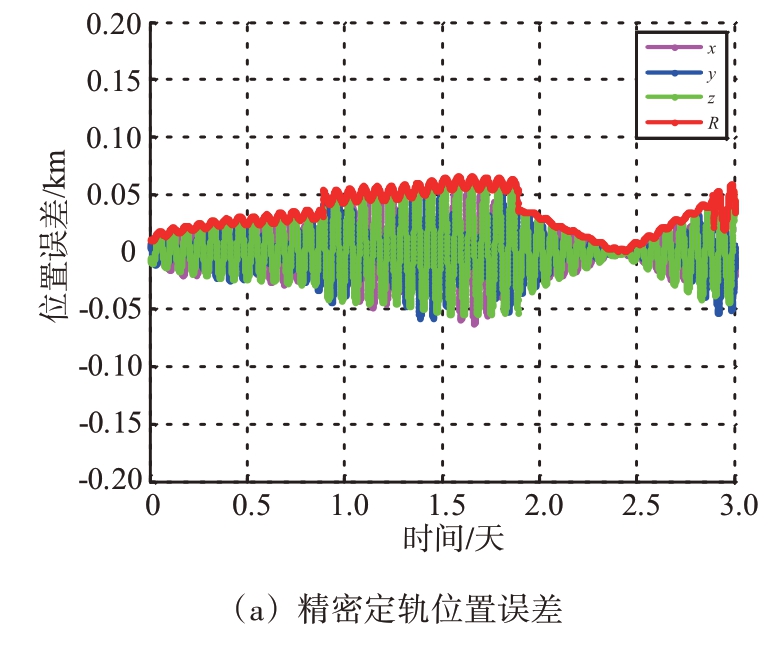
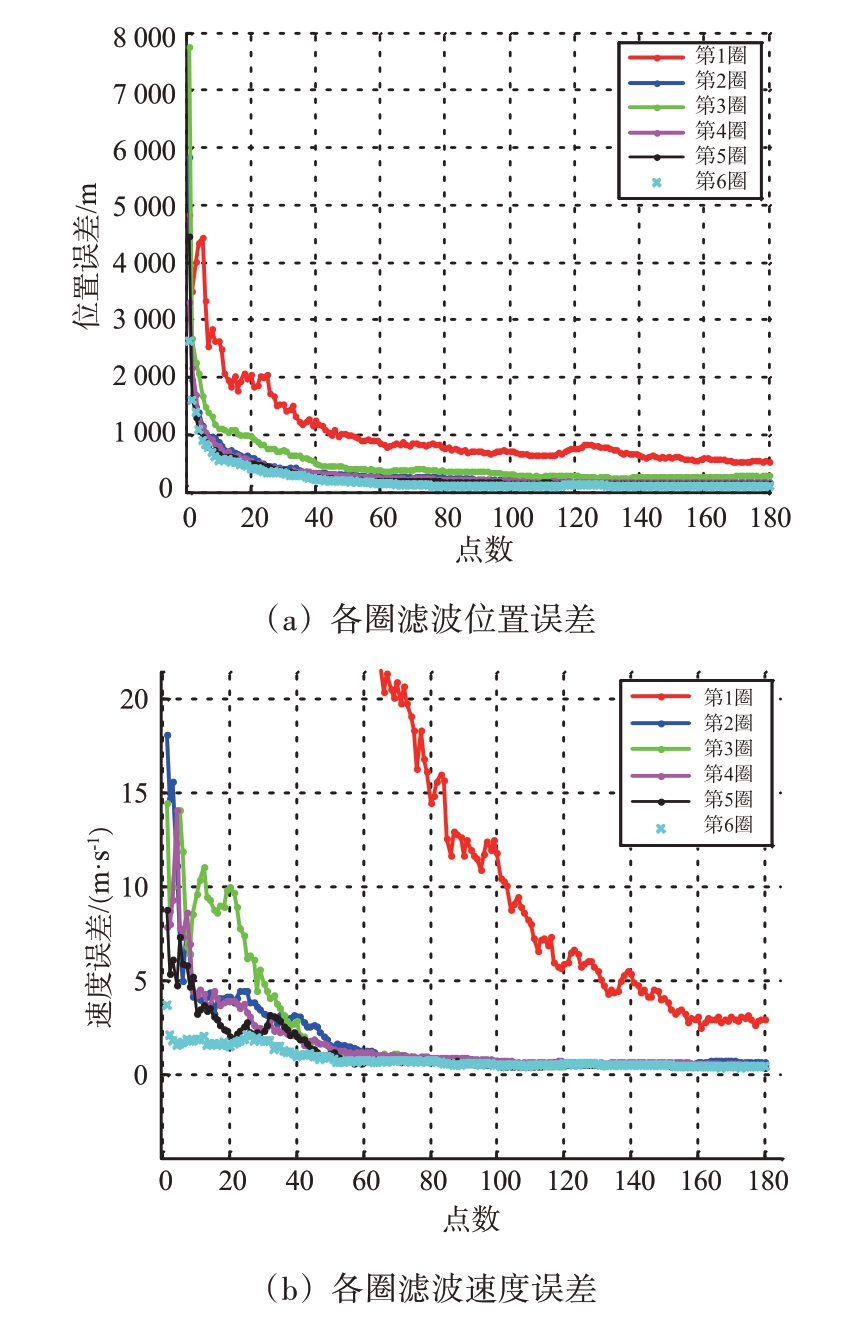
图5 场景3实时定轨各圈收敛图
针对场景3使用批处理法进行精密定轨，对比精密定轨结果如图6所示。
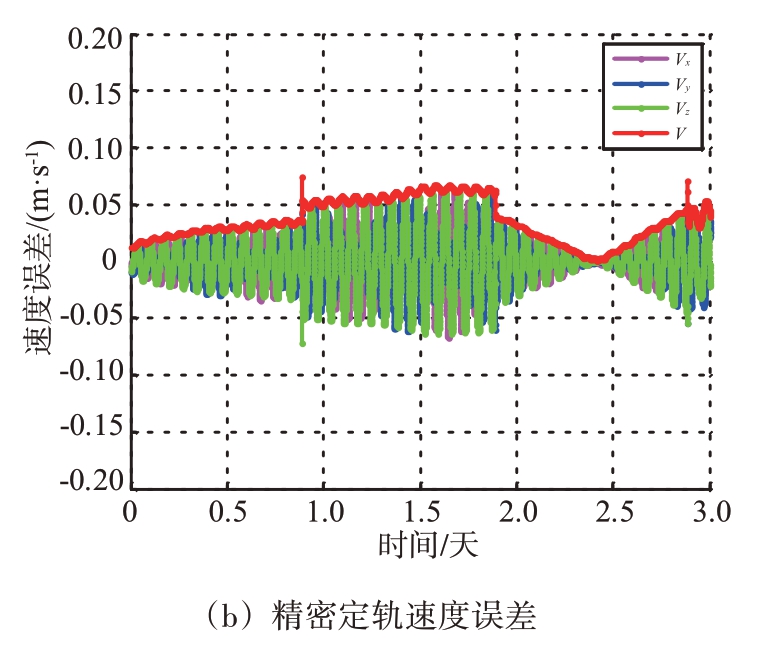
图6 3站探测数据精密定轨误差图
通过统计可知，精密定轨3 天最大位置误差66.28 m，最大速度误差0.07 m/s，且精度在定轨时间区间内较为均衡。但需要说明的是，精密定轨在计算时受初轨精度影响较大，初轨精度差易降低计算速度甚至导致计算失败。而实时滤波只需采用初始几点即可计算初轨坐标，虽然在每圈弧段初始时误差较大，位置误差可达到公里级，但每圈次跟踪60 点后滤波就已收敛，且通过多弧段滤波不断积累末点能够达到与精密定轨相同的精度量级。因此，对于缺少轨道信息的目标，多天测量后实时滤波在一定程度上可以替代精密定轨。
此外，从文中各仿真结果还可以看出，单弧段滤波的末点精度较差，位置误差可达数百米至公里级，而经过多弧段滤波积累可以显著提升目标指示精度。
3 结束语
面向特定的空间目标，尤其是缺少编目信息或编目信息精度较差的空间目标，完全依赖事后处理会影响雷达监视系统的实战能力。如何高效利用多装备探测数据，实现探测数据的实时处理，实时提供高精度目标指示，是太空态势监视领域亟待解决的问题。高精度实时目标定轨算法采用基于高精度空间目标轨道模型和空间目标轨道预报误差协方差传播理论的不敏卡尔曼（UKF）滤波，该方法有以下优势：1）无需初轨信息，简便，稳定性好，实时性强，可以用于单站测量，也可用于组网测量；2）优于传统滤波算法，该方法可以处理多装备多弧段滤波，实现精度提升；3）该方法可以处理弧段分布时间范围小于1 天的定轨场景，3 圈后位置精度可达到百米级，速度精度可达到分米级；对于时间跨度长于1天的场景，其最末点精度可达到与精密定轨相同的误差量级。总之，该实时定轨方法在实际工程中具有很好的应用前景。
［1］刘增文，张政川.国外地基空间目标监视雷达装备技术发展及其启示［J］.现代雷达，2022，44（6）:87-92.
［2］黄晓斌，张燕，肖锐，等.空间目标的雷达定轨实时识别问题研究［J］.雷达科学与技术，2021，19（1）:63-68.
［3］罗震龙，宋嘉政，褚福勇，等.基于SLR 数据的雷达探测精度分析方法［J］.雷达科学与技术，2021，19（6）:704-708.
［4］冯亚欣.基于长短期记忆的雷达目标数据处理方法研究［D］.哈尔滨：哈尔滨工业大学，2020.
［5］郭宇华，夏正欢，张涛，等.空间目标小型相控阵雷达探测技术［J］.航天器环境工程，2021，38（4）:446-452.
［6］周琳，刁伟峰，王祎.基于可观性分析的高精度空间目标跟踪方法［J］.雷达科学与技术，2021，19（5）:486-490.
［7］VERIS A I.Practical Astrodynamics［M］.Rome:Springer,2018.
［8］VETTER J.Fifty Years of Orbit Determination: Development of Modern Astrodynamics Methods［J］.Johns Hopkins APL Technical Digest,2007,27（3）:239-252.
［9］VALLADO D A.Fundamentals of Astrodynamics and Applications［M］.Hawthorne,CA:Microcosm Press,2013.
［10］ZHANG Qiang,GUO Xiang,QU Lizhong,et al.Precise Orbit Determination of FY-3C with Calibration of Orbit Biases in BeiDou GEO Satellites［J］.Remote Sensing,2018.10（3）:382-399.
［11］刘涵月.基于随机森林的低轨空间目标大气阻力系数确定研究［D］.武汉：武汉大学，2021.
［12］赵博，周庆勇，张旺，等.基于天地基测控的空间目标联合定轨研究［J］.光电工程，2011，38（11）:57-62.
［13］程昊文.航天器轨道理论在空间目标编目管理中的应用［D］.南京：南京大学，2012.
［14］MONTENBRUCK O,GILL E.Satellite Orbits-Models,Methods and Applications［M］.Berlin:Springer,2002.
［15］任夏，李铸洋，丁阳.抗差自适应滤波算法在实时定轨中的应用［J］.导航定位学报，2016，4（2）:26-28.
［16］任家栋.地球静止轨道目标跟踪与悬停控制研究［D］.哈尔滨：哈尔滨工业大学，2020.
［17］LI Lingwei,GUO Yiming,WU Xiwei,et al.Comparison of Three Filters Space Objects Parameters Estimation via Astrometric and Photometric Data［C］∥2021 40th Chinese Control Conference，Shanghai,China:［s.n.］,2021:1243-1248.
［18］金泽明，汪铃，刘柯，等.联合EKF和EKPF的空间非合作目标单目位姿估计［J］.宇航学报，2021，42（7）：907-916.
［19］韩蕾.低轨空间监视的天地协同轨道确定与误差分析［D］.长沙：国防科技大学，2008.
［20］闫瑞东，王荣兰，刘四清，等.空间目标碰撞预警的协方差计算与应用［J］.空间科学学报，2014，34（4）:441-448.
