0 引 言
随着电子信息技术的不断发展，雷达作为目标探测的主要手段已经被广泛应用于军事和民用领域，但同时雷达所面临的各种干扰则会严重降低雷达的性能［1］。基于数字射频存储器的欺骗干扰技术能够对雷达发射信号进行接收、加入延时、放大和转发，产生虚假目标信号以干扰雷达对真实目标的识别［2-3］。特别地，当距离欺骗目标位于雷达接收天线主瓣内时，雷达将面临主瓣欺骗干扰，传统的相控阵雷达较难实现对主瓣欺骗干扰的抑制［4］。
频控阵（Frequency Diverse Array,FDA）雷达因其相邻阵元的载波频率间存在一个频率偏移量，所以其发射方向图具有距离-角度依赖特性。由于在距离维上具有额外的自由度［5］，所以目前频控阵在距离相关的欺骗干扰抑制［6-8］、无线通信［9］、合成孔径成像［10］、杂波抑制［11］等多个方面得到了较多的应用。其中，文献［7］提出了一种主瓣内距离欺骗目标鉴别方法：雷达使用频控阵模式发射信号、相控阵模式接收信号，根据回波信号中包含目标个数的不同以实现对真实目标、干扰机、假目标等目标类型的鉴别。本文针对上述方法存在的不足，使用了一种干扰置零方法，对文献［7］所述的方法进行了改进和优化。
针对在均匀线阵结构下使用线性频偏的频控阵发射方向图存在的距离-角度耦合问题［3］，本文通过遗传算法优化得到一组非线性频偏，使用该组频偏设计的频控阵发射方向图不仅无距离-角度耦合且具有更窄的主瓣波束宽度和更低的旁瓣功率。
本文将干扰置零方法与基于遗传算法的频控阵发射方向图优化方法相结合，应用于距离假目标的鉴别。
1 频控阵阵列及发射方向图
常见的频控阵发射阵列结构如图1所示，其为具有等阵元间距的均匀线阵（Uniform Linear Array,ULA）。假设频控阵发射阵列共有N 个阵元，相邻阵元之间的间距均为d。设第一个阵元（参考阵元）的载波频率为f0，则第n个阵元的载频fn可表示为
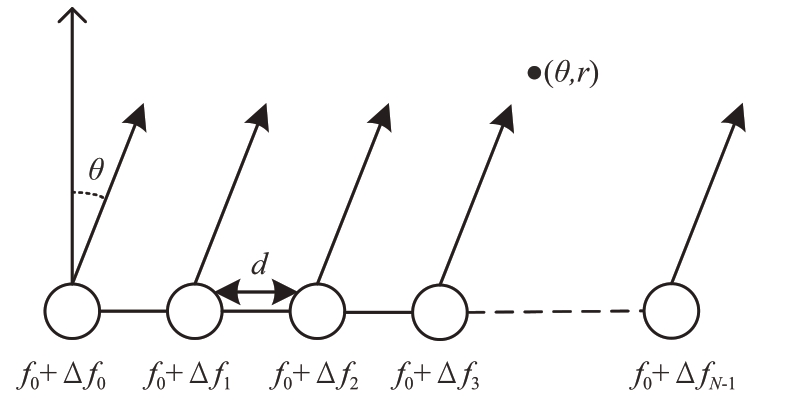
图1 频控阵阵列结构示意图
式中，△fn 为第n 个阵元的载频与参考阵元载频之间的频率偏移量，且△fn 远小于f0。一般△fn 满足线性变化，即
在图1所示的阵列结构中，记第n 个阵元的发射信号为
设空间中远场区位置存在一个目标，该目标与参考阵元的距离为r、与阵列法线的夹角为θ。此处为简化分析，不考虑发射信号在空间中传播时的衰减，得到N 个阵元的发射信号在(θ,r)位置处累加而得的和信号为
式中，c 表示信号在空间中的传播速度，rn 表示第n个阵元与目标的距离，有
将式（5）代入式（4），可将式（4）改写为
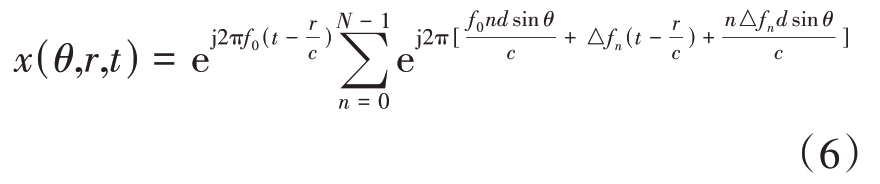
由式（6）得到频控阵阵列因子为
由于△fn远小于f0，所以式（7）中
且
接近于0，故
项可忽略。经过改写后的频控阵阵列因子为
对上式进行取模平方，可得到频控阵发射方向图表达式为
当△fn=0 时，所有阵元的发射信号载波频率相同，此时式（9）为
式（10）即为相控阵发射方向图表达式，其只与角度θ 有关。而频控阵发射方向图不仅与角度有关，还与距离和时间有关。固定t=0时刻，设阵元数为8，阵元间距为半波长，载频f0=10 GHz，使用线性频偏即△fn满足式（2），其中△f=5 kHz，得到的频控阵发射方向图如图2所示，其波束形状为弯曲的“S”型，具有距离-角度依赖性；固定其他参数不变，令△fn=0，得到的相控阵发射方向图如图3所示，其波束指向仅与角度有关。
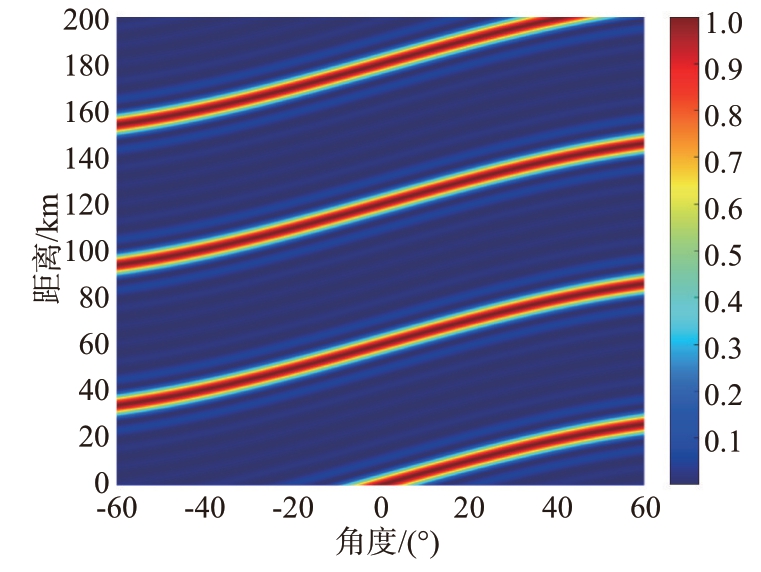
图2 频控阵发射方向图
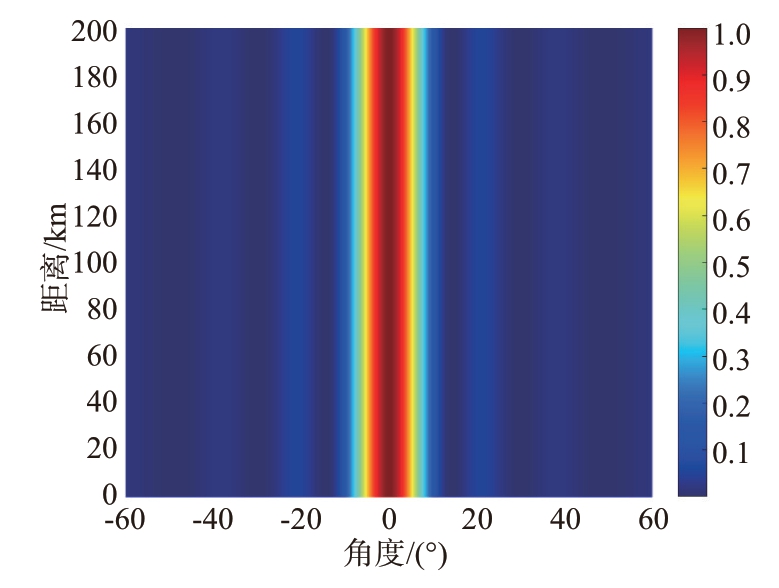
图3 相控阵发射方向图
2 频控阵发射方向图优化
如图2所示，当频控阵阵列每个阵元发射信号的频偏△fn 满足线性变化即式（2）时，其发射方向图存在多个波峰，目标的距离和角度可以存在多个对应解，即此时频控阵存在距离-角度耦合问题。该耦合问题能够造成目标的距离模糊。可以使用非线性变化的频偏如对数变化的频偏对频控阵发射方向图进行优化设计，以解决耦合问题［12］，即△fn满足
式中，△f为一定值频偏常量。
固定t=0时刻，阵元数为32，阵元间距为半波长，载频f0=10 GHz，目标位置为(20°,78 km)。△fn为对数变化即满足式（11），其中△f=30 kHz，得到的频控阵发射方向图如图4所示。使用对数变化的频偏时，发射方向图仅存在一个波峰，实现了解耦合的目的，但其主瓣宽度较宽，旁瓣功率较高。相比较于使用对数频偏，使用经过遗传算法优化得到的一组非线性频偏不仅能够实现解耦合的目的，同时也可以使发射方向图具有更窄的主瓣波束宽度和更低的旁瓣功率［13］。
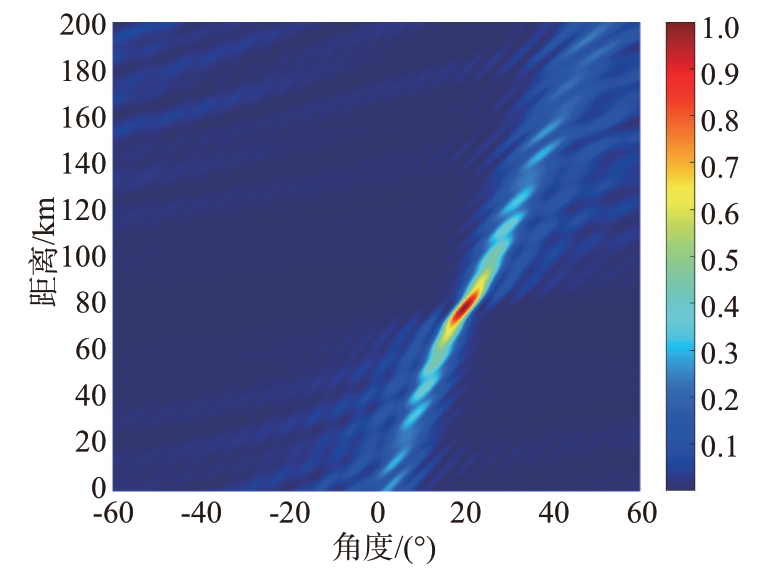
图4 基于对数频偏的频控阵发射方向图
使用遗传算法得到非线性频偏的流程如下：
a.划分空域。将期望频控阵波束主瓣照射的空间位置以及该位置周围的小范围区域作为目标区域，将空域中除目标区域以外的所有区域视为旁瓣区域。
b.初始化。将N 个阵元的N 个频偏所组成的变量χ=[△f0,△f1,…,△fN-1]作为个体，随机从[△fmin,△fmax]范围内利用二进制编码选择M 个个体作为初始种群P（0）。并设置最大遗传代数为G，初始种群代数g=0。
其中给定频偏范围[]△fmin,△fmax 是为了约束系统的带宽在一定的范围内，即系统带宽为B=△fmax-△fmin。
c.个体选择。记发射信号在旁瓣区域的能量和为
计算当前个体对应的
大小，并将
作为个体适应度函数值以对群体中的个体进行选择。本方法选取个体的准则为能够使
值最小的χ。
d.交叉、变异运算。对群体中经过步骤c后的个体的某些基因值进行交叉和或变异运算，以得到下一代种群。
e.终止算法。若当前种群代数g=G，则结束循环，得到当前最优解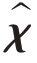
=[△f0,△f1,…,△fN-1]，否则继续步骤c。
使用经过遗传算法优化得到的一组频偏，阵元数为32，阵元间距为半波长，载频f0=10 GHz，目标位置(θ,r)=(20°,78 km)，固定t=0时刻，得到的频控阵发射方向图如图5所示。
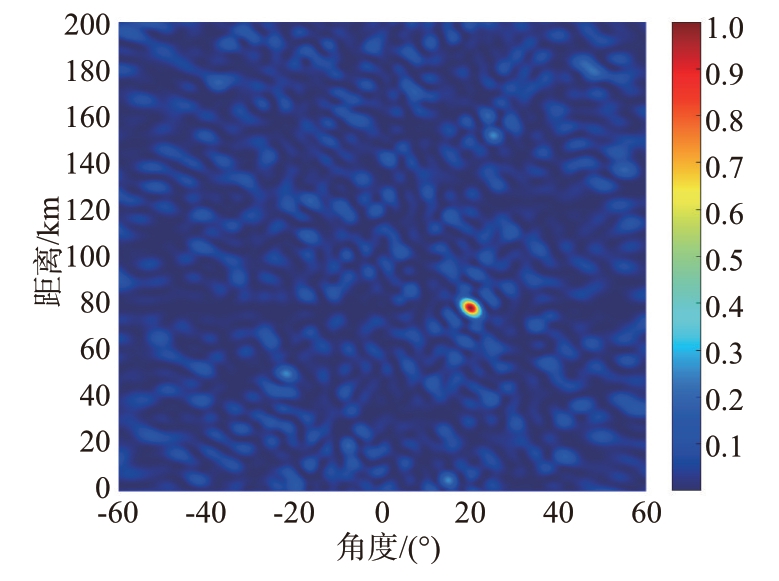
图5 基于遗传算法优化的频控阵发射方向图
图5与图4的参数对比结果如表1所示。使用经过遗传算法优化得到的频偏后，频控阵发射方向图波束主瓣的能量更加集中，同时方向图具有更窄的主瓣宽度和更低的旁瓣功率，具有更好的分辨率。所以本文接下来将使用经过遗传算法优化得到的频偏进行频控阵鉴别距离欺骗目标方法的研究。
表1 指向(20°,78 km)的频控阵发射方向图参数对比
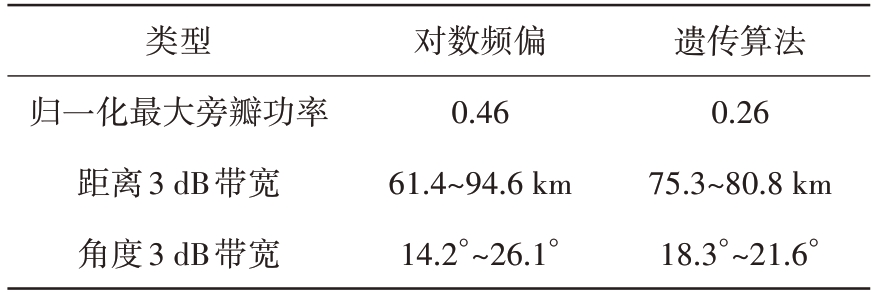
类型归一化最大旁瓣功率距离3 dB带宽角度3 dB带宽对数频偏0.46 61.4～94.6 km 14.2°～26.1°遗传算法0.26 75.3～80.8 km 18.3°～21.6°
3 干扰置零方法
一种常见距离欺骗目标干扰产生方式为空间中电子干扰机接收雷达的发射信号、加入延时、放大并转发，使雷达接收到该电子干扰机的转发信号后误认为该信号是空间中其他位置处目标的反射信号。特别地，如果电子干扰机与真实目标位于同一角度且电子干扰机转发形成的假目标也与真实目标位于同一角度，那么使用相控阵雷达将波束主瓣对准信号来向角度，对回波信号接收后雷达能够得到位于同一角度的多个目标的距离信息。但此时相控阵雷达无法区分何处目标为假目标，即受到了主瓣欺骗干扰。在这种情况下，能否准确鉴别假目标对雷达而言非常重要。
针对上述相控阵雷达无法鉴别主瓣内假目标的问题，文献［7］提出一种使用频控阵雷达鉴别假目标的方法：利用频控阵发射方向图的距离依赖性，依次将频控阵发射方向图的主瓣指向待鉴别目标位置处，再使用相控阵模式对回波信号进行接收。因为不同类型的目标的回波信号中含有的目标个数不同，所以可以根据回波信号中所含有的目标个数实现对不同位置处目标类型的鉴别。
但是在将波束主瓣指向待鉴别目标的位置处时其他位置的目标可能位于频控阵发射方向图较高旁瓣上，此时其他位置的目标仍能较好收到雷达发射信号，雷达仍能够收到其他位置目标的反射信号，受到其他位置目标信号的干扰。基于上述考虑，本文研究了一种干扰置零方法，使得在将频控阵发射方向图的主瓣对准需鉴别目标位置处时，其他目标位置处位于方向图的零陷上，避免了其他位置的目标仍能接收到雷达发射信号从而对雷达形成干扰的问题。本文的干扰置零方法如下：
为方便描述，假设在空间中同一角度的3个不同距离位置上分别存在真实目标、电子干扰机、假目标。经过相控阵雷达探测后得到其角度和距离大小分别为(θ0,r1)、(θ0,r2)、(θ0,r3)。由式（9）可知具有N个阵元的均匀线阵频控阵导向矢量为
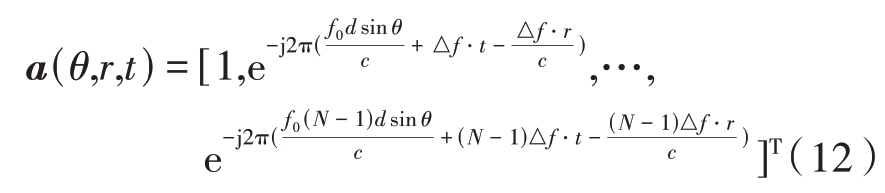
(θ0,r1)、(θ0,r2)、(θ0,r3)位置在频控阵模式下的导向矢量分别为
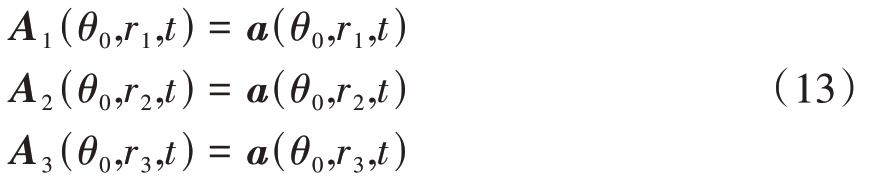
当有多个目标时同理。
若期望将频控阵波束主瓣指向(θ0,r1)的位置，在(θ0,r2)、(θ0,r3)的位置形成零陷，则首先构造需置零陷方向的方向矢量为
根据Aj构造其正交补空间为
之后将期望方向的导向矢量A1(θ0,r1,t)投影到该正交补空间，得到的结果为
将wout 作为权向量对频控阵各阵元的发射信号进行加权。经过加权后的频控阵发射方向图可以在将主瓣对准需鉴别目标位置处时使其他目标位置处位于方向图的零陷上。
将距离-角度二维空域按照距离维划分为G 个单元，按照角度维划分为H 个单元，即将整个空域共划分为GH 个单元。对于空间中第g个距离单元与第h个角度单元组成的空域，设其与阵列法线的夹角为θg、与参考阵元的距离为rh，则该处空域导向矢量为
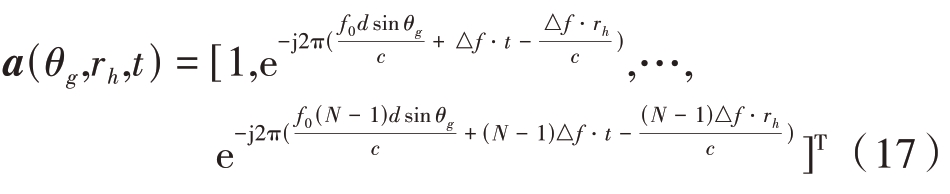
式中：g=1,2,…,G; h=1,2,…,H。
用式（16）的权向量对频控阵各阵元的发射信号进行加权后可得到频控阵发射方向图在第g 个距离单元与第h 个角度单元组成的空域的归一化幅度为
式中：g=1,2,…,G; h=1,2,…,H。
若期望将频控阵波束主瓣指向其他位置处并在其余目标位置处形成零陷时，同理。
4 仿真实验与分析
现仿真以下主瓣距离欺骗干扰场景：空间中(-10°,53 km)处存在一个真实目标，(-10°,93 km)处存在一个电子干扰机，该电子干扰机通过对雷达发射信号进行接收、延时、放大并转发，使雷达接收到该信号后误认为(-10°,133 km)处存在一个真实目标。首先使用相控阵雷达将发射波束和接收波束均指向-10°方向对回波信号进行接收，阵列为均匀线阵，阵元数为32，阵元间距为半波长，信号载频为10 GHz，得到的收发方向图如图6所示。此时3个目标均位于方向图波束主瓣上，所以雷达能够收到3 个目标的信号并得到3 个目标的角度和距离信息，但无法鉴别真假目标。
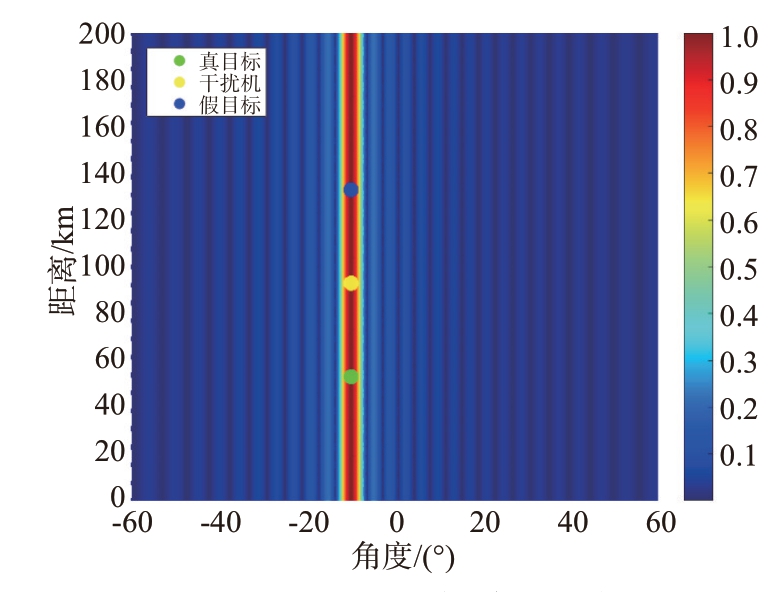
图6 指向-10°的相控阵收发方向图
4.1 将波束主瓣指向（-10°，53 km）
使用文献［7］的方法，首先将频控阵的发射波束主瓣指向(-10°,53 km)，将相控阵的接收波束主瓣指向-10°方向，阵列均为均匀线阵，阵元间距为半波长，信号载频10 GHz，频控阵各阵元发射信号的频偏为使用遗传算法优化得到的一组频偏，不使用本文的干扰置零方法，得到的雷达收发方向图如图7（a）所示。收发方向图上(-10°,93 km)处的归一化功率为0.033（即-14.81 dB），(-10°,133 km)处的归一化功率为0.077（即-11.14 dB）。在文献［7］方法的基础上，使用本文的干扰置零方法，阵列参数及信号参数同上，得到的收发方向图如图7（b）所示。收发方向图上(-10°,93 km)处的归一化功率为1.11×10-6（即-59.55 dB），(-10°,133 km)处的归一化功率为3.94×10-6（即-54.05 dB）。经过干扰置零后，(-10°,93 km)处的归一化功率下降了44.74 dB，(-10°,133 km)处的归一化功率下降了42.91 dB。
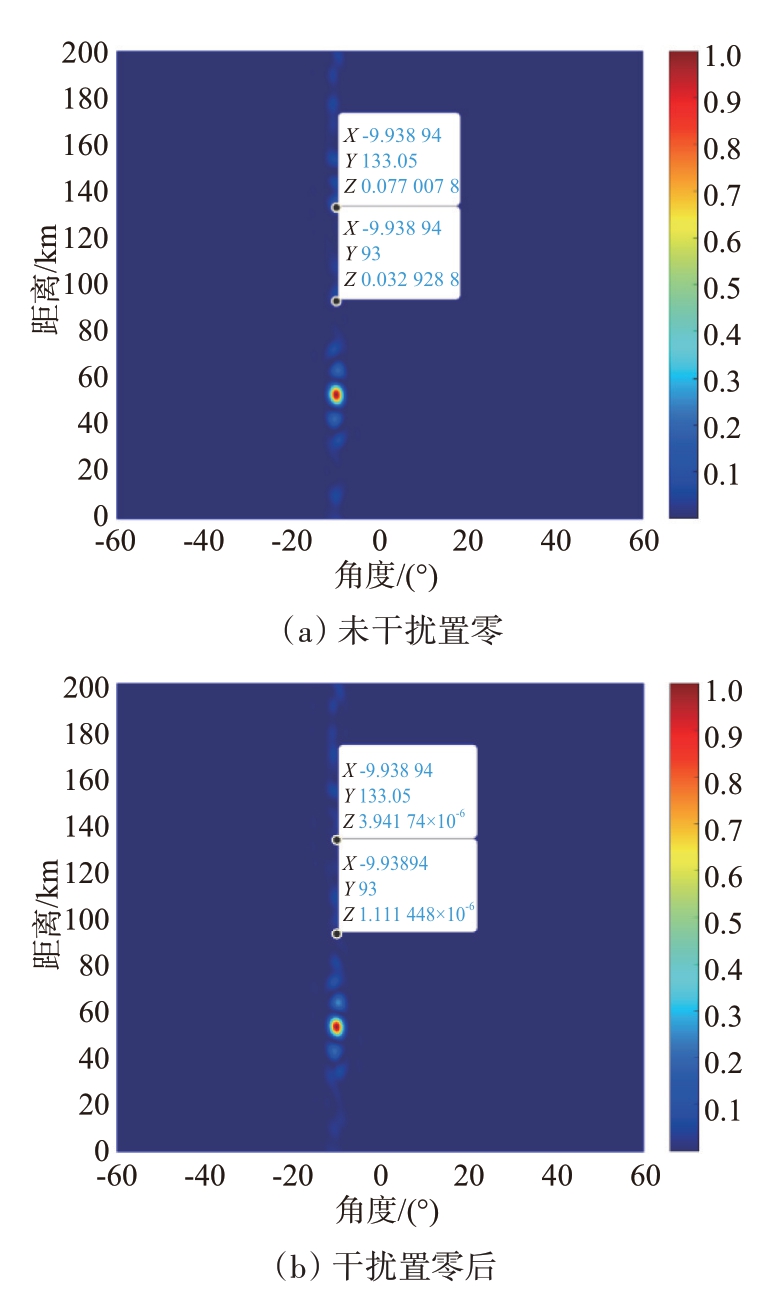
图7 指向(-10°,53 km)的频控阵收发方向图
使用了本文所述的干扰置零方法后，(-10°,93 km)位置和(-10°,133 km)位置就位于频控阵发射方向图的零陷上，此时能够有效避免电子干扰机若位于发射方向图较高旁瓣上仍能收到雷达发射信号并形成干扰的问题。在将波束主瓣对准真实目标位置时，雷达能够收到1 个目标的信号，即真实目标的反射信号。
4.2 将波束主瓣指向(-10°,93 km)
之后将频控阵发射波束主瓣对准(-10°,93 km)位置，不进行干扰置零，得到的收发方向图如图8（a）所示，(-10°,53 km)和(-10°,133 km)处的归一化功率均为0.034（即-14.69 dB）。干扰置零后得到的收发方向图如图8（b）所示，(-10°,53 km)处的归一化功率为2.94×10-6（即-55.32dB），（-10°，133km）处的归一化功率为5.86×10-6（即-52.32 dB）。经过干扰置零后，(-10°,53 km)处的归一化功率下降了40.63 dB，(-10°,133 km)处的归一化功率下降了37.63 dB。
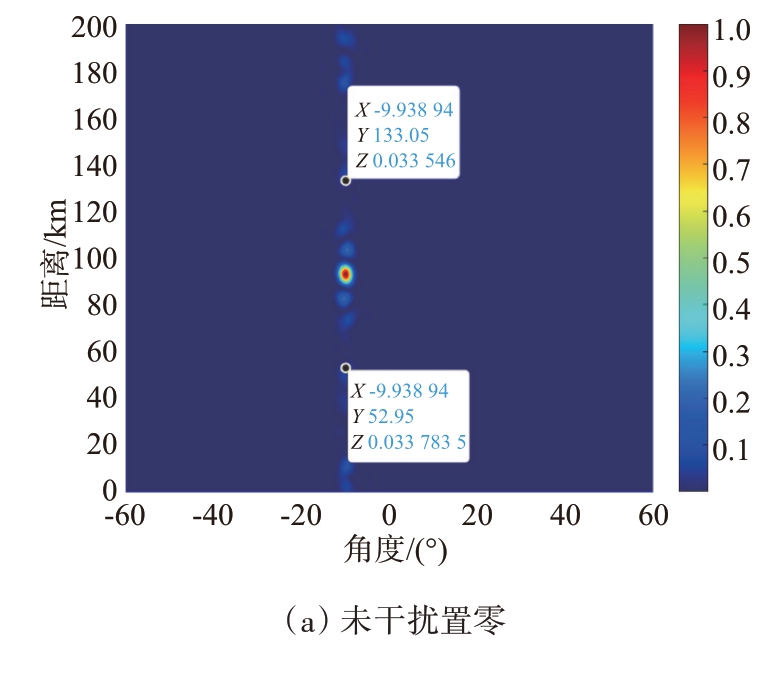
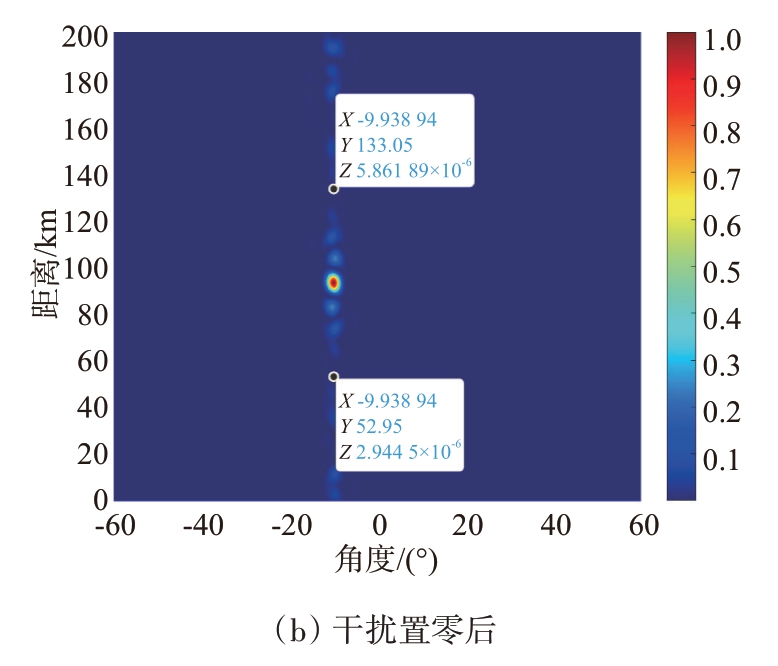
图8 指向(-10°,93 km)的频控阵收发方向图
干扰置零后，(-10°,53 km) 和(-10°,133 km)位置位于收发方向图的零陷上，有效避免了（-10°，53 km）处的真实目标若位于发射方向图较高旁瓣上时仍能较好收到雷达发射信号从而干扰雷达对(-10°,93 km)处目标的鉴别。将波束主瓣对准(-10°,93 km)时雷达能够收到2个目标信号，即电子干扰机的反射信号和电子干扰机产生的假目标信号。
4.3 将波束主瓣指向(-10°,133 km)
最后将频控阵发射波束主瓣对准（-10°，133 km），不进行干扰置零，得到的收发方向图如图9（a）所示，(-10°,53 km) 处的归一化功率为0.081（即-10.92 dB），(-10°,93 km)处的归一化功率为0.033（即-14.81 dB）。干扰置零后得到的收发方向图如图9（b）所示，(-10°,53 km)处的归一化功率为3.92×10-5（即-44.07 dB），(-10°,93 km)处的归一化功率为1.40×10-6（即-58.54 dB）。经过干扰置零后，(-10°,53 km)处的归一化功率下降了33.15 dB，(-10°,93 km)处的归一化功率下降了43.73 dB。
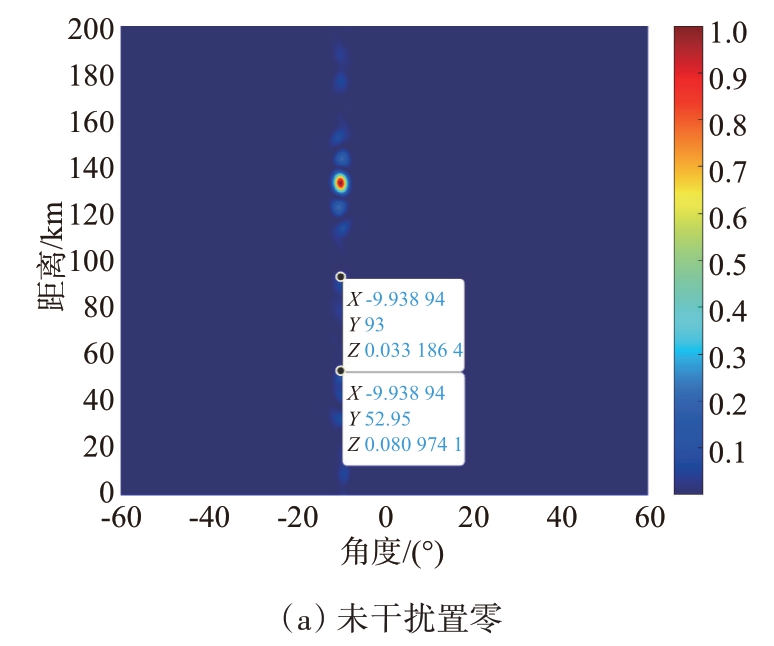
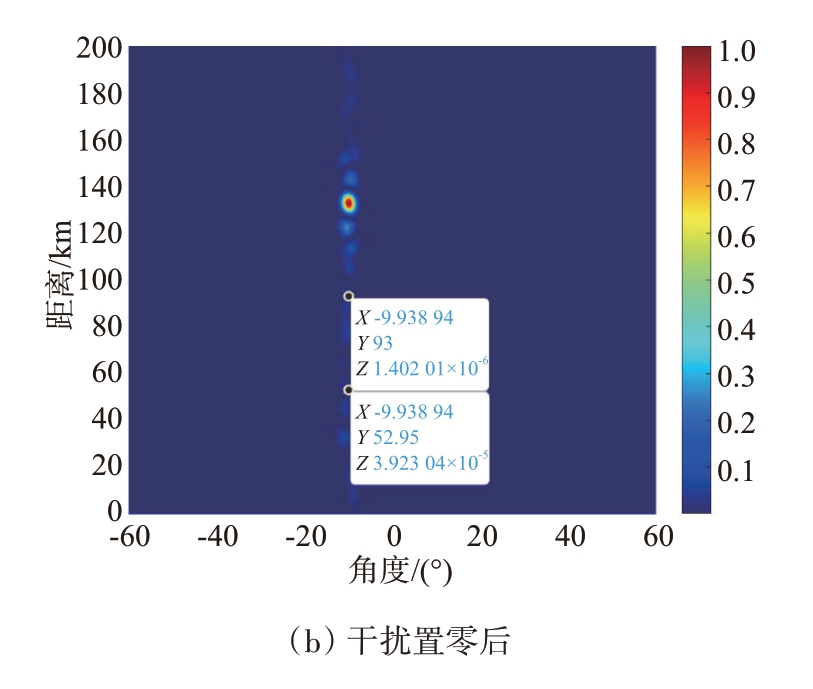
图9 指向(-10°,133 km)的频控阵收发方向图
干扰置零后，(-10°,53 km)和(-10°,93 km)处位于方向图的零陷上，有效避免了真实目标和电子干扰机处于方向图较高旁瓣上仍能较好收到雷达发射信号并对雷达鉴别(-10°,133 km)处的目标类型形成干扰。将波束主瓣对准(-10°,133 km)时,由于此处实际上无目标，所以雷达收不到目标信号。
4.4 总 结
综上所述，将频控阵发射波束主瓣依次对准(-10°,53 km)、(-10°,93 km)、(-10°,133 km) 位置，若回波信号中包含2个目标，则该处位置为电子干扰机；若回波信号中包含1 个目标，则该处位置为真实目标；若回波信号中无目标，则该处位置为电子干扰机转发形成的假目标。根据不同位置处的回波信号中所包含目标个数的不同可以实现目标类型的鉴别。仿真结果表明本文的干扰置零方法能够使当波束主瓣对准待鉴别目标位置时收发方向图上其余目标位置处的归一化功率下降超过30 dB。同时，本文使用遗传算法对频控阵发射方向图的优化能够实现方向图无距离-角度耦合的同时获得更窄的主瓣宽度和更低的旁瓣功率，提高了角度测量的分辨率。
5 结束语
本文首先使用遗传算法对频控阵发射方向图进行优化，在实现方向图无距离-角度耦合的同时获得了更窄的主瓣宽度和更低的旁瓣功率，提高了方向图分辨率。其次，针对雷达发射信号时采用频控阵模式、接收信号时采用相控阵模式的距离欺骗目标鉴别方法存在的不足，本文研究了一种干扰置零方法，使频控阵发射波束的主瓣对准需鉴别目标位置处时其他潜在目标位于方向图的零陷上，避免了其他待测目标位于频控阵发射方向图较高旁瓣上时雷达仍能接收其反射信号而受到干扰。仿真结果表明本文的方向图优化方法和干扰置零方法具有可行性和有效性，能够实现良好的目标鉴别效果。
［1］谭清莉，张艺乐，张伟，等.FDA-MIMO 雷达主瓣欺骗干扰对抗方法［J］.雷达科学与技术，2017，15（6）：671-676.
［2］LAN Lan,XU Jingwei,LIAO Guisheng,et al.Suppression of Mainbeam Deceptive Jammer with FDA-MIMO Radar［J］.IEEE Trans on Vehicular Technology,2020,69（10）：11584-11598.
［3］朱圣棋，余昆，许京伟，等.波形分集阵列新体制雷达研究进展与展望［J］.雷达学报，2021，10（6）:795-810.
［4］陈阳，田波，王春阳，等.FDA-MIMO 抗干扰技术进展及前景展望［J］.电光与控制，2022，29（8）:65-72.
［5］DING Zihang,XIE Junwei.Joint Transmit and Receive Beamforming for Cognitive FDA-MIMO Radar with Moving Target［J］.IEEESensorsJournal,2021,21（18）：20878-20885.
［6］WANG Yuzhuo,ZHU Shengqi.Main-Beam Range Deceptive Jamming Suppression with Simulated Annealing FDAMIMO Radar［J］.IEEE Sensors Journal,2020,20（16）：9056-9070.
［7］周恒亮，唐霜天，涂刚毅.频率分集阵列鉴别距离欺骗假目标方法［J］.现代防御技术，2019，47（3）:26-30.
［8］LIAO Yi,ZENG Guanghui,WU Chunlin,et al.Frequency Diverse Array Design for Deceptive Jamming Suppression Using Particle Swarm Optimization［C］∥2021 IEEE International Geoscience and Remote Sensing Symposium,Brussels,Belgium:IEEE,2021：2719-2722.
［9］WU Xuehan,SHAO Huaizong,LIN Jingran,et al.High-Speed User-Centric Beampattern Synthesis via Frequency Diverse Array［J］.IEEE Trans on Signal Processing,2021,69：1226-1241.
［10］ZHOU Yashi,WANG Wei,CHEN Zhen,et al.High-Resolution and Wide-Swath SAR Imaging Mode Using Frequency Diverse Planar Array［J］.IEEE Geoscience and Remote Sensing Letters,2021,18（2）:321-325.
［11］XU Jingwei,LIAO Guisheng,SO H C.Space-Time Adaptive Processing with Vertical Frequency Diverse Array for Range-Ambiguous Clutter Suppression［J］.IEEE Trans on Geoscience and Remote Sensing,2016,54（9）:5352-5364.
［12］王博，谢军伟，张晶，等.对数频偏FDA 方向图解耦优化［J］.系统工程与电子技术，2020，42（3）:505-512.
［13］熊杰.频控阵发射波束形成及其应用方法研究［D］.成都：电子科技大学，2018.
