0 引 言
合成孔径雷达(Synthetic Aperture Radar,SAR)因其可全天时、全天候工作及广域大刈宽等优点,在海洋遥感领域发挥出重要作用。目前复杂环境下的舰船目标检测仍是SAR 海洋遥感领域的难点问题,具体表现在近岸目标检测、密集目标检测和弱小目标检测等方面。极化合成孔径雷达(Polarimetric SAR,PolSAR)在单通道SAR 的基础上增加了更多极化通道,能够更完整地保留目标电磁散射特性,极大提升了目标检测和识别方面的性能[1],文献[2]展现了极化特征在目标恒虚警检测中的实际效果。文献[3]对目前极化SAR 图像舰船目标检测方法进行了详细综述,常用的极化检测器可分为特征融合舰船目标检测方法、慢动舰船目标检测方法等。其中特征融合检测方法中的极化最优化技术利用不同极化通道信息,遵循一定的优化目标函数,对PolSAR 图像进行特征融合处理,具有检测性能良好、物理可解释性强等优点,在极化检测中占有重要地位。因此本文聚焦该研究方向,展开基于最优化技术的极化检测器的改进和提升工作。基于优化技术的极化检测器主要分为目标特性已知时的和目标特性未知时的两类检测器。
在目标特性已知的极化最优化检测器方面:1988年Boerner 等人基于最大信噪比准则提出了极化匹配滤波器(Polarimetric Matched Filter,PMF)。1989年,Novak 等人从似然比检验角度提出了最优极化检测器(Optimal Polarimetric Detector,OPD),该方法达到了极化探测器的理论上限(需要目标的先验信息)[3]。杨健等以信噪比最大为优化目标,提出了极化对比增强(Optimization of Polarimetric Contrast Enhancement,OPCE)方法,取得较好的效果[4]。杨健等随后将散射机理融于OPCE 形成其广义方法(GOPCE),提升了目标检测效果[5-6]。杨栋文等提出一种基于最小杂信比子空间(Minimal Clutter to Signal Ratio)的极化对比增强方法并应用到舰船检测领域,发现在某些维数的子空间上其舰船目标检测性能优于传统的极化对比增强方法[7]。作者以信杂比和杂波起伏度的比值最大为优化目标提出了极化检测优化滤波器(Polarimetric Detection Optimization Filter,PDOF),并证明在复杂环境下该方法是目标先验信息已知时的最优极化检测器[8]。
在目标特性未知的极化最优化检测器方面:1982年Boerner 提出的能量检测器(SPAN)利用了极化回波的所有能量[9]。采用单位矩阵与SPAN的乘积代替OPD 中的目标协方差矩阵,即可得到单位似然比(Identity Likelihood Ratio Test,ILRT)检测器[10]。通过将极化散射矢量进行组合可形成功率最大合成检测器(PMS)[9-10]。1990年,Novak和Burl 提出了极化白化滤波器(Polarimetric Whitening Filter,PWF)[11],与上述其他方法相比,PWF的检测性能与OPD 最为接近[10-11]。Marino 提出以杂波能量最小为准则的极化凹口滤波器(Polarimetric Notch Filter,PNF)[12]。高贵等将PNF应用到了高海况情形、混合极化情形和干涉情形,均取得了较好效果[13]。2020年,刘涛等考虑电磁散射能量的现实物理意义,修改了PNF 表达式,并对其命名为新PNF(New PNF,NPNF),取得了较原PNF 更好的检测性能[14]。目前大部分场景下PNF 的性能仍低于PWF[15]。
考虑到将上述检测器进行融合有望提高目标检测性能,刘涛等利用改进的线性判别方法(Modified Linear Discriminant Analysis,MLDA)将上述检测器进行融合,发现PWF 与PDOF 的组合基本能够达到多种极化检测器融合的最佳效果,并因此提出了极化对角加载检测器(Diagonal Loading Detector,DLD)[16]。遗憾的是,而这二者进行组合的最优权重无法获得。因此本文的研究目的就是寻找求解PWF 和PDOF 线性组合的最优加权系数算法。第1节给出了DLD的数学模型及其约束条件。第2 节分别从3 个思路给出了基于ROC 曲线下面积(MAUC)、Fisher 线性判别准则(LDA)和口袋感知机学习算法(Pocket Perceptron Learning Algorithm,PPLA)的求解方法。另外针对基于MAUC的求解方法,结合LDA 设计出其快速实现算法。第3节利用仿真和实测数据分析了样本数目、杂波模型对检测性能的影响,并比较了计算速度。第4节给出了结论。
1 DLD检测器的数学模型
Novak 等人提出的PWF 物理机理是使杂波的起伏度最小,其表达式为[11]
式中:tr(·)是矩阵的迹,L是等效视数,i表示统计平均中第i个像素;s是极化散射矢量,si即为第i个像素的极化散射矢量,服从多维复高斯分布;C=![]() 是多视极化协方差矩阵;ΣC= E(C)是杂波极化协方差矩阵,E(·)表示数学期望,Σ-1C 表示杂波极化协方差矩阵的逆。
是多视极化协方差矩阵;ΣC= E(C)是杂波极化协方差矩阵,E(·)表示数学期望,Σ-1C 表示杂波极化协方差矩阵的逆。
PDOF 在复杂杂波背景和目标先验信息已知情况下的检测性能优于OPD,其表达式为[8]
式中G=Σ-1C ΣTΣ-1C,ΣT为目标极化协方差矩阵。
现构造PWF与PDOF的线性组合模型为
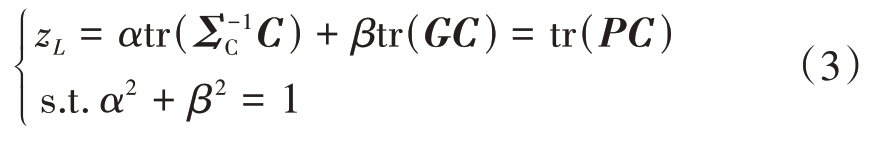
其中,P矩阵为
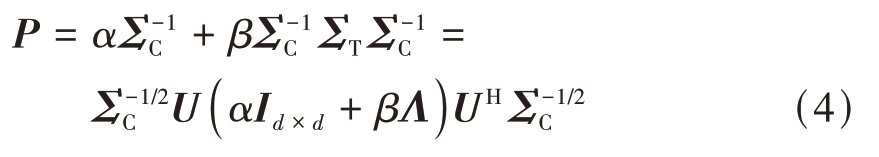
式中:Id×d 为d 维单位矩阵,在单像素检测技术中,d 一般为3,与极化协方差矩阵的维数相同;Λ 为非负实对角矩阵且满足![]() ,U 为酉矩阵。
,U 为酉矩阵。
因此该问题就转化为在满足α2+β2=1 的约束条件下寻找最优的α 和β 使得联合极化检测器检测量zL=tr(Σ-1/2CU(αId×d+βΛ) UHΣ-1/2CC) 具备最佳的检测性能。当然两个系数不进行归一化约束也可以,不影响最后的极化检测性能。
极化检测器的性能通常以受试者工作特征(Receiver Operating Characteristic)曲线来体现,其横坐标轴为虚警概率(Probability of False Alarm,PFA),纵坐标轴为检测概率(Probability of Detection,PD)。ROC曲线构成的曲线下面积(Area Under Curve,AUC)可以量化其检测性能[8]。AUC 的取值范围为[0,1],其表达式为
式中R(Pfa)表示ROC曲线,Pfa表示虚警概率变量。
然而,在实际工作中的雷达往往需要较低的PFA,当PFA 提高时,PD 接近于1,导致各检测器的AUC 较为接近。为了突出低虚警概率前提的重要性以及降低高信噪比导致AUC 饱和的影响,结合对数坐标系的优势,本文提出采取修正AUC(Modified AUC,MAUC)作为评价指标:
则最终的优化数学模型为
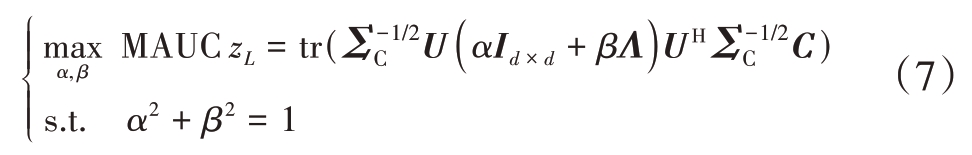
工作的难点是在MAUC 没有解析表达式的情形下求取两种检测器的最优线性加权系数。
2 线性模型求解方法
首先简化优化准则,从基于Fisher准则的LDA线性判别角度出发,通过最大化目标和杂波的类间散度并最小化它们的类内散度,得到近似最优线性权重。然后提出以曲线下面积最大为优化目标、基于数据利用曲线下面积(MAUC)的方法来求解式(7)中的优化模型。为了加快MAUC 参数搜索算法的求解速度,提出以LDA 解算结果为初值的快速参数搜索方法。最后,从二分类的角度出发,提出将PWF 和PDOF 作为两个特征,以最小分类错误为准则,利用PPLA 求取权重。3 种求解方法的关系图如图1所示。
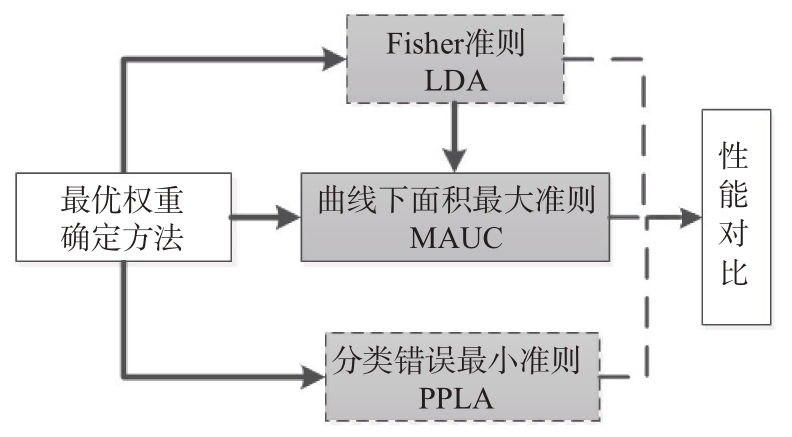
图1 线性模型求解方法关系图
2.1 基于LDA的求解方法
在求解线性组合加权系数中,LDA 是一种比较常用的机器学习方法,因此我们打算首先简化优化准则,利用LDA 方法初步求取其线性组合系数。当然此时的Fisher优化准则和式(7)不完全一样,但计算简单,预期能得到不错的结果。基于LDA 的线性组合优化本质上是比值问题[6],其经典表达式为
式中,z=[zPWF,zPDOF]T 为PWF 和PDOF 输出组成的高维Fisher 矢量,zT 为目标Fisher 矢量,zC 为杂波Fisher 矢量,x=[α,β]T 为线性组合权重系数,Var(·)表示变异系数,即均值与标准差的商,‖·‖为2 范数。式(8)的物理含义是最小化杂波与样本的类内距离并最大化类间距离,将式(8)整理可得到
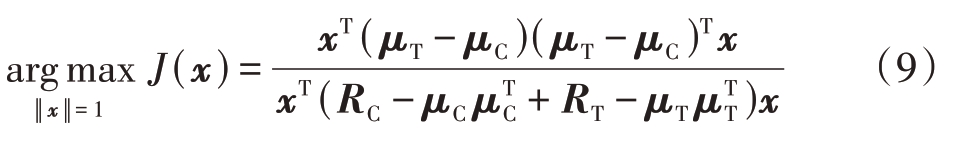
式中,RT 和RC 为Fisher 矢量所对应的特征协方差矩阵,μC 和μT 分别为杂波和目标特征Fisher 矢量的均值。利用广义特征值分解定理可得其最优加权系数为
式中,λk,fk(k=1,2)为矩阵(RC-μCμTC+RT-μTμTT)-1(RT-RC)的特征值和特征矢量,其中最大特征值所对应的特征矢量就是线性最优加权系数。
2.2 基于MAUC的求解方法
针对复杂海况,遍历参数[α,β],构造联合滤波矩阵P,计算其输出值,并确定门限范围即可计算MAUC。具体算法流程如算法1 所示。这种方法可适用于任何滤波矩阵。
算法1 基于MAUC的DLD线性求解算法

1)确定先验信息ΣC,ΣT,根据[α,β]确定变换矩阵;2)利用公式(3)计算杂波和目标对应的输出值;3)通过杂波输出值的范围确定门限范围,令门限递增,求取MAUC;4)遍历所有参数对[α,β],重复步骤2)~3)直到覆盖所有参数对;5)在参数对中,通过选择最大MAUC确定最优线性系数。
该算法的实现依托训练样本且遍历全部参数,耗时较长。由于α2+β2=1相当于围绕单位圆周进行搜索,为了提升速度可利用对称性结合正负定判决来确定DLD 输出的正负方向,可将搜索范围进一步限定在β >0 的上半圆。同时,将LDA所得结果作为该算法初值,可以进一步减少搜索时间。基于MAUC 的DLD 线性求解快速算法如算法2所示。
算法2 基于MAUC的DLD线性求解快速算法

1)确定先验信息ΣC,ΣT,以LDA方法确定的[α,β]作为初值;2)利用公式(3)计算杂波和目标对应的输出值;3)求取杂波输出和目标输出的均值,比较大小,确定DLD输出方向;4)通过杂波输出值的范围确定门限范围,令门限T递增,求取MAUC;5)遍历上半圆[α,β],重复步骤2)~3)直到覆盖上半圆;6)在参数对中,通过选择最大MAUC确定最优线性系数。
2.3 基于PPLA的求解方法
Rosenblatt提出的感知机是一种简单的二元分类模型[17]。但是感知机算法有一个强前提条件—数据必须是线性可分的。这意味着,如果我们无法保证样本是线性可分的,那么根据感知机算法执行的计算机程序可能会永远找不到合适的划分边界,陷入无限迭代之中,无法收敛。由于其无法解决线性不可分问题,因此一度遇冷。为了解决这个问题,Stephen 在文献中提出了口袋感知机算法PPLA[17]。其原理是在求解超平面的过程中,保存当前的最优解,当超过迭代次数后,算法输出保存的最优解。“口袋”中就始终拥有目前我们所见到的最优的划分平面,这就是“口袋算法”。值得注意的是,为了防止无限重复,我们必须预先规定一个迭代次数,当迭代次数超过设定值时,算法将会停止运行。因此迭代次数和初值对最优解的影响较大。将PWF 和PDOF 作为样本的两个特征,构造2×1 的感知机,其示意图如图2所示。由于偏置为一常数,从检测角度而言不影响性能,因此记录PWF 和PDOF 的权重并归一化,即可由PPLA 得到[α,β]。
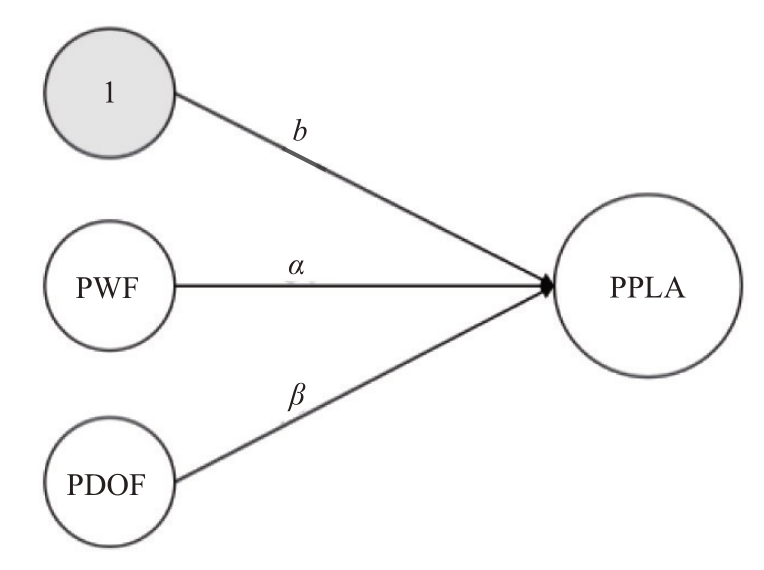
图2 基于PPLA的DLD线性权重求解
3 实验验证
3.1 实验流程设计
实验流程设计如图3所示。主要分为联合极化检测器的构建和PolSAR图像数据验证性能评估两方面。平行四边形分别表示输入和输出。带有灰色背景的矩形实框表示需要执行和处理,矩形虚框表示并行可选事项。钻石表示求解参数的确定。实验的核心在于两种极化检测器线性组合最优系数的求解。实验框架基本流程是通过粗选择(训练样本)估计目标和杂波的极化协方差矩阵,然后通过最有权重求解方法加权系数,最后用图像数据(测试样本)验证方法的有效性。
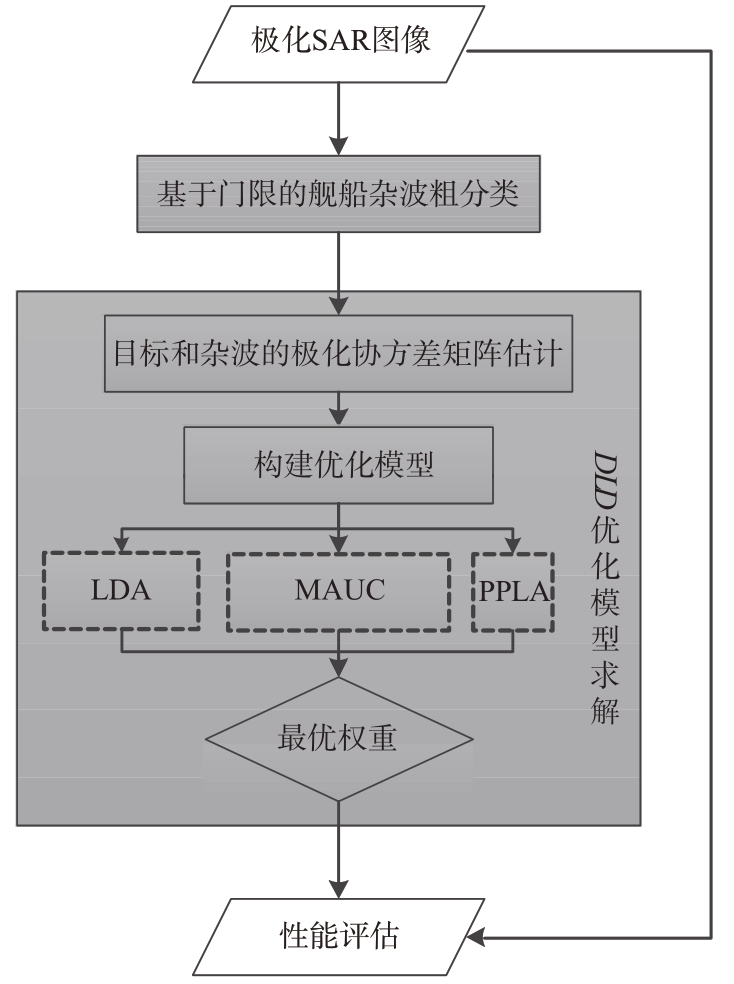
图3 DLD实验验证流程
3.2 PolSAR数据集描述
实验采取两个PolSAR数据集对所构建的DLD进行验证。第一个PolSAR数据集由加拿大全极化星载RADARSAT-2(RS-2)于2013年11月在加拿大北海地区的观测得出[18]。其数据格式为单视复(Single Look Complex,SLC)数据,波段为C波段(中心频率5.4 GHz),该图像方位向分辨率为7.6 m,距离向分辨率为5.2 m,入射角约为32°。舰船的实际位置信息由船舶自动识别系统(Automatic Identification System,AIS)获取。如图4所示,图像中有11艘舰船[18]。图中圆形边框表示在单极化通道中难以检测的目标。方框表示在单极化图像中能以正常检测的目标[18]。

图4 RadarSat 2数据中的北海区域
另一个极化SAR 数据集由NASA/JPL Airborne SAR(AIRSAR)在日本的Kojimawan 地区以L 波段观测得出[18]。该全极化数据获取于2000年10月。其距离视数为1,方位视数为9。该图像方位分辨为4 m,距离分辨率为3 m,在这个场景中有22艘船,如图5所示。其详细信息可以在https://vertex.daac.asf.alaska.edu/中查看[18]。
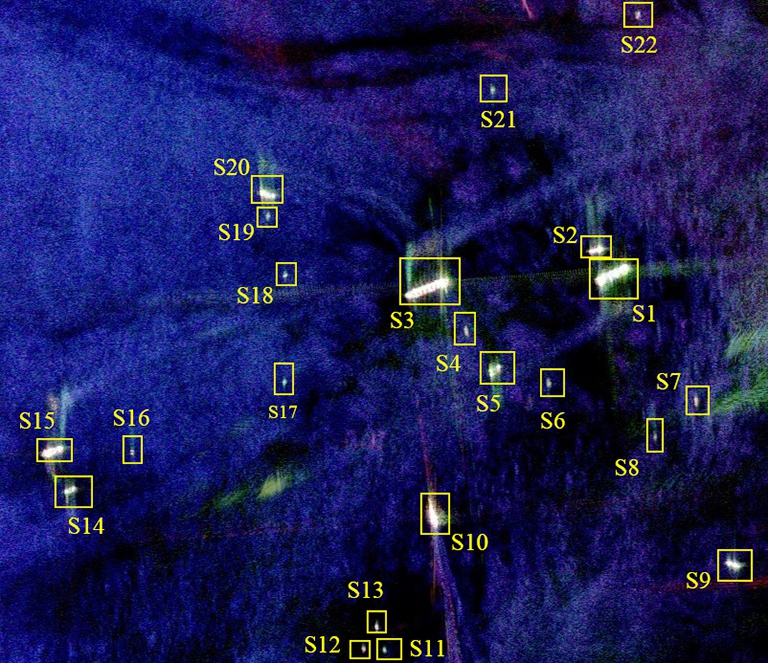
图5 AIRSAR数据中的Kojimawan区域
这两个数据集的海况均可以通过C 波段交叉极化进行反演[19]:RS-2北海的海面风速约为16 m/s,Kojimawan 的海面风速约为12.5 m/s,该两景图像均为中高海况,检测弱小舰船目标存在一定难度,适用于本文实验。同时为保证实验的有效性和标准性,本实验硬件计算平台统一采用Intel Core i7-9750H 处理器,NVIDIA GeForce GTX 1650 4G 显卡,24G 内存,软件平台是Windows 10 系统,Matlab2021。
3.3 仿真实验验证
仿真部分通过对来自RS-2 的实测PolSAR 数据中大面积纯海域进行统计平均,提取得到杂波协方差矩阵,以此为统计基础仿真Wishart 分布。在复杂海况下杂波协方差矩阵偏离Wishart 分布。多变量乘积模型可以用于描述复杂海杂波的统计特性[20-21],如K-Wishart 和g0-Wishart 模型。至于海面舰船目标,通常采用g0-Wishart 模型进行描述(纹理变量 服从归一化逆Gamma 分布,相干斑服从Wishart分布)[18,20]。在本仿真中,对杂波而言,KWishart 模型的形状参数为4,g0-Wishart 模型的形状参数为10;对舰船而言g0-Wishart 模型的形状参数为2。信杂比(Target to Clutter Ratio)是目标检测中的重要参数,TCR定义如下:
服从归一化逆Gamma 分布,相干斑服从Wishart分布)[18,20]。在本仿真中,对杂波而言,KWishart 模型的形状参数为4,g0-Wishart 模型的形状参数为10;对舰船而言g0-Wishart 模型的形状参数为2。信杂比(Target to Clutter Ratio)是目标检测中的重要参数,TCR定义如下:
式中,tr(ΣT- ΣC)表示目标功率,tr(ΣC)表示杂波功率。为仿真低信噪比复杂杂波情况下的弱小目标检测,仿真实验部分TCR设为0.5。
为探究不同杂波和目标模型中各求解方法所求DLD 参数的检测性能,对杂波K-Wishart分布-目标g0-Wishart分布(CKTG)以及杂波g0-Wishart分布-目标g0-Wishart 分布(CGTG),两种情形进行了分析。设定训练样本数量为5 000,测试样本数量为100 000。为了方便与其他极化检测器进行比较,同时给出了PWF、PDOF、OPD和PNF的ROC曲线。图6给出了CKTG情形下的参数搜索情况和各检测器的ROC曲线。求解所得线性组合参数可见表1。
表1 各求解方法所得参数及耗时(CKTG)
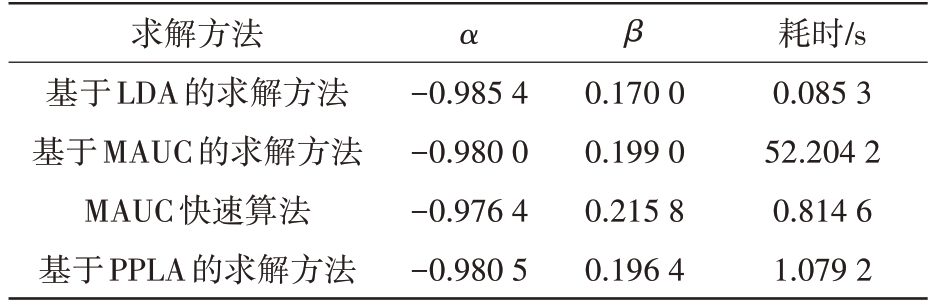
求解方法基于LDA的求解方法基于MAUC的求解方法MAUC快速算法基于PPLA的求解方法α β-0.985 4-0.980 0-0.976 4-0.980 5 0.170 0 0.199 0 0.215 8 0.196 4耗时/s 0.085 3 52.204 2 0.814 6 1.079 2
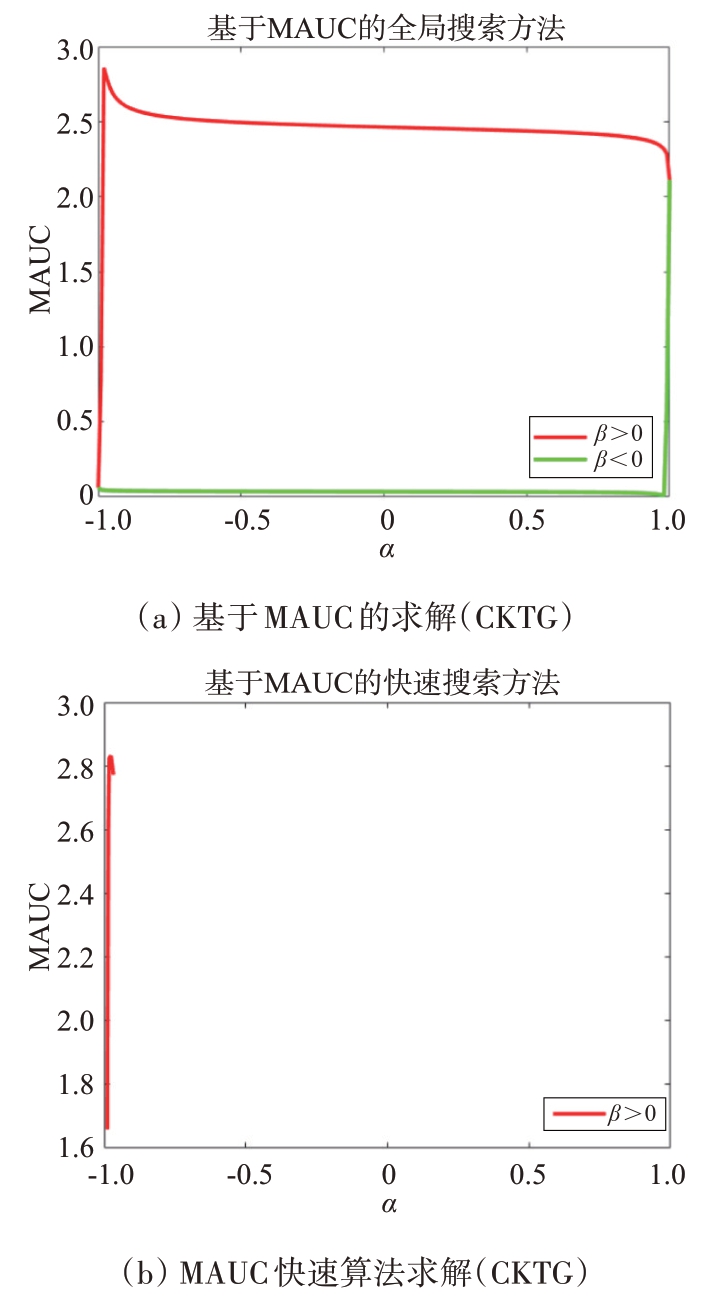
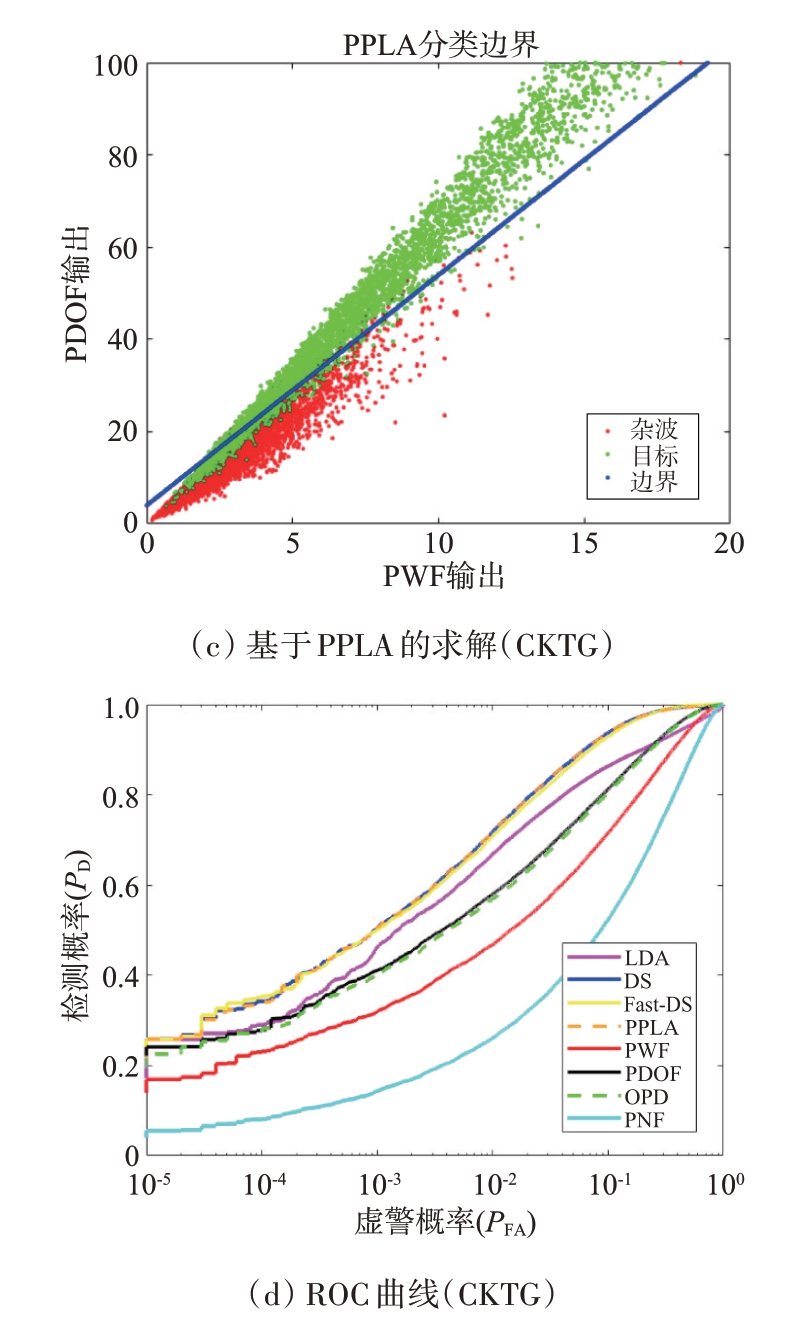
图6 CKTG情形下参数搜索情况及各检测器ROC曲线
图6(a)、(b)展示了基于MAUC 的求解方法及其快速算法的搜索情况。结合表1可知,MAUC 求解方法遍历[α,β]全局空间,其耗时较久,但能获取全部参数对应的检测性能;MAUC 快速算法以LDA 为初值,极大减小了搜索耗时,但如果LDA 的初值并不理想,有可能无法收敛到MAUC 的求解结果。图6(c)展示了PPLA 所求的二维边界。基于PPLA 的求解算法直接以PWF 和PDOF 的输出为二维特征在利用样本进行学习,其耗时与快速搜索算法接近,但没有陷入局部最优的风险。
观察图6(d),可发现在检测性能方面基于MAUC 的求解方法(全局搜索)≈MAUC 快速算法≈PPLA 算法>基于LDA 的线性求解方法>PDOF>OPD>PWF>PNF。图6及表1说明复杂海况下DLD具有明显良好的检测性能。CGTG情况与CKTG相似,为节省篇幅不再罗列。
3.4 实测数据验证
3.4.1 RS-2场景实验
该北海区域PolSAR 图像信杂比为31.912 4。由于先验信息目标和杂波协方差矩阵已知,利用舰船真实信息(GroundTruth),在大量杂波像素和一定量的目标像素中,随机选取目标像素数80%的数量作为目标和杂波样本,对DLD 进行参数求解,所得参数及相关指标如表2所示。
表2 各求解方法所得参数及耗时(RS-2场景)
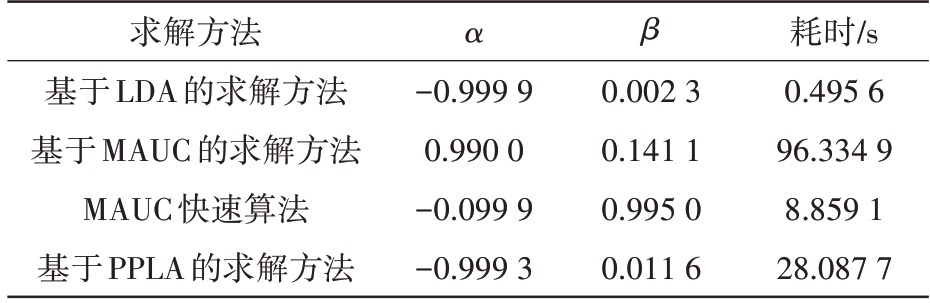
求解方法基于LDA的求解方法基于MAUC的求解方法MAUC快速算法基于PPLA的求解方法α β-0.999 9 0.990 0-0.099 9-0.999 3 0.002 3 0.141 1 0.995 0 0.011 6耗时/s 0.495 6 96.334 9 8.859 1 28.087 7
各求解方法对应的搜索情况以及不同极化检测器的检测结果如图7所示。
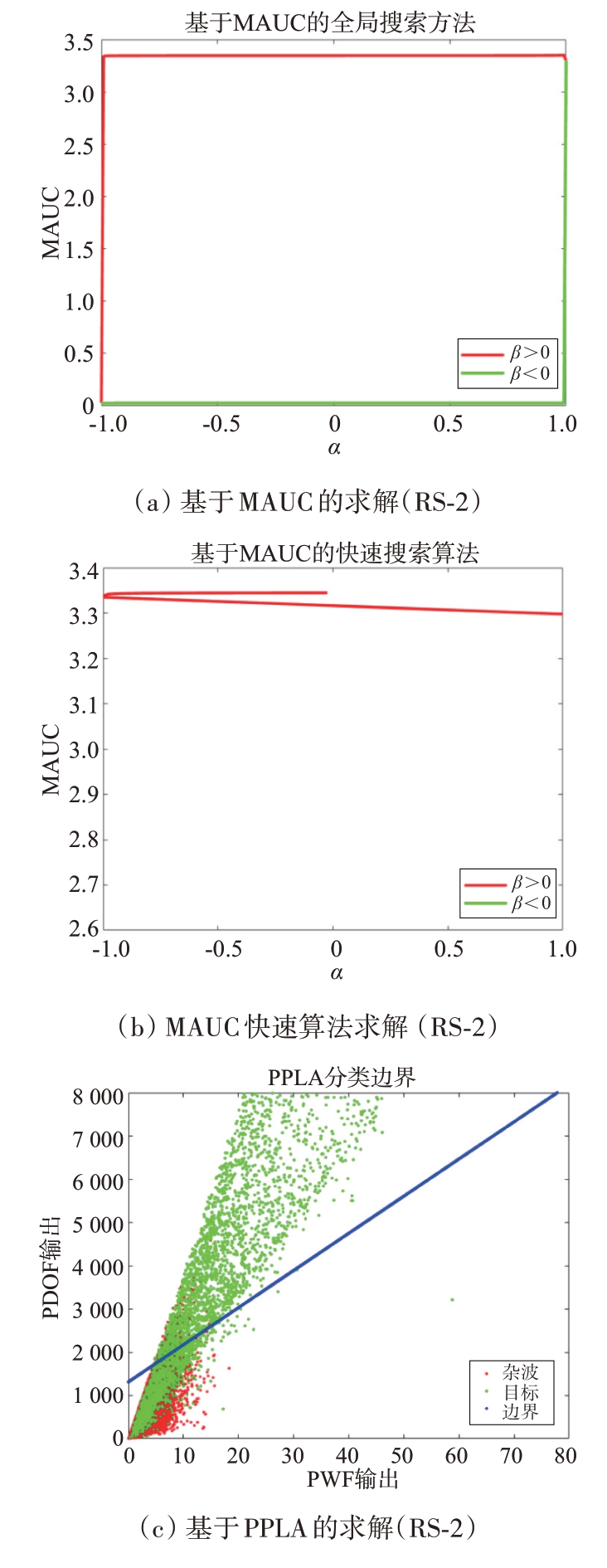
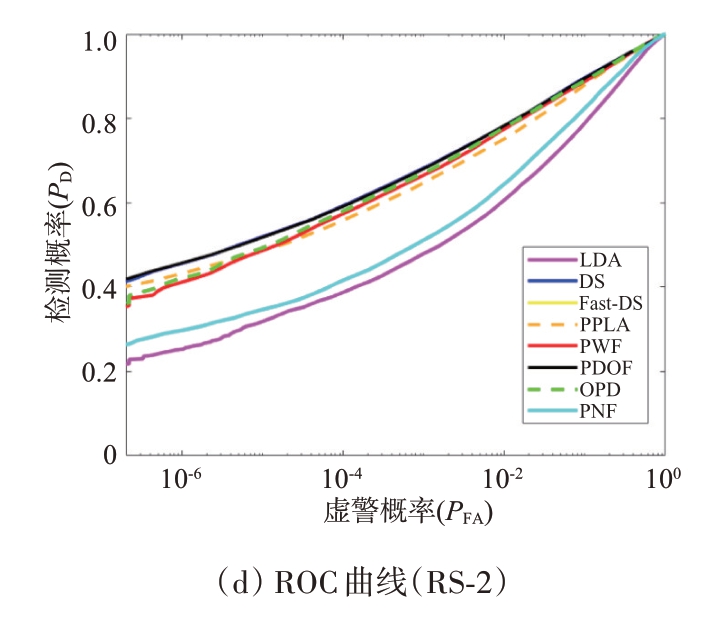
图7 RS-2场景参数搜索情况及各检测器ROC曲线
由于该场景杂波服从Wishart 分布[8]且信噪比较高,导致公式(4)中Λ 远大于Id×d,因此图7(a)中的MAUC 较为平稳。观察图7(d),可发现MAUC、Fast-MAUC 求解方法及和PDOF 几乎重叠,OPD 优于PWF,PWF 优于PPLA,说明在实际系统中,对线性不可分问题,在样本有限且不均衡时,感知机的性能受限。LDA的性能最差,这是因为杂波服从Wishart分布时,OPD和PWF性能极优,在有限样本下,LDA的性能上限不会超过PWF和PDOF。仔细观察图7(d)可发现利用MAUC求解所得DLD略优于PDOF。
3.4.2 AIRSARS场景实验
实验采用的AIRSAR-Kojimawan B 区图像信杂比为131.23,利用本文所提方法对DLD 进行参数求解,所得参数及相关指标如表3所示。
表3 各求解方法所得参数及耗时(AIRSAR)
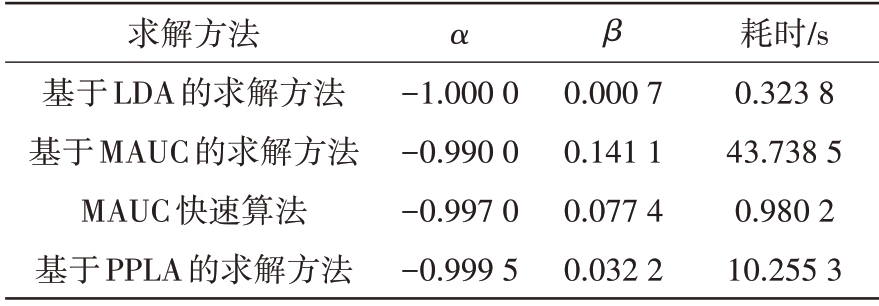
耗时/s 0.323 8 43.738 5 0.980 2 10.255 3求解方法基于LDA的求解方法基于MAUC的求解方法MAUC快速算法基于PPLA的求解方法α β-1.000 0-0.990 0-0.997 0-0.999 5 0.000 7 0.141 1 0.077 4 0.032 2
各求解方法对应的搜索情况以及不同极化检测器的检测结果如图8所示。
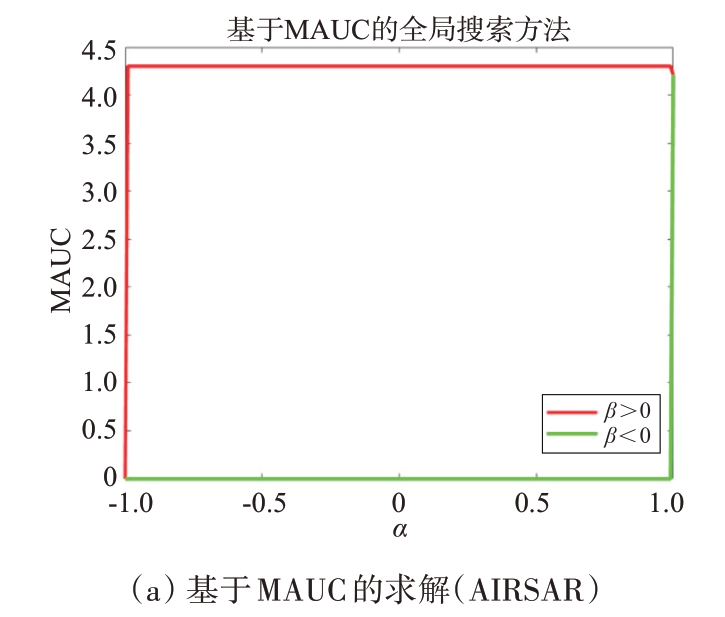
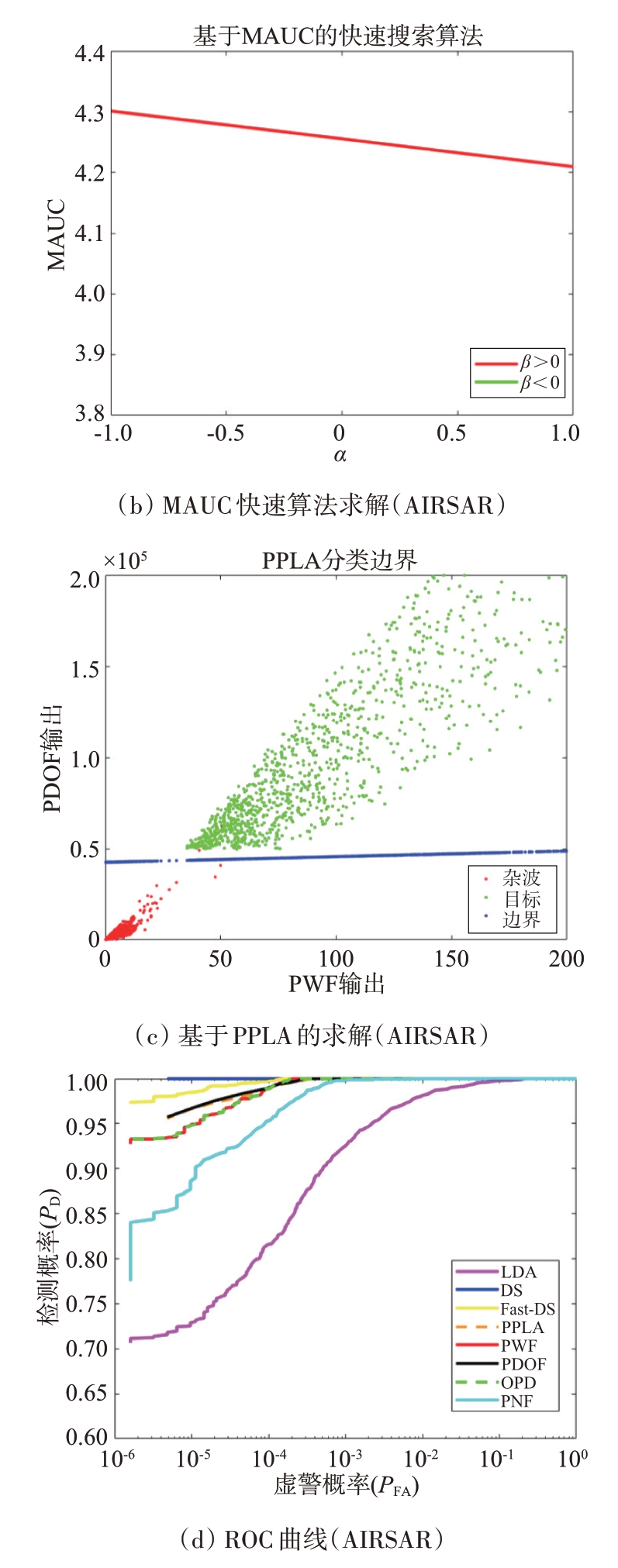
图8 AIRSAR场景参数搜索情况及各检测器ROC曲线
由于该场景相比于RS-2杂波环境服从K-Wishart 分布[8],在该场景下基于数据求解所得的DLD在检测性能上的提升更加明显。
4 结束语
本文重新构建了极化对角加载检测器的基本模型,在此基础上分别从准则简化、参数遍历和数据分类3 个路径提出基于Fisher 线性判别分析(LDA)、MAUC 准则及口袋感知机学习算法(PPLA)的3 种求解方法,得到PWF 和PDOF 的最优组合系数。经仿真和实测实验证明,在复杂海况环境下,DLD 具有优于PDOF 和PWF 的检测性能。在3种求解方法中,基于线性判别LDA的线性求解方法速度最快,但性能最差。基于MAUC 准则的线性求解方法性能最好,具有较强的鲁棒性,但耗时最长,以LDA 为初值的快速MAUC 方法可以有效解决耗时问题。基于PPLA 的方法性能与基于数据搜索的方法相当,耗时不如以LDA 为初值的快速搜索方法。后续将拓展机器学习算法,研究神经网络模型对极化信息挖掘的检测性能提升程度。
[1]王雪松,陈思伟.合成孔径雷达极化成像解译识别技术的进展与展望[J].雷达学报,2020,9(2):259-276.
[2]张嘉峰,朱博,张鹏,等.Wishart分布情形下极化SAR图像目标CFAR检测解析方法[J].电子学报,2018,46(2):433-439.
[3]刘涛,杨子渊,蒋燕妮,等.极化SAR图像舰船目标检测研究综述[J].雷达学报,2021,10(1):1-19.
[4]YANG Jian,YAMAGUCHI Y,BOERNER W M,et al.Numerical Methods for Solving the Optimal Problem of Contrast Enhancement[J].IEEE Trans on Geoscience and Remote Sensing,2000,38(2):965-971.
[5]YANG Jian,DONG Guiwei,PENG Yingning,et al.Generalized Optimization of Polarimetric Contrast Enhancement[J].IEEE Geoscience and Remote Sensing Letters,2004,1(3):171-174.
[6]YIN Junjun,YANG Junyou,XIE Chunhua,et al.An Improved Generalized Optimization of Polarimetric Contrast Enhancement and Its Application to Ship Detection[J].IEICE Trans on Communications,2013,96(7):2005-2013.
[7]YANG Dongwen,DU Lan,LIU Hongwei,et al.Novel Polarimetric Contrast Enhancement Method Based on Minimal Clutter to Signal Ratio Subspace[J].IEEE Trans on Geoscience and Remote Sensing,2019,57(11):8570-8583.
[8]LIU Tao,JIANG Yanni,MARINO A,et al.The Polarimetric Detection Optimization Filter and Its Statistical Test for Ship Detection[J].IEEE Trans on Geoscience and Remote Sensing,2021,60:1-18.
[9]BOERNER W M.KOSTINSKI A B,JAMES B D.On the Concept of the Polarimetric Matched Filter in High Resolution Radar Imaging: An Alternative for Speckle Radiation[J].Remote Sensing:Moving Towards the 21st Century,1988,1:69-72.
[10]CHANEY R D,BURL M C,NOVAK L M.On the Performance of Polarimetric Target Detection Algorithms[J].Aerospace & Electronic Systems Magazine IEEE,1990,5(11):10-15.
[11]NOVAK L M,BURL M C.Optimal Speckle Reduction in Polarimetric SAR Imagery[J].IEEE Trans on Aerospace&Electronic Systems,1990,26(2):293-305.
[12]MARINO A,CLOUDE S R,WOODHOUSE I H.Detecting Depolarized Targets Using a New Geometrical Perturbation Filter[J].IEEE Trans on Geoscience & Remote Sensing,2012,50(10):3787-3799.
[13]GAO Gui,GAO Sheng,HE Juan,et al.Ship Detection Using Compact Polarimetric SAR Based on the Notch Filter[J].IEEE Trans on Geoscience& Remote Sensing,2018,56(9):5380-5393.
[14]LIU Tao,YANG Ziyuan,ZHANG Tao,et al.A New Form of the Polarimetric Notch Filter[J].IEEE Geoscience and Remote Sensing Letters,2022,19:1-5.
[15]杨子渊,唐涛,蒋燕妮,等.极化SAR 图像中PNF 与PWF的CFAR检测性能对比[J].电波科学学报,2019,34(6):778-788.
[16]LIU Tao,YANG Ziyuan,MARINO A,et al.Joint Polarimetric Subspace Detector Based on Modified Linear Discriminant Analysis[J].IEEE Trans on Geoscience and Remote Sensing,2022,60:1-19.
[17]GALLANT S I.Perceptron-Based Learning Algorithms[J].IEEE Trans on Neural Networks,1990,1(2):179-191.
[18]LIU Tao,YANG Ziyuan,MARINO A,et al.PolSAR Ship Detection Based on Neighborhood Polarimetric Covariance Matrix[J].IEEE Trans on Geoscience and Remote Sensing,2020,59(6):4874-4887.
[19]ZHU Shuai,SHAO Wenzeng,MARINO A,et al.Semi-Empirical Algorithm for Wind Speed Retrieval from Gaofen-3 Quad-Polarization Strip Mode SAR Data[J].Journal of Ocean University of China,2020,19(1):23-35.
[20]LIU Tao,ZHANG Jiafeng,GAO Gui,et al.CFAR Ship Detection in Polarimetric Synthetic Aperture Radar Images Based on Whitening Filter[J].IEEE Trans on Geoscience and Remote Sensing,2020,58(1):58-81.
[21]LIU Tao,TANG Tao,YANG Ziyuan,et al.L-Distribution for Multilook Polarimetric SAR Data and its Application in Ship Detection[J].Science China(Information Sciences),2021,64(12):226-238.

