0 引 言
单脉冲作为一项主流技术被广泛应用于目标跟踪和精确制导等领域，精确估计目标角度是单脉冲雷达的基本要求。然而，单脉冲测角中需要面对的一个经典难题就是雷达3 dB 主瓣内存在不可分辨的双目标。Nickle 在文献［1］中基于传统三通道（和通道、方位差通道和俯仰差通道）单脉冲雷达提出了估计两个空间距离相近目标的参数拟合模型，但是该模型需要多个脉冲才能得到最优解。文献［2］在研究复单脉冲比统计分布的基础上，提出了使用矩法估计两个瑞利目标角度的方法。文献［3］利用最大似然原理改进了文献［2］的方法，从而提高了估计的准确性。然而，这些方法都需要充分的先验知识和连续的多个脉冲。Sherman在文献［4］中提出了一种使用两个脉冲且不需要先验信息的确定性方法用于估计不可分辨双目标的角度，但是当两目标具有相似的方位角或仰角时，该方法的估计结果会发生模糊。Lee 在文献［5］中对Sherman 的方法进行了改进，通过求解高次多项式克服了角度估计模糊的问题。但是，这两种方法都需要目标回波满足Sherman 条件，即在两个脉冲之间两目标的相位是独立变化的，而幅度比保持不变。
Zheng 在文献［6］中提出了一种解析的单脉冲双源分辨（Two-target Resolution,TR）算法，该算法使四通道（和通道、方位差通道、俯仰差通道和双差通道）单脉冲雷达（Four-Channel Monopulse Radar,FCMR）能够在单个脉冲内估计不可分辨双目标的角度，且不受限于Sherman 条件。Crouse 在文献［7］中简化了Zheng 的方法，使该方法具有较少的反三角函数运算。文献［8］提出了一种对文献［7］的补充算法，该算法可适用于发射4 个倾斜波束的比幅单脉冲雷达。以上方法尽管都使用单个脉冲实现了不可分辨双目标的角度估计，但估计角度模糊的问题依然存在。
针对估计角度模糊的问题，文献［9］提出了另外增设一组天线的解决方法，新增设的天线与初始的4个天线相比绕雷达视轴方向旋转了30°。类似地，文献［10］在双极化阵列中，通过将垂直极化子阵绕雷达视轴旋转了45°，构造交错子阵结构，实现了对两目标角度的无模糊估计。此外，文献［11］提出了一种基于子阵的四通道单脉冲方法用于数字阵列雷达的TR，通过坐标系旋转解决了角度模糊的问题。
然而，当单脉冲雷达配备非矩形阵列时，如圆形阵列、椭圆阵列或菱形阵列，TR算法会由于天线方向图的不一致而产生严重的估计误差。针对这一问题，文献［11］提供了一种解决方案，但其要求天线阵列上的每个阵元都配备单独的接收机，并且该方法牺牲了目标回波的部分功率。
本文提出了一种双脉冲双源分辨（Dual-pulse Two-target Resolution,DTR）方法，该方法适用于配备任意非矩形阵列的极化FCMR。该方法包括两部分:双脉冲解算和双极化融合，主要创新点如下:
1）本文推导了一种新的双脉冲解算方法，消除了由非矩形阵列引起的误差。利用目标回波的起伏特性，从接收到的两个连续脉冲中可以获得8个方程。据此，推导得到了两个关于目标角度的匹配函数。这两个匹配函数都有且只有一个零点，并分别对应了两目标的真实角度位置，因此通过搜索两个匹配函数的零点可以得到两个目标的精确角度估计。
2）本文通过双极化融合消除了角度估计模糊，同时提升了估计精度。基于全极化交错子阵（Full-polarization Interlaced Subarray Partition,FISP）结构的雷达，1）中的方法可以从雷达的两个主极化通道中稳定地获得两组估计结果，并且其中至少有一个极化通道的估计结果是无模糊的。因此，利用多个脉冲将单个极化通道的匹配函数进行锐化后（先多脉冲取平均，再取对数），再将两个极化通道的匹配函数对应加权，从而得到融合匹配函数，继而实现对两目标角度无模糊的、精确的估计。
1 信号模型
本文考虑配备了FISP 结构的非矩形天线阵列全极化单脉冲雷达，该雷达可以通过在不同极化通道中发射正交的波形获得目标的极化散射矩阵，从而保证了两个主极化通道的接收信号都具有足够的幅度响应。不失一般性，本文以圆形的天线阵列为例。FISP结构的子阵划分如图1所示。其中不同的颜色代表不同的子阵分区。在图1（a）中，水平极化（H）子阵划分为H00，H01，H10 和H11。在图1（b）中，垂直极化（V）子阵的划分相对于H 子阵顺时针方向旋转了β，β 是旋转角（本文中β=45°，若阵列形状为椭圆形或菱形时，β 的值应作相应调整）。
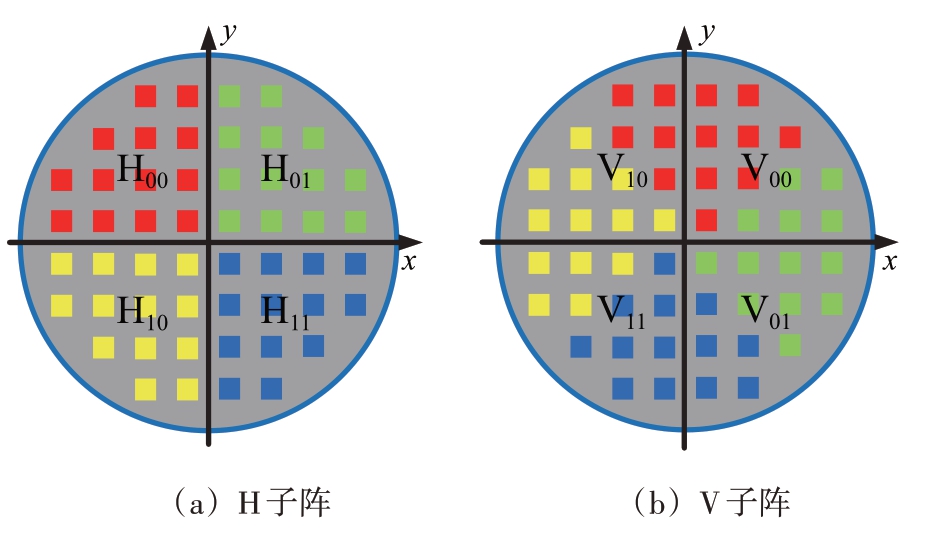
图1 圆形FISP阵列
图1 中，阵元间的列间距和行间距分别为a 和b。H子阵阵元的导向矢量为
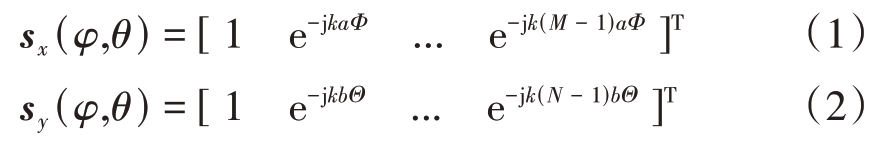
式中sx(φ,θ)是方位向导向矢量，sy(φ,θ)是俯仰向导向矢量，j 是单位虚根，k=2π/λ 是波数，λ 是波长。Φ=sin(φ)cos(θ), Θ=sin(θ)是目标在H 子阵上响应的空域相位角，其中φ 和θ 分别是目标的方位角和俯仰角。
V 子阵的导向矢量表达与H 子阵的导向矢量类似，区别在于两种极化子阵上的阵元对于目标的空域相位角的响应不同，其关系为
式中Φ′和Θ′是目标的空域相位角在V 子阵上的响应，β 是旋转角。为了叙述方便，下文的模型介绍均以H 子阵为例。每个子阵的导向矢量矩阵Smn(φ,θ)为［11］
式中Wmn ∈ℝM×N 是Hmn(m,n=0,1)子阵阵元的权值矩阵，其中的元素（只包含0 或1）与Hmn 子阵的阵元一一对应，属于Hmn 子阵的阵元为1，其余为0；⊙是Hadamard 乘积。则Hmn 子阵的方向图在(φ,θ)处的增益可以表示为
式中sij(φ,θ)是Smn(φ,θ)的元素。对于两个起伏目标，H子阵接收到的信号可以表示为
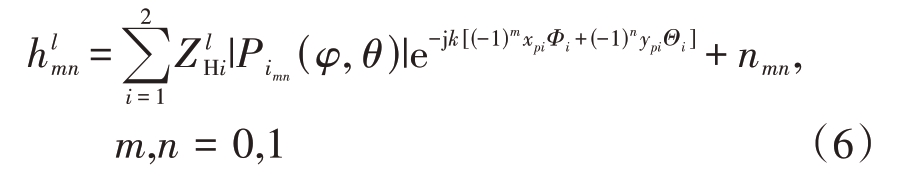
式中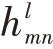
代表Hmn子阵接收到的第l(l=1,2)个脉冲的回波信号，
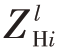代表H 极化通道接收的第i(i=1,2)个目标在第l 个脉冲回波的复幅度，nmn 是Hmn子阵输出的高斯白噪声，xpi和ypi分别是第i 个目标对于Hmn 的相位中心到y 轴和x 轴的距离（为了书写简便且不影响读者理解，下文省略相位中心的目标编号下标i）。当天线阵列的形状是矩形时，（xp,yp）是矩形子阵的几何中心，且与目标位置无关，并且|P00(φ,θ)|=|P11(φ,θ)|=|P10(φ,θ)|=|P01(φ,θ)|。但是，在非矩形天线阵列中，如圆形天线阵列、椭圆形天线阵列和菱形天线阵列，对于位于(φ,θ)的目标，xp和yp表示为
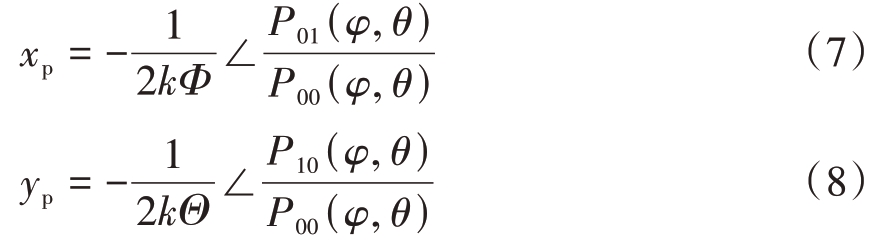
式中∠表示取复数的相位角，且|P00(φ,θ)|=|P11(φ,θ)|≠|P10(φ,θ)|=|P01(φ,θ)|。为了书写简洁，定义γ和δ:
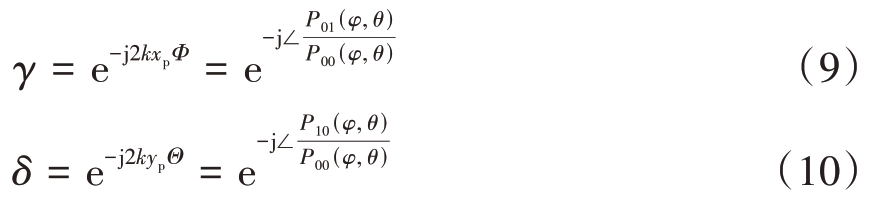
结合文献［11］中对子阵因子α 的定义:α=|P01(φ,θ)|/|P00(φ,θ)|，则H 通道和V 通道接收到两个脉冲的双目标的回波的模型可以表示为
式中:l 表示脉冲数；
γ′i 和δ′i是FISP 阵列V 通道的目标参数，与H 通道对应参数的含义相同。
2 提出的方法
本章的内容是DTR 方法的信号处理过程。DTR 方法被分为两部分:双脉冲解算和双极化融合。在2.1 节双脉冲解算中，详细推导了单极化通道利用两个脉冲无误差求解目标角度的过程，在2.2 节双极化融合中，介绍了如何利用FISP 阵列的两个主极化通道进行联合估计，从而在克服了角度模糊问题的同时提高了估计精度。
2.1 双脉冲解算
在本节中以使用H 通道接收信号求解角度的过程为例。对于接收到的两个脉冲回波（式（11）），其中有8 个未知量和8 个等式，这种情况在数学理论中是可解的，求解过程如下。
首先，利用克莱默法则求解两目标在每个回波中的复幅度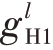
和
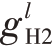，得
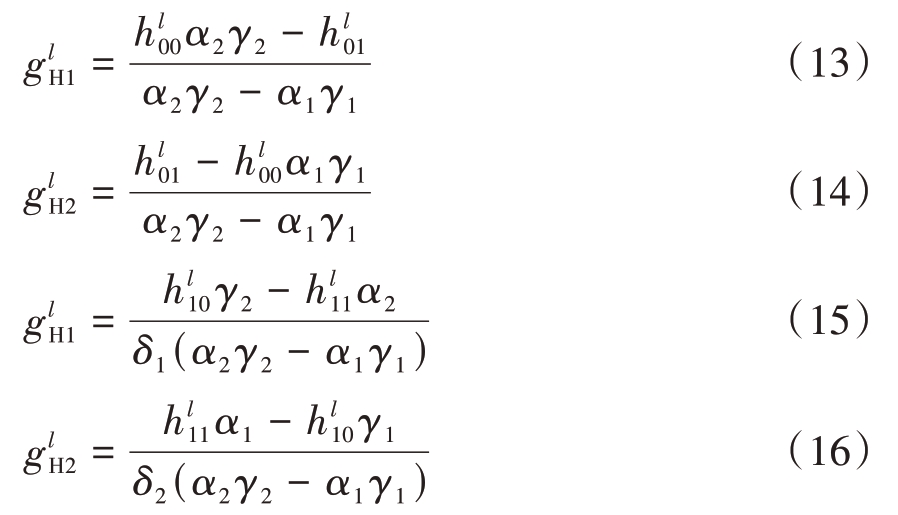
然后将式（11）与式（15）相比消去
，将式（12）与式（16）相比消去
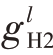，化简得
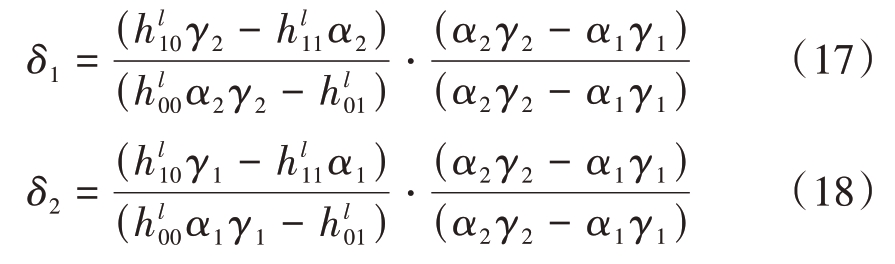
式中l=1,2，代表第l 个脉冲。在式（17）中将第一个脉冲得到的δ1 与第二个脉冲得到的δ1 作除法，即(l=1)/(l=2)，消去δ1，同理利用式（18）中两个脉冲的等式消除δ2，从而得到下面的等式:
式（19）中的未知量只有γi与αi，也即式（19）确立了单个目标的γi 与αi 的确定性关系。另一方面，将方程组（11）的第三行与第二行的位置进行调换，重复以上计算过程，可以得到单个目标的δi与对应的αi的确定性关系如下:
为了得到γi与αi和δi与αi的显性关系式，将式（19）和式（20）取模，化简得到
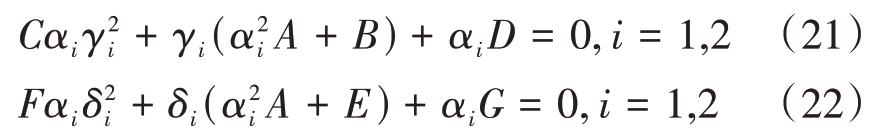
其中，
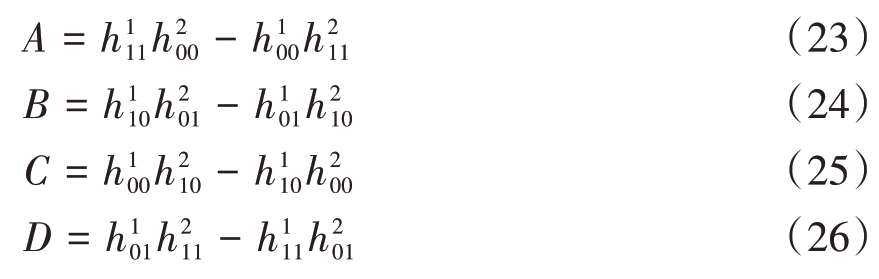
显然式（21）和式（22）分别是关于γi 和δi 的一元二次方程，求解该方程可以得到γi和δi与αi的显性关系式:
式（30）和式（31）表征了单个目标的γi 或δi 与αi 的关系，其中±，在i=1 时取加（减）号，i=2 时取减（加）号。由于本文使用的非矩形阵列，所以αi 未知，且无法解析表达［11］，于是想要得到γi 或δi 的解析形式的解是非常困难的。
但是，由式（7）已知γi, δi 和αi 都是关于(φ,θ)的函数，可以表示为fγ(φ,θ),fδ(φ,θ)和fα(φ,θ)。将式（21）和式（22）写为关于(φ,θ)的函数的形式，通过分析发现，式（21）在两目标对应的方位角处必定存在零点，式（22）在两目标对应的俯仰角处必定存在零点。又因为式（21）和式（22）是一元二次方程最多只有两个零点，因此式（30）和式（31）作为式（21）和式（22）的解，其4个值正好对应于两个目标的4个角度值。若将式（15）写作(φ,θ)的函数的形式，并进行整理得到式（32）和式（33）。
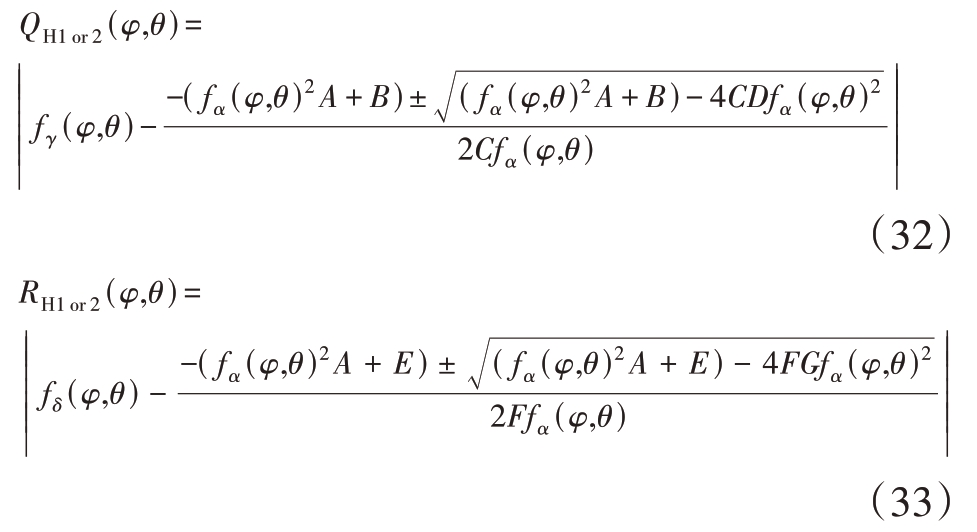
式（32）和式（33）的含义为:对位于(φi,θi)的两个目标，式（32）的QHi(φ,θ)在对应的φi 处是一条零域；式（33）的RHi(φ,θ)在对应的θi 处是一条零域。于是将QHi(φ,θ)与RHi(φ,θ)对应相加，就可以得到只在(φi,θi)处存在一个零点的函数，如下:
结合函数图像对式（37）进行说明。如图2 所示，以其中一个目标位于（1.5°,1°）为例，函数QH1(φ,θ) 在方位角1.5°附近有一条零域，函数RH1(φ,θ)在俯仰角1°附近有一条零域，而FH1(φ,θ)则在（1.5°,1°）处存在唯一的零点。于是通过在3 dB主瓣波束宽度范围内搜索式（34）的零点就可以精确估计目标的角度，该过程描述如下:
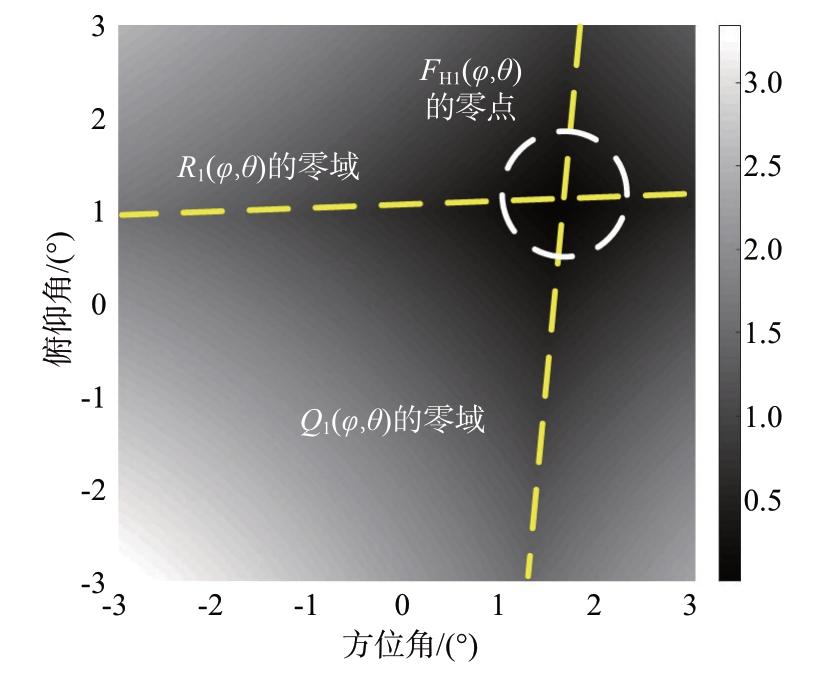
图2 函数FH1(φ,θ)在（1.5o,1o）处存在唯一零点示意图
至此，从H 通道得到了一组正确的角度估计结果。同理，从V 通道的接收信号中可以得到另外一组角度估计值，即
虽然上述过程消除了非矩形阵列带来的误差，但是若单独使用某个极化通道估计两目标角度仍然会存在估计结果模糊的问题。另外，由于H通道和V 通道的坐标系是交错的，并不会出现两个极化通道的估计结果同时模糊的情况。因此，若能够联合两个极化通道的估计结果则可以很好地解决角度模糊问题。
2.2 双极化融合
在上一节介绍了单极化通道的信号处理流程。两极化通道接收信号的主要不同点在于:对于同一个目标，其空域相位角的响应不同，如式（3）所示。当使用H 极化通道估计两目标角度时若两目标具有相同的方位角或俯仰角，那么其估计结果会产生模糊。当使用V 极化通道估计两目标角度时若两目标的角度关系刚好满足arctan((θ1-θ2)/(φ1-φ2))=±β，则其估计结果会模糊，其中β是V子阵相对于H子阵绕视轴的旋转角。
因此，为了解决角度估计模糊的问题，提升算法的估计性能，本文利用多个脉冲将两个极化通道的估计过程进行了联合处理，流程如下:
1）从l(l=2,4,6,…)个脉冲中分别得到两个极化通道的l 2组估计结果。
2）分别计算每个极化通道估计结果的方差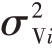
和σ2H（ii=1，2）。
3）分别计算两极化通道中式（23）～（29）中各个系数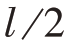
次估计的均值，得到单极化通道的均值匹配方程，如下:
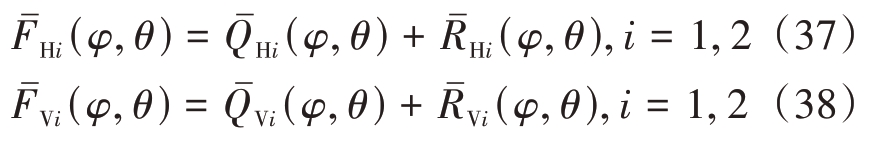
4）加权融合，若|σ2Hi - σ2Vi| ≤τ min(σ2Hi,σ2Vi)，将式（37）和式（38）的两个函数分别取对数然后根据权值相加，如下:
其中τ是选择门限，且
其中τ是选择门限，且
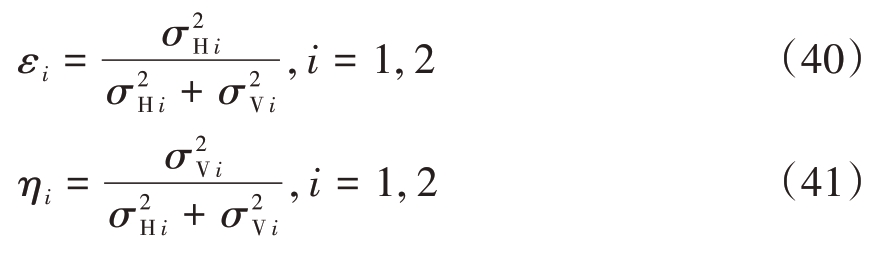
否则，若|σ2Hi-σ2Vi|＞τ min(σ2Hi,σ2Vi)，我们直接选择估计方差小的通道进行最终角度估计，即:若σ2Vi＞σ2Hi，则εi=1，ηi=0；若σ2Vi＜σ2Hi,则εi=0，ηi=1。需要注意的是，虽然计算均值使用的是l 个脉冲，但是可以使用更多的L（L ≥l）个脉冲来计算单极化通道的估计方差，以提升融合的性能。
最终的结果可以通过在3 dB 主瓣波束范围内搜索式（39）的最小值得到，如下:
3 仿真分析
本章基于圆形阵列对本文提出的DTR 方法和文献［7］中的传统TR 算法进行了一系列仿真分析。首先展示了两种算法的估计误差，证明了本文的DTR 方法可以消除非矩形阵列的影响，并解决了角度模糊的问题。之后，比较分析了两种算法的估计性能受两目标相对位置和信噪比（Signal to Noise Ratio,SNR）的影响。
在仿真中，考虑一个276 阵元的圆形阵列（每个子阵有69 个阵元），参考图1，其中a 和b 都是半波长。其余仿真参数如表1 所示。我们设置了6个仿真场景来验证DTR 方法的性能，两目标为瑞利目标且能量相等。其中有5 个场景两个目标的位置如表2 所示:场景1 是不存在角度模糊的场景；场景2 是在场景1 的基础之上改变了两目标的能量比；场景3是V 通道的估计结果会出现角度模糊的场景；场景4是H 通道估计结果产生角度模糊的场景；场景5 是两极化通道估计性能相近的场景。在所有仿真中τ=0.3，且式（35）、式（36）和式（42）的搜索精度为0.01°。
表1 仿真参数
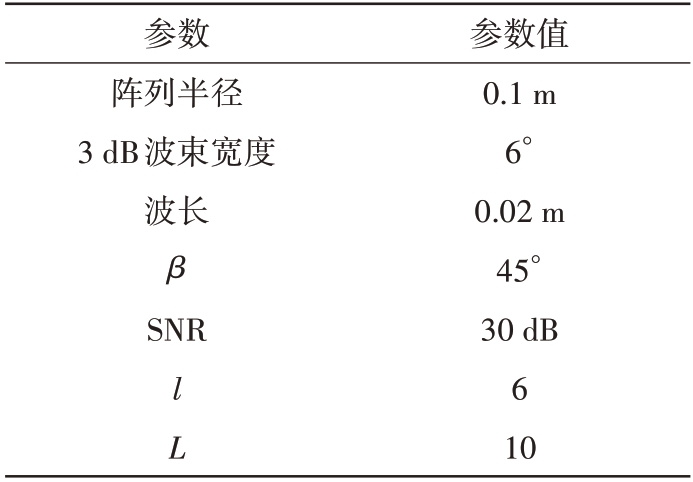
参数阵列半径3 dB波束宽度波长β SNR参数值0.1 m 6°0.02 m 45°30 dB 6 10 l L
表2 不同场景下的目标位置
场景1，2 3 4 5目标1（1.5°,1°）（1.5°,1.5°）（1.5°,1.5°）（1.5°,1.5°）目标2（-1.5°,-1°）（-1.5°,-1.5°）（-1.5°,1.5°）（-1.5°,0.2°）
对于仿真使用的雷达，其4个子阵生成的天线方向图如图3 所示，其中4 幅图从左到右从上到下依次对应于H00、H01、H10 和H11 子阵。从图中可以发现，每个子波束的方向图都是倾斜的椭圆，并且其任意一点的增益都满足|P00(φ,θ)|=|P11(φ,θ)|≠|P10(φ,θ)|=|P01(φ,θ)|。这里4 个天线方向图的不一致是导致TR 方法估计结果产生误差的根源。
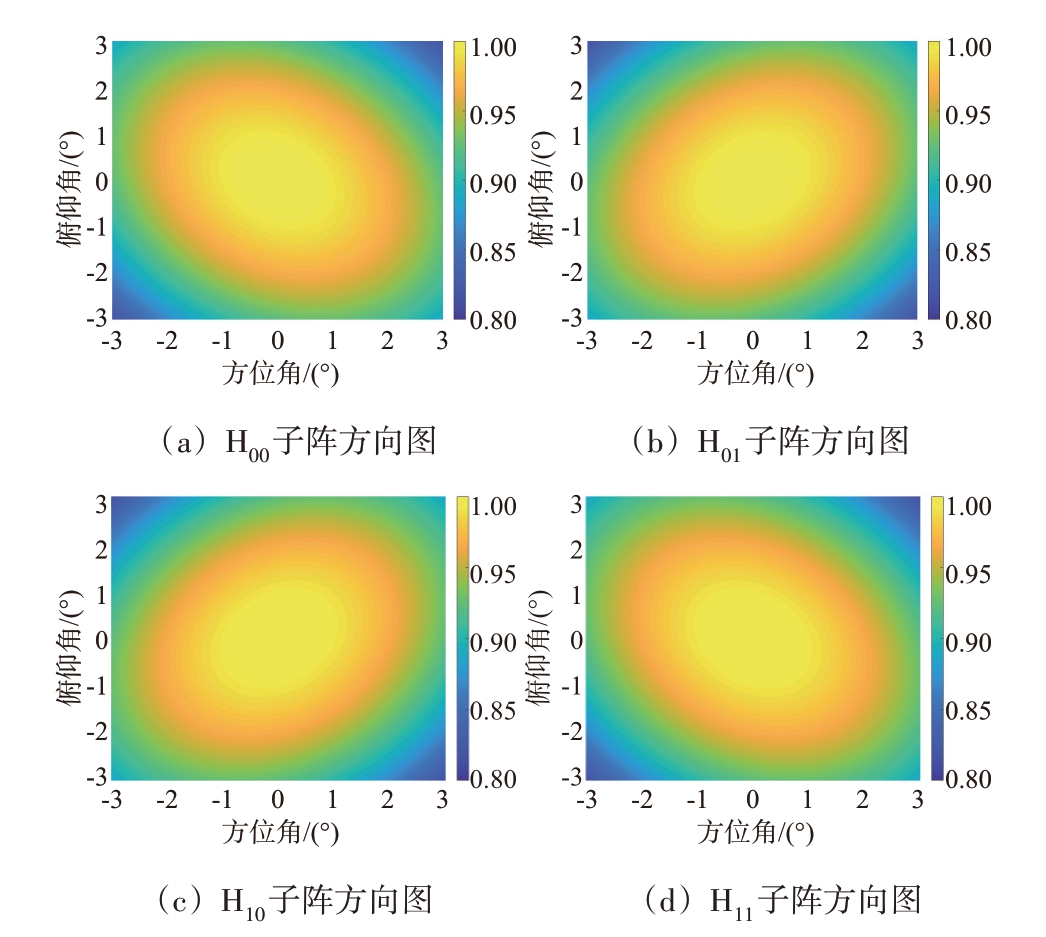
图3 子阵方向图
在下文的仿真结果中，图例标注含义如下:DTR（H）和TR（H）表示H 通道两种方法的估计结果；DTR（V）和TR（V）表示V 通道两种方法的估计结果；DTR（V+H）表示DTR方法融合后的估计结果。
在场景1中，我们证明了DTR方法能够消除非矩形阵列造成的估计误差。50 次蒙特卡洛的仿真结果如图4 所示。图中显示双目标的位置被DTR方法精确估计，然而TR 方法的估计结果产生了严重的偏差。另外粗略的比较图中TR 方法和DTR方法的估计点的离散程度可以看出，DTR 方法的估计精度远高于TR方法。
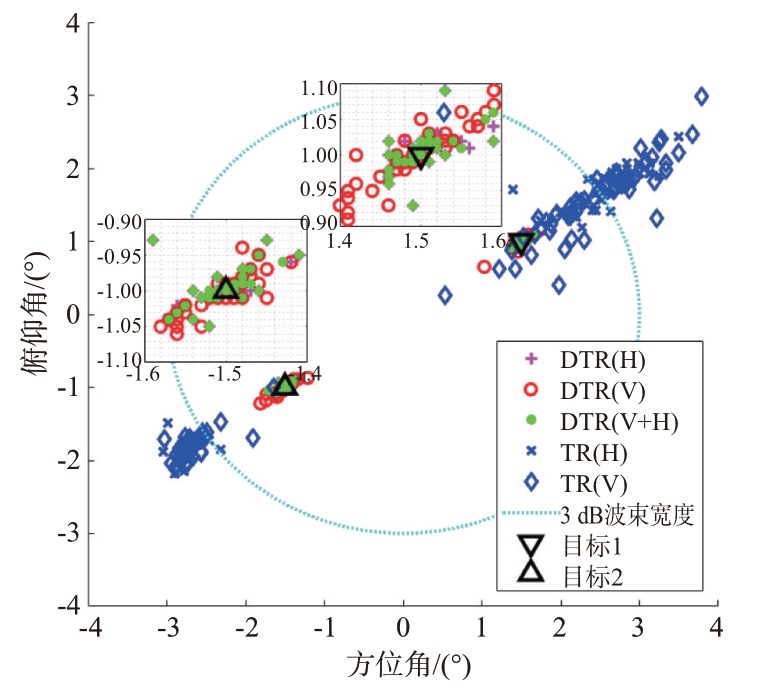
图4 场景1的双源分辨结果
此外，在场景1 的基础上，场景2 中考虑了目标2的能量比目标1的能量高出10 dB的情况，其估计结果如图5 所示。与等能量情况的图4 相比，两种方法的估计结果的中心位置并未发生明显变化，但是目标2的估计结果的离散程度有所下降。这说明两种方法估计结果的均值不受目标相对能量的影响，目标能量的变化只影响了估计结果的方差。
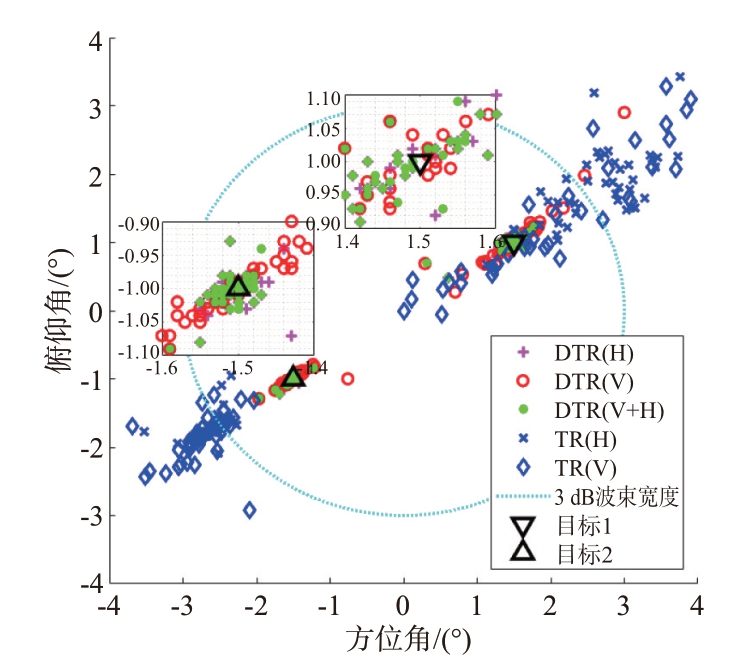
图5 场景2的双源分辨结果（SNR1=20 dB，SNR2=30 dB）
结合场景3 和场景4 的仿真结果，对DTR 方法解决角度模糊的能力进行了验证，对应场景的仿真结果分别如图6 和图7 所示。对比图4，可以发现在图6 中V 通道的估计结果发生模糊，图7 中H通道的估计结果出现了模糊，但是双极化融合后的估计结果在两图中都精确定位了两目标的位置。这也证明了针对这两种出现角度模糊的场景，DTR方法都能精确估计两目标角度。
图6 场景3的双源分辨结果
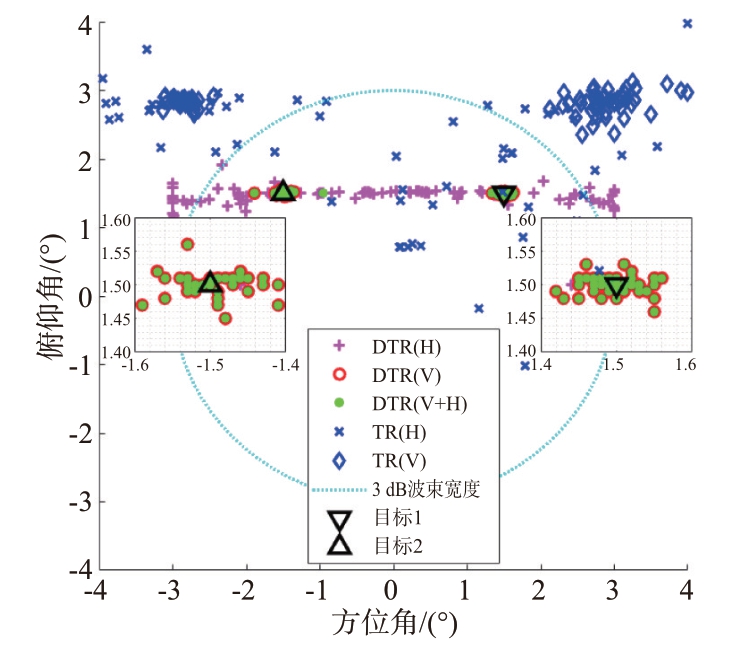
图7 场景4的双源分辨结果
进一步，我们考虑了两目标相对位置对估计性能的影响。进行1 000 次蒙特卡洛仿真后均方根误差（RMSE）随目标2 方位角变化的曲线如图8所示。在这个仿真场景中，目标1 的位置固定于（1.5°，1.5°）；目标2从（-1.5°，-1.5°）移动到（1.5°，-1.5°）。从图8 可以看出:1）DTR 方法估计结果的RMSE 比TR 方法估计结果的RMSE 要小得多；2）单极化通道估计结果的RMSE 随角度变化的起伏较大；3）DTR 方法融合后的估计结果随着目标角度的变化总是保持较低的RMSE；4）DTR 方法估计结果的RMSE 显示，当H 通道和V 通道估计结果的RMSE相差较大时融合后的结果与二者较小的保持一致，当H 通道和V 通道估计结果的RMSE 相差较小时，融合后的RMSE 小于二者单独的RMSE。这证明了DTR 方法中的双极化融合不仅解决了角度模糊这一问题，还对估计精度有所提升。
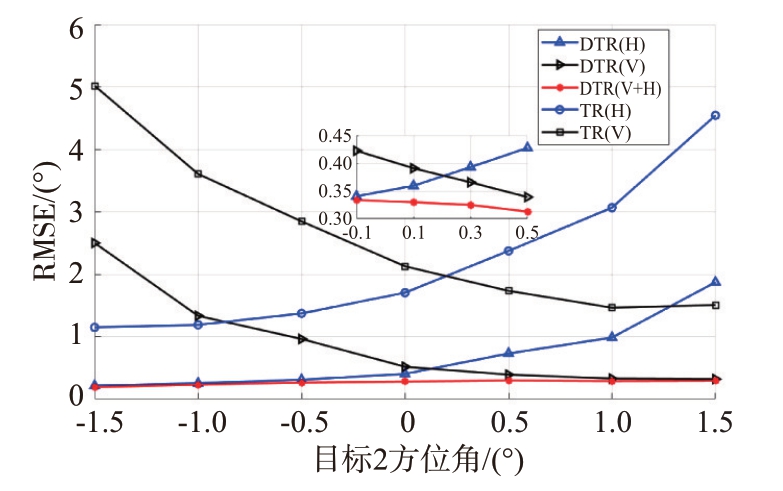
图8 RMSE随目标2方位角度的变化（SNR=20 dB）
最后，我们分析了两种方法在不同信噪比下的估计性能。当两目标位于场景5的位置时，经过1 000 次蒙特卡洛仿真，两种方法估计结果的RMSE 随SNR 变化的曲线如图9 所示。从图中可以看出:1）随着SNR 的增加RMSE 逐渐减小；2）DTR 方法的RMSE 显著小于TR 方法的RMSE；3）在DTR 的三种估计结果中，融合后的估计结果的RMSE始终小于单极化通道的RMSE。这证明了双极化融合方法对估计性能的提升非常稳定。
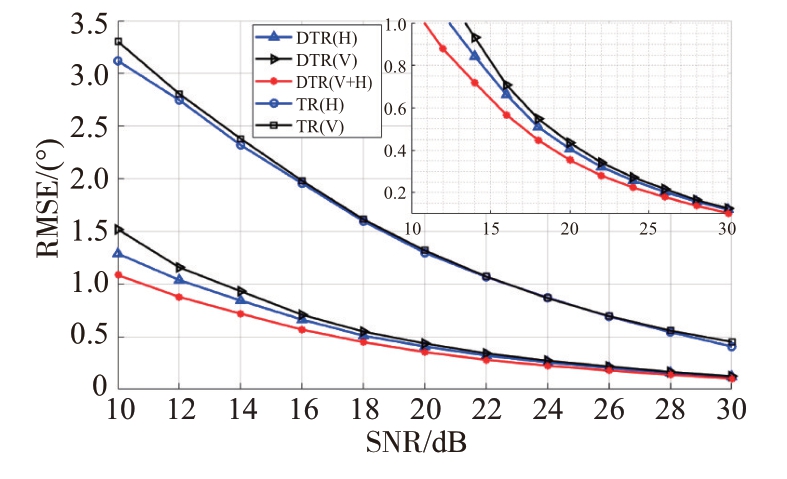
图9 RMSE随SNR的变化（场景5）
在本章的仿真中，我们证明了DTR 方法不仅消除了非矩形阵列造成的估计误差，而且相比于TR 方法具有更高的估计性能。可以得出以下结论，DTR 方法能够适用于配备非矩形阵列天线的极化单脉冲雷达（如圆形天线、椭圆形天线和菱形天线）进行精确双源分辨。
4 结束语
本文提出了一种用于极化四通道单脉冲雷达的双脉冲双源分辨算法（DTR）。所提的方法可以适用于装配各种形状天线阵列的四通道雷达，如矩形、圆形、椭圆和菱形。该方法使用两个连续的脉冲消除了非矩形阵列带来的角度估计的误差。基于应用FISP 架构的天线，该方法还可以通过两个极化通道的估计结果进行融合从而提升角度估计性能。总之，DTR 方法实现了对位于3 dB 主瓣内不可分辨双目标的快速、精确、稳定的角度估计。本文的仿真证明了所提方法对比传统TR 方法具有更加卓越的性能。
［1］NICKEL U.Superresolution Using an Active Antenna Array［C］∥IEE Conference Radar,London,UK:［s.n.］,1982:87-91.
［2］BLAIR W D,BRANDT-PEARCE M.Monopulse DOA Estimation of Two Unresolved Rayleigh Targets［J］.IEEE Trans on Aerospace and Electronic Systems,2001,37（2）:452-469.
［3］WANG Zhen,SINHA A,WILLETT P,et al.Angle Estimation for Two Unresolved Targets with Monopulse Radar［J］.IEEE Trans on Aerospace and Electronic Systems,2004,40（3）:998-1019.
［4］SHERMAN S M,BARTON D K.Monopulse Principles and Techniques［M］.2nd ed.Boston:Artech House,2011.
［5］LEE S P,CHO B L,LEE S M,et al.Unambiguous Angle Estimation of Unresolved Targets in Monopulse Radar［J］.IEEE Trans on Aerospace and Electronic Systems,2015,51（2）:1170-1177.
［6］ZHENG Yibin,TSENG Shuming,YU Kaibor.Closed-Form Four-Channel Monopulse Two-Target Resolution［J］.IEEE Trans on Aerospace and Electronic Systems,2003,39（3）:1083-1089.
［7］CROUSE D F,NICKEL U,WILLETT P.Comments on “Closed-Form Four-Channel Monopulse Two-Target Resolution”［J］.IEEE Trans on Aerospace and Electronic Systems,2012,48（1）:913-916.
［8］WANG Yufei,MA Jiazhi,SHI Longfei.Algorithm Supplement of Four-Channel Two-Target Resolution for Amplitude-Comparison Monopulse Radar［J］.Electronics Letters,2021,57（17）:647-649.
［9］JARDAK S,AHMED S,ALOUINI M S.Generalised Two Target Localisation Using Passive Monopulse Radar［J］.IET Radar,Sonar&Navigation,2017,11（6）:932-936.
［10］MA Jiazhi,SHI Longfei,LIU Jian.Improved Two-Targets Resolution Using Dual-Polarization Radar with Interlaced Subarray Partition［C］//2017 13th IEEE International Conference on Electronic Measurement & Instruments,Yangzhou,China:IEEE,2017:397-400.
［11］WANG Shengbin,XU Zhenhai,YANG Xiao,et al.Efficient and Unambiguous Two-Target Resolution via Subarray-Based Four-Channel Monopulse［J］.IEEE Trans on Signal Processing,2020,68:885-900.
