0 引 言
间歇采样转发干扰是一种利用DRFM 交替存储雷达信号并放大和转发的特殊干扰手段。它的提出解决了在雷达干扰领域收发隔离的难题,兼具了欺骗干扰和密集压制干扰能力。该技术在数字射频存储(DRFM)的支持下,降低了干扰机隔离度的要求,克服了全脉冲式干扰机延时大的问题,对发射的大时宽带宽信号的脉冲压缩雷达体制具有极强的干扰效果。而随着现在ISJ 出现各种变种,如间歇采样重复转发干扰[1]、移频转发干扰[2],干扰的复杂程度和不规律程度大幅提升,使得雷达辨识ISJ 的难度也急剧升高。ISJ 由于其自身特性,其周期和占空比等干扰参数较为固定,通过对干扰参数的估计能够实现针对干扰段的有效抑制。因此对于ISJ 的参数估计研究,能够极大提高雷达最终实现抗ISJ的可能性。
目前国内外存在一些对ISJ 参数提取方法的研究,但相对较少,这之中多数方法都采用了时频分析来实现。其中,文献[3]对雷达进行希尔伯特变换,获取干扰的切片数量、切片宽度和转发次数。该方法存在着计算量大的问题,且误差较大。文献[4]通过分数阶傅里叶变换和短时傅里叶变换结合,对短时分数阶傅里叶变换二维图像分析,能够获得干扰时宽参数和切片中心频率,进而实现干扰抑制,但主要针对频谱弥散干扰这样调频斜率变化明显的干扰类型,而对其他类型没有深入研究。文献[5]采用了滑动截断匹配滤波的方法,输出脉压后参考窗长和延时的二维幅度图,估计干扰切片宽度和转发周期。该方法需要形成参考窗长和延时的二维遍历图像,带来计算量大的问题,响应时间较长。文献[6]推导干扰经雷达匹配接收后的互模糊函数,分析函数定量关系,基于Randon 变换和最小二乘估计对干扰采样周期和占空比进行估计。但该方法受噪声影响仍然较大,难以满足雷达实际探测需求。文献[7]将参数估计问题转化为向量估计问题,然后利用交替方向乘子法(ADMM)进行分解,实现干扰切片宽度和数量估计,大大提高了ISJ 参数估计的精度和运行速度,但也存在着只针对了间歇采样直接转发干扰研究的问题,仍需要后续研究。除通过关键参数估计进行干扰针对性抑制外,部分文献直接对间歇采样转发干扰的特性进行分析,通过设计滤波器或改进发射信号的方式实现间歇采样转发干扰抑制。其中文献[8]借鉴OFDM 通过系统Partial FFT解调算法实现了间歇采样转发干扰分段滤波,但该方法分段后会造成信号频谱展宽重叠,滤除效果较弱。文献[9]通过对发射信号进行编码,在回波信号中实现假目标辨别,但该方法复杂度高,对雷达要求较高。因此,目前这些方法较难投入实际使用当中。
针对以上问题,本文以线性调频脉冲压缩雷达对抗ISJ 为对抗背景,提出一种在强干扰背景下的抗ISJ 算法。该方法首先基于文献[10],它将信息熵作为干扰类型的判断标准,但无法对干扰参数进行测定。本文对其进行改进,对雷达回波信号进行分段处理,并分别计算信息熵,通过二元检验区分干扰段和非干扰段,将参数估计问题转化为对于向量的处理和估计问题,实现对干扰切片宽度和转发周期的估计,再联合针对性的脉冲压缩方法,将估计的参数用于分段脉冲压缩的分段选取,判断分段之间的关系,最后对间歇采样转发干扰进行重构,并实现对干扰的抑制。
1 ISJ特性分析
若雷达发射信号为线性调频信号,那么可以表示为
式中,A 表示发射信号幅度,rect(·) 表示矩形脉冲,f0表示信号脉宽,k表示信号的调频斜率,且k=B/T。
假设目标位置距离雷达为R,那么回波信号可以表示为
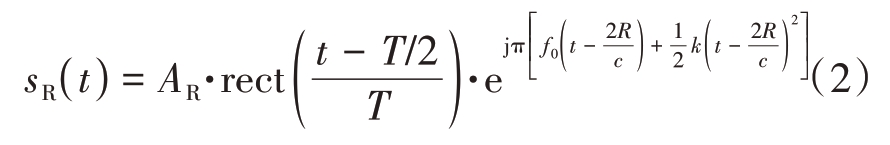
式中,AR表示回波信号幅度,其值可由雷达方程确定,c为光速,所以2R/c表示为信号发射到接收的时延。
ISJ是采用干扰机对雷达发射信号进行分段采样,再按照不同的方式进行转发,形成密集的假目标。间歇采样直接转发干扰(Interrupted Sampling Direct Jamming,ISDJ)、间歇采样重复转发干扰(Interrupted Sampling Repeater Jamming,ISRJ)和间歇采样循环转发干扰(Interrupted Sampling Cycling Jamming,ISCJ),ISDJ 相应的干扰信号模型如图1所示,而重复转发和循环转发则是将采样的信号进行多次转发,使形成的假目标更加复杂逼真。
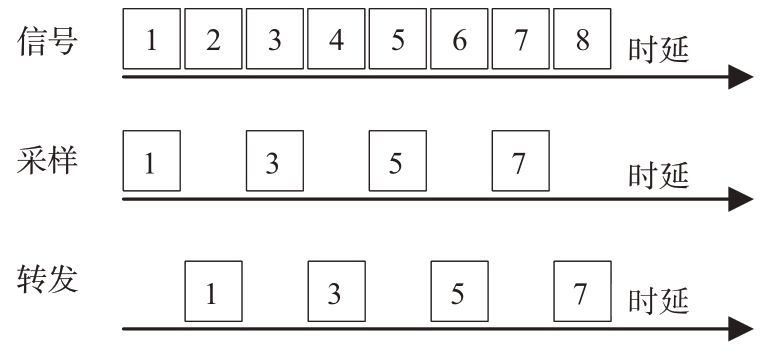
图1 ISDJ原理
干扰机采样雷达信号可以表示为
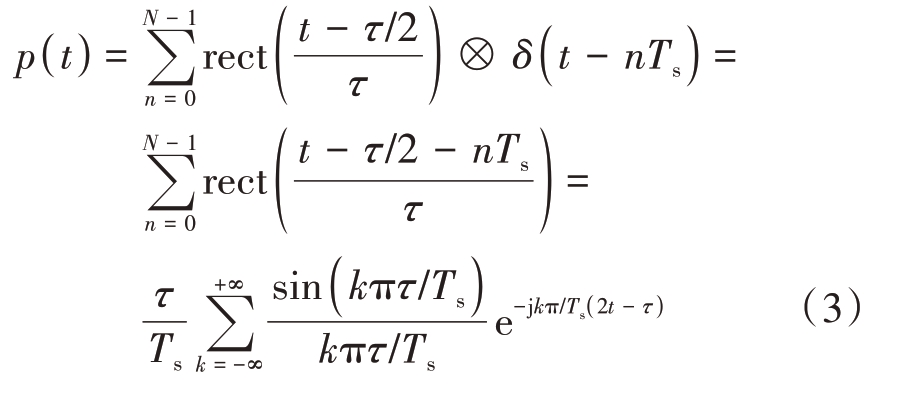
式中,τ 表示间歇采样的时宽,Ts 表示间歇采样的周期。
间歇采样直接转发干扰可以看作是对间歇接收信号的延迟直接转发,因此可以表示为

式中ts表示转发的延迟时间。
最终雷达接收到的实际回波信号sout则可以表示为
而间歇采样重复转发干扰和循环转发干扰可以看作是直接转发干扰的多次重复,具有相似的性质。直接采样转发干扰呈现的多个距离向假目标群,在重复转发和循环转发中,可以认为是进行了多次直接采样转发干扰,因此会在次假目标群中呈现等同于重复次数的假目标峰值,相比直接采样转发干扰假目标群更多,欺骗效果更好。
2 ISJ对抗方法
2.1 ISJ的分段信息熵参数估计方法
信息熵借用了热力学中熵的概念,用来对信息进行量化度量,信息中排除冗余之后的平均信息量即为信息熵。本文借助这个概念来对雷达回波信号中包含的信息量进行测量。
信息熵的定义为
式中,n 为底数,决定信息量的单位,本文取n=2,此时信息熵的单位为bit,s(x) 为待测量信号,且s(x)=0 时H=0。在信息熵中,该参数为集合中各事件发生的概率,而在该方法中,则是将整段信号看作一个整体,因此要求![]() ,在进行参数估计前,需对完整信号进行归一化处理。
,在进行参数估计前,需对完整信号进行归一化处理。
系统的混乱程度决定了信息熵的值。在文献[10]中采用信息熵实现了对信号和不同干扰的区分,且在干噪比较低的情况下仍能实现干扰检测。因此,本文将信息熵作为判断信号是否受到ISJ 影响的依据。当信号受到ISJ 影响时,由于ISJ 间歇收发的特性,可以认为其中存在未受干扰信号子段和受干扰信号子段,那么受干扰信号子段的信息熵会高于未受干扰信号段。
如图2 所示,对回波信号进行分段处理,可以将每一段作为该段内的点的代表,假设每一段代表该段的中心点位置,那么可以将对该段信号是否受干扰的判断转化为对中心点是否受干扰的判断。
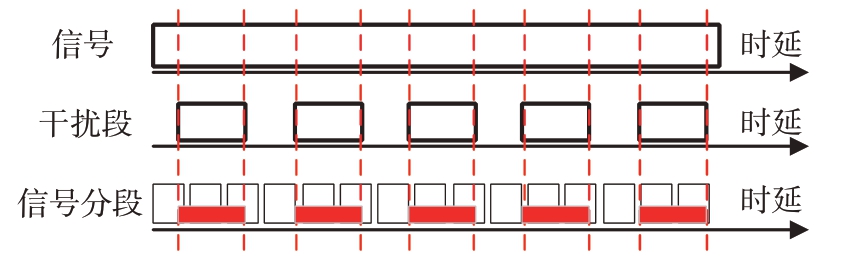
图2 分段信息熵原理
首先根据采样频率fs,有t=n/fs,T=N1/fs。假设将信号分段数为N,那么第k 段信号可以表示为
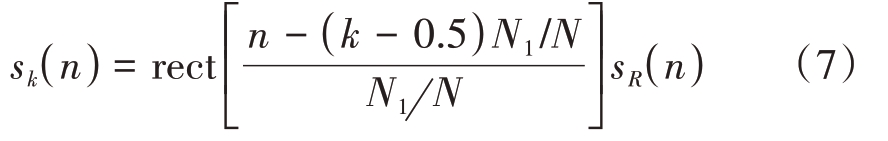
那么该段信息熵的计算结果为
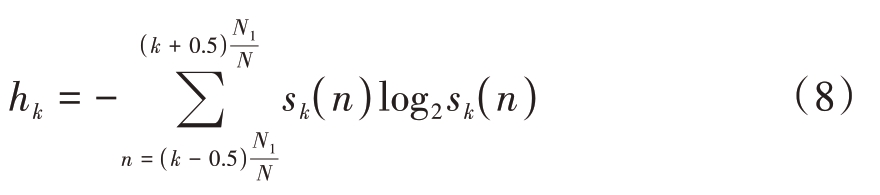
最终组成的信息熵向量为
由于分段可以认为将信号进行了稀疏处理,当信号子段代表的点不在干扰的边界上时,判断出的干扰位置存在误差,因此采用插值的方法对稀疏后的部分进行补充,此时分段信息熵组成的向量长度恢复到与信号长度一致。而又由于信号在求信息熵的过程中,噪声由于分段内求和而削弱,保证了最终结果的稳定性。
在干扰信号段和未受干扰信号段之中,信号子段的包含ISJ 的程度存在差异。根据ISJ 在信号子段的分布可以认为,存在几种类型:完全干扰段(hj)、主干扰段(hmj)、半干扰半信号段(hhalf)、主信号段(hms)、完全信号段(hs)。且存在以下关系:
为了区分受干扰子段和信号子段,将ISJ 的判定转化为一个二元检验问题,即
式中H0 表示信号子段hk 为目标回波的概率,H1 表示信号子段hk 为ISJ 的概率,h 表示辨别门限。信号子段hk代表中位置为![]()
信号子段为半干扰半信号(hhalf)时,其中心位置为干扰的边界点,那么选取该类型作为ISJ 二元检验的判定门限。
hhalf 的信息熵在不考虑噪声影响下可以表示为
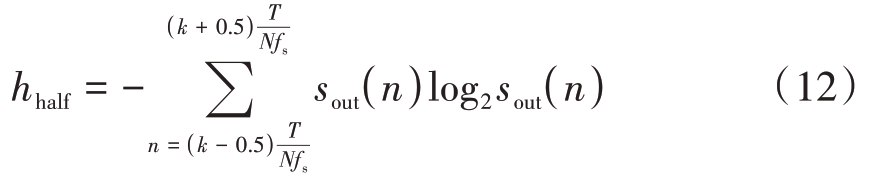
前一半不带干扰信号的信息熵值为
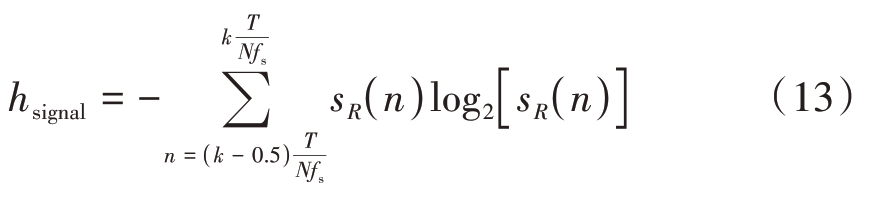
后一半带干扰信号的信息熵值为
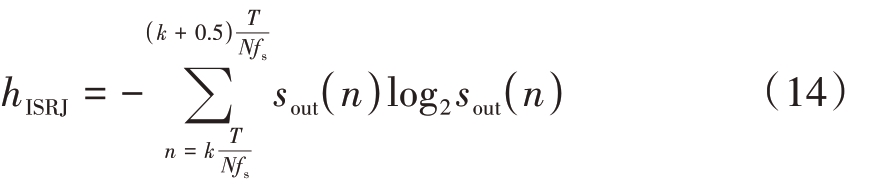
将式(5)、式(13)、式(14)代入式(12)得
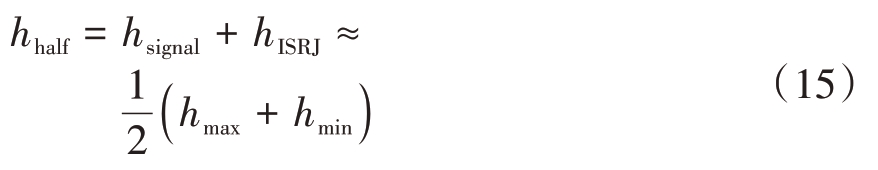
噪声的计算在信息熵中是非线性的,但从文献[10]实验中可以认为,在干噪比大于0 dB 时,噪声在其中的影响较小。那么,ISJ 的判定门限可以近似为雷达回波信号子段信息熵最大值和最小值的均值。如图3所示,确定干扰段和非干扰段位置后,即可将信号受ISJ 影响的干扰脉宽和周期估计出来。
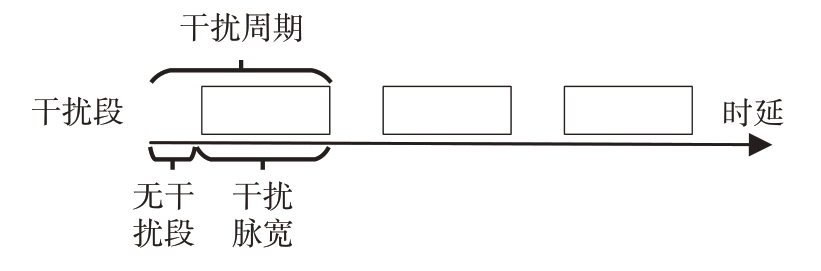
图3 ISJ二元检验结果图
但在实际计算中,噪声仍然会造成信息熵值的不稳定,另一方面,干扰段本身也会造成熵值波动,使得在干扰的判断过程中易出现错误。为了解决这个问题,对分段后的信息熵向量,采用滤波器对熵值进行平滑处理。此时的熵值向量波动减小,但以此估计会产生误差。
所以最终将平滑前后的信息熵进行融合判定,平滑后的结果确定干扰边界的范围,再根据平滑前结果确定精确值,估计得到干扰位置,以及干扰的采样宽度和转发周期。
2.2 基于分段脉冲压缩的ISJ重构
脉冲压缩是一种线性调频信号常采用的处理方式,也是匹配滤波理论很好的实际应用。传统匹配滤波方法采用完整发射信号作为参考函数,对回波信号进行处理,实现对目标能量的积累,并抑制了信号中的噪声,提高了距离分辨能力和精度。因此,在前文参数估计的基础上,我们在文献[11]的分段脉冲压缩方法基础上,提出一种根据非干扰段信号对干扰段进行区分的分段脉冲压缩方法,其基本思路为:采用前文参数估计得出的非干扰段作为信号匹配滤波的参考信号,根据时延对回波信号不同位置进行脉冲压缩。那么,该非干扰段在脉压结果中会在两个位置取得极大值,非干扰段自身所在位置以及采用该段作为干扰信号的所在位置。而当干扰段将前几次样本叠加时,由于匹配滤波是一种线性滤波,分段脉冲压缩对应的非干扰段会分别在叠加位置取得极大值,而叠加的样本来源于取得极大值的未干扰段,那么在进行该叠加段重构时,将模拟干扰机行为,将多段信号进行叠加,形成重构的干扰。据此,非干扰段和干扰段之间的相互关系得到确定。
分段脉冲压缩的输出可以表示为
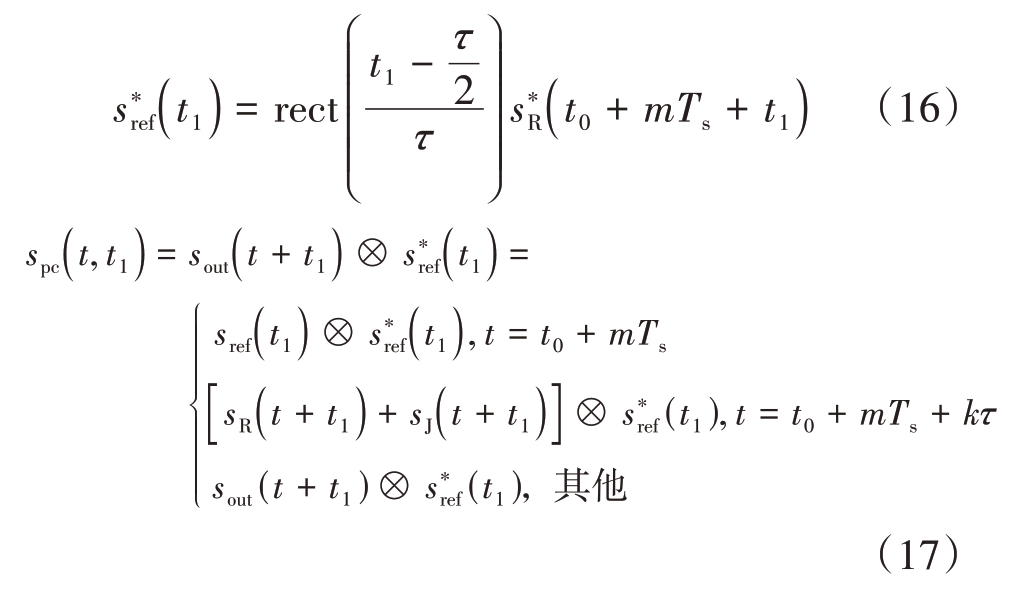
式中,sref 为参考信号,采用回波信号中的未受干扰段,t0为起始时延,位于回波干扰周期的起始位置,t1 为参考信号时延,表示脉冲压缩方向的时延,m为干扰周期数,“其他”为当t ≠t0+ mTs 且t ≠t0+mTs+ kτ的输出结果。
令k1为间歇收发形成的时延,则干扰部分可表示为sJ(t+t1)=sR(t+ t1-k1τ),那么当t=t0+mTs+ kτ时,可分为两种情况:
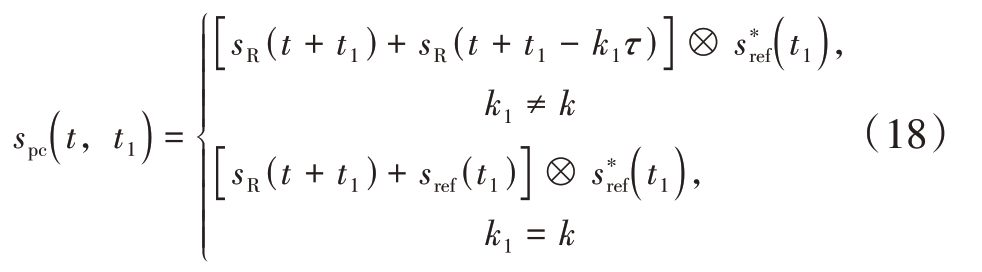
可以看出,在公式(17)和公式(18)中,t 决定了对回波信号段的选择,也就决定了脉冲压缩的结果,当t=t0+ mT表明用于脉压的信号与参考信号相同,t=t0+ mTs+ kτ 表明用于脉压的信号为干扰段之一,那么当k1=k 时,ISJ 所使用的采样信号与参考信号相同,该两个时刻分段脉冲压缩输出取极大值。因此,可以得出在t方向的结果关系如图4所示,被采样段分别再各自转发的位置形成了极值点。
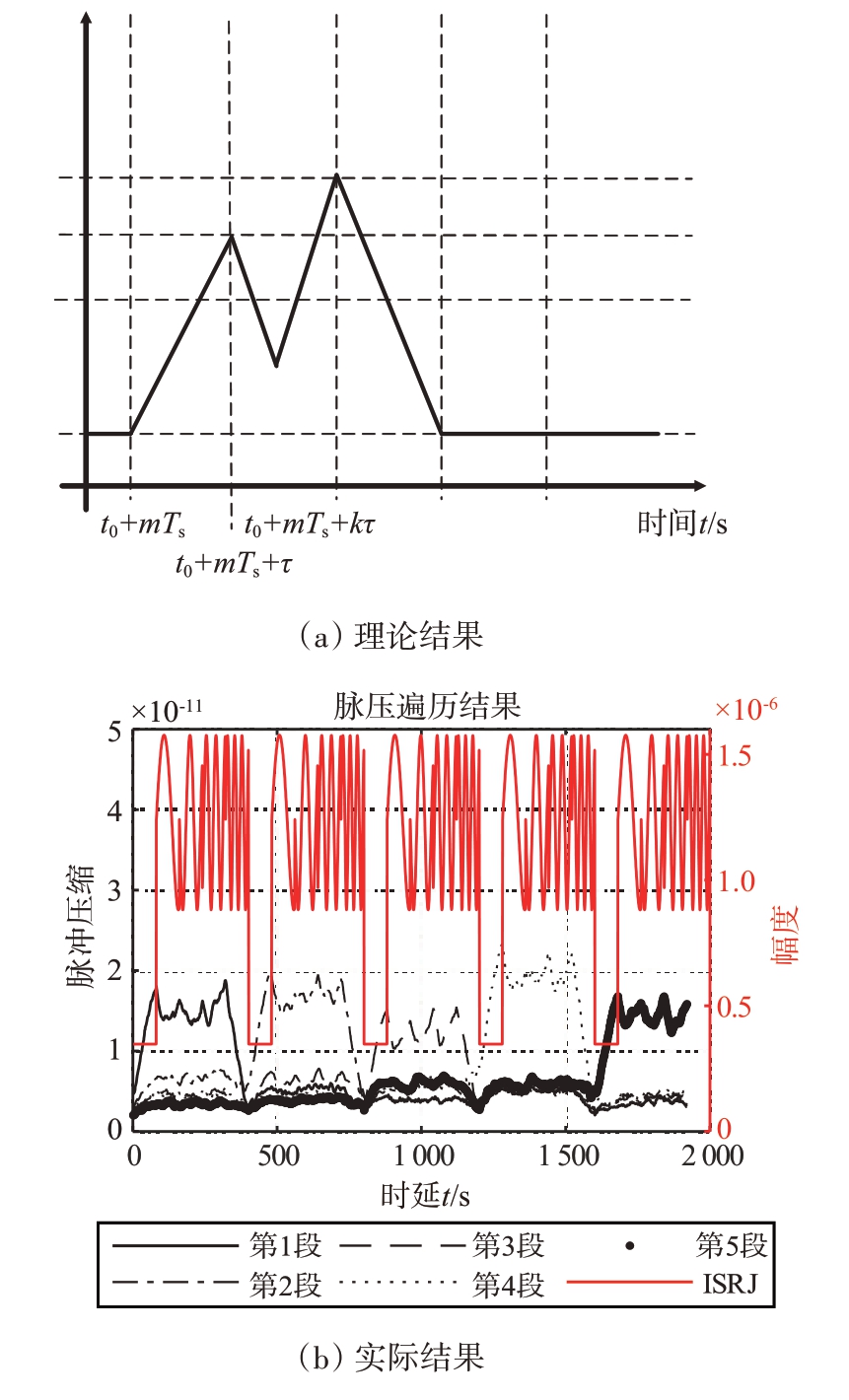
图4 分段脉冲压缩在t方向的结果
在对ISJ 的讨论中,存在复杂的转发情况,干扰机可能采样后立即转发也可以不立即转发。因此在进行分段脉压前,需要对是否是典型ISJ 模型进行判断。
当干扰机立即转发时,可以认为干扰转发脉宽是采样脉宽的倍数,且倍数为转发次数,即![]() 以此认为干扰机立即转发。本文考虑到干扰机为了增强干扰效果,多采用立即转发的形式,而不立即转发时,为了防止残留目标信息过多,转发间隔也不会过长,因此直接采用倍数关系判断。而不立即转发的情况本文尚未进行研究。
以此认为干扰机立即转发。本文考虑到干扰机为了增强干扰效果,多采用立即转发的形式,而不立即转发时,为了防止残留目标信息过多,转发间隔也不会过长,因此直接采用倍数关系判断。而不立即转发的情况本文尚未进行研究。
那么选择在信号子段分界点附近进行脉冲压缩。相较于对信号完整时延进行遍历,计算量低,运算速度快。
由此对线性调频信号内每段未受干扰信号进行处理,可以获得未受干扰段与干扰段之间的对应关系,同时也验证了干扰参数计算的准确性。根据干扰参数,也可以判断得到干扰类型。此时间歇采样转发干扰参数基本获得,可直接对干扰进行重构,采用干扰对消的方式可以对干扰进行抑制。
2.3 算法流程
经过分析,设计ISJ处理流程如图5所示,算法处理步骤如下:
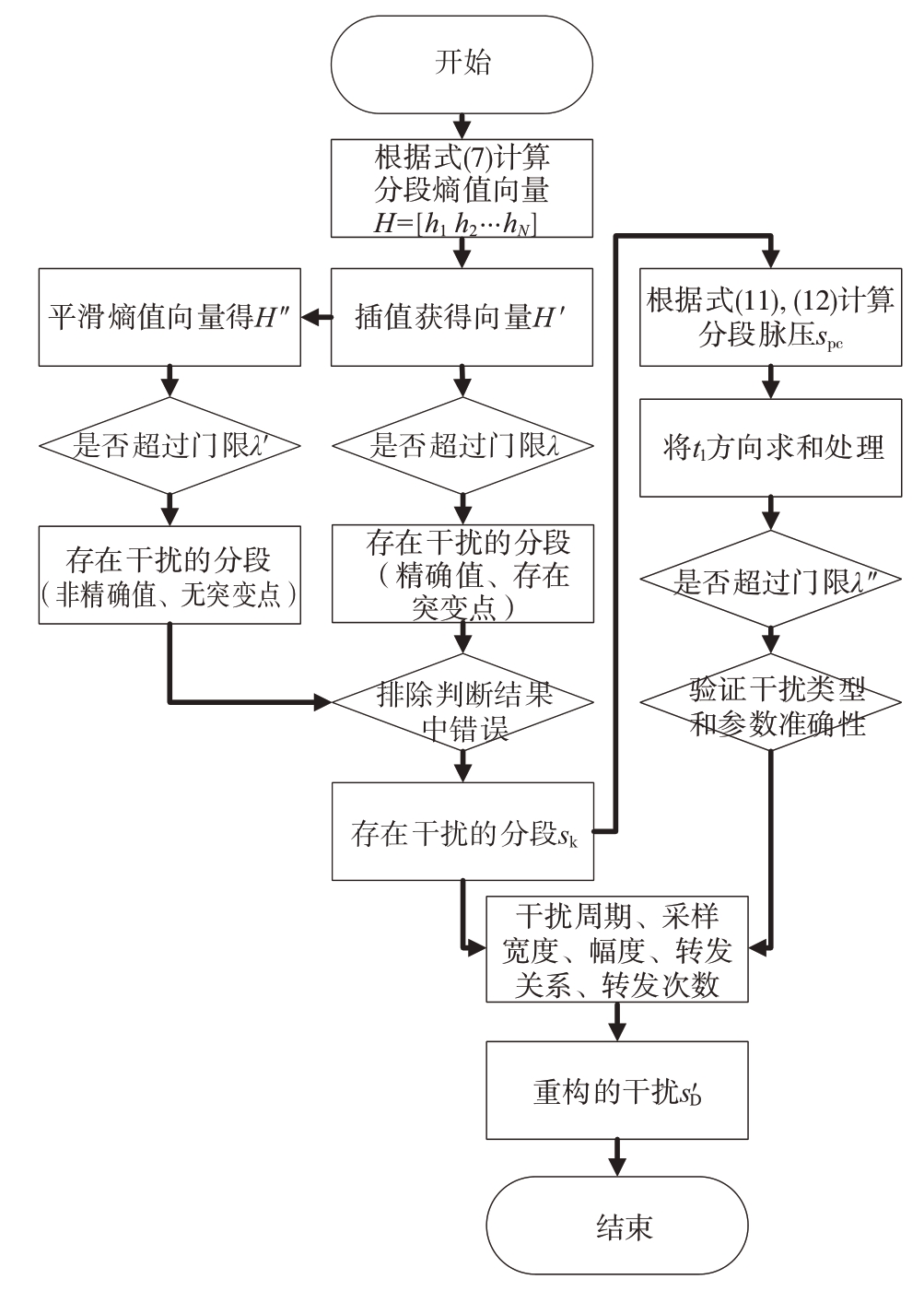
图5 抗ISJ信号处理流程
1)将雷达回波信号进行分段处理,根据分段计算信息熵,并通过插值法补充信息熵向量中缺少的点。
2)对平滑前熵值向量进行二元检验,此时由于噪声影响,获取参数中存在大量偏差。
3)对分段信息熵进行平滑处理,确定干扰参数的模糊范围。
4)将平滑后所得干扰参数范围作为平滑前参数估计结果的判断依据,去除参数估计中的突变点,得到准确干扰周期和采样宽度。
5)根据干扰参数进行分段脉压,获得干扰类型和转发宽度参数,并判断干扰类型和验证参数准确性。
6)依据获取的干扰参数重构干扰,并与受干扰回波信号进行对消,实现干扰抑制。
3 仿真分析
3.1 参数设置
为了对上述抗干扰方法进行仿真分析,对雷达仿真参数设计如表1 所示,采用的仿真平台为Matlab,计算机CPU型号为i7-10750H。
表1 仿真参数设置

参数信号类型载频f0脉冲宽度T带宽B采样频率fs探测距离参数值线性调频信号50 MHz 100 μs 10 MHz 20 MHz 3 km
仿真模拟中采用ISRJ 为例,模拟回波处理情况。由于间歇采样转发干扰间歇收发的特性,回波的干信比和干噪比与干扰采样占空比有关,因此设置采样脉宽τ=4 μs,采样周期Ts=20 μs,转发次数为4 次。设JSR=20 dB,JNR=5 dB,此时,信号基本被干扰完全遮蔽,受干扰回波脉冲压缩结果如图6所示。
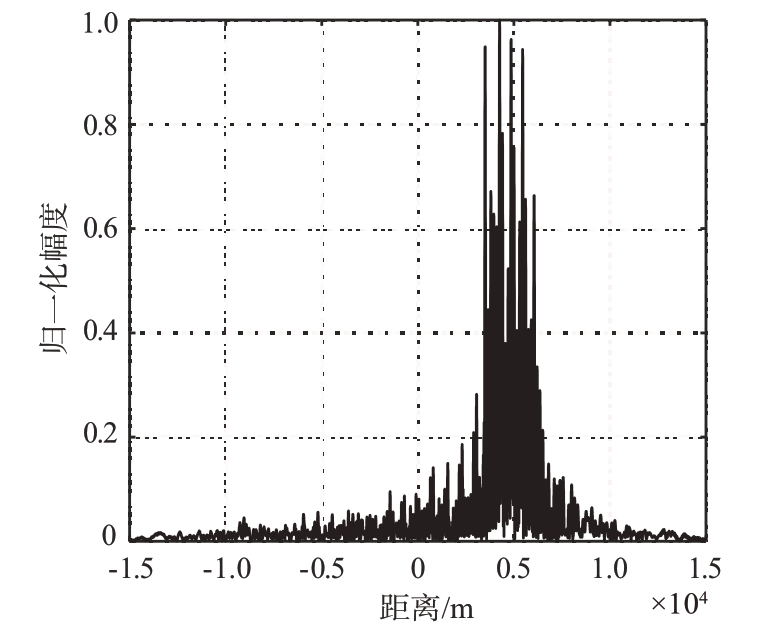
图6 受干扰回波脉压结果
可以看出,干扰信号与真实目标混合形成了多个主假目标峰和密集的次假目标,目标受到遮蔽,检测难度大,干扰难以去除。
3.2 分段信息熵处理效果
采用分段信息熵处理,设分段数为600。JNR=5 dB 时平滑前后二元检验效果如图7(a)、(b)所示,判定为回波时置0,为干扰时置1。得到的干扰边界位置如图7(c)所示,正值为上升沿,负值为下降沿。通过平滑处理的方式,分段信息熵法能够较稳定进行干扰检测。
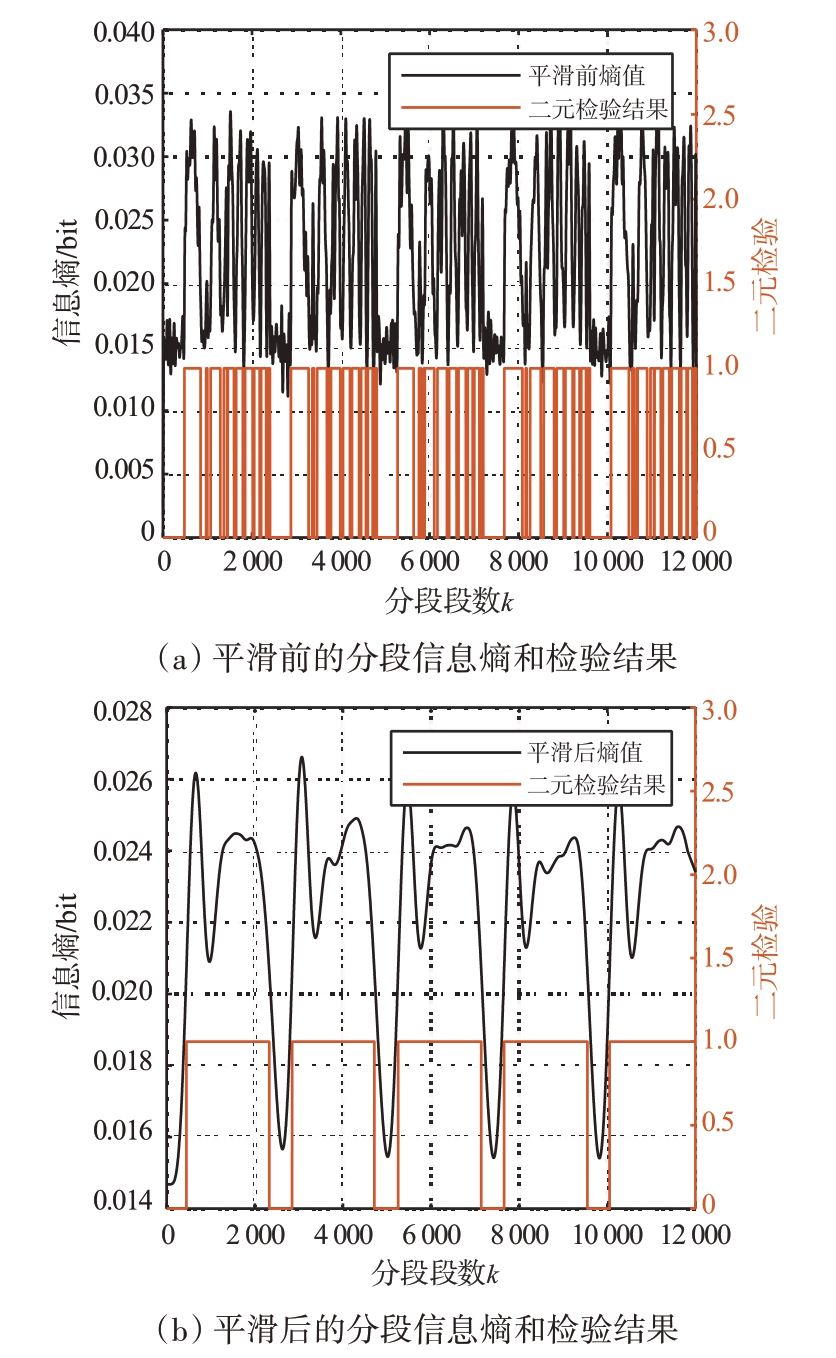
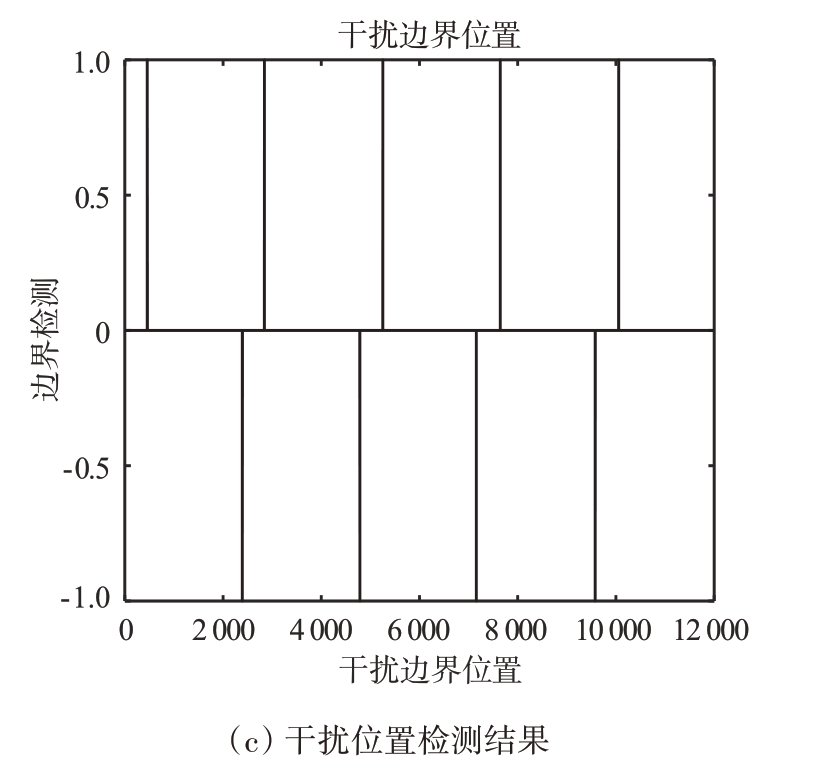
图7 分段信息熵处理效果
3.3 分段脉压处理效果
根据分段信息熵获取的参数,在干扰采样宽度和转发周期已知的情况下进行处理,可以得到对ISRJ脉压遍历结果如图8所示。
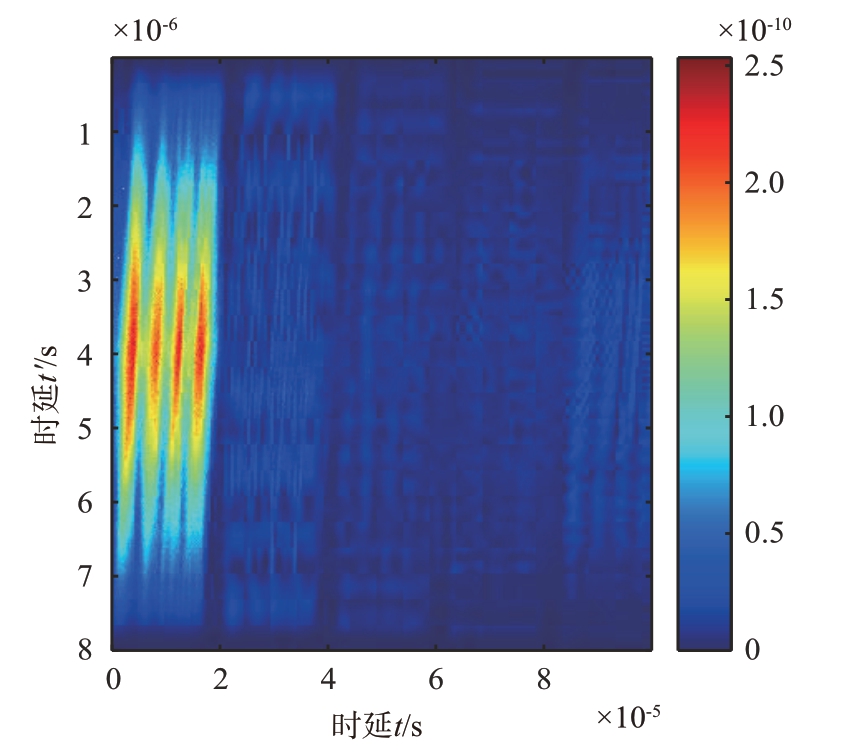
图8 脉压遍历效果
那么对脉压遍历结果在脉压时延方向上进行求和,得到回波信号与未受干扰段匹配程度一维图像为图4(b)。分段脉压降低了运算量,只对干扰子段边沿进行遍历,其中对第一段未受干扰段进行分段脉压效果如图9和图10所示。
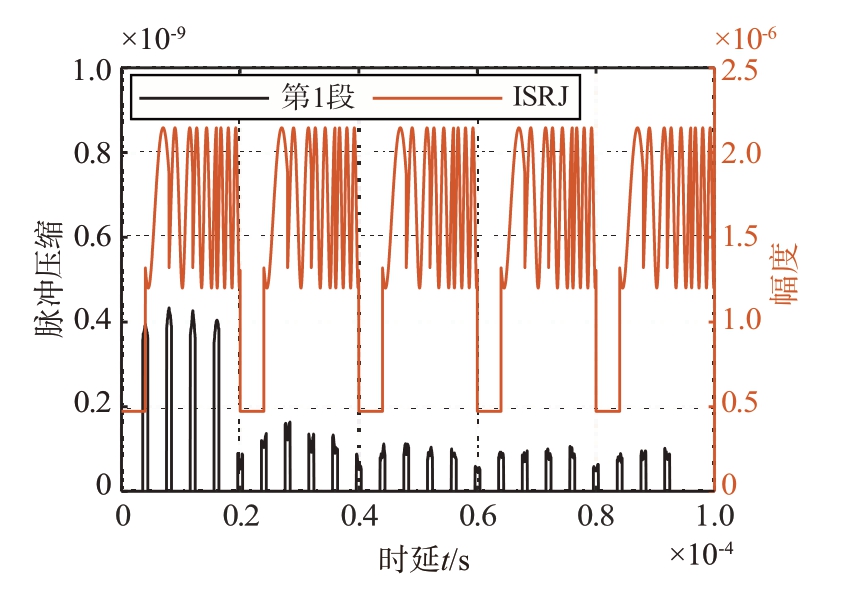
图9 分段脉压效果
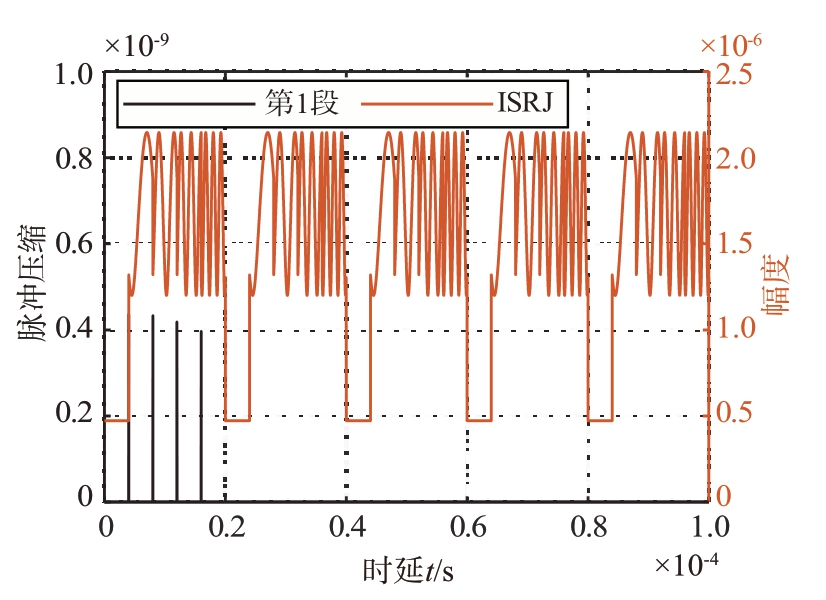
图10 分段脉压检测结果
此时可以判断出干扰采样段在干扰中所处位置,并还原干扰信号,如图11所示。
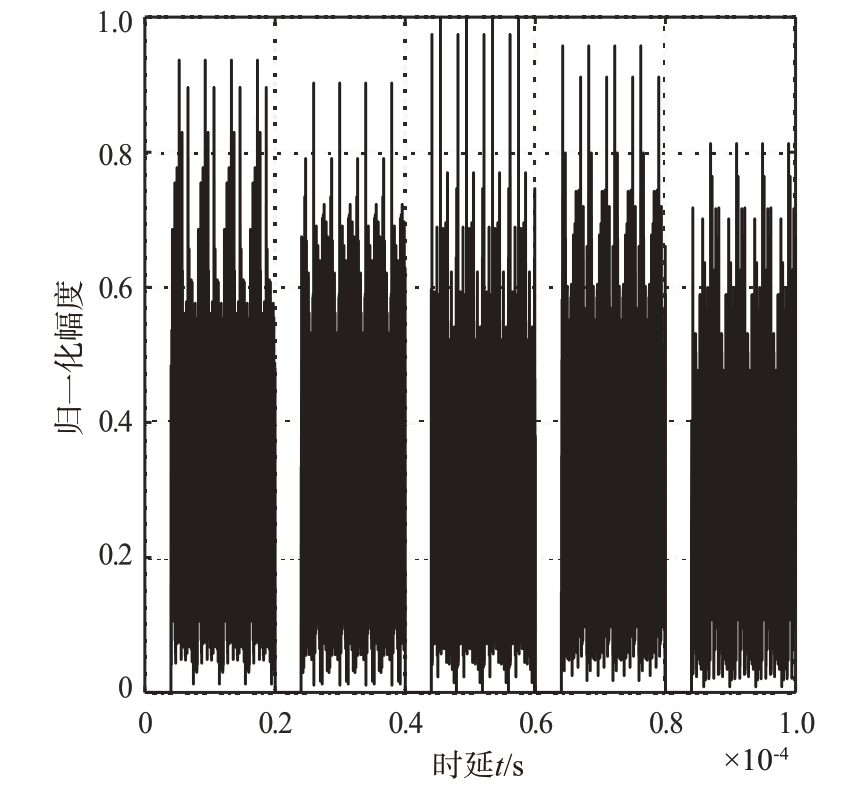
图11 干扰重构效果
3.4 性能分析
为了验证本文算法有效性,在干噪比为0~10 dB情况下,对该算法进行100次蒙特卡洛仿真。
计算不同干噪比条件下分段信息熵计算干扰参数对直接、重复、循环三种干扰模式的均方根误差,以ISJ 转发周期为例,分段信息熵测量误差随干噪比变化情况如图12所示。
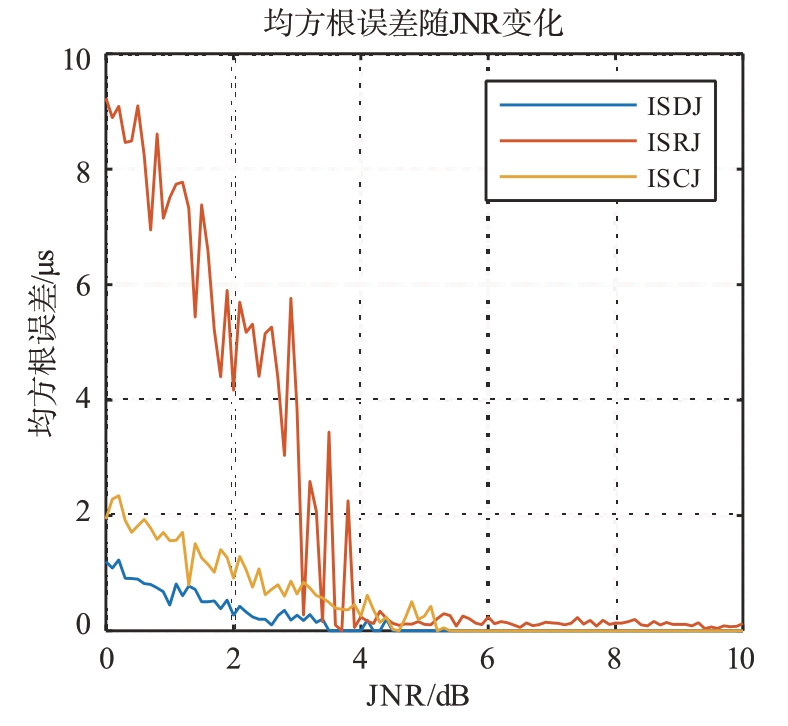
图12 JNR变化对不同干扰类型检测误差的影响
从图12可以看出,随着JNR 增大,估计的精确度有明显提升,当JNR 达到5 dB 时,估计的均方根误差降低到了0.05 μs,并趋于稳定。
在不同干信比条件下对算法的鲁棒性进行了测试,保持JNR=5 dB,计算干信比从低到高时的估计误差,计算结果如图13所示。
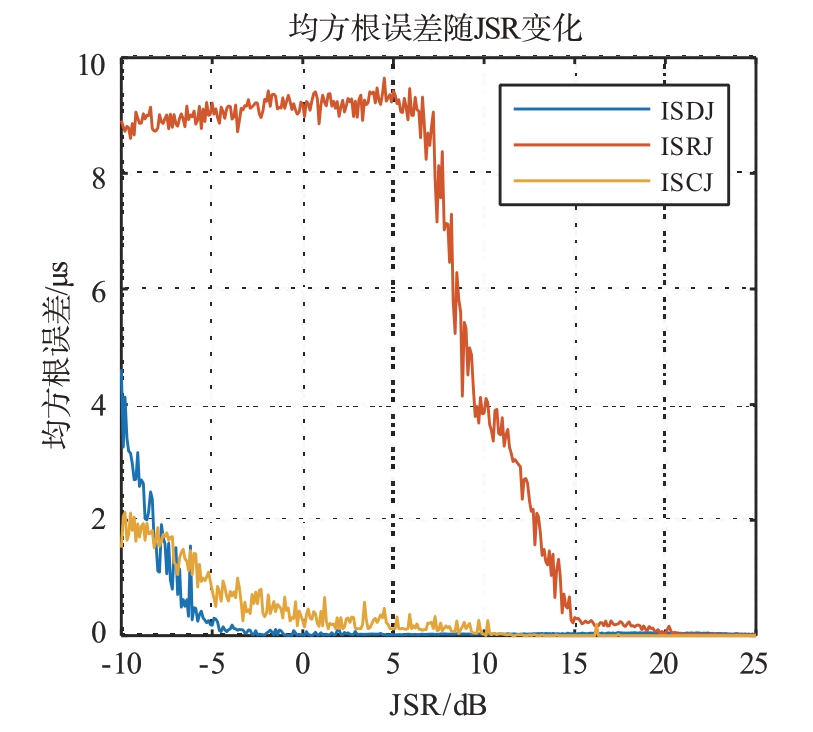
图13 JSR变化对不同干扰类型检测误差的影响
可以看出,算法对于ISDJ和ISCJ较为稳定,在JSR 大于5 dB 时较为稳定,而对于ISRJ 则需要当JSR大于15 dB时可以较为稳定地测量干扰参数。
为了测试该方法在分段数不同时的稳定性,调整分段数为300~500段进行估计,最终均方根误差和相应运行时间随分段数变化结果如图14所示。
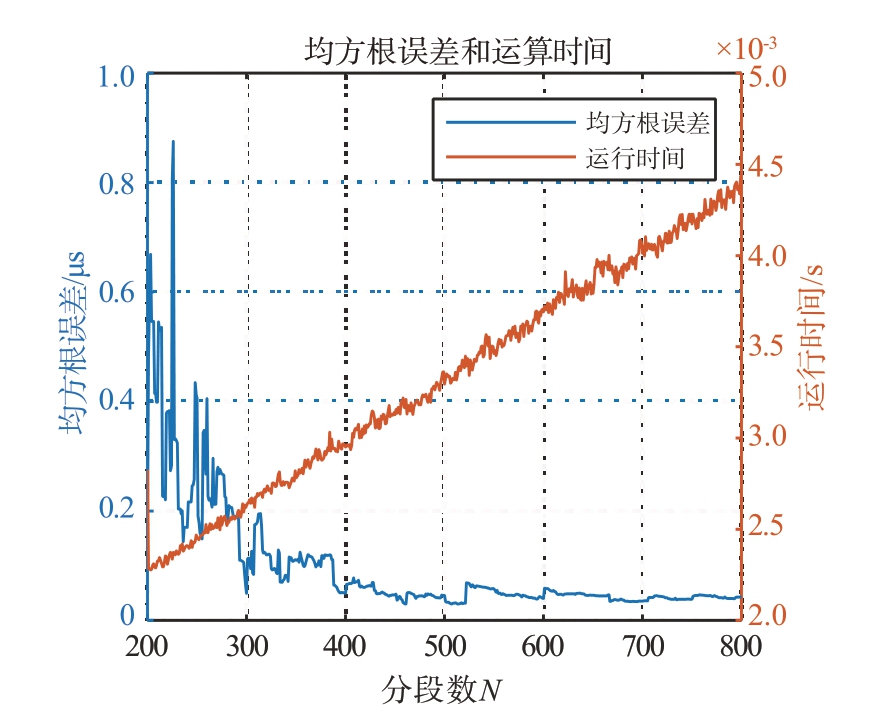
图14 分段数变化对检测误差和运行时间的影响
可以发现,随着分段数增多,估计结果均方根误差明显下降,在分段数达到400 段以后,误差降低明显,均方根误差达到0.1 μs以下,且趋于稳定。而运行时间则随分段数线性变化。
将本文参数估计方法与现有文献中的方法[2,5]进行对比,对比结果如图15所示。
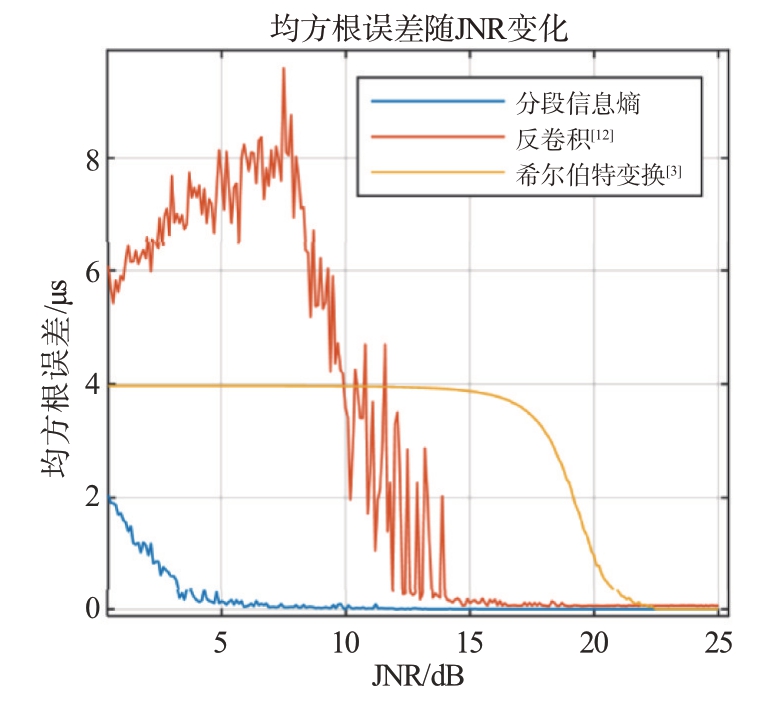
图15 JNR变化对不同方法检测误差的影响
在相同条件下,该方法的估计误差受JNR 影响相比反卷积法和希尔伯特变换法有明显下降,文献[12]采用反卷积的方法对ISJ 的参数进行估计,受干扰影响较大,在干噪比达到20 dB 以上时趋于稳定。文献[3]采用了时频分析和希尔伯特变换结合的方式来分析干扰模式和估计干扰参数,从图中可以看出,该方法在达到15 dB 以上时较为精确,噪声对该方法稳定性的影响仍然较大。此外,在文献[7]中采用的基于ADMM 的干扰切片宽度和数量估计方法经过迭代,在干噪比达到10 dB时,均方根误差趋于稳定,稳定值约为0.02 μs。相较而言,本文分段信息熵法能够实现在JNR 达到6 dB 时,估计的均方根误差达到0.05 μs,并趋于稳定。
仿真中分别统计了三种方法的运行时间,统计结果如表2所示。
表2 算法运行时间比较

方法本文反卷积法[12]希尔伯特变换法[3]运行时间/s 0.003 3 0.001 1 0.003 8
可以看到,在分段数为600段时分段信息熵方法的运行时间较快,处于中等水平,比希尔伯特变换法快但比反卷积法慢。
在经过分段脉压处理后,估计得到了信号段和干扰段之间的关系并重构了干扰,将干扰与原信号进行对消,其中导入干扰参数时,采用的均方根误差为0.1 μs,干扰假目标抑制效果约5 dB,脉冲压缩后的结果如图16所示。
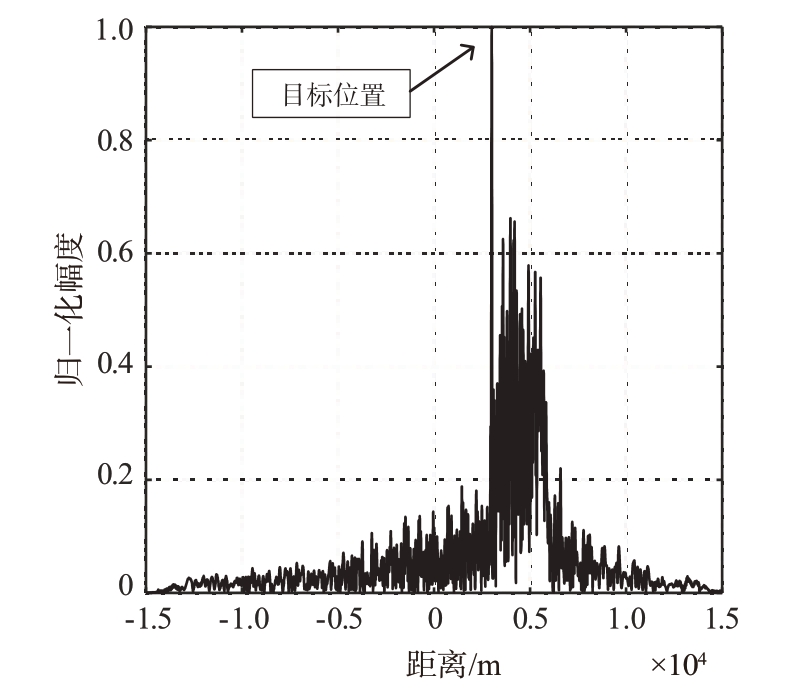
图16 对消后的脉压结果
可以看出,经过该方法处理后回波中的ISJ 受到了抑制。采用干扰重构对消方法在计算结果精确的情况下能够极大削弱ISJ 干扰效果,且估计误差越低时,采用干扰重构的抑制效果越好,因此对设备要求较高,并存在部分引入新干扰的风险,但影响较小。
4 结束语
间歇采样转发干扰针对大时宽带宽的雷达信号具有较高威胁。本文针对该问题将信息熵和脉冲压缩结合,基于分段的思想,将回波信号进行区分并获取间歇采样转发干扰参数以及与原信号的关系信息,最终进行重构和剔除。相较于传统方法,提高了在强噪声环境下的检测能力,同时运行速度较快,但在对干扰的剔除上仍然需要一定的改进以提升稳定性。仿真结果表明该方法在干噪比为6 dB 以上时,能够较为精确的判断干扰并进行去除,抑制效果可以控制在5 dB 以上,证明了该方法的可行性和有效性。
[1]刘忠,王雪松,刘建成,等.基于数字射频存储器的间歇采样重复转发干扰[J].兵工学报,2008,29(4):405-410.
[2]刘巧玲,李文臣,张文明,等.间歇采样移频转发干扰效果仿真分析[J].电子信息对抗技术,2009,24(1):48-50.
[3]ZHOU Chao,LIU Quanhua,CHEN Xinliang.Parameter Estimation and Suppression for DRFM-Based Interrupted Sampling Repeater Jammer[J].IET Radar,Sonar & Navigation,2018,12(1):56-63.
[4]杨小鹏,韩博文,吴旭晨,等.基于短时分数阶傅里叶变换的间歇采样转发干扰辨识方法[J].信号处理,2019,35(6):1002-1010.
[5]周超,刘泉华,曾涛.DRFM间歇采样转发式干扰辨识算法研究[J].信号处理,2017,33(7):911-917.
[6]周畅,范甘霖,汤子跃,等.间歇采样转发干扰的关键参数估计[J].太赫兹科学与电子信息学报,2019,17(5):782-787.
[7]尚东东,张劲东,胡婉婉,等.基于ADMM 的间歇采样转发式干扰的参数估计[J].雷达科学与技术,2021,19(4):417-422.
[8]李欣,王春阳,包磊,等.基于Partial FFT 的间歇采样转发干扰抑制方法[J].探测与控制学报,2018,40(6):43-49.
[9]WU Wenzhen,ZOU Jiangwei,CHEN Jian,et al.False-Target Recognition Against Interrupted-Sampling Repeater Jamming Based on Integration Decomposition[J].IEEE Trans on Aerospace and Electronic Systems,2021,57(5):2979-2991.
[10]蒋莹,何明浩,郁春来,等.基于熵理论的间歇采样转发干扰识别方法[J].现代防御技术,2016,44(3):104-109.
[11]张建中,穆贺强,文树梁,等.基于LFM分段脉冲压缩的抗间歇采样转发干扰方法[J].电子与信息学报,2019,41(7):1712-1720.
[12]MENG Yunyun,YU Lei,WEI Yinsheng,et al.A Novel Parameter Estimation Method of Interrupted Sampling Repeater Jamming[C]//2019 IEEE International Conference on Signal,Information and Data Processing,Chongqing,China:IEEE,2019:1-5.
