0 引 言
由于单脉冲雷达测角不受目标回波振幅变化影响,导致幅度调制的干扰方法失效,另外,国外典型单脉冲机载火控雷达角跟踪能力强,进入跟踪干扰源模式后,能够快速推算出目标距离,还可采用双机交叉定位实施攻击。所以,对单脉冲体制的机载火控雷达进行角度诱骗较难,需要从单脉冲雷达固有缺陷出发,通过干扰增大测角误差。近年来,协同干扰成为研究热点,文献[1-5]主要针对直线排列的多个干扰源组成多对干扰机,研究协同干扰的影响因素、干扰效果等,主要应用于空对面干扰场景;文献[6-8]主要对多源反向交叉眼干扰的干扰环路影响因素进行了分析,应用于多弹协同突防场景;文献[9]从协同干扰的理论发展、装备发展、应用难题以及研究趋势等4 个方面进行综合论述;文献[10]对多环路反向交叉眼干扰进行建模,分析了平台运动在不同干扰环路间引入的多普勒频率差,并分析了多普勒频率差补偿的敏感度和多普勒频率差对参数容限的影响。上述研究对于多源反向协同干扰提供了思路,但是,空空对抗中,多机编队只有在具有绝对优势,采用“墙形”战术时才可能呈直线排列,针对空空对抗多机协同干扰目标选择、干扰机动态编组还鲜见报道。
世界军事强国近几年空战对抗演习表明,战斗机协同作战已经成为当前和今后一段时期的主要作战样式,且随着高速数据链技术的发展,编队动态重组以及多机之间高速共享告警信息、干扰样式和干扰策略等成为现实。本文从多机信号级协同干扰出发,探索多机动态可重构协同干扰策略并选择最优干扰对象,拟为优化战斗机协同干扰提供借鉴。
1 问题描述
传统的协同干扰指战术级的协同干扰,即不同平台从不同方向或不同时段进行干扰,平台之间在干扰时序上区分同步和异步,干扰样式可根据干扰平台特性进行加载。战术级协同干扰面对机载有源相控阵雷达时,主要存在以下问题。
1.1 复杂电磁环境问题
战斗机空战中,突击编队执行空中火力打击、夺取制空权等任务时,面临敌防空体系的严重威胁。作战对象包括多种平台,涵盖不同体制雷达,频域几乎覆盖全频段,且成体系存在,一部发现,全网皆知,使空中进攻作战的电子干扰掩护面临复杂的电磁威胁环境,实施干扰难度加大。单机可同时干扰目标数量有限,面临大量空中、地/海面目标时,若各飞机独立实施干扰,必定存在漏干扰、重复干扰、干扰能量稀释等问题。
1.2 雷达跟踪干扰源问题
自卫干扰和随队支援干扰可在距离、速度上产生干扰效果,但无法降低雷达角度测量精度,雷达通过跟踪干扰源可获得准确的角度信息。双机通过三角定位和融合跟踪,可获取目标精确的距离、速度信息,满足火控攻击的精度需求。另外,从国外先进机载火控雷达和空空导弹作战能力来看,雷达受到干扰后,由于仍具备精确的角度测量能力,在体系支援下,仍可进行火控攻击引导。
1.3 战斗机干扰目标分配和资源选择问题
战斗机均具备同时干扰多目标功能,在体系对抗中,为提升战斗机复杂电磁环境下的干扰效能,应通过干扰目标选择、合理分配编队干扰资源,保证干扰目标的全覆盖,同时提高干扰信号的瞬时频域覆盖范围,提升多目标场景下的干扰能力。传统的干扰目标分配方法,很大程度上由威胁目标的威胁程度决定,而干扰资源的分配常常在任务规划阶段已经完成,对抗中,长机难以根据战场态势进行干扰资源实时分配。在远距离编队作战场景中,传统的干扰目标分配和干扰资源选择方法难以适应战场态势的变化,无法达成目标的最优选择和资源的最优分配。
2 双机协同干扰建模与分析
2.1 多机协同干扰数学模型
多机协同作战时,可以组合成为多个两源反向干扰系统,协同干扰飞机之间通过高速数据链传递告警信息、干扰策略、干扰样式和干扰信号特征参数等,容易实现干扰信号的幅度和相位的控制。典型多机协同干扰示意图如图1所示。

图1 协同干扰示意图
图1 中,A 表示机载火控雷达O 受到飞机A1、A2 协同干扰后指向的假目标,θe 表示干扰机天线半张角,θ1、θ2 分别表示飞机A1、A2 与机载火控雷达O 连线相对于雷达法向的夹角,θs表示由交叉眼干扰引起的雷达跟踪误差角大小,θr表示干扰双机连线旋转角,r1、r2分别表示飞机A1、A2与机载火控雷达的距离,rA 表示飞机A1 和A2 连线的中点到机载火控雷达中心的距离。双机协同干扰增益Gc为[11]
式中,ℜ表示取实部,a和φ分别为干扰信号的幅度比和相位差。单脉冲指示角θi与干扰双机连线θr、半张角θe之间的关系为
在协同干扰作用下单脉冲雷达测角误差为
根据图1中的几何关系有
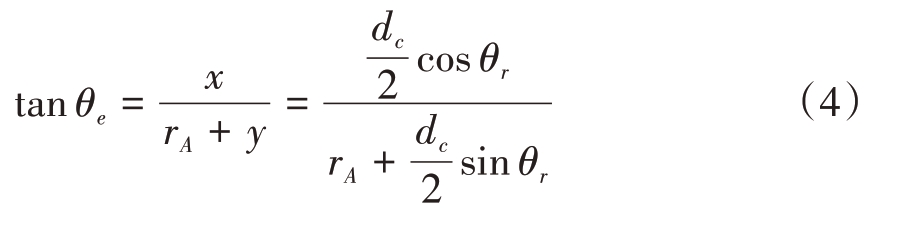
则
将式(1)和式(5)代入式(2)和式(3)即可得到测角误差:
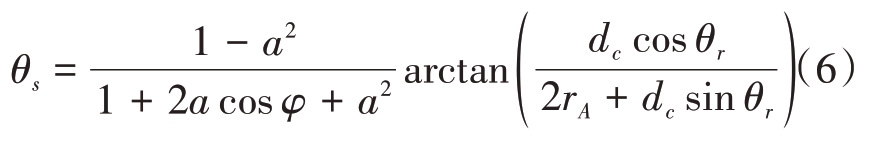
1)幅度比、相位差和旋转角对干扰效果的影响
协同干扰双机连线旋转角、干扰信号幅度比和相位差变化时,对机载火控雷达测角误差的影响如图2所示。
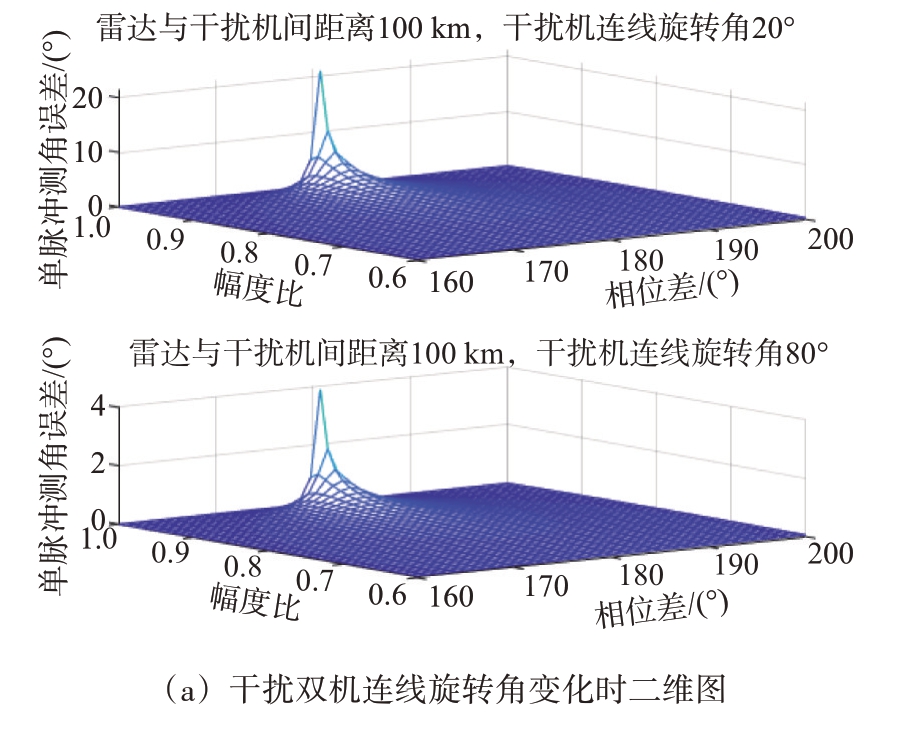
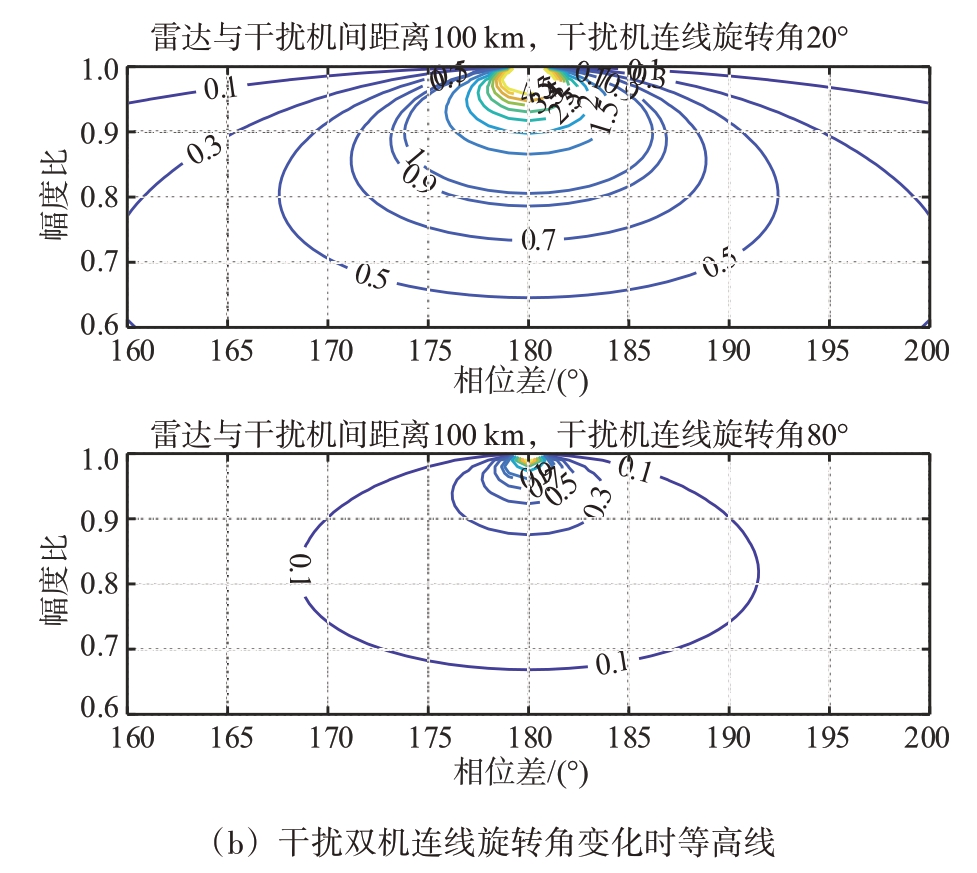
图2 测角误差随干扰信号幅度比和相位差变化
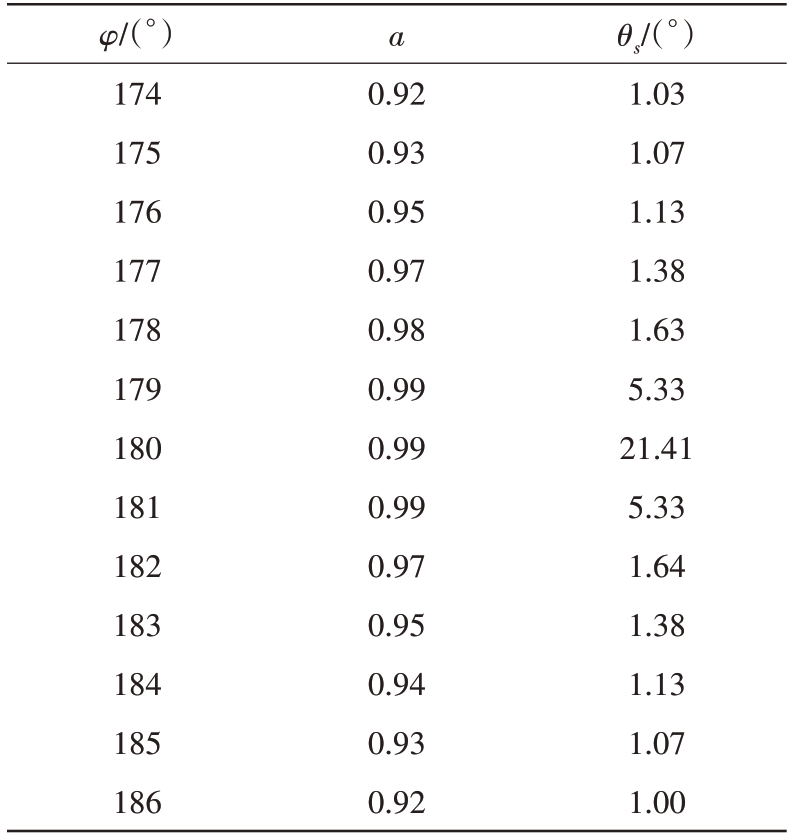
从图2 可以看出,干扰机距离雷达100 km、两干扰信号相位差为180°且幅度比接近1时,协同干扰导致雷达测角误差最大,且随着相位差越接近180°,同时幅度比越接近1 时,协同干扰对雷达测角误差影响变化率越大。当雷达与两干扰机距离、信号幅度比和相位差保持不变,干扰双机连线旋转角从0°增加到90°时,协同干扰对雷达测角误差影响越小。雷达与干扰机间距离为100 km 且干扰双机连线旋转角为20°时,测角误差大于1°时,相位差与幅度比取值范围如表1所示。
表1 测角误差大于1°时相位差与幅度比取值
φ/(°)174 175 176 177 178 179 180 181 182 183 184 185 186 a 0.92 0.93 0.95 0.97 0.98 0.99 0.99 0.99 0.97 0.95 0.94 0.93 0.92 θs/(°)1.03 1.07 1.13 1.38 1.63 5.33 21.41 5.33 1.64 1.38 1.13 1.07 1.00
从表1可以看出,协同干扰导致雷达测角误差增大,对协同干扰信号的幅度比和相位差均提出较高的要求,测角误差大于1°时,协同干扰信号幅度比要求在[0.92,1],且相位差在[174°,180°]。相位差为180°、幅度比为0.97 时,干扰机双机连线旋转角对测角误差的影响如图3所示。
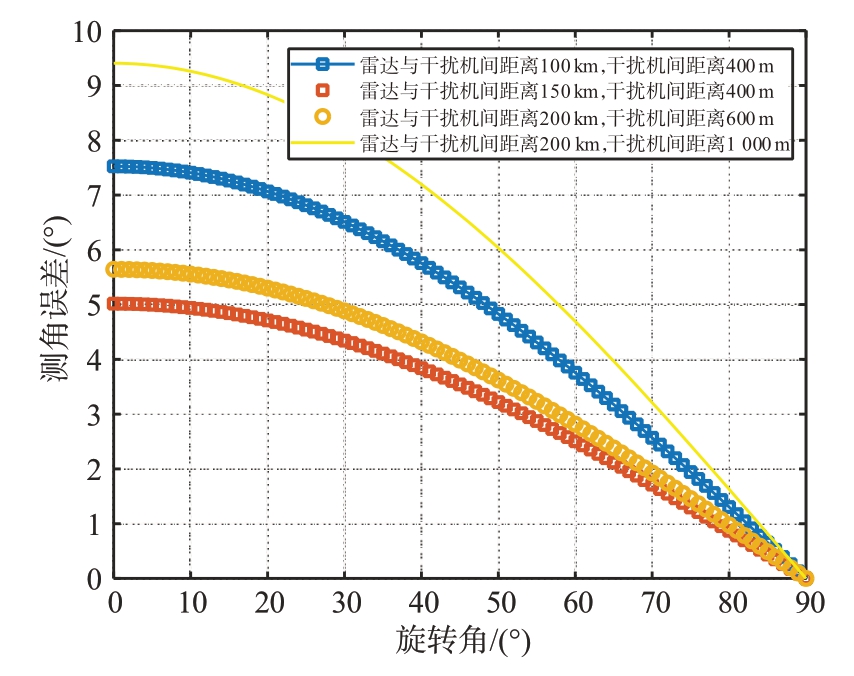
图3 干扰双机连线转角对测角误差的影响
从图3 可以看出,在雷达与干扰机距离、干扰机间距离均变化时,随着干扰双机连线旋转角从0°增加到90°,对测角误差的影响逐渐减小,说明要想达到好的干扰效果,干扰机双机连线要尽量对准干扰目标,如果因战术需要,双方机动导致干扰双机连线旋转角大于90°,此时协同干扰无效,可以关闭干扰,节省能量。
2)载目距离对干扰效果的影响
干扰机双机距离600 m、干扰双机连线旋转角为20°时,当雷达与干扰机间距离从150 km 增加到200 km 时,双机协同干扰对雷达测角误差的影响逐渐降低,降幅约5°,如图4所示。
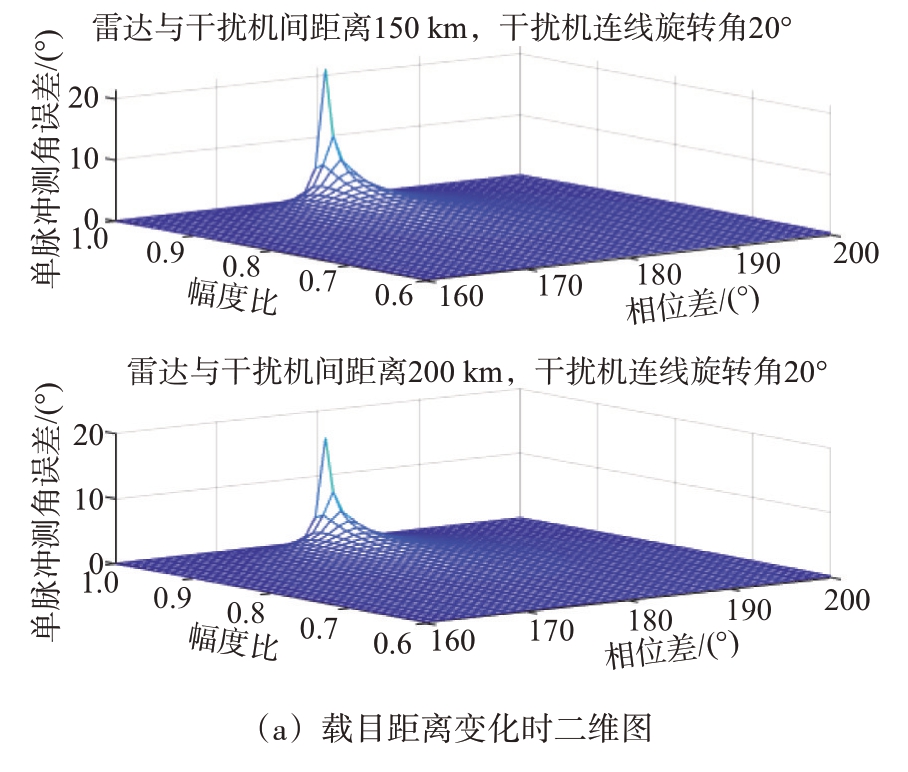

图4 测角误差随干扰信号幅度比和相位差变化
相位差为180°、幅度比为0.97 时,干扰双机连线旋转角对测角误差的影响如图5所示。
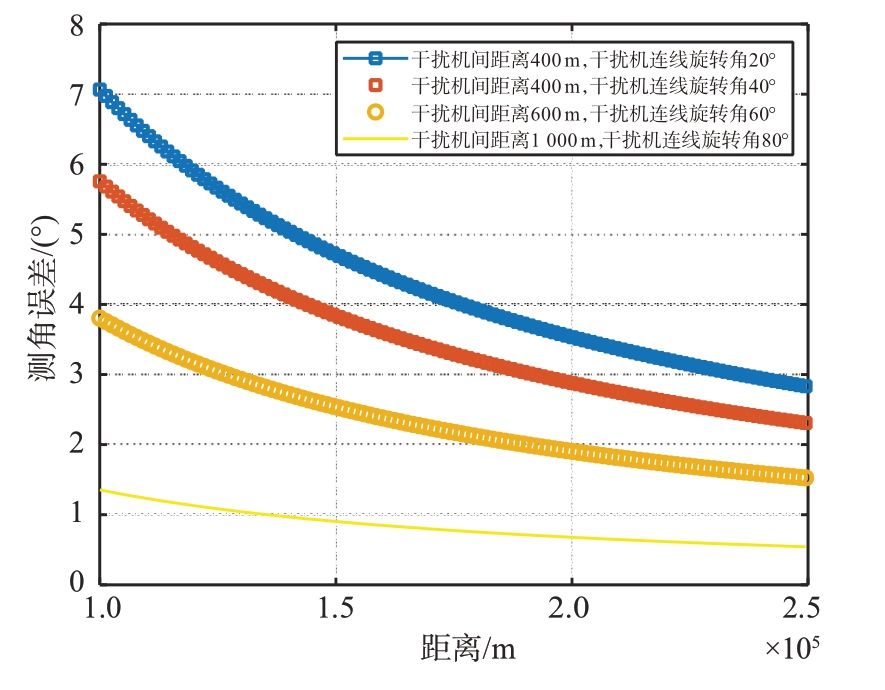
图5 雷达与干扰机间距离对测角误差的影响
从图5 可以看出,干扰机间距离、干扰双机连线旋转角变化时,随着雷达与干扰机间距离的增加,测角误差逐渐减小。
3)干扰机双机距离对干扰效果的影响
干扰双机连线旋转角为40°、雷达与干扰机间距离为250 km 时,当干扰机间距离从400 m 增加到600 m 时,协同干扰对雷达测角的影响逐渐增大,增幅约3°,如图6所示。
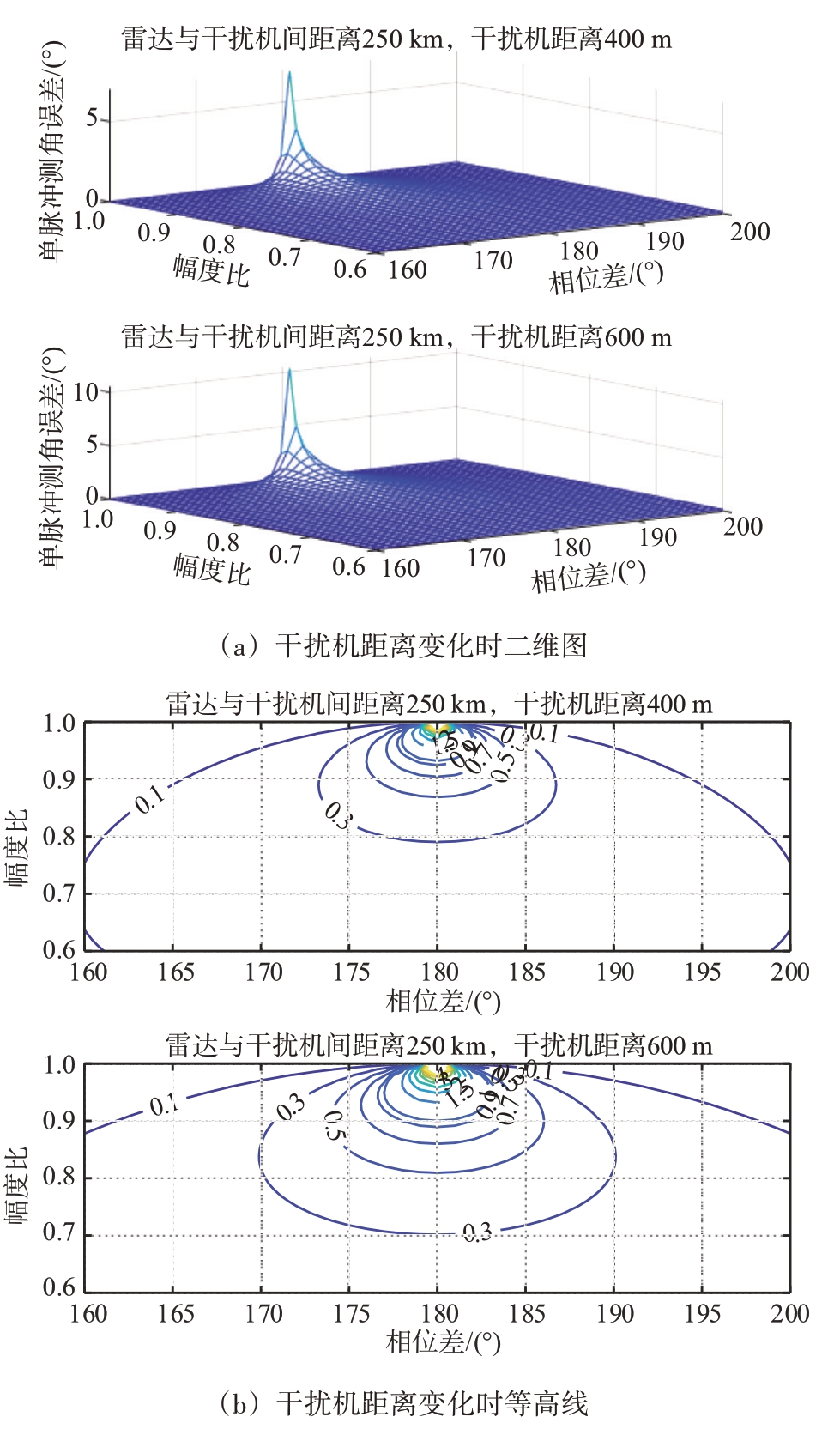
图6 干扰机双机距离对干扰效果的影响
相位差为180°、幅度比为0.97 时,干扰机间距离的变化对测角误差的影响如图7所示。
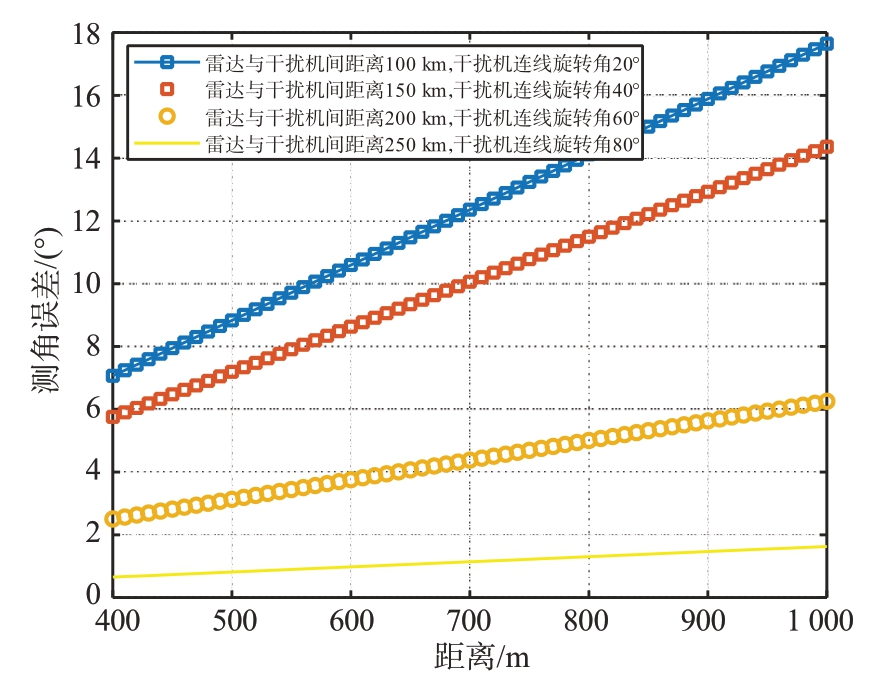
图7 干扰机间距离对测角误差的影响
从图7 可以看出,雷达与干扰机间距离、干扰双机连线旋转角不同时,随着干扰机间距离的增大,测角误差逐渐增大,说明了双机在雷达同一波束内时,增大干扰机间的距离,可以达到更好的干扰效果,但是,两干扰机间的距离大于雷达距离分辨率时,雷达能够分辨出两个目标,会导致干扰无效,且容易被雷达跟踪两个干扰源。
根据近距格斗和超视距空战特点,假设雷达与干扰机间距离为20~300 km,雷达角度分辨率为0.1~10 mrad,根据协同干扰要求两个干扰源必须在雷达角度分辨率内,则两干扰机间距离要求如图8所示。
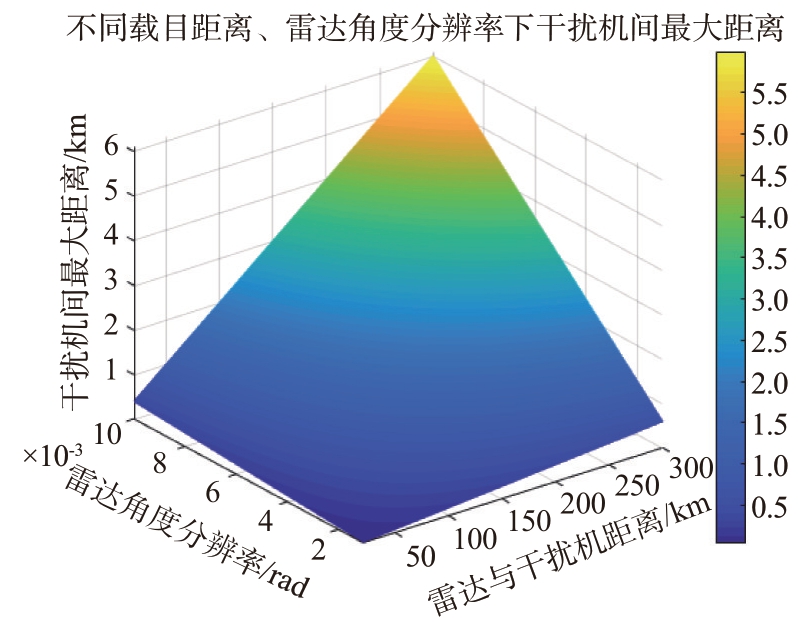
图8 协同干扰对干扰机双机距离要求
从图8可以看出,雷达角度分辨率和雷达与干扰机距离越小时,要求两干扰源距离越近,例如当雷达角度分辨率为5 mrad、雷达与两干扰源距离分别为20,80,150 和250 km 时,两干扰源之间的最大距离分别为80,320,600 和1 000 m。所以,协同干扰对干扰源间距提出了较高要求。
2.2 连通图模型
图理论在工程实践中应用非常广泛[12-13],根据多机协同干扰特点,将空战场景用连通图进行描述,其中,被干扰飞机和释放干扰的编队飞机看成连通图中的节点,被干扰飞机为固定节点,即每个时刻的连通子图中必须含有一个被干扰飞机,这些节点以及非固定节点连线的中点通过加权连接边进行连接,连通子图连接边的差值表示此协同干扰系统的稳定性。基于连通图找到每一时刻最优干扰连通子集,得到针对固定节点的最优协同干扰组合。
假设红蓝双方分别有m 架和n 架飞机,k 时刻针对红方第i 架飞机进行协同干扰的飞机为蓝方的Ln、L2和L5飞机,则连通图如图9所示。
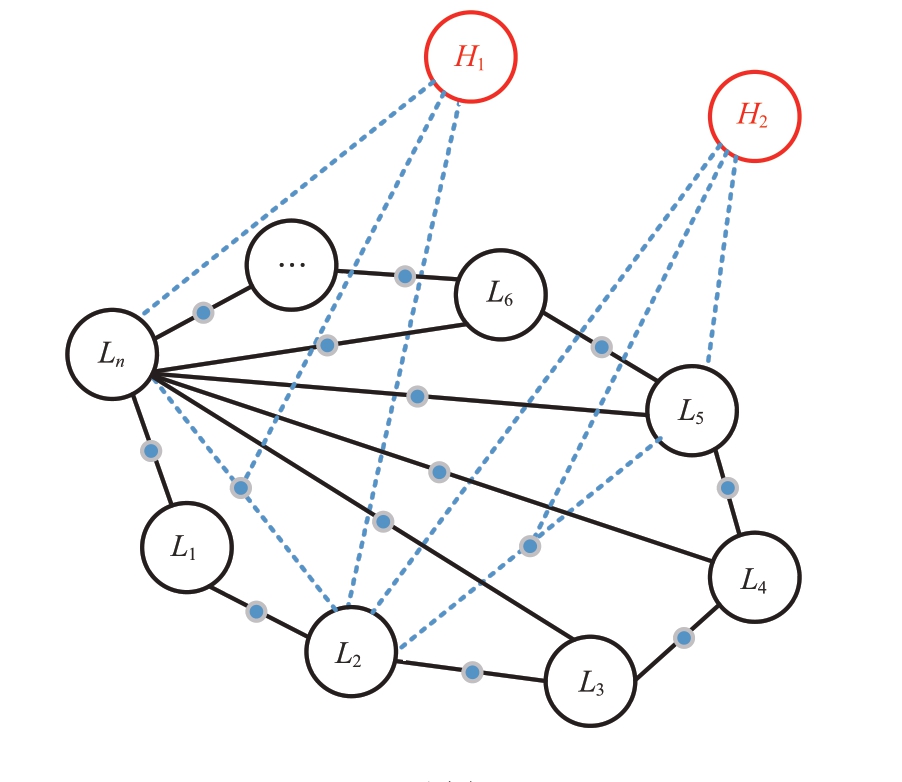
图9 k时刻连通图
记图9 中的k 时刻的连通子图为Gik=(Hki,Hkn i,Zkn i),其中,i=1,2,H 为固有顶点的集合,L为常规顶点的集合,Z 为常规顶点之间中点的集合。根据可能的红蓝双方位置关系来确定各顶点之间的连通关系,很显然,每个连通子图都为连通图G的一个子图,即G′ ⊆G,H′ ⊆H,Z′ ⊆Z。如果在红蓝双方飞机数量分别为m 架和n架的场景中,某一时刻连通子图的个数最多为m×C2n,以F-22 飞机为例,编队协同作战飞机数量不大于4 架,编队与编队之间再形成编队组合,且同一架飞机能够同时干扰的飞机数量也不大于4 架,所以,一般情况下,m≤4,n≤4。
2.3 连通子图动态可重构策略
连通子图动态可重构策略决定系统从k 时刻到k+1时刻采用哪些连通子图,实现动态可重构协同干扰,即根据 k 时刻的连通子图![]() 模型概率μ(k-1)、状态估计X(k-1)和观测值Z(k-1)来确定下一时刻的图
模型概率μ(k-1)、状态估计X(k-1)和观测值Z(k-1)来确定下一时刻的图![]() 根据协同干扰数学模型和典型作战场景飞机数量可知,连通子图最多为24 个,约束条件一般小于5 个,普通寻优算法能够很快实现,这里不再赘述。基于蚁群算法的算法流程图如图10所示。
根据协同干扰数学模型和典型作战场景飞机数量可知,连通子图最多为24 个,约束条件一般小于5 个,普通寻优算法能够很快实现,这里不再赘述。基于蚁群算法的算法流程图如图10所示。
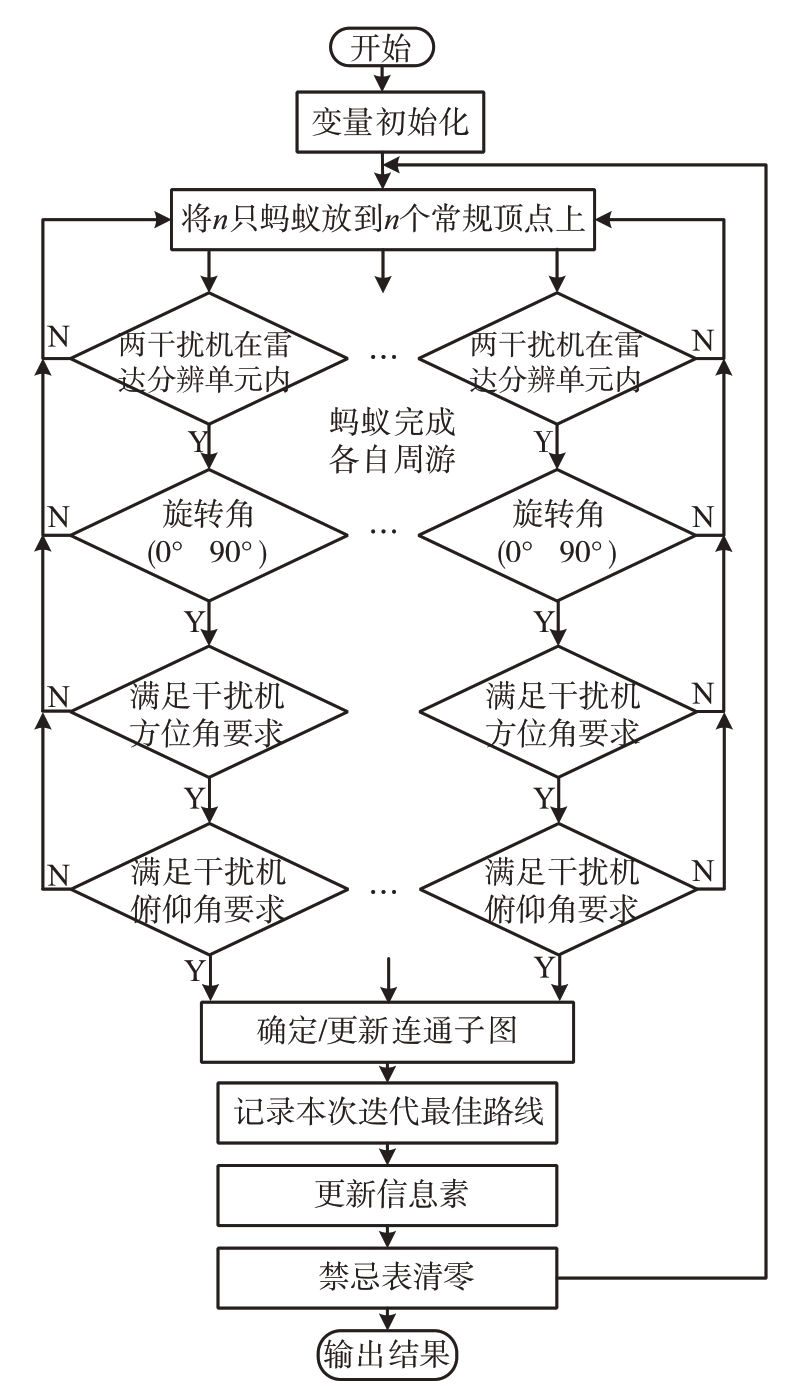
图10 算法流程图
某一时刻,n只蚂蚁完成各自周游后,在“确定/更新连通子图”阶段,针对某一个固定节点,可能存在多个连通子图并存的情况,一般按照下列条件择优:
1)同一干扰机同一时刻最多针对4 个目标释放干扰,即Gik≤4;
2)根据2.1节的分析,若k时刻针对固有顶点i存在多个协同干扰组合,即Lnik ≥2时,按照干扰双机连线旋转角越小、干扰机间连线越长、载目距离越小、前向干扰优先的原则,择优选择最优干扰机配对,确保Lnik=1。
上述动态可重构连通子图建立过程,如果因某种战术配合的需要,飞行员可实时介入,手动选择干扰目标和协同干扰组合,或者退出协同干扰,即飞行员操作权限高于动态可重构协同干扰权限。
3 实例仿真及分析
3.1 双机协同干扰典型作战场景
以典型的“磨刀匠”攻击战术为例,蓝方4机编队先进行迎头超视距攻击,4 机编队采用2 机分别组成协同干扰系统进行干扰,如果攻击未果或者攻击导致红方还有剩余兵力,则在超视距攻击结束后利用高度优势,继续进行迎头攻击,在最高点附近4 机编队采取机动混编方式,4 机编队根据协同干扰要求,在空中动态重组,确保协同干扰效果和提高协同干扰资源利用率。典型作战场景如图11所示。
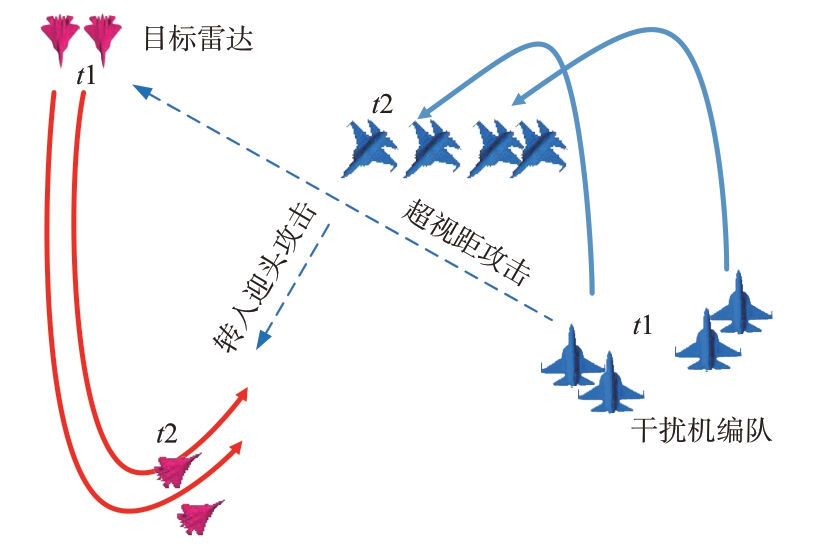
图11 “磨刀匠”攻击战术典型作战场景
假设红蓝双方均为隐身战斗机,且在实施协同干扰时,同时使用距离波门拖引干扰,即平台回波信号对协同干扰效果的影响可忽略。假设初始条件为:红蓝双方距离280 km,红方双机高度6 500~7 000 m,速度500~600 km/h,蓝方4 机高度9 000~10 000 m,速度550~650 km/h,蓝方飞机前后向干扰方位角±70°、俯仰角±40°,干扰距离大于300 km,编队共享的友机位置误差r<50 m。红蓝双方对抗航迹如图12所示。
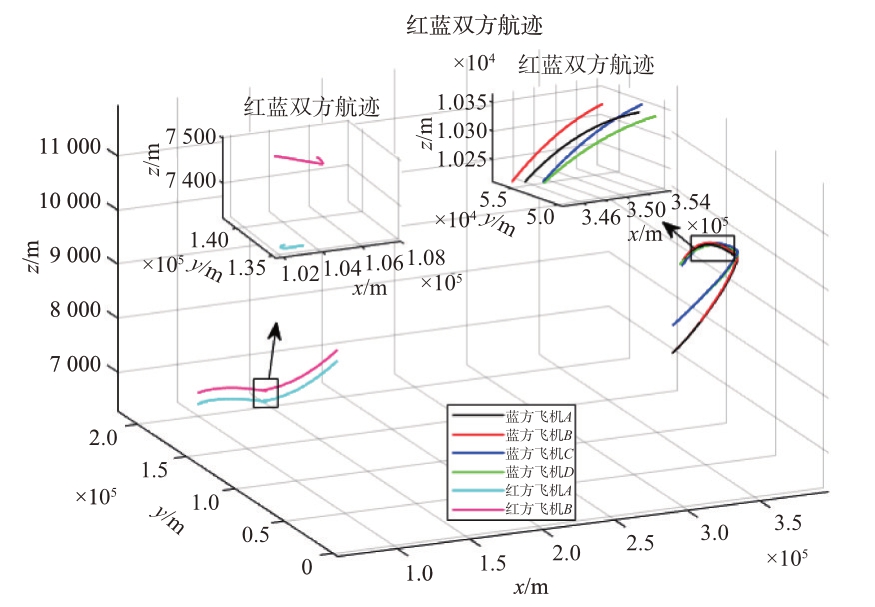
图12 红蓝双方对抗航迹
3.2 仿真结果及分析
当协同干扰信号幅度比为0.97、相位差为180°时,基于连通图的最优干扰结果如图13所示。
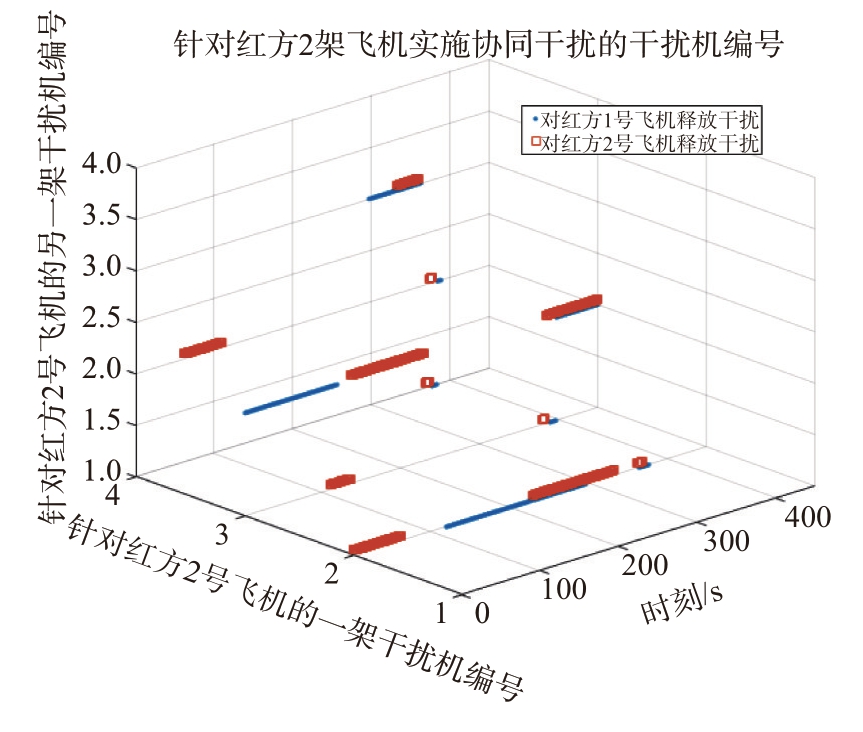
图13 最优干扰配对及目标分配结果
从图13 可以看出,针对红方1 号飞机的协同干扰,超视距阶段和迎头攻击阶段主要集中在蓝方3 号和2 号飞机协同干扰,回转阶段在蓝方4 架飞机之间进行了快速动态重构;针对红方2号飞机的协同干扰,超视距阶段主要集中在蓝方2 号和1号协同干扰,以及3 号和2 号协同干扰,回转阶段在蓝方4 架飞机之间进行了快速动态重构。这里仅列出某一时段的最优干扰连通子图,如表2所示。
表2 372~378 s最优干扰连通子图(Hki,Lnik)
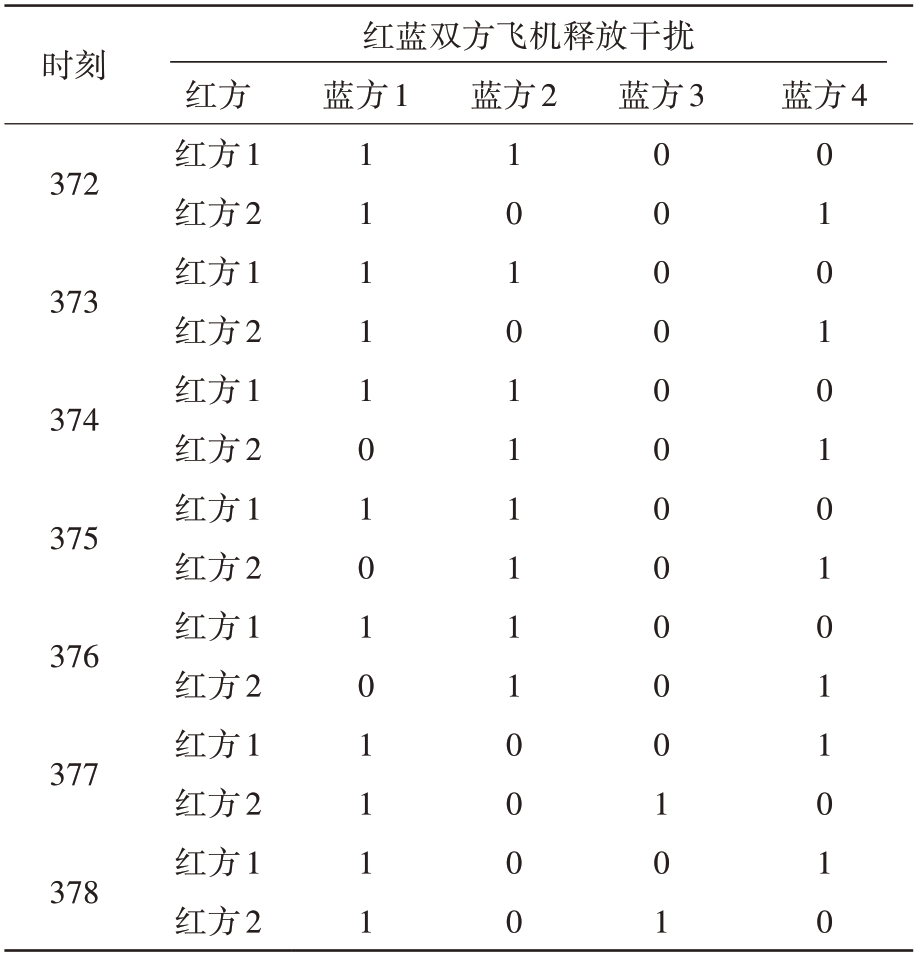
时刻红蓝双方飞机释放干扰蓝方2蓝方1蓝方3蓝方4 372 373 374 375 376 377 378红方红方1红方2红方1红方2红方1红方2红方1红方2红方1红方2红方1红方2红方1红方2 1 1 1 1 1 0 1 0 1 0 1 1 1 1 1 0 1 0 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 1 0 1 0 1 0 1 0 1 0 1 1 0 1 0
基于连通图的动态可重构协同干扰算法是针对每一个干扰目标进行寻优,很好地解决了干扰目标分配问题,同时,寻优结果为干扰机协同配对结果,在“确定/更新连通子图”阶段,同步解决了干扰资源优化选择的问题。对应表2 中最优连通子图的边矩阵如表3所示。
表3 372~378 s最优干扰连通子图边矩阵(Hki,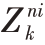 )
)
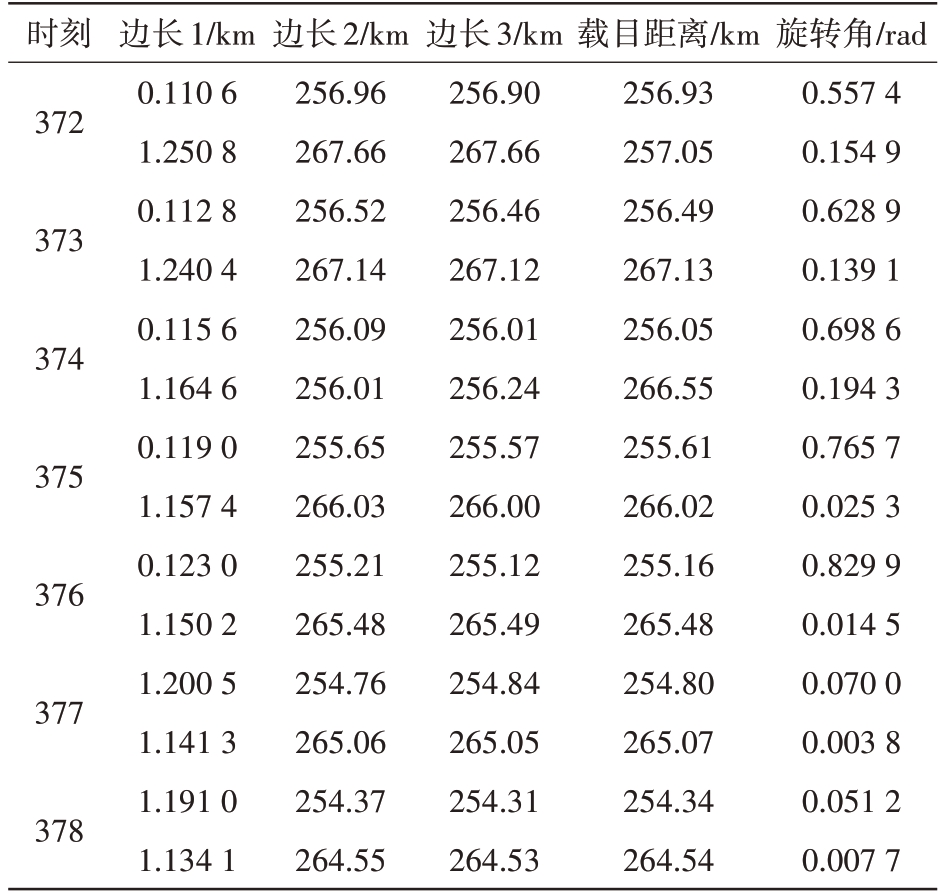
时刻372 373 374 375 376 377 378边长1/km 0.110 6 1.250 8 0.112 8 1.240 4 0.115 6 1.164 6 0.119 0 1.157 4 0.123 0 1.150 2 1.200 5 1.141 3 1.191 0 1.134 1边长2/km 256.96 267.66 256.52 267.14 256.09 256.01 255.65 266.03 255.21 265.48 254.76 265.06 254.37 264.55边长3/km 256.90 267.66 256.46 267.12 256.01 256.24 255.57 266.00 255.12 265.49 254.84 265.05 254.31 264.53载目距离/km 256.93 257.05 256.49 267.13 256.05 266.55 255.61 266.02 255.16 265.48 254.80 265.07 254.34 264.54旋转角/rad 0.557 4 0.154 9 0.628 9 0.139 1 0.698 6 0.194 3 0.765 7 0.025 3 0.829 9 0.014 5 0.070 0 0.003 8 0.051 2 0.007 7
从表2 和表3 可以看出,被干扰目标到双机的距离差值很小,从连通子图上看,协同干扰双机和被干扰目标3 个顶点构成的三角形近似为等腰三角形,旋转角小,符合2.1 节关于旋转角对干扰效果的影响分析。根据第2.1 节建立的双机协同干扰模型,不同幅度比和相位条件下,基于连通图的动态可重构协同干扰对测角误差的影响如图14至图17所示。
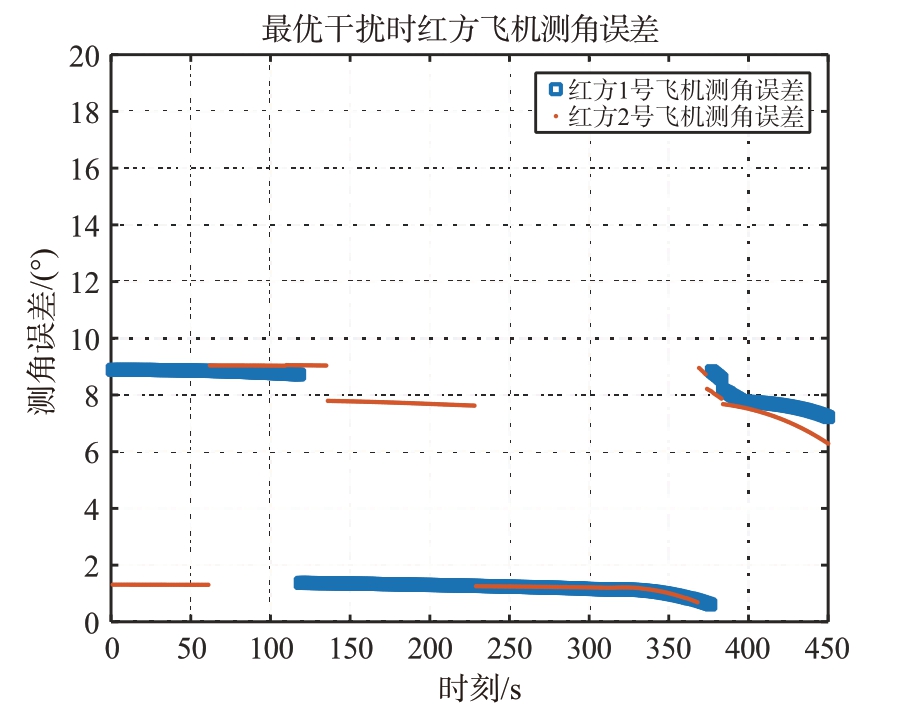
图14 a=0.97、φ=180°时最优干扰结果
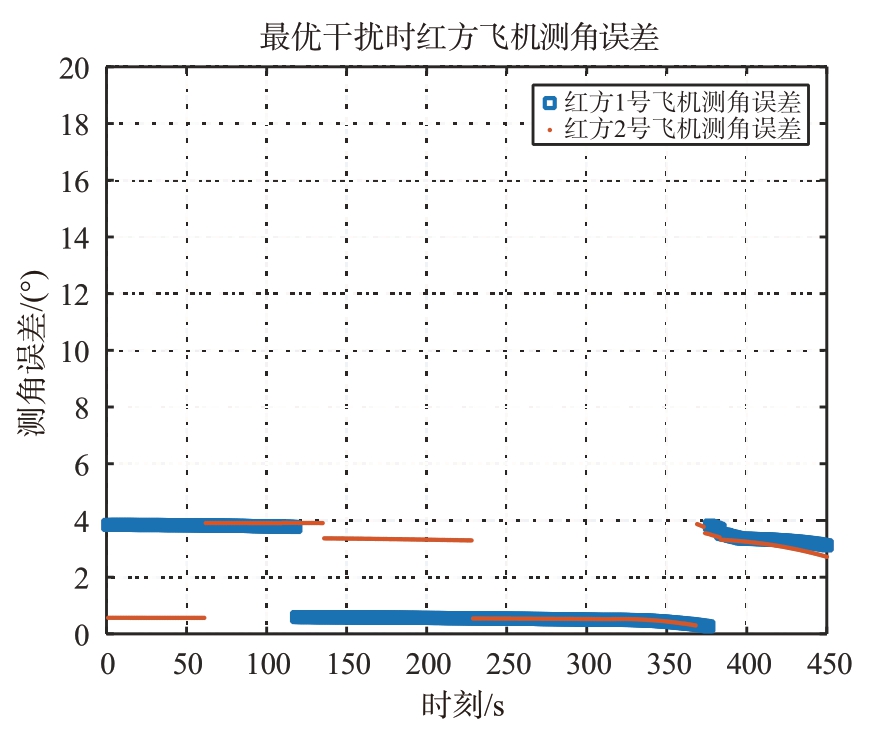
图15 a=0.97、φ=178°时最优干扰结果
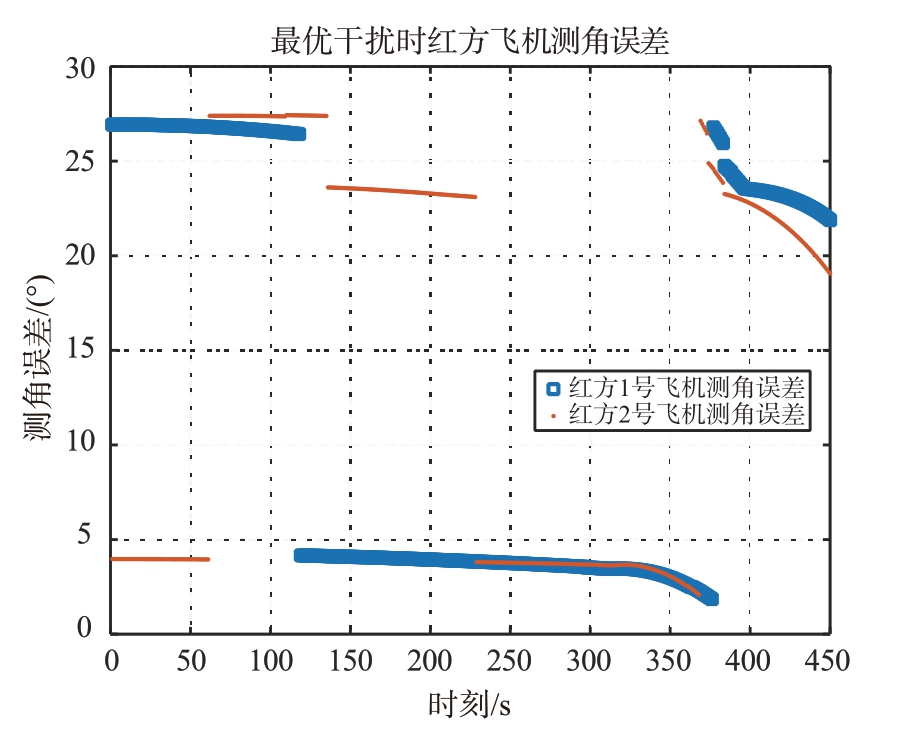
图16 a=0.99、φ=180°时最优干扰结果
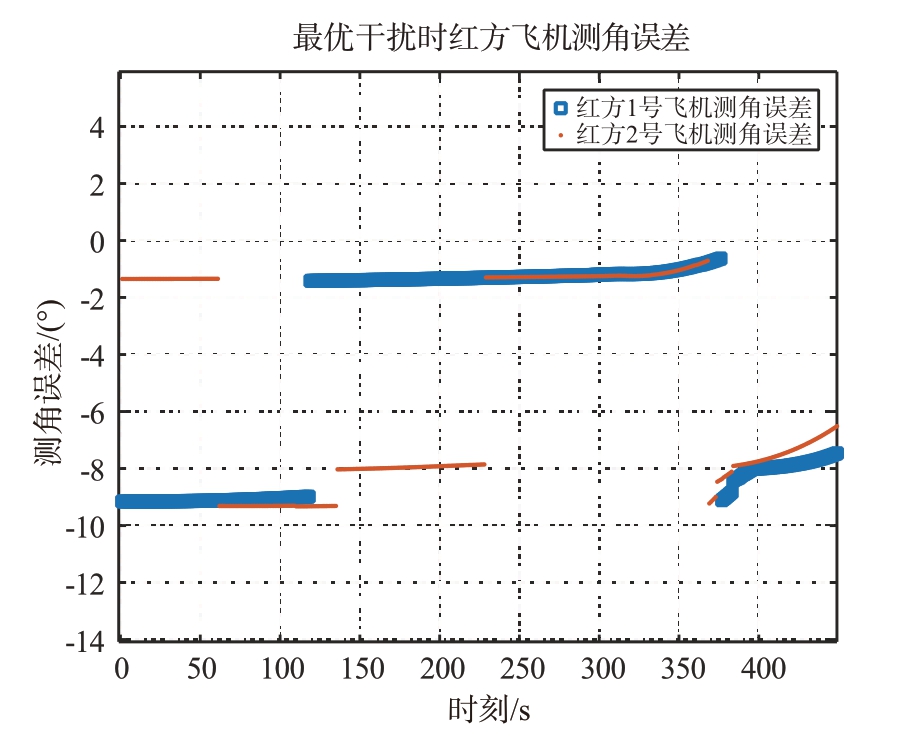
图17 a=1.03、φ=180°时最优干扰结果
从图14 至图17 可以看出,通过动态可重构的协同干扰方法,可以对机载火控雷达测角误差带来约2°到28°的影响,随着干扰双机的动态组合,对测角误差的影响也在变化,从而很好地解决了雷达跟踪干扰源的问题;双机干扰信号的幅度比越接近1、相位差越接近180°时,双机协同干扰对机载火控雷达测角误差的影响越大;当幅度比大于1时,对机载火控雷达测角误差的影响会反相。
在Inter(R)Core(TM)i7-5820 的Win 7 电脑上运行Matlab R2019a,完成450 次协同干扰动态可重构寻优,用时0.002 798 s,算法耗时完全满足协同干扰策略制定和目标分配对时间的要求。
4 结束语
本文建立了双机协同干扰数学模型和基于连通图的多机动态可重构协同干扰方法,有效解决了针对空战电子对抗中复杂电磁环境、雷达跟踪干扰源以及干扰目标选择和资源分配的问题。在隐身飞机密集编队突防过程中,如何快速进行多机协同干扰作战效能评估,为飞行员和指挥员快速决策提供支撑,将是下一步研究重点。
[1]YANG Degui,LIANG Buge,ZHAO Dangjun.Cross-Eye Gain Distribution of Multiple-Element Retrodirective Cross-Eye Jamming[J].Journal of Systems Engineering and Electronics,2018,29(6):1170-1179.
[2]MA Jiazhi,SHI Longfei,XIAO Shunping,et al.Mitigation of Cross-Eye Jamming Using a Dual-Polarization Array[J].Journal of Systems Engineering and Electronics,2018,29(3):491-498.
[3]CHEN Jiabei,SHI Qingzhan,HUANG Zhaoyu,et al.Performance Analysis of Multi-Group Three-Tuple Cross-Eye Jamming[J].Journal of Systems Engineering and Electronics,2022,33(1):80-90.
[4]LIU Wei,MENG Jin,ZHOU Liang.Method of Four-Element Retro-Directive Cross-Eye Jamming Based on DoA[J].IEEE Access,2020,8:76896-76902.
[5]LIU Tianpeng,WEI Xizhang,PENG Bo,et al.Tolerance Analysis of Multiple-Element Linear Retrodirective Cross-Eye Jamming[J].Journal of Systems Engineering and Electronics,2020,31(3):460-469.
[6]SONG Zhiyong,LI Guanqing,FU Qiang.Principle Analysis of Coherent Two-Point Source Jamming Based on Amplitude Comparison Monopulse[C]// The 3rd International Conference on Electronic Information Technology and Computer Engineering,Xiamen,China:IEEE,2019:919-923.
[7]CHENG Yun,LIU Tianpeng,HUO Kai,et al.Analysis of Performance of Shipborne Cross-Eye Jamming Against Anti-Ship Missile[J].Photonics & Electromagnetics Research Symposium,2019(12):2763-2769.
[8]LIU Wei,MENG Jin,ZHOU Liang.Research on RectangularArrayRetrodirectiveCross-EyeJammingMethodConsidering Target Echo[C]// 19th IEEE International Conference on Communication Technology,Xi′an,China:IEEE,2019:224-227.
[9]刘天鹏,魏玺章,刘振,等.交叉眼干扰研究综述[J].雷达学报,2019,8(1):140-153.
[10]肖扬,罗明.多环路反向交叉眼干扰多普勒频率差研究[J].雷达科学与技术,2021,19(6):661-668.
[11]DU PLESSIS W P,ODENDAAL J W,JOUBERT J.Extended Analysis of Retrodirective Cross-Eye Jamming[J].IEEE Trans on Antennas and Propagation,2009,57(9):2803-2806.
[12]刘胜久,李天瑞,谢鹏,等.网络能量在混合图中的研究与应用[J].湖南大学学报(自然科学版),2021,48(6):105-111.
[13]严迎建,赵聪慧,刘燕江.基于多维结构特征的硬件木马检测技术[J].电子与信息学报,2021,43(8):2128-2139.
