0 引 言
空时自适应处理技术（Space-Time Adaptive Processing,STAP）自提出以来，因其对杂波和干扰有着良好的抑制作用［1-5］，引起了学术界的广泛关注。随着STAP 技术广泛应用于机载雷达，作为雷达对抗方，积极开展有针对性的干扰方法研究显得尤为重要。
STAP在进行目标检测时一般将处理的数据按照距离不同分为待检测数据和训练样本数据，待检测数据中杂波、干扰特征是未知的，需要从训练样本数据中估计得到［6-7］。当前主流的干扰方法是向待检测单元或训练样本单元中注入假目标，使得从训练样本中估计得到的杂波、干扰特征与待检测数据中的杂波、干扰特征偏差加大，从而影响目标检测结果。文献［8］提出了一种频移假目标干扰方法，形成的干扰假目标可影响自适应处理器对目标速度信息的检测结果，但干扰维度较为单一。文献［9］针对自适应技术对迅速变化的信号环境自适应性差的特点，提出了一种快变干扰的概念，为后续研究提供了一种新思路，但未能给出相应的数学模型和实现方法。文献［10］研究了一种散射波欺骗干扰方法，干扰机利用角反射器生成的假目标能同时在方位和多普勒两个维度对STAP进行欺骗干扰，但能量利用效率较低，实施难度大。文献［11］提出了一种改进的延时混叠干扰方法，有效增加了假目标的生成数量。
结合以上分析，本文提出了一种针对STAP 的调频转发干扰方法。该方法使用不同调频参数对接收信号进行频率调制，在目标前后生成多个假目标，破坏训练样本独立同分布条件，干扰STAP的目标检测过程。
1 STAP基本原理
假设雷达工作在正侧视状态，天线采用N 个阵元的均匀线阵，一个相干处理间隔（Coherent Processing Interval,CPI）内的脉冲数为M，将第n 个阵元第m 次快拍接收的数据记为x（n, m），则第n个阵元接收到的数据为
将X(n),n=1,2,…,N排成NM × 1的形式，则一个距离单元的回波数据为
H0 和H1 分别表示目标不存在和存在两种假设，待检测距离单元的数据X 表示为以下两种形式:
式中，Xn 表示除目标外的噪声、杂波、干扰分量，b为目标回波幅度，S为目标空时导向矢量。
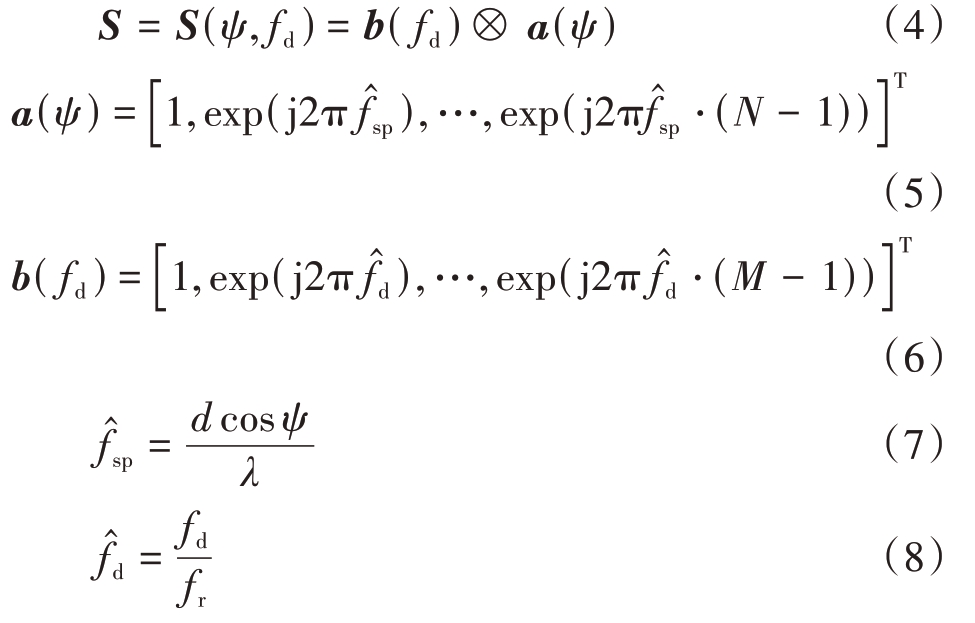
a(ψ)、b( fd)分别为目标空间和时间导向矢量，d、λ、ψ、fr 分别为阵元间距、信号波长、锥角、脉冲重复频率。
设自适应权矢量为W，则STAP 系统自适应输出为
当待检测距离单元杂波、干扰、噪声协方差矩阵已知的情况下，自适应最优权矢量为
式中R为杂波、干扰、噪声协方差矩阵，定义如下:
输出信干噪比（Signal to Interference Plus Noise Ratio,SINR）是衡量STAP性能的一个常用指标，定义如下:
式中σ2 为单个阵元热噪声功率，ξt 为单个阵元接收到的目标信噪比。
在白噪声环境下，R 为单位矩阵，此时最优输出信噪比值（Signal to Noise Ratio,SNR）为
为方便量化自适应算法性能，将该算法输出信干噪比相对无干扰环境下最优输出信噪比的损失定义为［1］
在实际情况中R 不可准确获得，通常使用训练样本估计出样本协方差矩阵
代替，过程如图1所示。
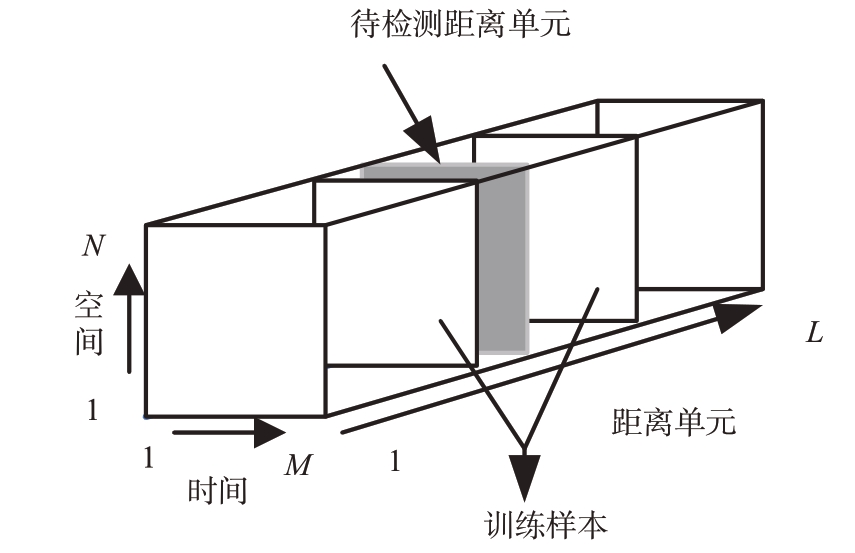
图1 估计样本协方差矩阵过程
利用估计得到的样本协方差矩阵代替真实的协方差矩阵会导致STAP 输出信干噪比有一定的损失，为了将该损失降低至3 dB 以内，要同时满足以下两个条件。一是训练样本要满足独立同分布条件；二是训练样本数L ≥2MN-3［12-13］。为了防止自适应滤波器在抑制杂波时将目标滤除，训练样本要剔除目标单元及其相邻几个单元的数据。
2 干扰目标对STAP系统影响
由上述STAP 基本原理可知，待检测单元的样本协方差矩阵与训练样本有关。在选取训练样本估计待检测单元的杂波和干扰协方差矩阵过程中，若训练样本内包含干扰信号，将破坏训练样本独立同分布的条件，影响自适应系统目标检测结果［14］。
为了简化分析训练样本中的干扰目标对STAP系统检测目标性能的影响，假设检测单元中仅有一个目标，空时导向矢量为S，训练样本中也仅有一个干扰目标，干扰功率为σ2j，空时导向矢量为Sj。由干扰目标产生的协方差矩阵为
因回波信号中杂波、干扰、噪声之间相互独立，协方差矩阵为各分量协方差矩阵之和:
式中Rcn=Rc+ Rn为杂波、噪声协方差矩阵之和。
由Sherman-Morrison 公式对式（16）求逆展开可得
式中I为单位矩阵，为简化公式方便分析，定义
将式（17）代入式（14）中分析干扰目标对STAP系统输出信干噪比损失LSINR 的影响。因式（14）中σ2、MN都为固定常数，所以仅需分析k=SHR-1S的变化情况。
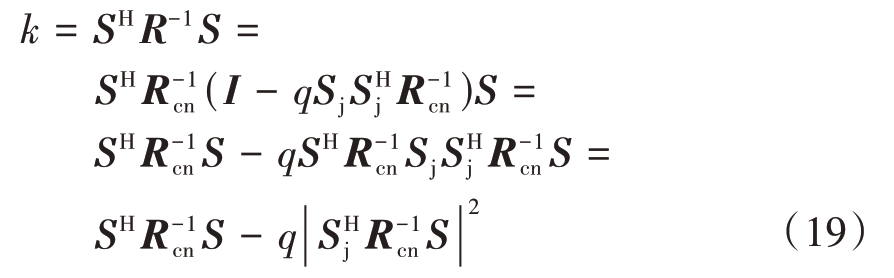
在式（19）中，定义
因Rcn 为正定矩阵，
且σ2j ≥0，因此对式（18）分析可知，q ≥0。结合公式（18）、（19）可知，当干扰信号功率σ2j 增大时，LSINR 增大。但当干扰信号功率足够大时，q →
，此时再增加干扰功率，LSINR也不会有太大变化。
当σ2j 一定时，干扰信号与目标信号的归一化多普勒频率越接近，l 越大，LSINR 也随之增大。设Sj=bj ⊗aj（bj和aj分别为干扰目标时间和空间导向矢量），因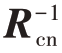
对角线元素通常远大于其他矩阵元素，可近似看作δI［15］，则将式（20）展开可得
为简化分析，干扰采用自卫干扰方式，即目标、干扰空间导向矢量均已固定，则
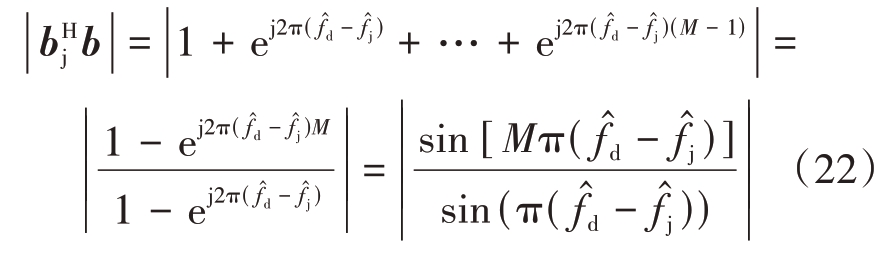
当
|较小时上式可简化为
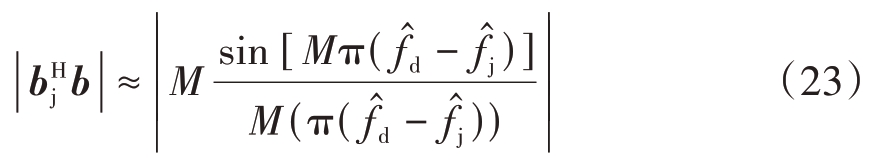
式（23）可看作一个辛克函数，当干扰、目标归一化多普勒差值
|越小时，
|值越大，STAP 输出信干噪比损失越大。随着
差值增大，
|的值迅速衰减，其半功率波束宽度为θ0.5 ≈1 M，即当
时，可认为干扰目标对目标通道LSINR几乎无影响。
图2 给出了目标通道LSINR 随干扰目标强度和归一化多普勒频率变化情况，其中M=16，N=16，目标和干扰方位相同，目标归一化多普勒频率为0.19，干扰目标强度为干扰目标经训练样本L 平均后的功率。由此可得出以下结论:1）目标通道LSINR随干扰目标强度增大而增大，但干扰信号强度增大到一定值后，目标通道LSINR 不再有明显变化；2）当干扰目标归一化多普勒频率与目标归一化多普勒频率越接近时，目标通道LSINR 越大，目标信号有被对消的风险。当干扰目标与目标归一化多普勒差值大于半功率波束宽度时，可认为干扰目标对目标通道LSINR无影响。
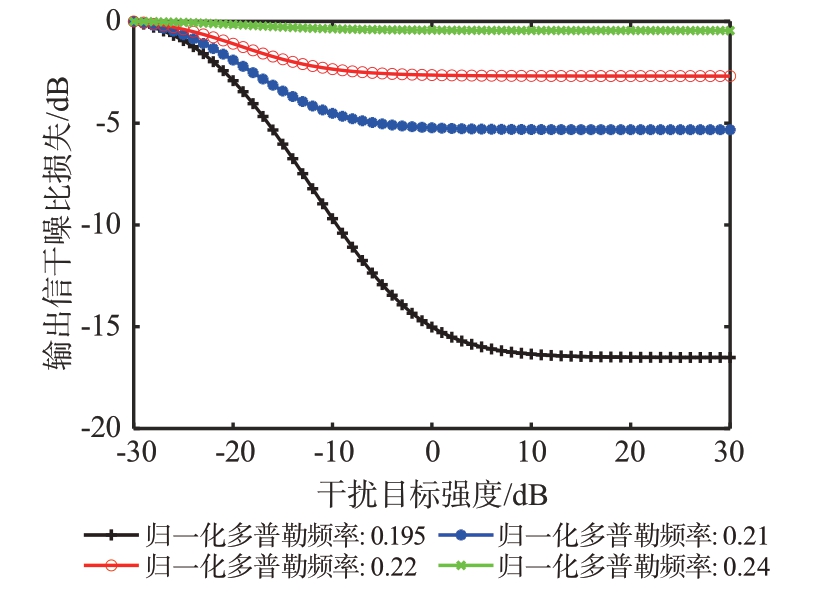
图2 目标通道输出信干噪比损失变化情况
3 调频转发干扰信号模型
由上节分析可知，目标距离单元的训练样本内包含干扰假目标，可对STAP 系统目标检测性能产生影响。同样地，STAP 系统在对干扰目标进行检测时，干扰目标距离单元的训练样本内包含目标或者其他干扰目标时，也会对干扰目标的检测结果产生影响。结合线性调频信号在距离-多普勒频移之间存在强耦合的特性，本节提出一种新的调频转发干扰方法。该方法思路如下:干扰机对接收信号进行频率调制，生成距离和多普勒频率都可控的干扰假目标，破坏训练样本独立同分布条件，干扰STAP的目标检测过程。
由第2节结论可知，当目标检测单元的训练样本内包含与目标归一化多普勒频率相同的假目标时，能有效减小目标输出，降低STAP系统目标检测性能。当生成多个归一化多普勒频率互不相同的干扰假目标时，即使这些干扰目标互相落入对方的训练样本内，STAP 也无法将其对消，因此可在距离、多普勒两个维度对自适应系统构成欺骗干扰，有效解决了文献［8］所提方法干扰维度单一的问题。
3.1干扰信号模型
设雷达发射时宽为T，带宽为B 的线性调频脉冲信号，信号可表示为
式中，f0 为信号载频，μ=B/T 为调频斜率。干扰机对接收到的雷达信号附加频移量fj，此时干扰信号可表示为
经脉冲压缩处理后，干扰输出表达式为
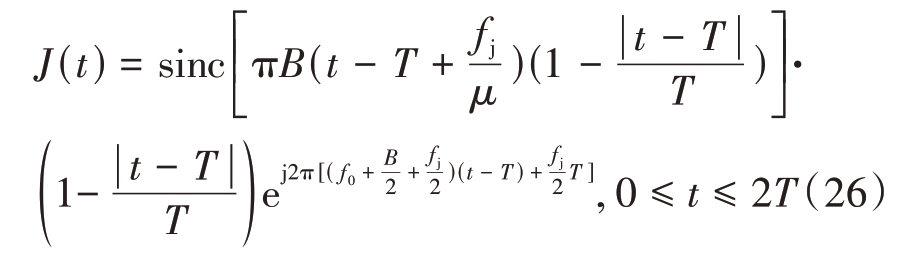
由式（26）可知，当频移量fj ＞0 时，干扰信号经脉压处理后峰值输出将导前目标，反之延后目标。干扰信号峰值位置与附加频移量值成正比，通过设置不同的频移量，可产生距离分布不同的假目标，干扰信号相对目标信号时延为
此外频移量还会影响干扰信号脉冲压缩效果，干扰信号的脉冲压缩比为
由式（28）可知，干扰附加的频移量越小，脉冲压缩效果越好，为防止因脉冲压缩失配导致干扰信号功率损失过大，干扰附加的频移量不宜过大，一般要求|fj|＜B 2。
如图3所示，假设干扰机接收到的信号为s(t)，频率产生器产生干扰信号所需的频移量，将s(t)与频移量相乘，最后将产生的各干扰脉冲相加输出，得到
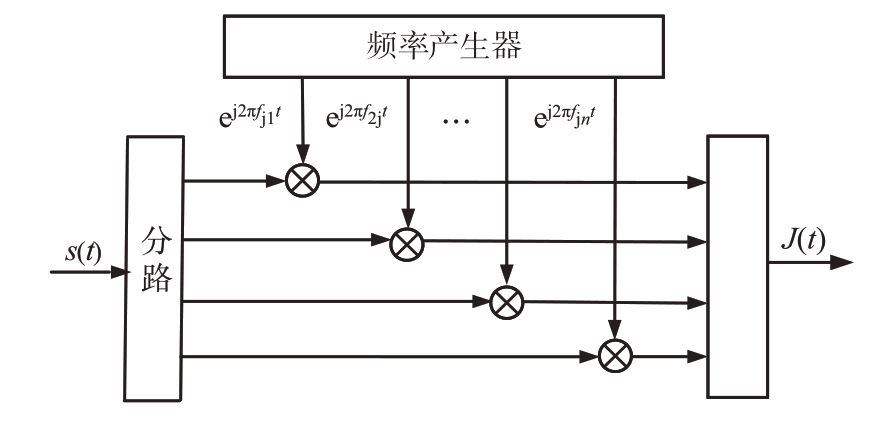
图3 调频转发干扰原理
由式（29）可以看出，干扰机输出的干扰信号包含了多个不同多普勒频率的脉冲，通过设置不同频移量，干扰机可产生距离分布不同假目标。
3.2 频率调制方法
由公式（6）、（8）可知，当干扰信号附加的频移量是脉冲重复频率fr的整数倍时，干扰信号与目标信号的时间导向矢量和归一化多普勒频率相同。此时调频转发干扰频移量设为
式中K 为整数值。由公式（27）可知，通过设置K 值可控制假目标的距离分布，当这些假目标落入待检测单元的训练样本时，可引起目标信号输出信干噪比损失加大，甚至会导致目标信号被对消，STAP系统检测目标的性能将严重下降。
类似地，为了防止干扰机生成的假目标被STAP对消，调频转发干扰频移量可设为
式中M 为一个相干处理间隔内的脉冲数，0≤i＜M。通常由(i/M)fr 引起的时延量可忽略不计，因此还是需要通过设置K 值来控制干扰假目标距离分布。由第2节分析可知，任意两个干扰信号之间归一化多普勒频率差值都大于等于1/M时，干扰信号无法被STAP 对消。当目标距离单元附近存在多个类似的干扰假目标时，可引导雷达错误跟踪，起到掩护目标的作用。
4 仿真分析
根据频移量设置的不同，调频转发干扰有不同的干扰效果，设计仿真实验，用于证明干扰的有效性。
基本仿真参数:雷达发射信号为线性调频信号，载频f0=1.5 GHz，信号脉宽T=20 μs，带宽B=10 MHz，脉冲重复频率fr=2 000 Hz。天线采用均匀线阵正侧视观察，阵元间隔d=λ 2，阵元个数N=16，一个CPI内脉冲数M=16，信噪比为0 dB，杂噪比为25 dB。载机飞行高度为9 km，飞行速度v=100 m/s，载机与目标距离为30 km，目标方位角为0°，目标归一化多普勒频率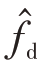
=0.19，目标位于2 000 距离单元处，训练样本数L=2MN=512。
仿真实验1：无干扰情况下STAP处理结果
无干扰情况下，训练样本满足独立同分布条件，可以较好地估计出待检测单元中的杂波协方差矩阵，雷达回波信号经自适应处理后可以有效滤除杂波，得到目标方位和多普勒频率信息。图4为无干扰时STAP 处理结果，由图4（a）可以看出，目标在距离门2 000 和归一化多普勒0.19 处被检出，杂波输出得到极大抑制。由图4（b）和图4（c）可知，空时二维功率谱在对角线处具有低增益，在方位角0°，归一化多普勒频率0.19 处有较高增益，由此可见，经STAP 处理后，沿对角线分布的杂波被有效滤除，目标被成功检出。图4（d）为无干扰情况下目标距离单元输出信干噪比损失曲线，仅在归一化多普勒频率0处有一用于抑制杂波的凹口。
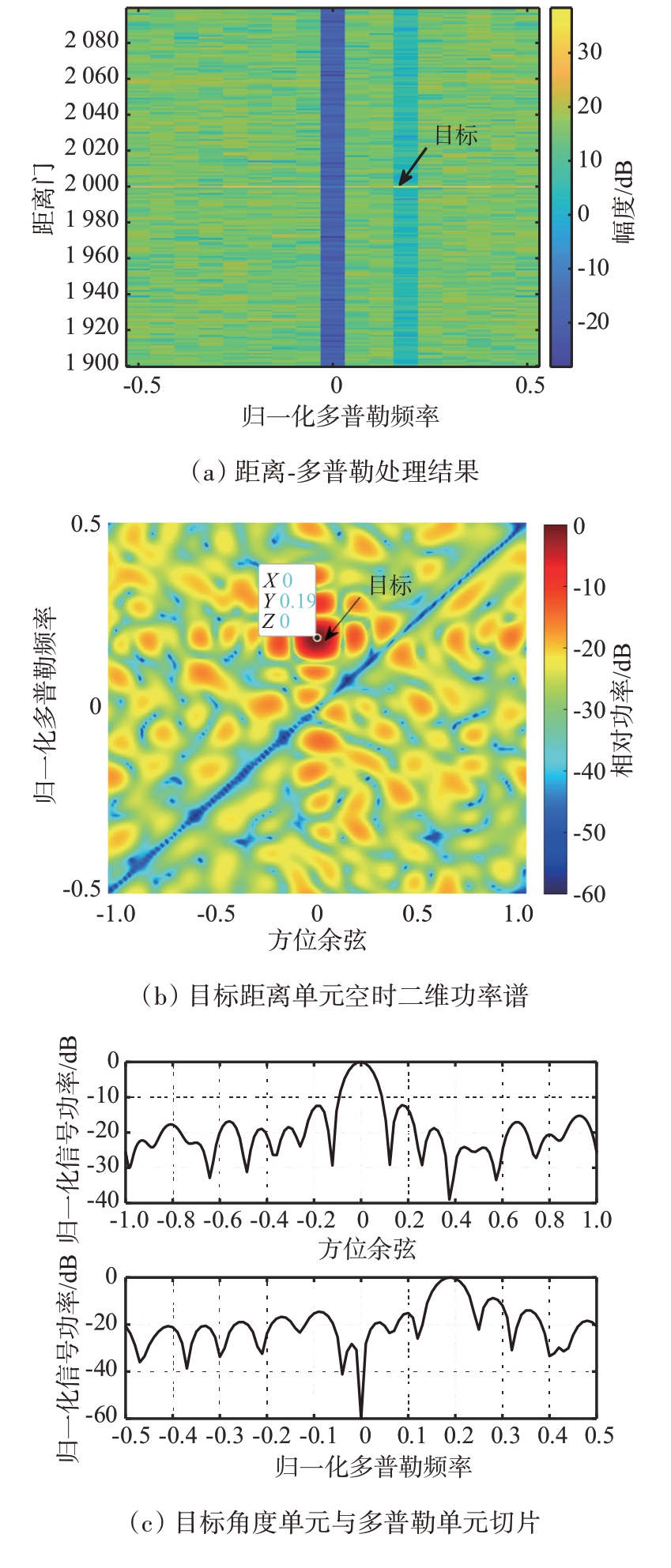
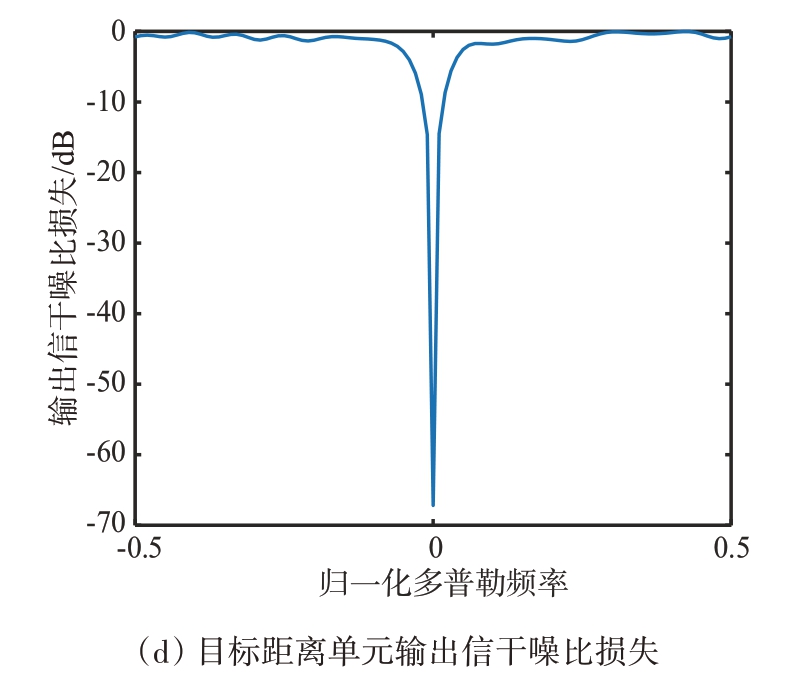
图4 无干扰情况下处理结果
仿真实验2：在目标距离单元附近产生与目标归一化多普勒频率相同的干扰假目标，分析干扰对STAP系统检测目标性能的影响
干扰参数:干扰机采用自卫干扰方式，设置5个干扰假目标，干信比为10 dB，根据公式（30）,为使假目标归一化多普勒频率值与目标归一化多普勒频率相同，干扰附加频移量应设为[4 MHz,3 MHz,2 MHz,-1 MHz,-2 MHz]。
图5给出了调频转发干扰效果，其中干扰假目标在脉冲压缩后距离单元分布情况如图5（a）所示，干扰信号的峰值因频率失配导致有所减小，分别位于1 920、1 940、1 960、2 020、2 040 距离单元处，由此可见，可以通过调整频移量来控制假目标距离分布。因附加频移量都为fr的整数倍，所以产生的干扰信号归一化多普勒频率都与目标信号相同，结合图4和图5可以看出，当训练样本内存在多个与目标归一化多普勒频率相同的干扰目标时，STAP系统在归一化多普勒频率0.19 处的输出信干噪比有36.31 dB的损失，目标输出受到抑制，在图5（b）、图5（c）和图5（d）中已无法有效检测出目标信息。
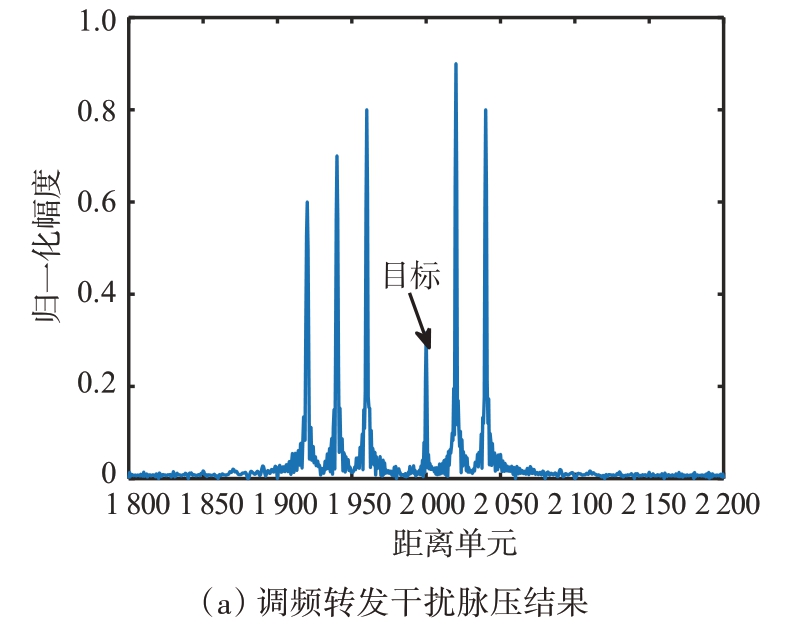
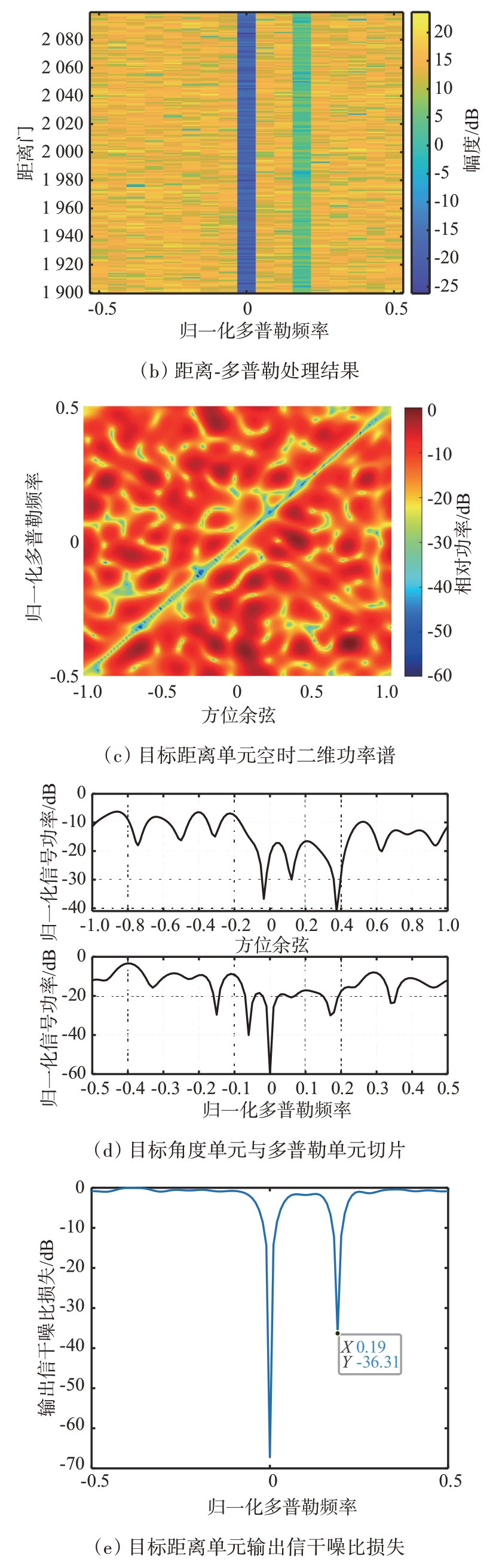
图5 调频转发干扰效果
仿真实验3：在目标距离单元附近产生无法被STAP对消的干扰假目标，分析假目标对目标掩护作用
干扰参数:干扰机采用自卫干扰方式，设置5个干扰假目标，干信比为10 dB，根据公式（31），为使生成的假目标不被STAP系统对消且能对目标起到良好的掩护作用，干扰附加频移量应设为[(4 M+125)Hz,(3 M+250)Hz,(2 M+375)Hz,(-1 M+500)Hz,(-2 M+625)Hz]。
图6给出了调频转发干扰效果，其中干扰假目标在脉冲压缩后距离单元分布情况如图6（a）所示，干扰信号峰值分别位于1 920、1 940、1 960、2 020、2 040 距离单元处。如图6（b）所示，在为每个干扰脉冲调制上相应的频率后，任意两个干扰信号之间的归一化多普勒频率差值都大于等于1/M，STAP 系统无法将这些假目标对消，因此在多个距离单元和多普勒通道处检测出干扰假目标，实现对STAP 多维度欺骗干扰。如图6（c）、（d）所示，在方位角0°，归一化多普勒频率0.19 处检测到目标。如图6（e）、（f）所示，因干扰目标数目较多，仅展示出干扰目标4 所在距离单元的空时二维功率谱及其切片图，从图中可以看出在方位角0°，归一化多普勒频率0.44 处检测到干扰目标。图6（g）为该干扰下目标距离单元输出信干噪比损失曲线，目标距离单元的训练样本内存在多个干扰目标，自适应系统在这些干扰目标所在的归一化多普勒频率处的输出都有不同程度的损失。因干扰信号与目标信号归一化多普勒频率差值也都大于等于1/M，所以目标输出信干噪比没有明显损失。通常干扰信号幅值大于目标信号，当目标距离单元附近出现多个类似无法被对消的假目标信号时，可引诱雷达错误跟踪，有效起到掩护目标的作用。
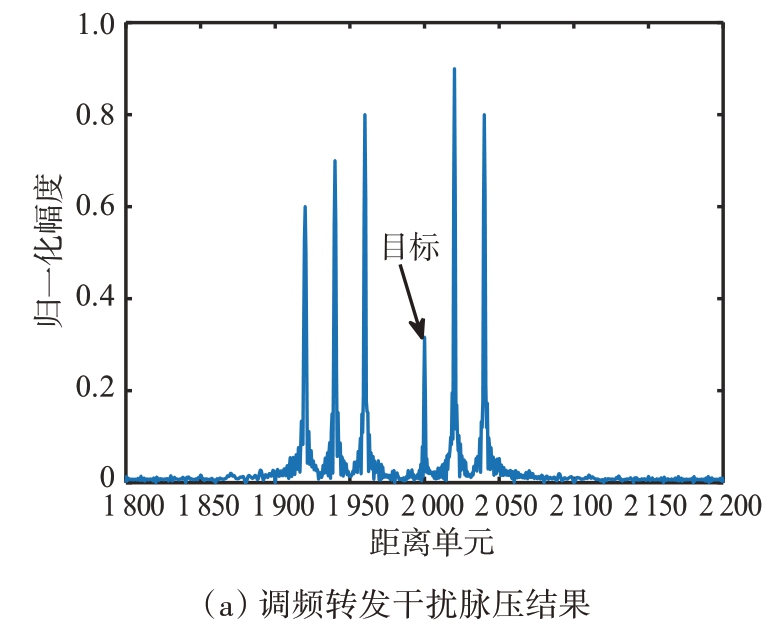
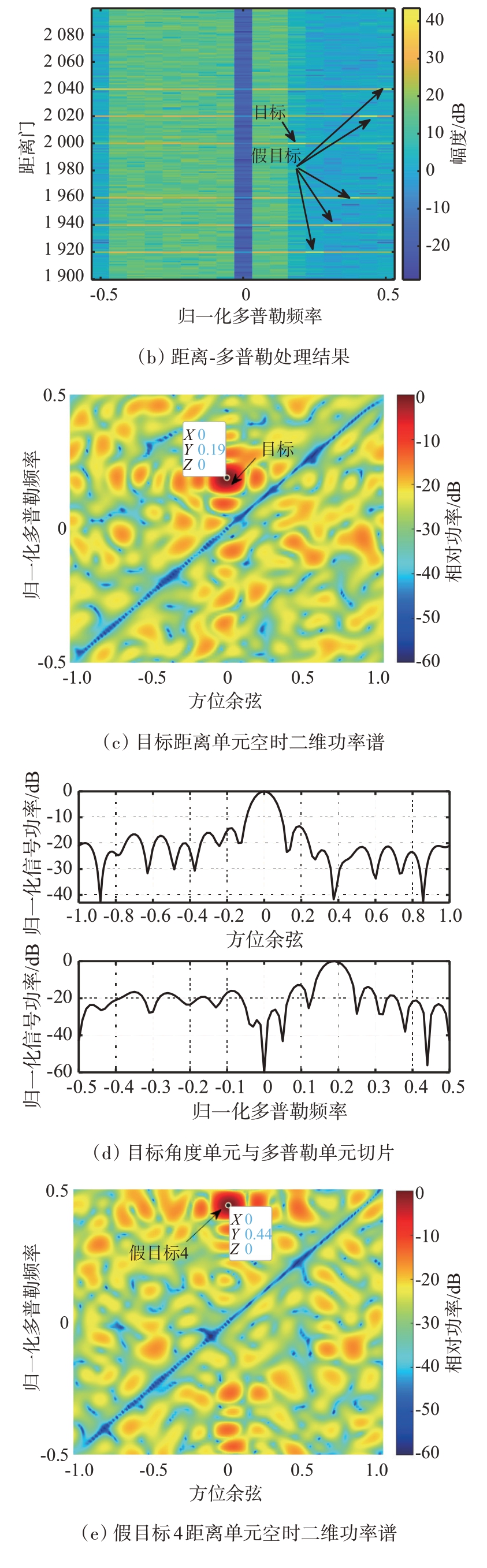
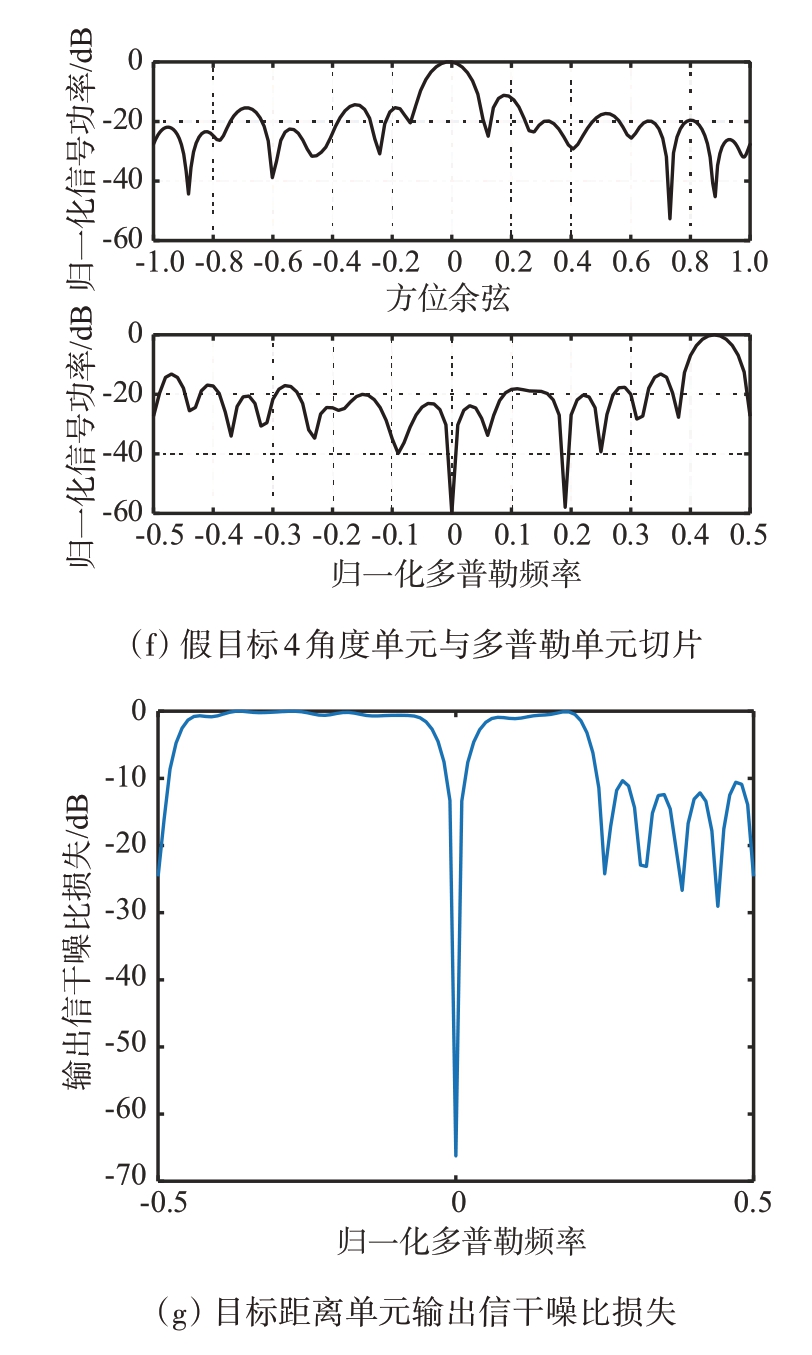
图6 假目标掩护效果
5 结束语
本文根据自适应处理过程中训练样本需要满足独立同分布这一条件，详细分析了当训练样本中存在干扰目标时对自适应系统检测目标的影响，然后在此基础上提出了一种新的调频转发干扰方法。该方法通过对干扰机接收信号加以频率调制，在目标周围生成多个距离分布可控的假目标，破坏训练样本独立同分布条件，从而影响自适应处理器检测目标结果。最后通过三个仿真实验，证明了该方法产生的假目标既可有效降低空时自适应处理系统的目标检测性能，也可诱导空时自适应系统错误跟踪，起到有效掩护目标的作用。
［1］WARD J.Space-Time Adaptive Processing for Airborne Radar［R］.USA:MIT Lincoln Laboratory,1994.
［2］LI Y W,XIE W C,MAO H H,et al.Clutter Suppression Approach for End-Fire Array Airborne Radar Based on Adaptive Segmentation［J］.IEEE Access,2019,7:147094-147105.
［3］王晓明，杨鹏程，邱炜.基于稀疏重构的机载雷达KASTAP 杂波抑制算法［J］.雷达科学与技术，2020，18（5）:546-550.
［4］CUI N,DUAN K Q,XING K,et al.Beam-Space Reduced-Dimension 3D-STAP for Nonside-Looking Airborne Radar［J］.IEEE Geoscience and Remote Sensing Letters,2022,19:1-5.
［5］WU D,ZHU D Y,SHEN M W,et al.Clutter Suppression for Wideband Radar STAP［J］.IEEE Trans on Geoscience and Remote Sensing,2022,60:1-18.
［6］SUN G H,HE Z S,TONG J,et al.Knowledge-Aided Covariance Matrix Estimation via Kronecker Product Expansions for Airborne STAP［J］.IEEE Geoscience and Remote Sensing Letters,2018,15（4）:527-531.
［7］段克清，李想，行坤，等.基于卷积神经网络的天基预警雷达杂波抑制方法［J］.雷达学报，2022，11（3）:386-398.
［8］薛冰心，张友益.基于频移假目标对机载雷达STAP 技术干扰效果的研究［J］.舰船电子对抗，2012，35（1）:11-13.
［9］唐孝国，张剑云.机载相控阵雷达STAP 原理及其干扰方法研究［J］.电子设计工程，2012，20（15）:71-74.
［10］谌诗娃，张剑云，贺平，等.对空时自适应处理技术的散射波欺骗干扰研究［J］.现代雷达，2016，38（1）:76-80.
［11］赵燕慧，汤建龙，李骥阳，等.对降维STAP机载雷达的延时混叠转发干扰方法分析［J］.系统工程与电子技术，2020，42（8）:1718-1725.
［12］REED I S,MALLET J D,BREENAN L E.Rapid Convergence Rate in Adaptive Arrays［J］.IEEE Trans on Aerospace and Electronic Systems,1974,10（6）:853-863.
［13］SALEH O,RAVAN M,RIDDOLLS R,et al.Fast Fully Adaptive Processing: A Multistage STAP Approach［J］.IEEE Trans on Aerospace and Electronic Systems,2016,52（5）:2168-2183.
［14］熊元燚，谢文冲.干扰目标环境下机载雷达非均匀STAP 检测器性能分析［J］.空军预警学院学报，2020，34（4）:266-270.
［15］陈小舟，邢庆君，张立东.对机载预警雷达STAP 的慢时调频干扰方法［J］.系统工程与电子技术，2021，43（11）:3177-3184.
