0 引 言
基于合成孔径雷达（Synthetic Aperture Radar,SAR）的地面运动目标检测（Ground Moving Target Indication，GMTI）一直是近年来雷达领域的研究热点［1-4］。众所周之，由于运动目标存在目标径向速度，导致其在SAR 图像中存在方位偏差［5］，运动目标精确定位问题一直是一个重要问题。目标定位误差表示SAR 图像上运动目标测量位置与真实目标位置之差。目标定位误差可以评估目标径向速度测量精度是否满足要求，定位结果是否准确。在多通道SAR-GMTI系统中，目标定位精度主要受通道间干涉相位精度影响。一旦干涉相位中存在噪声，必然会影响目标定位精度。国内外提出了多种方法［6-9］实现运动目标精确定位。Ender 等［9］采用克拉美罗界（Cramér-Rao Bound，CRB）来分析SAR-GMTI 系统的定位误差性能，但克拉美罗界只给出了定位误差最小情况下的分析结果。Cerutti-Maori 等［10］应用微分法及误差传递模型来估计定位误差，该方法缺乏在相位误差、基线误差等条件下对定位精度影响的深入分析。
本文从概率统计角度讨论了目标定位精度问题。假设定位性能主要受噪声影响，推导了运动目标的干涉相位误差的概率密度函数。这种采用概率密度函数描述定位误差的一个突出优点是可以在方案设计和参数评估阶段预测估计星载SAR-GMTI的目标定位性能，另外本文还为不同参数条件下的在轨SAR-GMTI系统性能比较提供了一种新的分析思路。
1 采用多通道技术抑制杂波
当前大多数GMTI 系统均采用多通道技术［6-13］进行杂波抑制，本文讨论聚焦多通道SAR-GMTI系统。杂波抑制的一个重要步骤是根据实测数据来估计杂波向量。假设每个像素内包含一个运动目标，则N幅SAR图像对应像素的复信号A1,A2,…,AN可以表示为
式中，i 表示第i 个天线，S1,S2,…,SN 分别为N 幅图像中对应的运动目标信号，且Si=S1exp(-jφt,i),
λ 为工作波长，Vr 和V 分别表示目标径向速度和平台速度，d 表示两个接收天线相位中心之间的距离，ni 表示第i 个天线的噪声信号，c 表示杂波分量。理想情况下，各个天线接收的杂波信号应完全相同。
在目标信噪比（Signal-to-Noise Ratio,SNR）足够大的条件下（SNR ＞20 dB），可以采用干涉仪（Along-Track Interferometry,ATI）技术［14-15］精确估计运动目标的径向速度Vr。但是当SCNR 相对较小时，干涉相位测量精度较低，导致径向速度Vr 的测量精度和目标定位精度严重下降。因此，必须尽可能抑制杂波信号以便于获得较高的SCNR。由式（1）可知，理想情况下，N 幅复图像中的杂波向量完全相同，该杂波向量C 可以用原点指向点C(x,y)的向量表示。图1 中，N 个点A1(x1,y1)，A2(x2,y2)，…，AN(xN,yN)表示N幅复图像a1,…,aN。这N 个向量均匀分布在以点C(x,y)为圆心，半径均为r的圆上，易得这N个向量的表达式为
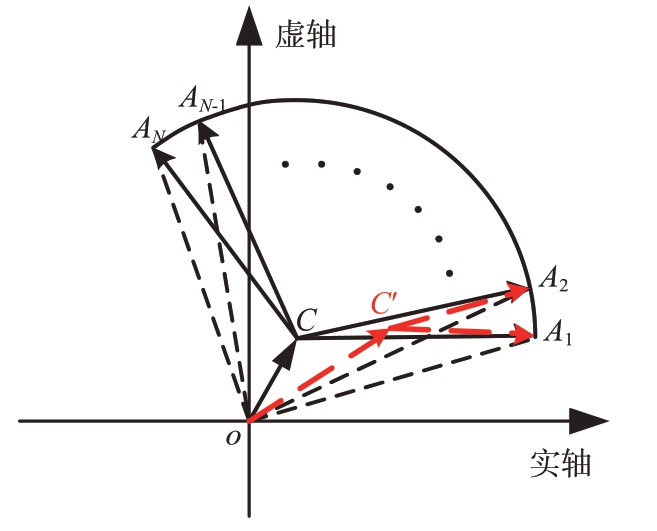
图1 采用ATI方法杂波相消时N幅配准的SAR图像之间的干涉相位关系
为求解运动目标的真实位置，需要对目标重新定位。由于卫星/飞机平台快速运动，地面杂波的主瓣杂波谱会明显展宽，位于主瓣杂波谱的慢速运动目标通常会被掩盖，难以检测；要完成对动目标角度的精确测量和定位至少需要3 个子孔径［6］（通道）。此处结合图1，对该原理进行简单说明。圆上任意两个向量OA1和OA2表达式分别为
OA1和OA2分别表示两个通道复信号，杂波相消就是同时减去相同的杂波分量OC。但由图1可知到点A1 和A2 距离相同的点C 和C′有无穷个，式（3）也可表示为
杂波抑制后没有多余的空域自由度进行目标定位了。因此，至少需要3 个孔径，即3 个向量OA1、OA2 和OA3，依据三点共圆原理，可以唯一确定圆心，即先准确估计杂波分量C再进行抑制。
典型的方法是将沿航向均匀排列的3 个天线子孔径分成1、2 和2、3 两组完成杂波相消，利用相消后的两个相位进行干涉测向，按照测得的目标距离和目标所在的多普勒通道，对目标的径向速度进行估计并对运动目标进行重新定位。
基于上述分析，假设在下文的讨论中杂波被充分抑制。杂波抑制后，目标矢量的起始点就变成原点。
2 定位误差的概率密度函数
本节重点分析噪声对运动目标定位的影响。假设杂波信号被完全抑制，则目标定位精度主要受噪声的影响。以一个包含3部天线的SAR-GMTI系统为例，“通道1和通道2”以及“通道2和通道3”两两杂波相消后，目标信号与噪声信号构成的两个复向量I1和I2的表达式如下:
与式（1）不同的是，式（3）中不包含杂波向量（假设采用DPCA 及STAP 等技术已经将杂波完全抑制），则I1和I2的干涉相位可以表示为
式中，angle(·)表示复向量的辐角，[·]*表示取共轭。
式（4）中值得注意的是，只有在不存在噪声背景下，杂波抑制后两个复向量的干涉相位才等于运动目标的真实干涉相位。只要存在噪声，I1和I2的干涉相位必然与真实目标的干涉相位存在偏差。假设干涉相位主要是受白噪声N1 和N2 影响，且N1和N2的数学期望为0，方差为σ2，则可以推导出干涉相位误差的概率密度函数。根据文献［16］，白噪声N1 和N2 的相位在
区间上服从均匀分布，很容易得出N1 和N2 相位差θ 的概率密度函数
假设目标信号与噪声信号之间满足独立同分布，可得
式中，φt为式（1）中运动目标干涉相位，E[·] 为数学期望，且
令R=|S|，则式（8）可以变换为
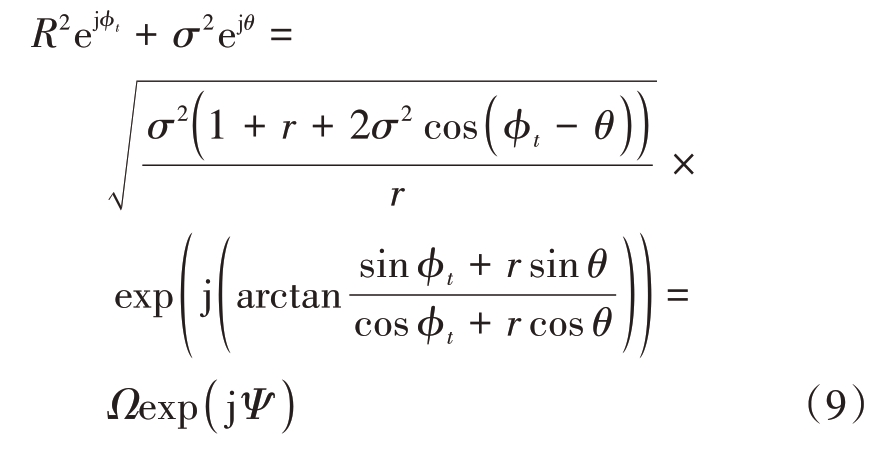
式中，r=σ2/R2，且r 的数学期望E[r] 与信噪比SNR 成反比，令
式（8）中复向量的相位Ψ 与运动目标干涉相位φt之差为Δφ，且Δφ正切值由下式给出:
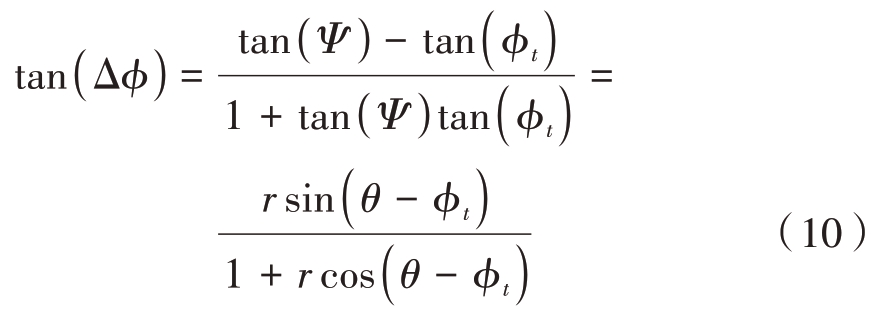
令α=θ-φt，对式（8）两侧变量α 求偏导，可知当cos α=-r 时，求得tan(Δφ) 极值为
因此，当Δφ 范围是
时，tan(Δφ)的值域为
cos α=-r 在区间[-π,π]上有两个根，分别是α1=-arccos(-r)和α2=arccos(-r)。当α ∈(α1,α2)时，函数tan(Δφ)是单调递增的；当α ∈(-π,α1)及α ∈(α2,π)时，函数tan(Δφ)是单调递减的。
将cos α看作未知变量，则由式（11）可得:
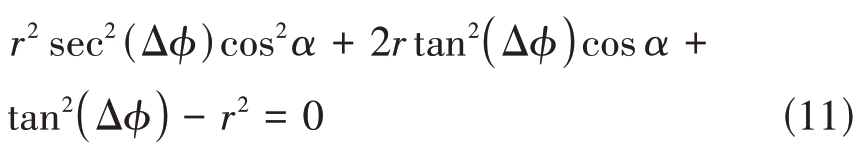
式中，α的值域为[0,2π]。
根据一元二次方程求根公式可得
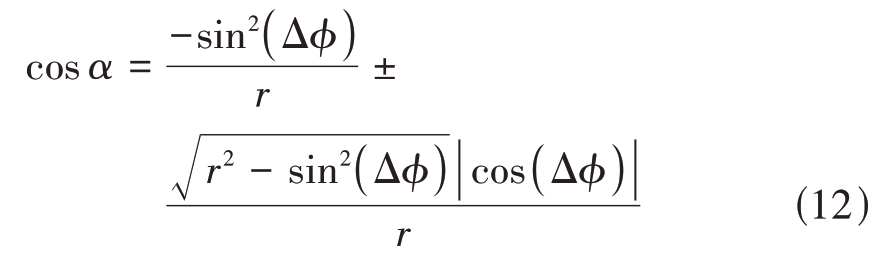
Δφ的概率密度函数fΔφ(Δφ) 是变量Δφ的分段函数，因此我们可以分别在两个区间
上推导fΔφ(Δφ) 的表达式。为便于进一步推导，令A=
分段函数fΔφ(Δφ)，当
时，
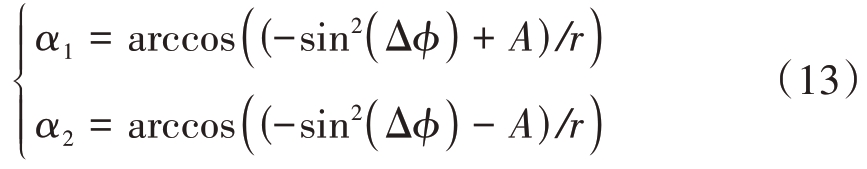
式（13）两侧同时对变量Δφ求偏微分，可以得到
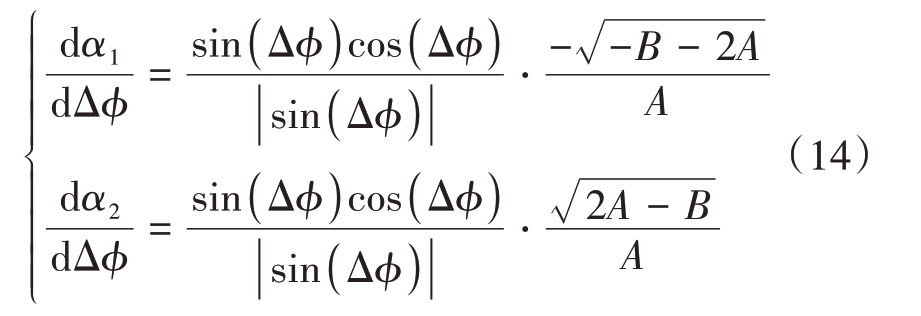
当
时，
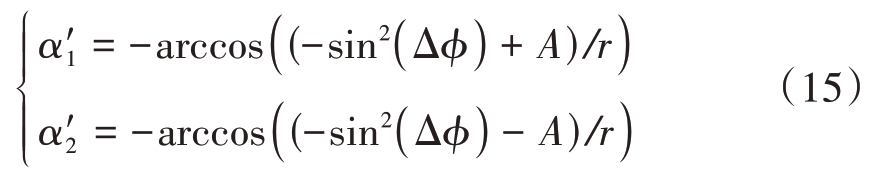
注意，式（15）中用α′1 和α′2，以便与式（13）中α1和α2进行区分。
则微分系数表达式为
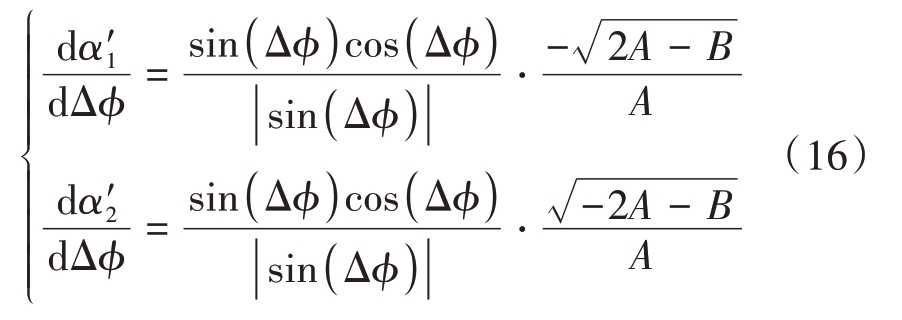
根据概率密度函数（PDF）的非负性，相位误差Δφ的概率密度函数表达式如下:
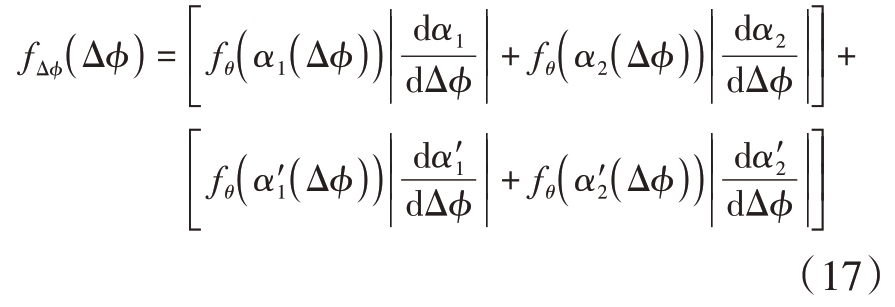
采用图2对上述结果进行解释，假设运动目标位于复平面的第一象限，其幅度大小为R，运动目标干涉相位为φt。上文提及噪声信号可以被认为是幅度为σ2，相位θ服从均匀分布的复向量。考虑到噪声矢量具有随机性，不论噪声位于哪个象限（例如图2 中噪声位于第一象限，其他象限结论类似），相位差Δφ 均表示目标和噪声和矢量与目标矢量之间的夹角，即目标定位问题实质上是目标矢量与噪声矢量竞争的结果。
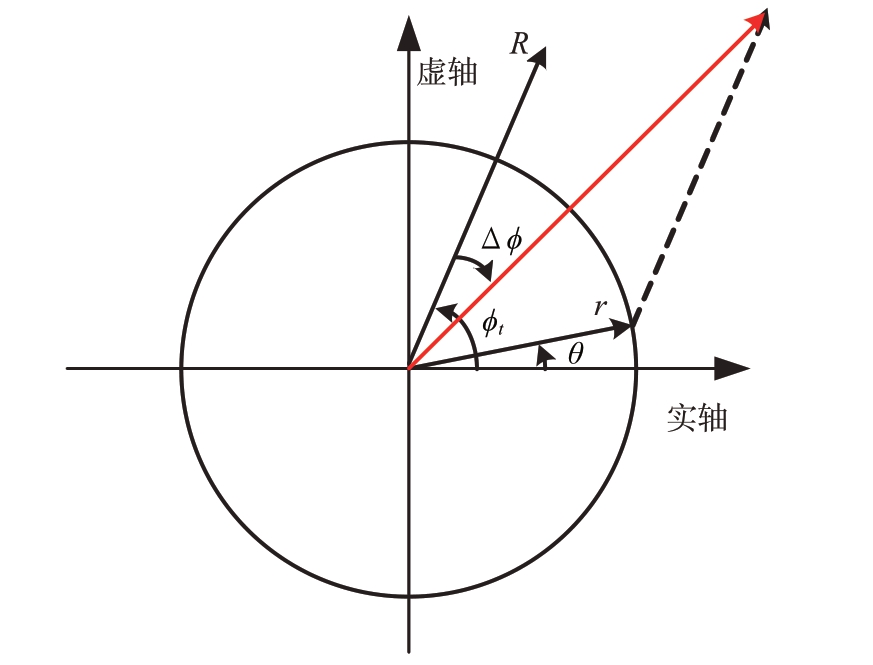
图2 相位误差产生原因说明（图中目标和噪声向量均位于第一象限）
换言之，相位误差主要受目标信噪比的影响。事实上，SNR 远大于1的情况对于探测运动目标是非常有利的，反之SNR远小于1的情况表明目标被噪声遮挡难以探测。此处，有三种情况需要解释。第一种情况，当Δφ=0时，目标向量和噪声向量矢量方向相同，则目标信号被增强，有利于获得较高的定位精度；第二种情况，当Δφ=π 时，即目标信号矢量和噪声矢量方向相反，则目标信号被抵消，目标定位精度由剩余信号能量与噪声比值（SNR）决定；第三种情况，当目标矢量与噪声矢量相互垂直，相位误差Δφ最大，此时目标定位误差也最大。
3 定位性能分析
本节从两个方面针对上面的分析进行性能分析仿真。一方面，采用推导的概率密度函数（PDF）来分析运动目标定位误差。另一方面，分析信噪比对目标定位性能的影响。假设星载SAR 下视角为50°，表1 给出了3 个国外典型的单基星载SAR/GMTI 系统［17］的主要参数，这三个SAR/GMTI 系统分别为TerraSAR-X、RADARSAT-II 和Cosmo-Skymed，它们都有双通道GMTI 试验模式，相邻天线通道（或相位中心）的间距分别为2.39 m，7.5 m 和3 m。注意，每个卫星都具有M 个天线通道，例如TerraSAR-X（M=12）,RADARSAT-II（M=16）以及Cosmo-Skymed（M=5），这样有助于采用空时自适应处理技术抑制杂波。
表1 国外3个典型星载SAR-GMTI系统的雷达参数
参数波长天线长度天线数量载频中心斜距TerraSAR-X 0.031 1 m 4.784 m 2 9.6 GHz 761 km RADARSAT-II 0.055 5 m 15 m 2 5.405 GHz 1 156 km Cosmo-Skymed 0.031 1 m 6 m 2 9.65 GHz 909 km
根据文献［18］，目标径向速度Vr 的表达式如下:
值得注意的是式（18）中的Vr，d 和Δφ 是不考虑基线误差时的理想值。
定位误差是干涉相位误差Δφ的函数:
式中，Rs表示卫星平台到运动目标间的中心斜距。
由图3 可知，当信噪比（SNR）为10 dB 时，TerraSAR-X、RADARSAT-II和Cosmo-Skymed 3个星载SAR-GMTI 系统的最大定位误差分别为158.74 m，136.37 m和150.38 m，它们对应的概率值为1，表明上述3 个SAR-GMTI 系统定位精度大于该取值概率较大。对这三个星载SAR-GMTI系统进行比较，从图3 可以看出目标定位误差落入[]0,100 m 区间的概率分别是0.442，0.472 和0.533。事实上，目标定位误差与不同天线参数密切相关。图3 中，TerraSAR-X 的目标定位误差比其他两个系统要大，这主要是由于TerraSAR-X 的方位口径小于另外两个星载SAR-GMTI系统，其基线较短。
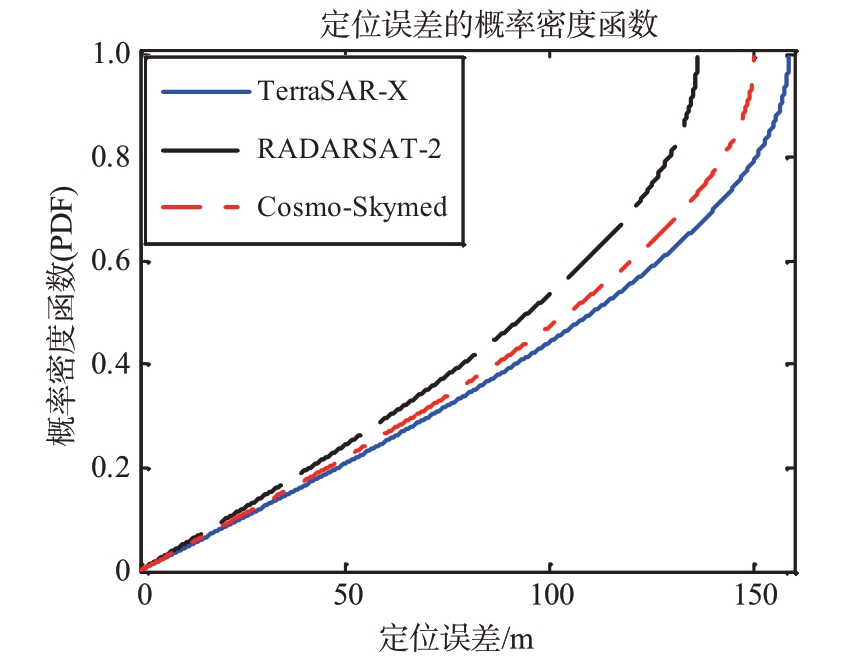
图3 3种星载SAR-GMTI系统的目标定位概率密度函数曲线（图中设定目标信噪比为10 dB）
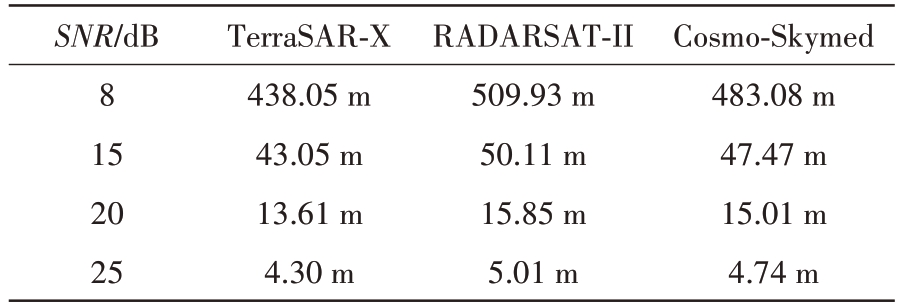
影响定位精度的另外一个重要因素是目标信噪比。表2给出3种星载SAR-GMTI系统在不同信噪比条件下的最大定位误差。
表2 不同星载SAR-GMTI系统不同信噪比条件下的最大目标定位误差
SNR/dB 8 15 20 25 TerraSAR-X 438.05 m 43.05 m 13.61 m 4.30 m RADARSAT-II 509.93 m 50.11 m 15.85 m 5.01 m Cosmo-Skymed 483.08 m 47.47 m 15.01 m 4.74 m
以TerraSAR-X 为例，图4 分别给出了信噪比10，15和20 dB 条件下的目标定位误差概率密度函数。由图4 可知，SNR 较低时目标定位误差较大，反之当SNR 较高时，出现较小的目标定位误差的概率显著增加。当信噪比分别为10，15 和20 dB时，定位误差为9 m 的概率分别为0.037，0.114 和0.384，表明目标信噪比在定位性能上起着重要作用，提高目标定位精度的首要因素就是提高目标信噪比。换言之，要达到一定目标定位精度，目标信噪比必须要达到某个门限值。例如，为了将定位误差控制到10 m 以内，要求目标信噪比不小于22 dB。
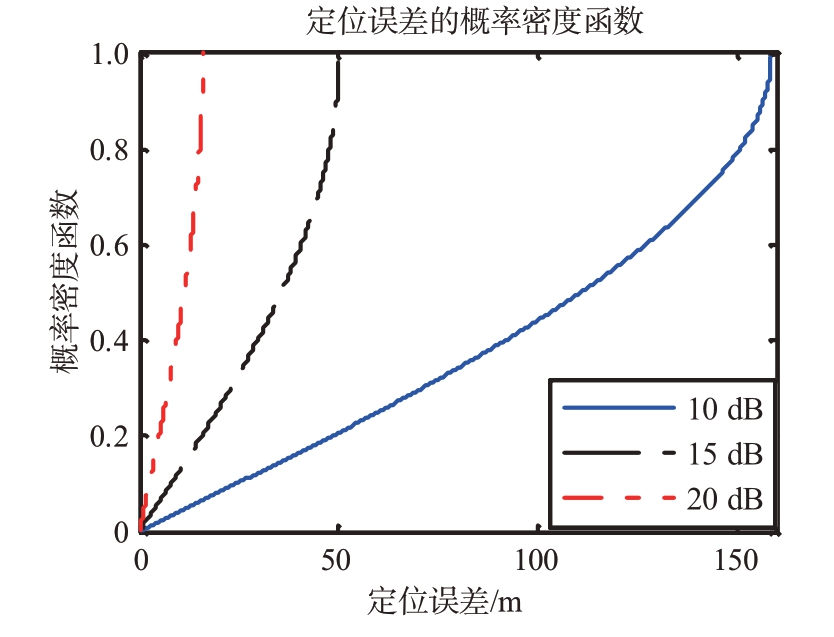
图4 目标信噪比分别为10，15和20 dB时TerraSAR-X对应的定位误差概率密度函数
事实上，星载SAR 斜距可达几百公里甚至上千公里，即使较小的相位误差从卫星传导到地面也会造成明显的定位误差。为了获得较高目标定位精度，需要提高雷达系统功率孔径积，进而提高目标信噪比。注意，上述推导及分析结果是在理想条件下得到的，实际情况中可能不一定完全满足，但上述分析结果也是有意义的，可以为星载SAR-GMTI 系统理论分析和参数设计提供重要分析工具。
4 基线误差对定位性能的影响
上一节，我们分析了噪声对定位误差的影响。事实上，星载SAR-GMTI系统定位误差还受一些非理想因素（例如地球自转、大气扰动、轨道误差等）影响。这些非理想因素在文献［19-20］进行了深入讨论，此处就不作详细讨论。本文只考虑由于热胀冷缩现象引起的基线变化对目标定位的影响。根据式（18），可以得出当基线误差存在时，定位误差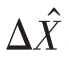
和径向速度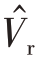
表达式分别为
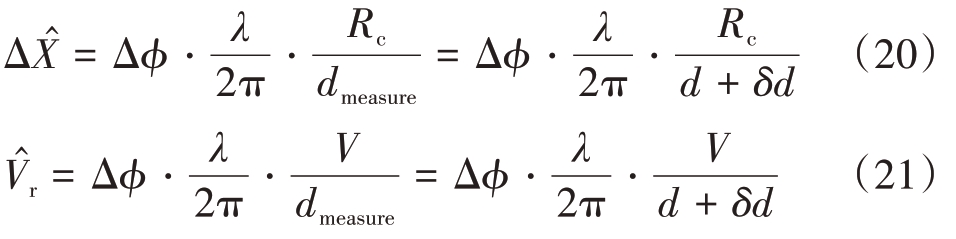
式中，dmeasure 表示测量基线值，d 表示两通道之间的实际基线值。二者之差用δd=|dmeasure-d|表示。
由于基线测量值dmeasure 存在误差，实际中即使Δφ是准确的，用dmeasure估计得到的目标径向速度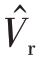
也是存在误差的。由基线误差导致的速度估计误差由下式给出:
由式（22）容易推导得出基线引起的额外定位误差δRreloca表达式如下:
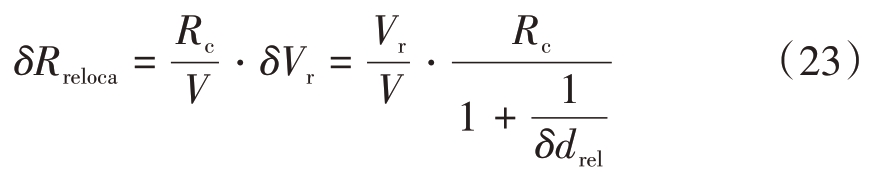
式中，δdrel=δd/d 为δd 和d 的比值，此处命名为相对基线误差。当δdrel ≪1，δRreloca ≈
· Rc· δdrel。
当径向速度为常数时，定位误差与相对基线误差成正比。本文以TerraSAR-X 为例来研究基线误差对定位误差的影响。仿真中假设基线误差δd均值为0，方差σ2 为（δd）2，即δd 值域为（-Δd,Δd）。图5给出定位误差δRreloca随径向速度Vr和相对基线误差δdrel的变化关系。垂直坐标表示径向速度Vr，其变化范围从0～50 m/s，水平坐标δdrel 表示相对基线误差，其变化范围从0%～5%，颜色表示不同定位误差（m）。以定位误差15 m 为门限，黑线上方区域表示定位误差小于15 m的情况。例如，图5中，当δdrel=1% 和Vr=10 m/s 时，定位误差为9.94 m。
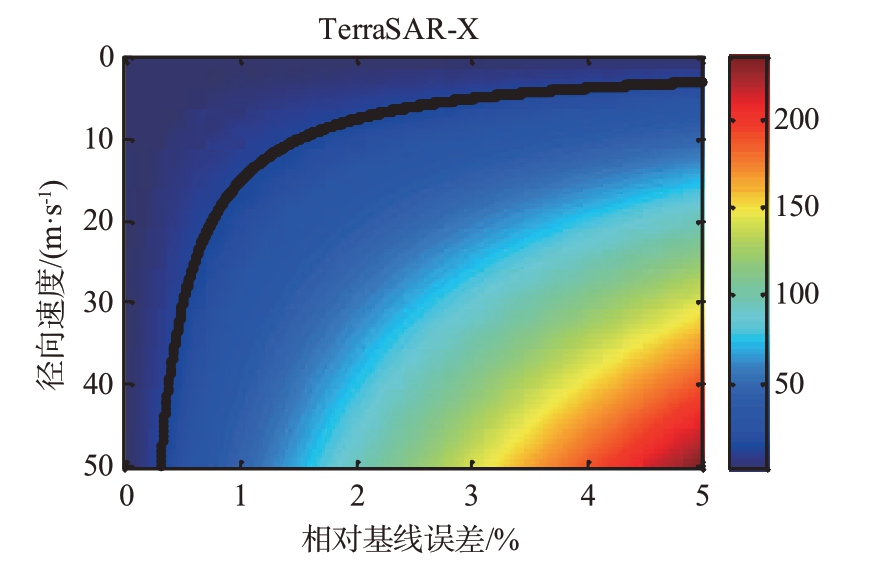
图5 目标定位误差随径向速度和相对基线误差的变化曲线
最后，我们同时考虑噪声和基线误差影响，并分析给出目标定位误差的概率密度曲线。图6中，绿色、红色和黑色曲线分别对应d-Δd，d 和d+Δd 三种情况。换言之，目标定位误差的PDF 是一类介于d-Δd和d+Δd之间的PDF曲线簇。
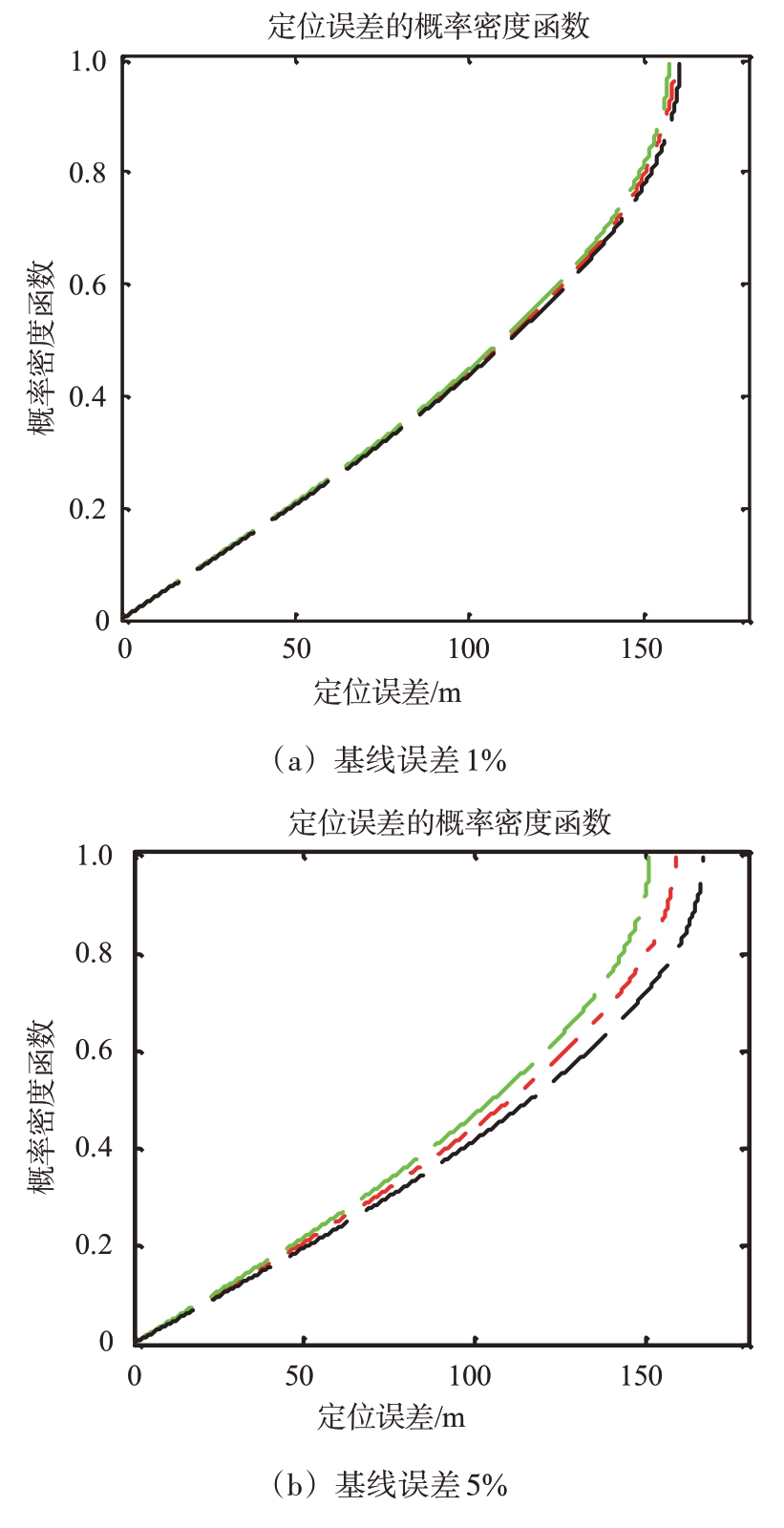
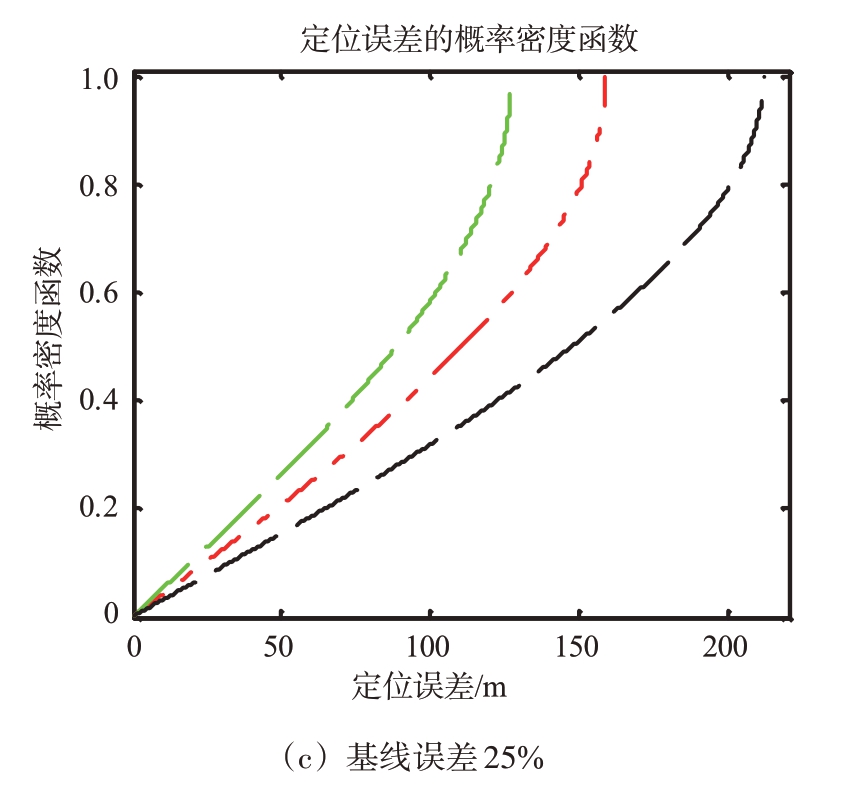
图6 当相对基线误差分别为1%，5%和25%时对应的目标定位精度
如图6（a）所示，当基线误差δdrel 只有1%时（Δd=0.023 9 m），3条概率密度函数曲线几乎完全重合，表明该基线误差对定位影响相对较小。当基线误差δdrel 达到5%的时候（Δd=0.119 6 m），概率密度函数曲线簇出现了分化，此时基线误差对定位精度影响比较明显。为了分析基线误差的影响，仿真计算了一种更极端的情况，但δdrel 大于25%（Δd=0.598 0 m）时，黑色和绿色概率密度函数曲线出现了明显差异。注意δdrel=25%为较极端情况，实际系统中不常见。事实上，由于黑色和绿色曲线分别表示误差上界和下界，随着d的变化可以得到一束分布介于绿色和黑色曲线为边界的概率密度函数曲线簇。对于RADARSAT-II 和Cosmo-Skymed系统，也可从仿真计算中得出类似结论，此处不再赘述。
5 结束语
本文首先针对GMTI系统中至少需要3个子孔径同时实现杂波抑制和目标精确定位的基本原理提出了全新的几何解释。在此基础上，本文指出目标理论位置和实际位置偏离主要是由于复噪声影响，导致ATI方法测得的目标干涉相位与实际干涉相位存在误差。受概率统计思想启发，基于高斯白噪声模型假设推导了一种新的运动目标定位误差的概率密度函数模型，该统计模型充分发掘多通道技术探测目标时的相位差异。本文提出的概率分析对星载和机载SAR-GMTI 系统以及分布式卫星GMTI 系统［21-23］均适用，拓展后可推广分析分布式卫星系统的目标检测性能。
注意本文研究目标主要是针对地面慢速运动目标，未来需要深入研究快速或高机动运动目标的定位误差的统计特性。另外，对于星载SARGMTI 系统，由于卫星运动速度远大于地面目标的运动速度，运动目标方位向速度引起的散焦问题可以忽略。但是对于高机动空中目标或者临空高速飞行器，实现目标精确定位难度较大，作为开放性研究领域，后续需要深入研究，一些新技术［24］可能作为有益探索解决此类问题。
［1］ZHANG Shuangxi,JIANG Zheyi,CHEN Junli,et al.An Effective Clutter Suppression Approach Based on Null-Space Technique for the Space-Borne Multichannel in Azimuth High-Resolution and Wide-Swath SAR System［J］.IEEE Trans on Geoscience and Remote Sensing,2022,60:1-28.
［2］韩超垒，杨志伟，张庆君，等.距离-多普勒-频带域3DAWP-MRF分类辅助的SAR-GMTI杂波抑制方法［J］.电子学报，2021，49（12）:2339-2348.
［3］王宇，曹运合，齐晨，等.基于高超声速平台前斜视多通道SAR-GMTI 杂波抑制方法［J］.电子与信息学报，2020，42（2）:458-464.
［4］MU Huilin,ZHANG Yun,JIANG Yicheng,et al.CV-GMTINet: GMTI Using a Deep Complex-Valued Convolutional Neural Network for Multichannel SAR-GMTI System［J］.IEEE Trans on Geoscience and Remote Sensing,2022,60:1-15.
［5］RANEY R K.Synthetic Aperture Imaging Radar and Moving Targets［J］.IEEE Trans on Aerospace and Electronic Systems,1971,7（3）:499-505.
［6］YADIN E.A Performance Evaluation Mode for a Two Port Interferometer SAR-MTI［C］// Proceedings of the 1996 IEEE National Radar Conference,Ann Arbor,MI,USA:IEEE,1996:261-266.
［7］HU Ruixian,LIU Baochang,WANG Tong,et al.A Knowledge-Based Target Relocation Method for Wide-Area GMTI Mode［J］.IEEE Geoscience and Remote Sensing Letters,2014,11（4）:748-752.
［8］HAN Jiusheng,CAO Yunhe,YEO T S,et al.A Novel Hypersonic Vehicle-Borne Multichannel SAR-GMTI Scheme Based on Adaptive Sum and Difference Beams Within Eigenspace［J］.Signal Processing,2021,187:1-16.
［9］ENDER J H G,GIERULL C H,CERUTTI-MAORI D.Improved Space-Based Moving Target Indication via Alternate Transmission and Receiver Switching［J］.IEEE Trans on Geoscience and Remote Sensing,2008,46（12）:3960-3974.
［10］CERUTTI-MAORI D,KLARE J,BRENNER A R,et al.Wide-Area Traffic Monitoring with the SAR/GMTI System PAMIR［J］.IEEE Trans on Geoscience and Remote Sensing,2008,46（10）:3019-3030.
［11］GUO Yifan,LIAO Guisheng,LI Jun,et al.A Novel Moving Target Detection Method Based on RPCA for SAR Systems［J］.IEEE Trans on Geoscience and Remote Sensing,2020,58（9）:6677-6690.
［12］LONG Yajun,ZHAO Fengjun,ZHENG Mingjie,et al.A Novel Azimuth Ambiguity Suppression Method for Spaceborne Dual-Channel SAR-GMTI［J］.IEEE Geoscience and Remote Sensing Letters,2021,18（1）:87-91.
［13］HE Xiongpeng,LIAO Guisheng,ZHU Shengqi,et al.Range-Ambiguous Clutter Suppression for the SAR-GMTI System Based on Extended Azimuth Phase Coding［J］.IEEE Trans on Geoscience and Remote Sensing,2020,58（11）:8147-8162.
［14］SOUMEKH M.Moving Target Detection and Imaging Using an X Band Along-Track Monopulse SAR［J］.IEEE Trans on Aerospace and Electronic Systems,2002,38（1）:315-333.
［15］CHEN C W.Performance Assessment of Along-Track Interferometry for Detecting Ground Moving Targets［C］//Proceedings of the 2004 IEEE Radar Conference,Philadelphia,PA,USA:IEEE,2004:99-104.
［16］BARHAT M.Signal Detection and Estimation［M］.Boston:Artech House,1991.
［17］李春升，王伟杰，王鹏波，等.星载SAR 技术的现状与发展趋势［J］.电子信息与学报，2016，38（1）:229-240.
［18］VACHON P W,CAMPBELL J W M,GRAY A L,et al.Validation of Along-Track Interferometric SAR Measurements of Ocean Surface Waves［J］.IEEE Trans on Geoscience and Remote Sensing,1999,37（1）:150-162.
［19］GODARA L.Error Analysis of the Optimal Antenna Array Processors［J］.IEEE Trans on Aerospace and Electronic Systems,1986,22（4）:395-409.
［20］SUN Qingyang,SHU Ting,TANG Mang,et al.Effective Moving Target Deception Jamming Against Multichannel SAR-GMTI Based on Multiple Jammers［J］.IEEE Geoscience and Remote Sensing Letters,2020,17（3）:441-445.
［21］陈乐平，安道祥，周智敏，等.机载双频曲线SAR 系统与试验［J］.雷达科学与技术，2021，19（3）:248-257.
［22］刘浩，吕洋，李川.一种机载GMTI 雷达点迹凝聚方法研究［J］.雷达科学与技术，2022，20（1）:87-91.
［23］詹珍贤，许唐红，胡帅帅，等.无人机载Ku 波段有源相控阵天线［J］.雷达科学与技术，2020，18（2）:151-155.
［24］WANG Bao,LIN Xianqi,KANG Yuxin,et al.Low-RCS Broadband Phased Array Using Polarization Selective Metamaterial Surface［J］.IEEE Antennas and Wireless Propagation Letters,2022,21（1）:94-98.
