0 引 言
雷达探测空中目标,不同于地面目标跟踪,可以利用交通运输网等先验信息辅助目标跟踪,雷达通常只能利用探测到目标的空间相对位置、运动特征等特征对目标进行跟踪,难以获得观测区域内的飞行器航道信息进行辅助。实际上,由于地形、流量控制、洋流、气象条件、燃料等因素,空中、海上等雷达目标也遵循特定的航道运动,以便快速到达目标位置,而这些航道信息蕴含在目标的运动轨迹中。因此,可以对一定区域内一定时间段内积累的目标运动轨迹进行分析处理,从中获得隐含的区域内航道信息,作为先验辅助信息,在气象、电磁环境复杂的情况下帮助雷达进行目标跟踪,提高探测效率和情报质量。
目前大部分工作是对地面道路[1-2]、海(河)面舰船[3]进行航道提取。Li 等人[4]提出改进的动态时间规整算法(DTW)实现时间序列的分类与聚类,该方法能够较为精确的度量序列差异,但DTW时间复杂度为O(m·n),即与对比的两条序列的采样点数之积正相关,因此当轨迹数目多,长度大时,该算法效率较低。Guo等人利用高斯分布对道路上的GPS点进行建模,从中抽取路网信息[5]。由于GPS 精度高,道路上的运动点偏移概率小,因此采用高斯分布对GPS 点进行建模行之有效;对于雷达探测的空中目标而言,航道并不可见且探测获得点迹的位置精度和稳定性远低于GPS,导致高斯分布难以在大量航迹点上对其准确建模,提取航道。另一类方法将轨迹点视为图像中的像素点,提取航道[6-7]。但在由不同采样率获得的航迹集合上,这种方法难以进行合适的平面网格化,获取“像素”。对于水面目标,大部分航道提取工作基于位置精度较高的AIS 信息提取水面航道,如Lee 等人[8-12]利用AIS 建立核密度函数或密度聚类等方法,获取航道轮廓,再提取轮廓中心线作为航道。
目前大部分提取航道的方法是基于合作式目标,可获取其主动提供的准确定位信息,然而在雷达探测中,有时难以获取由目标提供的准确定位,只有被动探测数据。被动探测由于系统误差、随机误差、环境噪声等原因,精度有限,即使目标是沿着某航道运动,其结果也可能存在偏差。因此我们提出一种基于密度拟合的航道挖掘方法,在无先验知识且不引入利用航迹点时间关联性的情况下,将航迹作为最小处理单元,实现精细化航道提取的目标。
1 问题背景与基本定义
本文我们将给出在无先验知识的条件下,从积累的雷达数据中提取热门航路的方法,基于密度拟合区域航道挖掘方法(Density based Fitting Method for Route Extraction,DFRE)。具体来说,积累的雷达数据由一个区域内的目标航迹点组成,包含经度、纬度、时间等信息。我们的方法目前只考虑二维平面内的航道挖掘,并未考虑空间高度;忽略航迹中各点的时间关系,将每条航迹视为一个处理单元,找到区域内的热点航路。热点航路由一系列斜率参数及起始点经纬坐标组成的线段集合表示。
1.1 方法框架
本文提出的方法包含航迹参数拟合及拟合参数聚类两个部分。根据目标航迹特征可知,大部分航道呈直线状,少量航道可呈多条直线组成的折线/曲线状。因此本文方法首先利用最小二乘方法对航迹数据集进行拟合,获得各航迹在二维平面上斜率和截距两个拟合参数,再使用基于密度的空间聚类方法DBSCAN 对拟合参数进行聚类。DBSCAN方法是一种无监督聚类方法,无需提前进行模型训练,不受聚类形状限制(只要空间分布连续),可应用于未知聚类数目的聚类。因此对于本方法中未知拟合参数空间分布的情况,DBSCAN方法适用。
1.2 参数聚类
DBSCAN方法将聚类对象抽象为空间中的点,某点的密度由其半径δ(δ-邻域)内的点迹数目定义。根据点的密度,空间中的点可分为核心点、边缘点和噪声点。其中,点密度不低于阈值γ的为核心点,位于核心点密度范围内但自身点密度小于γ的为边缘点,其他则为噪声点。DBSCAN通过循环迭代完成聚类。
所有的聚类点初始标记为未访问。随机选取一个未访问的p 点,若p 的δ 邻域内点数不少于γ,则标记p 为类别Li且已访问。将其δ-邻域中不带类别标签(噪声不是簇标签)的点加入Li候选集;若点数小于γ,那么p被标记为噪声且已访问。对于Li候选集合中的某个点p*,聚类时可能有两种情况。
情况1: p*没有被访问。在这种情况下,p*被标记为已访问且类别Li。若p*δ-邻域中点数不小于γ,则将其邻域中所有未被标记类别的点放入Li候选集。
情况2: p*已被访问。p*是Li的边缘点,标记为Li。
上述过程在所有聚类点上迭代进行,直到它们都已访问且被标记类别(或噪声)。
2 基于密度拟合的区域航道挖掘流程
2.1 航迹参数拟合
具体航道提取流程如算法1所示,首先对每条航迹进行航迹拟合(算法2),输出每条航迹的参数集合H={(kh,bh,starth,endh)}Hh=1。集合中由拟合参数kh、bh及起始点位置starth、endh表示相应航迹,利用聚类算法将相近的航迹参数聚为一类(算法3),此处选择数值较小的聚类邻近阈值,保证聚类的精确性。之后对属于同一类的航迹根据起始终结位置进行接续处理(算法4),保证初步提取航道的连续性,避免由于航迹点迹缺失或航迹结束导致的航道不完整。较小的聚类邻近阈值虽能保证聚类的精确性,但易导致一些属于同一类的航迹被分为几类。因此在完成航道接续后,根据各条航道可能存在或交叉或邻近的位置关系,利用算法再进行一次航道合并(算法5)和接续(算法4),得到最终的区域航道信息。
算法1:基于密度拟合区域航道挖掘(DFRE)

输入:航迹集合T={tm|tm=(xm1,ym1),(xm2,ym2),…,(xmN,ymN)}Mm=1,拟合精度acc_threshold,划分单元length_unit,距离阈值δk,δb,连接阈值σc,合并阈值σk,σlat,σlon输出:航道参数集合H={(kh,bh,starth,endh)}Hh=1(starth,endh为航道起始、终结坐标)1Γ=FFT(T,acc_threshold,length_unit);2Λ=FPC(Γ,δk,δb);3Θ=CFT(Λ,δc);4H=MNR(Θ,σk,σlat,σlon);
对航迹的参数拟合过程由算法2所示,假设某目标航迹tm 由点迹序列组成{(xm1,ym1),(xm2,ym2),(xm3,ym3),…,(xmN,ymN)},其中x 为经度,y 为纬度,各航迹点迹数目N 并不相同。由该点迹拟合获得的直线段斜率和截距如下式所示,对于沿某经线运动的航迹,其k 值无穷大(即x=c)。对于此类航迹,采用以纬度为x,经度为y 进行拟合。将式中x与y互换,即可得到以沿经线运动的航迹的拟合参数。用(km,bm)参数对表示每条航迹(第2行)。
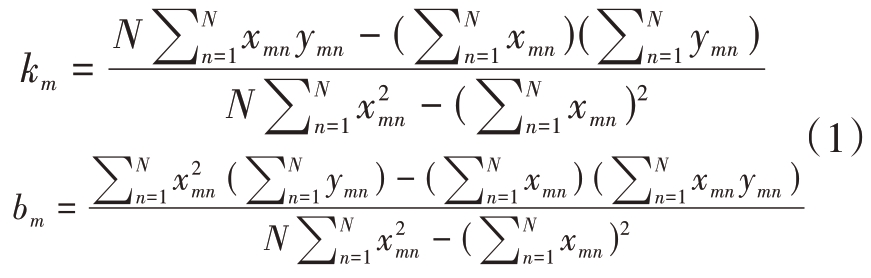
随后判断当前拟合是否满足拟合精度阈值,本方法以航迹中各点的纬度与由各点经度经拟合参数获得的拟合纬度间的绝对差值的均值作为衡量标准(第3行)。若满足精度阈值,则该拟合参数及对应的航迹起始终结点坐标组成向量(km,bm,startl,endl)放入集合Γ(第5 行),若不满足阈值,则将其放入分段航迹集合(第7行)。对该集合内的各条航迹进行分段,每p个航迹点作为一独立航迹(p 取值视数据情况调整,本文实验中p 取20),进行与上述过程类似的参数拟合及精度判断,满足阈值要求的分段航迹补充进集合Γ,反之则舍弃不用(第9~13 行)。注:本文中所指航迹起始为当前航迹中经度最小点和终结为当前航迹中经度最大点,与航迹实际产生过程无关。此外,当前算法基于k 值存在的情况,若趋向于无穷大(航迹平行于经线),则将纬度视为x、经度视为y,同时将算法中涉及到的经纬度互换即可。
算法2:航迹参数拟合(FFT)

输入:航迹集合{tm|tm=(xm1,ym1),(xm2,ym2),…,(xmN,ymN)}Mm=1,拟合精度acc_threshold,航迹划分单元length_unit输出:满足精度的航迹参数集合Γ={(kl,bl,startl,endl)}L l=1(startl,endl分别为航迹起始、终结点坐标)1for m=1 to M 2按照公式(1)计算航迹tm的拟合参数(km,bm);3计算拟合精度accm=(∑n=1 N|kmxmn+ bm-ymn|)/N;4if accm ≤acc_threshold 5(km,bm,startl,endl)放入Γ;6else 7将tm放入分段航迹集合{}t′s S s=1;8endfor 9for s=1 to S 10将航迹t′s划分为长度为length_unit的多个子航迹;11计算各个子航迹的拟合参数并计算拟合精度;12满足拟合精度的子航迹参数(ks,bs,starts,ends)加入集合Γ;13endfor
2.2 拟合参数聚类
在实际情况中,飞行器沿着航道运动,因此在收集到的航迹数据中可以看出在一些区域,某些位置航迹沿某个方向呈现平行聚集情况,如图1(a)所示。因此在对航迹进行参数拟合后,聚类拟合参数,从平行聚集的航迹集中抽取相应的航道参数。具体聚类提取方法如算法3 所示。以航迹参数集合Γ={(kl,bl,startl,endl)}Ll=1、用于聚类度量的距离阈值δk,δb 为输入,对参数k 与参数b 分别聚类。对航迹l,将参数k 与kl 距离不超过δk 的航迹编号分别与l 构成元素(l,lδi k)分别放入集合Ak,对参数kb 进行同样操作(第1~4 行),得到集合Ab。两个集合交集即为同时满足k与b聚类要求的航迹对(第5 行)。对集合中出现的每一个航迹编号l,将与l 满足距离关系的编号与l 归为同一类,同时以该类中的编号为参数距离衡量参考,将与其满足距离关系的编号归为当前类别,以此类推,当前类别不断延伸,直至不再有新编号加入该类别,则该类别完成聚类(第7~23行)。
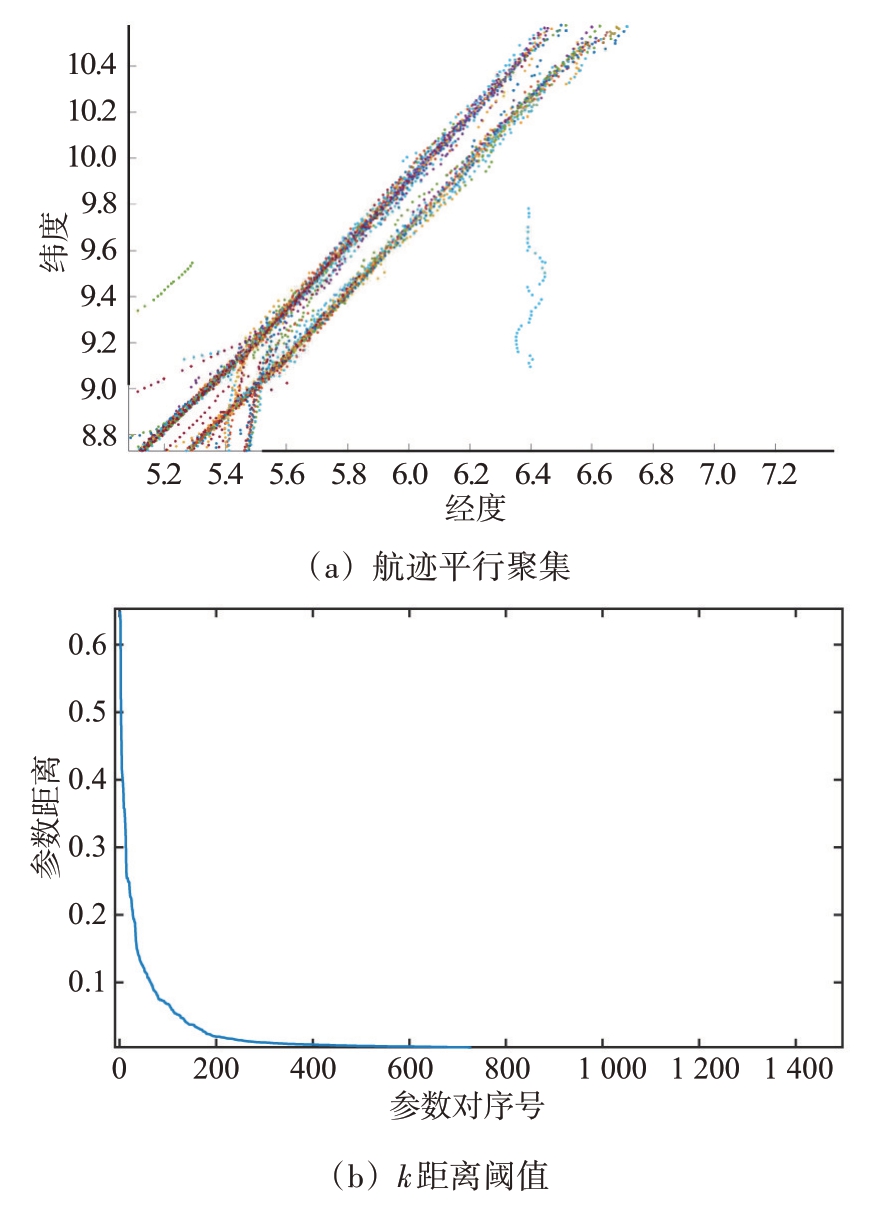
图1 航迹分布及聚类参数统计
由于聚类过程是基于距离关系类别集合不断扩充的过程,若距离阈值δk,δb过大,则会导致所有航迹编号聚为同一类;若阈值过小,则会导致聚类失败。因此,我们随机选取了训练集中20%的数据,计算并统计这些航迹参数间的距离,如图1(b)所示。为保证同一类别内的高内聚性,避免粗粒度聚类导致航道提取不准确,我们以拐点所在区域内较小的距离值作为距离阈值,达到航迹参数聚类效果。
算法3:拟合参数聚类(FPC)

输入:航迹参数集合Γ={(kl,bl,startl,endl)}Ll=1,距离阈值δk,δb输出:拟合航迹聚类集合Λ={(kl,bl,startl,endl,C)}L l=1 1for l=1 to L 2将拟合斜率k位于[kl-δk,kl+ δk]区间内的航迹编号lδk i(l,lδk i)I 存入集合Ak={}L i=1l=1;3将拟合截距b位于[bl-δb,bl+ δb]区间内的航迹编号lδb i(l,lδb j)I 存入集合Ab={}L j=1l=1;4endfor 5Akb=Ak ⋂Ab;6C=1,BC=∅;7for l=1 to L 8if l已被访问9 continue;10else 11将l放入集合BC,每个满足(l,lδkb) ∈Akb且lδkb ∉BC的航迹编号lδkb放入集合BC;12l标记为已访问;13e指向BC中第一个元素;14while e不为∅15每个满足(e,eδkb)∈Akb且eδkb ∉BC的航迹编号eδkb放入集合BC;16e标记为已访问;17e指向BC中下一个元素;18endwhile 19BC中编号的类别标记为C;20C++,BC=∅;21将BC中航迹编号对应的参数向量(kg,bg,startg,endg,C)加入集合Λ;22endif 23endfor
2.3 拟合航迹连接
由于不同航迹不同的起始位置和终结位置,归属同一类的航迹参数会存在位置重叠或者不连续的情况。为了去除重叠,同时保证航道连贯,我们利用拟合航迹连接算法进行航迹去重和接续处理。具体过程如算法4 所示。对于某一航迹参数类别,将该类别中的参数向量按照航迹起始点的经度依升序排序(第2行)。
令s1 表示初始连接航迹,s2 表示最新连接上的航迹,e 表示当前待连接航迹,若e 与s2 存在重叠或者二者端点的经度差(e 的起始点和s2 的终结点)不超过连接阈值,则e连接至s2航迹,s2向当前连接航迹中结束点经度最大的航迹,e 指向下一待连接航迹(第5~8,14 行);若e 与s2 不满足条件,则中断当前连接过程,以s1 航迹的起始为起始,s2 航迹终结为结束,从s1 到s2 的航迹参数k 与b 的均值为参数,表示经连接产生的航道,同时下一待连接航迹作为新的初始(最新)连接航迹s1 和s2 表示,e 则指向s1和s2所示航迹的下一条航迹(第10~12,14行)。
上述过程循环直至所有类别内的航迹参数都完成连接评估,完成航道提取。
算法4:拟合航迹连接(CFT)

输入:拟合航迹聚类集合Λ={(kl,bl,startl,endl,C)}Ll=1,连接阈值σc输出:航道(迹)链集合Θ={(kg,bg,startg,endg)}G g=1 1for each C 2根据start_lon值对同属C类别的航迹参数向量排序;3s1=1,s2=s1,e=s1+1;4while e ≤||C 5 if starte_lon ≤ends2_lon+ σc //若e航迹开始经度不超过s2航迹结束经度的σc扩展6 if ende_lon >ends2_lon //若e航迹结束经度大于s2航迹结束经度7 s2=e;8 endif 9 else 10以s1至e所有航迹的k,b均值为合并航迹k,b均值,以s1航迹的起始为起始,11s2航迹的结束为结束,存入集合Θ;12s1=e,s2=s1;13endif 14e=e+1;15endwhile 16以s1至e所有航迹的k,b均值为连接航迹的k,b均值,以s1航迹的起始为起始,e航迹的结束为结束,存入集合Θ;17endfor
2.4 邻近航迹合并
虽然在航迹参数聚类后进行航迹连接,初步提取出了连贯的航道,但聚类中使用的距离阈值较小,导致有些邻近航迹可能并未被归属同类。因此我们在初步提取的航道上再进行邻近航道合并,去除重叠航道。具体过程由算法5所示。对某航道t,根据其参数kt,在集合Θ中找到满足阈值σk的航道编号,放入同一分组(第2行)。分别计算该分组内的航道i 与t 的距离,若二者存在交点或二者经度交叠部分的纬度差值不超过阈值σlat(若二者斜率参数绝对值之和大于2,则为纬度交叠部分的经度差值不超过阈值σlon),则记t 与i 为一组邻近航道对,放入集合Q(第3~13 行)。对邻近航道对集合Q,利用FPC算法在航道参数做一次聚类和航迹连接(第15、16行),避免由于邻近关系引入的参数误差,保证航道方向、位置的准确性和航道连贯性。
通过本方法提取出的航道可用于后续该区域内的目标跟踪。当环境复杂,杂波较多时,可将跟踪航迹与航道匹配,利用航道帮助过滤异常点,防止目标跟偏,航迹断批。
算法5:邻近航道合并(MNR)

输入:航迹(道)集合Θ={(kl,bl,startl,endl)}Ll=1,合并阈值σk,σlat,σlon输出:航道参数集合H={(kh,bh,starth,endh)}H h=1 1for t=1 to L 2将ki ∈[kt,kt+ σk]的航道编号i放入集合I;3for each i ∈I 4 if航道i与航道t存在交点5(t,i)放入集合Q;6 elseif 航道i与t的经度存在重叠部分且该部分最大距离(纬度差值)不超过σlat 7(t,i)放入集合Q;8 elseif||ki+||kt >2 9 if航道i与t的纬度存在重叠部分且该部分最大距离(经度差值)不超过σlon 10(t,i)放入集合Q;11endif 12endif 13endfor 14endfor 15基于集合Q运行FPC算法第6~23行,获得集合ϒ;16H=CFT(ϒ,δc);
3 实验结果及分析
3.1 实验设置
本文在实测航迹数据集上进行算法性能测试。航迹数据集包含同一区域不同时间的三次采集结果,共计包含2 501 条航迹。随机抽取其中1 600条作为训练集,剩余数据作为测试集,测试提取获得的航道是否能符合区域内航迹情况。训练集和测试集中的航迹分布如图2 所示。测试集和训练集中的航道分布基本一致,因此可用测试集对从训练集中抽取出的结果进行航道匹配性测试。
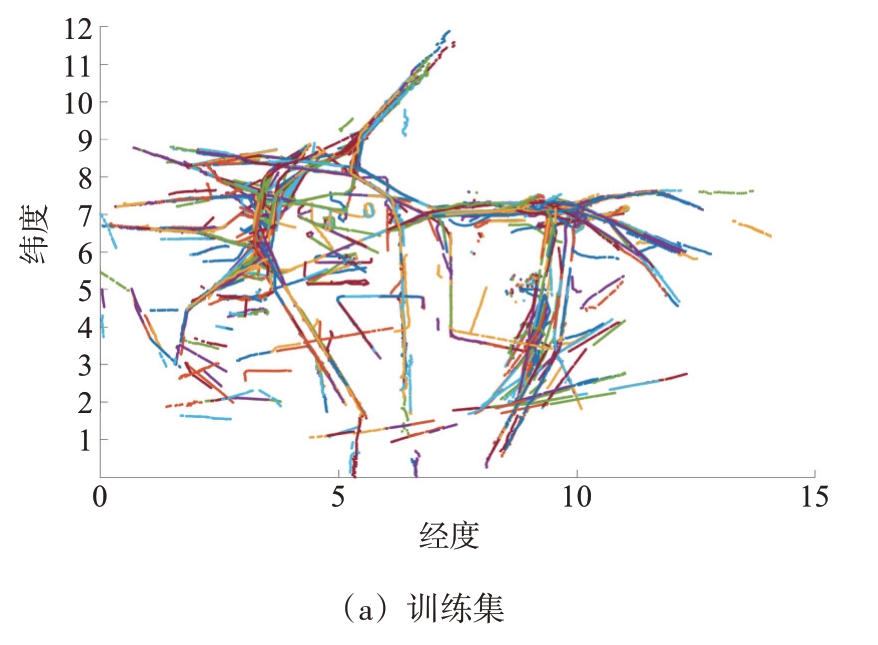

图2 航迹数据集
3.2 实验结果分析
我们将基于区域热点的航道骨架提取算法作为控制对比组,与本文方法做实验对比。图3(a)为控制组方法从训练集中提取的航道,图3(b)为本方法从训练集中提取的航道与测试集航迹的对比图,其中蓝色点线为航道,绿色点为测试集航迹。观察可知,对比组方法虽然航道连通性高,基本勾画出航迹分布轮廓,但航道走向勾画精准度不高;本方法航道间连通性较低,但对整体航道走向勾画较为精准。为衡量提取航道与测试航迹的匹配性,我们以航迹与航道是否处于同一区域、航迹点与航道间的距离,以及航迹匹配上的航道点的整体航向衡量航迹航向的匹配度。
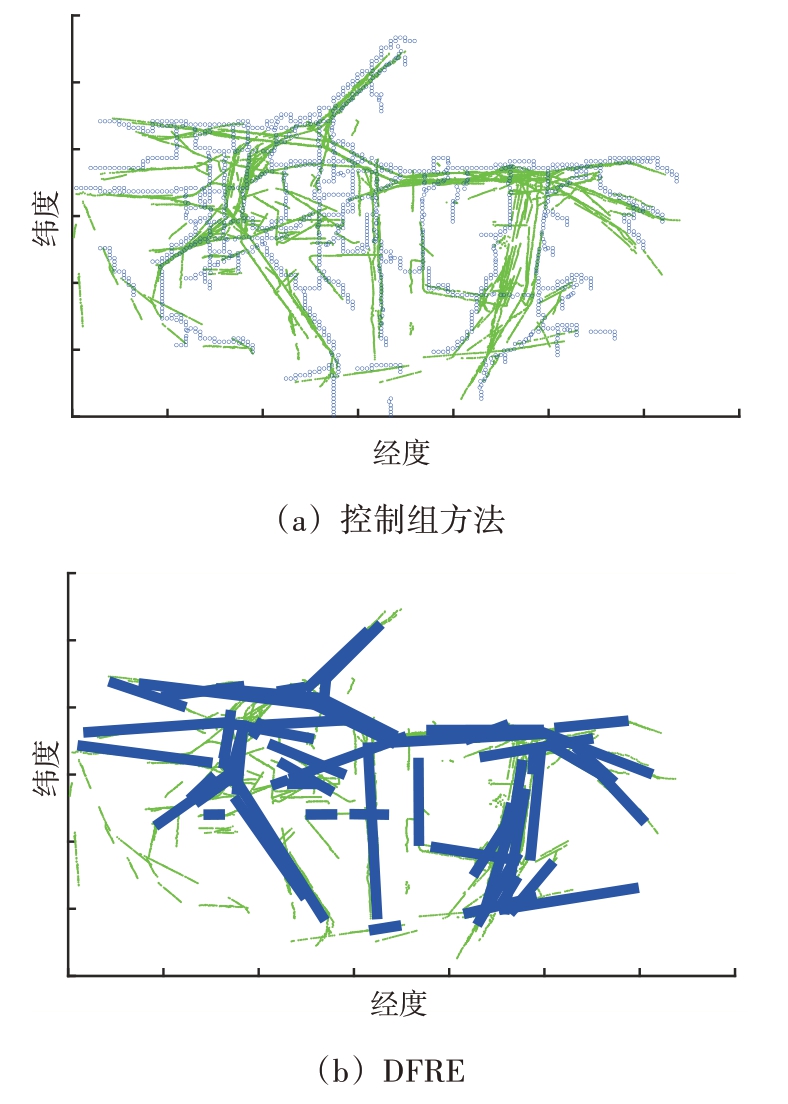
图3 航道提取对比
具体来说,在航迹与航道存在经度或纬度重叠的部分,统计航迹点与航道间距离不超过设定阈值、航向匹配的航迹点数目,计算匹配的航迹点数目与该航迹总航迹点数目的占比。由于篇幅有限,表1 仅展示了两种不同距离阈值,不同匹配比例下的两种航道对测试集航迹的匹配性。从表中可知,在控制变量的条件下,匹配到的航迹数目和距离阈值成正相关。与对比组结果相比,本方法所获得航道的匹配度普遍大幅度优于对比组方法,要求的匹配度越高,本方法的优势越明显。虽然对比组方法将勾画出连通的整体航道,但受限于航道骨架提取需将区域网格化的要求,难以对航道方向进行精确提取,同时易受少量异常值影响,导致航道精确度差,匹配度较低;而本方法利用了参数拟合的思想,避免了区域网格化引入的不必要误差,保证了航道的精确度。
表1 航道-航迹匹配统计
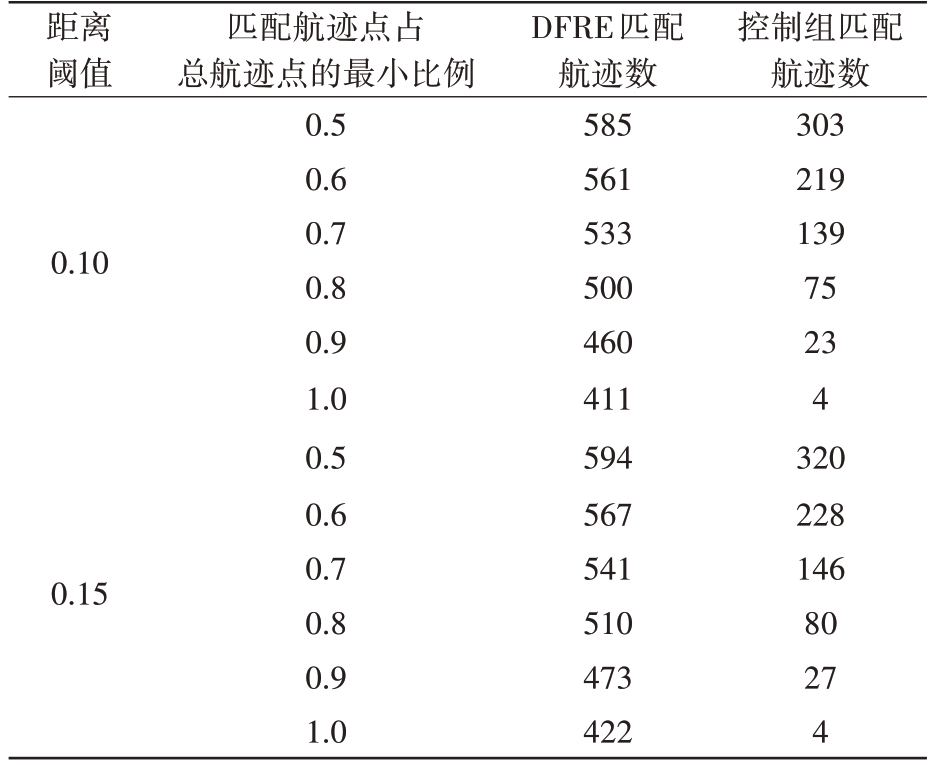
距离阈值0.10 0.15匹配航迹点占总航迹点的最小比例0.5 0.6 0.7 0.8 0.9 1.0 0.5 0.6 0.7 0.8 0.9 1.0 DFRE匹配航迹数585 561 533 500 460 411 594 567 541 510 473 422控制组匹配航迹数303 219 139 75 23 4 320 228 146 80 27 4
图4 展示了在距离阈值0.1°时,匹配上航道的航迹结果,图中红色点迹即为匹配上的航迹点。图中黑色虚线圆圈标识了航道匹配较差的区域。对比提取航道的训练航迹集,圆圈1内的训练集本身的航迹较为稀疏,是否存在航道难确定,为避免提取有误,本算法忽略相应航迹;圆圈2 内的区域较小,训练集内航迹杂乱,未能形成明确航道,因此测试集中出现于此处的航迹未能有航道匹配。对比方法中虽然航迹也有匹配,但由于航道不平滑,整体匹配精度较低,此外圆圈3 内的航迹未被匹配,说明对比方法更为偏重对航迹存在区域的轮廓描述,轮廓内航道的精细化提取较弱。
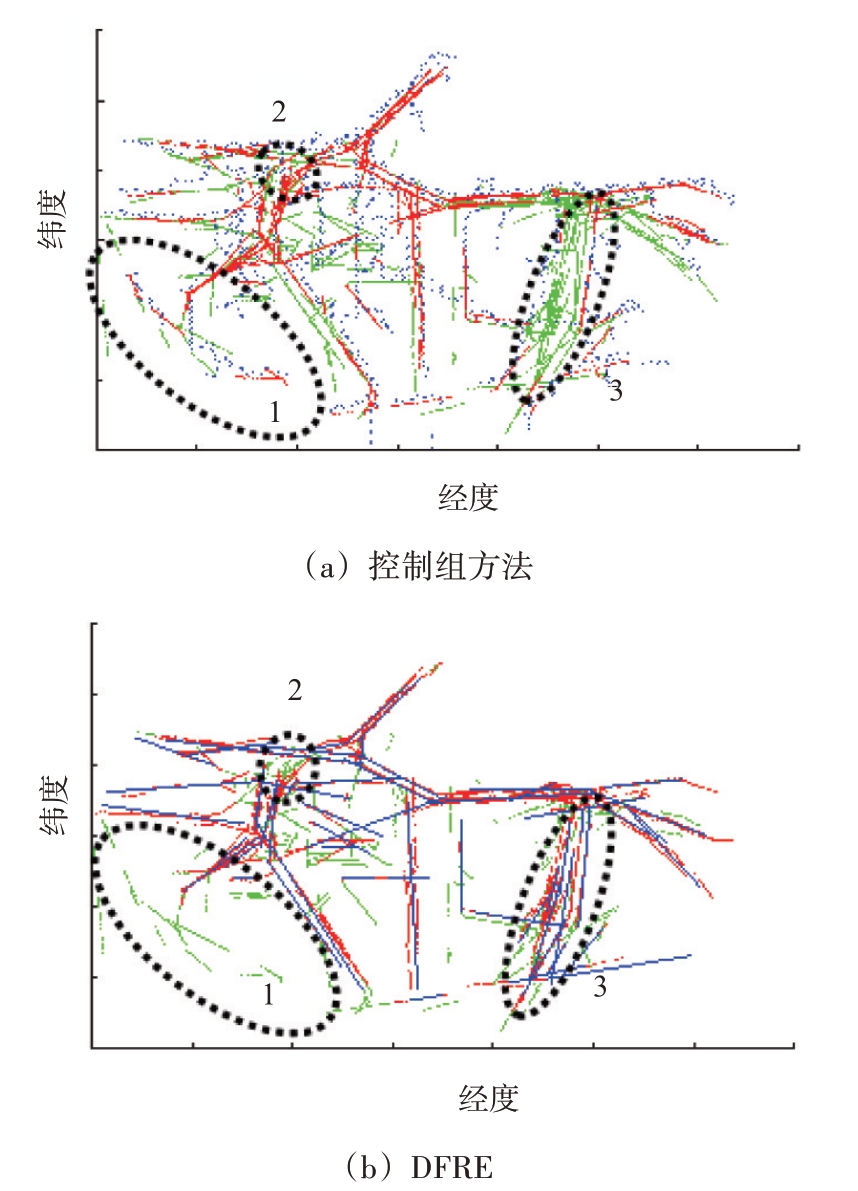
图4 测试集航迹与提取出的航道对比
通过上述对比分析,可以看出本方法具有较强的精细化航道提取能力,在没有先验知识的情况下,能够从积累的历史航迹信息抽象区域内目标运动轨迹,精确有效地提取区域内航道,为航迹跟踪、目标推断提供信息支撑。
4 结束语
本文研究了在不使用额外辅助信息的条件下,如何从航迹数据集中精细化提取航道,提出了一种基于密度拟合的区域航道挖掘方法。由于燃料、成本、飞行安全等限制,大部分航迹近似直线,因此该方法采用直线拟合的方法获取航迹表征参数(对于少数非直线航迹进行分段拟合),基于航迹参数实现邻近航迹的聚类,在同类航迹中进行航道提取,最终根据航道始末位置进行航道连通,完成整个区域的航道挖掘。通过分析和对比试验,本方法效率高且提取出航道具有较高的精细度,能够在无先验知识的条件下有效地挖掘区域内热点航道信息。
[1]焦春雨,常文革.超宽带SAR图像道路提取算法适应性研究[J].雷达科学与技术,2012,10(6):600-606.
[2]TANG Luliang,REN Chang,LIU Zhang,et al.A Road Map Refinement Method Using Delaunay Triangulation for Big Trace Data[J].ISPRS International Journal of Geo-Information,2017,6(2):45.
[3]PALLOTTA G,VESPE M,BRYAN K.Vessel Pattern Knowledge Discovery from AIS Data: A Framework for Anomaly Detection and Route Prediction[J].Entropy,2013,15(6):2218-2245.
[4]LI Huanhuan,LIU Jingxian,YANG Zaili,et al.Adaptively Constrained Dynamic Time Warping for Time Series Classification and Clustering[J].Information Sciences,2020,534:97-116.
[5]GUO Tao,IWAMURA K,KOGA M.Towards High Accuracy Road Maps Generation from Massive GPS Traces Data[C]//Proceedings of 2007 IEEE International Geoscience and Remote Sensing Symposium,Barcelona,Spain:IEEE,2008:667-670.
[6]LIU Xuemei,BIAGIONI J,ERIKSSON J,et al.Mining Large-Scale,Sparse GPS Traces for Map Inference: ComparisonofApproaches[C]//Proceedingsofthe18thACM SIGKDD International Conference on Knowledge Discovery and Data Mining,Beijing,China:ACM,2012:669-677.
[7]LI Jianjiang,CHEN Wei,LI M,et al.The Algorithm of Ship Rule Path Extraction Based on the Grid Heat Value[J].Journal of Computer Research and Development,2018,55(5):908.
[8]LEE J S,SON W J,LEE H T,et al.Verification of Novel Maritime Route Extraction Using Kernel Density Estimation Analysis with Automatic Identification System Data[J].Journal of Marine Science and Engineering,2020,8(5):375.
[9]LEE H T,LEE J S,YANG H,et al.An AIS Data-Driven Approach to Analyze the Pattern of Ship Trajectories in Ports Using the DBSCAN Algorithm[J].Applied Sciences,2021,11(2):799.
[10]SON W J,CHO I S.Analysis of Trends in Mega-Sized Container Ships Using the K-Means Clustering Algorithm[J].Applied Sciences,2022,12(4):2115.
[11]KIM Y J,LEE J S,PITITTO A,et al.Maritime Traffic Evaluation Using Spatial-Temporal Density Analysis Based on Big AIS Data[J].Applied Sciences,2022,12(21):11246.
[12]LEE J S,CHO I S.Extracting the Maritime Traffic Route in Korea Based on Probabilistic Approach Using Automatic Identification System Big Data[J].Applied Sciences,2022,12(2):635.
