0 引 言
靶标设计和优化对提升武器系统性能有着重要的支撑作用,靶标雷达特性预估和分析则是靶标设计优化的重要基础。多次散射结构广泛存在于各类靶标外形结构和靶场应用之中,如靶场角反射器及其阵列的使用、飞机进气道结构、舰船复杂上层建筑形成的多次散射结构等[1-2]。如何准确、高效地实现对含多次散射复杂靶标雷达特性的快速预估和分析,仍然是电磁散射建模领域的重要研究课题[3-4]。高频电磁散射建模方法具有计算效率高、物理机理清晰、工程应用性强的优点,非常适合于大型靶标宽带雷达特性的快速计算和分析[5]。
然而,在靶场尤其是大型靶标设计的实际工程应用中,为了获取合理的设计结果,需要大量重复计算和优化,现有高频计算方法依然难以满足靶标设计高效性的需求,靶标雷达特性快速预估和分析面临诸多困难和挑战。这些挑战和困难主要来自以下几个方面。首先,对电大尺寸靶标的高分辨一维距离像(HRRP),二维雷达图像(SAR)等目标宽带雷达特性的需求加剧了电磁计算的困难[6]。靶标宽带电磁散射特性仿真必须克服雷达宽带信号多个频点和目标多姿态采样所带来计算量大的挑战[7]。其次,为了满足靶标特性计算精度的需求,含多次散射结构(靶场角反射器及其阵列、腔体等)在电磁建模过程中,需要计入三次及三次以上的电磁高阶耦合作用,开展三次以上的高频射线追踪。这类多次的射线追踪过程极其复杂,计算非常耗时,导致靶标雷达特性预估面临计算效率低下的问题[8]。第三,含多次散射结构靶标涉及复杂多次电磁散射机理,对其宽带雷达特性形成机制的分析同样面临巨大挑战。多次散射形成的等效视在中心(距离像位置或者散射中心位置)往往偏离目标区域[9],对多次散射机理和等效视在中心位置的分析,目前还缺乏有效的分析手段。
为了提升电大尺寸复杂目标高频方法计算效率,研究者们采用加速算法和并行计算技术改进高频仿真过程中最耗时的射线追踪模块。Suk 等人提出利用多分辨率网格算法减少射线管的数量从而减少计算量[10];Glassner 等人提出空间划分算法,利用面元之间的空间关系,通过减少射线追踪过程中求交判断的次数来减少计算量[11];随后KDTree 和八叉树等算法在此基础上不断发展[12];国内浙江大学团队利用GPU 平台同时计算众多射线管,通过并行计算来提高计算效率[13-14]。
除了上述加速算法和GPU 并行技术,CPU 多核技术近年来迅猛发展,为并行电磁计算的发展创造了发展空间和条件[15-16]。本文针对含多次散射复杂靶标雷达特性的快速计算难题,提出了一种CPU 多核并行技术、GPU 硬件加速技术和KDTree 遍历技术相结合的靶标电磁散射加速计算方法。在此基础上,建立了带腔舰船、角反射器阵列与舰船等含多次散射复杂靶标的电磁散射(高频)模型,可以满足大型靶标进行快速评估的需求。
针对多次散射特性分析困难,本文进一步提出了多次散射距离像位置快速预测方法。通过多次散射射线分集结合射线路径相位理论预估,预测了多次散射等效视在中心的位置。将多次散射等效视在中心理论预估位置与高频仿真雷达特性进行比较,揭示了腔体等含多次散射结构复杂的多路径散射机理与作用过程。通过具体数值算例,建立了靶标多次散射雷达特性与其多次散射几何结构之间的映射关系。
本文结构安排如下:首先针对靶标雷达特性仿真效率低下的问题,提出了基于三种计算机加速技术的靶标电磁散射高频建模加速方法。然后,针对多次散射特性分析困难,基于电磁场射线理论相位预估,发展了一种多次散射距离像位置快速预测方法。最后,通过数值仿真和分析,表明了本文方法的有效性。
1 靶标电磁散射加速计算方法
图1 展示了传统的靶标雷达特性高频建模流程。
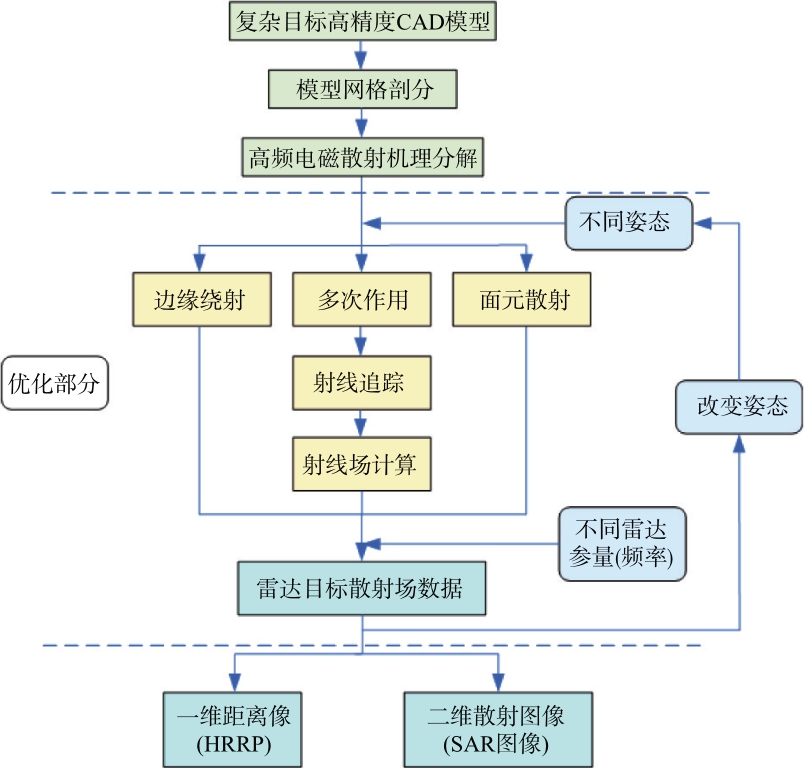
图1 雷达目标特性获取流程图
针对靶标建模对象,首先需要建立对应的高精度CAD 模型,并将目标表面剖分为若干面元,后续根据目标的点面信息进行电磁计算。在对模型预处理之后,将目标散射贡献按照高频散射机理进行分解,可将复杂目标电磁散射贡献分解为边缘绕射场、面元散射及多次射线场等贡献之和。在给定计算姿态下,通过射线追踪确定电磁场的传播路径,并结合物理光学法计算该姿态下的总射线场。进一步可结合时频变换获取宽带雷达特性数据,包括高分辨一维距离像数据以及合成孔径雷达二维图像数据。上述建模流程中,复杂多次射线追踪和大量的目标宽姿态宽频带采样是电磁计算耗时的两个主要原因。
在射线追踪过程中,需要所有射线和所有面元两两进行照亮判断,此时的时间复杂度为O(N2),N 为面元数量。针对电大尺寸复杂靶标高频区散射,N 往往数以万计,此时要获取雷达宽带特性数据的计算代价是巨大的。尤其是当目标存在多次散射结构时,每一次反射点记录需要重复射线与面元两两判断的过程,成倍地增加了计算时间。考虑到射线追踪的过程中,各个射线之间的追踪互不相关,非常适合大规模并行计算。本文通过GPU 平台来对多次射线追踪进行加速。GPU 上有大量的计算单元,在每个计算单元上创建线程进行射线的追踪运算,实现所有射线并行追踪的功能,此时射线追踪的时间复杂度降为O(N)。同时,利用目标各面元的空间位置关系,进一步引入KD-Tree 数据结构,仅对射线与发射方向附近的面元进行求交测试,此时射线追踪的时间复杂度进一步下降到O(log2N)与O(N)之间。
传统仿真串行地依次计算每一个姿态和频点下的回波数据,使得目标宽频带和宽姿态采样的计算非常耗时。考虑到各个姿态下的计算流程相同,且计算过程中的中间数据互不相关,本文采用功能更为强大的CPU 来创建指定数量的多线程实现并行计算。由CPU 创建的每一个子线程在射线追踪环节都将访问GPU,之后继续在CPU 端完成后续的射线场计算。而GPU 作为计算过程中的共享资源,在被其中一个子线程访问时,需要阻止其他线程的访问。本文利用OpenMP 编程模型来协调线程和管理共享资源,使得雷达目标多姿态并行计算顺利进行。如图2 所示,通过OpenMP 中的critical指导语句设立临界区,临界区内的内容同一时刻只能有一个线程访问,将访问GPU 的代码块放置在临界区内,可以保证同一时刻只有一个线程在访问GPU,从而实现了共享资源的保护。
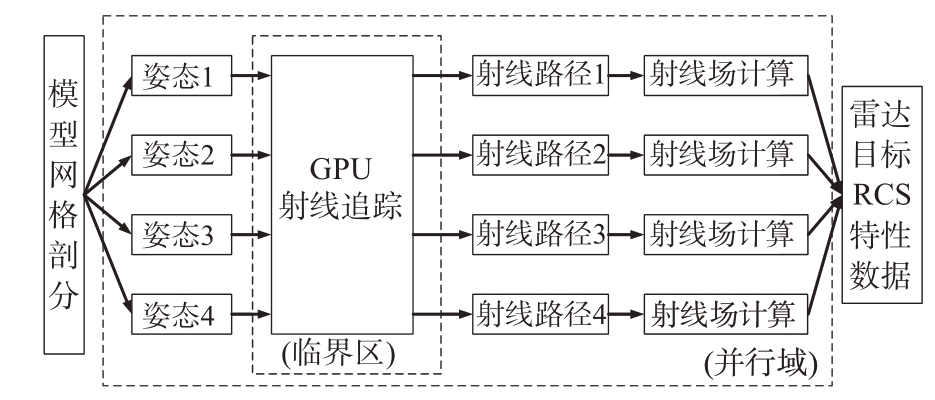
图2 多姿态并行计算模型
在上述过程中,子线程数量并非越多越好,需要确定合理的子线程数量。由于不同线程之间对共享资源GPU 存在竞争关系,当创建一定数量的线程之后,GPU 将达到满负载工作状态,整体效率不会再因为线程数量增多而增加。本文根据线程在GPU 和CPU 上运行的时间长短来创建合理数量的线程。如果把GPU 端进行射线追踪的时间记为A,把CPU端后续射线场计算部分的时间记为B,那么最合理的线程数N可以由式(1)得到:
图3 展示了两种不同情况的用时占比。第一种情况下,GPU 上用时与CPU 上用时相等,此时创建的最佳线程数为2。第二种情况下CPU 上用时情况为GPU 上的2 倍,最佳线程数为3。两种情况下,GPU 上线程运行状况如图4 所示。可以看出,此时GPU 已经达到满负载工作,无法通过创建更多的线程来提高系统效率。
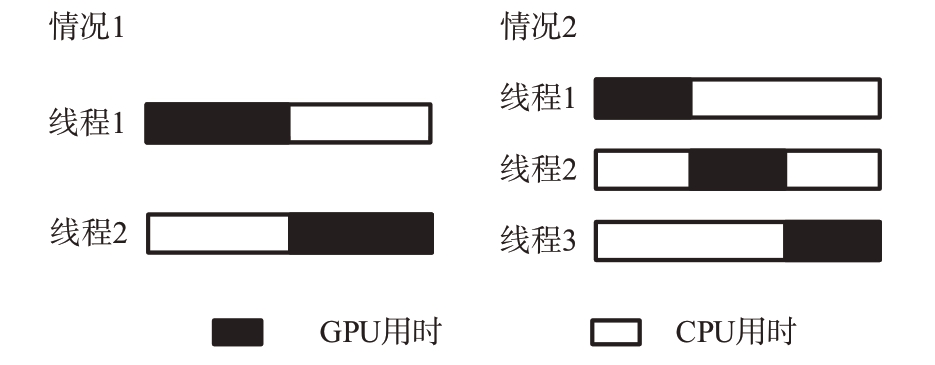
图3 GPU用时不同占比的两种情况
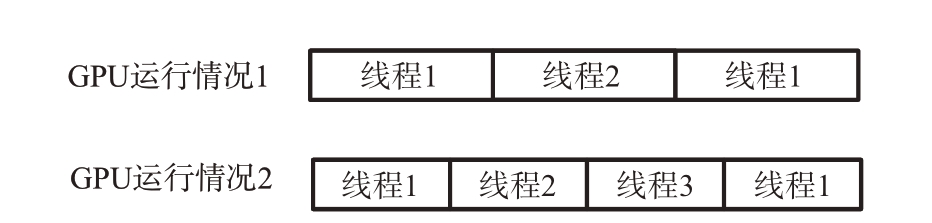
图4 两种情况下GPU运行情况
2 多次散射距离像位置预测方法
本文提出了多次散射距离像位置快速预测方法。通过多次散射射线分集结合射线路径相位理论预估,预测了多次散射等效视在中心的位置。
针对复杂目标多次散射,本文通过射线追踪记录电磁波与目标相互作用的反射点,获取电磁波传播过程中的射线路径集合,计算每一条射线的光程。根据射线光程可以快速推导多次散射等效视在中心的位置,即距离像位置或者散射中心位置。一维距离像峰值的射线理论预测值X 可以按式(2)计算:
式中L 为光程,R 为目标参考系原点到雷达的距离。为了说明光程的计算过程及其物理含义,本文选取多次散射典型结构,以矩形腔体为例,进行具体的分析。当雷达入射方向与腔体横截面平行时,射线在一个平面内传播,此时可以清晰简洁地分析横截面上射线的传播路径,并给出峰值预测结果。
以腔体口径面为界,将射线分为腔体内部射线以及腔体外部射线,然后分别计算光程。图5给出了腔体内部一条射线在口径面某一点入射,经四次反射后返回雷达的传播路径。
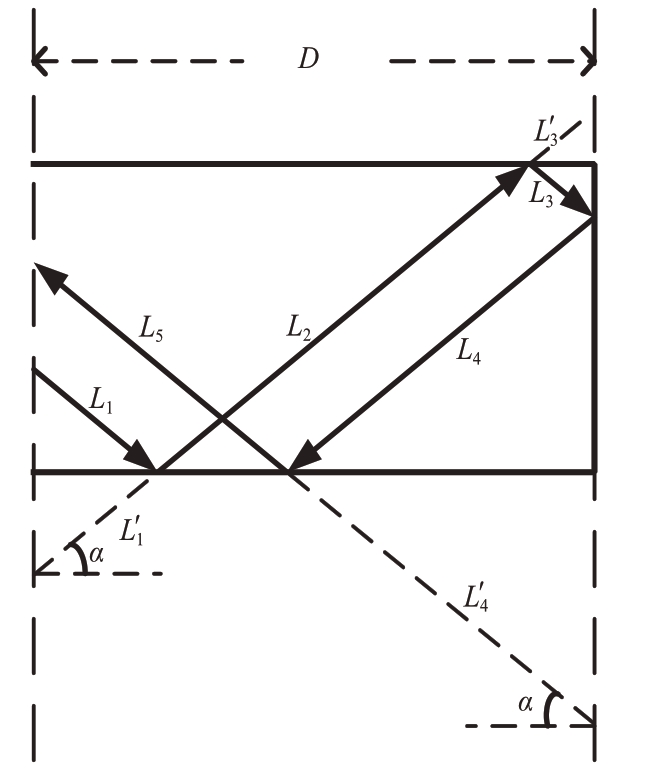
图5 腔体内部射线追踪情况
按反射情况可以将腔体内部的射线分为5段,分别标记为L1,L2,L3,L4,L5。将L1,L3,L4 段以腔内壁为轴翻转,根据几何反射原理,翻转后的L′1,L2,L′3在同一条直线上,L′4,L5 在同一条直线上,由此可以得到该射线长度为
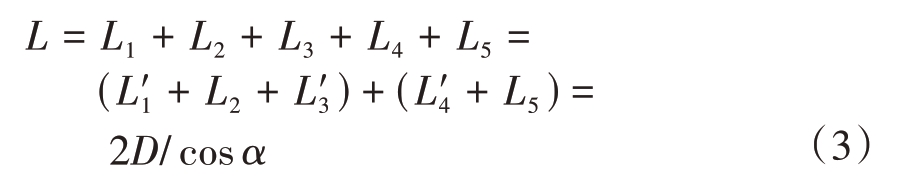
由式(3)可以看出,射线光程在腔体内的长度仅由入射角度α和腔体深度D决定,与入射位置无关。所以对于在口径面其他点入射的射线,光程均相等。而当反射次数增加时,同样可以通过上述方式计算光程。
图6 用于说明如何计算腔体内外总的射线长度。为方便分析,如图建立二维坐标系,并将入射射线与口径面的交点和出射射线与口径面的交点记为y1,y2,与雷达的距离记为a,b,则腔体外射线长度可记为a + b。根据几何关系,可以得到入射方向和反射方向平行,此时腔体外光程可以为y1y2中点到雷达距离的两倍,所以需要先求得y1y2 中点。根据几何关系,有如下关系式:
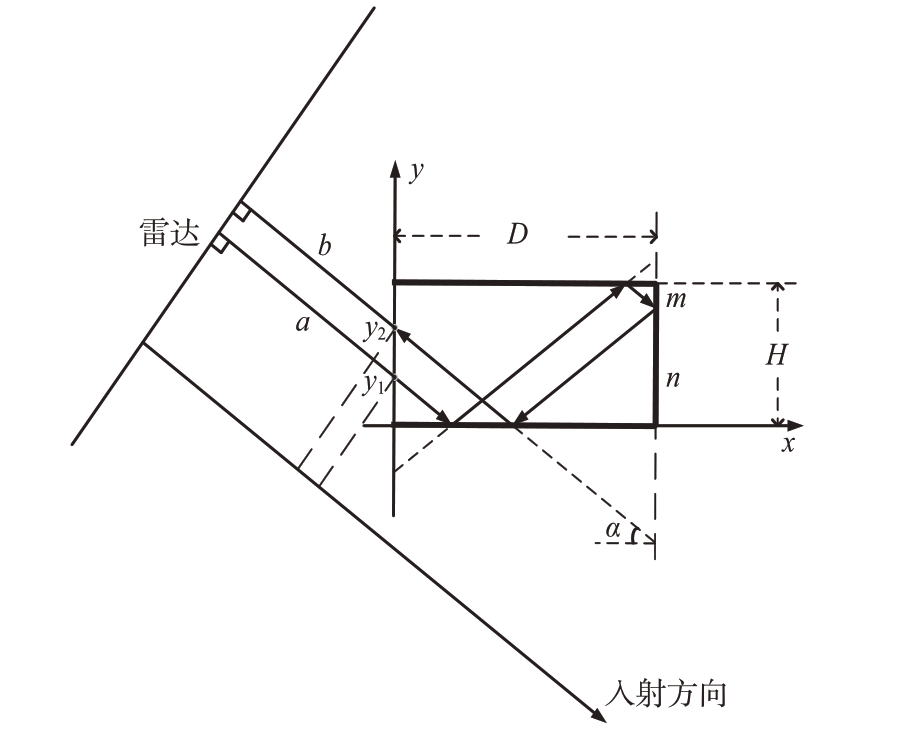
图6 自由空间中射线路径图
式中m,n为腔体底部被接触点分割的两部分,且二者之和为腔体底部长度H,可以求得
式(5)说明入射点与出射点的中点位置坐标仅受入射角度和腔体尺寸影响,从不同点入射的射线在腔体外的长度也相等。所以,针对矩形腔体,在同一入射姿态α 下形成的所有4 次反射的射线路径光程相同,一维距离像位置相同。
图7 是预测腔体目标一维距离像的示意图。A,B 分别为射线入射时与口径面的交点以及反射时与口径面的交点在雷达径向方向的投影。O 点为目标坐标系原点在雷达径向方向上的投影,记坐标原点与雷达之间的距离为R,OA,OB 分别为O点和A,B 点之间的距离,有R = a + OA = b + OB。一维距离像的峰值坐标可以由式(6)求出,其中OA + OB 的值可以通过上文求出的y1y2 中点和雷达间的距离求出。
图7 自由空间中腔体目标成像示意图
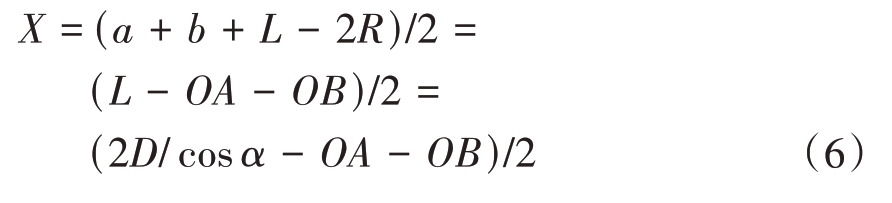
3 靶标雷达特性仿真与分析
三面角和腔体是靶标设计中常见的具有多次散射的典型结构,本节首先通过本文加速方法,获取三面角和矩形腔体两种结构的雷达特性。并将矩形腔体距离像射线理论预估位置与高频仿真距离像特性进行比较,两者吻合一致。进一步,针对带腔舰船、角反射器阵列与舰船复合目标开展了仿真与特性分析,仿真结果表明了本文方法的有效性。本文仿真环境如下:CPU 型号为Intel Core i7-9700,内存大小为16G,内含8 核。GPU 型号为NVIDIA GeForce GTX 1660Ti,显存大小为8 192 MB。
3.1 三面角
三面角的几何模型如图8 所示,面元数为34 292,点数量为17 361。入射射线与z 轴夹角记为俯仰角θ,入射射线在XOY 平面上的投影与x 轴夹角记为方位角φ。三面角雷达参数设置如下:θ角范围为0°~90°,φ角为45°,频率为3 GHz,极化方向为垂直极化。
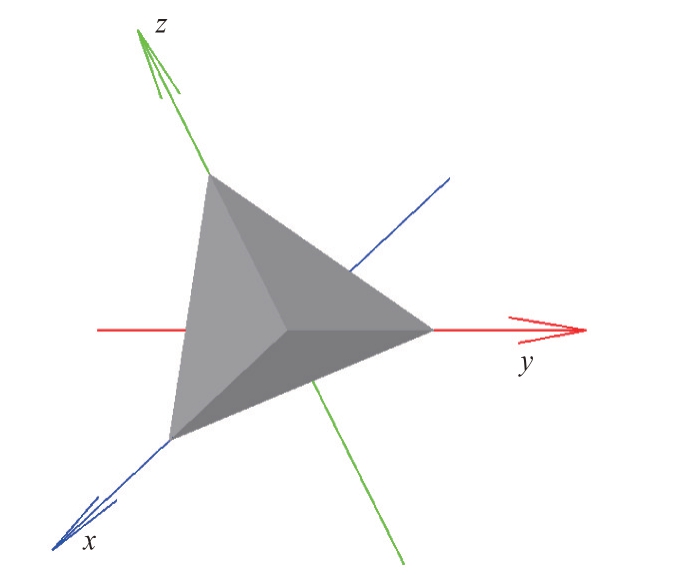
图8 三面角模型
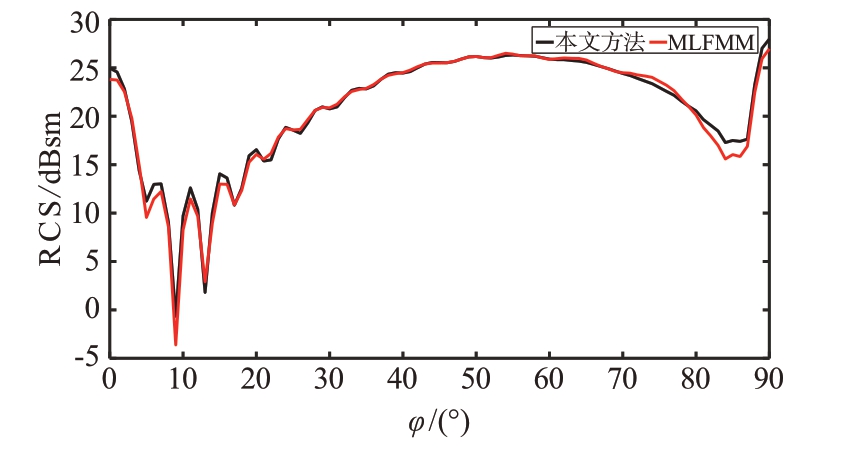
图9 三面角RCS结果对比
分别在无加速、利用GPU和KD-Tree数据结构加速射线追踪过程以及CPU 和GPU 混合编程三种情况下记录所需用时,加速情况如表1所示。此时线程调用GPU 的时间与在CPU 端运行的时间相近,所以通过OpenMP的协调,与不调用OpenMP相比提高了约两倍的计算效率。
表1 不同方法计算三面角RCS曲线耗时对比
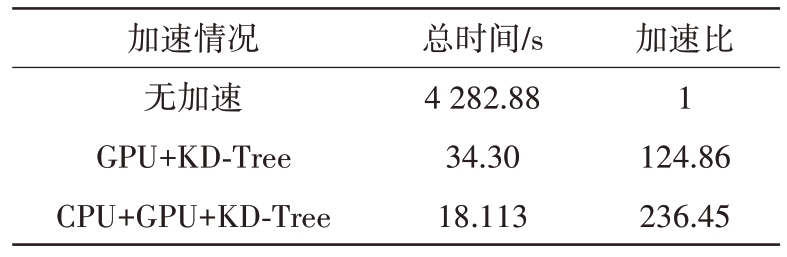
加速情况无加速GPU+KD-Tree CPU+GPU+KD-Tree总时间/s 4 282.88 34.30 18.113加速比1 124.86 236.45
3.2 腔体目标
矩形腔体算例尺寸如图10所示。
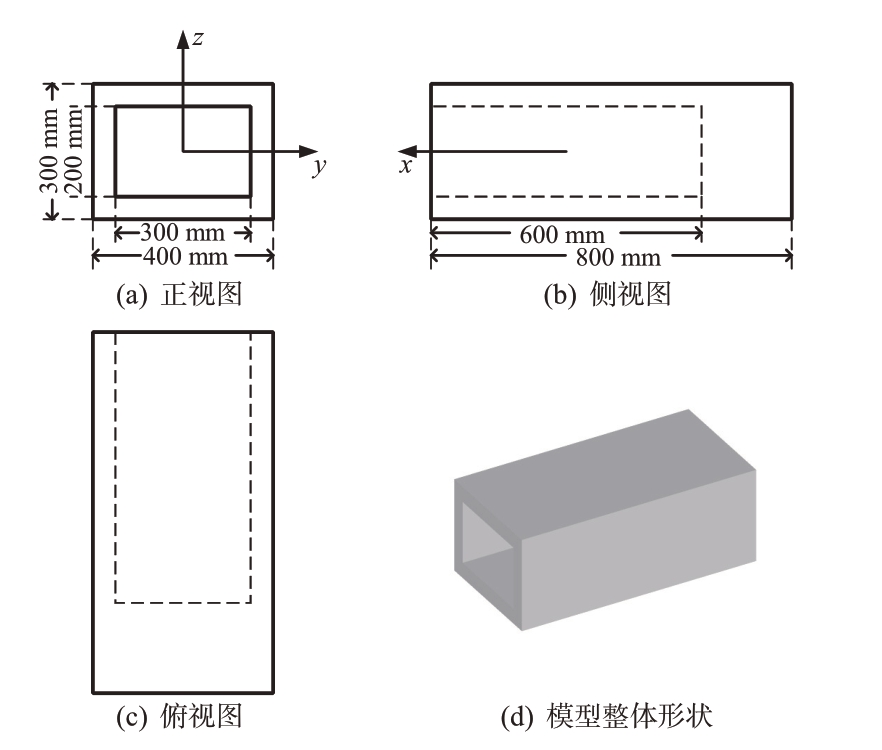
图10 矩形腔体模型尺寸
腔体目标雷达参数设置如下:θ 角为90°,φ 角范围为0°~90°,频率为10 GHz,极化方向为垂直极化,商用软件FEKO 所用方法为高频方法,计算结果相比如图11所示。
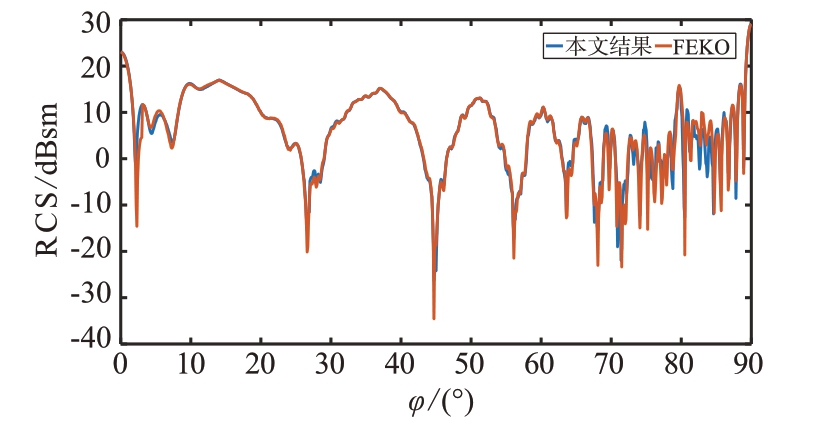
图11 腔体目标RCS结果对比
选取RCS 曲线中的极大值点,计算当φ = 37°时的一维距离像。不模糊距离为3 m,成像分辨率为0.01 m。图12 给出了腔体目标在该入射角度下一维距离像的数值结果。仿真结果表明,腔体目标在该入射角度下形成了一个强散射中心,距离像峰值坐标为0.43 m。用本文射线路径相位理论预估的方法计算得到的结果为0.433 1 m,符合仿真结果,说明通过目标的几何结构预测目标的一维距离像峰值坐标方法的可靠性。
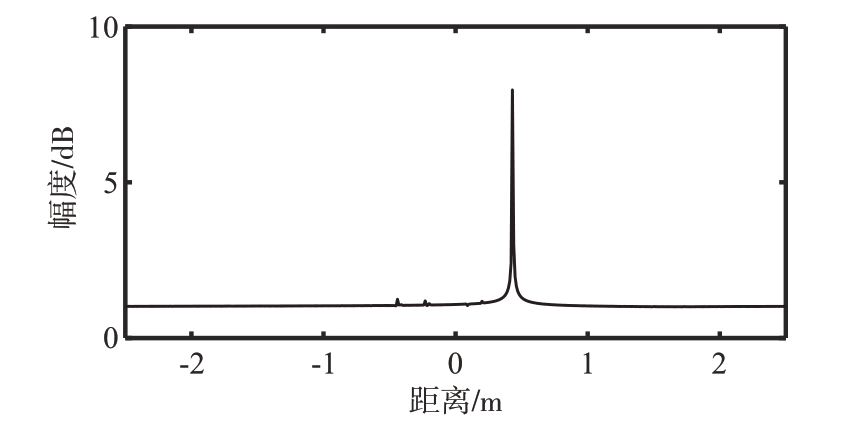
图12 腔体目标一维距离像(θ = 90°,φ = 37°)
选取RCS曲线中的其他极值点,分别计算φ角度为51.3°,60.2°,66.1°和73°情况下的一维距离像,不模糊距离为5 m,成像分辨率为0.01 m。结果如图13所示。

图13 不同入射角度下的腔体目标一维距离像
不同姿态下的射线长度不同,所以得到的距离像峰值位置也不同。由图可见,随着入射角增大,即入射射线与腔体口径法向的夹角增大,射线经由腔体反射形成的强散射中心逐渐远离参考原点。同时,口径面在雷达方向的投影面积减小导致进入腔体的射线减少,一维距离像的峰值强度也逐渐减小。
在实际工程中,射线不一定在一个平面内传播,多次反射的结构也可能是不规则的,此时同样可以根据本文射线追踪方法得到射线光程,进而预测目标的一维距离像。选取俯仰角θ = 82°,方位角φ = 37°的姿态进行射线追踪和分析,目标姿态如图14所示。
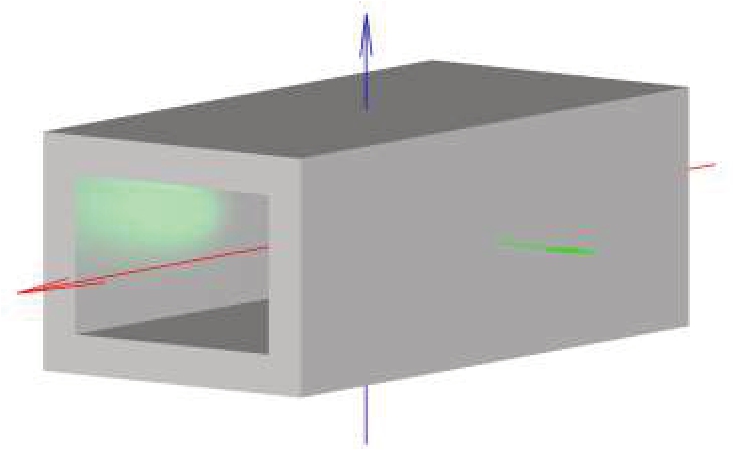
图14 腔体目标姿态图(θ = 82°,φ = 37°)
通过记录所有射线路径,可以计算得到所有射线长度均为1.824 0 m。坐标原点到雷达接收点之间的距离为0.471 7 m,根据射线路径相位理论预估方法可计算目标一维距离像中峰值的理论坐标X = 0.440 3 m。该姿态下仿真得到的一维距离像结果如图15 所示,图中峰值坐标为0.44 m,与通过射线追踪预测的坐标一致,说明了通过射线长度预测目标一维距离像峰值的普适性。

图15 腔体目标一维距离像(θ = 82°,φ = 37°)
3.3 带腔舰船目标
图16所示为某一驱逐舰船模型,舰船长166.7 m、宽17.2 m、高33 m,船舱部件之间存在多种多次散射结构。在舰船的船头、中部和船尾存在明显的腔体部件,腔体部件长8 m、宽5 m、高3 m。后文分别以前腔、中腔和后腔指代。舰船除3个腔体部件以外关于x轴对称。
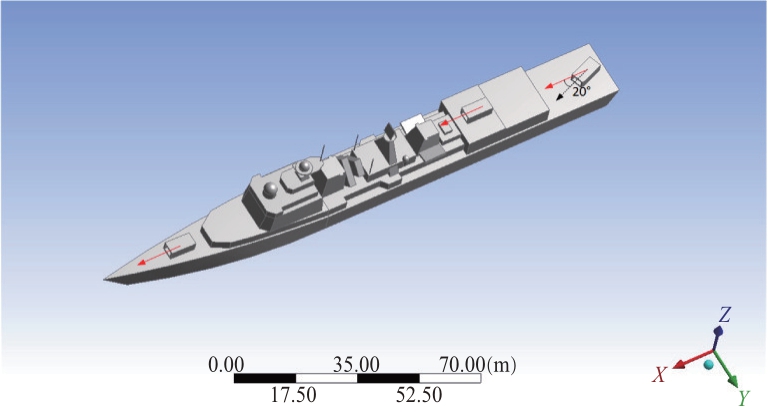
图16 带腔舰船几何模型
雷达参数设置如下:θ 角为90°,φ 角范围为0°~360°,频率为10 GHz,极化方向为垂直极化,计算结果如图17 所示。φ 角为0°时探测方向正对船头,散射贡献主要来自船体前部的平板结构。在90°和270°处RCS 达到峰值,此时主要散射贡献来源于船侧的平板结构。在俯仰角为90°的情况下,关于x 轴对称目标的全姿态RCS 曲线也具有对称性,关于方位角为0°和180°对称。后腔是唯一不关于x 轴对称的部件,在方位角为20°~110°的范围内后腔散射贡献主要来自于腔体内部的多次散射作用,在方位角为110°、200°和290°时,后腔散射贡献主要来自于腔体外壁的一次作用,这些方位角对应的RCS 值略高于对称姿态下的RCS 值。对含腔目标而言,如果射线追踪的次数过少,则无法计入部分角度下腔体的散射贡献,会影响对应角度下RCS的计算精度。
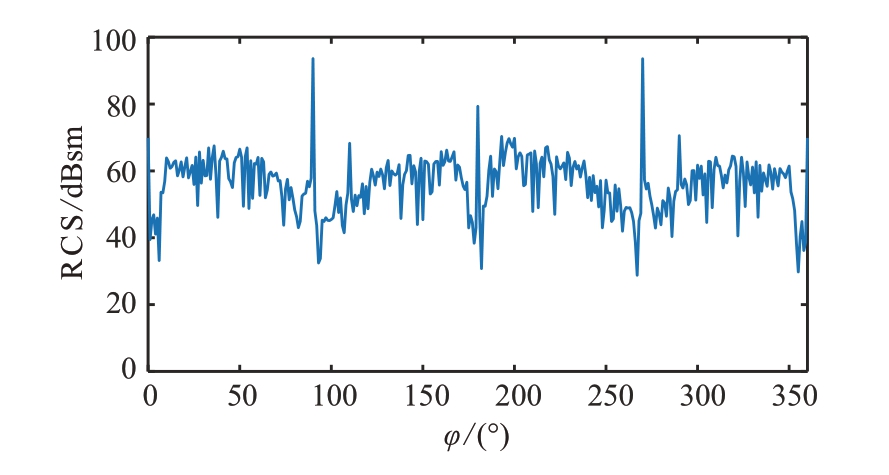
图17 带腔舰船全姿态RCS结果图
图18为带腔舰船目标在俯仰角为65°,方位角为37°姿态下的一维距离像,简易舰船为不包含3个腔体部件的舰船模型。对带腔舰船目标的几个较强的峰值进行分析,形成峰值的等效散射源与目标几何结构的对应关系如图19 所示,射线理论预估和仿真结果对比如表2 所示。其中1,3,4 号峰值点分别由3个腔体部件形成,前腔和中腔开口方向与船头一致,然而前腔截面偏离XOY 面角度约3°,导致其距离像幅度较低。2 号峰值点为船体中部船舱各平板之间的三次作用形成。
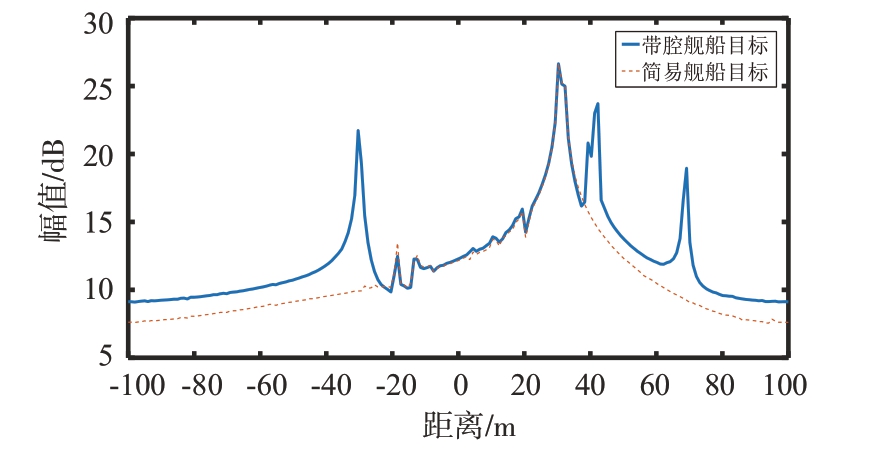
图18 带腔舰船与简易舰船一维距离像对比图

图19 一维距离像峰值与目标几何结构对应关系示意图
表2 舰船目标一维距离像位置验证
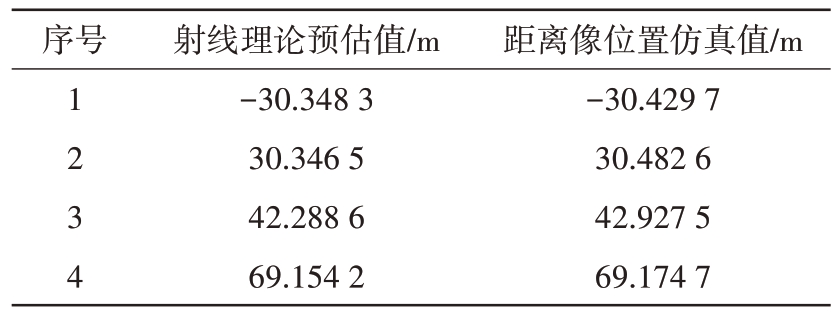
序号1 2 3 4射线理论预估值/m-30.348 3 30.346 5 42.288 6 69.154 2距离像位置仿真值/m-30.429 7 30.482 6 42.927 5 69.174 7
腔体结构不仅在某些角度下能形成强散射中心,腔体内部的多次散射还能影响其等效视在中心与部件几何中心投影之间的位置关系。如图20所示,前腔与中腔的开口方向一致,在该入射姿态下具有相同的光程,视在中心与几何中心投影均相距5.2 m。后腔在该入射姿态下的散射贡献来源于腔体内壁与底部的二次作用,视在中心与几何中心投影距离为3.4 m。可以看出,多次散射使得目标的等效散射源偏离了原有目标空间范围,偏离程度随着射线光程的增加而增大。
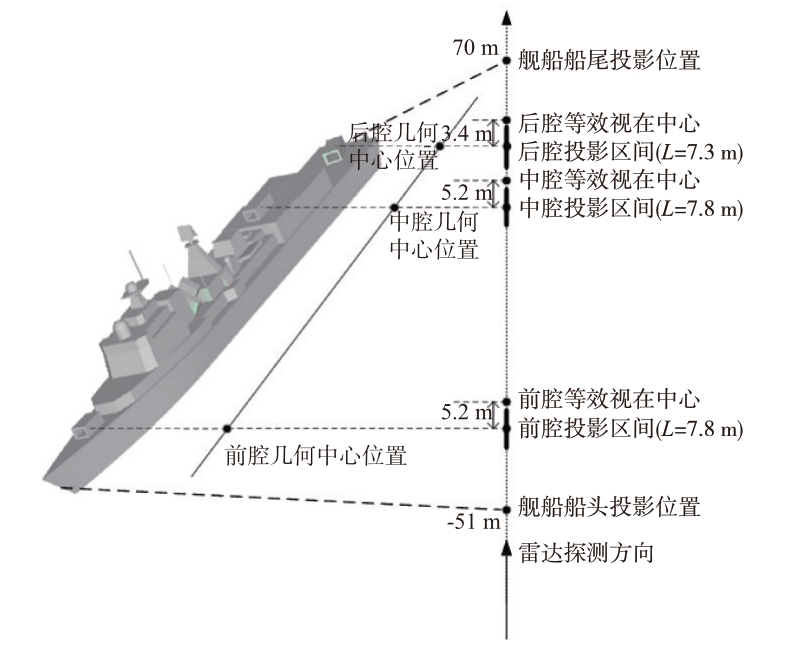
图20 腔体等效视在中心与腔体几何结构关系示意图
3.4 角反阵列与舰船复合目标
本文以图21所示的角反阵列与舰船复合模型为例,快速评估复合模型的散射特性及角反阵列回波干扰信号的有效性。舰船长119 m、宽10.8 m、高12.88 m,角反射器阵列分别包含边长为0.5 m、1 m、2 m 的角反射器各4 个,这些角反射器开口朝向各不相同,复合模型的网格数量为278 000。
图21 角反射器阵列与舰船目标复合模型
当雷达参数为俯仰角60°,中心方位角45°,中心频率10 GHz,极化方式为垂直极化,分辨率为1 m 时,获取图23 所示的复合模型SAR 图像数据需对22 500个不同参数(150个频点、150个方位角点)的目标RCS 进行采样计算,不同方法的耗时如表3所示。本文提出的CPU多核并行技术、GPU硬件加速技术和KD-Tree 遍历技术相结合的靶标高频电磁散射加速方法与传统高频仿真方法相比,将普通性能计算机获取单幅大型舰船与角反射器阵列复合散射SAR图像的耗时由186 h降至0.35 h,可实现大型舰船靶标散射特性的单机快速评估。此时线程调用GPU 的时间远小于在CPU 端运行的时间,所以通过OpenMP 的协调,与不调用OpenMP相比提高了约6倍的计算效率。
表3 不同方法计算单幅大型舰船与角反射器阵列复合散射SAR图像的耗时对比
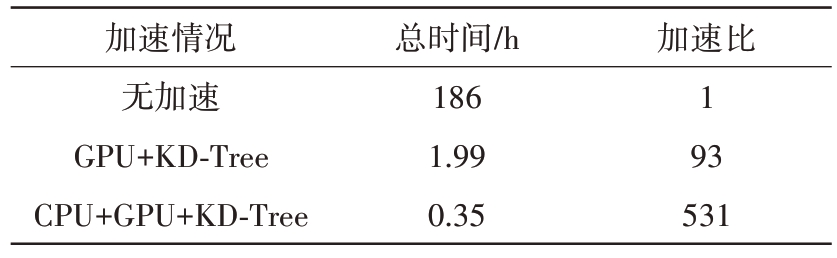
加速情况无加速GPU+KD-Tree CPU+GPU+KD-Tree总时间/h 186 1.99 0.35加速比1 93 531
图22为舰船与角反阵列复合散射的一维距离像特性,雷达参数设置如下:俯仰角为60°,方位角为45°,极化方向为垂直极化,不模糊距离为150 m,分辨率为1 m。图中蓝色点状区域为目标在雷达视线方向的投影示意,依据距离像峰值与目标几何结构的对应关系可知,6 个峰值点全部由开口朝向雷达的9个角反射结构三次散射形成。其中,1,4,5号峰值点分别由3对位于同一雷达分辨单元的角反射结构形成,而2,3,6号峰值点则分别由单个角反射器形成。图23为舰船与角反阵列复合模型的SAR图像,图中的9个强散射中心同样全部由这9个角反射结构的三次散射机理形成。
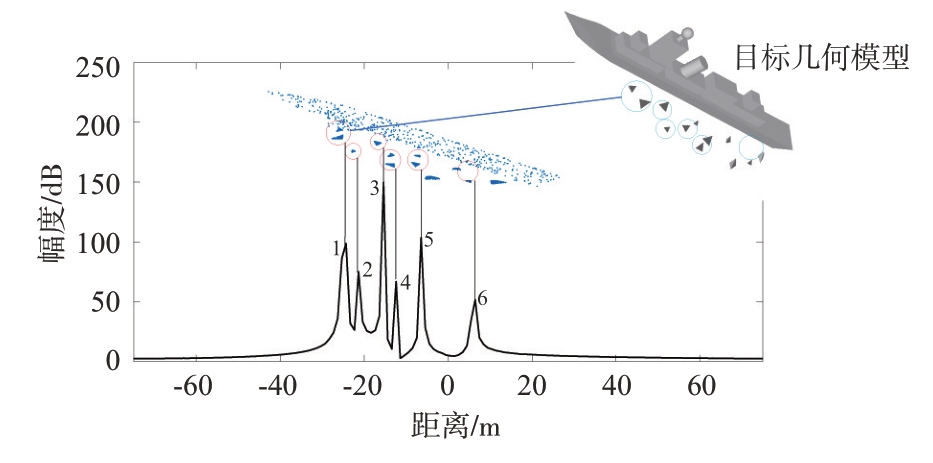
图22 三面角阵列与舰船复合模型距离像
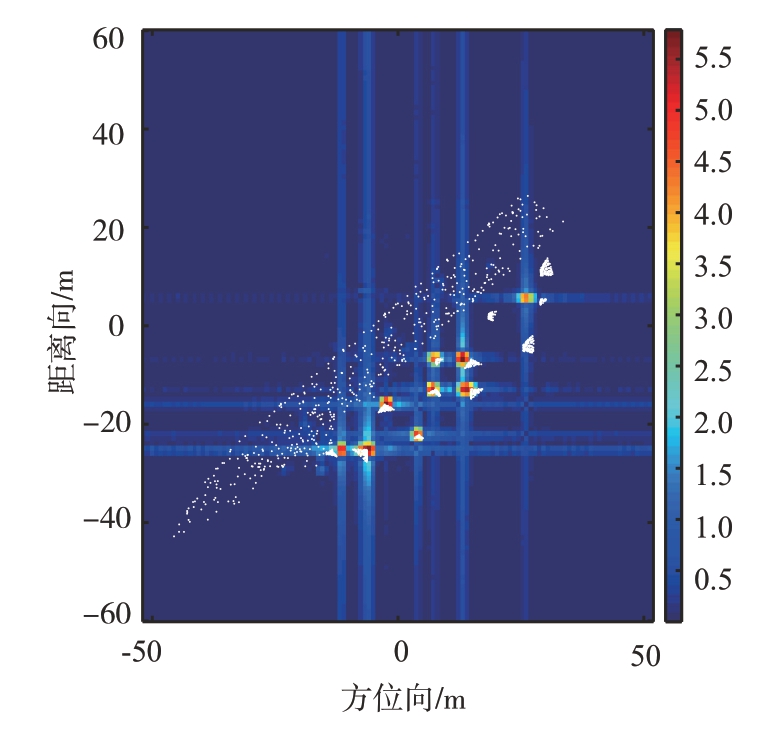
图23 三面角阵列与舰船复合模型二维图像
通过上述分析可以发现,在雷达观测的一维距离像和SAR 图像特性中,边长0.5 m 的角反射器产生的强后向散射回波足以掩盖舰船目标自身的回波信号,且由于雷达对角反射器三次散射机理的等效视在位置位于三面角顶点,因此,在舰船周围放置合适尺寸及方向的角反阵列,可以完全改变舰船的雷达特性。
4 结束语
本文针对靶标特性建模的需求,提出了结合OpenMP 和GPU 混合编程的加速算法,提高了获取雷达目标回波数据的效率。对于存在多次作用结构体的目标,本文计算了雷达目标包含高阶散射场的总体回波信息,通过与FEKO 对比验证了计算结果的准确性。通过对不同方法计算的用时说明了本文方法的高效性,并利用雷达目标特性数据获得目标的一维距离像和SAR 图像,根据射线理论预测一维距离像峰值坐标,解释了距离像峰值的物理意义,雷达图像所展示出的特征与目标几何形状有较好的关联性,说明了计算结果的可靠性。
[1]赵京城,娄长玉,李家碧,等.一种方形腔体的目标散射特性及测量方法[J].北京航空航天大学学报,2022,48(12):2415-2424.
[2]郭立新,魏仪文.复杂动态海面与目标电磁散射及回波仿真研究现状与展望[J].雷达学报,2023,12(1):76-109.
[3]朱雪慧,余泽太,覃潇潇,等.基于动态RCS的舰船雷达回波仿真与分析[J].雷达科学与技术,2019,17(5):543-549.
[4]孙佳兴,姚慧婧.基于联合处理的复杂目标RCS估计方法[J].雷达科学与技术,2022,20(2):181-186.
[5]王超.高频电磁散射建模方法及工程应用[D].北京:中国传媒大学,2009.
[6]殷红成,郭琨毅.目标电磁散射特性研究的若干热点和难点问题[J].电波科学学报,2020,35(1):128-134.
[7]郝晓军,杨晓帆,赵宏宇,等.基于RCS静态宽带数据的雷达目标成像算法[J].太赫兹科学与电子信息学报,2022,20(3):208-212.
[8]殷红成,朱国庆,董纯柱,等.基于自适应射线管分裂的多次反射计算方法[J].系统工程与电子技术,2013,35(4):700-706.
[9]XIAO Guangliang,GUO Kunyi,SHENG Xinqing. Parametric Scattering Center Modeling for a Conducting Deep Cavity[J].IEEE Antennas and Wireless Propagation Letters,2021,20(8):1419-1423.
[10]SUK S, SEO T I, PARK H S, et al. Multiresolution Grid Algorithm in the SBR and Its Application to the RCS Calculation[J]. Microwave & Optical Technology Letters,2001,29(6):394-397.
[11]GLASSNER A S.Space Subdivision for Fast Ray Tracing[J]. IEEE Computer Graphics and Applications, 1984, 4(10):15-24.
[12]MACDONALD J D, BOOTH K S. Heuristics for Ray Tracing Using Space Subdivision[J]. Visual Computer,1990,6(3):153-166.
[13]SONG Tao, LIAO Huanyu, SUBBARAYAN G. Efficient Local Refinement near Parametric Boundaries Using KDTree Data Structure and Algebraic Level Sets[J]. Algorithms,2022,15(7):245.
[14]TAO Yubo,LIN Hai.GPU-Based Shooting and Bouncing Ray Method for Fast RCS Prediction[J]. IEEE Trans on Antennas&Propagation,2010,58(2):494-502.
[15]PAJOT A, BARTHE L, PAULIN M, et al. Combinatorial Bidirectional Path-Tracing for Efficient Hybrid CPU/GPU Rendering[J]. Computer Graphics Forum, 2011, 30(2):315-324.
[16]GAO Pengcheng,TAO Yubo,BAI Zhihui,et al.Mapping the SBR and TW-ILDCs to Heterogeneous CPU-GPU Architecture for Fast Computation of Electromagnetics Scattering[J]. Progress In Electromagnetics Research, 2012,122(1):137-154.
