0 引 言
基于阵列传感器的辐射源被动定位在雷达、声呐、通信、电子对抗等领域中均具有重要的应用［1-2］。相对于窄带辐射源信号，宽带辐射源信号更有利于目标检测、参量估计和目标特征提取，在实际中获得了更广泛的应用［3-4］。然而，与日趋成熟的窄带辐射源定位技术相比，围绕宽带辐射源的定位研究起步较晚，尤其是考虑阵列结构对算法的影响，以及辐射源在传播过程中普遍存在的多径效应等问题，相关研究亟需进一步发展与完善。
最早，基于阵列的无源定位技术研究主要考虑均匀线阵结构。均匀圆阵相对于均匀线阵具有360°的全方位角覆盖，几乎不变的方向图以及额外的俯仰角信息，因此，其更具结构优势［5-6］。当前，针对宽带辐射源信号的定位方法主要以基于统计推断类［7-8］方法和基于信号子空间方法［9-10］为主。前者易收敛到局部极值导致结果出错，后者需要辐射源角度参数的先验信息，且二者均存在计算复杂度较大的问题。另外，针对相干辐射源信号的定位，采用的解相干方法主要包含空间平滑算法［11-12］和矢量重构类算法［13-14］。然而，这些解相干处理算法仅适用于均匀线阵。针对均匀圆阵下的解相干方法主要采用相位模式激励的方法，将均匀圆阵转化成一个虚拟的均匀线阵，由此将空间平滑和均匀圆阵连接起来，但是它要求相干源信号必须与阵列共面，限制了算法的应用。
因此，本文主要瞄准军事中广泛运用的宽带线性调频（Linear Frequency Modulated，LFM）信号，基于均匀圆阵的阵列结构优势，在综合现有研究方法的基础上，提出一种快速有效的宽带相干LFM 信号定位方法。首先，算法利用LFM 信号在分数阶傅里叶域的能量聚焦性［15-16］，对接收数据进行分数阶傅里叶变换，通过提取阵列接收数据在分数阶傅里叶域的峰值输出，实现对宽带相干LFM 信号的窄带化处理；其次，借鉴均匀线阵下空间平滑的原理，通过均匀圆阵的轴向虚拟等距平移，计算单次平移和前后两次平移阵元接收数据的自协方差矩阵和互协方差矩阵，构造空间平滑矩阵，从而实现均匀圆阵下相干辐射源信号的解相干处理；最后，利用空间平滑矩阵大特征值对应的特征向量，得到相邻阵元接收数据的相位差，结合相位差反演参数估计方法［17］直接得到LFM 信号二维角度参数估计的闭式解。仿真实验验证了算法的有效性，同时结合参数估计的克拉美罗界（Cramer-Rao Lower Bound，CRLB）［18］，研究分析了算法的估计性能。
1 信号模型
双均匀圆阵下宽带相干LFM 信号模型如图1所示。以圆心为坐标原点，建立三维直角坐标系，坐落在xy 平面上的圆阵子阵1 半径设为R，M 个阵元均匀分布在圆阵上，考虑K 个相干宽带LFM 信号，第k个LFM 信号方位角ϕk为x轴按逆时针方向出发到信号与圆点的连线在xy 平面上的投影所成的角度；俯仰角θk 为z 轴到信号与圆点连线的角度。圆阵子阵2 可以看作子阵1 在z 轴上向下平移d 个单位得到。此外，虚线部分假设为双圆阵向下平移形成的虚拟圆阵，用于相干信号的解相干。
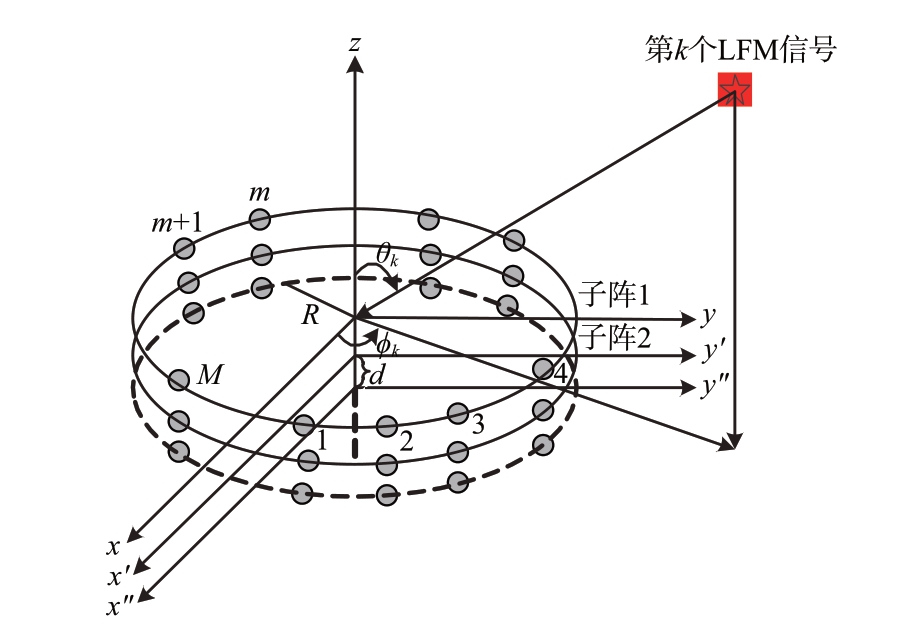
图1 信号模型
2 算法描述
2.1 宽带LFM信号窄带化处理
宽带信号定位处理主要分为两步，第一步需要将宽带信号进行窄带化处理，第二步利用窄带下的辐射源定位方法获取信号的位置参数。因此，算法首先考虑宽带LFM 信号的窄带化处理算法。根据文献［15］，利用LFM 信号在分数阶傅里叶域的能量聚焦性，通过对接收数据进行分数阶傅里叶变换，提取其峰值输出，可以获得一个具有时不变导向矢量的类窄带信号模型。
在不考虑噪声的情况下，子阵1第m 个阵元接收数据在分数阶傅里叶域的第k 个LFM 信号峰值输出有如下的表达式：
式中，S0,k(ε0,k,κ0,k)表示假设的子阵1 中心阵元接收数据在分数阶傅里叶域的第k 个LFM 信号的峰值输出，εm,k 和κm,k 分别表示峰值点对应的横纵坐标，且满足关系式ε0,k=ε1,k=…εM,k和κm,k=κ0,k+fsτm,k cos ε0,k，
表示新模型下的导向矢量，其表达式可以近似为
注意到，新模型下是时不变的导向矢量，可以直接采用窄带下的信号源定位方法。
子阵1 阵元接收数据在分数阶傅里叶域峰值输出的矢量形式可以表示为
式中，
表示假设的中心阵元接收数据在分数阶傅里叶域K 个信号对应的峰值输出矢量矩阵，
表示子阵1 中M 个阵元在分数阶傅里叶域的峰值输出的噪声矢量矩阵。
子阵2 阵元接收数据在分数阶傅里叶域峰值输出的矢量形式可以表示为
式中，
。
2.2 均匀圆阵平滑解相干
空间平滑算法是一种有效的解相干方法，通过子阵平滑来恢复接收数据协方差矩阵的秩，但是一般只适用于均匀线阵。在信号模型介绍部分，通过圆阵的轴向平移可以发现变化的时延与线阵下子阵的平移带来的时延变化近似，因此可以通过圆阵的轴向虚拟平移模拟线阵的子阵平移，从而实现圆阵下相干信号的解相干。
2.3 LFM信号角度参数估计
至此，通过估计获得各个宽带相干LFM 信号的角度参数值完成了对信号的定位。图2 给出了本文提出的基于均匀圆阵的宽带相干LFM 信号定位方法的流程图。
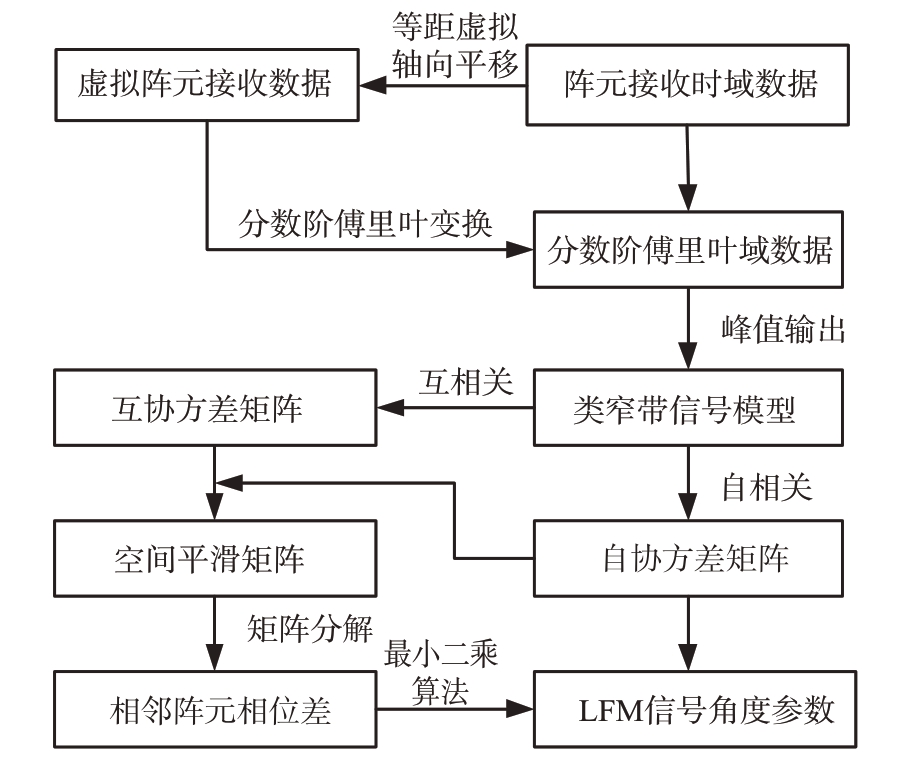
图2 均匀圆阵下宽带相干LFM信号定位方法流程图
3 仿真实验
本节通过MATLAB 仿真实验验证提出的方法对宽带相干LFM 信号定位的有效性，同时和现有方法进行对比以此评估算法性能。实验中，考虑由各8个阵元构成的双均匀圆阵，接收数据中包含的噪声假设为加性高斯白噪声，信噪比定义为信号和噪声的功率比
，在性能对比中采用均方根误差（Root-Mean-Square Error，RMSE），定义为
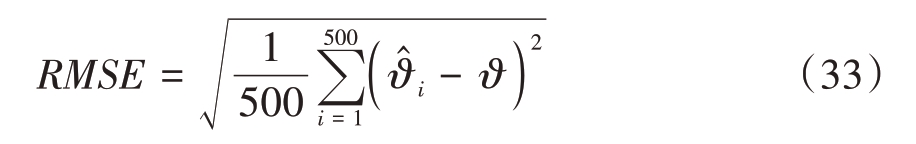
式中，
代表第i次实验下估计得到的参数值，ϑ表示对应参数的真值，蒙特卡洛仿真实验次数假设为500次。
3.1 算法有效性验证
这一小节用于验证本文提出方法对宽带相干LFM 信号定位的有效性。实验中考虑两个相干宽带LFM 信号，起始频率和带宽假设为f0 = 1 GHz，带宽B = 100 MHz；均匀圆阵大小固定为R = λ/2，两个LFM 信号的方位角和俯仰角分别假设为(10.5°,50.1°) 和(-10.2°,79.8°)；采样点数N =16 384，信噪比设为SNR = 10 dB；圆阵虚拟平移2次，每次平移距离d = λ/2。
图3 给出了阵元接收数据在分数阶傅里叶域的时频图和采用本文提出的算法估计得到的辐射源角度参数的二维直观图。从图3（a）所示结果中可以看出，两个相干的宽带LFM 信号在分数阶傅里叶域只形成了一个谱峰，通过提取峰值输出，可以实现宽带LFM 信号的窄带化处理。图3（b）给出了实验参数下采用本文提出的解相干算法后估计得到的LFM 信号的角度参数。其中，红色的十字表示LFM 信号真实的位置，蓝色的点代表的是50次蒙特卡洛仿真实验得到的估计结果。从图示结果可以看出，采用本文提出的解相干方法后得到的辐射源角度位置的估计结果贴近真实值，算法能够有效解决均匀圆阵下宽带相干LFM 信号的角度估计问题。
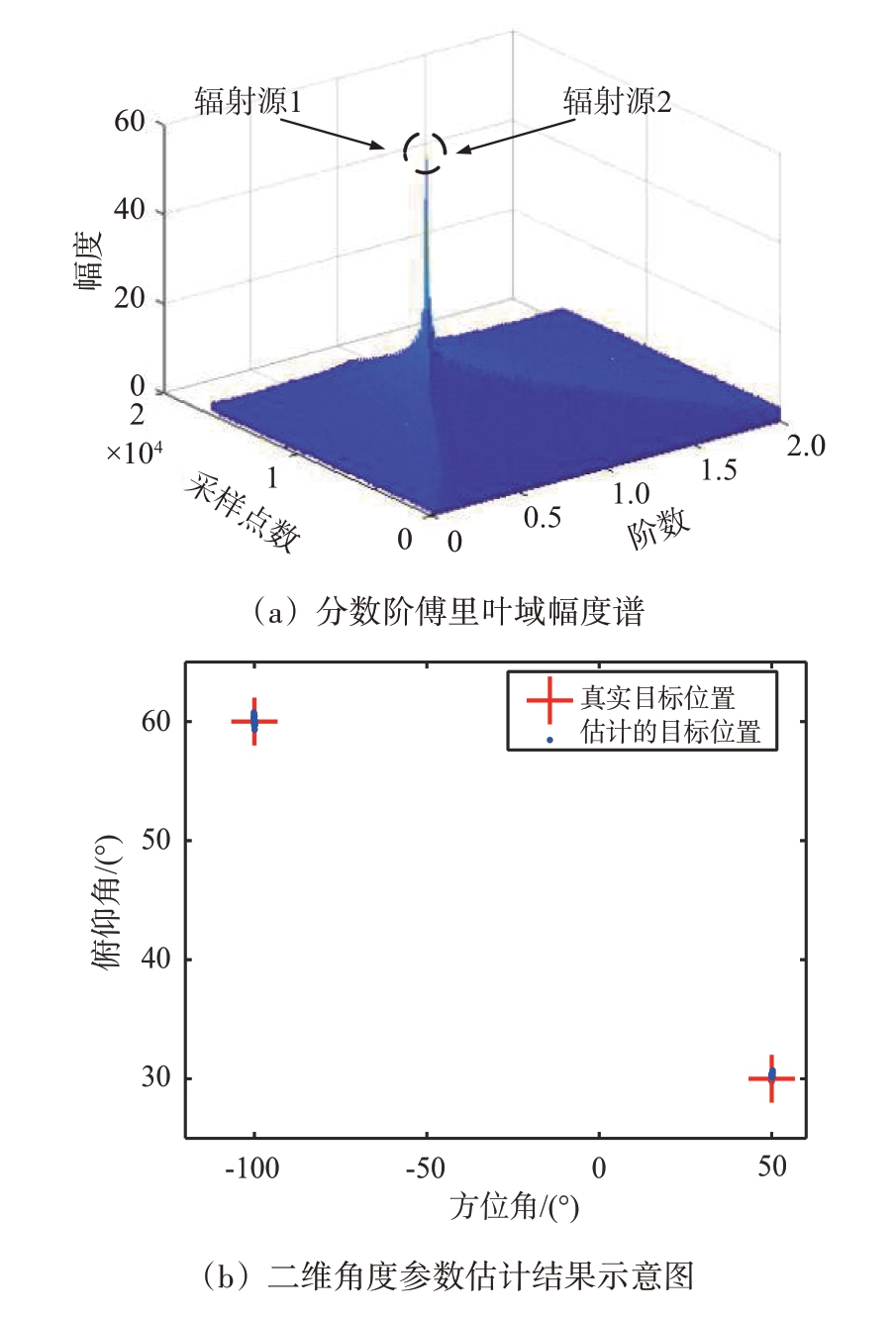
图3 算法有效性验证
3.2 算法估计性能分析
这一小节用于验证本文提出算法对宽带相干信号角度参数的估计性能。值得注意的是，经查阅相关文献后发现目前还未有同等条件下解决宽带相干辐射源角度参数估计的文献资料，因此在实验中只与CRLB［18］进行性能对比。图4 中带“方框”的蓝色的线为通过500次蒙特卡洛仿真实验下算法对LFM 信号1 角度参数估计的RMSE；带“方框”的红色的线是实验条件下LFM信号1角度参数估计的CRLB；带“圆圈”的蓝色的线为通过500 次蒙特卡洛仿真实验下算法对LFM 信号2 角度参数估计的RMSE；带“圆圈”的红色的线是实验条件下LFM 信号2角度参数估计的CRLB。从图示结果可以看出尽管本文提出的算法参数估计的性能不能与CRLB相比拟，但是当信噪比高于10 dB时，方位角估计的误差小于0.2°，俯仰角估计的误差小于0.5°。
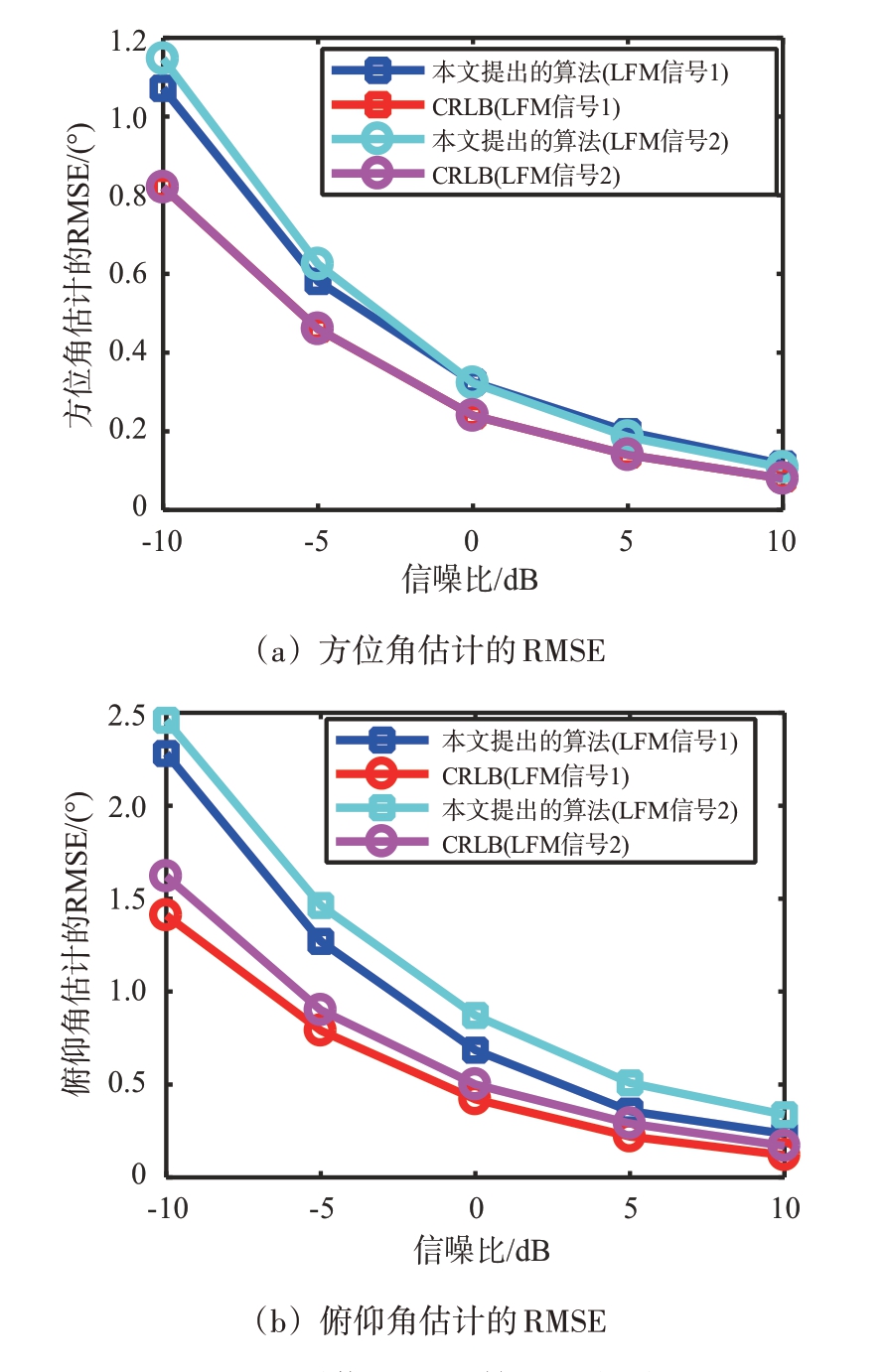
图4 不同信噪比下算法性能分析
进一步地，仿真实验还考察了不同采样点数下算法参数估计的性能，同样加入CRLB 进行对比。采样点数N从1 000变化到9 000，每次变化间隔2 000，图5给出了信噪比为10 dB 下角度参数估计的RMSE 随采样点数的变化。与图4 情形类似，参数估计的RMSE值随采样点数的增大逐渐减小，且RMSE 数值虽然不能贴近CRLB，但是当采样点数大于9 000时，方位角估计误差小于0.2°，俯仰角估计误差小于0.3°。
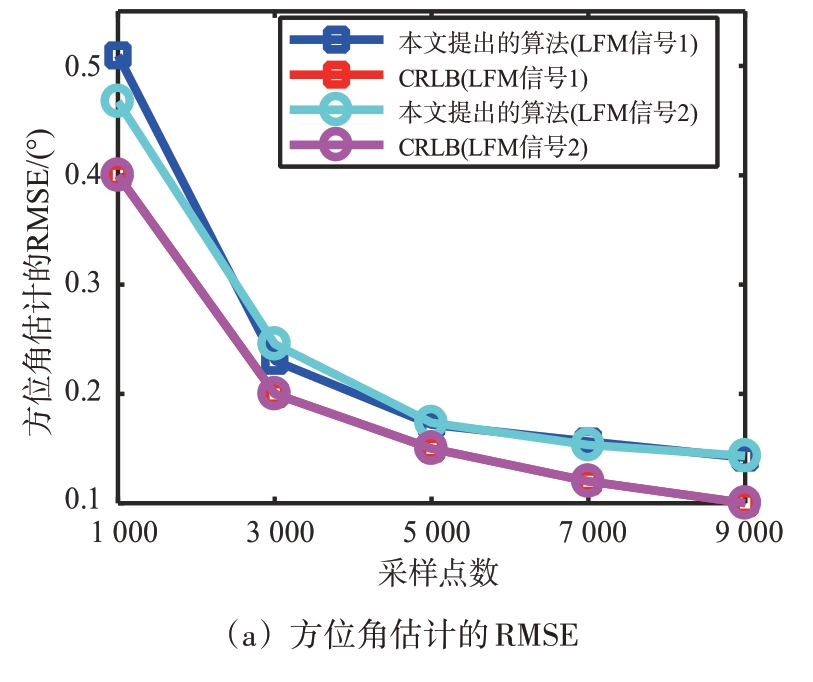
图5 不同采样点下算法性能分析
4 结束语
本文提出的均匀圆阵下宽带相干LFM 信号定位算法首先通过提取LFM 信号在分数阶傅里叶域的峰值输出，实现宽带LFM 信号的窄带化处理；其次，算法通过圆阵的轴向虚拟等距平移，计算每次平移和相邻两次平移间接收数据的自协方差矩阵和互协方差矩阵来构造空间平滑矩阵，实现“类平滑”的解相干处理；最后，将构造的空间平滑矩阵结合相位差反演参数估计算法得到宽带相干LFM信号二维角度参数的闭式解。仿真实验验证了算法的有效性。
［1］晏辉，司伟建.基于均匀圆阵相干信源的二维DOA 估计［J］.雷达科学与技术，2022，20（4）:464-469.
［2］周成伟，郑航，顾宇杰，等.互质阵列信号处理研究进展：波达方向估计与自适应波束成形［J］.雷达学报，2019，8（5）:558-577.
［3］李小琳，张文俊.Nested阵列宽带LFM 信号二维DOA估计［J］.上海大学学报，2020，26（4）:506-517.
［4］张家成，邱天爽，栾声扬，等.脉冲噪声下基于循环相关熵和稀疏重构的宽带信号DOA 估计［J］.电子与信息学报，2020，42（11）:2587-2591.
［5］陈鑫，刘振，魏玺章。基于旋转均匀圆阵的单近场源参数估计解模糊算法［J］.电子学报，2017，45（3）:584-590.
［6］CHEN Xin, LIU Zhen, WEI Xizhang. Unambiguous Parameter Estimation of Multiple Near-Field Sources via Rotating Uniform Circular Array［J］. IEEE Antennas and Wireless Propagation Letters,2017,16:872-875.
［7］BUCRIS Y, COHEN I, DORON M A. Bayesian Focusing for Coherent Wideband Beamforming［J］. IEEE Trans on Audio Speech&Language Processing,2012,20（4）:1282-1296.
［8］CHEN J C, HUDSON R E, KUNG Y. Maximum-Likelihood Source Localization and Unknown Sensor Location Estimation for Wideband Signals in the Near-Field［J］.IEEE Trans on Signal Processing, 2002, 50（8）:1843-1854.
［9］WAX M, SHAN Tiejun, KAILATH T. Spatio-Temporal Spectral Analysis by Eigenstructure Methods［J］. IEEE Trans on Acoustics, Speech, and Signal Processing, 1984,32（4）:817-827.
［10］VALAEE S, KABAL P. Wideband Array Processing Using a Two-Sided Correlation Transformation［J］. IEEE Trans on Signal Processing,1995,43（1）:160-172.
［11］周豪，胡国平，汪云.基于自适应步长萤火虫-多重信号分类算法的低空目标波达方向估计［J］.雷达学报，2015，4（3）:309-316.
［12］杜永兴，李晨璐，秦岭，等.多径环境下阵列波达方向估计及互耦校正［J］.微波学报，2019，35（3）:24-33.
［13］李磊，李国林，刘润杰.基于相干积累矩阵重构的波达方向估计新方法［J］.雷达学报，2015，4（2）:178-184.
［14］刁鸣，安春莲.独立信号和相干信号DOA 估计新方法［J］.系统工程与电子技术，2011，33（12）:2582-2586.
［15］CHEN Xin, LIU Zhen , WEI Xizhang. Fast FRFT-Based Algorithm for 3-D LFM Source Localization with Uniform Circular Array［J］.IEEE Access,2018,6:2130-2135.
［16］杨利民，苏卫民，顾红，等.基于二维映射的LFM UWB雷达动目标速度估计［J］.雷达学报，2012，1（3）:232-237.
［17］JUNG T J,LEE K K.Closed-Form Algorithm for 3-D Single-Source Localization with Uniform Circular Array［J］.IEEE Antennas and Wireless Propagation Letters, 2014,13:1096-1099.
［18］王永良，陈辉，彭应宁，等.空间谱估计理论与算法［M］.北京：清华大学出版社，2004.
