0 引 言
采用数字波束形成技术的两维相控阵雷达具备方位、俯仰相扫和同时多波束能力，广泛应用于防空预警雷达和空间目标探测雷达［1］。对于大型相控阵雷达，通常采用圆形布阵或四周切角的多边形布阵以提高能量的利用率。
矩形布阵雷达通常采用多波束比幅测角［2］或者两维和差波束测角。为了消除波束扫描引起的波束展宽以及不同载频波束宽度不一致的影响，通常转换到正弦空间坐标系下，即U-V 空间测角［3-4］。该方法只需要建立一条俯仰和差曲线和一条方位和差曲线即能实现威力范围内所有指向的测角。文献［5］研究了低数据量条件下测角曲线建立方法。文献［6］给出了和差波束测角的精度分析。文献［7］研究了和差波束测角在抗主瓣干扰条件下的应用。但是，对于圆形平面阵等非矩形阵，U-V空间测角曲线相对波束中心的偏差存在耦合关系，通过单条U空间测角曲线和单条V空间测角曲线不能实现两维精确测角。文献［8］研究了非矩形阵列单脉冲测角的方法，但仅利用了不同偏角和差曲线共零点的特点，并没有对和差测角曲线进行修正。
本文提出了一种采用曲线拟合以及迭代处理的方法实现圆形布阵雷达两维测角，运算简单，易于工程实现。
1 阵列模型
如图1 所示的圆形平面阵，阵元排布如图2 采用矩形栅格排列，水平间距为dx，垂直间距为dy。任意阵元相对于阵面中心的坐标为(cx,cy)，则阵列的导向矢量为
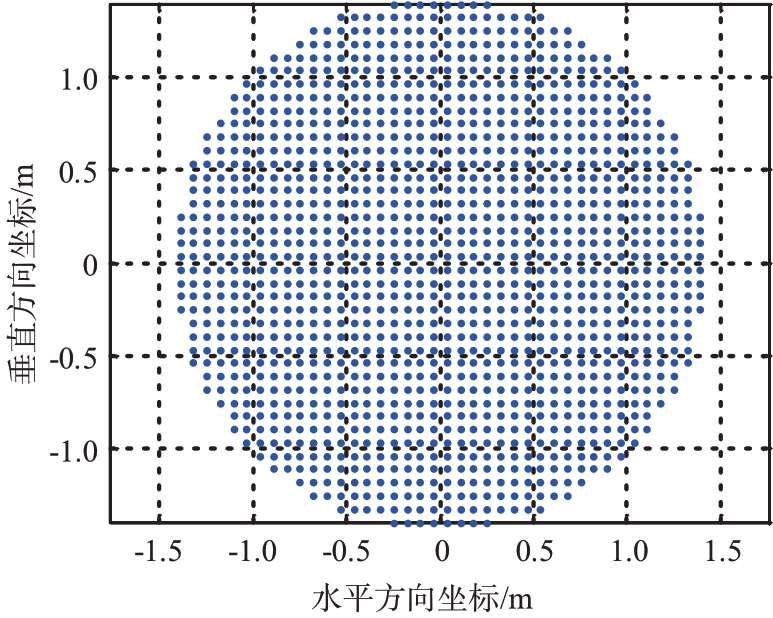
图1 圆形平面阵阵元排布
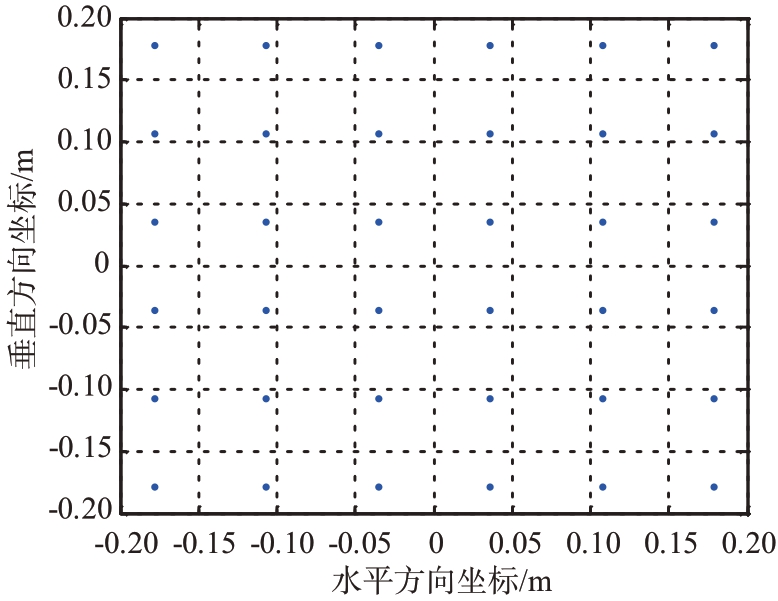
图2 阵元排布（局部放大）
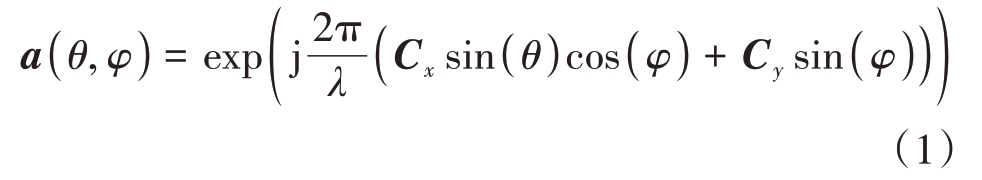
式中，Cx =[cx0,cx1,…,cxN-1]，Cy =[cy0,cy1,…,cyN - 1]，θ 为方位角，φ 为俯仰角，N 为总阵元数。该阵列两维方向图可以表示为
式中wn 为窗函数，θ0 为方位指向角，φ0 为俯仰指向角。
圆形平面阵列的方向图如图3 所示，图4 为等高线图，可以看出，圆形平面阵列的方向图主瓣为圆形区域，当目标和主瓣中心存在偏角时，方向图在U-V 空间的剖面和不存在偏角时明显不同，因此，在和差曲线建表时不能共用没有偏角时所建的表。
图3 三维方向图
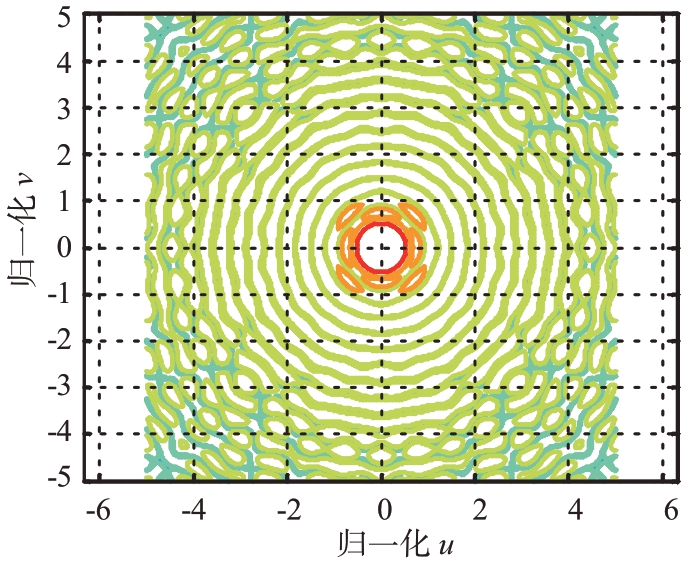
图4 等高线图
2 和差波束测角
和差波束测角实现简单，且相对于波束扫描法（最大幅度法）具有较高的测量精度，因此在工程中广泛应用。其核心思想为通过和差波束输出的复信号构建归一化角误差信号，再利用归一化角误差信号查表计算出目标回波相对于波束中心指向的偏角。但是传统的查表曲线需要建立不同波长、不同扫描角等多组曲线，为了解决该问题，通常在正弦坐标系（U-V空间）建表，且对波长进行归一化处理，令
，代入式（1）得
构建u方向和v方向角误差信号：
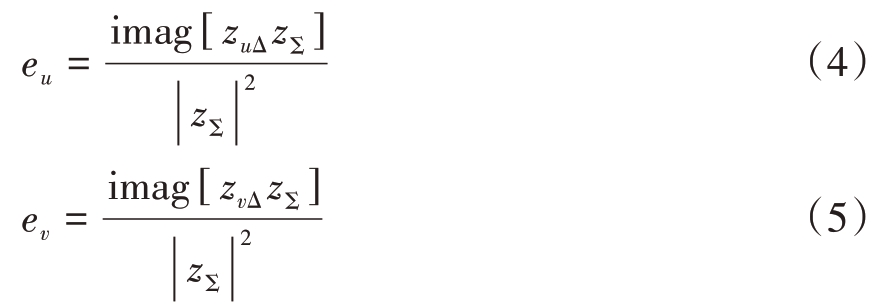
式中，zΣ 表示和波束，zuΔ 表示方位差波束，zvΔ 表示俯仰差波束。对于矩形排布阵列，u、v 两维是完全正交的。可以分别建立u、v 各一条归一化误差曲线，根据式（6）即可得到方位角和俯仰角的测量值：
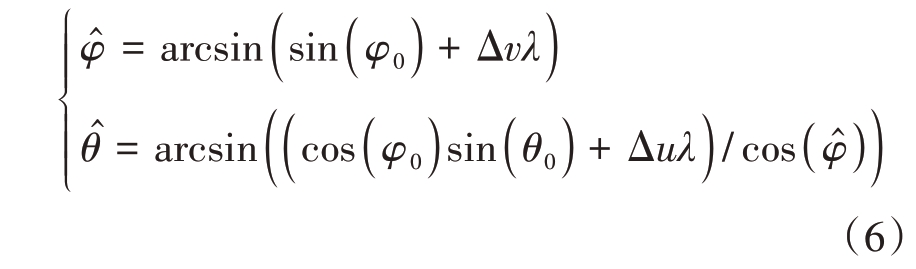
但是，对于圆形阵列，对于不同的Δv，u维归一化误差曲线有所不同，对于不同的Δu，v 维归一化误差曲线有所不同，如图5 和图6 所示。因此，不能只用一条u方向归一化曲线和一条v方向归一化曲线测角，必须在上述方法基础上改进。
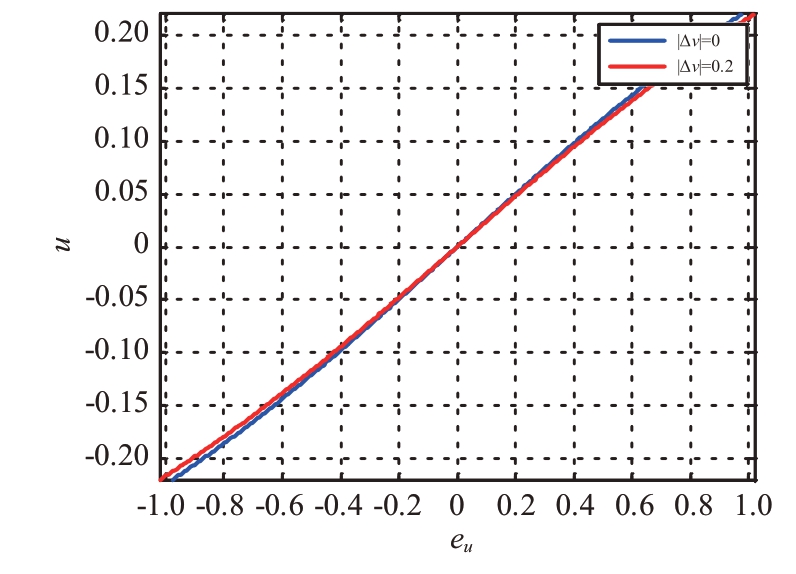
图5 u方向归一化误差曲线
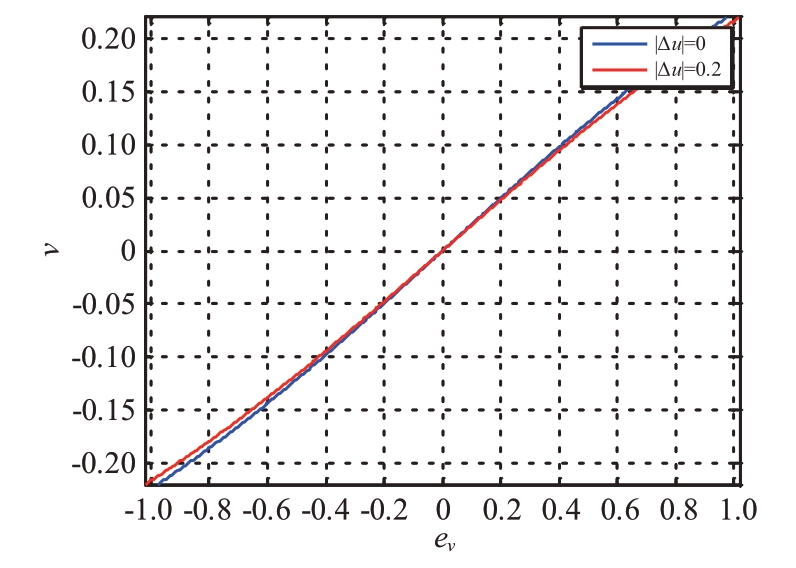
图6 v方向归一化误差曲线
要精确测角必须建立多条测角曲线，为了工程实现简便，可以按以下方法进行处理。
对于上述归一化曲线，以u 方向为例，对于给定的Δv，该曲线可以采用多项式拟合：
式中，cu0，cu1，cu2，cu3 为拟合系数，对于不同的Δv，归一化曲线对应拟合系数不同，且-Δv 和Δv 对应的归一化曲线完全相同。因此，cu0，cu1，cu2，cu3 可以看作是自变量为|Δv|的函数。经过分析cu0，cu2 的值非常小，可以取作0，则
cu1，cu3随|Δv |变化曲线如图7和图8所示。
图7 拟合系数cu1随 |Δv| 变化曲线
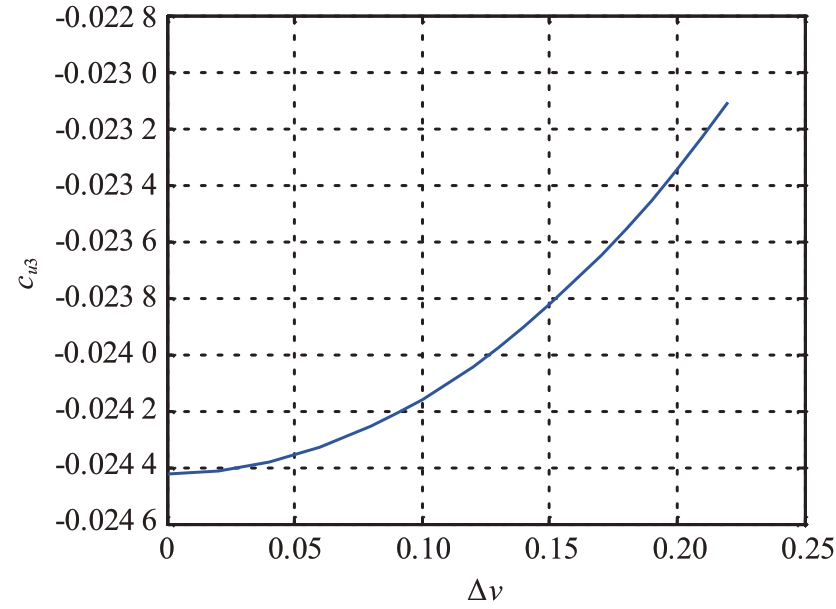
图8 拟合系数cu3随 |Δv| 变化曲线
对cu1，cu3进行曲线拟合
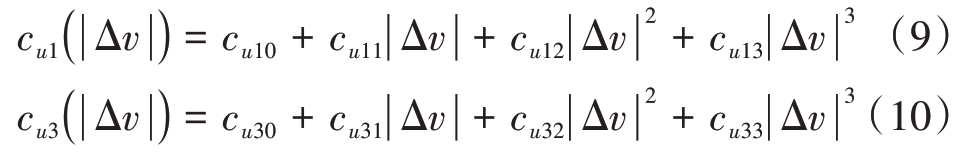
同理，对于v方向有
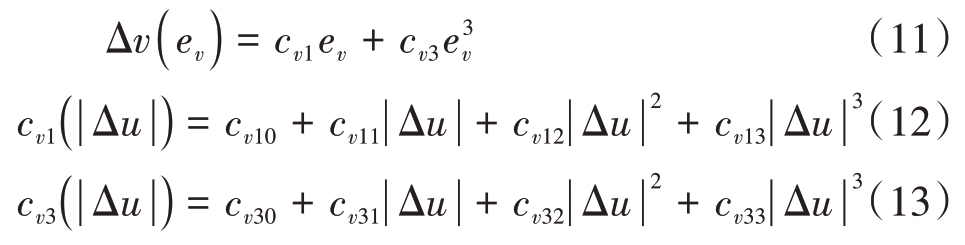
具体的算法步骤：
第一步：根据式（4）、式（5）计算出角误差信号eu和ev；
第二步：令Δu = 0，根据式（12）、式（13）计算出cv1 和cv3，再根据式（11）计算出Δv 的第一次估计
；
第三步：令
，根据式（9）、式（10）计算出cu1 和cu3，再根据式（8）计算出Δu 的第一次估计
；
第四步：令
，根据式（12）、式（13）计算出cv1 和cv3，再根据式（11）计算出Δv 的第二次估计
；
第五步：令
，根据式（9）、式（10）计算出cu1 和cu3，再根据式（8）计算出Δu 的第二次估计
；
第六步：将
代入式（6）即可得到方位角和俯仰角的估计值。
3 仿真结果分析
雷达工作时，波束在一定范围内扫描，目标位置未知，目标会出现在波束宽度内任意位置。可以作如下仿真：假设雷达工作频率2 300 MHz，波束指向法线方向，目标在波束宽度内（方位-1.5°～1.5°，俯仰-1.5°～1.5°）均匀分布，分别采用改进前后的测角方法，对比测角性能。
首先采用改进前U-V 空间和差波束测角，此时，仅用一条u 方向归一化曲线和一条v 方向归一化曲线测角。测角结果如图9 所示。对比真值和测量值可以看出，目标偏离波束中心指向位置越大测角误差越大。究其原因是因为目标偏离波束中心指向时归一化曲线发生了变化，因没有修正带来了偏差。
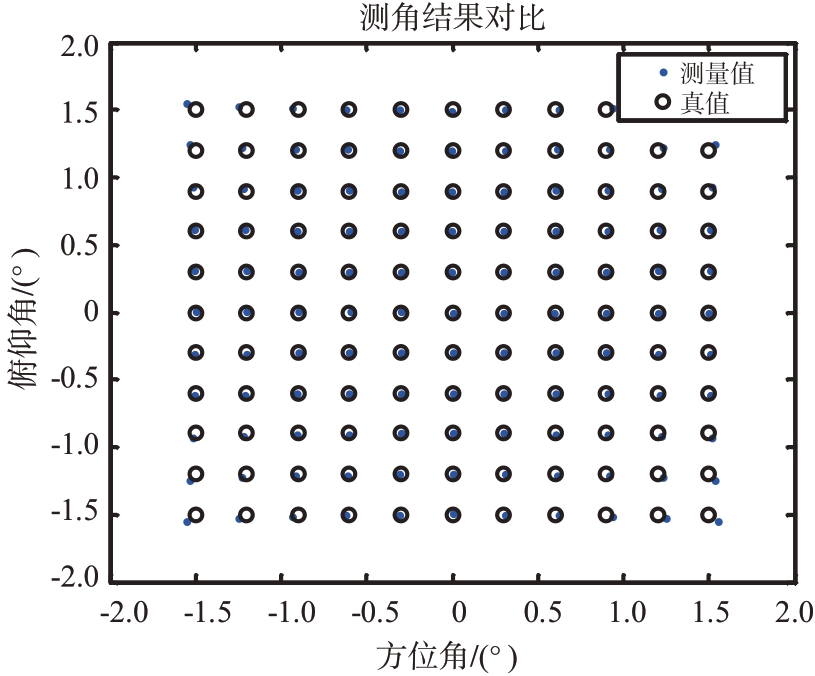
图9 改进前U-V空间和差波束测角
再采用改进后U-V 空间和差波束测角，此时，采用迭代的方式，逼近目标位置所对应的归一化曲线。测角结果如图10所示。对比真值和测量值可以看出，测角结果和目标偏离波束中心指向位置没有关系，均达到了较小的测角误差。
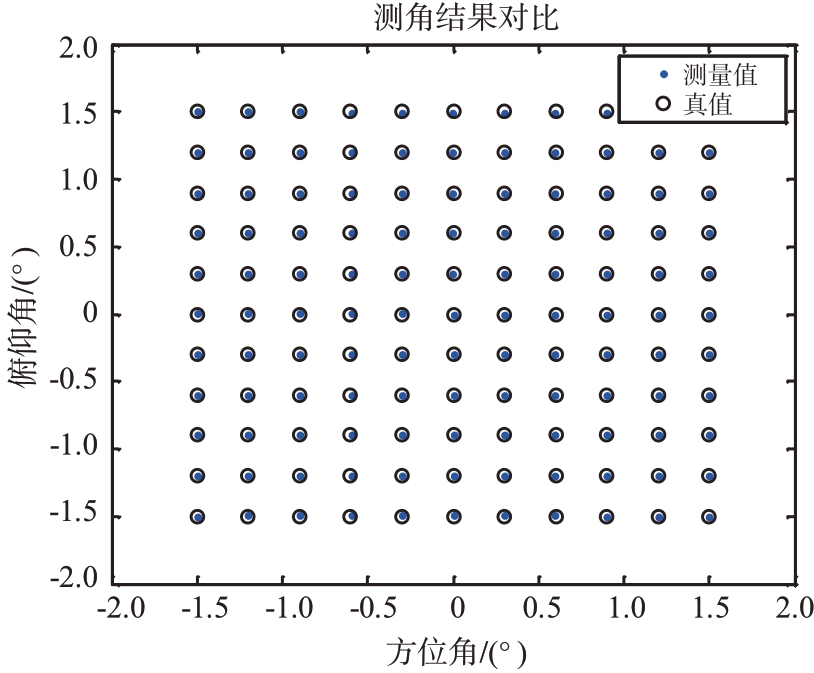
图10 改进后U-V空间和差波束测角
采用同样的仿真参数，假设目标在波束宽度均匀分布，以方位角为例，改进前后的测角误差对比如图11所示，可以看出，改进后的测角误差大幅减小。
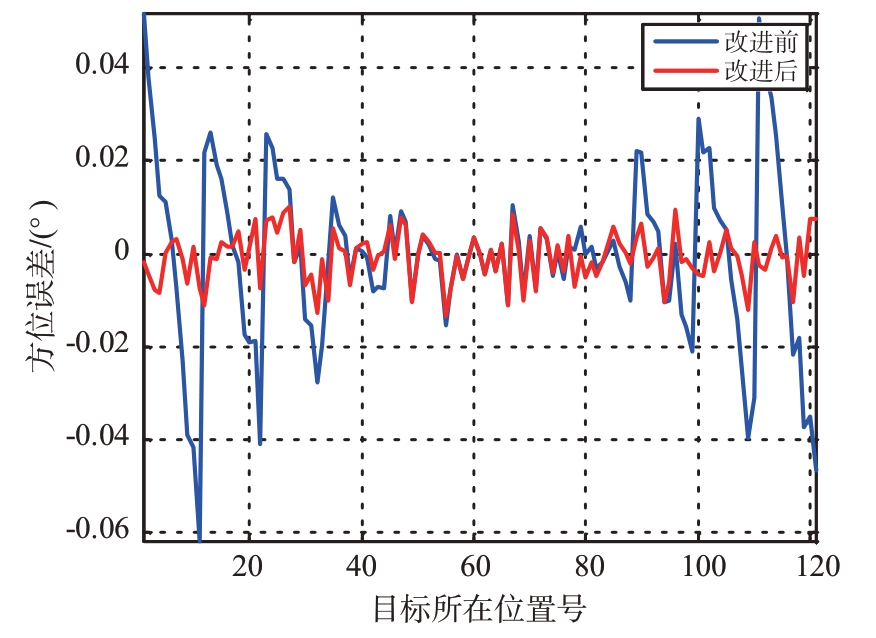
图11 改进前后测角误差对比
4 结束语
基于和差波束的单脉冲测角方法在两维相控阵雷达中广泛使用。对于矩形阵列，通常转换到UV 空间建立误差曲线，对频率归一化后只需方位、俯仰两条误差曲线即可实现精确测角。对比圆形阵列和矩形阵列的方向图可以看出，圆形平面阵列的方向图主瓣为圆形区域，当目标和主瓣中心存在偏角时，方向图在U-V 空间的剖面和不存在偏角时明显不同。若只采用在主瓣中心位置建立的方位、俯仰两条误差曲线测角，在目标偏离主瓣中心时存在较大误差。
本文针对圆形平面阵列采用常规U-V 空间测角方法误差较大的问题，提出了一种迭代处理的方法，以逼近最优的归一化曲线，有效减小了测角误差。经分析，该方法对于圆形平面阵列外的非矩形阵列同样适用，仿真结果证明了该方法的有效性和可行性。
［1］张光义.相控阵雷达原理［M］.北京：国防工业出版社，2009．
［2］李磊，宁勇，李麒鹏，等.多波束比幅测向波束交叠与测向精度的研究［J］.航天电子对抗，2021，37（6）：28-31．
［3］杨雪亚，刘张林.子阵级和差波束形成及测角方法研究［J］．中国电子科学研究院学报，2015，10（1）：82-86．
［4］崔向阳，付学斌，朱永杰，等.两维相控阵UV 域测角分析及应用［J］.火控雷达技术，2021，50（4）：45-48．
［5］王磊，邹佳龙，贾文渊.低数据量的相控阵雷达多波束鉴角曲线生成方法［J］.空天预警研究学报，2022，36（1）：19-22．
［6］方棉佳，吕涛.单脉冲和差波束测角的精度研究［J］.雷达科学与技术，2013，11（6）：645-649．
［7］陈希信，龙伟军，张庆海.一种低副瓣自适应单脉冲测角方法［J］.中国电子科学研究院学报，2021，16（5）：496-498．
［8］饶灿，李荣锋.主瓣干扰下多点约束自适应单脉冲测角方法［J］.雷达科学与技术，2011，9（3）：232-236．
