0 引 言
采用SAR 技术，将收发天线沿着长线阵的轨迹等速移动并辐射相参信号，从而实现等同于长线阵的方位向高分辨率［1］。线性合成孔径阵列可以通过条带模式进行数据采集［2］，这种模式下随着雷达中心频率的增加至毫米级，SAR 系统获得的方位向分辨率能力也随之更高。近年来，基于CMOS 的调频连续波雷达能够将模拟单元与射频单元集成到一个紧凑芯片中［3］，这使超宽带毫米波雷达系统小型化并低成本化，被广泛用于健康监测、武器藏匿检查、建筑结构检查等视觉失灵领域的高分辨率近场成像［4-9］。传统的SAR成像系统采用由单个阵元构成的密集阵列，而MIMO阵列则由多个阵元构成的子阵进行信号收发，实现了数据采集时间的减少。
对于单个阵元，现阶段长期使用的SAR 全息成像方法是基于RMA 的波数域方法［10］，为了提高计算速度常常需要在时间-空间域、频率-波数域通过Stolt 插值法得到均匀采样的后向散射信号数据后进行快速傅里叶变换（Fast Fourier Transform,FFT）［11］，然而这种插值过程繁琐，成像效率较低。本文讨论了引入NUFFT 代替Stolt 插值的方法，极大提高了RMA 重建图像速度［12-16］，这对于相比单个阵元复杂度更高的MIMO 的采用有着重要意义［17］。
在实际应用中，MIMO 阵列不同阵元拾取的后向散射信号之间存在着相位或者距离不匹配［18］，同时多站雷达的收发天线之间存在耦合的情况［19］，未经过校准的SAR 成像存在严重的伪影。本文提出了通过对平行于平面MIMO-SAR 阵列的金属平面板照射后拾取的散射信号进行分析，实现192个虚拟子阵列阵元的同时校准。
1 MIMO-SAR成像
1.1 虚拟阵列拓扑结构
如图1所示，将射频板与数据采集板的级联板安装在由两个丝杆步进电机组成的平面扫描平台上。通过丝杆步进电机的带动级联板横向扫描和斜向复位，实现了收发天线阵列在整个平面内的位置移动。
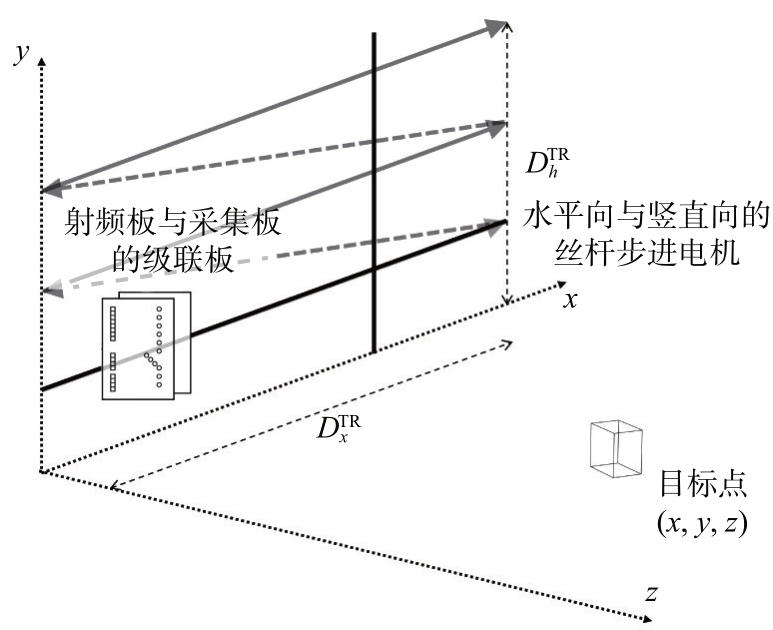
图1 级联板扫描机械运动结构
虚拟阵元位置是由TX 天线和RX 天线在空间上位置卷积产生［20］。在近场条件下，若天线空间位置rT 和rR 详细表示为(x t,yt,zt)和(x r,yr,zr)，目标位置表示为( x′,y′,z′) ，收发天线空间位置中点到目标点距离为R，则我们可以将新的虚拟阵元与目标之间的往返距离表示为［21］
如图2所示，发射天线TX1和接收天线RX1可以构成虚拟天线阵列的一个阵元CH1，其位置由TX1 和RX1 的空间位置卷积产生，所有的2 个TX天线和4个RX天线可以构成8个虚拟阵元位置。
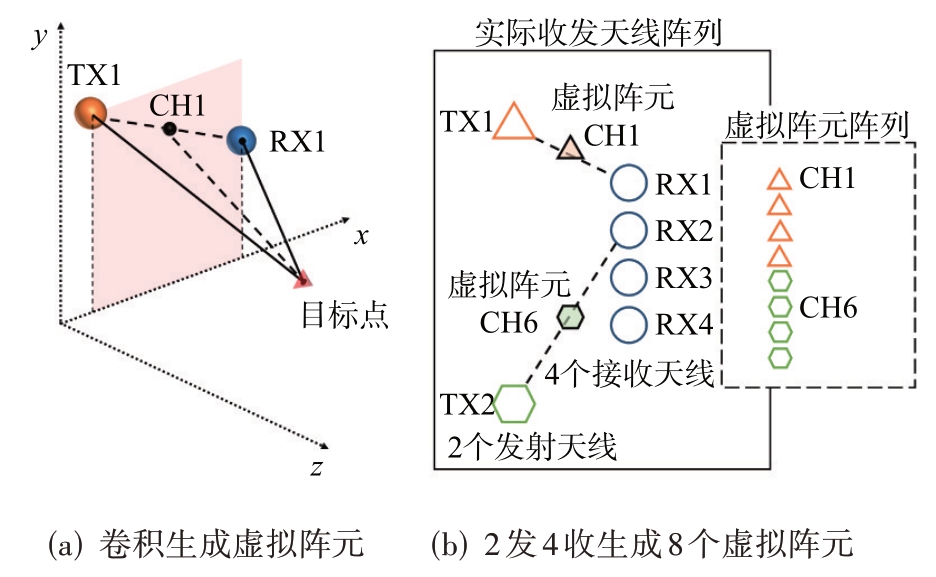
图2 MIMO拓扑结构
如图3所示，如果对天线阵列水平和竖直位移进行合理的调整，则可以获得一个更大的虚拟阵列。
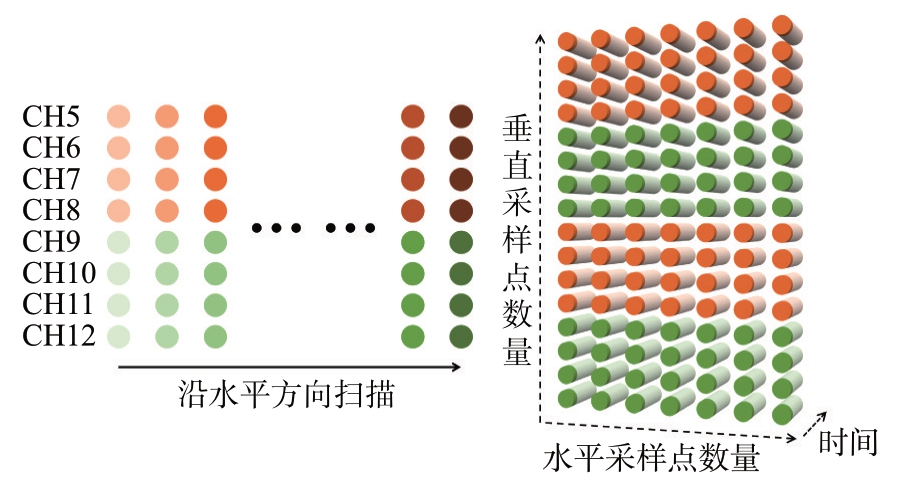
图3 子阵列构成200 mm×200 mm扫描孔径阵列
1.2 基于NUFFT改良的RMA
经典的SAR 数据成像主要有基于时域的后向投影算法［22］（Back-Projection Algorithm, BPA）和基于波数域的RMA［23］，两者在SAR 成像聚焦原理上具有一致性，但在成像过程中RMA 的速度要明显快于BPA［24］，因此本文选择以RMA为基础，进行图像复现。
可以进行如下总结：
基于NUFFT的波数域三维全息图像重建算法：
1）对回波信号建立波数域上的模型s(u,v,k,h)；
2）对u 和v 在波数域上进行3D-FFT，得到S(ku,kv,k,kz)；
3）通过乘以
，引入补偿；
4）在ky 通过Stolt 插值使得后面的FFT 运算得以实现/在方位向上使用NUFFT代替插值；
5）通过对(ku,kv)维上的降维积累，实现4D 数据降维为3D；
6）利用3D-IFT 解得目标点发射率的估计值
；
7）实现图像重建。
2 基于反射面的MIMO阵列校准
MIMO 阵列成像系统的实际使用中，各个通道之间存在时间延时、通道响应、系统噪声等导致的误差。本文对各个误差的产生原因不作更为细致的分析，对客观存在的不同通道之间的系统误差值进行计算，从而实现MIMO阵列校准［28-29］。
同时，对于多站雷达采集信号进行range-FFT分析，结果如图4所示。可以更清晰地看到除了在理论位置附近获得了一个幅值尖峰，在离天线较近位置处也有一个由收发天线耦合造成的幅值尖峰，本文在下述校准过程中对互耦的影响也进行了补偿。
图4 点目标回波信号的range-FFT结果
2.1 基于金属反射面的MIMO阵列校准方法
本文使用平面金属反射面作为成像校准目标进行实验，其特点在于当虚拟阵列平面和收发天线阵列相平行且金属平面足够大时，虚拟阵元均落于金属反射面投影内，可以认为每个阵元与目标始终保持相等的距离。此时通道之间的差异全部来自于系统误差。
如图5所示，目标物体平面金属反射面平行虚拟阵列平面放置，距离为z0，则对于每一个虚拟阵元距离目标的距离均为z0。本文假定虚拟阵列平面上有一组额外的收发天线对构成的虚拟阵元，理想条件下，忽略信号振幅和残余视频相位项，采集到的后向散射信号为
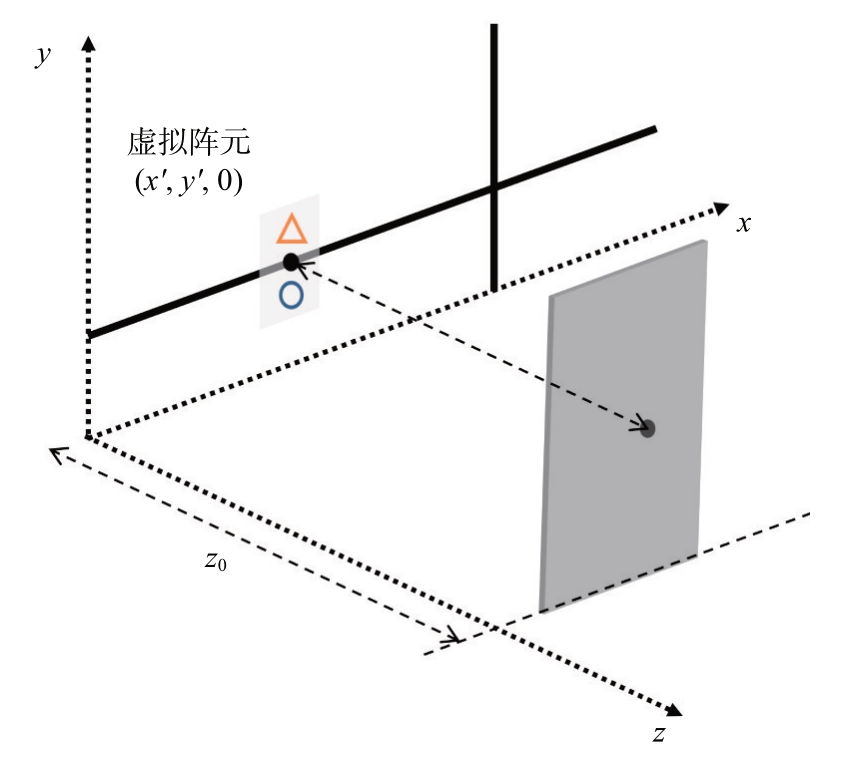
图5 利用平行金属平面进行采样
式中，fb = Kτ 为拍频信号的频率，ϕ = 2πf0τ 为拍频信号的相位，可以看出均与信号往返时延τ 有关，式中τ = 2z0/c。假设对拍频信号在时域上均匀采样，采样周期为Ts，采样频率为N，则可以由s(t)连续信号得到离散信号s[ n ]= s(nTs)，式 中n =[0,1,2,…,N - 1]。通过对采样拍频信号进行N 点离散傅里叶变换（DTFT）得到
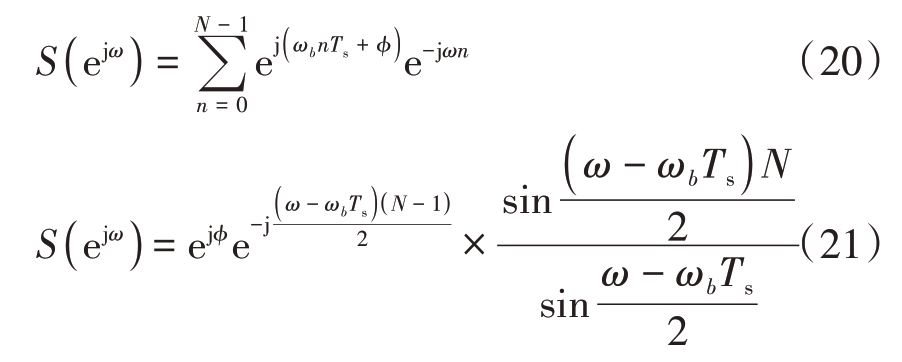
式中，ωb = 2πfb = 4πKz0/c 为拍频信号角频率。由于拍频信号是在时间上的均匀采样，上式的采样版本可以通过range-FFT获得。
将上述生成的理想后向散射信号s(t)作为参考信号，将实际采集到的信号与其进行对比，从而得到对应通道的校准参数。对于某个MIMO 虚拟阵元采集到的未校准信号
，存在收发增益al、系统时延
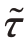（包括仪器带来的系统延迟τi、收发天线耦合导致的时延τ）l，忽略热噪声和残余视频相位项，则未校准信号可表示为
式中，
为信号剩余复增益系数，fi = Kτi 为参考信号s(t)的拍频。假设有
，则可以认为ωl即为我们需要的校准参数，即
式中，s*(t)为s(t)的复共轭。从而将估算ηi 与fi 转化为估算噪声中的单频
式中Wl( f)表示为
如果ωl(t)是在时域上的均匀采样，则可以通过FFT 得到Wl(f)的离散型。最后对于复增益系数ηi可以通过对
中插入估算得到的
来计算。
2.2 192个虚拟通道的MIMO阵列校准
在本文实验中，采用雷达天线的横向扫描构建虚拟阵列，对每个通道的后向散射信号而言，信号相位变化有
式中，k 为波数，D 为虚拟阵元与目标的往返距离，Δd = D/2 为单程距离，λ 为波长，f 为频率，c 为光速，考虑到对于平行金属反射面照射，在各个阵元位置上Δd 值不变，因此信号相位应该为常数φ =4πfΔd/c。对一次单行横向扫描采样结果进行相位分析，选取其中1 个通道进行相位展开，得到相位信息如图6 所示，x 轴为采样帧序列，y 轴为采集信号的相位值。可以清晰地看到，在整个扫描过程中，相位值相当稳定，整体在2 rad 以内，这种情况下对于金属平面的扫描结果可以等效于每一个通道始终对于距离不变的目标进行扫描。
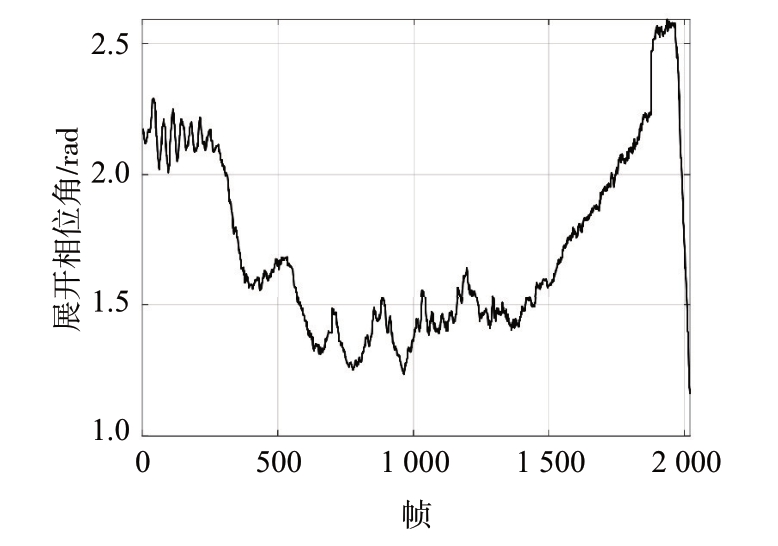
图6 单对天线在不同阵元采集信号相位角变化
经过对本文装置的分析，认为图像最左段与最右段出现的相位抖动情况，来自于扫描天线在加速移动中带来的扫描架振动；而在图像中段出现绝对值小于1.5π 的相位变化，来自于实验金属平面本身在加工中不够光滑导致。这种误差在对于使用点目标顶点校准时也同时产生影响。
同时，如果对于点目标进行照射，对于理想的信号相位角应当是一条抛物线，但是实际可以看到信号相位角变化过程中有明显的振动，如图7所示，这正是扫描架机械振动带来的影响，因此对于这种情况需要进行函数拟合使得曲线更为平滑。
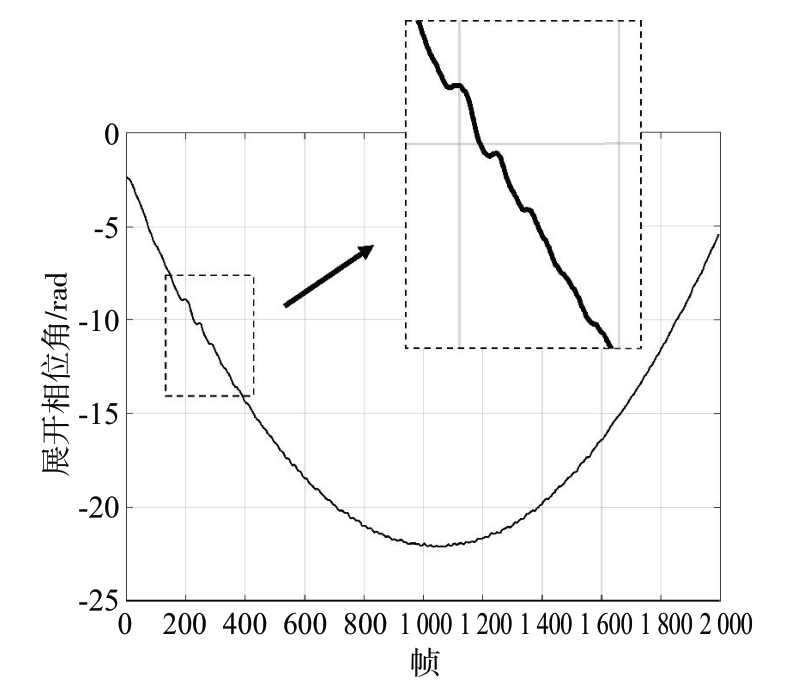
图7 机械振动带来的信号相位的微小变化
如图8所示，本文对图4中的实验抽取了20个通道的结果进行了拟合，拟合结果和预想的平面结果基本吻合。
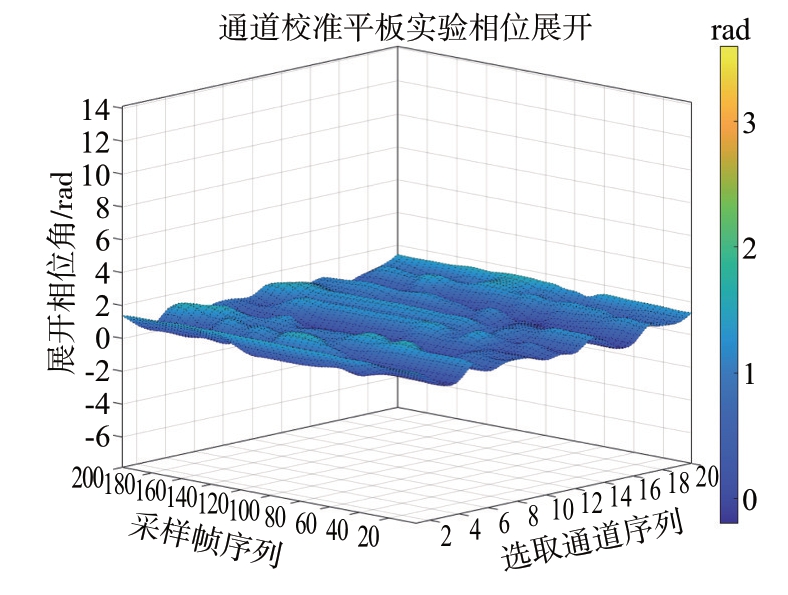
图8 部分阵元散射信号相位采集
根据对金属平面的扫描得到每个通道采集信号的距离和相位信息进行分析，得到了192个通道不匹配的具体数值。这192 个通道中的144 个负责距离向成像，48 个通道负责方位向成像。根据2.1节对于不同通道之间偏差的计算可以得到如图9 所示的距离偏差和相位偏差结果，通过乘以加权值矩阵补偿偏差至同一基线，即实现了多通道相位信息校准。
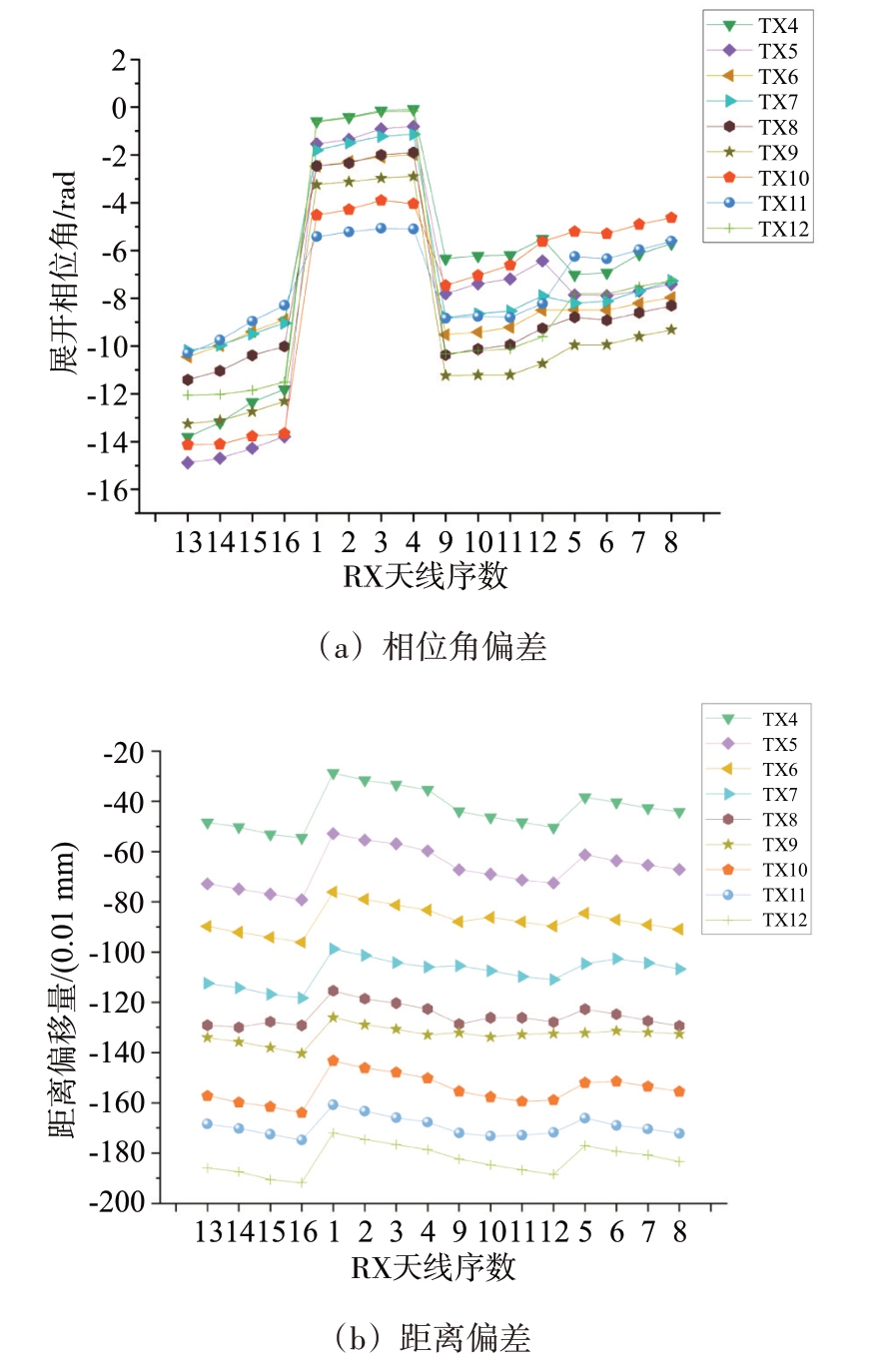
图9 144通道在计算上的偏差
2.3 在金属平面倾斜情况下的距离估算
在2.1 节中进行多通道校准时，需要金属平面和虚拟阵元二维平面平行，而在实际操作放置实验装置时这一理想条件很难实现。本节就金属平面倾斜放置的情况下，对多通道校准系数产生的影响进行讨论。
如图10 所示，在笛卡儿坐标系中，平面MIMO阵列位于xOy 面上，目标平面相对MIMO 阵列倾斜放置。假设平面无限大，平面方程为aX + bY +cZ + d = 0；选取虚拟阵列上任一阵元，位置为(m,n,0)，则经过该虚拟阵元且与目标平面垂直的直线方程为
；假设虚拟阵元在目标平面上的投影为(m′,n′,l′)，则知(m′,n′,l′)满足
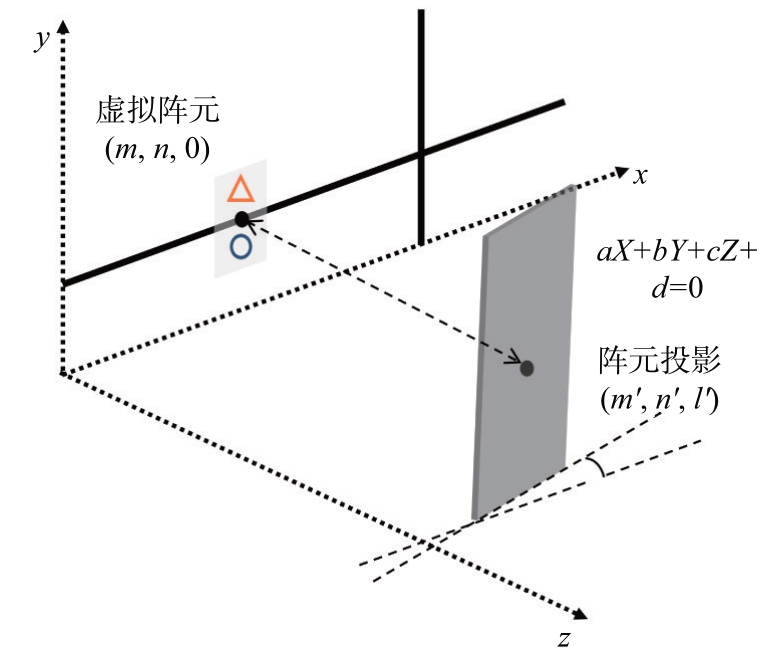
图10 利用倾斜金属平面进行采样
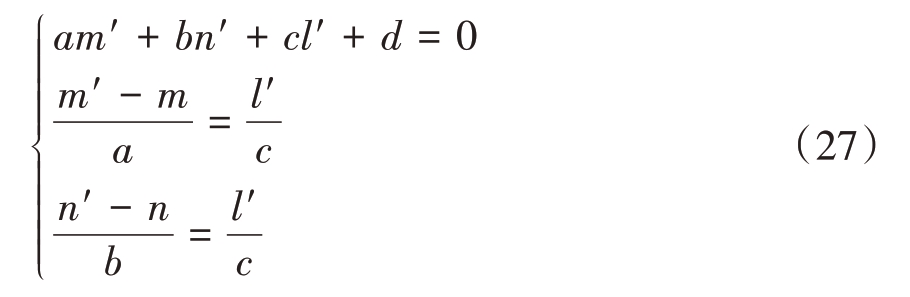
求解得到
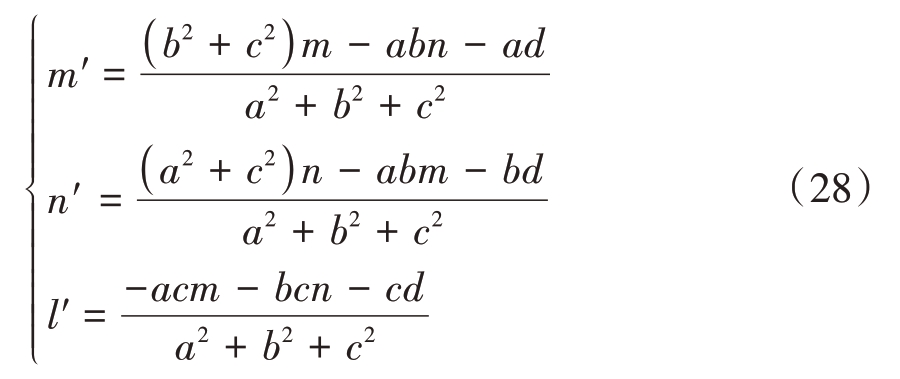
则此时阵元距离反射平面距离从2.1节的z0更新为
3 MIMO-SAR成像系统搭建
本文构建了一套基于W 波段的毫米波调频连续波雷达成像实验平台，以验证本文所提成像算法的重构效果与校准算法的有效性。
3.1 系统硬件组成
本文采用基于平面阵列的SAR 成像，考虑到数据采样后处理的简便性，雷达平台在横纵方向的运动均采用逐行光栅扫描，即在横向完成一行的扫描后移回初始位置，同时纵移一定距离，然后在新的纵向位置上完成横向单行扫描。雷达运动扫描平台的控制、射频板雷达信号的发送、数据采集板的后向散射数据接收，均由上位机控制。设计成像平台硬件架构如图11所示。
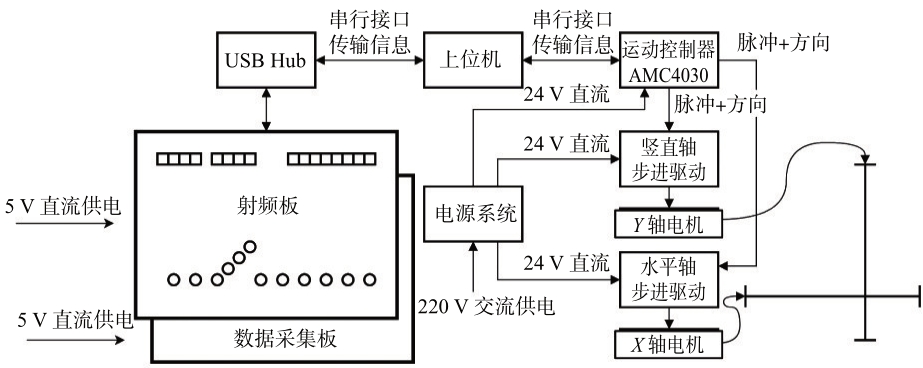
图11 设计成像平台硬件架构
本文中上位机对射频板和数据采集板级联而成的信号收发模块发出指令，采集到的雷达数据通过以太网传输回上位机以进行后处理。采用两根丝杆步进电机垂直交叉构成一个二维运动结构，并将水平轴步进电机安装在竖直轴电机上。安装完成的成像平台实物图如图12所示。
图12 硬件平台系统
3.2 系统软件组成
考虑到雷达运动平台和信号收发模块在时间上的同步性，因此不能直接使用毫米波雷达成像的配套工具。毫米波MIMO-SAR 成像系统处理流程如图13所示，包括雷达运动与数据采集模块、校准模块和图像重构模块。本文设计了一个可视化用户操作界面，如图14所示，集合了雷达运动和数据采集、保存的功能，实现了输入运动参数和信号参数后对整个成像平台的快速工作配置，并解决了运动模块和信号收发模块的在时间同步性上的问题，完成了信号采集与数据保存的一键化实现。
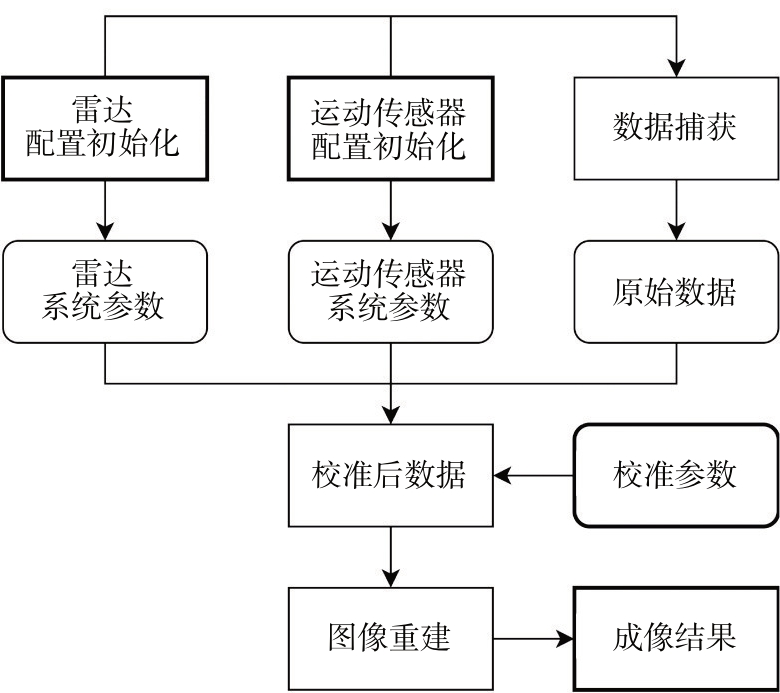
图13 MIMO SAR成像系统处理流程
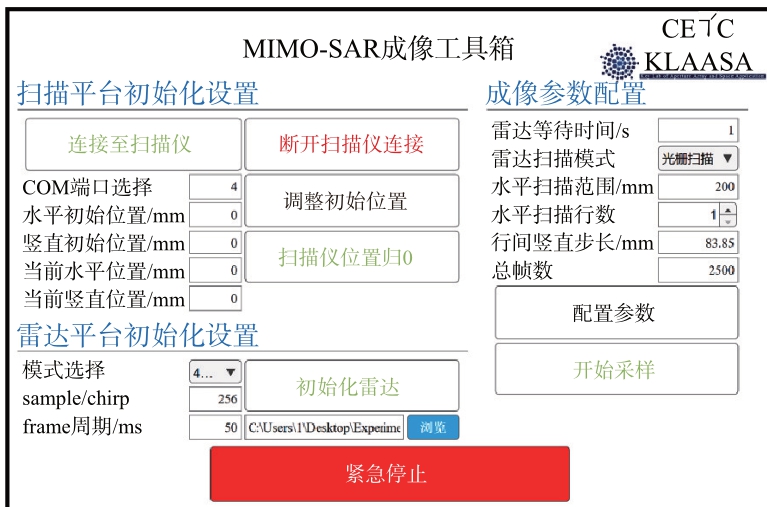
图14 软件操作界面
在可视化用户操作界面中，可以直接修改平台运动参数和信号参数，包括了雷达的水平和垂直初始位置、扫描模式选择、横向扫描距离、纵向移动距离、帧周期、数据保存路径等配置。
4 实验成像与分析
4.1 实验参数设计
根据方位向理论分辨率与距离的关系以及Nyquist 采样定律的要求，设置成像实验采用的雷达参数如表1 所示，合成孔径参数配置如表2 所示。上位机发出指令对MIMO-SAR 成像平台基本参数进行配置，将雷达采集板中的原始中频数据通过千兆网口传输回上位机存储，再对实际采集的数据进行后处理得到可直接用于后续算法处理的数据立方体。
表1 成像实验雷达参数
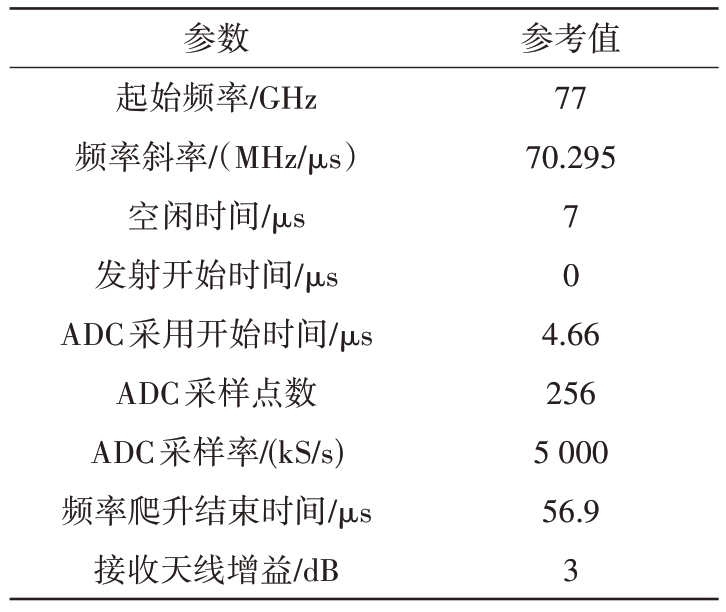
参数起始频率/GHz频率斜率/（MHz/μs）空闲时间/μs发射开始时间/μs ADC采用开始时间/μs ADC采样点数ADC采样率/(kS/s)频率爬升结束时间/μs接收天线增益/dB参考值77 70.295 7 0 4.66 256 5 000 56.9 3
表2 合成孔径参数 mm
参数x轴方向合成孔径y轴方向采样间隔y轴方向合成孔径参数值200 83.85 200
4.2 点目标成像分析
对于已有成像系统实际应用中的成像分辨率测算，可以利用点目标扩展函数（Point Spread Function, PSF）对某一点目标的解析能力进行描述。通过对某一理想点目标进行成像，分析其PSF函数-3 dB 宽度，以此作为对成像分辨率的评价指标。
本文实验中，角反目标与扫描平面距离为100 mm，扫描孔径为200 mm×200 mm，横向、纵向步进扫描间隔设置均为1 mm，具体仿真参数采用4.1 节参数。利用采集到的信号对点目标进行图像重建，得到如图15 所示的成像结果，可以观察到清晰明亮的单个点目标，其平面坐标位置与真实目标位置相一致。以重建点目标图像为原点，沿水平方向和垂直方向分别有多个旁瓣，如图16所示，对于能量较低的旁瓣，可以通过设置动态范围将其滤除。理想点目标成像结果的亮斑大小可定性说明成像系统的分辨率性能。对于理想点目标，其空间体积可以忽略，根据调频连续波雷达分辨率理论
图15 点目标成像结果图
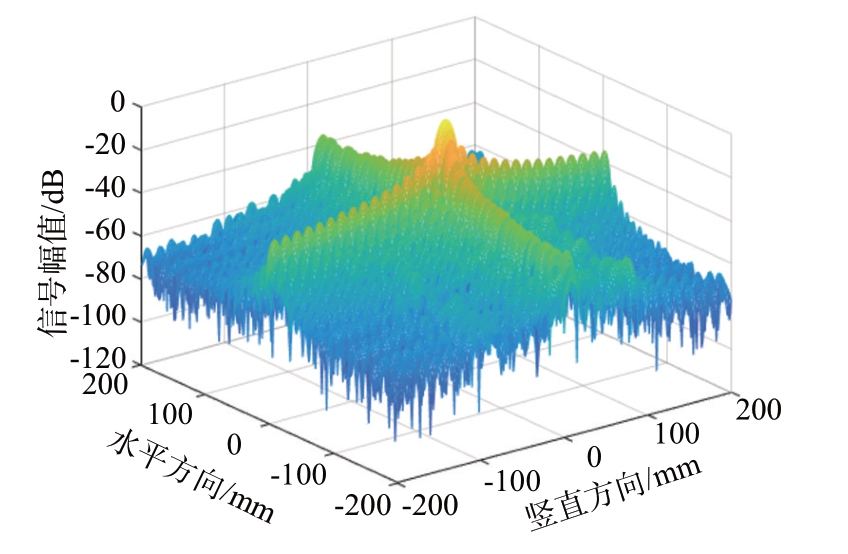
图16 PSF的二维展示
得到计算理论分辨率为10 mm。而对于图15 的成像结果，可以采用PSF对实际成像分辨率进行大致估算，如图16 所示。将成像结果分别沿着水平轴方向和竖直轴方向做切面，对所得结果的幅值量进行归一化处理并取dB 计算，如图17 所示。观察分析主瓣-3 dB 宽度范围可知，本文雷达成像平台的成像分辨率约为9.5 mm，这与前述所说的理论值基本符合。与理论计算值基本一致。
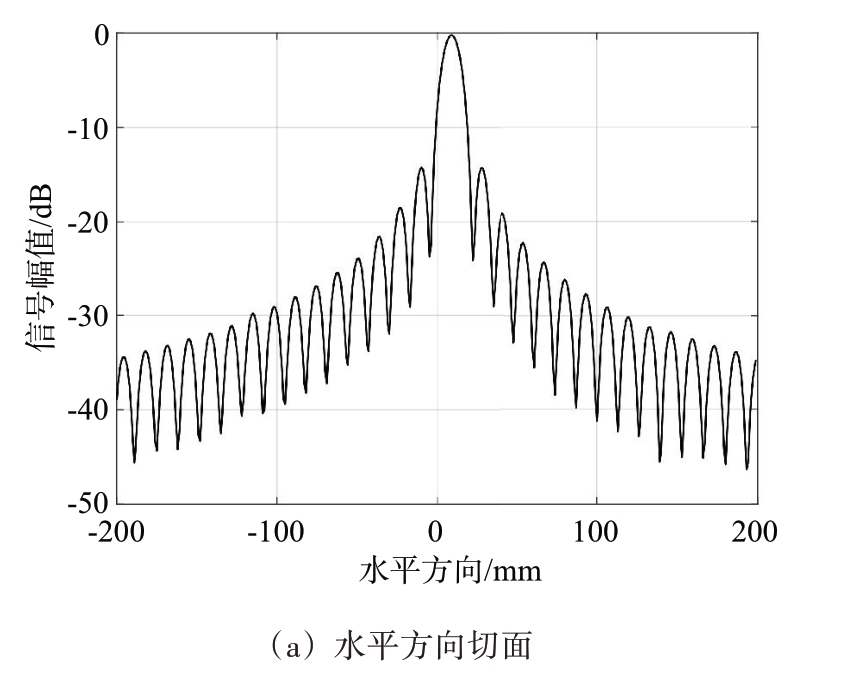
图17 PSF切面展示
进一步观察，可以看到水平方向相比垂直方向整体上分辨率一致，但波形明显更为光滑，分析原因为水平方向运动扫描间隔更小。
4.3 MIMO-SAR成像
4.3.1 金属尺成像
选择金属直尺作为成像目标。钢制直尺长度为120 mm，宽度为25 mm，竖直平行立于距离雷达发射平面前，目标直尺上方有一个直径7 mm 的圆形孔洞，方便验证成像的准确性。目标中心位置与雷达扫描平面中心位置基本对齐，距离雷达扫描平面中心距离约100 mm，成像目标在x 轴方向的长度约为25 mm，y轴方向长度约为120 mm。设置水平和垂直两个方向运动平台扫描孔径范围大小均为200 mm。x 轴方向雷达运动步进间隔为1 mm，y 轴方向步进间隔为1 mm，采样步进值满足空间采样定律理论值。扫描目标如图18所示。
图18 钢尺目标实际图像与尺寸
对于实验所得数据分别直接利用1.2 节中改进的RMA 进行图像重建和基于2.1 节进行多通道校准后再进行图像重建，两次实验的成像结果如图19所示。
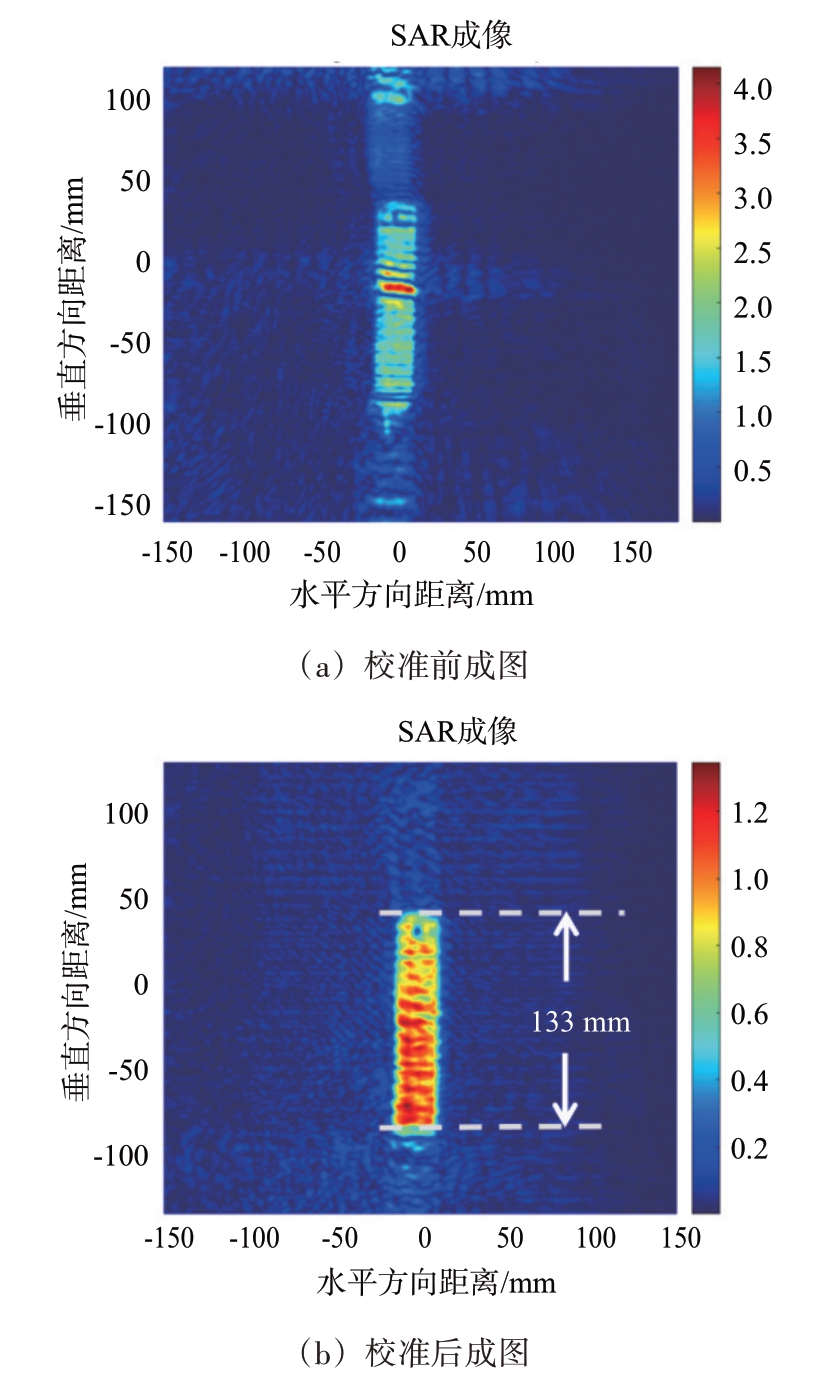
图19 未校准图像与校准后图像对比
可以看出，在校准前，MIMO-SAR 成像带有严重的伪影和虚焦的情况，经过校准，两种情况都得到了改善，并且钢尺上方的圆形空洞有较清晰的成像结果。
值得注意的是，实验如果采用0.9 mm 孔径的单发单收毫米波雷达实现阵列孔径为200 mm×200 mm SAR 成像，数据采集时间约为8 080 s；本文采用了MIMO-SAR，可以实现了86 个通道的同时扫描，则实现相同阵列孔径SAR 成像理论机械扫描时间最低可降为原来的1/86，而对于200 mm×200 mm SAR 成像需要采集时间则为120 s，这显著提高数据采集的速度。
4.3.2 镂空铝箔成像
将印有“CETC”和“KLAASA”镂空字样的铝箔附着在泡沫板上，在距离射频板约200 mm 进行扫描采样。采用获得的校准数据对采样结果进行校准，得到的成图效果如图20所示。
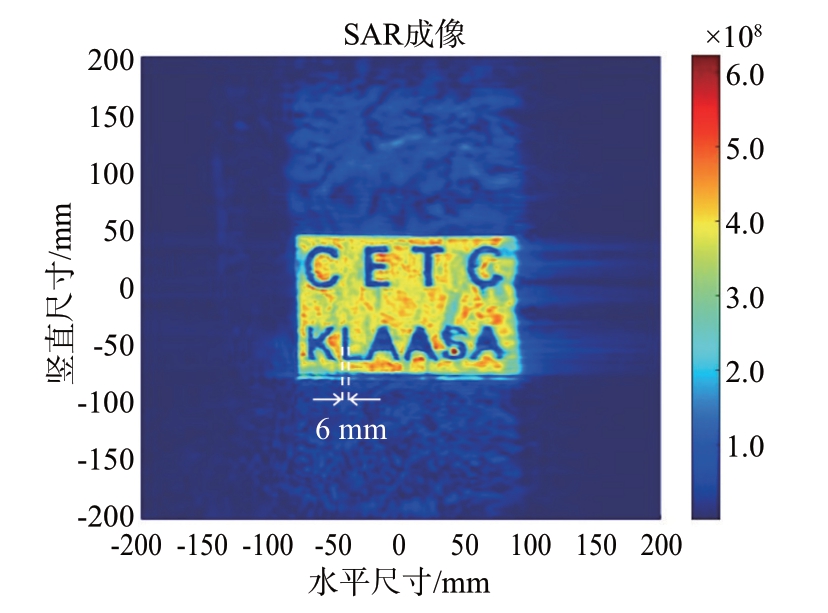
图20 对小尺寸镂空图像进行成像处理
成像结果相对理想，可以根据成像目标的尺寸可以看到在对于6 mm 的小尺寸目标成像有良好的效果，这验证了在整个实验装置不移动的情况下，通过一次校准数据获得后，可以稳定用于之后成像校准计算中。
5 结束语
本文主要讨论了在近场MIMO-SAR 成像中采用RMA 实现图像重现并通过引入NUFFT 对其运算速度进行优化；对于采用MIMO系统讨论了利用照射金属反射面实现多通道的快速校准，有效减少了多基地雷达带来的成像伪影。本文搭建了200 mm×200 mm 孔径大小的SAR 平台，通过校准后的图像良好地重现了原目标尺寸，成像分辨率达到了2.5 mm。相较于原有的单通道SAR 成像，本文实现了86 个虚拟通道的SAR 成像，使得机械扫描时间理论最高可以缩短至原来的1/86，这对需要实现快速SAR成像的应用场景有重要的意义。
［1］丁鹭飞，耿富录，陈建春.雷达原理［M］.5版.北京：电子工业出版社，2014.
［2］HAMIDI S,SAFAVI-NAEINI S.3D Near-Field Millimeter-Wave Synthetic Aperture Radar Imaging［C］//2021 IEEE 19th International Symposium on Antenna Technology and Applied Electromagnetics, Winnipeg, MB, Canada:IEEE,2021:1-2.
［3］侯本栋.弹载平台FMCW SAR成像方法研究［D］.西安：西安电子科技大学，2018.
［4］OLOUMI D, WINTER R S C, KORDZADEH A, et al. Microwave Imaging of Breast Tumor Using Time-Domain UWB Circular-SAR Technique［J］.IEEE Trans on Medical Imaging,2020,39(4):934-943.
［5］BHARGAVA D, RATTANADECHO P. Microwave Imaging of Breast Cancer: Simulation Analysis of SAR and Temperature in Tumors for Different Age and Type［J］.Case Studies in Thermal Engineering,2022,31:101843.
［6］DI MEO S, FAVA A, PASIAN M. Numerical Quantitative Evaluation of the Skin Impact in Breast Cancer Imaging at mm-Waves［C］//2022 16th European Conference on Antennas and Propagation,Madrid,Spain:IEEE,2022:1-5.
［7］HE Xiongpeng, YU Yue, GUO Yifan, et al. Ground Moving Target Detection with Nonuniform Subpulse Coding in SAR System［J］. IEEE Trans on Geoscience and Remote Sensing,2023,61:1-18.
［8］AHMED S S. Microwave Imaging in Security-Two Decades of Innovation［J］. IEEE Journal of Microwaves.2021,1(1):191-201.
［9］刘劲涛，张泽生，顾昌展，等.基于微型化FMCW 雷达的抗振乘员健康监测［J］.雷达科学与技术，2022，20(4)：391-396.
［10］VU V T, PETTERSSON M I, BATRA A, et al. Fourier Transform of SAR Data Cube and 3-D Range Migration Algorithm［J］. IEEE Trans on Aerospace and Electronic Systems,2022,58(3):2584-2591.
［11］YANG Chen, WANG Ninghao, LI Xinze, et al. A United Bandpass-Angular Weighting Template for Stolt’s f-k in Coherent Plane-Wave Compounding［C］//2021 IEEE International Ultrasonics Symposium (IUS), Xi’an, China:IEEE,2021:1-4.
［12］ WANG Jianping, CETINKAYA H, YAROVOY A.NUFFT Based Frequency-Wavenumber Domain Focusing Under MIMO Array Configurations［C］//2014 IEEE Radar Conference,Cincinnati,OH,USA:IEEE,2014:1-5.
［13］张铁男.毫米波三维全息成像图像重构算法研究［D］.南京：南京理工大学，2016.
［14］卢浩琴，朱莉，高传斌，等.基于不同窗函数的NUFFT全息成像算法［J］.微波学报，2021，37(S1)：199-202.
［15］BREGLIA A,CAPOZZOLI A,CURCIO C,et al.NUFFTBased Interpolation in Backprojection Algorithms［J］.IEEE Geoscience and Remote Sensing Letters, 2021, 18(12):2117-2121.
［16］SONG Jiayu, LIU Qinghuo,TORRIONE P, et al. Two-Dimensional and Three-Dimensional NUFFT Migration Method for Landmine Detection Using Ground-Penetrating Radar［J］.IEEE Trans on Geoscience and Remote Sensing,2006,44(6):1462-1469.
［17］ZHUGE Xiaodong,YAROVOY A.Frequency-Wavenumber Domain Focusing Under Linear MIMO Array Configurations［C］//2012 IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany:IEEE,2012:2125-2128.
［18］徐哲.毫米波雷达MIMO-SAR 成像研究［D］.哈尔滨:哈尔滨工业大学，2020.
［19］ZHU Rongqiang, ZHOU Jianxiong, TANG Liang, et al.Frequency-Domain Imaging Algorithm for Single-Input-Multiple-Output Array［J］. IEEE Geoscience and Remote Sensing Letters,2016,13(12):1747-1751.
［20］Machado S, Mancheno S. Automotive FMCW Radar Development and Verification Methods［D］. Sweden: University of Gothenburg,2018.
［21］YANIK M E. Millimeter-Wave Imaging Using MIMOSAR Techniques［D］. USA:The University of Texas at Dallas,2020.
［22］ARIKAN O, MUNSON D C. A New Back-Projection Algorithm for Spotlight-Mode SAR and ISAR［J］. Proceeding of SPIE,1989,1058:107-117.
［23］JIN M Y, WU Chialin. A SAR Correlation Algorithm Which Accommodates Large-Range Migration［J］. IEEE Trans on Geoscience and Remote Sensing,1984, 22(6):592-597.
［24］杨辉，朱国富.后向投影算法和距离迁移算法在超宽带SAR 聚焦中的比较［J］.电子技术，2008，45(11)：53-55.
［25］GAO Xiangyu, ROY S, XING Guanbin, et al. Perception Through 2D-MIMO FMCW Automotive Radar Under Adverse Weather［C］//2021 IEEE International Conference on Autonomous Systems, Montreal, QC, Canada:IEEE,2021:1-5.
［26］ZHU Rongqiang, ZHOU Jianxiong, JIANG Ge, et al.Range Migration Algorithm for Near-Field MIMO-SAR Imaging［J］. IEEE Geoscience and Remote Sensing Letters,2017,14(12):2280-2284.
［27］WANG Jianping, AUBRY P, YAROVOY A. 3-D Short-Range Imaging with Irregular MIMO Arrays Using NUFFTBased Range Migration Algorithm［J］. IEEE Trans on Geoscience and Remote Sensing,2020,58(7):4730-4742.
［28］TIAN Xianzhong, GUO Qijia, CHANG Tianying, et al.Phase Self-Calibration for Millimeter Wave MIMO Imaging［C］//2018 43rd International Conference on Infrared,Millimeter, and Terahertz Waves, Nagoya, Japan:IEEE,2018:1-2.
［29］IKRAM M Z, ALI M, WANG Dan. Joint Antenna-Array Calibration and Direction of Arrival Estimation for Automotive Radars［C］//2016 IEEE Radar Conference, Philadelphia,PA,USA:IEEE,2016:1-5.
