0 引 言
SAR 因具有全天时、全天候、作用距离远和高分辨率等特点,在空间探测、民用遥感和军事侦察等领域被广泛应用。SAR 系统复杂,参数众多且相互关联、相互制约,若能借助计算机软件进行参数设计,便可以大大节约设计人员的工作量,所以系统参数的合理选择成为了SAR设计的关键。
目前,已有许多学者针对SAR 系统参数的设计方法进行了相关研究,王睿详细地介绍了SAR条带模式的PRF、天线长度等参数的选取方法[1]。张卫华等讨论了如何在条带SAR 参数设计过程中实现高分辨率指标,给出了星载SAR 几何关系、PRF 等参数的选取方法[2]。段秋萍系统地介绍了SAR 条带模式的设计方法和流程[3]。杨淋等提出了星载P波段SAR的系统分析流程,结合其特点分析了系统体制选择、工作频率和极化方式选择,给出了系统等噪声系数、PRF、距离方位模糊、天线口径等关键参数的设计[4]。总体而言,已有文献通常只是给出了SAR 系统设计的设计流程,但在提高SAR 系统参数设计方法的自动化程度方面的论述相对较少。对于脉冲重复频率这一重要参数的选取,通常需要设计人员根据斑马图进行手工选取,使得工作量增大,效率降低。当利用仿真平台发现性能指标评测结果不完全满足用户要求时,仍然需要操作人员不断地手工调节SAR 系统设计参数,使得SAR系统设计费时费力。
本文针对SAR 系统参数设计过程自动化方法进行了研究。首先,针对PRF 和波位位置的选取进行了优化设计[5]。然后,针对方位分辨率、距离分辨率、方位模糊比等技术指标的评测结果不满足用户要求时,利用PID 控制器对方位向天线尺寸、信号带宽、PRF等参数进行自动调节。最后,通过仿真结果验证了所提出设计方法的合理性。
1 PRF的优化选取设计
1.1 传统方法
PRF是合成孔径雷达重要的参数之一,它的选择将受到雷达速度、飞行高度、天线长度、入射角度、脉冲宽度及测绘带宽等参数的约束,并直接影响到雷达的性能。PRF 的选择也会影响到发射信号峰值功率、数据率等参数值,并改变雷达距离模糊和方位模糊的大小。所以选择合适的PRF 是雷达系统参数设计中较为重要的一步[6]。
目前,传统的方法主要依靠设计人员根据斑马图来完成PRF 和波位(波束中心入射角)的选取[7-9]。如图1 所示,给出了SAR 系统设计中PRF选取所需要的斑马图示例。通常情况下,设计人员进行选取时需要注意以下三点:
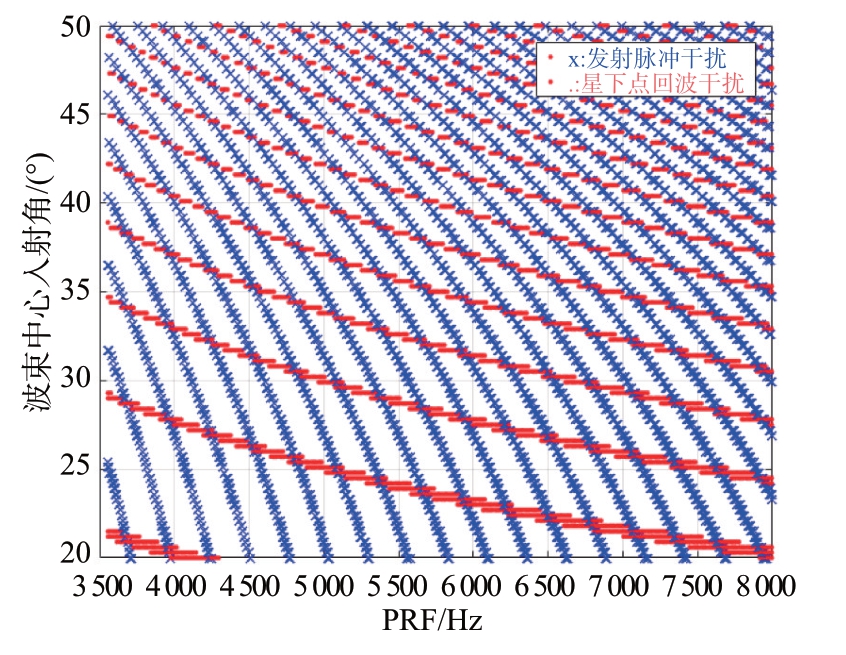
图1 斑马图示例
1)为减少数据率,PRF应尽量小;
2)波位对应的测绘带两端应与星下点干扰和发射脉冲干扰保持一段间隔;
3)选取一套波位所对应的测绘带宽时,为保证图像的连续和完整性,测绘带应存在重叠。
由此看来,人工根据斑马图选取PRF 和波位需要考虑诸多因素[10-11]。目前只能通过观察的方式进行寻优,并且需要耗费大量时间进行PRF 和波位组合的合理性验证,导致SAR 系统参数设计极为繁琐。
1.2 优化设计
本文为了使参数设计更加便捷高效,从优化的角度出发,建立优化模型来快速确定PRF 和波位位置。目标函数为寻求最小的雷达数据率,其中,PRF和入射角作为两个自变量,分别为x1和x2。约束条件包括PRF 的取值范围、入射角的取值范围、避开发射脉冲干扰时PRF 和入射角的取值范围以及避开星下点回波干扰时PRF 和入射角的取值范围。
目标函数如下:
约束条件如下:

式中,Frac表示取小数部分,Int表示取整数部分,N为主波束内距离单元的个数,Q为每个采样点的量化位数,Nhead 为头数据的典型位数,H 为卫星高度,C 为光速,Tr 为脉冲宽度,PRI 为脉冲重复间隔,τg为接收机保护时间,vs 为卫星速度,ρa 为方位分辨率,Wg,max为最大测绘带宽,θn,min为近端入射角,θf,max为远端入射角,cos x2,n 为波束范围内的近端距离,cos x2,f为波束范围内的远端距离。
2 PID控制应用于SAR参数自动化调节设计
2.1 SAR参数自动化调节原理
在实际应用中,SAR 系统会受到噪声、天线方向图、硬件系统误差等因素的影响,可能会使得根据理论设计的参数无法满足用户指标要求。此时只能由设计人员不断调节参数,浪费时间和精力。所以,SAR 系统参数设计应具备自适应性。即根据用户指标要求的变化,自动调整相关参数,缩短调节时间,保证SAR 系统设计结果的合理性,提高系统响应的时效性。随着科学技术的发展,利用软件进行PID控制被广泛应用于信号处理、智能控制等领域[12]。PID 控制算法简单,具有一定的抗干扰能力,鲁棒性好,并且反应速度快,具有一定的时效性,可以满足SAR 系统参数设计过程自动化的需求。如图2 所示,给出了基于PID 的SAR 系统参数自动化调节的原理图。在SAR 系统参数设计过程中,利用PID 的线性控制策略,计算雷达指标的实际输出和期望输出之间的系统偏差e(t),将其作为PID 控制器的输入。通过对系统偏差e(t)进行加权,得到控制信号u(t)后,驱动受控对象,使得系统偏差e(t)朝减小的方向变化,从而达到SAR系统参数的自动化调节。PID 控制器的控制规律公式为
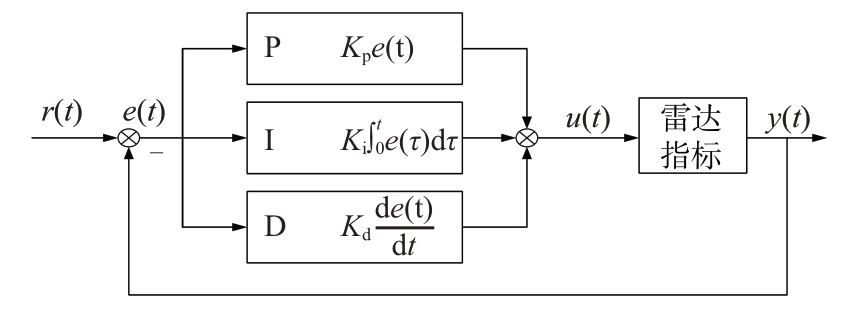
图2 基于PID的SAR参数自动化调节原理图
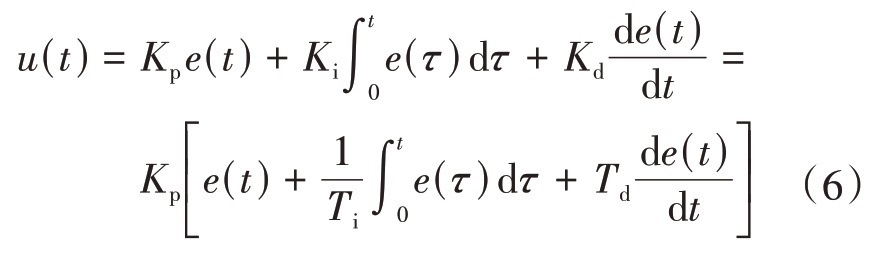
式中,e(t)为系统偏差,Kp 为比例控制加权系数,Ki为积分控制加权系数,Kd 为微分控制加权系数,Ti为积分时间常数,Td为微分时间常数。
本文添加PID 控制器对SAR 参数设计进行自动化调节。当系统受到外界干扰时,其输出结果就会发生相应的改变。经过一段时间后,系统的输出结果将会达到平稳状态。其控制过程比较简单,具有较强的鲁棒性,提高了SAR 系统参数设计的自动化程度。
2.2 指标分析
在SAR 系统仿真中添加一个PID 控制器进行系统参数调节,需要将控制算法数字化。数字式PID 控制算法可分成两种,如表1 所示,给出了两种不同PID 算法适用领域以及优缺点。本文采用位置型控制算法来得到空间分辨率以及模糊比对系统参数影响的某一确定值。
表1 两种不同PID算法适用领域以及优缺点

名称位置型控制算法适用领域计算机输出的u()k可直接控制执行机构(如阀门)缺点需要遍历偏差信号,累积误差相对更大增量型控制算法数字控制器输出的是控制量的增量优点输出值和执行机构的位置(如阀门开度)一一对应,便于获取误动作时影响小,便于实现无扰动切换,不产生积分失控积分截断效应大,有静态误差溢出的影响大;
位置型PID控制表达式为
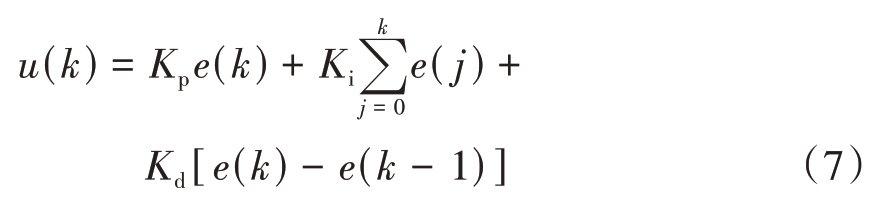
式中,k 表示采样序号,k=0, 1, 2,…, u(k)表示第k次采样时刻系统被控对象的输入值,e(k)表示第k次采样时刻系统的偏差,e(k - 1)表示第k - 1次采样时刻系统的偏差。
工作人员在进行SAR 系统参数设计时,通常需要考虑很多技术参数。SAR 的不同工作模式下相关参数和技术指标之间互相约束,当某一参数发生变化时,往往会影响到多个指标。因此,并不是所有的参数都适合PID 控制进行调节。为了解决这一问题,首先需要对SAR 系统设计过程中涉及到的参数进行理论分析,然后确定出适合PID控制调节的参数,从而实现评测结果不满足用户要求时系统的自动调节。本文以SAR 条带模式为例,对相关参数和技术指标进行了理论分析。
首先,对SAR 条带模式的方位分辨率ρa 进行适用性分析,ρa的计算公式为
式中,la代表方位向天线尺寸。由式(8)可知,方位向分辨率和天线尺寸呈线性关系,由于方位分辨率只与一个参数有关,当使用PID控制针对方位向天线尺寸进行调节时,可以使仿真得到的方位向分辨率达到预设值,同时确定此时的方位向天线尺寸。方位向天线长度变化将会引起脉冲重复频率下限、天线增益、系统灵敏度和方位模糊比这些指标产生变化,所以需要检查当前情况下的指标合理性。
其次,对SAR 条带模式的距离分辨率ρr 进行适用性分析,ρr的计算公式为
式中,Br代表信号带宽。
如图3所示,给出了距离分辨率和信号带宽的关系图。距离向分辨率的改变只与信号带宽有关,二者近似为线性关系。当使用PID控制针对信号带宽进行调节时,可以使仿真得到的距离像分辨率达到预设值,同时确定此时的带宽。带宽的变化将会导致噪声功率的改变,间接地改变了距离向峰值和积分旁瓣比的数值大小,所以需要检查当前情况下的指标合理性。
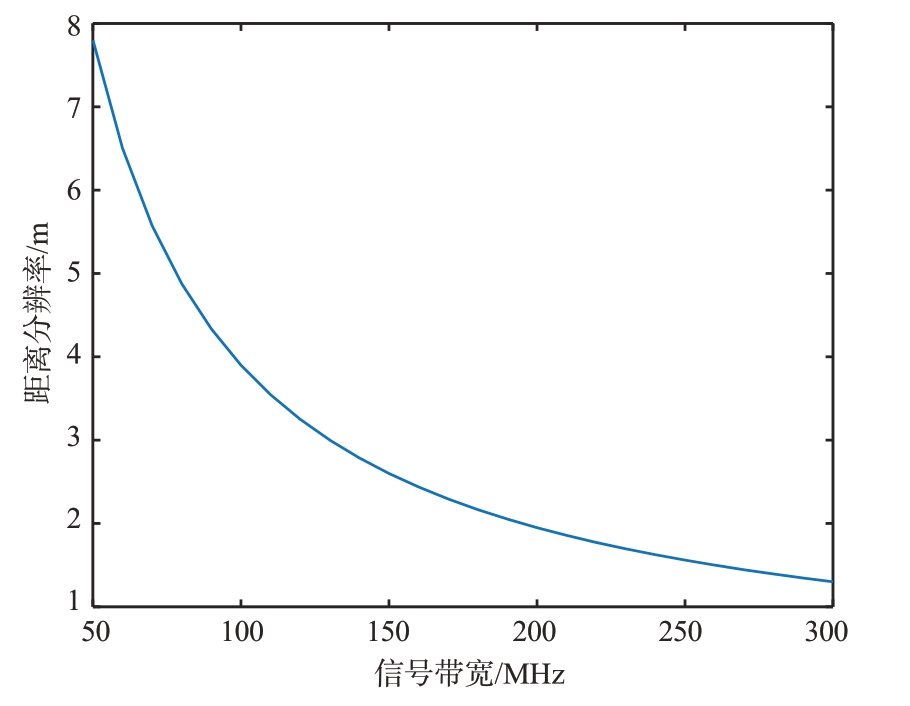
图3 距离分辨率和信号带宽的关系图
下一步,对SAR 条带模式的距离模糊比(Range Ambiguity to Signal Ratio,RASR)进行适用性分析,RASR的计算公式为
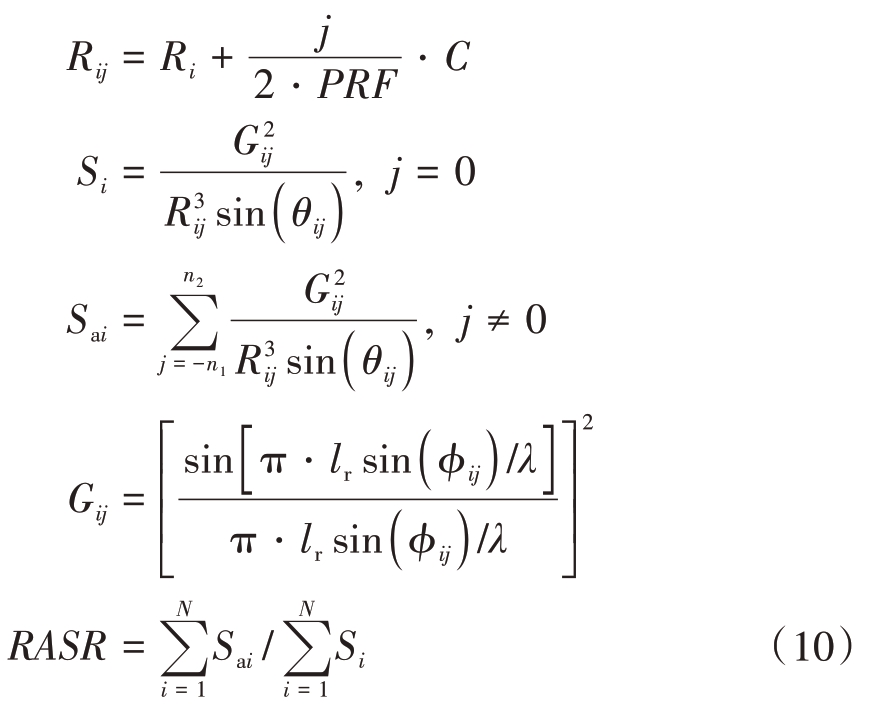
式中,i 是主波束内距离单元的序号,j 是模糊区的序号,Ri 是主波束内第i 个距离单元对应的斜距,S是回波功率,N 是主波束内距离单元的个数,θij 是第i 个距离单元的第j 个模糊区对应的入射角,n1和n2 分别是近端模糊区的下限序号和远端模糊区的上限序号,ϕij 是第i 个距离单元的第j 个模糊区与波束中心线的夹角。
如图4所示,给出了距离模糊比和PRF的关系示意图。二者关系呈非线性,并不适合PID控制参与系统调节。
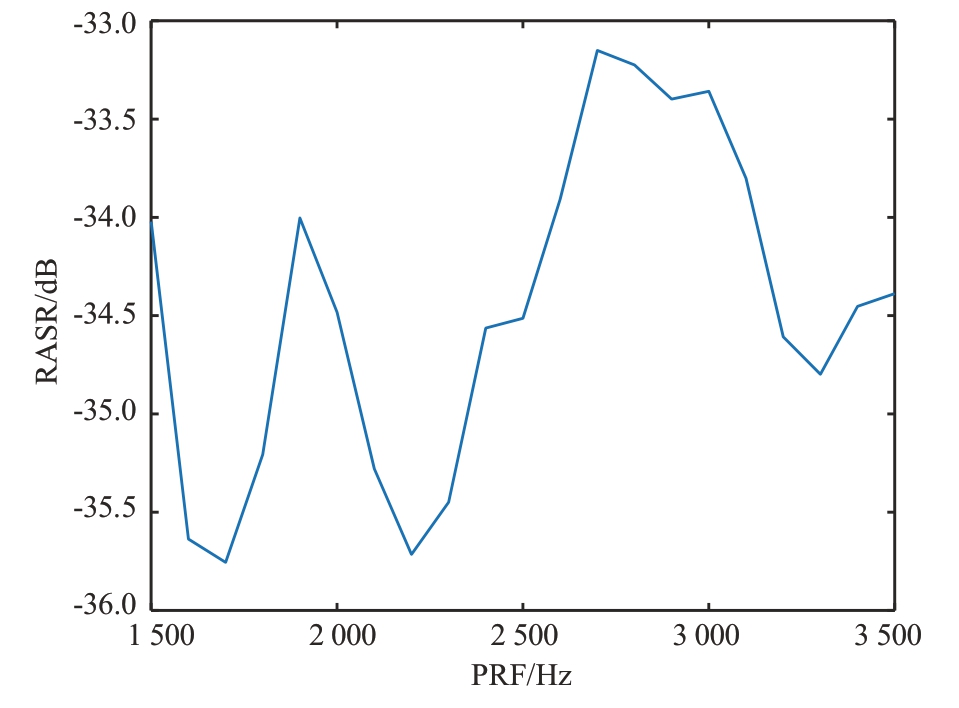
图4 距离模糊比和PRF的关系
最后,对SAR 条带模式的方位模糊比(Azimuth Ambiguity to Signal Ratio,AASR)进行适用性分析,AASR的计算公式为
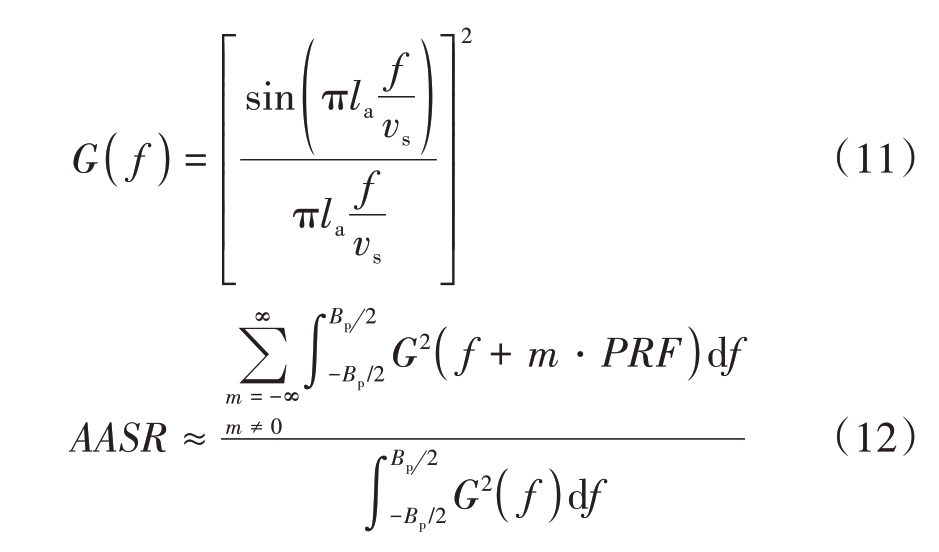
式中,Bp为多普勒带宽,f为多普勒频率。
如图5所示,给出了方位模糊比与PRF的关系示意图。PRF与方位模糊比之间的关系近似线性,当使用PID控制针对PRF进行调节时,可以使仿真得到的方位模糊比达到预设值,同时确定此时的PRF,PRF 的改变将会引起系统灵敏度变化,所以需要检查当前情况下的指标合理性。
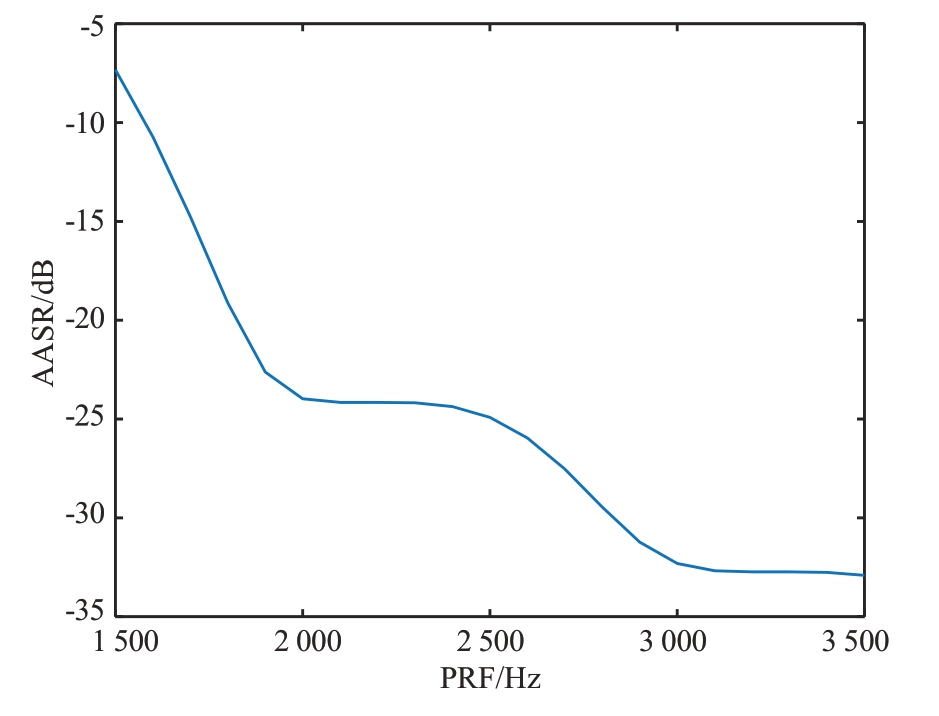
图5 方位模糊比和PRF的关系
2.3 参数自动化设计流程
如果在SAR 系统的参数设计过程中考虑天线方向图和系统噪声等因素后,理论设计的方位分辨率、距离分辨率、方位模糊比三项指标往往无法满足用户要求,此时利用PID控制器针对方位向天线尺寸、信号带宽、PRF三项参数作自动调节,直到指标符合要求。本文采用经验试凑法来完成PID控制器参数的整定[13-14],根据经验和系统的响应随参数变化的趋势,比较快速、方便的调节参数使系统达到目标要求。对利用PID 控制器进行SAR 参数自动化调节的设计流程进行了总结,其主要步骤如图6所示。
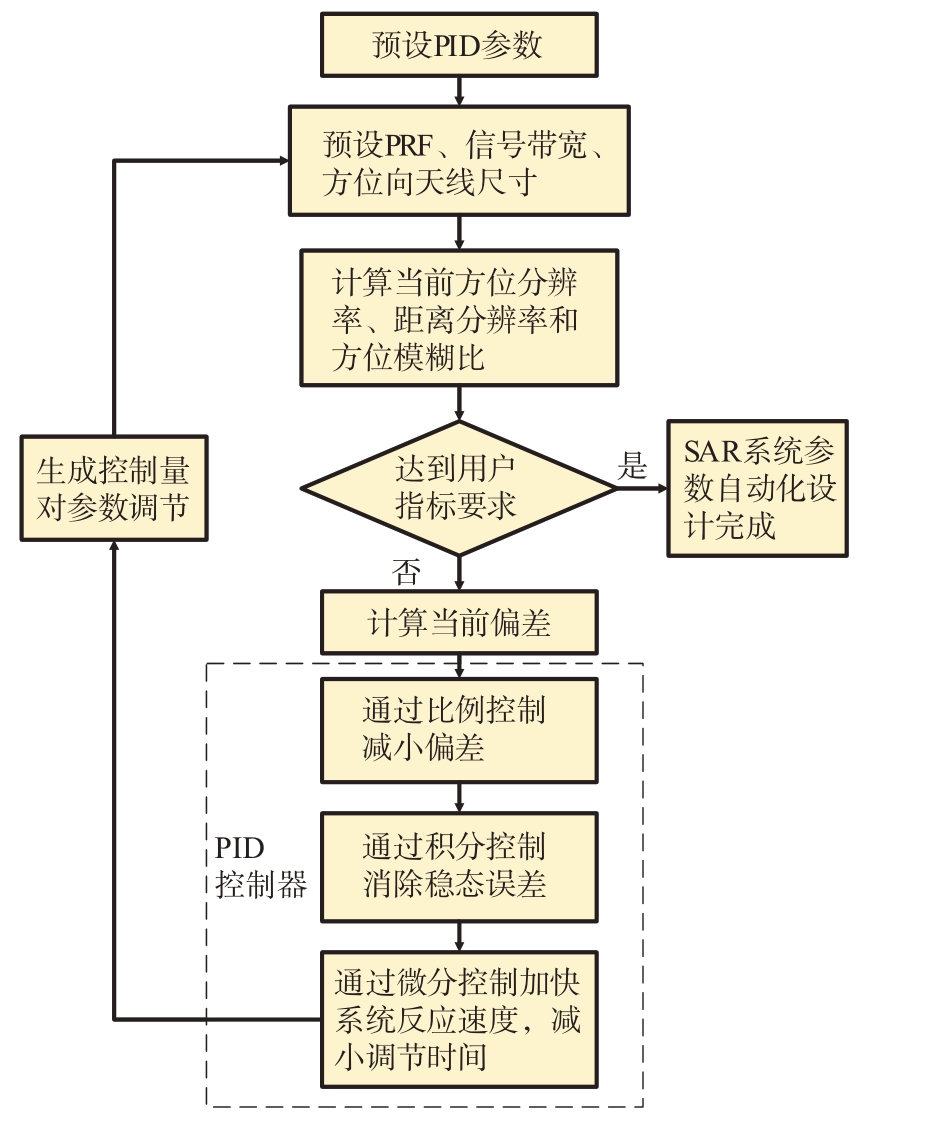
图6 PID控制应用于SAR参数自动化调节设计流程图
3 仿真结果与分析
3.1 PRF优化设计的结果分析
MATLAB中的fmincon函数通常用来求解非线性优化问题。借助fmincon 函数求解1.2 节中的目标函数,能够快速地确定出PRF、波位和数据率的值。如表2所示,当需要选取多个PRF和波数中心入射角的组合时,可以通过改变PRF 和波束中心入射角的下限的方式得到参数选取结果和数据率。相较于传统的依靠斑马图选取PRF,该方法极大地减少了工作人员在设计PRF 和波位组合时花费的时间和精力。
表2 利用优化求解模型得到的PRF和波位参数选取结果以及数据率
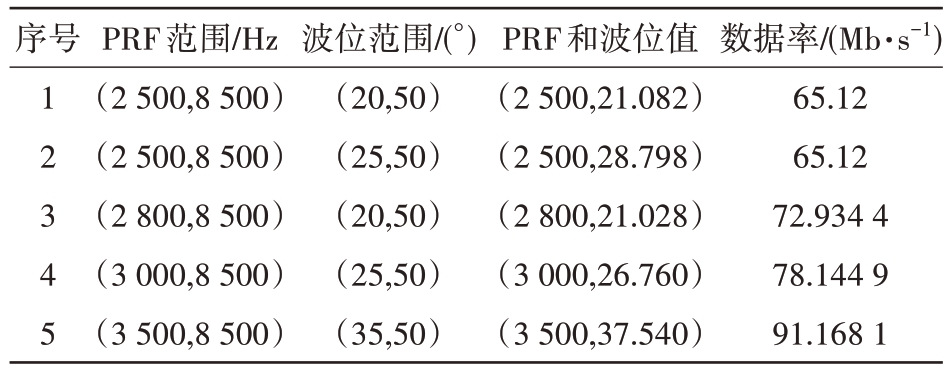
序号1 2 3 4 5 PRF范围/Hz(2 500,8 500)(2 500,8 500)(2 800,8 500)(3 000,8 500)(3 500,8 500)波位范围/(°)(20,50)(25,50)(20,50)(25,50)(35,50)PRF和波位值(2 500,21.082)(2 500,28.798)(2 800,21.028)(3 000,26.760)(3 500,37.540)数据率/(Mb·s-1)65.12 65.12 72.934 4 78.144 9 91.168 1
3.2 系统参数自动化调节的结果分析
为了解决SAR 系统参数设计得到的部分技术指标与用户实际要求存在一定偏差的问题,本文利用PID控制来完成SAR系统参数的自动化调节。首先,计算当前时刻的指标偏差,作为PID 控制器的输入值。然后,经过比例控制减小偏差、积分控制消除稳态误差及微分控制加快系统反应速度,减小调节时间。最后,生成控制量对PRF、信号带宽、方位向天线尺寸作调节,再判断当前时刻的指标是否达到用户要求直到指标达标,结束SAR 系统参数自动化设计。如表3 所示,给出了PID 调整方位分辨率、距离分辨率和方位模糊比三项指标的相关参数预设值。根据表3的参数值,按照上述循环过程得到了如图7所示的实验结果图。从图7可以看出,利用PID控制进行SAR系统参数自动化调节是可行的,PID 参数值的差异仅对指标收敛到目标值的快慢有较小的影响。通过利用PID 控制不断进行方位向天线尺寸、信号带宽和PRF 的自动调节,使得从SAR 图像中提取的方位分辨率、距离分辨率和方位模糊比与目标设定值越来越接近,最终达到设定值。相较于人工调整参数,该法使SAR 系统参数设计更加便捷高效。实现了SAR系统参数向用户指标要求调节的自动化过程。
表3 相关参数预设值
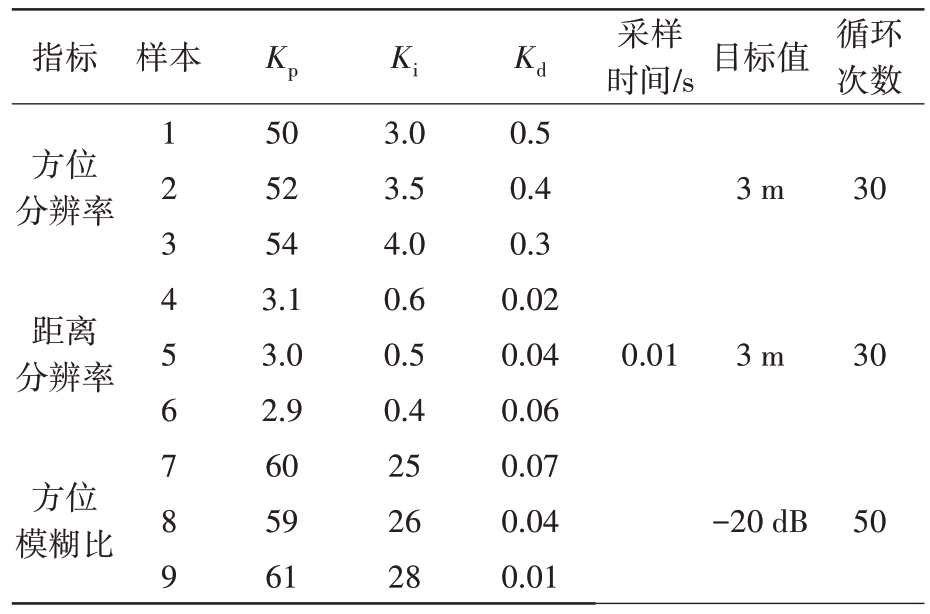
指标样本Kp Ki Kd采样时间/s 目标值 循环次数方位分辨率3 m 30距离分辨率0.01 3 m 30方位模糊比123456789 50 52 54 3.1 3.0 2.9 60 59 61 3.0 3.5 4.0 0.6 0.5 0.4 25 26 28 0.5 0.4 0.3 0.02 0.04 0.06 0.07 0.04 0.01-20 dB 50
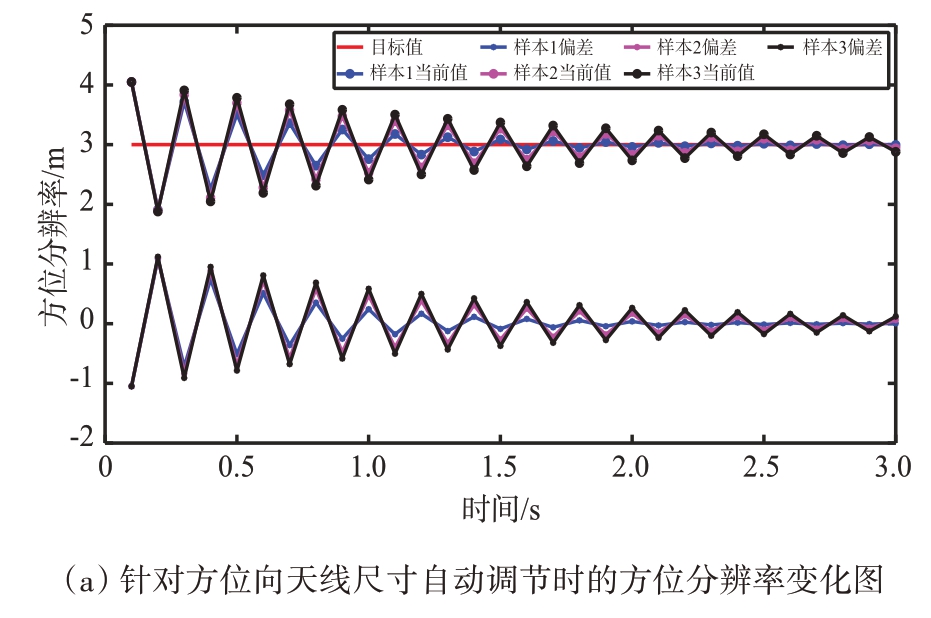
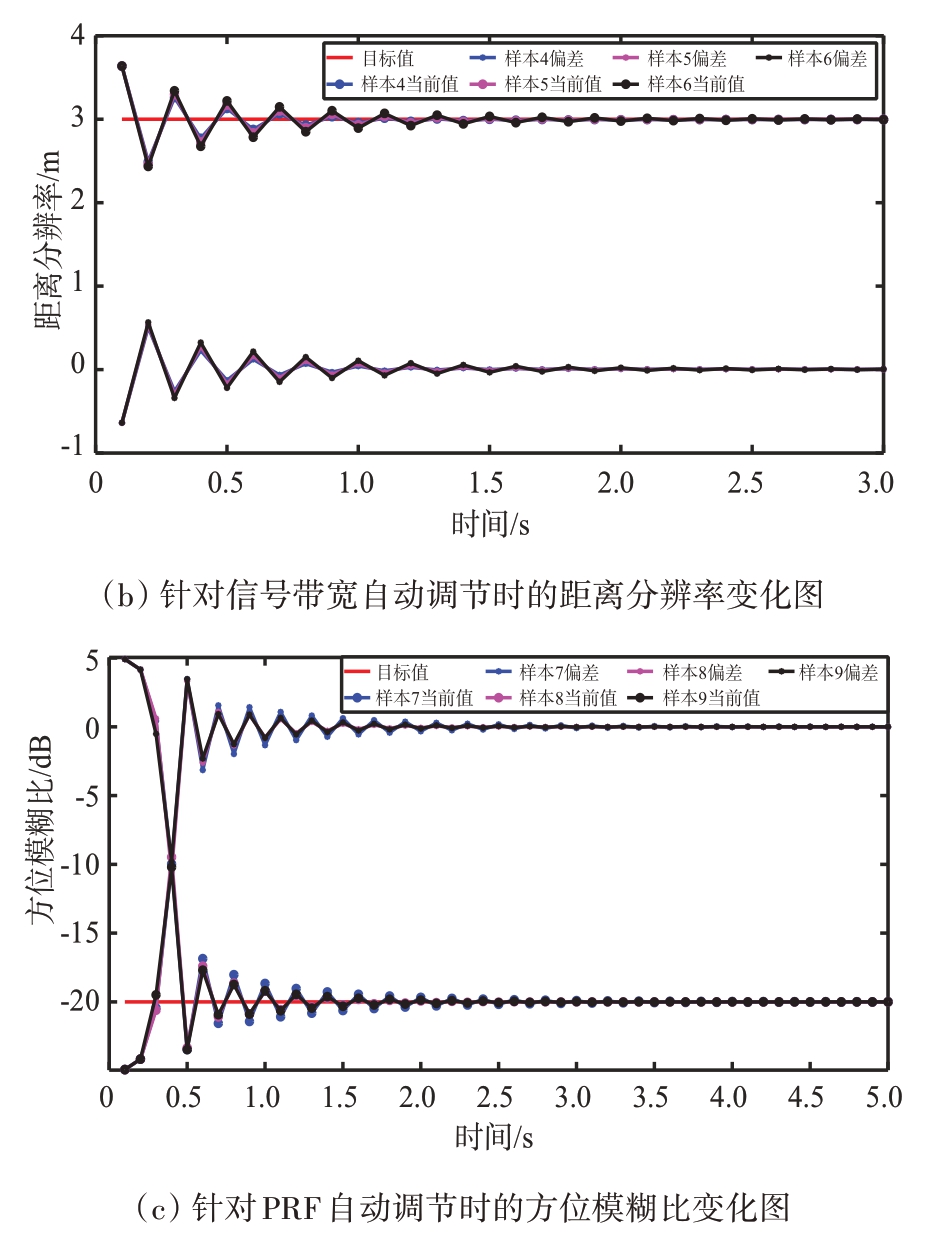
图7 仿真结果图
4 结束语
本文提出了一种SAR 系统参数自动化设计的方法。首先,针对部分参数仍需手工选取的现状建立了最优化求解模型,并给出了PRF 和波位位置的优化选取结果,使参数设计流程更加高效便捷。然后,针对SAR 系统参数设计过程中部分技术指标的评测结果不满足用户需求时无法自动调节的现状,采用PID 控制器对方位向天线尺寸、信号带宽、PRF 等参数进行自动调节,使得方位分辨率、距离分辨率、方位模糊比等技术指标向用户需求值逐步靠近。通过仿真实验验证了该方法的可行性,实现了SAR系统参数设计过程的自动化。
[1]王睿.星载合成孔径雷达系统设计与模拟软件研究[D].北京:中国科学院研究生院(电子学研究所),2003.
[2]张卫华,王立刚.高分辨率星载SAR系统关键参数的设计[J].雷达科学与技术,2004,2(4):230-234.
[3]段秋萍.合成孔径雷达系统参数设计、回波仿真及应用研究[D].北京:中国科学院研究生院(电子学研究所),2007.
[4]杨淋,赵宁,姚佰栋,等.高分辨率星载P 波段SAR 系统参数设计[J].雷达科学与技术,2017,15(1):19-28.
[5]郭媛,索志勇,王婷婷,等.弹载SAR系统参数优化设计方法[J].系统工程与电子技术,2020,42(7):1478-1483.
[6]陈粤,禹卫东.星载SAR 方位多通道TOPS 成像模式参数设计[J].雷达科学与技术,2022,20(2):142-149.
[7]ZHU Daiyin, XIANG Tianshun, WEI Wei, et al. An Extended Two Step Approach to High-Resolution Airborne and Spaceborne SAR Full-Aperture Processing[J]. IEEE Trans on Geoscience and Remote Sensing, 2021, 59(10):8382-8397.
[8]薛莲,周鹏,张振华,等.多模式小卫星SAR机载挂飞试验的飞行路线规划与雷达参数设计[J].海洋科学,2021,45(5):62-73.
[9]SUN Zhicao,WU Junjie,PEI Jifang,et al.Inclined Geosynchronous Spaceborne-Airborne Bistatic SAR:Performance Analysis and Mission Design[J]. IEEE Trans on Geoscience and Remote Sensing,2016,54(1):343-357.
[10]张润宁,王旭莹,王志斌.星载高分宽幅SAR技术发展趋势分析[J].航天器工程,2022,31(1):1-9.
[11]姚佰栋,盛磊,孙光才,等.大椭圆轨道SAR 系统设计及关键技术研究[J].雷达科学与技术,2020,18(4):373-380.
[12]吕德深,梁承权.模糊理论和PID 相结合的激光雷达智能控制系统[J].激光杂志,2021,42(7):157-160.
[13]张继荣,张天.基于改进粒子群算法的PID 控制参数优化[J].计算机工程与设计,2020,41(4):1035-1040.
[14]崔恒荣,秦雅,卞玮章.基于模糊控制参数自整定的舰载雷达三轴稳定控制[J].雷达与对抗,2020,40(1):57-60.
