0 引言
低空风切变作为极端恶劣天气中危险系数极高的一种大气现象,具有变化时间短、作用范围小、强度大等特点[1],严重威胁了民航的飞行安全。低空风切变现象多半发生在飞机的起飞和降落阶段,尤其降落阶段最为危险。降落阶段飞机准备降落跑道,由于飞机距离地面的高度较低,如果遭遇低空风切变,驾驶员反应不及极其容易发生飞行事故,对待低空风切变这一危险气象我们只能尽量规避。因此,研究低空风切变检测,给飞机及时提供预警信息以避免飞行事故就非常必要。低空风切变的检测流程一般可分为杂波抑制、低空风切变风速估计、平均F 因子计算、低空风切变危险性判决这四个步骤[2],低空风切变风速估计是其中至关重要的一步,若风速估计失准,就会直接导致低空风切变检测结果不准确,因而准确估计低空风切变风速具有重要意义。
机载气象雷达是用于实时警戒和预报危险气象的主要探测工具之一[3],在其探测低空风切变时,地杂波回波信号因其广而强的特征掩盖了低空风切变回波信号,因此首先需要抑制杂波,杂波抑制之后才能进行低空风切变风速的估计。在抑制杂波过程中,当抑制掉与其重叠的低空风切变信号时,低空风切变信号发生缺失,使得风速估计结果的准确性大大降低。因此研究数据缺失情况下的低空风切变风速估计具有重要意义。
目前,已有多种低空风切变风速估计方法被提出[4-6],但所提方法均没有考虑数据缺失的情况。迄今为止,谱估计非参数化法是一种主流的缺失数据恢复方法。CLEAN 算法是最早被提出的一种常用于缺失数据的谱估计方法,该算法以迭代的方式对数据进行拟合并去除正弦波[7],被广泛应用于图像重建问题;缺失数据振幅相位估计(Gappeddata APES,GAPES)算法是基于APES 对缺失数据的最小二乘准则的最小化[8],被应用于合成孔径雷达(SAR)成像问题;缺失数据迭代自适应(Iterative Adaptive Approach,M-IAA)算法使用IAA 频谱估计来检索丢失的数据,通过时域的方法对缺失数据进行了恢复[9],适用于IID 样本数较少甚至单个样本的情况,多被应用于雷达成像领域。上述缺失数据恢复算法普遍运算量较大,且应用于数据缺失情况下的低空风切变风速估计中未有相关文献报道。
基于上述问题,本文提出了一种数据缺失情况下基于M-SPICE 的低空风切变风速估计方法。该方法首先构造数据缺失模型,然后通过M-SPICE算法求解目标函数,不断迭代更新得到估计算子和协方差矩阵,最后恢复得到缺失数据重构出完整的风切变数据,进而估计风场速度。该方法能很好地提高缺失数据的恢复精度,实现了数据缺失情况下低空风切变风速的准确估计。
1 信号模型
机载气象雷达探测低空风切变示意图如图1所示,天线阵列呈线性排列,由N 个阵元等间隔组成,载机平台在高度为H 处以速度V 匀速直线运动,其中θ0 和φl 分别表示低空风切变风场目标的方位角和俯仰角。则第l(l=1,2,…,L)个距离单元雷达回波数据y(l)表示为
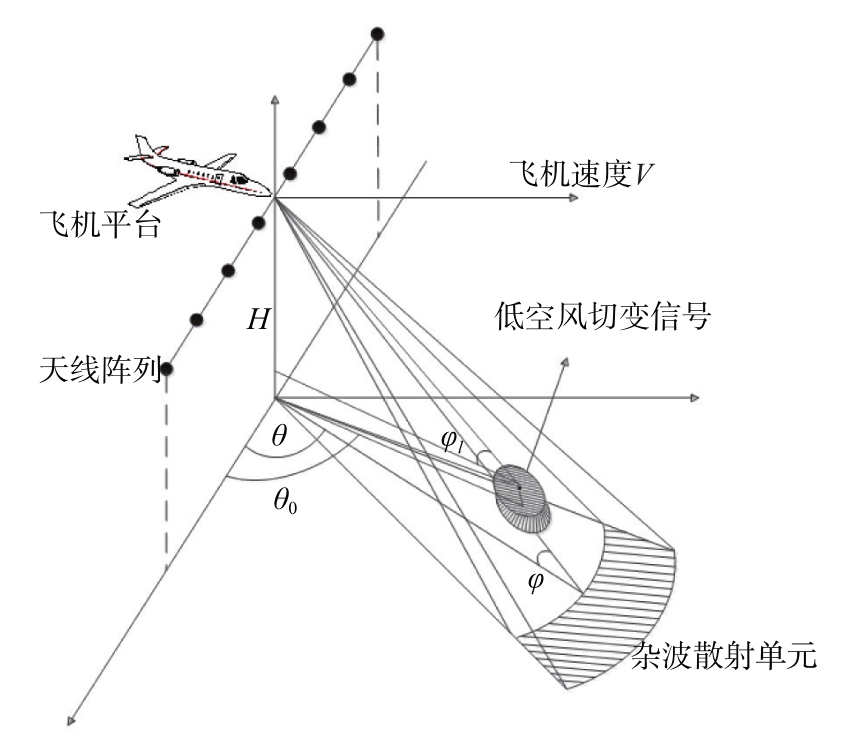
图1 机载气象雷达探测低空风切变示意图
式中,s(l)为第l 个距离单元内低空风切变风场产生的雷达回波信号,c(l)为第l 个距离单元内的地杂波信号,n(l)为第l个距离单元的高斯白噪声。
低空风切变是一种分布式目标,单个距离单元的低空风切变回波信号中包含多个散射粒子,将每个散射粒子的幅度、相位相加,得到一个距离单元的低空风切变回波信号s(l):
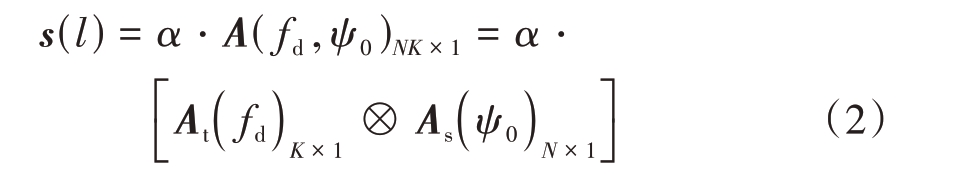
式中,⊗为Kronecker积,α 为低空风切变信号的复幅度,fd 为低空风切变信号的多普勒频率,ψ0 为低空风切变信号的空间锥角,且cos ψ0=cos θ0 cosφl,A(fd,ψ0)NK× 1 为低空风切变信号的空时导向矢量,其中时域导向矢量At(fd)K× 1 和空域导向矢量As(ψ0)N× 1的表达式[10]分别为
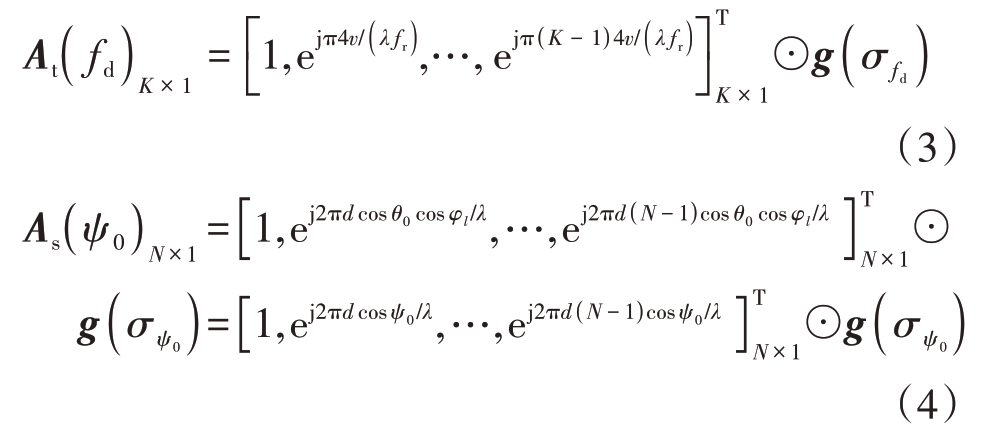
式中,⊙为Hadamard积,T 为转置,![]() 分别为低空风切变信号的频率扩展函数和角度扩展函数[11]。
分别为低空风切变信号的频率扩展函数和角度扩展函数[11]。
地杂波信号仿真采用的是Ward 模型,其仿真原理为:首先依据雷达参数确定距离分辨率,然后再根据角度分辨率将雷达辐射范围进行角度划分,最后根据角度和距离分辨率将第l 个距离单元的地杂波划分为M 个杂波散射单元,将所有杂波散射单元的信号叠加就得到一个距离单元内的地杂波信号。则第l个距离单元的地杂波信号c(l)可表示为
式中,M 为杂波散射单元总数,P 为雷达接收功率,cRCS 为杂波散射单元的反射系数,Rl 为第l 个距离单元的杂波散射单元与载机平台之间的斜距,F(θl,m)为雷达天线方向图,a(fd,m,ψs,m)为杂波散射单元NK×1维的空时导向矢量,可表示为
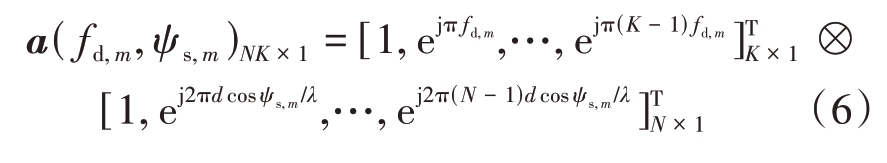
2 基于M-SPICE的低空风切变风速估计方法
基于M-SPICE 的低空风切变风速估计方法首先抑制杂波,然后通过M-SPICE 算法迭代得到估计算子,再利用估计算子计算协方差矩阵,进而恢复得到缺失的风切变数据,最后将恢复出来的缺失数据重构成完整的风切变数据,实现风场速度的准确估计。该方法可主要分为杂波抑制、缺失风切变数据的恢复和低空风切变风速估计三部分,下面将进行详细阐述。
2.1 基于正交投影STAP的杂波抑制
通过雷达接收到的不同距离单元回波数据可计算得到其协方差矩阵,则第l 个距离单元的协方差为
式中,L 为距离单元总数,H 表示共轭转置,y(l)为雷达接收到的第l 个距离单元的回波数据。将R̂(l)进行特征分解[12],可得
式中:λi 为![]() 的特征值,ui 为其对应的特征向量,U=[u1,u2,…,uNK],Λ 为各特征值构成的对角矩阵,Λ=diag[λ1,λ2,…,λNK];D 为杂波协方差矩阵中的前D 个较大特征值,其对应的特征向量构成杂波子空间,剩余L- D 个较小特征值对应的特征向量构成噪声子空间[13]。
的特征值,ui 为其对应的特征向量,U=[u1,u2,…,uNK],Λ 为各特征值构成的对角矩阵,Λ=diag[λ1,λ2,…,λNK];D 为杂波协方差矩阵中的前D 个较大特征值,其对应的特征向量构成杂波子空间,剩余L- D 个较小特征值对应的特征向量构成噪声子空间[13]。
然后构建与杂波子空间正交的投影矩阵对消杂波,可以表示为
投影矩阵Pc 对雷达回波数据y(l)进行投影变换后得到剩余数据y͂(l),可以表示为
同时投影矩阵Pc 对风切变信号的空时导向矢量G(l)进行投影变换后变为
则第l个距离单元的协方差矩阵变为
投影变换后求解STAP 权矢量,即在线性约束准则下转化为求解最优权矢量问题:

通过最小均方误差准则求解式(13),即可得到最优权矢量:
式中,μ为常数,ωl 为正交投影STAP算法求得的最优权矢量,且将用于后面低空风切变风速的估计中。
2.2 基于M-SPICE算法的缺失风切变数据恢复
在2.1 节进行杂波抑制后,部分低空风切变信号发生了缺失,这将会导致低空风切变风速估计准确性大大降低,因此有必要将缺失的低空风切变信号恢复出来,再估计低空风切变的风场速度。
雷达回波信号可以看作由不同方向和不同多普勒频率信号的叠加,将表示回波信号方向的角度域均匀离散化为Ns= ρsN 个网格、多普勒域均匀离散化为Nt= ρt K 个网格(ρs 和ρt 分别表示离散化系数),则整个空时域被离散化为Q= Ns Nt 个网格,第l个待检测单元的信号可表示为
式中:Q 为划分的网格总数;αl,q为第l个距离单元、第q个单元网格信号的幅度值;n为噪声向量,其协方差矩阵为![]() ;空时字典A 由多个单元网格的空时导向矢量a(fd,q,ψs,q),(q=1,2,…,Nt,q=1,2,…,Ns)构成,表示为
;空时字典A 由多个单元网格的空时导向矢量a(fd,q,ψs,q),(q=1,2,…,Nt,q=1,2,…,Ns)构成,表示为
将空时字典写成向量形式表示为A=[a1,a2,…,aQ]。
基于M-SPICE 算法恢复缺失的风切变数据,首先需要进行数据缺失模型的建立,然后根据M-SPICE算法求解估计算子,用求得的估计算子计算出协方差矩阵,进而利用有效数据和缺失数据在时域具有相同谱成分的关系恢复得到缺失数据[14]。下面分别介绍缺失数据恢复的模型建立、估计算子和协方差矩阵的求解及缺失数据时域恢复的详细过程。
1)建立数据缺失模型
根据杂波抑制之后的信号建立数据缺失模型,用Lg 表示有效单元数,Lm 表示缺失单元数,L=Lg+ Lm 为完整单元数。构造Lg×1 有效数据选择矩阵Sg,从![]() 中选择出有效数据组合成一个Lg×K 维矩阵,表示为有效数据矩阵yg,构造Lm×1 缺失数据选择矩阵Sm,将缺失的数据矩阵组合成Lm× K 维矩阵,表示为缺失数据矩阵ym,有效数据矩阵yg 表达式及其对应的空时导向矢量表达式可表示为
中选择出有效数据组合成一个Lg×K 维矩阵,表示为有效数据矩阵yg,构造Lm×1 缺失数据选择矩阵Sm,将缺失的数据矩阵组合成Lm× K 维矩阵,表示为缺失数据矩阵ym,有效数据矩阵yg 表达式及其对应的空时导向矢量表达式可表示为

则第l 个距离单元的有效数据协方差矩阵可以表示为
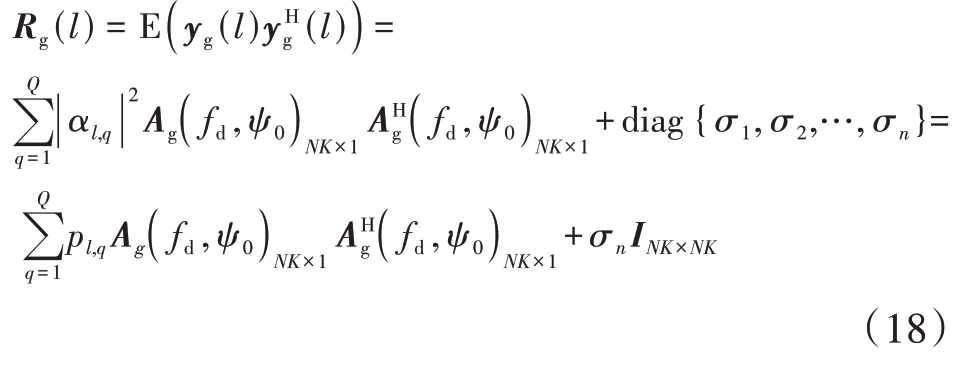
式中:![]() 被称为估计算子,是未知量;
被称为估计算子,是未知量;![]() 为每个网格对应的空时导向矢量;σn为接收机噪声功率,视为已知量。
为每个网格对应的空时导向矢量;σn为接收机噪声功率,视为已知量。
2)利用M-SPICE 算法求解估计算子和协方差矩阵
为了求解得到估计算子pl,q,可通过M-SPICE算法,优化求解其目标函数的最小值,其目标函数及约束条件如下[15]:
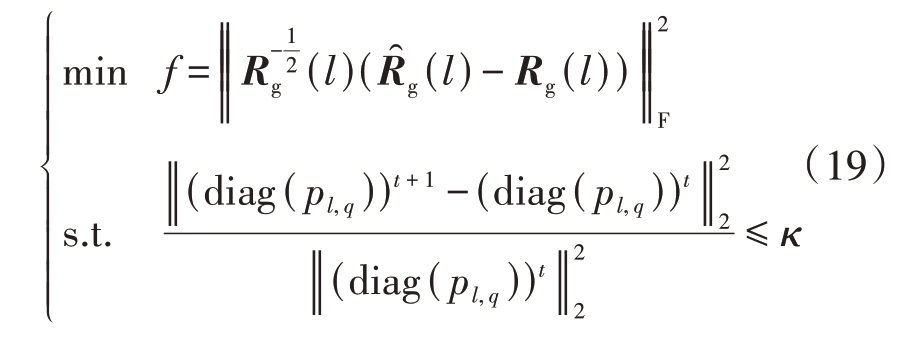
式中,diag(pl,q)为由估计算子pl,q 构成的空时二维谱的功率对角矩阵。为方便表示,将diag(pl,q)记为B,则式(19)可以表示为
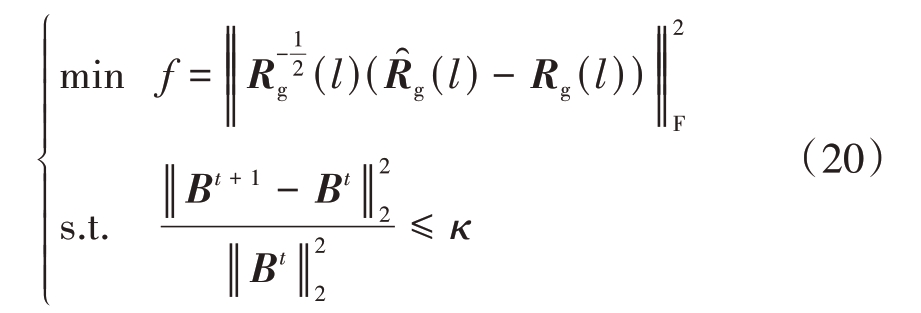
式中:f为M-SPICE 算法的目标函数;权矩阵![]() 为
为![]() 的平方根矩阵;κ 为M-SPICE 算法精度水平的阈值;
的平方根矩阵;κ 为M-SPICE 算法精度水平的阈值;![]() 为第l个距离单元有效数据矩阵的最大似然估计,其表达式为
为第l个距离单元有效数据矩阵的最大似然估计,其表达式为
将式(21)代入式(20)的目标函数中,并将Frobenius范数展开化简得到
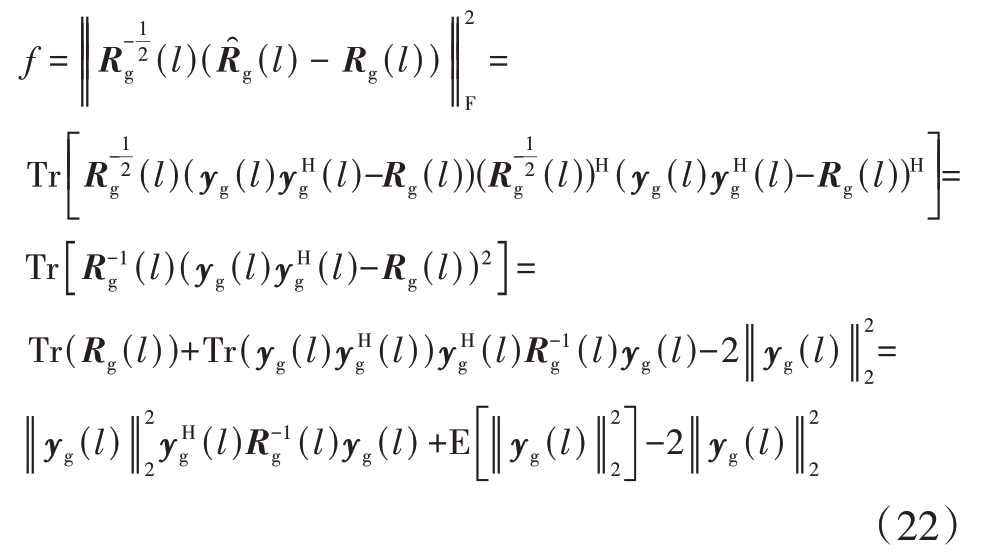
由于第l 个距离单元的有效数据矩阵yg(l)是由低空风切变目标和噪声叠加而成的,所以yg(l)的L2范数平方的数学期望可以表示为
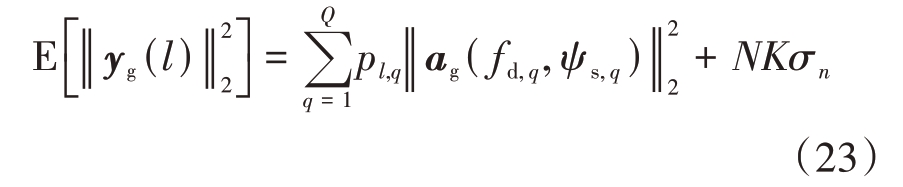
于是,进一步将目标函数f写为
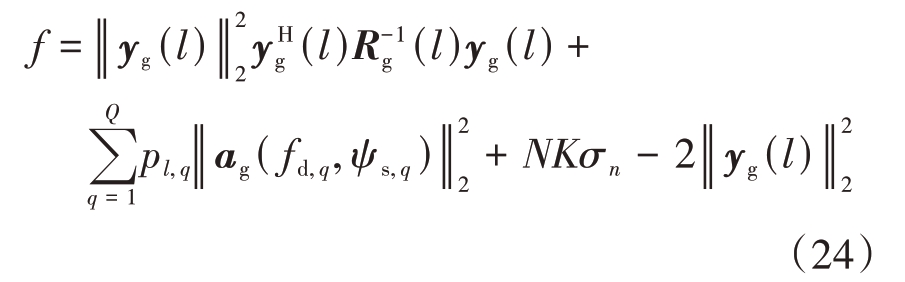
由于![]() 是已知的,可视为常数,为了简化计算,将式(24)两边同时除以
是已知的,可视为常数,为了简化计算,将式(24)两边同时除以![]() 得到
得到
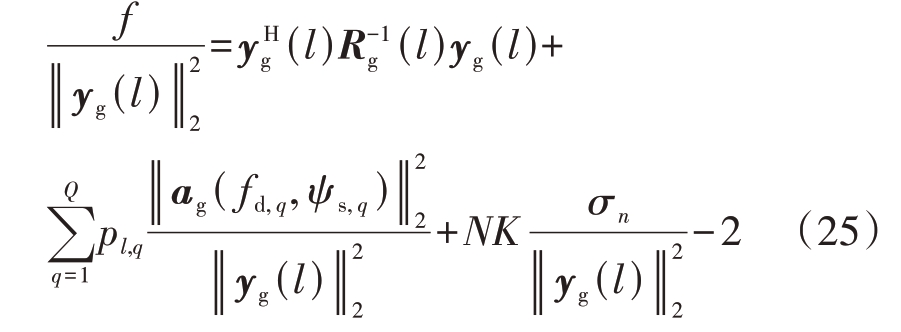
式(25)中后一项为常数,不影响求解式(24)最小值问题的结果,即可以忽略,从而将目标函数f 写成f1,表达式为
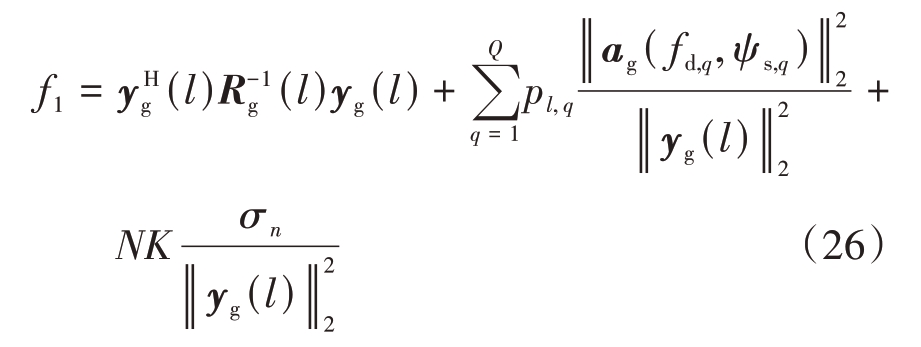
目标函数f1 是一个凸优化问题,根据Rojas 等人[16]的研究可知,求解式(26)的最小值问题可以转换为等式约束最优化问题:
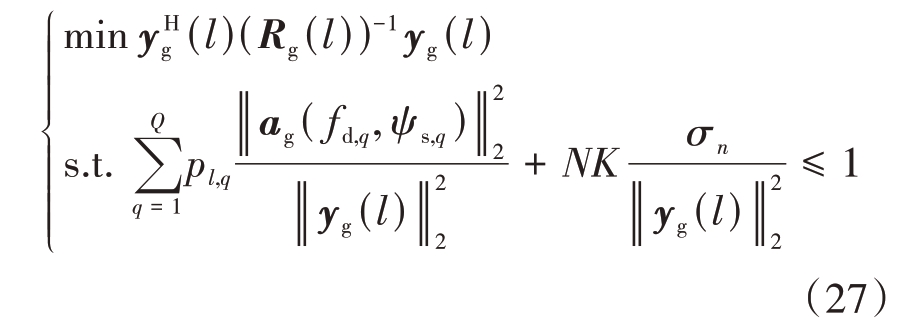
为了求解式(27),将式(27)中的有效数据协方差矩阵Rg(l)表示为[17]
式中,Θ=[Α1,ΙΝΚ]为一个由风切变信号和噪声组成的NK×(Q+ NK)维空时字典,则将式(28)代入到式(27)中,可以写为
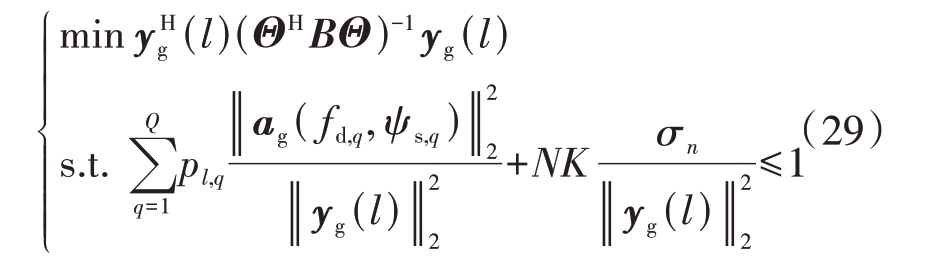
为了方便求解式(29)的最小值问题,引入一个新的矩阵Ψ:
即

将式(31)代入式(29)得
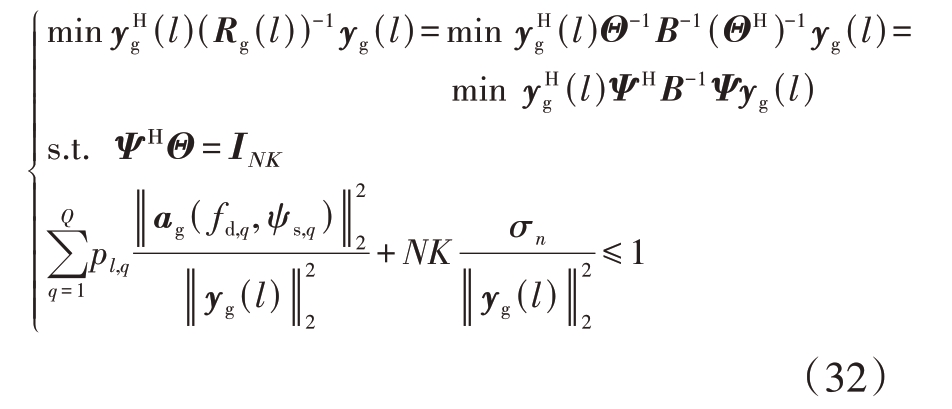
根据拉格朗日乘子法[18]和柯西瓦茨不等式[19],可得到该最小值问题的解为
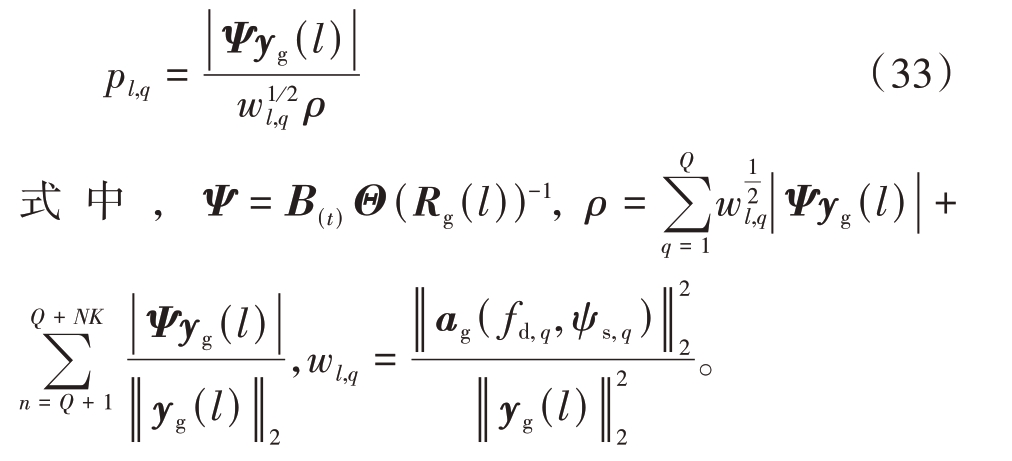
具体求解(Rg(l))(t)和B(t)的过程可以表示为
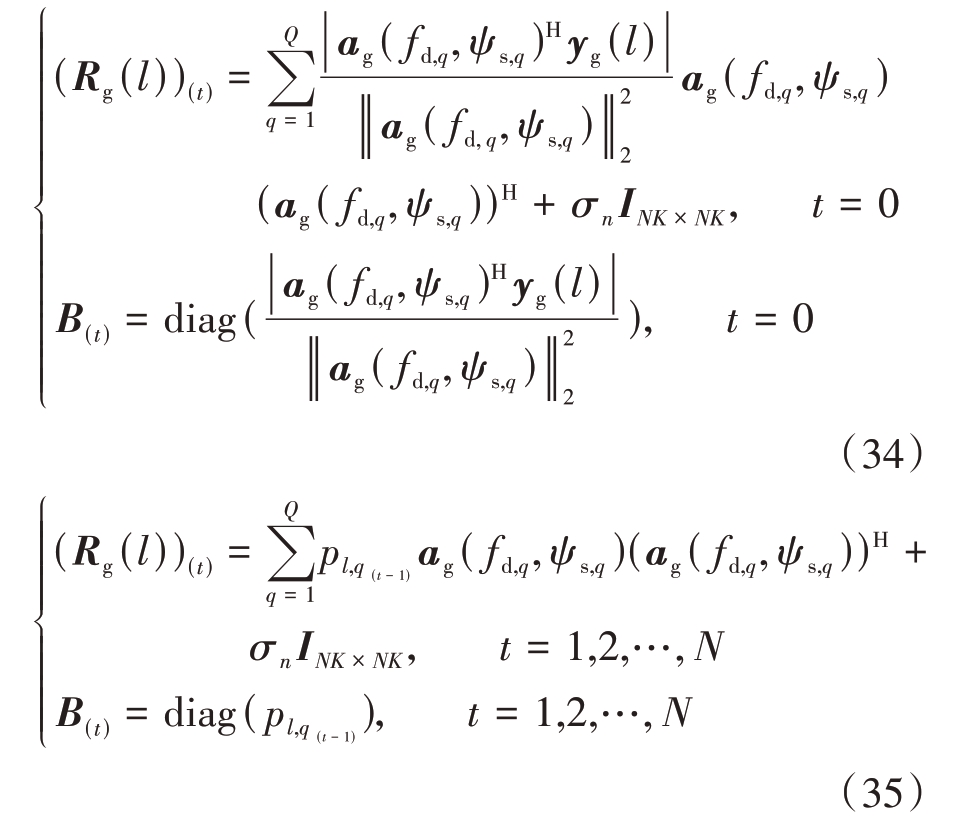
M-SPICE 算法首先通过式(34)计算得到初始值(Rg(l))(0)和B(0),然后根据式(33)得到![]() ;其次判断
;其次判断![]() 是否满足式(19)的约束条件,若满足则
是否满足式(19)的约束条件,若满足则![]() 为最终的估计算子,若不满足,则通过式(35)进行迭代,直到满足式(19)的约束条件终止迭代,即最后一次迭代得到的值
为最终的估计算子,若不满足,则通过式(35)进行迭代,直到满足式(19)的约束条件终止迭代,即最后一次迭代得到的值![]() 为所需的pl,q;最后将pl,q代入式(18)得到有效数据协方差矩阵。
为所需的pl,q;最后将pl,q代入式(18)得到有效数据协方差矩阵。
3)缺失数据时域恢复
有效数据和缺失数据在时域具有相同的谱成分,利用有效数据通过2.2 节优化目标函数不断迭代求解有效数据协方差矩阵,只需要用最后一次迭代值恢复缺失数据:
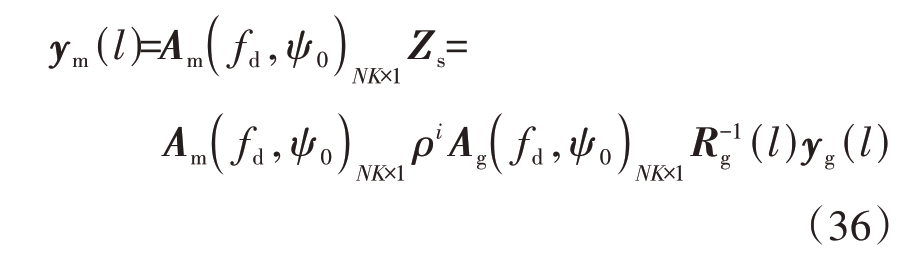
式中,![]() 是由缺失导向矢量构成的矩阵,可表示为
是由缺失导向矢量构成的矩阵,可表示为![]() 是式(33)中ρ第i次迭代得到的值。
是式(33)中ρ第i次迭代得到的值。
将恢复出来的缺失数据补全到缺失的距离单元,然后根据有效数据选择矩阵Sg 和缺失数据选择矩阵Sm 之间的关系![]() ,得到重建全数据
,得到重建全数据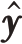 ̂。
̂。
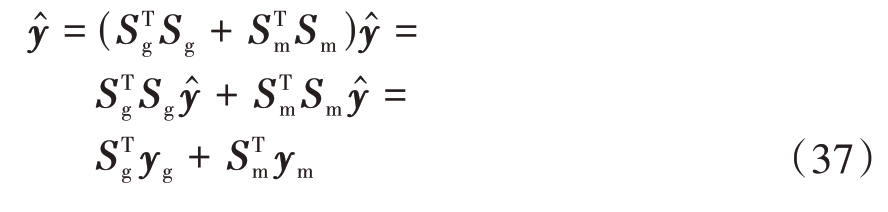
2.3 低空风切变风速估计
根据式(14)知,已经得到了抑制杂波后的最优权矢量ωl,发生缺失的低空风切变信号经过2.2节恢复后得到了完整的低空风切变信号,因此可以由以下表达式计算得到各个距离单元内的归一化多普勒频率:
第l 个距离单元的低空风切变风速估计结果为
3 方法流程
数据缺失情况下基于M-SPICE 的低空风切变风速估计方法流程图如图2所示。
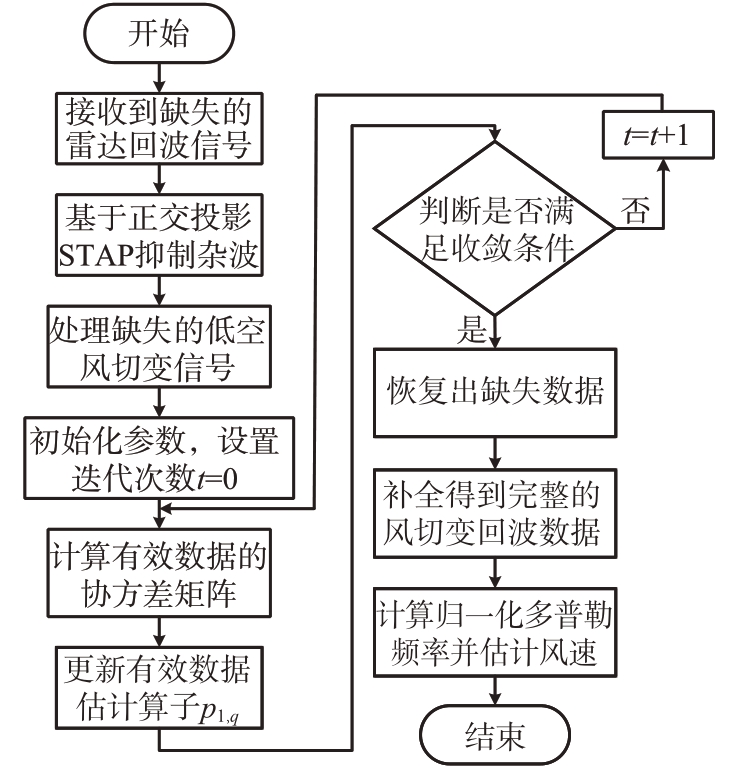
图2 数据缺失情况下基于M-SPICE的低空风切变风速估计方法流程图
4 仿真结果及分析
4.1 仿真条件描述
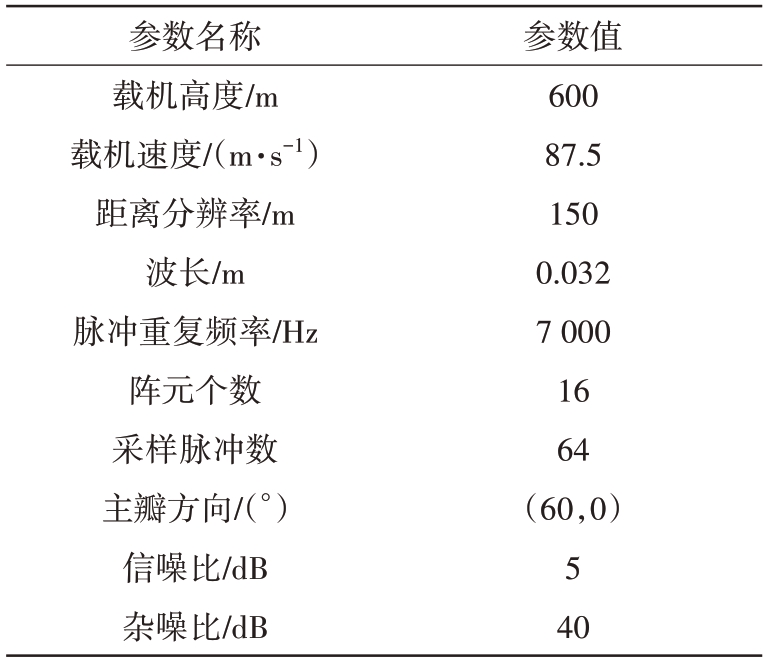
假设低空风切变场位于载机前方12.5 km 处,风场的水平风速范围为-50~50 m/s,实验仿真中其他参数如表1所示。
表1 载机和雷达主要仿真参数
参数名称载机高度/m载机速度/(m·s-1)距离分辨率/m波长/m脉冲重复频率/Hz阵元个数采样脉冲数主瓣方向/(°)信噪比/dB杂噪比/dB参数值600 87.5 150 0.032 7 000 16 64(60,0)5 40
4.2 仿真结果分析
图3为机载气象雷达回波信号的空时二维谱。从图3可以看出,地杂波回波信号在空时域呈半椭圆形分布,且地杂波回波信号功率强烈,主瓣方向尤为明显;低空风切变信号呈一条窄带分布于杂波主瓣位置处,分布范围小。由此可知,低空风切变回波信号相较于地杂波回波信号分布十分微弱,低空风切变回波信号多普勒信息几乎被地杂波回波信号所淹没,所以必须将地杂波回波信号完全消除,才能实现后续的低空风切变风速估计。
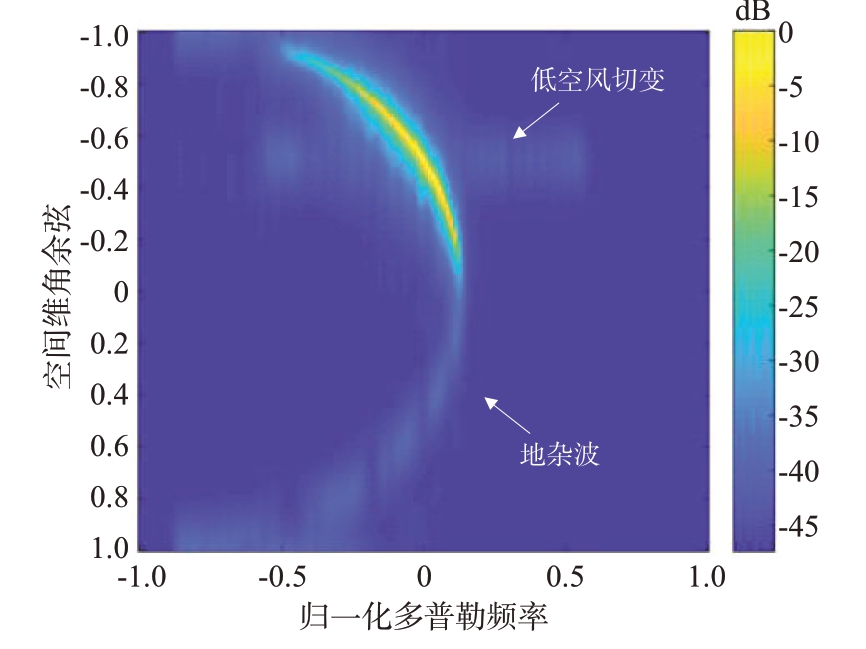
图3 机载气象雷达回波信号空时二维谱
图4所示为杂波抑制后的低空风切变信号距离多普勒。由图4可知,在零多普勒频率处形成明显的凹口,地杂波信号被完全抑制。低空风切变信号具有显著的反“S”型变化特征,但反“S”形状不连续,这意味着在抑制杂波时也抑制掉了部分低空风切变信号,导致部分距离单元的低空风切变数据缺失。
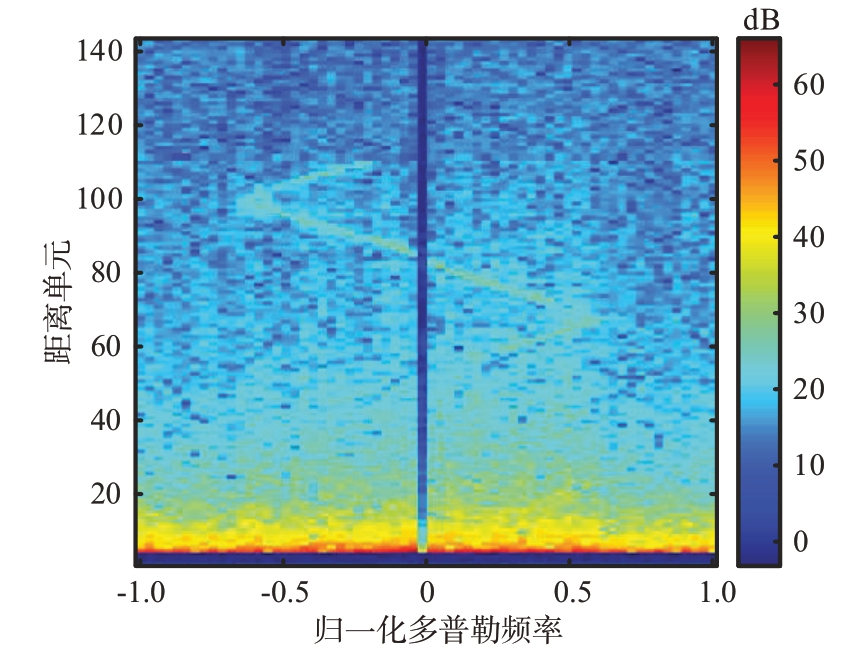
图4 杂波抑制后的低空风切变信号距离多普勒
图5所示为低空风切变数据缺失的风速估计结果图。从图5可以看出,与低空风切变信号的原始速度分布结果相比,部分距离单元的低空风切变信号发生缺失,进而导致风速估计的准确性大大降低,所以应该通过数据恢复方法,将缺失的数据恢复出来才能准确估计低空风切变风速。
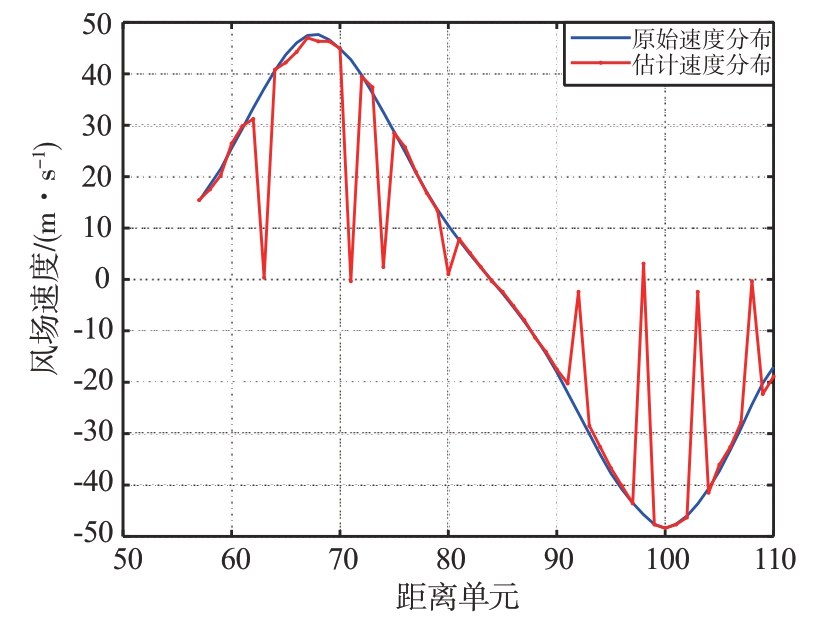
图5 低空风切变数据缺失的风速估计结果
图6 为基于M-SPICE 方法恢复缺失数据后的风速估计结果。可以看出缺失数据恢复后的风速估计值较贴合原始速度分布值,说明本文所提方法恢复精度高,风速估计结果较好。图7所示为第92号距离单元缺失数据恢复后的频谱图,从图7中能够直观看出,缺失的数据可以被完整恢复出来。
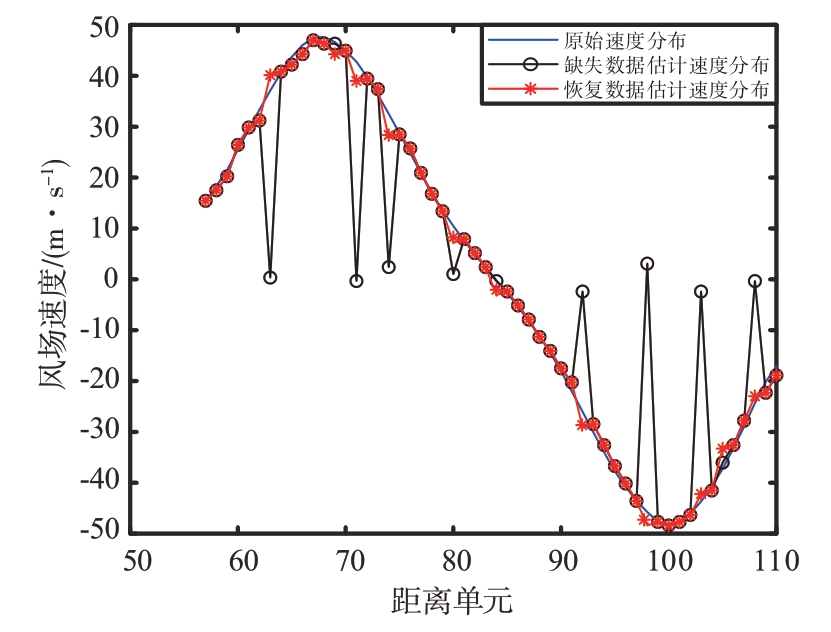
图6 基于M-SPICE方法恢复缺失数据后的风速估计结果
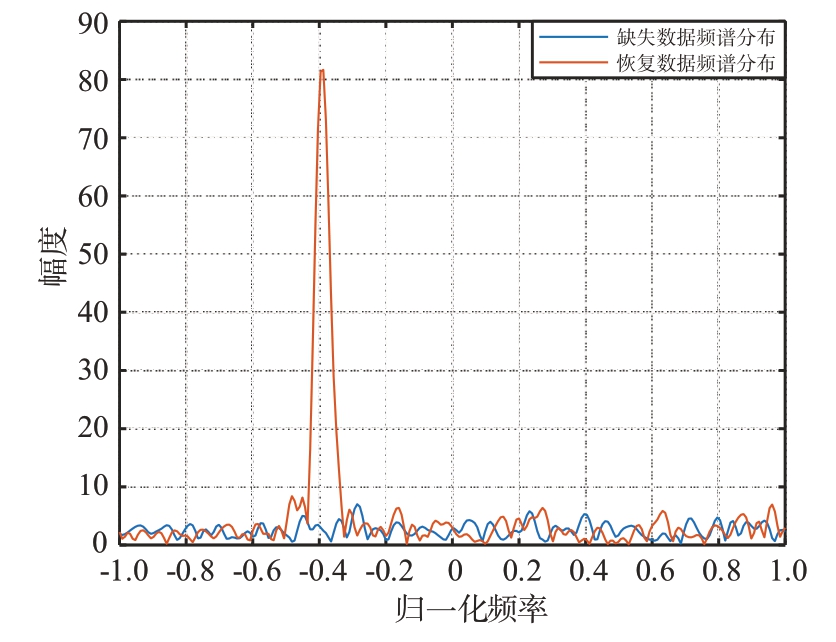
图7 第92号距离单元缺失数据恢复后的频谱分布
图8所示为本文方法、GAPES、MIAA 方法在同一数据缺失条件下的风速估计对比图。从图8 可以看出本文方法恢复缺失数据表现出良好的性能,可以准确估计风速且数据恢复精度更高。而GAPES、MIAA 方法恢复缺失数据的精度低,没有准确恢复出个别距离单元缺失的风切变信号,从而导致风速估计不准确。
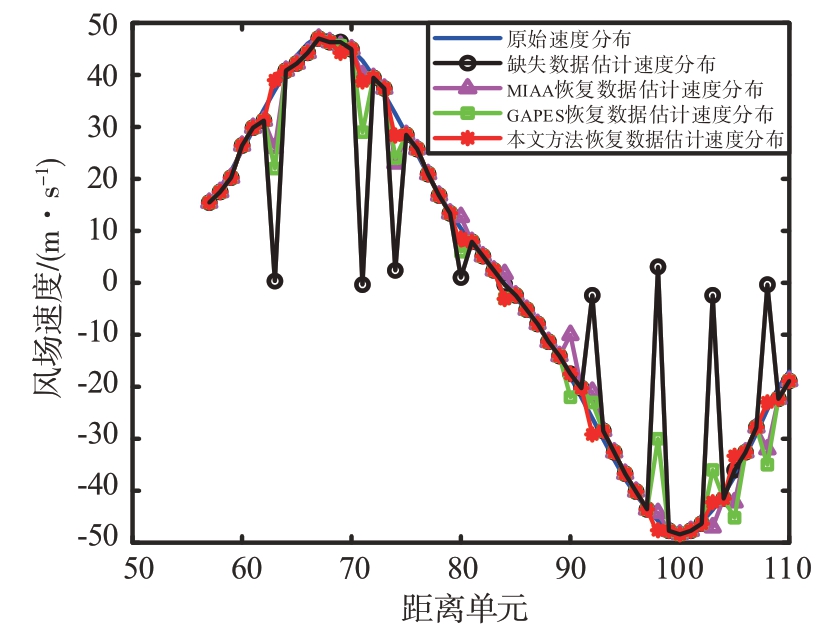
图8 不同恢复方法的低空风切变风速估计对比
表2所示为本文方法与GAPES、MIAA 方法完成缺失数据恢复后风速估计的运行时间对比,从表中可以看出其他两种方法由于迭代收敛速度慢,导致整个运行时间较慢,而本文方法因其循环最小化优势具有更快的迭代收敛速度,大大减少了运行时间。
表2 不同恢复方法运行时间对比
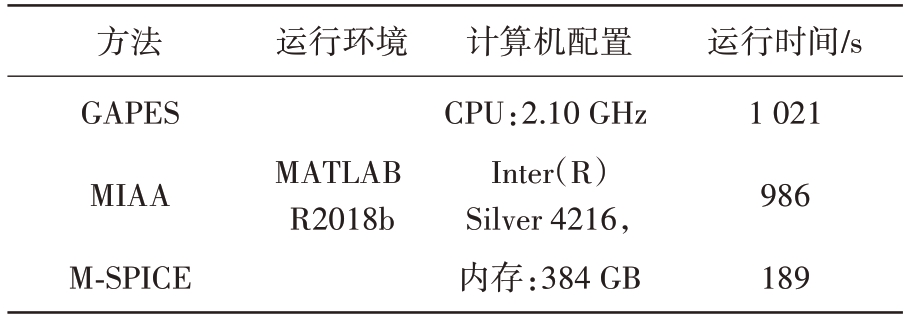
方法GAPES MIAA M-SPICE运行环境MATLAB R2018b计算机配置CPU:2.10 GHz Inter(R)Silver 4216,内存:384 GB运行时间/s 1 021 986 189
基于实际风速数据缺失分别对数据缺失的位置和不同缺失率这两种情况进行实验验证,并使用均方根误差和相对误差两个指标来评估MSPICE 方法的恢复性能,每组实验重复100 次,取均方根误差和相对误差的平均值。
图9 为风场数据在不同位置缺失时基于MSPICE算法恢复结果图,其中图9(a)为风场前半部分位置数据缺失恢复结果图,图9(b)为风场后半部分位置数据缺失恢复结果图,图9(c)为整个风场数据随机缺失恢复结果图。表3 为风场数据在不同位置缺失恢复后的均方根误差对比和相对误差对比,从表中可以看出,风场数据在不同位置缺失时,M-SPICE方法的均方根误差和相对误差变化较小,可以说明M-SPICE 方法在风场数据任何位置缺失情况下都能够较好地恢复出缺失数据。
表3 风场数据在不同位置缺失时基于M-SPICE算法的误差比较
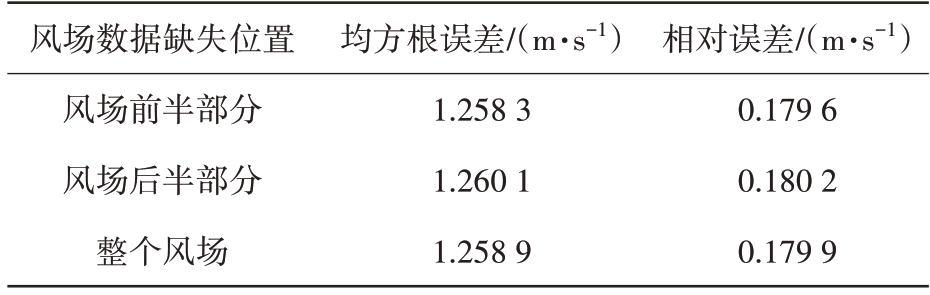
风场数据缺失位置风场前半部分风场后半部分整个风场均方根误差/(m·s-1)1.258 3 1.260 1 1.258 9相对误差/(m·s-1)0.179 6 0.180 2 0.179 9
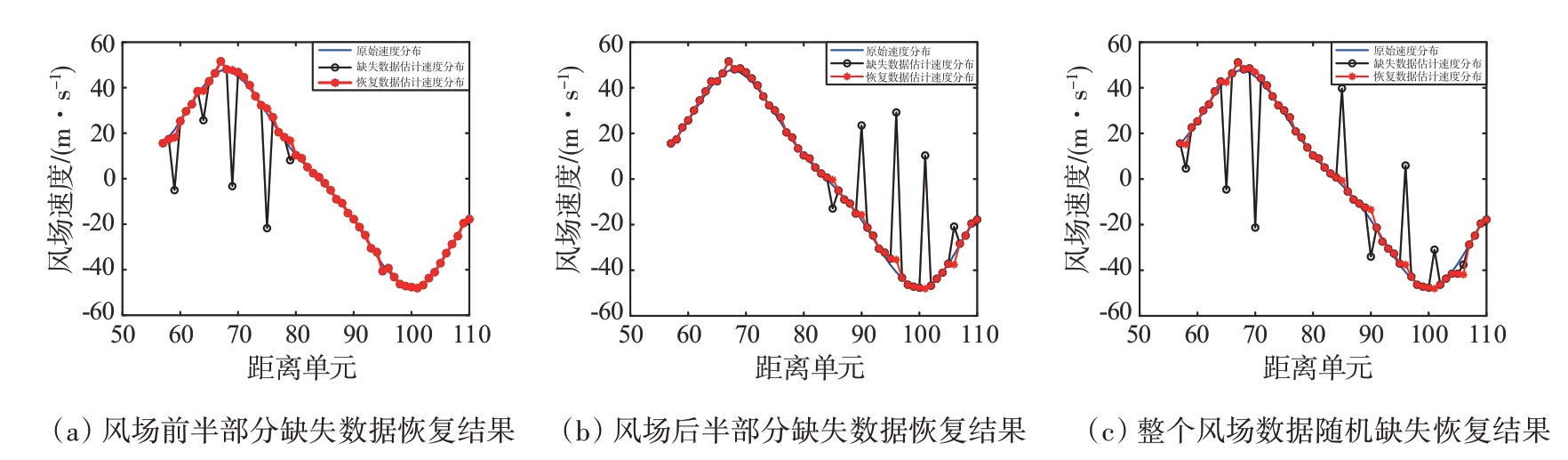
图9 风场数据在不同位置缺失时基于M-SPICE算法恢复结果
图10 为风场数据不同缺失率时基于M-SPICE算法恢复结果图,其中图10(a)为风场数据缺失率为5%时的恢复结果图,图10(b)为风场数据缺失率为10%时的恢复结果图,图10(c)为风场数据缺失率为20%时的恢复结果图。表4 为风场数据不同缺失率时恢复后的均方根误差对比和相对误差对比,从表中可以看出,随着数据缺失率的升高,MSPICE 方法的均方根误差和相对误差逐渐增大,但该方法仍能有效恢复出缺失数据,具有良好的数据恢复性能。
表4 风场数据不同缺失率时基于M-SPICE算法的误差比较

风场数据缺失率5%10%20%均方根误差/(m·s-1)1.208 3 1.255 7 1.348 4相对误差/(m·s-1)0.172 0 0.179 4 0.192 3
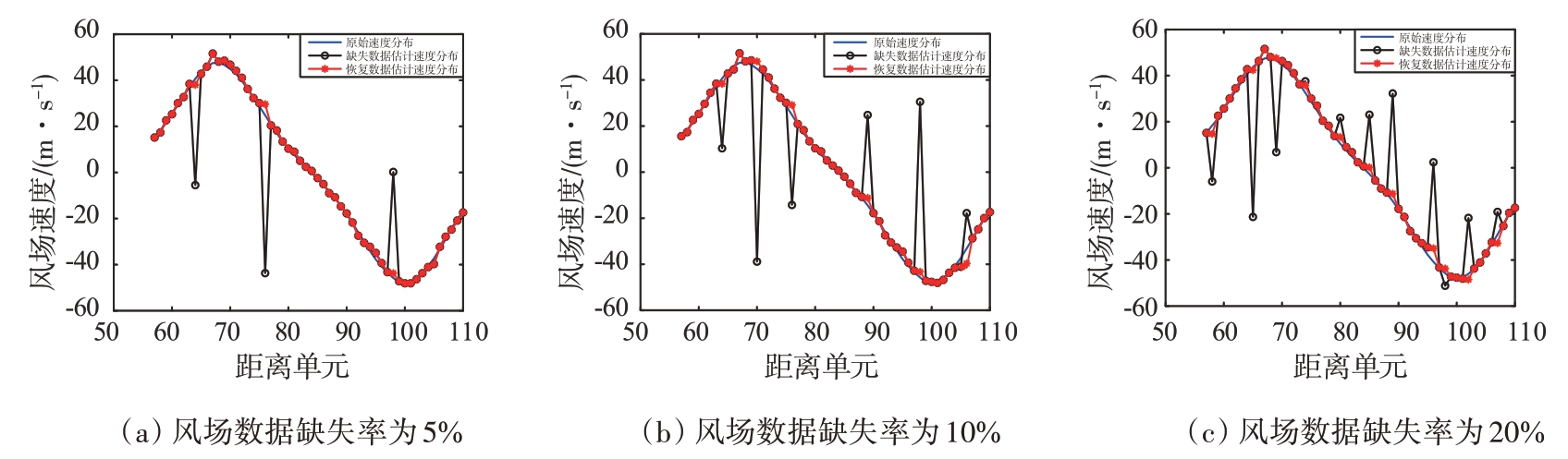
图10 风场数据不同缺失率时基于M-SPICE算法恢复结果
5 结束语
本文将稀疏迭代协方差算法应用到机载气象雷达缺失数据处理中,针对雷达回波数据缺失导致低空风切变风速估计不准问题,提出了一种基于缺失数据稀疏迭代协方差估计的低空风切变风速估计方法。该方法利用已知的有效数据,通过不断迭代得到的估计算子,恢复得到缺失的低空风切变信号,进而对风场速度进行精确估计。实验结果证明该方法可以高精度恢复出缺失的低空风切变信号,并且运算量小,相较于GAPES、MIAA两种恢复方法具有更少的运行时间。本文方法在雷达回波数据发生缺失的情况下,对于准确估计低空风切变风速具有实际意义。
[1]LI Hai,ZHENG Lei,MENG Fanwang.Low-Altitude Windshear Estimation Method Based on Four-Dimensional Frequency Domain Compensation for Fuselage Frustum Conformal Array[J].Sensors,2023,23(1):371.
[2]宋迪.基于RD-STAP 的线性调频连续波低空风切变检测方法研究[D].天津:中国民航大学,2020.
[3]刘琴,李明磊,汪玲,等.机载气象雷达目标的三维建模方法研究[J].雷达科学与技术,2022,20(4):435-441.
[4]李海,谢伶莉,张志宁.复杂地形环境下基于CL-KASTAP 的低空风切变风速估计方法[J].电子与信息学报,2021,43(12):3647-3655.
[5]李海,雍从建,范懿,等.幅相误差下基于CMCAP-JDL的低空风切变风速估计[J].信号处理,2020,36(4):502-510.
[6]李海,宋迪,呼延泽,等.LFMCW 体制下基于TDPC-JDL的低空风切变风速估计方法[J].系统工程与电子技术,2020,42(7):1504-1509.
[7]SCHWARZ U J.Mathematical-Statistical Description of the Iterative Beam Removing Technique(Method CLEAN)[J].Astronomy and Astrophysics,1978,65:345.
[8]LARSSON E G,STOICA P,LI Jian.Amplitude Spectrum Estimation for Two-Dimensional Gapped Data[J].IEEE Trans on Signal Processing,2002,50(6):1343-1354.
[9]STOICA P,LI Jian,LING Jun.Missing Data Recovery via a Nonparametric Iterative Adaptive Approach[J].IEEE Signal Processing Letters,2009,16(4):241-244.
[10]BRINGI V N,CHANDRASEKAR V.Polarimetric Doppler Weather Radar:Principles and Applications[M].UK:Cambridge University Press,2005.
[11]BOYER E,LARZABAL P,ADNET C,et al.Parametric Spectral Moments Estimation for Wind Profiling Radar[J].IEEE Trans on Geoscience &Remote Sensing,2003,41(8):1859-1868.
[12]黄凤青.基于子空间方法杂波抑制的慢动目标检测[D].桂林:桂林电子科技大学,2020.
[13]时艳玲,王磊,李君豪.基于投影空间下奇异值分解的海面小目标CFAR 检测[J].系统工程与电子技术,2022,44(2):512-519.
[14]STOICA P,LARSSON E G,LI Jian.Adaptive Filter-Bank Approach to Restoration and Spectral Analysis of Gapped Data[J].The Astronomical Journal,2000,120(4):2163-2173.
[15]STOICA P,BABU P,LI Jian.SPICE:A Sparse Covariance-Based Estimation Method for Array Processing[J].IEEE Trans on Signal Processing,2011,59(2):629-638.
[16]ROJAS C R,KATSELIS D,HJALMARSSON H.A Note on the SPICE Method[J].IEEE Trans on Signal Processing,2013,61(18):4545-4551.
[17]熊丹丹,刘剑锋,赵红景天,等.基于稀疏迭代协方差矩阵的谐波参数快速估计方法[J].信号处理,2021,37(8):1419-1429.
[18]STOICA P,BABU P,LI Jian.New Method of Sparse Parameter Estimation in Separable Models and Its Use for Spectral Analysis of Irregularly Sampled Data[J].IEEE Trans on Signal Processing,2010,59(1):35-47.
[19]欧阳顺湘.协方差不等式的若干证明及其注记——兼论大学数学各学科教学的融合[J].大学数学,2022,38(5):81-88.



