0 引言
无源双基地雷达（Passive Bistatic Radar,PBR）利用外辐射源发射的电磁波实现目标的探测［1］，其工作过程中不发射电磁波，具有电磁隐蔽性，因此对PBR 的探测与干扰是较为困难的。其次PBR 本身没有电磁波发射装置，相比于常规的有源雷达，其体积更小，机动性更强，造价更便宜。而针对电磁频谱拥挤环境下，PBR 工作不占用有限的频谱资源，是一种“绿色”雷达，近些年来，受到了广泛的关注［2］。
PBR 一般具备了两个通道，分别是参考通道和监视通道［3］。参考通道可以用于接收外辐射源发射的信号，而监视通道则用于接收经目标反射的回波信号。将参考通道的数据与监视通道的数据进行互模糊函数的计算，可以实现目标在距离延迟-多普勒频率二维平面上的检测［4］。监视通道中不可避免地会接收到外辐射源发射的信号，该信号传播距离短，且没有经过目标的反射，其功率常常远大于目标回波信号，从而构成了直达波干扰（Direct Path Interference,DPI）。若监视通道中存在DPI，在利用参考通道的数据进行互模糊函数计算中，会在距离延迟-多普勒频率二维平面上存在较大的干扰分量，极大影响了周围弱目标的检测性能。因此DPI 的抑制一直是PBR 信号处理中的重要问题［4-7］。
针对DPI 的抑制问题，目前有三种途径:一种是物理遮蔽法［8］，其是在外辐射源与接收机之间构建遮挡物，降低DPI 进入监视通道的功率；第二种是空域滤波法［9-11］，其是在接收端采用阵列天线，通过控制接收波束，减弱进入接收机的DPI 功率；第三种是时域滤波法［12-14］，其是以参考通道信号为期望信号，通过构建自适应滤波器对DPI 及其多径信号进行滤除。每种途径都能在一定程度上实现DPI 的抑制，而本文提出了一个新的DPI 抑制途径，即采用架设在接收机附近的智能反射表面（Intelligent Reflect Surface,IRS）实现接收通道中DPI的功率约束，并最大化反射回波功率。
智能反射表面［15］是一种无源低功耗器件，其最为突出的特色是能够通过低功耗的控制电路，实现对入射电磁波的反射方向的控制，目前针对智能反射面的应用主要面向6G 无线通信领域［16］，用来提高频谱利用效率［17］、物理层安全［18］、用户的感知与定位等方面［19-20］。在雷达通信一体化方向［21］，利用IRS可以保证用户通信质量的前提下实现目标的探测。IRS 也可以用于提高雷达的探测性能［22］，特别是在无视线（Non-Line of Sight,NLOS）情况下的目标探测问题引起了人们的重视［23］。截至目前，尚未见到相关公开文献将IRS应用于无源雷达的性能的改善。
本文的主要贡献是提出将IRS 应用于无源雷达中的直达波抑制的新技术途径，通过在监视通道附近放置一个无源IRS，可以将DPI 约束在一定范围内，最大化反射回波的功率。在本文第1节对IRS 辅助的PBR 的回波信号进行了建模。在第2节将DPI 抑制问题转换为一个非凸的二次约束二次规划（Quadratic Constrained Quadratic Programming,QCQP）问题，对于该问题采用坐标上升法［24］，将DPI 功率约束在指定范围内，最大化接收反射回波的功率。在第3 节对算法的性能进行了仿真分析，分析结果表明，在接收机附近放置中等尺寸的IRS，SINR 可以提升8 dB 左右。最后给出了全文的结论，并指出下一步研究的内容。
1 数据模型
考虑如图1所示的场景，外辐射源T 向空间发射电磁波信号，并假定该空间内存在目标P，监视通道接收机R 和智能反射表面S 用于目标的探测。监视通道接收机获得的信号主要是由外辐射源发射的信号经过4 条路径获得的:第1 条是直接从外辐射源T 到达监视通道接收机R 的直达波信号①，该信号也称之为直接路径干扰，其未经过反射，且传播路径端，路径损耗小。第2条是经过目标反射的回波信号②，该信号可用于目标的探测，由于该路径经过了一次反射，路径损耗较大，其功率远低于直接路径干扰。第3 条是经过智能反射表面反射的直接路径干扰信号③。第4 条首先经过目标反射后，再经过智能反射表面反射的回波信号④。这里假定IRS放置在监视通道接收机附近，考虑到路径损耗，忽略了首先经过IRS 反射，再经目标反射的回波。
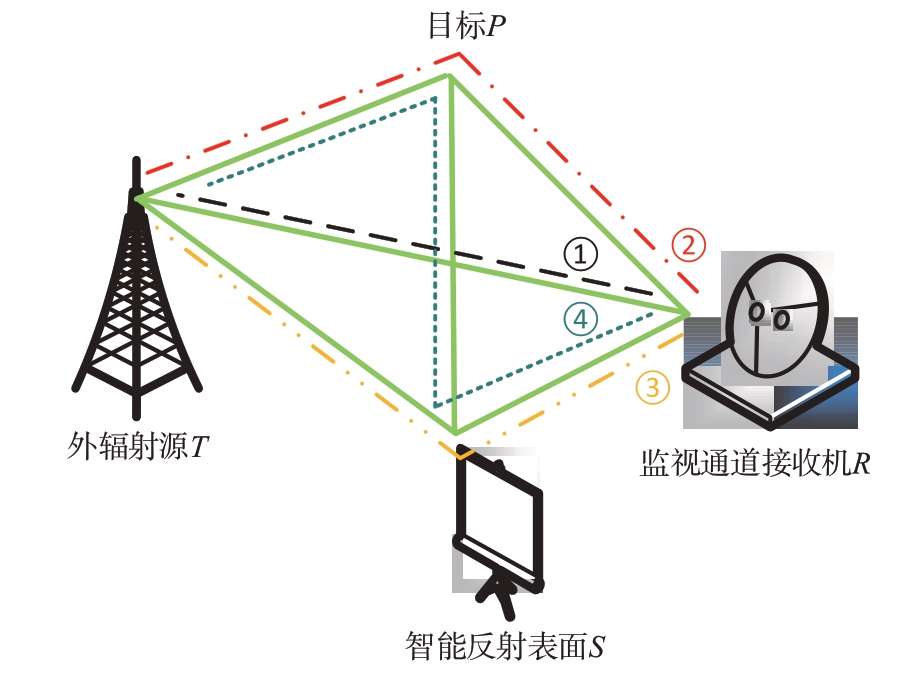
图1 IRS辅助PBR直达波抑制示意图
在上述考虑的场景中，信号③和信号④来自IRS 的反射信号，可以通过改变IRS 各个单元的相位实现对反射信号的控制。要进行DPI的抑制，可以通过优化IRS各个单元的相位，控制反射波的方向，使得IRS反射信号③能够在一定程度上抵消直达波信号①的同时，IRS 反射信号④能够与回波信号②通过相参累积得到增强。
结合上述分析，监视通道接收信号经过下变频后的基带信号可以表示为
式中下标分别对应接收的4 种类型的信号，n（t）为噪声信号。现对每个类型的信号进行分析。
对于信号①是直达波信号，其可以表示为
式中s（t）为外辐源发射的信号的基带形式，rTR表示外辐射源T 到监视通道接收机R 的距离，c 表示电磁波传播速度，该信号的复幅度α0可以利用雷达方程计算得到:
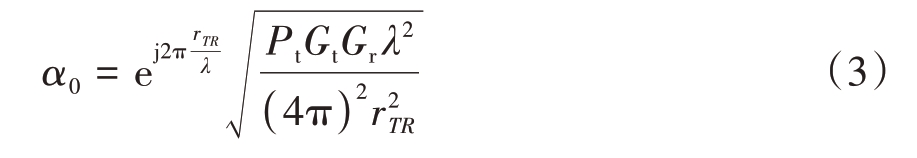
式中Pt为外辐射源发射机输出功率，Gt为外辐射源天线增益，这里假定外辐射源为全向天线，Gr为监视通道接收机天线增益，这里也假定为全向接收，λ表示雷达工作波长。
外辐射源发射的信号经过目标反射的回波信号②可以表示为
式中rTP和rPR分别是外辐射源T 到目标P 的距离，以及目标P 到监视通道接收机R 的距离。该信号的复幅度可以表示为
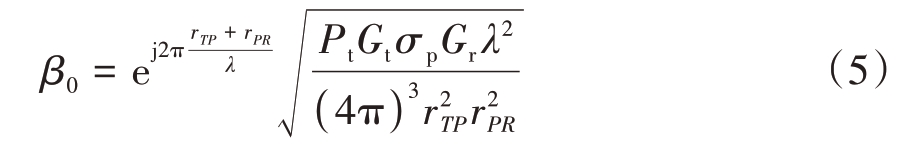
式中σp表示目标的雷达散射截面积。
外辐射源辐射的信号经过IRS 反射后进入接收机的信号③可以表示为
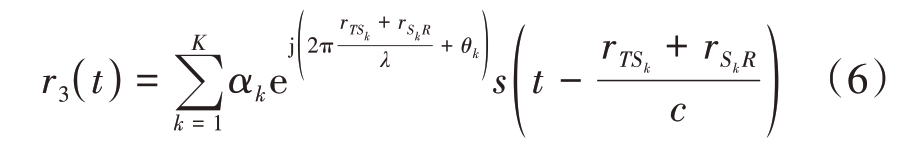
其中假定IRS 由K 个相位可控的单元构成，rTSk 和rSkR 分别是外辐射源T 到IRS 的第k 个单元的距离，以及IRS 的第k 个单元到监视通道接收机的距离，θk表示IRS 第k 个单元的相位值，信号幅度αk可以表示为
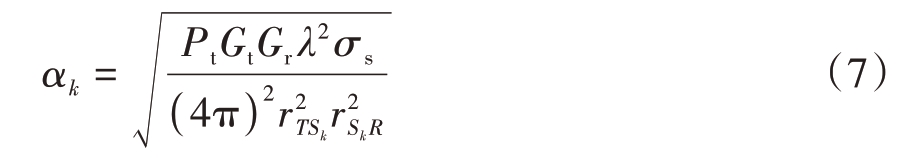
式中σs表示IRS每个单元的雷达散射截面积。
外辐射源发射的信号经过目标后，再经过IRS反射进入监视通道接收机的信号④可以表示为
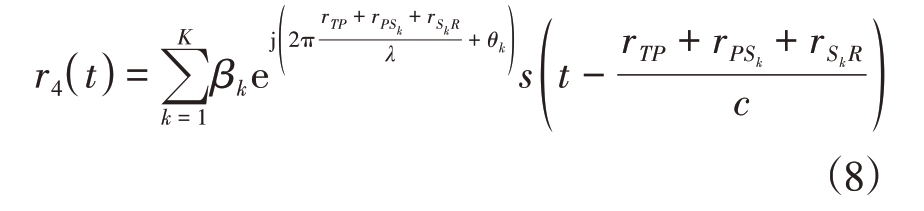
式中rPSk表示目标P 到IRS 的第k个单元的距离，该信号幅度βk可以表示为
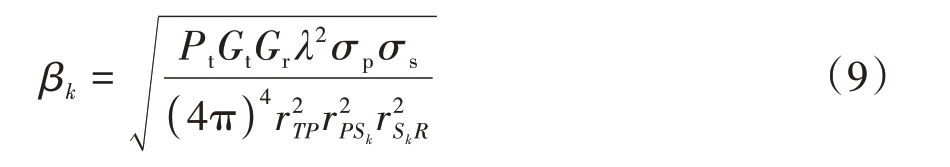
本文假定IRS 放置在靠近监视通道接收机附近，而且外辐射源发射的信号为窄带信号，经过IRS 不同单元反射信号的时间延迟对信号包络的幅度和时延的影响都可以忽略，那么经过IRS的反射信号③可以进一步表示为
式中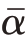
表示αk的平均值，并假定已知，且
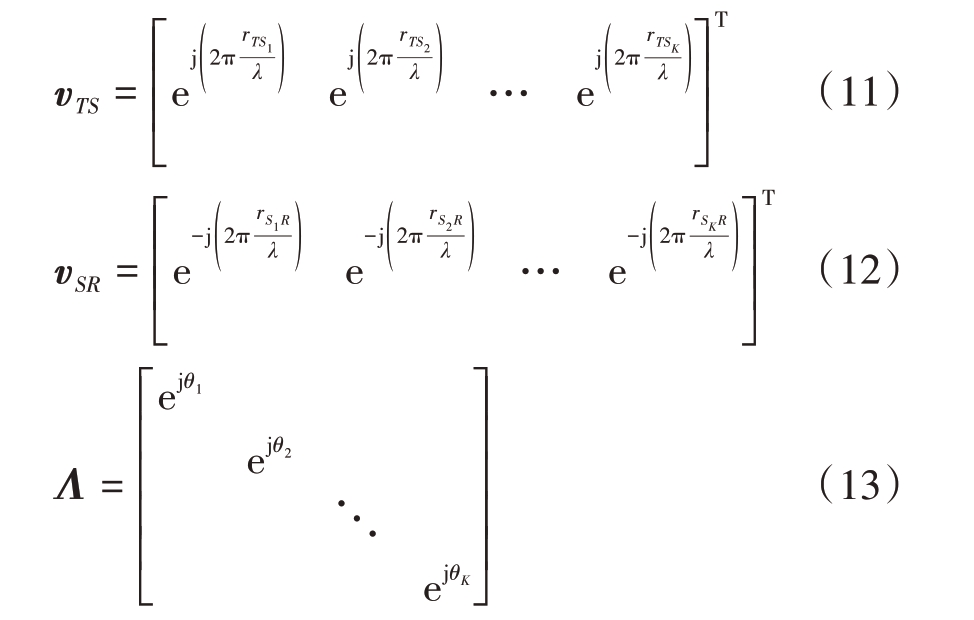
同理，信号④也可以进一步表示为
式中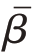
表示
的平均值，并假定已知，以及
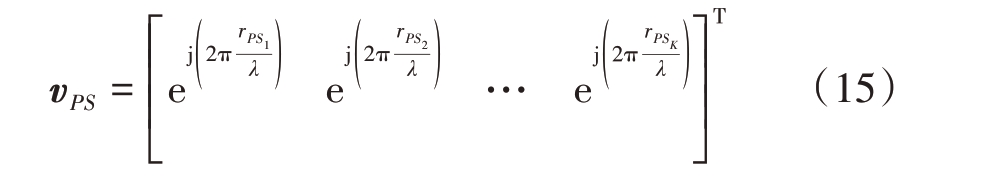
综上所述，监视通道接收的基带信号可以表示为
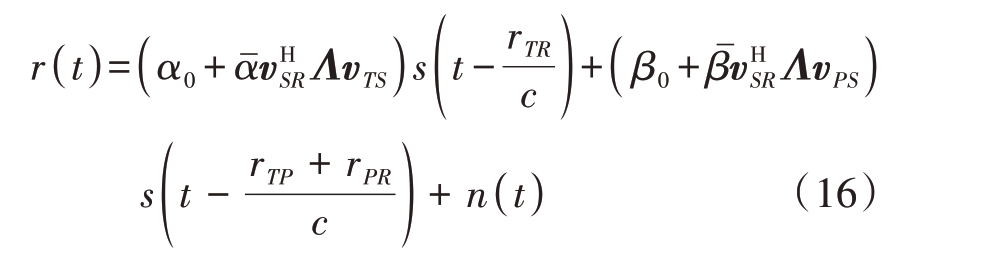
该信号由3 项构成，其中第1 项指的是DPI 分量，第2项指的是有用信号分量。虽然两个分量在时间上存在区别，但是考虑到DPI 的功率较强，即便经过互模糊计算，DPI的影响仍不能忽略。
2 DPI抑制
将IRS放置在监视通道接收机附近，使得监视通道的数据包含了可控分量，因此可以通过设计IRS的相位矩阵Λ减少DPI的分量，即优化问题为
该方法虽然可以保证监视通道接收数据中的DPI分量最小化，但同时可能导致有用信号分量功率损失。因此本文考虑在保持DPI 功率一定的约束条件下，有用信号分量的最大化问题。并进一步还考虑到RIS的相位并不能连续可调，因此相位值来自离散集合Ω:
式中M 为相位的离散程度，如M=2 表示相位只能取0或π。由此可以得到如下的优化问题:
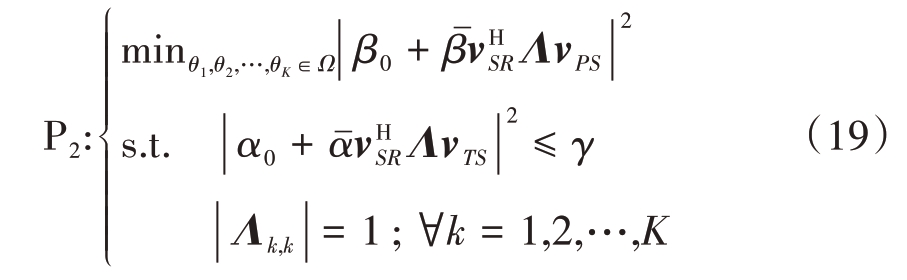
式中γ 表示约束值。该优化问题是二次约束二次规划问题，但是优化变量被约束为模1，因此该问题是一个非凸问题，常规的有效优化方法并不能直接适用。解决该问题的方法途径之一就是采用半定规划松弛（Semidefinite Relaxation,SDR）方法［25］，其基本思路是去掉对变量的模1 的约束，得到的最优解就是一个K 维方阵。如果该矩阵秩为1，那么就容易得到最优解，但通常情况下最优解的秩大于1，需要进行秩1分解，通常的解决办法是采用高斯随机化方法求得。得到的最终值还需要量化为离散的相位。第二种可行的方法是采用流形优化（Manifold Optimization,MO）的思路［26］，这是因为优化变量的模1 约束实际上定义了一个斜流形，通过计算该流形上的黎曼梯度，就可以确定搜索方向，再通过一定的操作，可以将更新的权值拉回（retraction）到流形上。本文结合IRS 的相位取离散值的特点，采用坐标上升（Coordinate Ascent,CA）法进行计算。
由于问题（19）是一个带有约束的优化问题，采用CA 方法也能得到较好的解决。CA 方法首先要在可行域内找到一个可行解，考虑到矩阵Λ 是对角矩阵，可以利用
式中
，符号⊙表示Hadamard 乘积，即对应元素相乘。为了更快找到一个可行解λ（0），可以利用投影矩阵构造:
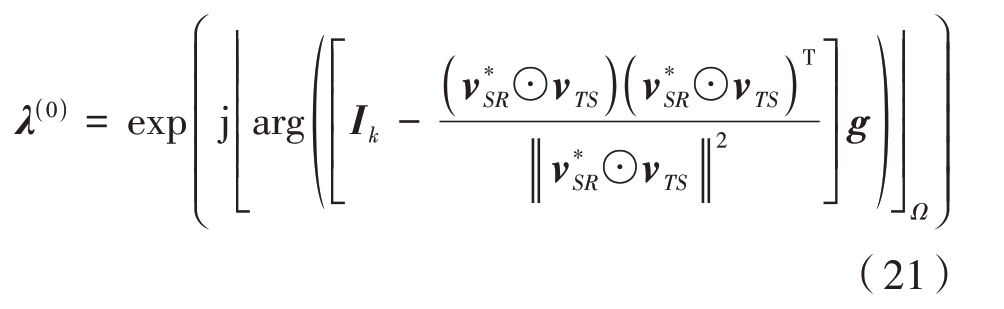
式中g 是一个单位协方差的零均值复高斯随机矢量。其基本思路是构造一个随机矢量，将其投影到与
正交的子空间上，从而使得
最小。IK是K×K 的单位矩阵，arg 算子表示计算复数的角度，𠃊𠃎Ω表示将相取集合Ω 中最接近的值。在获得初始解λ（0）后，还需代入到式（19）中约束条件进行验算，如果不满足约束条件，还需重新计算，直到获得一个初始可行解。
利用初始可行解λ（0），可以采用迭代的方法对可行解进行更新。具体而言就是对第n 次得到的可行解λ（n）的第k 个元素的相位分别取集合Ω 的值，然后代入到优化问题（19）中的约束条件中，如果满足可行解条件，就比较优化目标函数值，取最大值作为第k个元素的更新值，否则不对该分量进行更新。上述过程实际上就是求解如下优化问题:
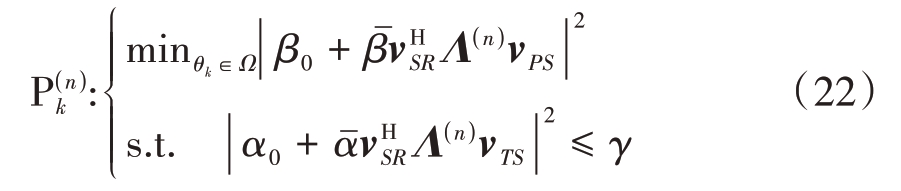
由于集合Ω 是离散的，因此很容易得到更新的可行解λ（n+1），当无法获得更好的可行解之后，可行解任何分量都不再更新，那么就得到了优化问题（19）的一个最优解。需要指出的是，坐标上升法得到的最优解不能保证是全局最优，其受初始可行解的影响较大，因此在实际操作中，往往需要随机化多个初始可行解进行分别计算，取目标函数值最大值对应的解作为最优解，从而可以获得更为稳定的性能。
3 仿真分析
在计算机仿真中，假设外辐射源辐射功率为200 W，发射天线增益为20 dB，监视通道天线采用全向接收，接收增益为0 dB，系统工作波长为0.1 m，目标的雷达散射截面积为1 m2，IRS 的每个单元的雷达散射截面积为0.01 m2。在距离设置上，外辐射源到监视通道接收机和IRS 距离均为10 km，到目标的距离为8 km；目标到接收机和IRS的距离为8 km。在缺省情况下，IRS 与监视通道接收机的距离为1 m，IRS 由K=50 个可控单元构成，每个可控单元的相位离散取值，离散程度M=30。在优化算法中，初始可行解随机取10 个值分别进行迭代计算，噪声功率假定为Pn，信号包络s（t）的功率为Ps。
为了评估优化效果，定义了信干噪声比:
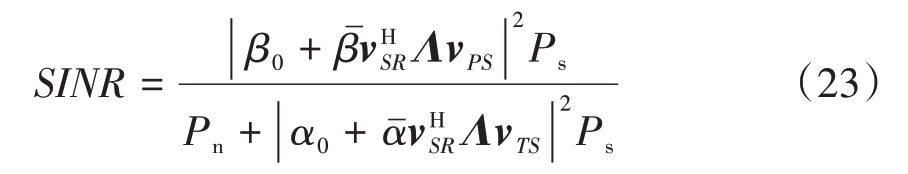
作为对比，考虑无IRS 辅助情况下的信噪比作为基准:
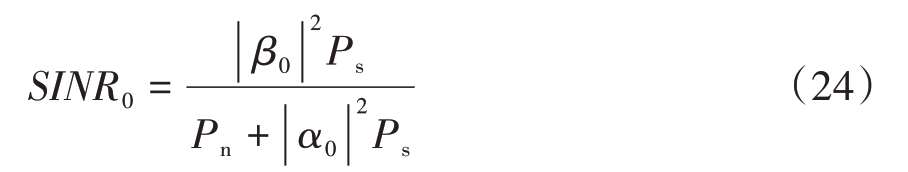
由此可以得到SINR 改善因子
。考虑另外两种反射面，一种是假定IRS各个相位是随机分布的情况（Rnd），从而可以模拟漫反射情况。另一种假定IRS 各个相位都为0，这样可以模拟镜面反射情况（Mir）。
首先分析IRS 的两个主要参数对SINR 改善因子的影响。考虑IRS 的各个阵元相位离散程度M的取值，从图2（a）可以看出，当M>4 之后，再增加M 的值，η 的变化趋于平稳，并且稳定在7～8 dB 附近。这说明在应用IRS 进行DPI 抑制时，IRS 并不需要连续的相位调整，而仅仅取少量几个离散的相位值就可以达到较好的效果，从而有利于简化控制电路，降低IRS的设计成本。IRS的尺寸越大，可以有更多的自由度控制DPI，为此图2（b）给出了仿真结果。可以看出，随着阵元个数K 的增大，η也得到了显著的增大。作为对比，即便阵元个数足够大，对于漫反射和镜面反射而言，对η 的贡献几乎可以忽略。这是因为增大阵元个数K，可以增加回波的强度，但如果不对IRS的阵元相位进行控制，DPI的强度也会增大。
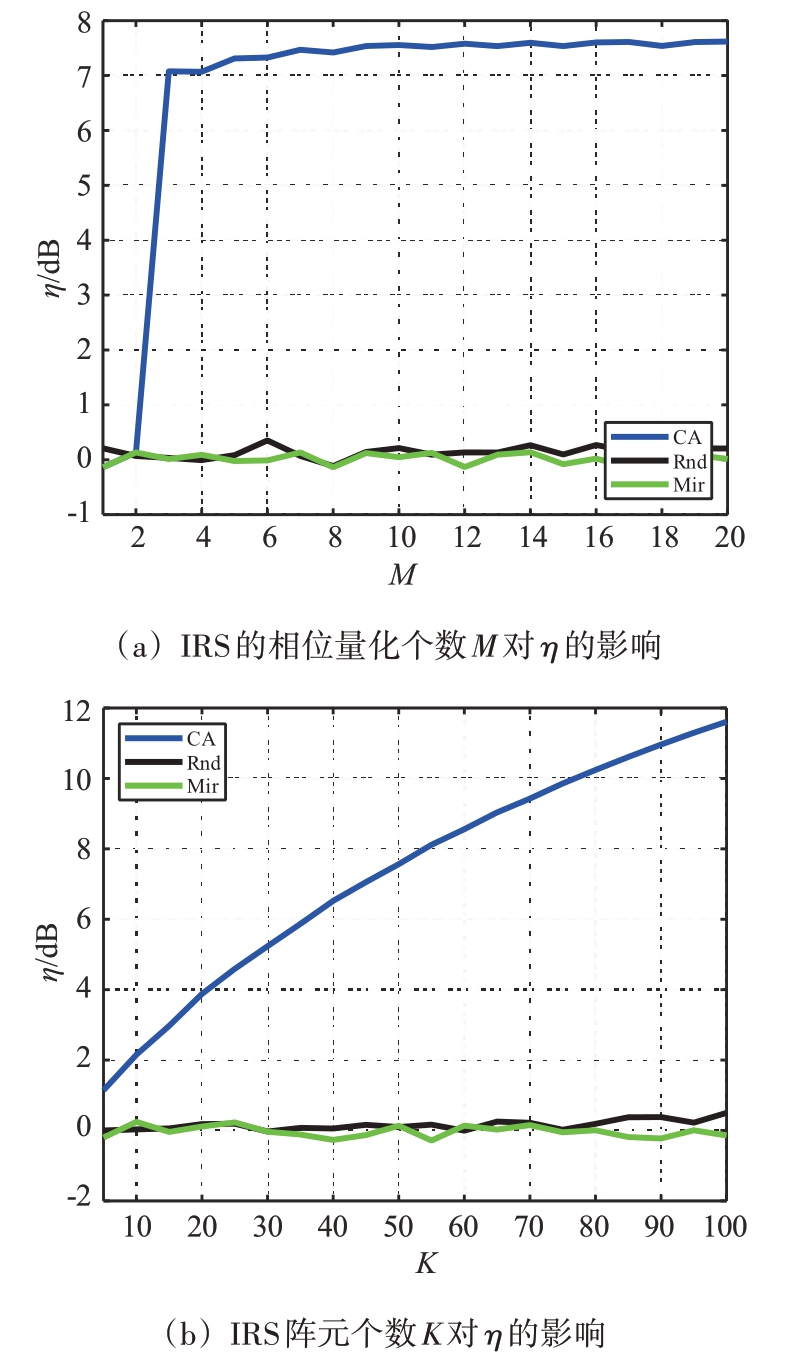
图2 IRS的主要参数对SINR改善因子的影响
本文假定IRS靠近监视通道接收机放置，为此需要分析IRS 与监视通道接收机的距离rSR对SINR改善因子的影响，其主要通过路径损耗产生了影响。仿真结果如图3所示。分析结果表明，IRS 越靠近接收机，获得的SINR 改善因子就越大。需要指出的是，对于漫反射表面，如果距离接收机足够近，也能获得少许的增益，但随着rSR的增大，会迅速衰减。镜面反射表面的放置不受rSR的影响，其主要与放置的方向有关。当然通过对IRS的优化，其改善因子明显优于其他两种情况。
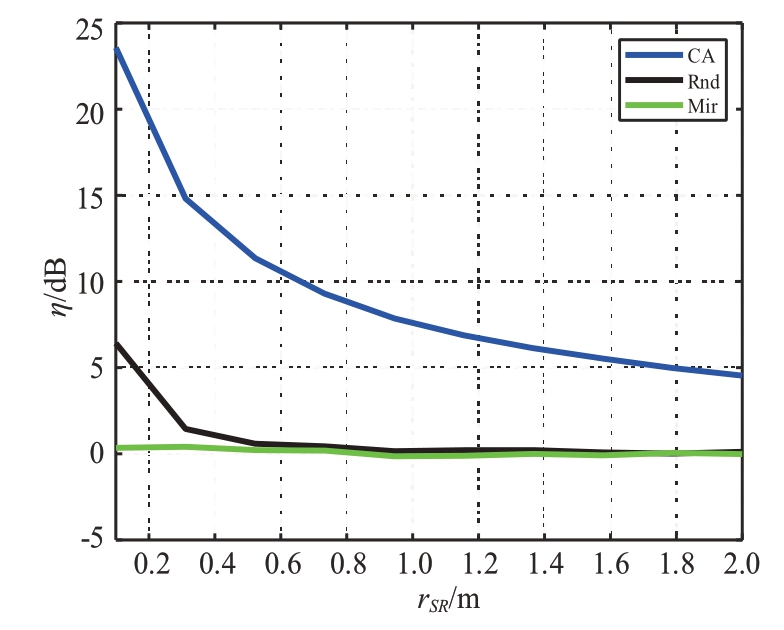
图3 IRS放置距离对SINR改善因子的影响
4 结束语
无源双基地雷达的直达波干扰的抑制是其信号处理的一项重要内容。本文提出了一种IRS 辅助的直达波干扰抑制方法，其本质上还是属于空域滤波方法。通过设置在监视通道附近的IRS，可以约束DPI分量的同时，最大化接收信号分量。从计算机仿真来看，对于中等尺寸的IRS，SINR 改善因子可以得到8 dB。如果进一步增大IRS 的阵元个数，或者进一步将IRS 靠近接收端，改善因子还可以进一步的提升。
需要指出的是，将IRS应用于无源双基地雷达的DPI抑制目前还处于初步研究阶段，因此文中考虑的都是一些理想条件下的情况，例如没有考虑到IRS的实际的物理特性［27］，如相位的控制与反射信号幅度之间可能存在关联。进一步采用有源IRS［28］，可以通过控制放大器增益调整反射信号的强度，可以为优化问题提供更多的自由度。
［1］GRIFFITHS H,BAKER C J.An Introduction to Passive Radar［M］.Norwood:Artech House,2017.
［2］MELVIN W L,SCHEER J A.Principles of Modern Radar［M］.London:Scitech Publishing,2014.
［3］KUSCHEL H,CRISTALLINI D,OLSEN K E.Tutorial:Passive Radar Tutorial［J］.IEEE Aerospace and Electronic Systems Magazine,2019,34（2）:1-19.
［4］MALANOWSKI M.Signal Processing for Passive Bistatic Radar［M］.Norwood:Artech House,2019.
［5］ZHANG Xin,LI Hongbin,HIMED B.A Direct-Path Interference Resistant Passive Detector［J］.IEEE Signal Processing Letters,2017,24（6）:818-822.
［6］FAZLOLLAHPOOR M,DERAKHTIAN M,KHORSHIDI S.Rao Detector for Passive MIMO Radar with Direct-Path Interference［J］.IEEE Trans on Aerospace and Electronic Systems,2020,56（4）:2999-3009.
［7］JING Tong,HUANG Gaoming,TIAN Wei,et al.Cramér-Rao Lower Bound Analysis for Stochastic Model Based Target Parameter Estimation in Multistatic Passive Radar with Direct-Path Interference［J］.IEEE Access,2019,7:106761-106772.
［8］WATSON B C,GUERCI J R.Non-Line-of-Sight Radar［M］.Norwood:Artech House,2019.
［9］GAO Yongchan,LI Hongbin,HIMED B.Joint Transmit and Receive Beamforming for Hybrid Active-Passive Radar［J］.IEEE Signal Processing Letters,2017,24（6）:779-783.
［10］CHABRIEL G,BARRÈRE J.Adaptive Target Detection Techniques for OFDM-Based Passive Radar Exploiting Spatial Diversity［J］.IEEE Trans on Signal Processing,2017,65（22）:5873-5884.
［11］SHEN Ji,YI Jianxin,WAN Xianrong,et al.Robust DOA Estimation for Passive Radar with Target Signals Mixed in the Reference Channel［J］.IEEE Geoscience and Remote Sensing Letters,2021,18（3）:456-460.
［12］GARRY J L,BAKER C J,SMITH G E.Evaluation of Direct Signal Suppression for Passive Radar［J］.IEEE Trans on Geoscience and Remote Sensing,2017,55（7）:3786-3799.
［13］MELLER M.Cheap Cancellation of Strong Echoes for Digital Passive and Noise Radars［J］.IEEE Trans on Signal Processing,2012,60（5）:2654-2659.
［14］MA Yahui,SHAN Tao,ZHANG Yimin,et al.A Novel Two-Dimensional Sparse-Weight NLMS Filtering Scheme for Passive Bistatic Radar［J］.IEEE Geoscience and Remote Sensing Letters,2016,13（5）:676-680.
［15］ZHANG Hongliang,DI Boya,SONG Lingyang.Reconfigurable Intelligent Surface-Empowered 6G［M］.Berlin:Springer,2022.
［16］崔铁军，金石，章嘉懿，等.智能超表面技术研究报告［R］.IMT-2030（6G）推进组，2021.
［17］MONDAL A,AL JUNAEDI A M,SINGH K,et al.Spectrum and Energy-Efficiency Maximization in RIS-Aided IoT Networks［J］.IEEE Access,2022,10:103538-103551.
［18］WEI Lai,WANG Kezhi,PAN Cunhua,et al.Secrecy Performance Analysis of RIS-Aided Communication System with Randomly Flying Eavesdroppers［J］.IEEE Wireless Communications Letters,2022,11（10）:2240-2244.
［19］PAN Cunhua,ZHOU Gui,ZHI Kangda,et al.An Overview of Signal Processing Techniques for RIS/IRS-Aided Wireless Systems［J］.IEEE Journal of Selected Topics in Signal Processing,2022,16（5）:883-917.
［20］ZHANG Hongliang.Joint Waveform and Phase Shift Design for RIS-Assisted Integrated Sensing and Communication Based on Mutual Information［J］.IEEE Communications Letters,2022,26（10）:2317-2321.
［21］LIU Rang,LI Ming,LIU Yang,et al.Joint Transmit Waveform and Passive Beamforming Design for RIS-Aided DFRC Systems［J］.IEEE Journal of Selected Topics in Signal Processing,2022,16（5）:995-1010.
［22］BUZZI S,GROSSI E,LOPS M,et al.Foundations of MIMO Radar Detection Aided by Reconfigurable Intelligent Surfaces［J］.IEEE Trans on Signal Processing,2022,70:1749-1763.
［23］SOLOMITCKII D,HEINO M,BUDDAPPAGARI S,et al.Radar Scheme with Raised Reflector for NLOS Vehicle Detection［J］.IEEE Trans on Intelligent Transportation Systems,2021,23（7）:9037-9045.
［24］ZHANG Dingcai,WU Qingqing,CUI Miao,et al.Throughput Maximization for IRS-Assisted Wireless Powered Hybrid NOMA and TDMA［J］.IEEE Wireless Communications Letters,2021,10（9）:1944-1948.
［25］WANG Fangzhou,LI Hongbin,FANG Jun.Joint Active and Passive Beamforming for IRS-Assisted Radar［J］.IEEE Signal Processing Letters,2022,29:349-353.
［26］JIANG Zhengming,RIHAN M,ZHANG Peichang,et al.Intelligent Reflecting Surface Aided Dual-Function Radar and Communication System［J］.IEEE Systems Journal,2022,16（1）:475-486.
［27］ÖZDOGAN Ö,BJÖRNSON E,LARSSON E G.Intelligent Reflecting Surfaces:Physics,Propagation,and Pathloss Modeling［J］.IEEE Wireless Communications Letters,2020,9（5）:581-585.
［28］RIHAN M,GROSSI E,VENTURINO L,et al.Spatial Diversity in Radar Detection via Active Reconfigurable Intelligent Surfaces［J］.IEEE Signal Processing Letters,2022,29:1242-1246.
