0 引言
雷达是信息化战争中的重要预警装备,常年担负着战斗值班,时刻守卫着国土安全,平时即是战时。为了提高雷达的任务执行率和作战性能完好性,雷达预测性维护在雷达维修中越来越受重视。雷达功放组件是固态雷达发射机的重要组成部分,相较雷达其他现场可更换单元(Local Replaceable Unit,LRU)故障率高,是预测性维护的主要内容之一。目前雷达功放组件的维修主要以换件修理为主。若能在雷达的日、周、月等维护中提前更换即将故障的功放组件,即实现功放组件的预测性维护必将大大提升维护的针对性和有效性。为此,需要对功放组件的参数进行监测和预测。对于现代雷达系统,要监测和预测每个LRU的所有参数几乎是不可能的,若能找出一个或几个可直接测量的参数进行监测及预测,就可将监测节点降低到可接受程度的同时可靠地预测雷达各部分出现的故障,并在维护中预先更换备件[1]。输出功率是衡量功放组件是否故障的重要指标,很多雷达以输出功率的大小来设置功放组件故障阈值,故对功放组件的输出功率预测进行研究对雷达的预测性维护具有重要意义。
从公开发表的成果来看,部分文献对雷达指标和性能参数预测进行了研究[2-6]。其中,文献[2]利用一种改进的灰色模型预测了雷达的备件消耗;文献[3]和[4]分别利用差分整合移动平均自回归模型(Autoregressive Integrated Moving Average model,ARIMA)和长短期记忆网络(Long Short-Term Memory,LSTM)模型预测了某船用雷达的发射功率;文献[5]利用ARIMA模型和径向基函数神经网络(Radial Basis Function Neural Network,RBFNN)模型预测了某雷达的发射功率;文献[6]利用离散输入过程神经网络(Discrete Process Neural Network,DPNN)模型预测了某雷达激光测距机的相关参数。但上述研究的样本数据变化趋势平缓,与本文实际监测到的雷达功放组件输出功率变化特征不符,且预测时长偏短没有考虑保障实际对预测时长的要求。为此,本文通过多个功放组件全寿命周期输出功率监测数据,重点研究不同变化趋势下预测时长与预测精度的关系,旨在为实现功放组件的预测性维护提供一定的参考。由于功放组件输出功率数据是典型的时间序列,而ARIMA 模型和神经网络中的深度学习模型LSTM在预测时间序列上具有优势,故本文采用ARIMA模型和LSTM模型进行功放组件输出功率预测。
1 预测模型
1.1 ARIMA模型
ARIMA(p, d, q)模型是自回归(Auto Regression,AR)模型、移动平均模型(Moving Average,MA)和差分法的结合,包含p、d、q 三个参数,其中p 为AR 模型参数,d为对数据进行差分的阶数,q为MA模型参数。
1)AR模型
AR 模型可描述当前值与历史值之间的关系,用变量自身的历史时间数据对自身进行预测,一个p阶AR模型可写为
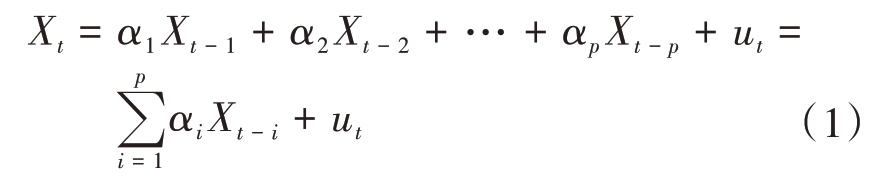
式中:Xt为t时刻的值;p 为AR 模型的阶数,表示用几期的历史值来预测当前值;αi 为模型参数;ut 为随机扰动项。
AR 模型要求时间序列数据必须具有平稳性且预测值与前期历史值具有相关性。
2)MA模型
如果AR 模型中的随机扰动项ut 是白噪声,则称AR(p)为一个纯自回归过程;如果ut不是一个白噪声,则通常认为它是一个q阶的移动平均,即为
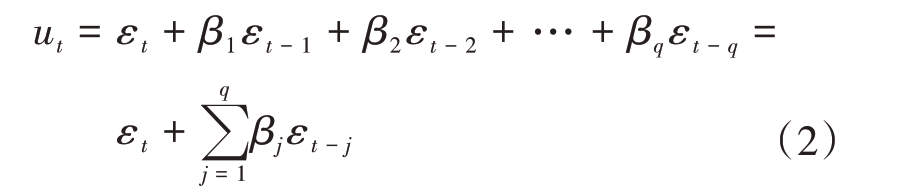
式中:εt 为白噪声;q 为MA 模型的阶数;βj 为模型参数。
当AR 模型中Xt= ut,表示时间序列的当前值与历史值没有关系,只依赖历史白噪声的线性组合,此时AR模型就变为MA模型。
3)ARIMA模型
将AR(p)模型和MA(q)模型进行组合就得到了一个自回归移动平均模型ARMA(p,q):
式(3)表示:一个随机时间序列可通过一个ARMA(p, q)模型来表示,即该序列可由其自身的过去或者滞后值以及随机扰动项来解释;如果时间序列是平稳的,即它的行为不会随着时间的推移而变化,则可通过该序列的过去行为来预测未来。
当需要预测的时间序列不满足平稳性时,可以通过差分法得到平稳序列,即对于非平稳时间序列可先进行d阶差分,转化为平稳时间序列后再利用ARMA(p,q)模型进行预测。故ARIMA(p,d,q)模型就是AR(p)模型、MA(q)模型和d 阶差分法的结合。
1.2 LSTM 模型
LSTM 是一种特殊的循环神经网络(Recurrent Neural Network,RNN)。典型的RNN 模型结构如图1所示,左边为RNN 模型折叠结构,右边为RNN模型展开结构。RNN 模型的特殊之处在于同一层各个节点之间也存在连接关系,即隐藏层中各个节点的输入由两部分组成:前一时刻的状态和现在时刻的输入,这种特殊的结构使得RNN 具有使用和挖掘序列间信息特征的能力,可以用公式表示为
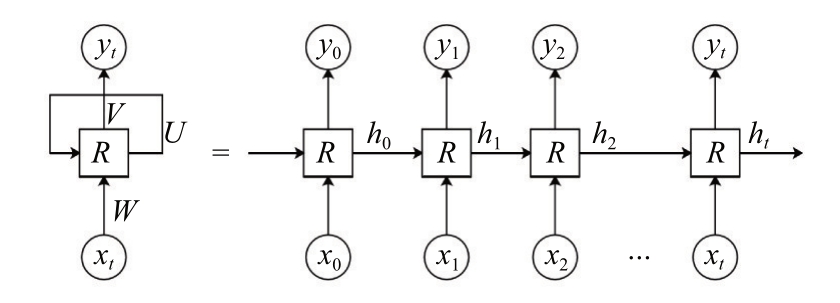
图1 RNN模型结构
式中:ht 为隐藏层节点当前状态值;f 为非线性激活函数,通常为线性整流函数relu(x)=max(0,x)或双曲正切函数tanh(x)=(ex-e-x)/(ex+e-x);U为隐藏层到隐藏层之间的权重连接矩阵;W 为输入层到隐藏层之间的权重连接矩阵。
RNN各节点的输出为
式中:yt 为节点输出值;g 为非线性激活函数,通常为sigmoid 函数,即sigmoid(x)=1/(1+e-x);V 为隐藏层到输出层之间的权重连接矩阵。
U、V、W 在每次循环步骤中都是相同的,即参数共享。
虽然理论上RNN 已经可解决时间序列中的“依赖”问题,但是实践中当时间序列较长时,RNN的学习和训练会出现梯度消失或梯度爆炸的问题,进而导致模型无法更新或收敛。为了解决上述问题,可对RNN 的神经元节点进行重新设计,并引入“门”机制。这种RNN 的变体就是LSTM 神经网络,其神经元节点的结构如图2所示。
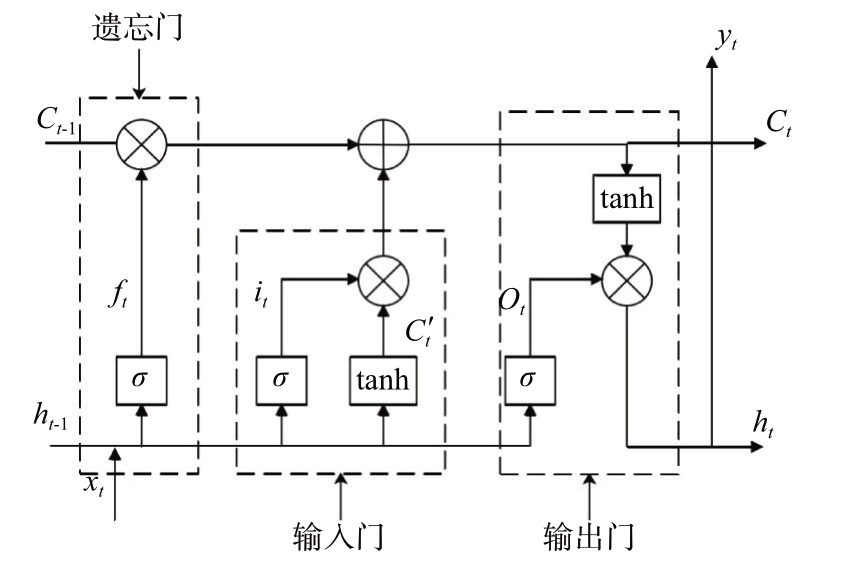
图2 LSTM网络神经元节点结构
图2 的上方有一条水平贯穿线Ct,它代表“长期记忆”,上面的数据信息会在整个网络中传递。图2 的下方也有一条水平线ht- 1,它不贯穿整个网络,只在相邻两个神经元节点之间传递,代表“短期记忆”。长短期记忆之间通过遗忘门、输入门和输出门进行控制。
遗忘门的数学表达式为
输入门的数学表达式为
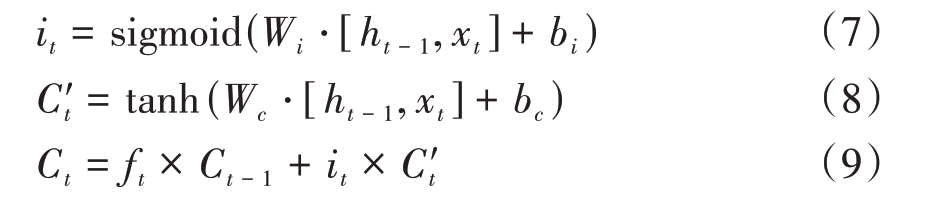
输出门的数学表达式为
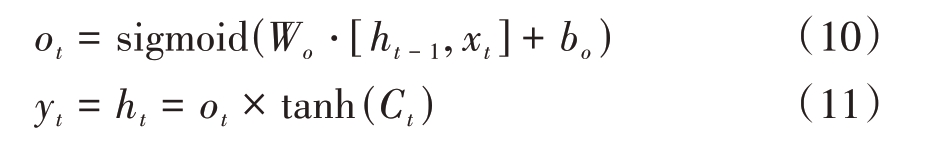
式(6)~(11)中,Wf、Wi、Wc、Wo 是对应于遗忘门ft,输入门it、Ct 和输出门ot 的权重;bf、bi、bc、bo 是相应的偏置参数。
2 预测实验与结果分析
2.1 数据样本说明
数据样本来自某型雷达2020年10月至2022年8月的功放组件输出功率监测数据。在此期间共有7 个功放组件发生故障(编号为1~7 号),选取该7 个功放组件被更换前1 000 h 内的输出功率数据进行预测实验。7 个功放组件的输出功率数据如图3所示。其中图3(a)为直接采样数据,每隔90 s 采样一次,即每小时采样40 次,每个功放组件共有40 000个输出功率原始数据,时间单位为90 s;图3(b)为对每小时的输出功率求平均后的数据,共有1 000个数据,时间单位为h。
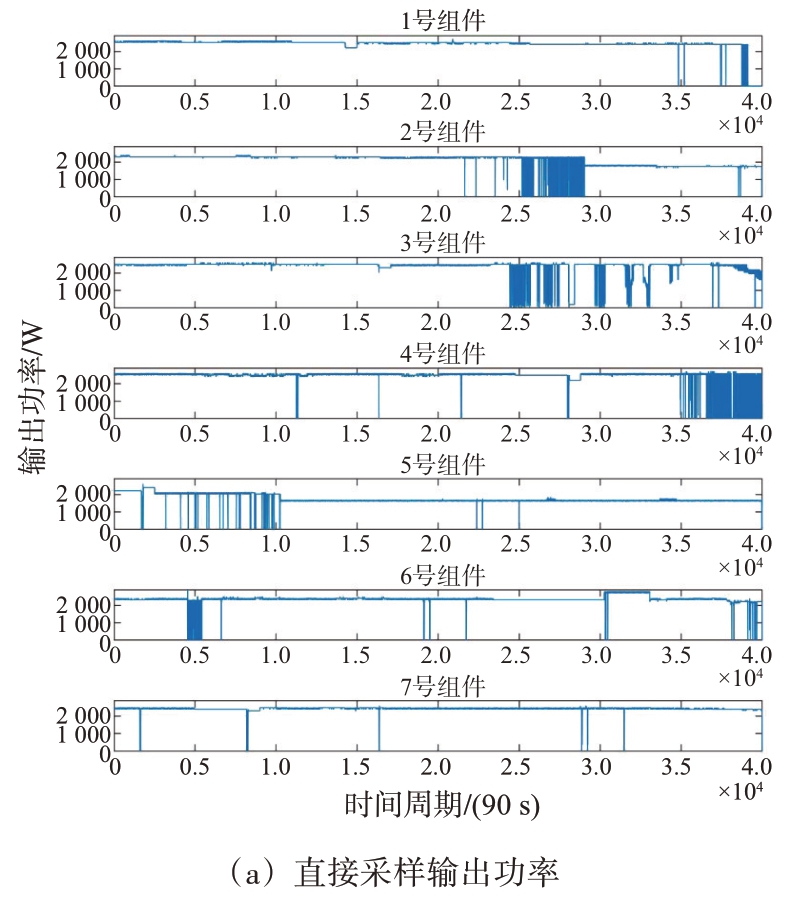
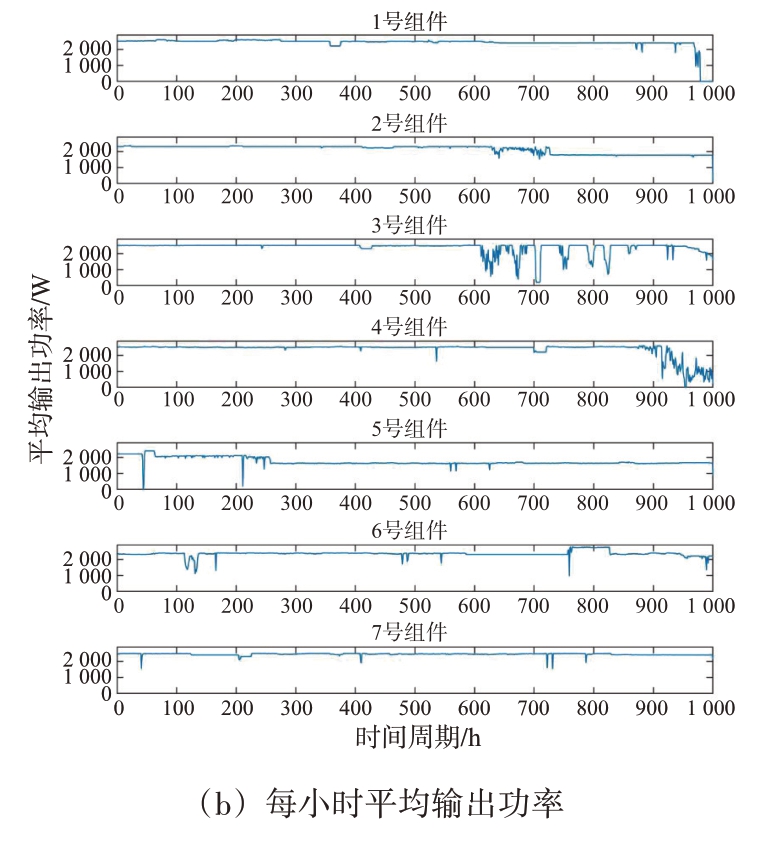
图3 功放组件输出功率监测数据
通过图3 可知,7 个雷达功放组件都有长时间的平稳工作期;其中,3号和4号组件有比较明显的缓慢劣化工作期;1 号和6 号组件的劣化工作期很短,可称为快速劣化工作期;2 号、5 号和7 号组件无明显劣化工作期,表现为突发性故障,这是难以预测的。下面将在MATLAB 2019a 平台上分别对雷达功放组件的平稳工作期、缓慢劣化工作期和快速劣化工作期的输出功率进行预测实验。
2.2 建模过程和参数设置
2.2.1 ARIMA建模过程
ARIMA 建模过程如图4所示。首先,对时间序列数据进行平稳性检验并确定差分阶数。这里选择了两种常用的互补平稳性测试方法,即Augmented Dickey-Fuller(ADF)和Kwiatkowski-Phillips-Schmidt-Shin(KPSS)。只有当ADF 的返回值为1且KPSS为0时,历史测量数据才是平稳序列,而其余的返回值则被判断为非平稳序列。若数据为非平稳性序列则进行差分运算直至通过ADF 和KPSS 准则的平稳性测试。其次,确定ARMA 模型阶数。利用自相关函数(ACF)和偏自相关函数(PACF)法,确定ARIMA 模型阶数。最后,为了检验模型的参数是否合适,还要进行残差检验。残差为原始数值减掉模型拟合出的数值后的残余值。如果残差为随机正态分布、不自相关,则说明残差是一段白噪声,有用的信号已经都被提取到ARIMA模型中了。此时建模完毕,可以进行预测。
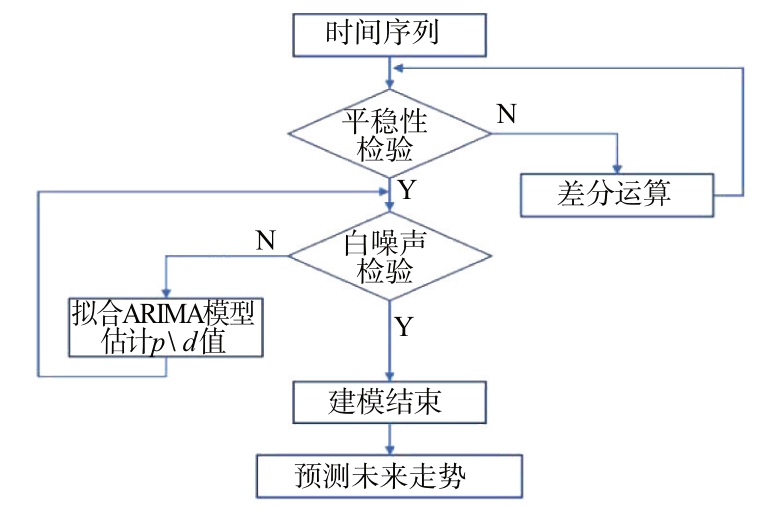
图4 ARIMA程序设计流程
2.2.2 LSTM参数设置
利用MATLAB 2019a 平台自带的深度学习工具箱(Deep Learning Toolbox)进行LSTM 网络的建模、训练和预测。相关参数设置如下:指定LSTM层有200 个隐含单元;求解器设置为“adam”,并进行250 轮训练;为了防止梯度爆炸,将梯度阈值设置为1;指定初始学习率0.005,在125 轮训练后通过乘以因子0.2来降低学习率。
2.3 平稳工作期功率预测
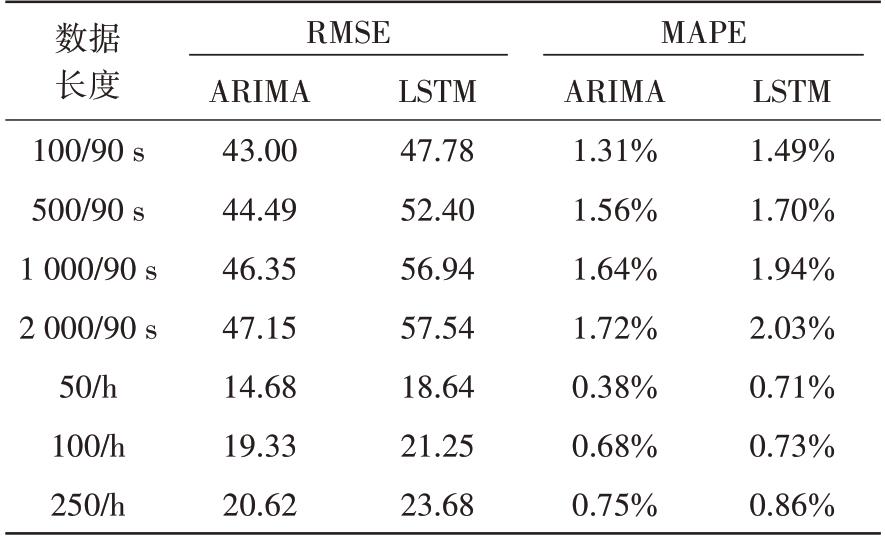
随机选取1~7号组件的平稳工作期进行预测,例如选取7号组件410~710 h之间的输出功率样本进行预测实验,如图5所示。图5(a)为原始监测功率输出序列数据,图5(b)为按小时求平均后的序列数据。实验过程如下:首先确定数据长度;然后随机抽取10 个时间段的监测数据分别采用ARIMA 模型和LSTM 模型进行预测实验,其中前90%用于训练,后10%用于预测;最后计算两个预测模型10次预测的平均RMSE(Root Mean Square Error)和平均MAPE(Mean Absolute Percentage Error)。整个实验在i7-8565U CPU、8.00 GB内存、Windows10操作系统的计算机上完成。预测实验结果如表1所示。
表1 平稳工作期输出功率预测结果
数据长度100/90 s 500/90 s 1 000/90 s 2 000/90 s 50/h 100/h 250/h RMSE MAPE ARIMA 43.00 44.49 46.35 47.15 14.68 19.33 20.62 LSTM 47.78 52.40 56.94 57.54 18.64 21.25 23.68 ARIMA 1.31%1.56%1.64%1.72%0.38%0.68%0.75%LSTM 1.49%1.70%1.94%2.03%0.71%0.73%0.86%
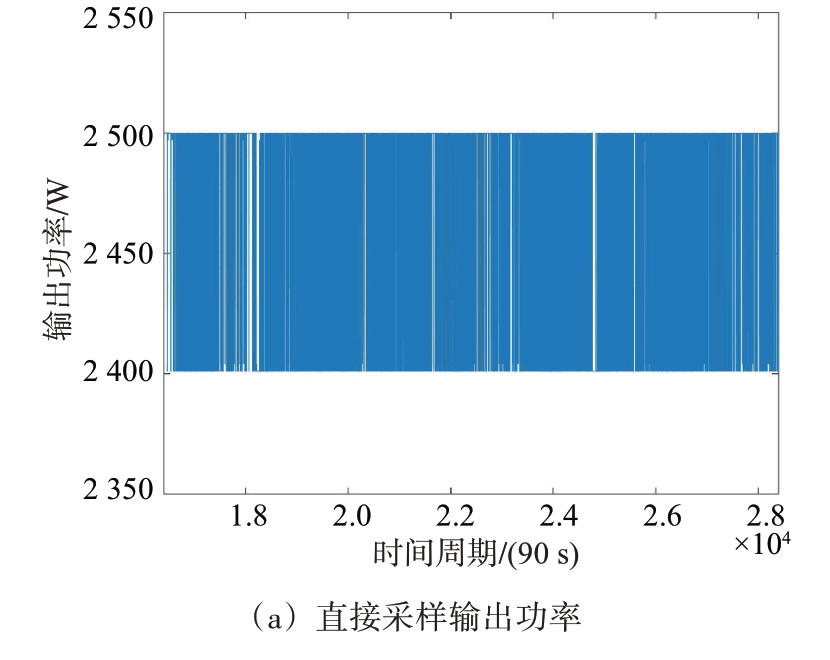
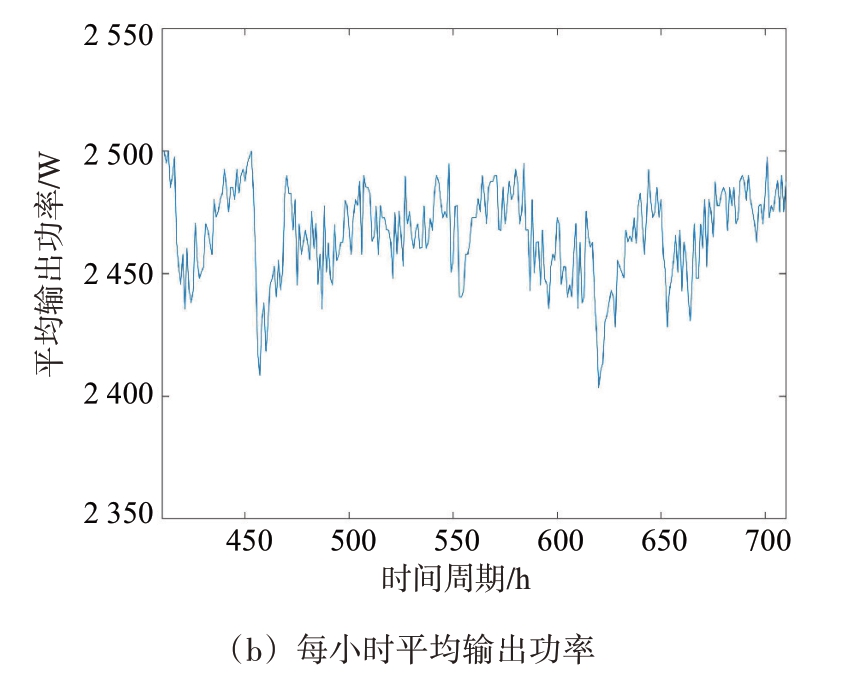
图5 7号组件平稳工作期输出功率监测数据
从表1 可以看出:1)ARIMA 模型的预测精度略优于LSTM 模型,但相差不大;2)数据长度和预测时长显著变长,预测精度变差并不明显;3)求平均后序列数据的预测精度要高于原始序列数据的预测精度,这是由于求平均后的序列相对原始序列更加平滑,而原始监测序列值在2 400~2 500 之间变化,变化比较激烈。另外,由于求平均后数据量变小,预测计算量也会相应变小。
由上述结果可知,在平稳工作期进行功率预测时,ARIMA 模型和LSTM 模型并没有显著差异;长期预测和短期预测区别不大,故平稳期可进行长期预测且可将原始监测数据进行分段求平均后再预测,这样既可以提高预测精度又可以减少预测计算量,具体分段长度可根据预测需求调整和确定。
其他组件的平稳工作期输出功率预测结果与上述结论一致,在此不一一赘述。
2.4 缓慢劣化期预测
选取3 号、4 号组件800~1 000 h 之间的输出功率样本进行预测实验,其中4号组件输出功率如图6所示。在劣化期往往会出现间歇故障[7],间歇故障会导致原始输出功率序列在0 到正常值之间剧烈变化。图6(a)为原始监测功率输出序列数据,图6(b)为按小时求平均后的序列数据。输出功率预测的主要目的之一是在维护中为功放组件的提前换件修理提供决策依据。由于更换功放组件耗时较长,一般需要在周维护中进行,但若雷达非24小时值班,值班间歇超过4 h,也可在日维护中进行。故功放组件有效预测时长至少为雷达的一个值班时间,通常为6~12 h,所以进行小时为步长的平均功率预测更有意义。
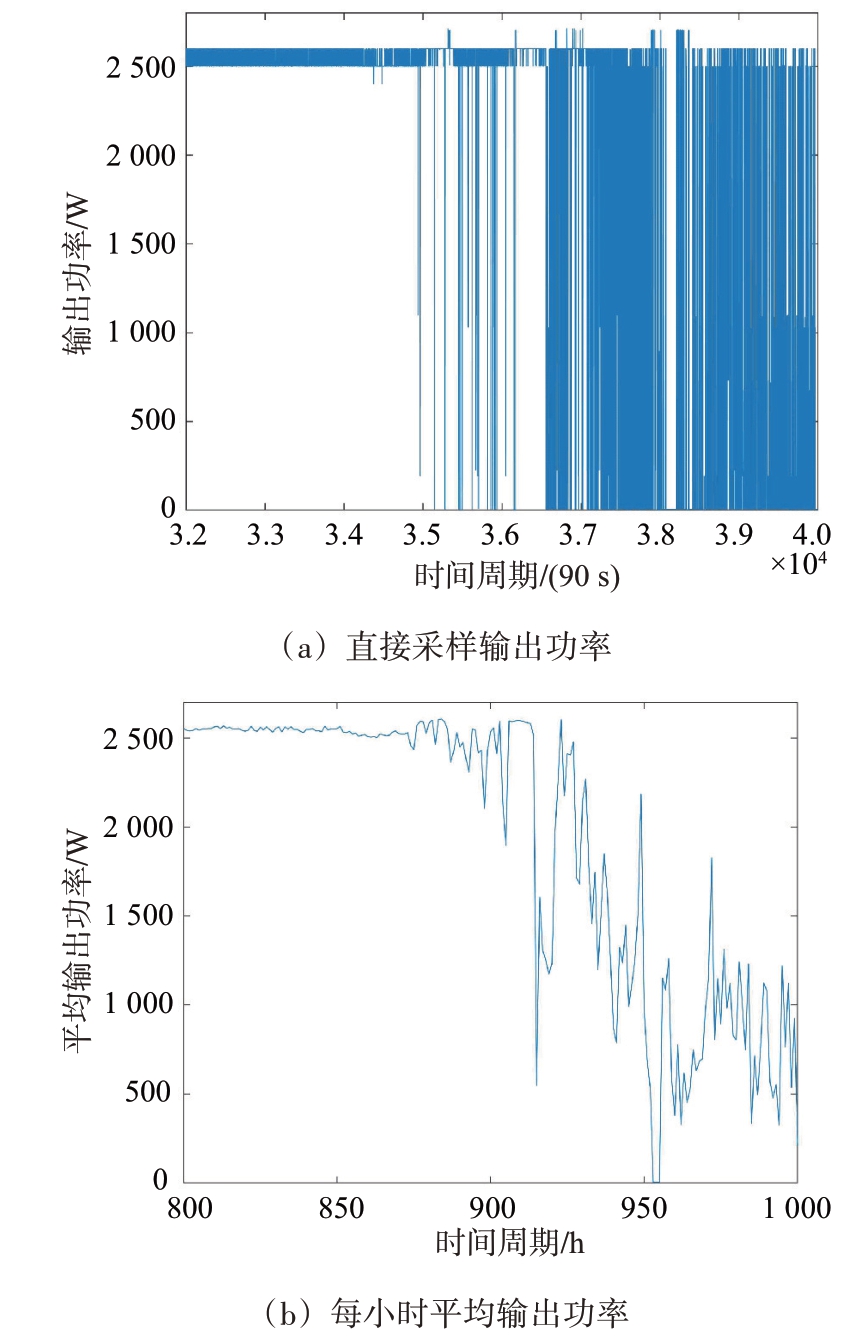
图6 4号组件劣化工作期输出功率监测数据
实验过程如下:首先选择数据时长为60 h(前90%用于训练,后10%用于预测),相应地预测时长为6 h,在此基础上逐渐增加数据时长;每段时间序列分别采用ARIMA 模型和LSTM 模型进行预测并计算RMSE(Root Mean Square Error)和MAPE(Mean Absolute Percentage Error);实验平台与2.3节一样,预测实验结果如表2、表3所示。
表2 3号组件缓慢劣化工作期输出功率预测结果

时间序列/h 801~860 801~880 801~900 801~930 801~960 801~1 000 RMSE MAPE ARIMA 63.70 89.08 52.83 247.36 232.00 440.92 LSTM 34.25 70.01 61.19 249.87 329.10 544.85 ARIMA 2.15%2.57%1.41%5.25%7.61%21.02%LSTM 0.91%2.66%1.69%5.39%11.37%25.66%
表3 4号组件缓慢劣化工作期输出功率预测结果
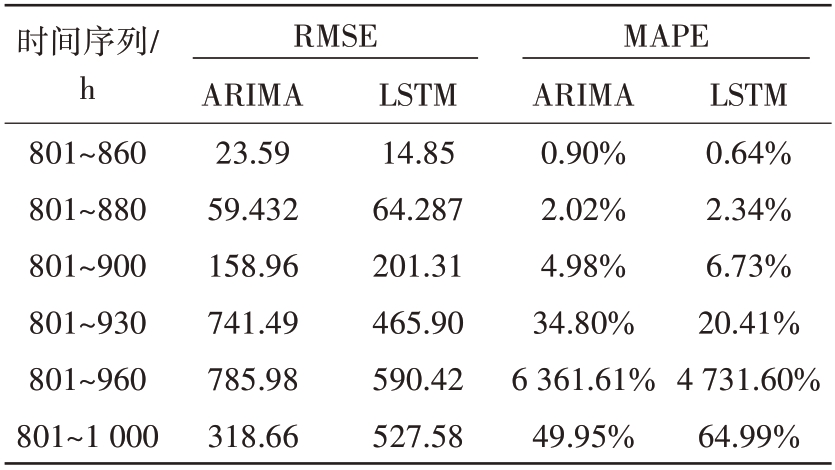
时间序列/h 801~860 801~880 801~900 801~930 801~960 801~1 000 RMSE MAPE ARIMA 23.59 59.432 158.96 741.49 785.98 318.66 LSTM 14.85 64.287 201.31 465.90 590.42 527.58 ARIMA 0.90%2.02%4.98%34.80%6 361.61%49.95%LSTM 0.64%2.34%6.73%20.41%4 731.60%64.99%
从表2、表3可以看出:1)ARIMA模型和LSTM模型的预测效果相当;2)与平稳工作期的输出功率预测相比,缓慢劣化工作期的预测精度明显变差;3)数据长度和预测时长显著变长,预测精度也显著变差,尤其当监测值变化剧烈时,如图7所示,此时两种预测模型的预测值与监测值的偏差都很大,难以完成有效预测。
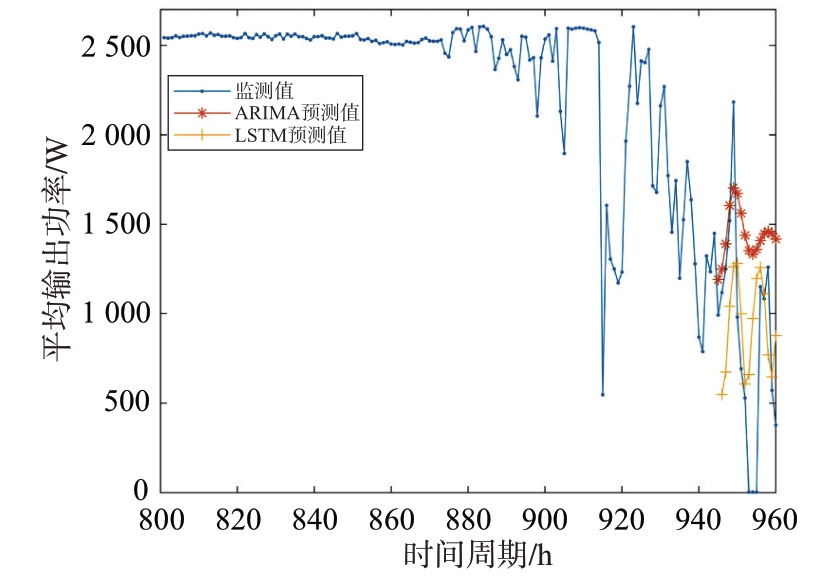
图7 4号组件缓慢劣化期输出功率监测与预测
由上述结果可知,缓慢劣化工作期的预测精度主要取决于预测时长和监测值变化的剧烈程度,当预测时长较短且监测值变化平缓时(见表2前4行、表3前3行),预测效果好,否则难以完成有效预测。
2.5 快速劣化期预测
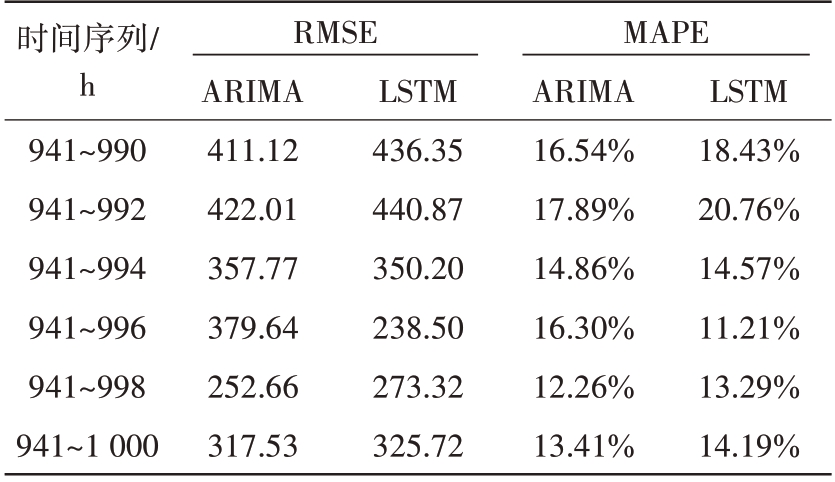
选取1号组件920~980 h和6号组件940~1 000 h之间的输出功率样本进行预测实验,其中1号组件输出功率如图8所示。这里与2.4 节一样,只进行小时为步长的平均功率预测。实验过程如下:首先选择数据时长为50 h(前90%用于训练,后10%用于预测),相应地预测时长为5 h,在此基础上逐渐增加数据时长至60 h;每段时间序列分别采用ARIMA 模型和LSTM 模型进行预测并计算RMSE(Root Mean Square Error)和MAPE(Mean Absolute Percentage Error);实验平台与2.3 节一样,预测实验结果如表4、表5所示。
表4 1号组件快速劣化工作期输出功率预测结果
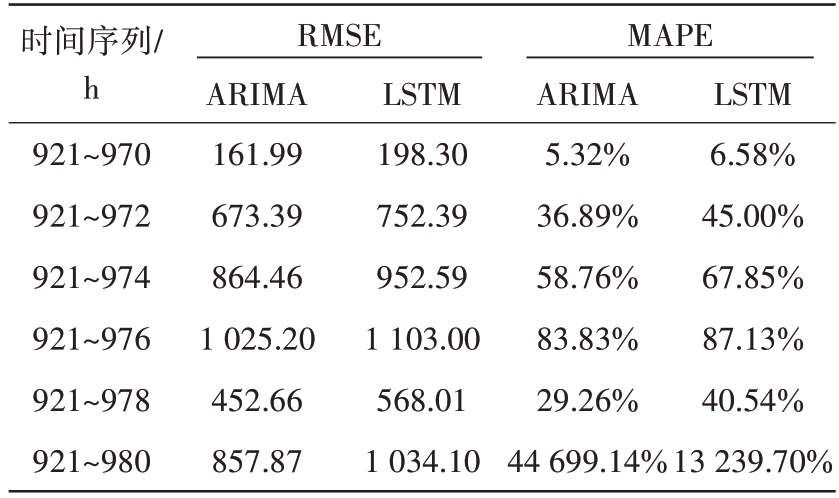
时间序列/h 921~970 921~972 921~974 921~976 921~978 921~980 RMSE MAPE ARIMA 161.99 673.39 864.46 1 025.20 452.66 857.87 LSTM 198.30 752.39 952.59 1 103.00 568.01 1 034.10 ARIMA 5.32%36.89%58.76%83.83%29.26%44 699.14%LSTM 6.58%45.00%67.85%87.13%40.54%13 239.70%
表5 6号组件快速劣化工作期输出功率预测结果
时间序列/h 941~990 941~992 941~994 941~996 941~998 941~1 000 RMSE MAPE ARIMA 411.12 422.01 357.77 379.64 252.66 317.53 LSTM 436.35 440.87 350.20 238.50 273.32 325.72 ARIMA 16.54%17.89%14.86%16.30%12.26%13.41%LSTM 18.43%20.76%14.57%11.21%13.29%14.19%
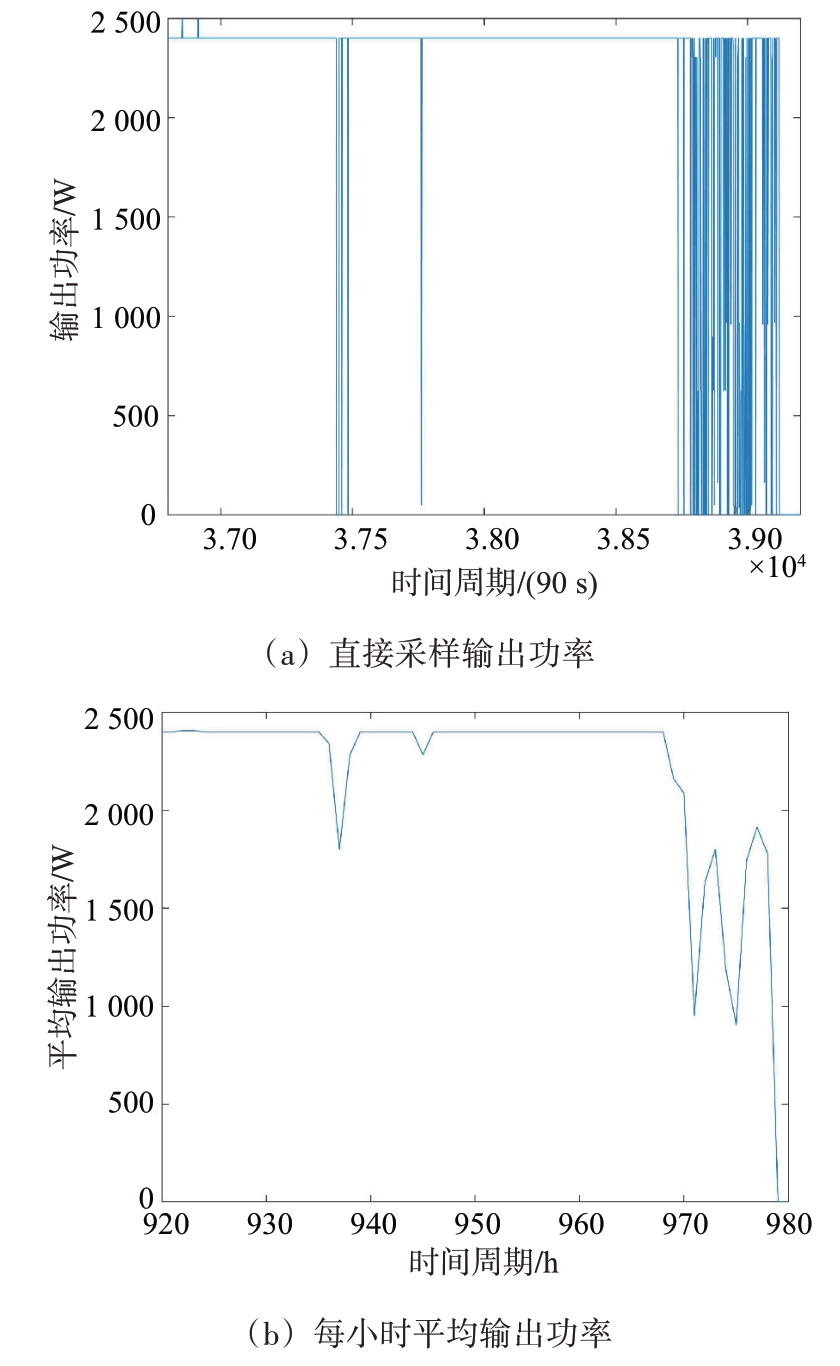
图8 1号组件劣化工作期输出功率监测数据
从表4、表5 可以看出:1)与缓慢工作期的输出功率预测相比,快速劣化工作期的预测精度明显变差;2)由于劣化期较短,且监测值变化剧烈,劣化规律难以捕捉,两种预测模型的预测值与监测值的偏差都较大,难以完成有效预测。
由上述结果可知,快速劣化工作期的输出功率是难以有效预测的,即难以进行满足预测性维护要求的输出功率预测。值得注意的是,当预测时长短且监测值变化不剧烈时,雷达性能参数的预测效果往往是比较好的[3-5],但此时的预测时长满足不了预测性维护的需求,即预警时间偏短难以完成有效的维护操作。
3 结束语
本文利用ARIMA 模型和LSTM 模型对功放组件全寿命周期的输出功率预测进行了研究,重点研究了功放组件不同工作阶段、变化特征和预测时长与预测精度的关系。研究结果表明,功放组件都有长时间的平稳工作期,在此期间预测效果好,长期预测和短期预测的预测精度区别不大;有的功放组件具有缓慢劣化工作期,当预测时长较短且监测值变化平缓时预测效果好,否则难以预测;有的功放组件只有快速劣化工作期,甚至表现为突发性故障,由于劣化期较短且监测值变化剧烈,劣化规律难以捕捉,无法完成有效预测;ARIMA 模型和LSTM 模型的预测效果没有显著差别,预测精度主要取决于预测时长和监测值变化特征。上述结果说明,时间序列预测方法只对部分功放组件输出功率劣化预测有效,为此还需要研究其他预测方法。希望本文能够为雷达设备故障预测技术的研究、发展和应用提供一些参考。
[1]欧阳霄,杨辉,朱东济,等.基于ARIMA 和神经网络的单脉冲雷达设备故障预测研究[J].计算机测量与控制,2021,29(10):83-87.
[2]徐飞,杨士英,魏祥生,等.基于改进灰色预测模型的雷达备件消耗预测[J].雷达科学与技术,2015,13(6):609-614.
[3]ZHAI Yuting,LIU Dongli,CHENG Zhanxin,et al.A Novel Prognostic Model of the Degradation Malfunction Combining a Dynamic Updated-ARIMA and Multivariate Isolation:Forest Application to Radar Transmitter[J].Electronics,2022,11(12):1-16.
[4]ZHAI Yuting,FANG Shaojun.A Degradation Fault Prognostic Method of Radar Transmitter Combining Multivariate Long Short-Term Memory Network and Multivariate Gaussian Distribution[J].IEEE Access,2020,8:199781-199791.
[5]WU Jie,LV Yongle.Adaptive Prediction Algorithm Based on ARMA and RBFNN Models for Radar Performance[C]// 3rd Annual International Conference on Information System and Artificial Intelligence,Suzhou,China:[s.n.],2018:1-8.
[6]李靖.基于大数据分析的现役雷达故障预测技术研究[D].西安:西安电子科技大学,2018.
[7]吕克洪,程先哲,李华康,等.电子设备故障预测与健康管理技术发展新动态[J].航空学报,2019,40(11):18-29.
