0 引言
相控阵天线通过简单对相位合成控制可使波束对空间自由扫描，经过多年发展已广泛地应用于雷达探测与目标分析等领域。传统相控阵天线的所有阵元辐射都源自于同一激励源信号，通过对每个阵元射频部分独立的移相器结构控制，实现调控相位/时延控制的累计偏移量，进而控制波束指向完成波束的空域扫描。此外，利用天线系统的工作频率的有意变化从理论上可以实现波束的空间扫描，即频率扫描天线。但是这两类天线阵列都存在一个弱点［1］，即在每个扫描周期/快拍内，波束指向只与方向角有关，而与距离参量无关。但是在某些应用场景中，比如电磁对抗环境下存在距离相关性干扰或地/海杂波抑制需求，再或者要求阵列波束在同一快拍周期内可以覆盖针状波束较小距离范围，其本质特征要求就是波束指向模型中存在角度与距离的复合相关项。2006年，文献［2］中首次提出了新体制频率分集阵（Frequency Diverse Array,FDA）概念，其基本原理是通过附加很小的频偏（频偏远远小于其载频）控制后合成波束的信号频率中心略有偏移，但其主要频率成分是相同的，形成具有距离角度相关性方向图，此概念提出伊始就引起美国国防研究机构的高度兴趣和热切关注［3-4］。而在中近场天线阵列的FDA 研究可有效拓展大孔径天线阵列测量范围，改进角度-距离解耦条件下测量精度，但相关研究却迟迟未见报道，其主要难度在于中近场传播非线性特征与FDA 的非线性叠加，使得数学模型更为复杂，表达式表征更加困难，性质特征更不明显。
本文在传统频率分集阵列研究的基础上，提出了适应天线阵列近场条件的FDA 新数学算法，针对阵列近场条件，首先利用经典近场的菲涅尔近似以及新近提出基于差分迭代近似两种方法推导，得到近场FDA 波束的不同表达新算法结构，其次针对新提出算法的数学关系式中距离、角度等关键参数特征分析，针对其中距离-角度耦合关系等深入讨论，再次开展数值计算和算法仿真对比，实验结果表明:新提出的算法解决了FDA 近场条件使用的模型条件限制，算法较好地解释了近场时距离-角度参数非线性耦合或独立关系，可以较好地支撑未来天线阵列近场，FDA 各种应用的深入分析与研究需要。
1 频率分集阵算法的基本原理
1.1 频率分集阵列基本概念
频率分集阵是相邻阵元上信号附加一个远小于载频的频率增量Δw，如图1所示第1个阵元的辐射频率为w0，而第m个阵元的信号频率为
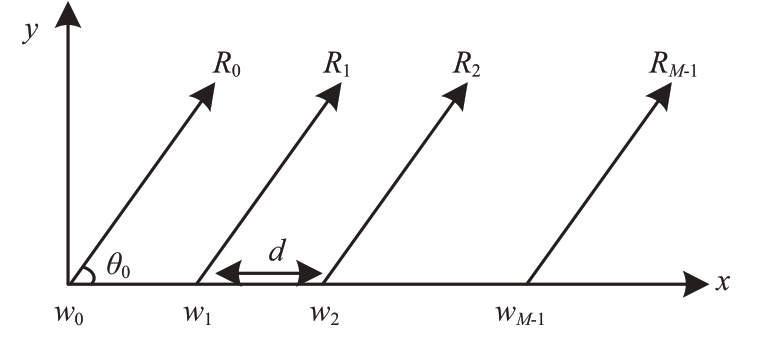
图1 频率分集阵列结构示意图
式中，M为阵元数。
由传统阵列分析，M个天线单元总合成电磁场强度为
假设均匀线性阵列满足远场基本条件［2］，即wn= w0+ nΔw，kn= k0+ nΔk，Δk=2π/Δλ，Rn= R0-nd cos θ并忽略关于n的二次项，可得到
式中ψ=Δwt+ k0dcos θn-ΔkR0。并得到
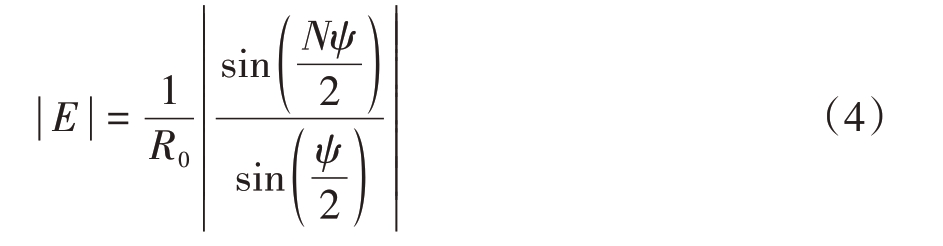
式（3）和式（4）是后续大量研究的基础和依据，但它只适用于远场条件，即
。
1.2 天阵阵列近场特性与传播近似研究
传统天线阵列中近场合成效应研究一般都采用菲涅尔近似模型形式，如图2所示，针对三角形ΔONK，由几何余弦定理有
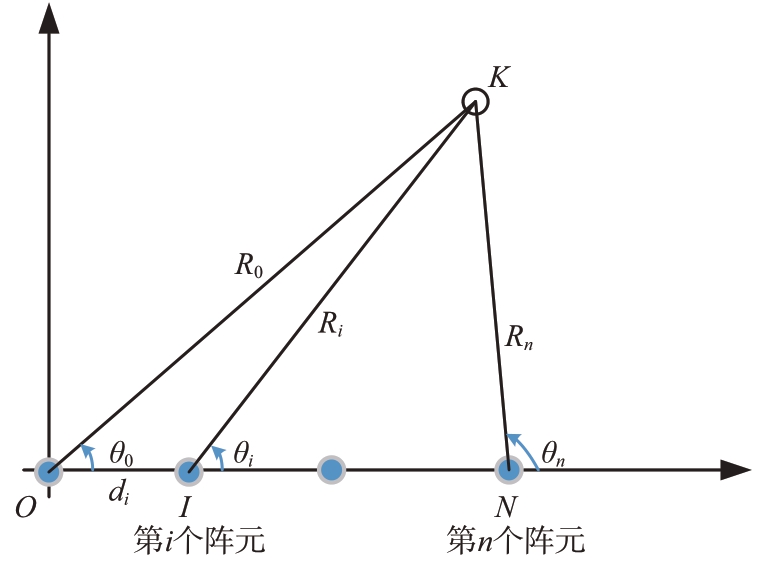
图2 频率分集阵列中近场结构示意图
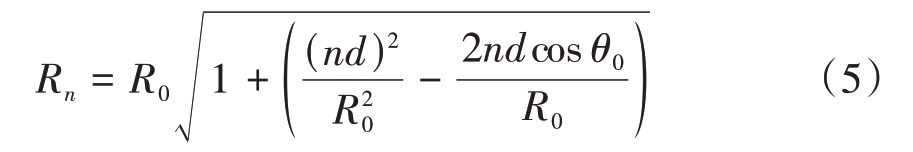
通过对
代数式的标准泰勒级数研究，可得式（5）的高阶标准多项式近似表达，考虑表达式中变量阶数的合理性、计算运算量和模型近似度等因素，一般认可采用变量二阶近似式即菲涅尔近似，其具体表达式如下:
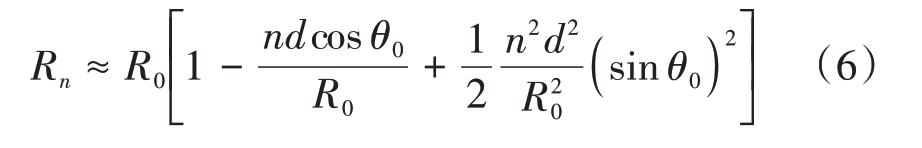
针对FDA 基本关系式（2），引入式（6）的近似表达并推导演绎相关数学模型，可得到FDA 在天线阵列近场条件下新模型的数学关系式。
同时作者在近期阵列中近场技术研究中，提出了基于几何结构的三角函数关系迭代的中近场距离估计新算法并发表于相关领域期刊［5］,区别于传统菲涅尔近似关系式，新提出算法结构与初值和迭代次数相关，如
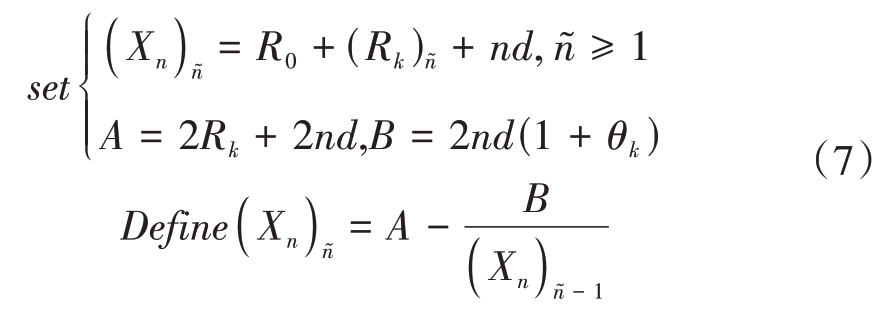
式中()n͂表示对操作数的第n 次迭代估计值。经过推导可得表达式:
同理针对FDA 基本关系式，引入式（8）的近似表达并推导，也可得到FDA 在天线阵列近场条件下新模型的数学关系式。
2 近场频率分集阵算法推导
2.1 基于菲涅尔近似的近场FDA表达式
针对天线阵列近场条件，将式（6）代入式（2）得到
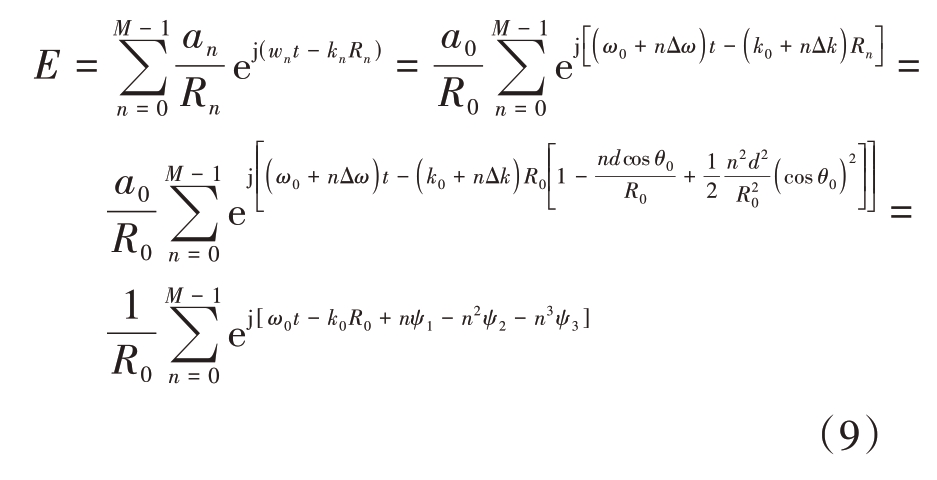
式中，n的各阶次系数项有
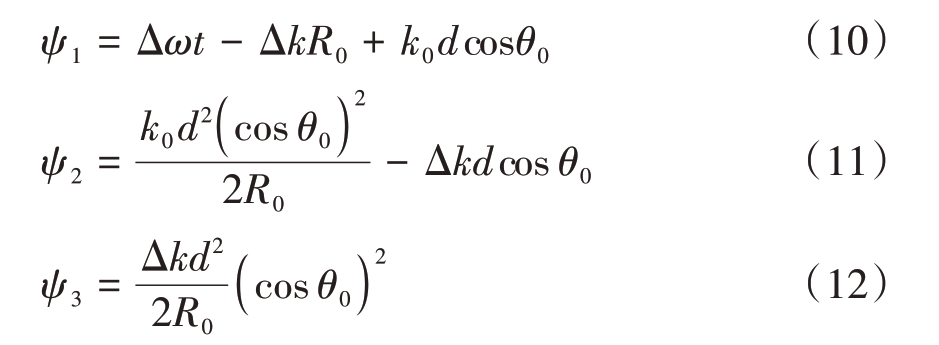
对于近场天线阵列有
约束，由式（9）～（12）可知，其近场信号合成的各分量耦合成分更多更复杂，其数学规律杂乱晦涩。因此需要考虑特殊条件下的先验性距离-角度解耦信号合成现象，系统则通过对未知参数在目标空间中搜索的方式验证其表现的特性与效能。
考虑最大程度简化复杂成分项，首先研究ψ3近似为零条件，有Δf ≪M2 约束；其次分析ψ2=0条件:
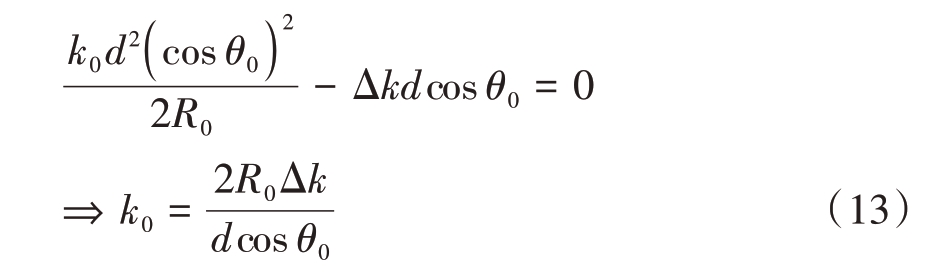
由式（13）可知，当信号参数确定后，合成结果对预期目标的距离与角度余弦呈现反比例关系。此时如约定距离或角度为某参数值，并采用宽频带信号选择合适的频率分量，则可以实现对另一个参数的搜索匹配。将式（13）代入式（10），得到
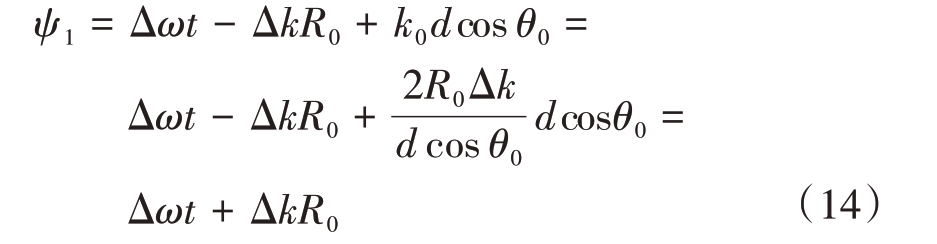
如果先验约定角度，此时合成信号只与目标距离有关，可是实现特定条件下的距离扫描，由式（9）有
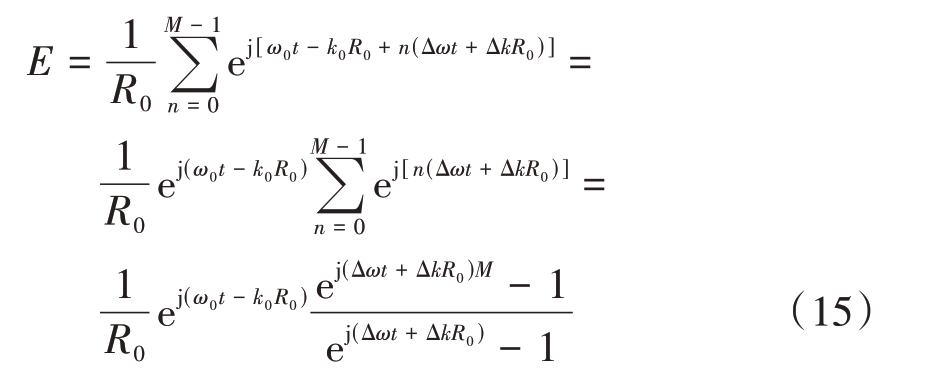
如果先验约定距离，则合成信号只与目标角度有关，可实现特定条件下的角度扫描。
2.2 基于差分迭代近似的近场FDA表达式
针对天线阵列近场条件，将式（8）代入式（2）得到
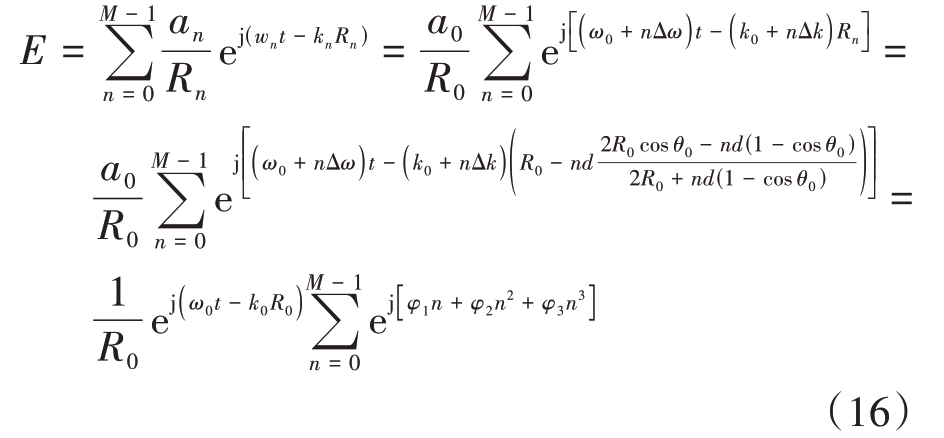
式中，n的各阶次系数项有
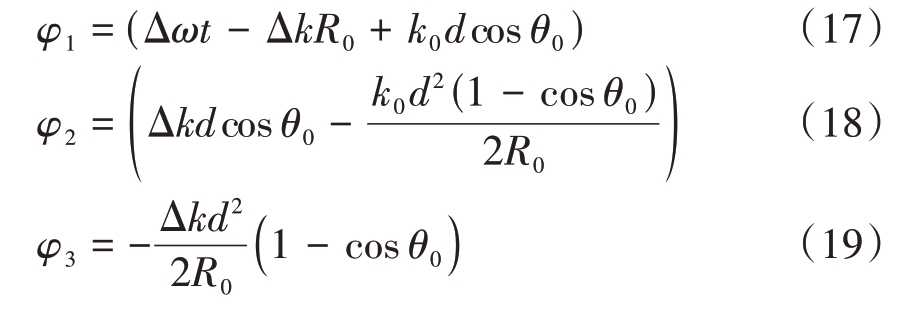
对于近场天线阵列，由式（16）～（19）可知，其近场信号合成的各分量耦合成分也十分复杂，非线性规律与性质突出。借鉴在菲涅尔近似近场FDA 新算法的分析过程，发现一些特殊条件下的算法新特征。
针对φ3 ≈0 条件，有Δf ≪M2 约束；其次分析φ2=0条件:
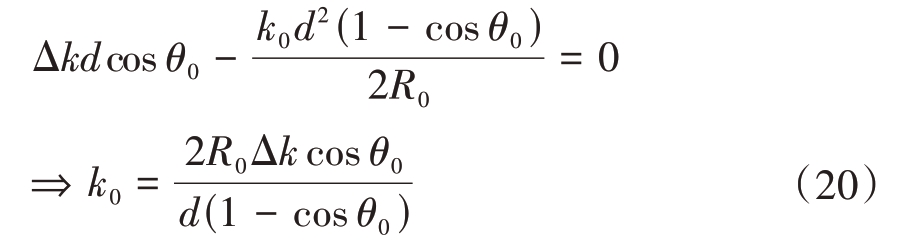
由式（20）可知，当信号参数确定后，合成结果对预期目标的距离与角度余弦呈现非线性关系。此时如约定距离或角度为某参数值，并采用宽频带信号选择合适的频率分量，也可以实现对另一个参数的搜索匹配。将式（20）代入式（10），得到
如式（21）所示，基于差分迭代近似的近场FDA 算法保留有距离-角度相关性，且非线性特征更为强烈。由式（15）、（21）两种形式算法的应用分析可知，对于近场天线阵列FDA 响应的对目标先验搜索都可以实现距离-角度耦合探测。
2.3 相关处理与算法的性能比较
传统远场条件下电波空间传播以平行波模型表达，并通过此近似可以得到简化形式［6-7］，而对于近场条件距离-角度间耦合非线性特征更为明显，针对FDA 处理的研究就涉及更少，鲜有报道。本文算法研究借鉴了传统天线阵列中近场研究利用菲涅尔近似模型和新近研究提出的基于差分迭代模型近似的新算法思路，推导得到新的近场FDA算法。从文献的研究分析可知，菲涅尔近似在45°～90°范围内近似精度更高，差分迭代算法在0°～45°范围内近似精度更高。新算法相对于传统相控阵体制的天线阵列近场合成有一个明显的优势特征，即通过FDA 技术显著改善了阵列间距不满足无模糊数距离条件时的模糊栅瓣数量激增现象。
3 对所提算法仿真和性质分析
针对均匀线阵的近场区域范围内目标定位性质进行仿真分析，数值计算验证:1）基于菲涅尔近似的近场FDA 算法结果和测量效能；2）基于差分迭代近似的近场FDA 算法结果和测量效能；3）针对这两种算法相互进行对比分析，总结其各自性能优缺点。
设定算法仿真近场目标区域范围为
，设定典型工作频谱为100 MHz，均匀线阵采用五阵元，间距为
无模糊布置。
3.1 基于菲涅尔近似的近场FDA算法仿真分析
针对式（15），按照如上所述仿真条件，开展近场FDA 合成目标检测计算分析，首先在距离维开展分析，之后考虑关联角度维的平面联合分析。
如图3所示，基于菲涅尔近似新FDA算法具有距离-角度的非相关性，考虑到信号的周期重复等因素带来的模糊性，在一个独立测量范围内，其主信号对栅瓣的距离抑制超过20 dB，具有良好的空间分辨率。
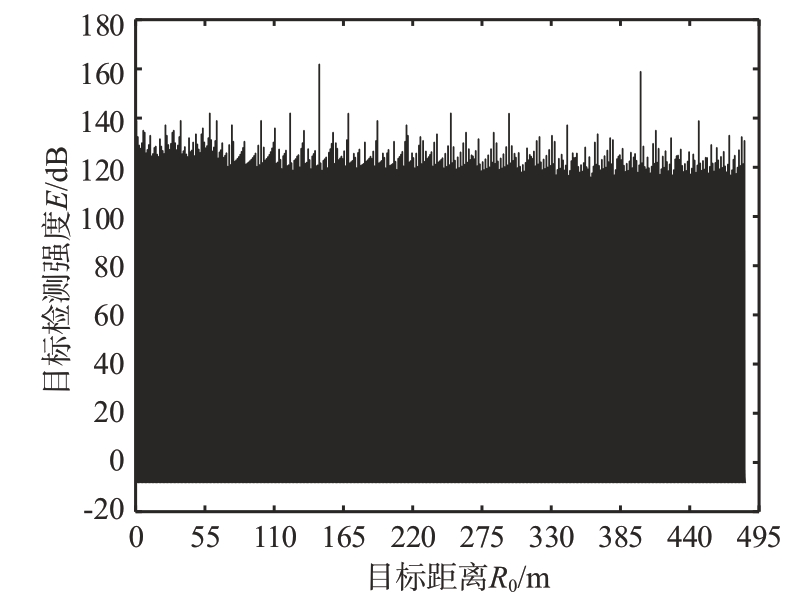
图3 基于菲涅尔近似的近场FDA算法距离检测图
如图4所示，基于菲涅尔近似新FDA算法在二维平面内实现对目标距离和角度的独立观测和测量。如果不考虑发射角度的先验约束，在二维平面范围内全响应条件下有多个模糊目标位置。如式（15）所示，当对到达角范围进行先验设定时，随着天线阵列阵元数增加可以有效减少模糊空间位置的个数；对于检测主目标峰值的杂散抑制则与阵型和阵列间距相关联；而具体信号的检测最佳效能实际上需要依据目标的特征相匹配。
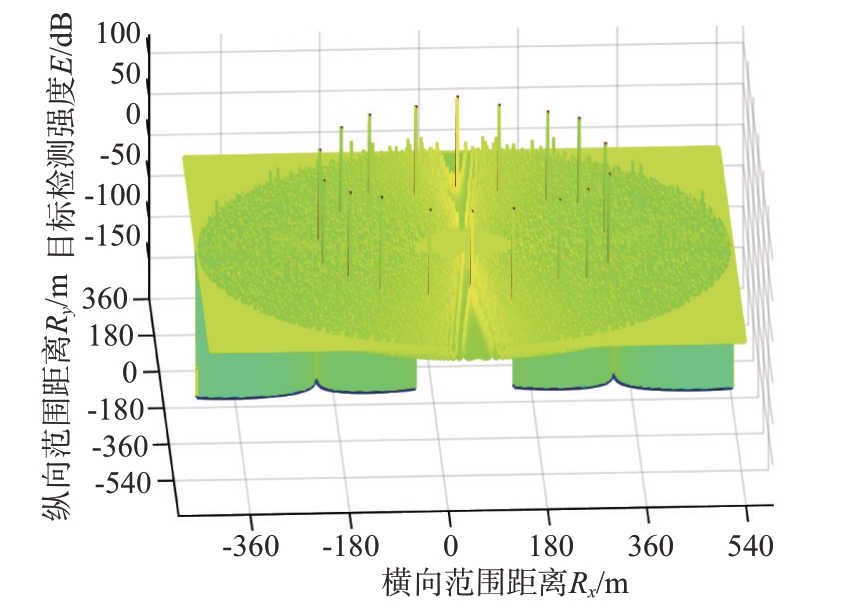
图4 基于菲涅尔近似二维空间近场FDA算法目标检测图
3.2 基于差分迭代近似的近场FDA近似仿真分析
针对式（21），按照如上所述仿真条件，开展近场FDA 合成目标检测计算分析，首先在距离维开展分析，之后考虑关联角度维的平面联合分析。
如图5所示，由于表达式（21）存在复杂数学关系结构，式中存在多个信号参数和目标距离、角度等因素且相互关联耦合，因此受信号参数影响，在一定范围内其目标角度-距离因素数值上存在多组等价模糊关系。图上显示在多个角度上，沿着距离方向存在一系列目标模糊位置点，这些点满足合成的副瓣和栅瓣特征，而在目标位置上存在最大值的检测峰值。
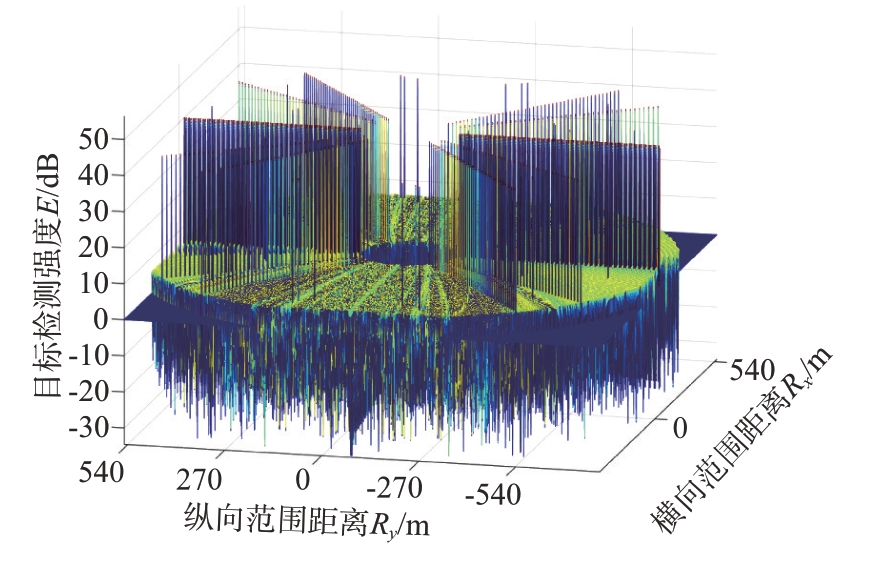
图5 基于差分迭代近似二维空间近场FDA算法距离检测图
根据阵列工作频段、阵列结构和尺寸，同时满足阵列中近场区域范围覆盖，合理设计其工作参数［8-9］，选择频率增量等信号参数，可以有效降低和抑制副瓣、栅瓣出现，降低阵列近场模糊程度。经过经典优化设计后，其基于差分迭代近似二维空间近场FDA算法目标检测结果如图6所示。
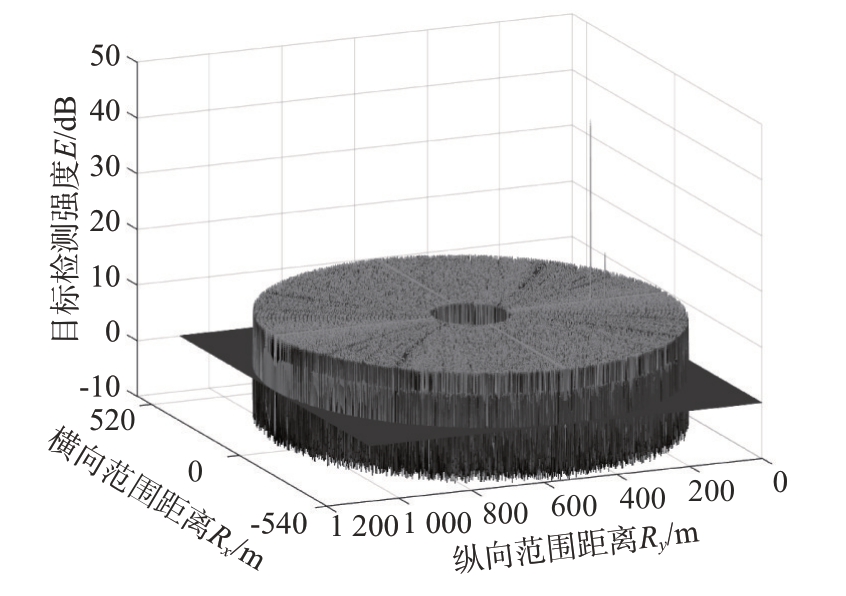
图6 基于差分迭代近似二维空间近场FDA算法距离检测图
经过信号参数优化和通过先验解模糊处理的基于差分迭代近似近场FDA 算法可以实现对近场目标的检测能力，具有和基于菲涅尔近似近场FDA 算法效能相一致的结果。对比两种近似算法的目标检测效果，其对比误差基本如图7所示，在近场0°～90°范围以45°为界，在0°～45°，迭代差分模型近似算法误差优于菲涅尔近似算法，精度约提升0.5‰～2‰（越接近45°指标越接近），从45°到135°，菲涅尔近似算法优于迭代差分模型近似算法，精度约提升0.5‰～2‰（越接近45°指标越接近，在90°处达到最大约6‰）。
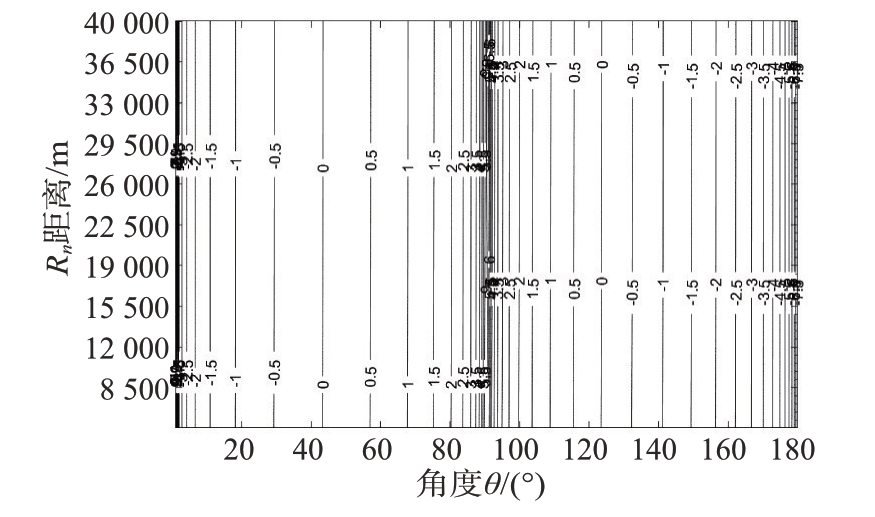
图7 中近场菲涅尔近似与差分迭代近似误差比较图
4 结束语
本文所提算法研究工作，首先针对近场FDA技术利用菲涅尔近似和差分迭代近似生成了新的应用条件下的新算法、新数学关系式，可以引导后续更多深入研究；其次讨论并分析了基于菲涅尔近似的近场FDA 算法，明确其距离-角度非相关特征，后续通过数值仿真并展示验证；再次针对基于差分迭代近似的近场FDA 算法分析和讨论，通过借鉴FDA 信号参数优化方法实现了近场解模糊、解距离-角度相关能力；最后针对两种不同的近场FDA 算法进行目标检测误差比较，并给出性能结果，对比分析结论。本文所提近场FDA 算法优势和特征较为突出，对于解决近场FDA 技术体制应用难题提供有益的指导。
［1］WANG Wenqin.Multi-Antenna Synthetic Aperture Radar［M］.New York:CRC Press,2013:376-381.
［2］ANTONIK P,WICKS W C,GRIFFITHS H D,et al.Frequency Diverse Array Radars［C］//Proceedings of the IEEE Radar Conference,Verona,NY:IEEE,2006:470-475.
［3］AYTUN A.Frequency Diverse Array Radar［D］.Monterey,California:Naval Postgraduate School,2010.
［4］ANTONIK P.An Investigation of a Frequency Diverse Array［D］.London:University of College London,2009.
［5］ZHAO Yan,TAO Haihong,CHANG Xin.An Accurate Near-Field Distance Estimation Differential Algorithm［J］.Chinese Journal of Electronics,2022,31（5）:851-859.
［6］WANG Wenqin,ZHENG Zhi.Frequency Diverse Array with Range-Dependent Transmit Beampattern［C］//2015 9th European Conference on Antennas and Propagation,Lisbon,Portugal:IEEE,2015:1-5.
［7］WANG Wenqin,SHAO Huaizong,CAI Jingye.Range-Angle-Dependent Beamforming by Frequency Diverse Array Antenna［J］.International Journal of Antennas and Propagation,2012（8）:61-70.
［8］项喆，陈伯孝.频率分集阵列的距离角度解耦的波束形成（英文）［J］.雷达学报，2018，7（2）:212-219.
［9］XU Jingwei,LAN Lan,HE Xiongpeng,et al.System Design and Signal Processing for Frequency Diverse Array Radar［J］.Journal of Beijing Institute of Technology,2021,30（1）:19-31.
