0 引言
脉冲压缩是现代雷达的一种重要体制,它既能克服雷达作用距离与分辨率的矛盾,也是雷达反隐身抗电子干扰以及对抗ARM 的有力手段[1]。脉冲压缩是通过发射较大时宽的脉冲信号,加大发射的平均功率,从而提高雷达作用距离;在雷达接收端通过接收经过脉冲压缩后的窄脉冲信号,从而获得较高的雷达距离分辨率[2]。依据调制信号波形,雷达脉冲压缩采用的信号可分为线性调频(LFM)信号、非线性调频信号和相位编码信号。由于LFM 信号结构简单,多普勒性能良好,并且不会引起信噪比损失,因此是目前应用最为广泛的脉冲压缩信号。该信号的缺点是在脉冲压缩后常会产生较高的距离旁瓣,影响雷达的小目标检测能力。
针对LFM 信号脉冲压缩后距离旁瓣较高的问题,国内外对此已有相关研究成果。文献[3]提出一种基于最小二乘迭代的旁瓣抑制方法,获得了较小的主瓣展宽比和峰值旁瓣比,但缺点是迭代系数不易控制,且计算量较大;文献[4-5]通过频谱修正方法抑制脉压后的旁瓣,但抑制效果不明显,且导致主瓣展宽和信噪比损失增加;文献[6]提出了一种窗函数双向加权法,获得了较低的峰值旁瓣,不过却严重地展宽了主瓣;文献[7]通过在时域中设计了一种新的窗函数,但该窗函数旁瓣抑制比不高,且带来了信噪比损失的增加;文献[8]应用加权网络方法降低旁瓣,通过先计算出输出信号的能量谱密度,然后计算脉冲压缩的传递函数,该方法计算量较小但旁瓣抑制比不高;文献[9]提出了应用人工神经网络的方法,通过控制雷达接收波形与输出波形之间的映射关系来抑制旁瓣,但该方法计算量较大,且鲁棒性较低。就工程设计而言,窗函数加权脉冲压缩是最容易和最常见的旁瓣抑制方法。窗函数加权技术引入具有海明窗、凯塞窗、布莱克曼窗以及泰勒窗等传输函数的加权网络进行旁瓣抑制[10]。
常用脉冲压缩的窗函数加权法分为单向加权法和双向加权法,传统的窗函数单向加权法通过在接收端对匹配滤波器系数时域窗函数加权来抑制旁瓣,双向加权法是在单向加权法的基础上,对发射信号再进行窗函数时域加权,从而进一步的抑制旁瓣[11]。不过这两种常用的窗函数加权法都是以不同程度的主瓣展宽获取峰值旁瓣的降低,相对单向加权法,双向加权法脉压后的旁瓣更低,但带来了更严重的主瓣展宽增加,导致雷达距离分辨率严重下降[12]。
本文试图回归窗函数的本身研究,在LFM 信号加权窗函数脉冲压缩的理论基础上,通过数学方法对常用的窗函数进行分析并加以改进,寻求一种在雷达脉冲压缩后主瓣展宽不变前提下,降低脉冲压缩信号峰值旁瓣的新方法。
1 窗函数线性组合法的基本原理
单向窗函数加权脉压和双向窗函数加权脉压的过程分别为
式中:s(t)为发射信号;h(t)为对应的匹配滤波器系数;w(t)为窗函数;y(t)为脉压输出;“⊗”表示卷积。在窗函数特性研究中[13],发现海明窗和汉宁窗的结构相似[14],都由一个常数和余弦函数加权组成,它们的表达式分别如下:
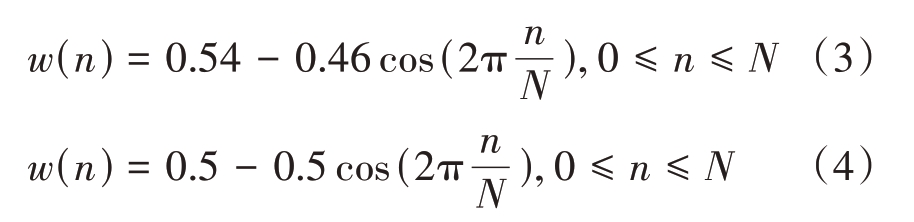
对这两种窗函数的表达式分析可知,海明窗、汉宁窗可分解为矩形窗和余弦函数窗的线性组合,但这两种组合结构相同的窗函数旁瓣抑制能力却有较大差异,因此,基于这两种一次余弦窗的思想,本文引出了窗函数的线性组合法,过程如下:
式中,w1和w2为窗函数线性组合法的两种基窗函数,w3为线性组合后的窗函数,a 为组合系数。为了在理论中证明窗函数线性组合法的旁瓣抑制能力,将上述组合后的窗函数w3与线性调频信号进行加窗脉冲压缩,设其脉压后的信号为y(t),由公式(1)可得窗函数线性组合法的组合窗w3加窗脉压过程为
则脉压输出信号y(t)的总能量E为

将公式(5)代入可得
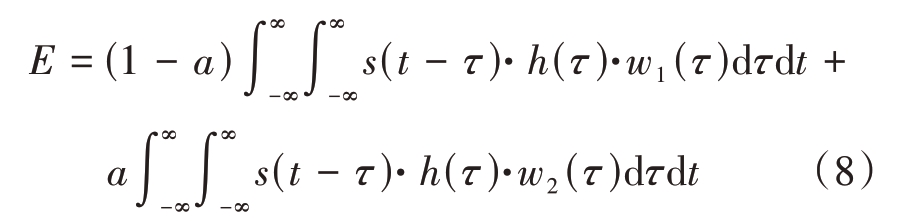
式中,第一项和第二项分别为基窗函数w1和w2分别做脉冲压缩输出的总能量,将其分别设为E1和E2,则
假设E1 > E2,则
由于脉压输出总能量为主瓣能量与旁瓣总能量之和,若这三种窗函数w1、w2、w3脉压后主瓣不变,由E < E1 可得此时线性组合窗w3脉压后的旁瓣总能量低于基窗函数w1脉压后的旁瓣总能量。同理,当E1 < E2时,可得线性组合窗w3脉压后的旁瓣总能量低于基窗函数w2脉压后的旁瓣总能量。因此,窗函数线性组合法理论上可在主瓣不变时,降低脉压后的旁瓣。
为了检验窗函数线性组合法的旁瓣抑制效果,取基窗函数w1与w2分别为三角窗与汉宁窗、变形布莱克曼窗与海明窗的两种线性组合窗,变形布莱克曼窗表达式为
式中,w0 为布莱克曼窗的表达式,窗函数组合原理如公式(5)所示。将这两种线性组合窗分别与线性调频信号做单向加窗脉压与双向加窗脉压,该过程分别如公式(1)与公式(2)所示。为了使线性组合窗获得理想情况下极低的旁瓣[15],令其脉压输出信号y(t)主瓣不变,所有旁瓣的总能量无穷小(近似为0),由此即可推导出线性组合窗中组合系数a的值,该过程如下:
式中,t1,t2是信号y(t)的主瓣起点和终点,通过对y(t)求微分后取其零点而得。所求两种线性组合窗的组合系数a 分别为0.74 和0.7,为检验这两种组合窗的加权脉压效果,设置时宽T=20 μs,带宽B=4 MHz,采样频率Fs=20 MHz,输入信号为调频斜率K=B/T 的LFM 信号,本文所有仿真条件均与此相同。这两种线性组合窗与其基窗函数脉冲压缩结果对比如图1和图2所示。
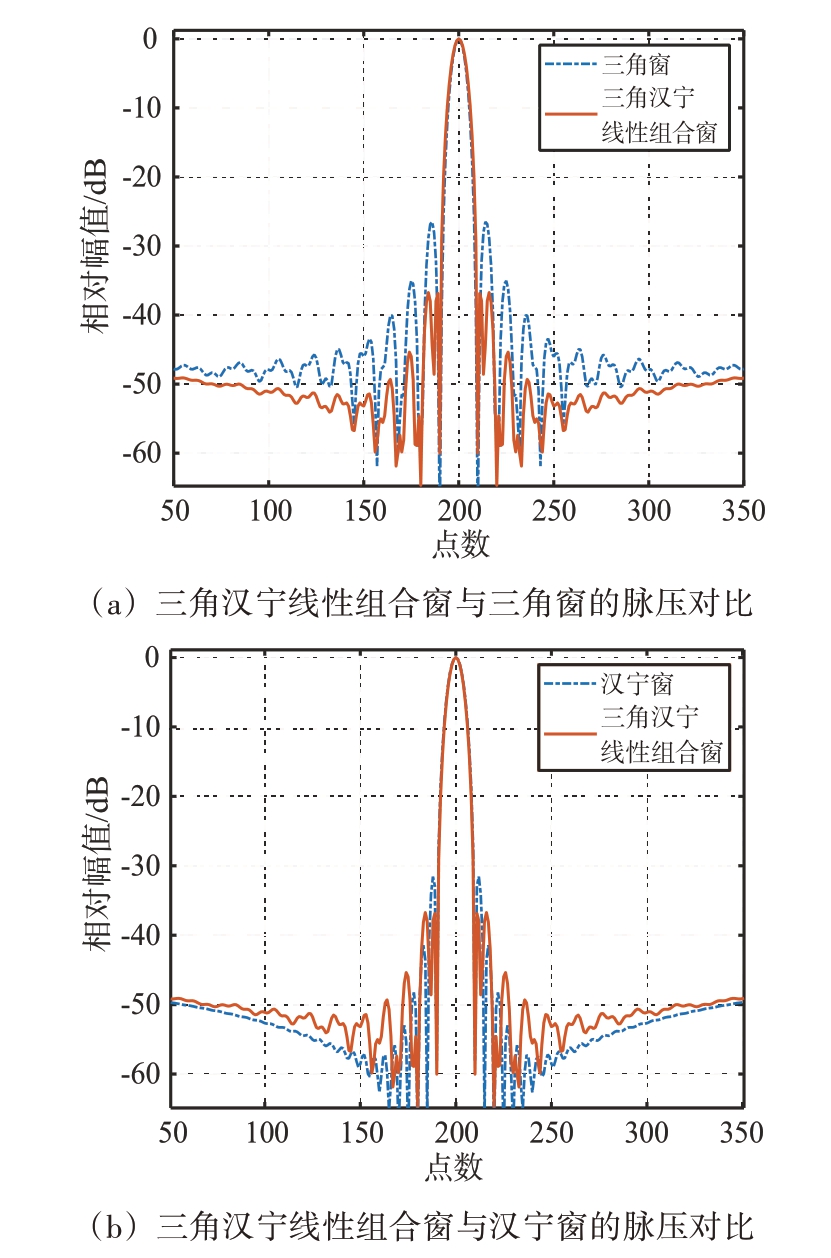
图1 三角窗、汉宁窗与它们的线性组合窗的脉压对比
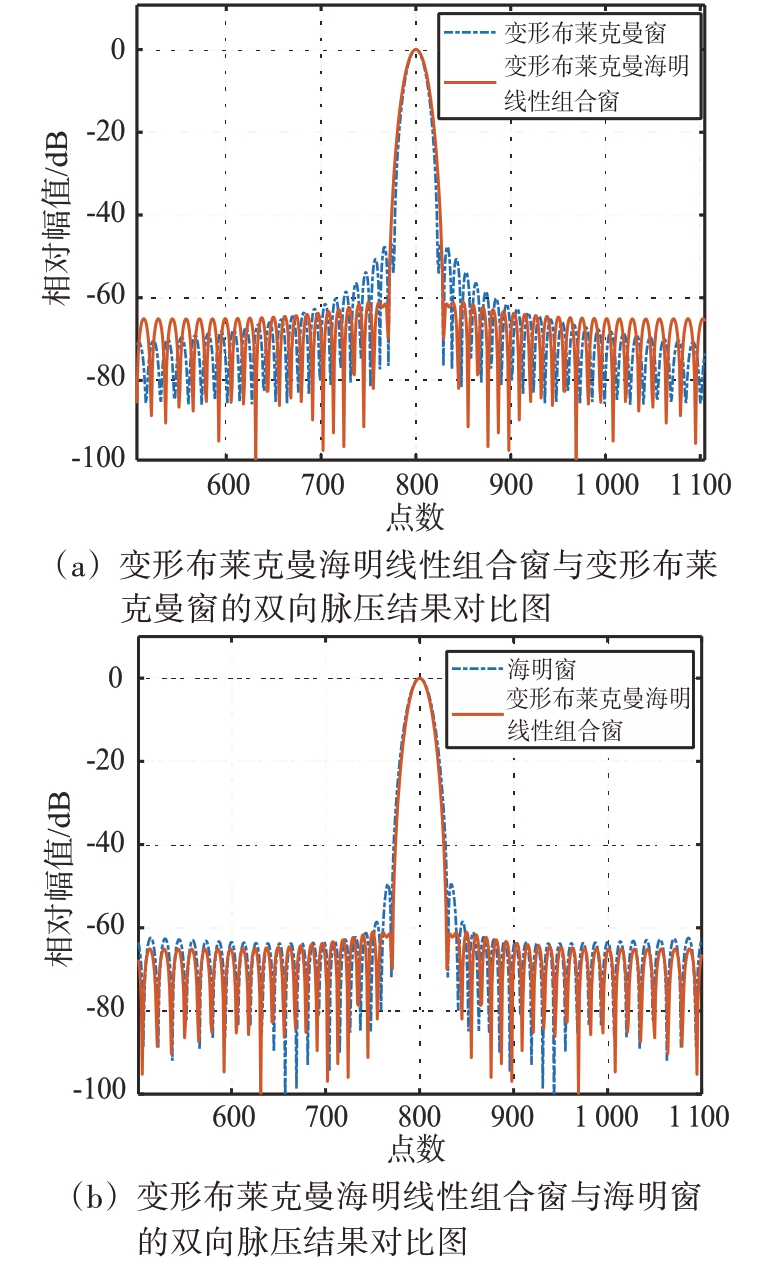
图2 变形布莱克曼窗、海明窗与它们的线性组合窗的双向脉压结果对比
由仿真结果可知,这两种线性组合窗分别做单向加窗脉压与双向加窗脉压后,与对应的基窗函数相比,脉压输出的主瓣宽度基本不变、峰值旁瓣降低,三角汉宁线性组合窗相比它的基窗函数峰值旁瓣降低5 dB 以上,变形布莱克曼海明线性组合窗相比它的基窗函数峰值旁瓣降低10 dB 以上,这两种线性组合窗远区旁瓣较高,不过该影响相对较小。
综上所述,窗函数线性组合法在它的基窗函数基础上,理论上可在主瓣不变时降低脉压信号旁瓣,并且通过仿真实验验证该方法在一些窗函数组合中的旁瓣抑制效果得到提高。
2 一种改进的窗函数非线性组合法
在雷达脉冲压缩中,有些情况下需要很低的旁瓣,从而获取更高的目标检测率[16]。因此,本节对窗函数线性组合法改进,寻求在主瓣宽度不变下,将脉压输出的旁瓣进一步降低。对此,通过对窗函数线性组合法中引入一个参数r 改进该方法的组合关系,使窗函数线性组合法由传统的线性组合关系变为非线性组合关系,改进的窗函数非线性组合法如下:
式中,w'3为非线性组合后的窗函数,w1、w2为基窗函数,a 为组合系数,r为可变参数。为了证明改进的窗函数非线性组合法旁瓣抑制效果,将其与窗函数线性组合法进行脉压结果对比,脉冲压缩过程如公式(1)所示,设窗函数线性组合法与改进的窗函数非线性组合法脉压输出信号分别为y3(t)和y'3(t),它们的脉压输出总能量差ΔE为
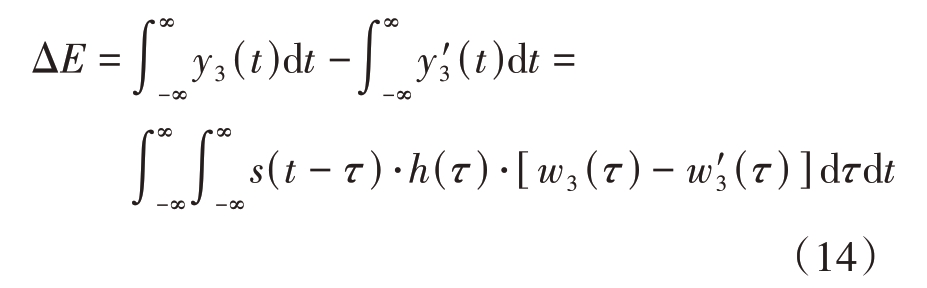
设Δw3(τ)= w3(τ)- w'3(τ),根据公式(5)与公式(13)可得
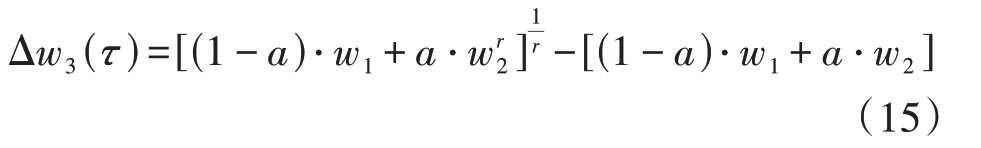
当a趋近于1时,1-a趋近于0,此时(1- a)⋅w1可近似为0,则
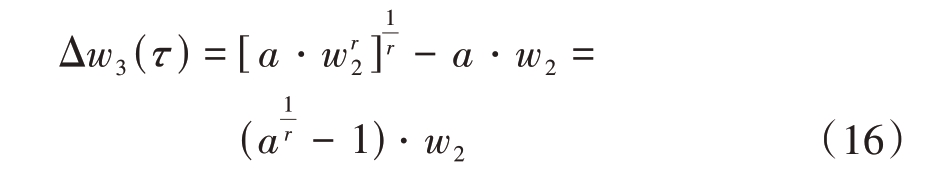
故当0 < r <1,a →1+时,有
将上式代入ΔE中可得
同理,当r >1,a →0-时,也可推得ΔE >0。故当参数r >0 时,存在组合系数a 使得改进的窗函数非线性组合法脉压输出总能量低于窗函数线性组合法,由于脉冲压缩输出总能量为主瓣能量与旁瓣总量之和,若脉压输出信号主瓣不变,则此时改进的窗函数非线性组合法脉压输出旁瓣总能量低于窗函数线性组合法。因此,通过上述理论分析,证明在主瓣不变下,改进的窗函数非线性组合法相比窗函数线性组合法可取得更低的旁瓣。
为了检验改进的窗函数非线性组合法的旁瓣抑制效果,取与第2 节相同的基窗函数w1、w2分别为三角窗与汉宁窗、变形布莱克曼窗与海明窗的两种非线性组合窗,并对这两种组合窗分别进行单向加窗脉压和双向加窗脉压,脉压过程分别如公式(1)和公式(2)所示。为了便于对比,令改进的窗函数非线性组合法的参数r 为自变量,组合系数a 为因变量,通过对不同r 值的非线性组合窗脉压峰值旁瓣取最理想结果,求出此时组合系数a的值,该过程如公式(12)所示,参数r 取不同值时两种非线性组合窗的组合系数a 的值以及加窗脉压的峰值旁瓣比和主瓣展宽结果分别如表1、表2所示。
表1 不同参数r下的三角窗、汉宁窗及它们的组合窗单向加窗脉压结果

窗函数类型三角窗汉宁窗线性组合窗参数r取值组合系数a值非线性组合窗1 1 1 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2 2.2 2.4 2.6 2.8 0 1 0.73 0.89 0.83 0.77 0.73 0.72 0.76 0.82 0.88 0.93 0.96 0.97 0.98 0.99主瓣展宽1.45 1.63 1.58 1.67 1.65 1.62 1.58 1.54 1.51 1.51 1.51 1.52 1.53 1.54 1.54 1.54峰值旁瓣比/dB-26.50-31.56-36.73-37.64-37.19-36.91-36.73-36.93-37.92-39.70-41.78-42.83-43.00-42.20-42.01-42.12
表2 不同参数r下的海明窗、变形布莱克曼窗及它们的组合窗双向加窗脉压结果
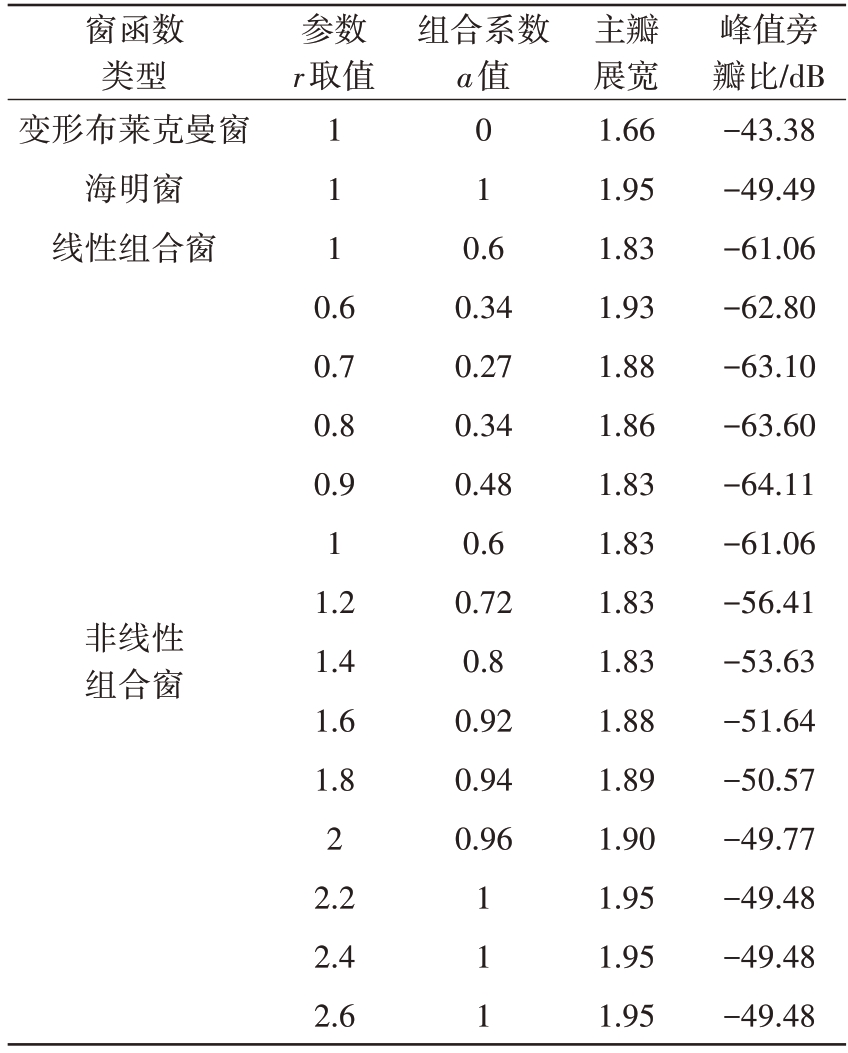
窗函数类型变形布莱克曼窗海明窗线性组合窗参数r取值组合系数a值非线性组合窗1 1 1 0.6 0.7 0.8 0.9 1 1.2 1.4 1.6 1.8 2 2.2 2.4 2.6 0 1 0.6 0.34 0.27 0.34 0.48 0.6 0.72 0.8 0.92 0.94 0.96 1 1 1主瓣展宽1.66 1.95 1.83 1.93 1.88 1.86 1.83 1.83 1.83 1.83 1.88 1.89 1.90 1.95 1.95 1.95峰值旁瓣比/dB-43.38-49.49-61.06-62.80-63.10-63.60-64.11-61.06-56.41-53.63-51.64-50.57-49.77-49.48-49.48-49.48
两种非线性组合窗的主瓣展宽、峰值旁瓣与参数r 值的变化关系分别如图3 和图4所示。由图3 和图4 可知,随着r 值的增加,两种非线性组合窗脉压后的主瓣展宽先降低而后趋于饱和;峰值旁瓣先提高再降低又提高,最后趋于饱和,这种非线性变化的原因是当参数r 靠近1 时,r 与1/r 都接近为1,影响较弱,所以此时组合系数a的存在产生干扰作用,主瓣展宽和峰值旁瓣趋于饱和是由于1/r随着r 的增大而趋于0,使得非线性组合窗形式趋于相同。因此,由于非线性组合窗脉压后的峰值旁瓣随着参数r 呈非线性变化,会出现峰值旁瓣极小值点,故两种非线性组合窗相比其对应的线性组合窗的主瓣展宽不变下可获得更低的峰值旁瓣。
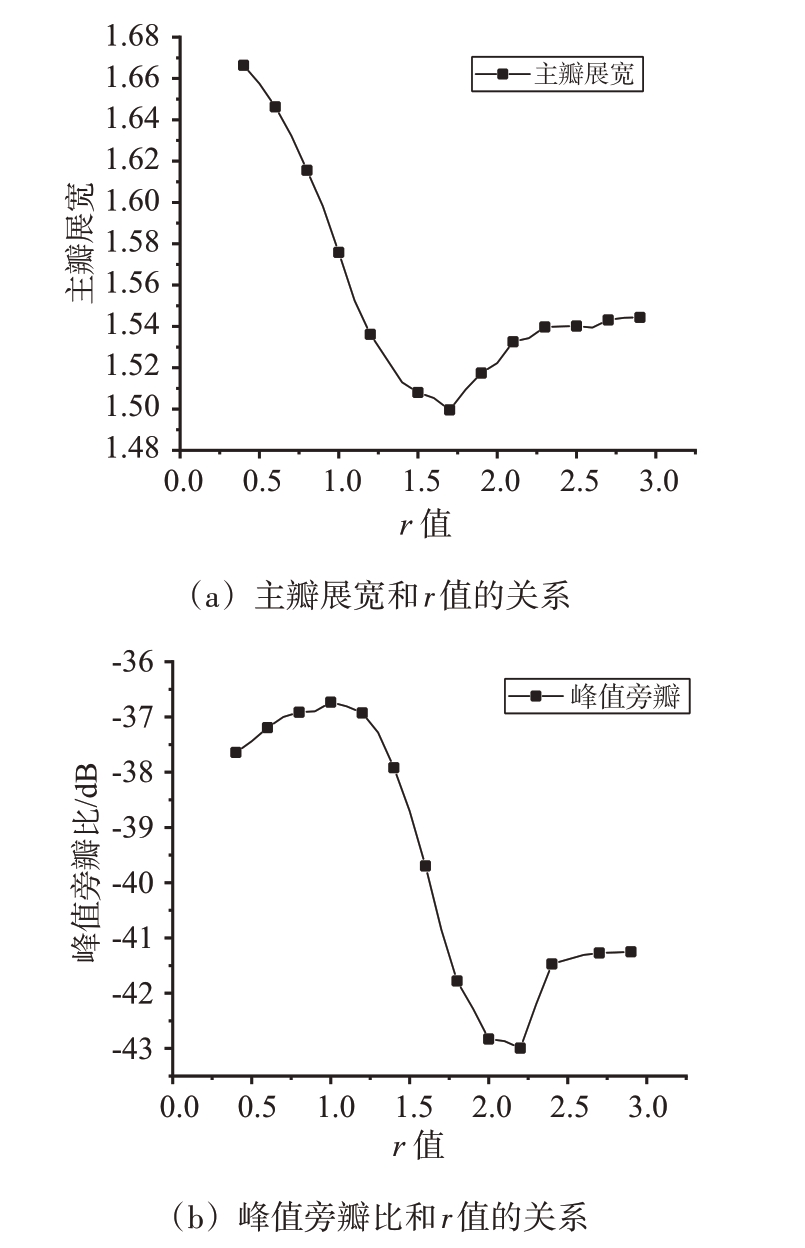
图3 三角汉宁非线性组合窗脉冲压缩性能和r值的关系
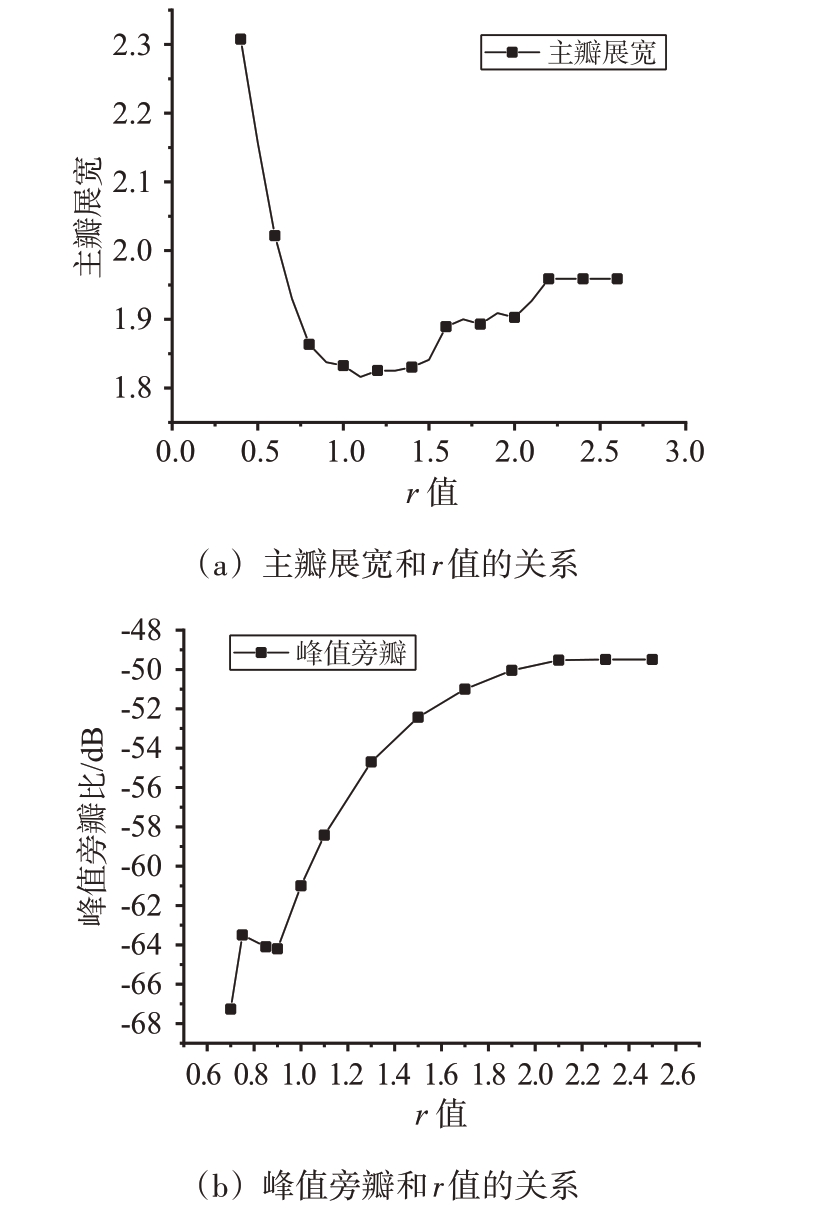
图4 变形布莱克曼海明非线性组合窗脉冲压缩性能和r值的关系
分别取上述表1 和表2 中相对其线性组合窗的主瓣不展宽、峰值旁瓣最低的三角汉宁非线性组合窗和变形布莱克曼海明非线性组合窗,它们的参数分别为r=2.2、a=0.96 与r=0.9、a=48,将这两种改进非线性组合窗与其线性组合窗以及基窗函数分别进行单向加窗脉压与双向加窗脉压,脉压结果如图5 和图6所示。由图5 和图6 的脉压结果可知,两种非线性组合窗在主瓣宽度不变下,峰值旁瓣大幅降低,相比对应的线性组合窗峰值旁瓣分别降低7 dB 和3 dB 以上,相比对应的基窗函数峰值旁瓣分别降低12 dB和13 dB以上。

图5 三角窗、汉宁窗及它们的非线性组合窗、线性组合窗的脉压结果对比
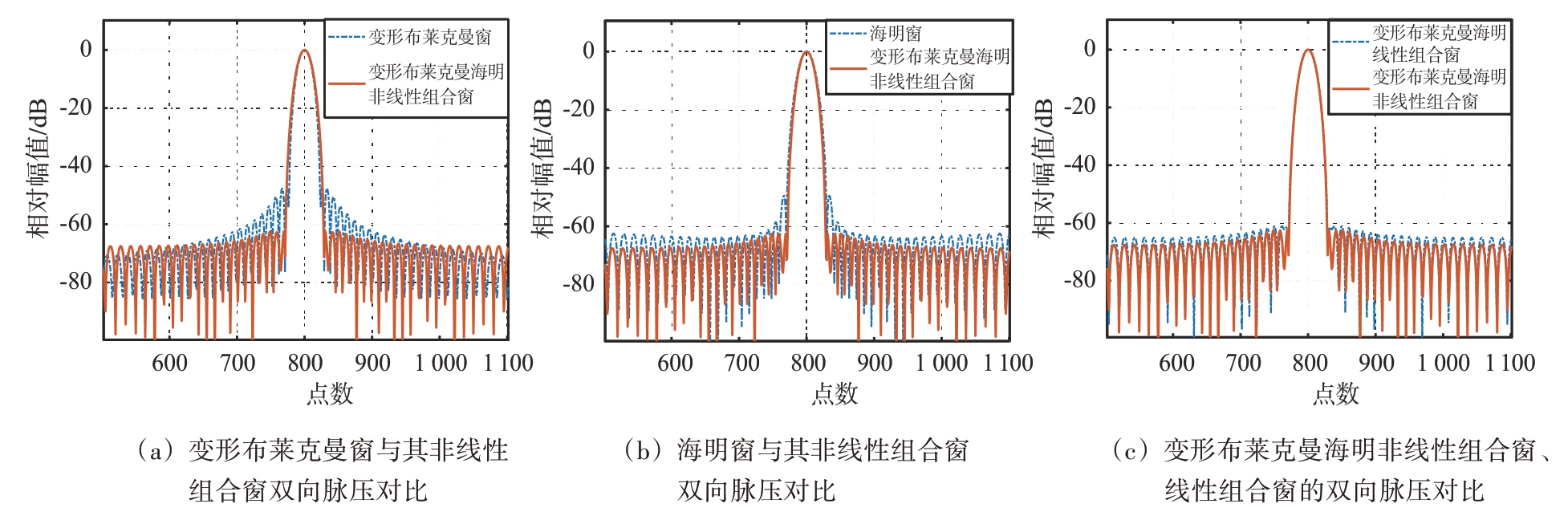
图6 变形布莱克曼窗、海明窗及它们的非线性组合窗、线性组合窗的双向脉压结果对比
综上所述,在窗函数线性组合法的基础上,改进的窗函数非线性组合法理论上可在主瓣展宽不变下,进一步降低脉压后的旁瓣,并通过仿真实验验证了该方法在一些窗函数组合中的旁瓣抑制效果也进一步提高。
3 改进的窗函数非线性组合法实验分析
3.1 改进的窗函数非线性组合法脉压效果检验
为了验证改进的窗函数非线性组合法在不同窗函数中使用效果,本节将几种常用的窗,分别是二次幂函数窗、三角窗、汉宁窗、海明窗以及布莱克曼窗,与主瓣展宽、峰值旁瓣可调的凯塞窗用改进的窗函数非线性组合法进行组合,为了便于对比,所取凯塞窗的主瓣宽度分别与这几种常用窗相同,对应凯塞窗阶数k 分别为3.3,4.9,5.7,6.6 和8.5,比较在相同主瓣展宽下,这几种常用窗与凯塞窗以及它们的非线性组合窗的脉压效果。改进的窗函数非线性组合法与上文相同,过程如下:
式中w'3 为非线性组合后的窗函数,w1为二次幂函数窗、三角窗、汉宁窗、海明窗或布莱克曼窗,w2为与w1主瓣宽度相同的凯塞窗,a、r 为使得组合窗主瓣不展宽、峰值旁瓣取最低值时的参数,该参数的求解过程与第2 节相同。二次幂函数窗的表达式如下:
与上文相同,设置时宽T=20 μs,带宽B=4 MHz,采样频率Fs=20 MHz,输入的LFM 信号调频斜率为K=B/T。表3给出了这几种常用窗函数与凯塞窗以及它们的非线性组合窗在相同主瓣展宽下的脉冲压缩结果,由于LFM 信号脉压后的旁瓣峰值会受到时宽带宽积的限制,因此为了便于对比,该表格中的峰值旁瓣比为窗函数频率响应的旁瓣峰值,主瓣展宽与信噪比损失为加窗脉压后结果。
表3 相同主瓣展宽下几种窗函数与凯塞窗以及它们的非线性组合窗的脉压结果对比
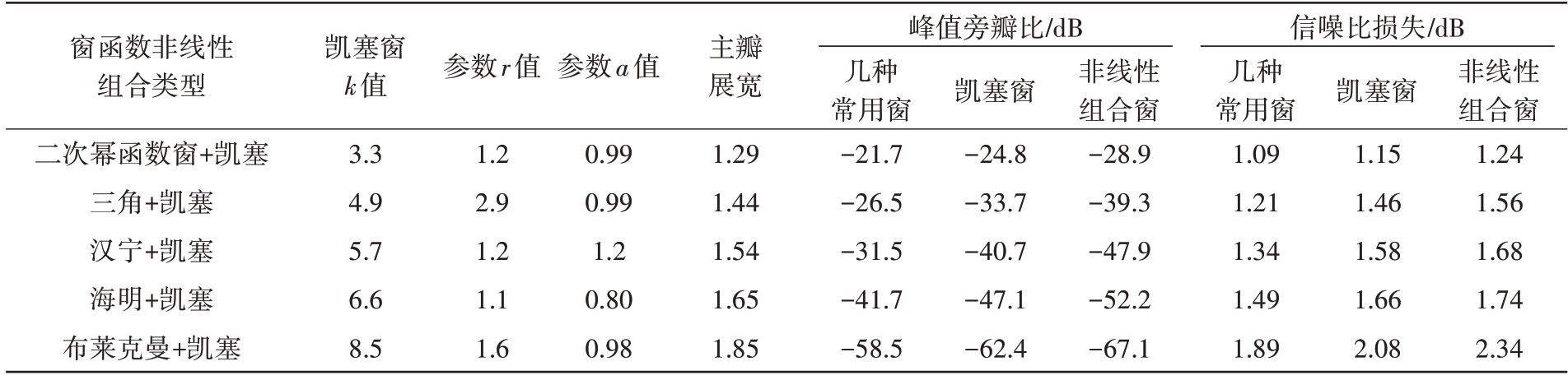
窗函数非线性组合类型二次幂函数窗+凯塞三角+凯塞汉宁+凯塞海明+凯塞布莱克曼+凯塞凯塞窗k值3.3 4.9 5.7 6.6 8.5参数r值参数a值0.99 0.99 1.2 0.80 0.98主瓣展宽1.29 1.44 1.54 1.65 1.85峰值旁瓣比/dB 信噪比损失/dB 1.2 2.9 1.2 1.1 1.6几种常用窗-21.7-26.5-31.5-41.7-58.5凯塞窗-24.8-33.7-40.7-47.1-62.4非线性组合窗-28.9-39.3-47.9-52.2-67.1几种常用窗1.09 1.21 1.34 1.49 1.89凯塞窗1.15 1.46 1.58 1.66 2.08非线性组合窗1.24 1.56 1.68 1.74 2.34
图7 给出了这几种常用窗函数与凯塞窗及其非线性组合窗在相同主瓣展宽时的脉压结果对比。
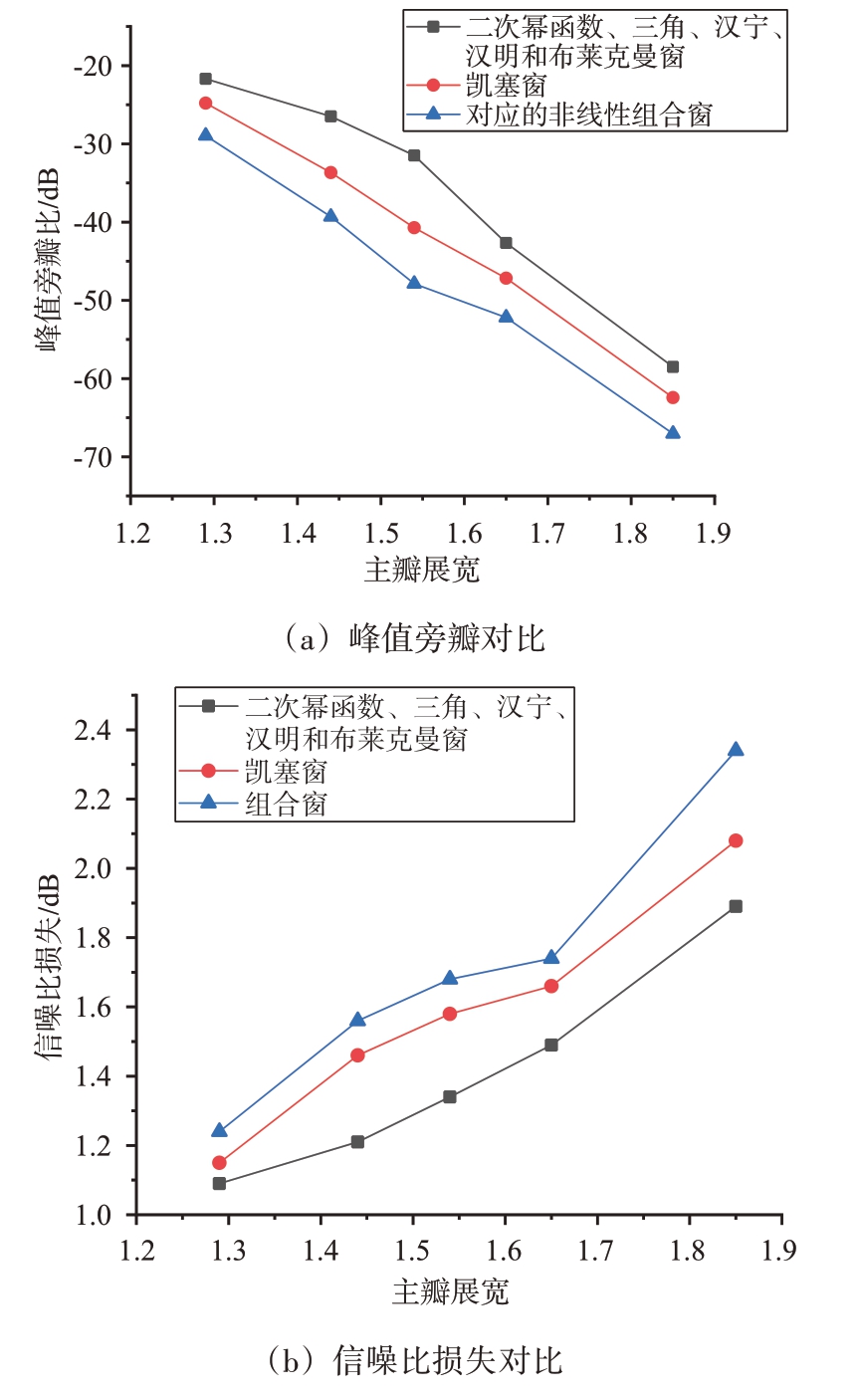
图7 相同主瓣展宽下几种窗函数与凯塞窗以及它们的非线性组合窗的脉冲压缩结果对比
由表3可以看出,这几种不同基窗函数的非线性组合窗脉压后的主瓣展宽、峰值旁瓣比、信噪比损失等性能各不相同。由图7(a)可知,在相同的主瓣展宽下,几种非线性组合窗的峰值旁瓣最低,其次是凯塞窗,几种常用窗函数的峰值旁瓣最高,几种非线性组合窗相比凯塞窗峰值旁瓣降低4 dB以上、相比几种常用窗函数降低7 dB 以上;由图7(b)可知,相同的主瓣展宽下,几种非线性组合窗信噪比损失相比其他窗函数增加了0.1~0.5 dB,该影响相对较小。
综上所述,本文改进窗函数非线性组合法应用在多种常用的窗函数中,加窗脉压均可达到主瓣展宽不变、峰值旁瓣降低的效果,并且在相同主瓣展宽下的旁瓣抑制能力相比凯塞窗进一步提高。
3.2 改进的窗函数非线性组合法在多目标问题的应用和分析
由于在雷达信号的多目标检测中,若大目标的旁瓣过高则会产生虚假目标,无法准确地检测出小信号和小目标[17];若是脉压后信号主瓣宽度过大,则会导致分辨率下降,无法检测出两个临近的目标[18]。故本文以三目标检测为例,检验改进的窗函数非线性组合法多目标检测能力,为了便于对比,以上文中主瓣展宽相同的三角窗、k=4.7的凯塞窗以及它们的非线性组合窗为代表,分别检验这三种窗面对多个目标的检测能力,其中该非线性组合窗中的参数与上文相同。
由于以上3种窗的峰值旁瓣比不同,于是设置3 个强弱不等的目标,分别在第100、130、150个采样点上。仿真条件设置时宽T=20 μs,带宽B=4 MHz,采样频率Fs=20 MHz,发射信号为调频斜率K=B/T的LFM 信号,仿真参数与上文一致。仿真结果如图8所示。
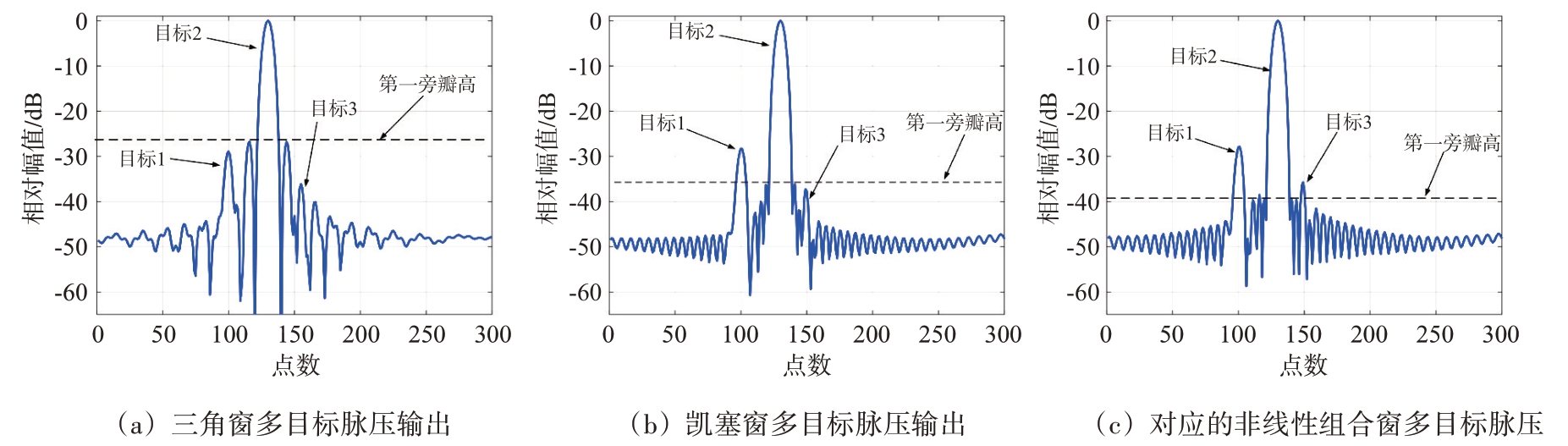
图8 三角窗、凯塞窗(k=4.7)以及它们的非线性组合窗多目标加窗脉压输出
由图8(a)可知,由于三角窗峰值旁瓣过高,导致第二个目标附近有很多较高的副瓣,这些副瓣强度超过另外两个目标,因此无法准确的区分另外两个目标。图8(b)是k=4.7 的凯塞窗多目标脉压输出,其旁瓣有所下降,使第一个目标可以被区分,但是第三个较弱的目标淹没在与其相邻的第二个大目标的旁瓣中。图8(c)是以三角窗和凯塞窗(k=4.7)为基窗函数的非线性组合窗多目标脉压输出,有着较低的旁瓣,可以很清楚地分辨这三个目标。
通过仿真实验,验证了上述非线性组合窗多目标加窗脉压具有较好的旁瓣性能,在主瓣宽度不变下,相比其基窗函数旁瓣抑制能力大大提高,适用于多目标的检测。本节基于改进的窗函数非线性组合法的其他几种非线性组合窗皆做过多目标检测仿真,效果良好,不再赘述。
4 结束语
针对雷达脉冲压缩中主瓣展宽与旁瓣抑制相矛盾的问题,本文提出了一种以常用窗函数为基窗函数的改进窗函数非线性组合法。通过对窗函数加权脉冲压缩的理论分析,首先证明窗函数线性组合法的旁瓣抑制能力,在此基础上,进一步证明本文所提的改进窗函数非线性组合法可以在主瓣展宽不变的前提下,将加窗脉压的旁瓣抑制能力相比窗函数线性组合法进一步提高。在改进窗函数非线性组合法的仿真实验中,验证了该方法应用在多种常用窗函数时,都可以在主瓣展宽不变、信噪比损失增加低于0.5 dB 的前提下,将峰值旁瓣相比凯塞窗降低4 dB 以上、相比几种常用窗函数降低7 dB 以上,并且在多目标检测仿真中,改进的窗函数非线性组合法也取得了比较理想的效果。
[1]AKHTAR J.High-Resolution Neural Network Processing of LFM Radar Pulses[C]//2023 IEEE International Conference on Acoustics,Speech and Signal Processing,Rhodes Island,Greece:IEEE,2023:1-5.
[2]FRASIER S J,ARGENTI F,FACHERIS L.Predistortion for Very Low Pulse-Compression Sidelobes in Solid-State Meteorological Radar[J].IEEE Geoscience and Remote Sensing Letters,2023,20:1-5.
[3]田达,王根弟,卢鑫.雷达信号时差频差定位关键技术研究[J].航天电子对抗,2011,27(1):45-49.
[4]王静,罗丰,付韶峰.谱修正旁瓣抑制技术的研究与应用[J].电子科技,2010,23(1):32-34.
[5]邹彬彬,陈晶晶,荆成财,等.谱修正技术在脉冲压缩信号检测中的应用[J].声学技术,2014,33(3):275-279.
[6]王传志,李学华,孙清,等.调频信号超低副瓣脉冲压缩算法[J].现代电子技术,2018,41(13):25-28.
[7]蒋忠礼,葛俊祥,郑启生.一种抑制雷达脉冲压缩旁瓣的新方法[J].现代雷达,2021,43(5):24-31.
[8]LU Qianrong,WANG Xiji,WANG Zhicheng,et al.Robust Adaptive Pulse Compression Under Encode-Decoder Network for Synthetic Aperture Radar[C]//2021 7th Asia-Pacific Conference on Synthetic Aperture Radar,Bali,Indonesia:IEEE,2021:1-5.
[9]戴永鹏.超宽带MIMO 雷达图像增强方法研究[D].长沙:国防科技大学,2021.
[10]GALUSHKO V.On Application of Taper Windows for Sidelobe Suppression in LFM Pulse Compression[C]//2020 IEEE Ukrainian Microwave Week,Kharkiv,Ukraine:IEEE,2020:995-1001.
[11]宁千千.抑制脉冲压缩旁瓣的算法研究[J].国外电子测量技术,2019,38(6):53-56.
[12]PEI Jiazheng,HUANG Yong,GUAN Jian,et al.Robust Adaptive Pulse Compression Method Based on Two-Stage Phase Compensation[J].IEEE Trans on Geoscience and Remote Sensing,2022,60:1-18.
[13]刘萍,邹林,周云,等.基于NLFM 的超低旁瓣脉冲压缩方法研究[J].雷达科学与技术,2014,12(5):527-531.
[14]刘金,宋红军.基于二次约束二次规划的窗函数设计方法[J].西安科技大学学报,2020,40(3):458-463.
[15]ZHU D,DONG X,LIN W.Pulse Compression with Very Low Sidelobes in a Spaceborne Weather Radar[C]//IGARSS 2008 IEEE International Geoscience and RemoteSensingSymposium,Nanjing,China:IEEE,2008:252-255.
[16]VAN ZYL A C,WIEHAHN E A,CILLERS J E,et al.Optimised Multi-Parameter NLFM Pulse Compression Waveform for Low Time-Bandwidth Radar[C]//International Conference on Radar Systems(RADAR 2022),Hybrid Conference,Edinburgh,UK:IEEE,2022:289-294.
[17]LIU Xinyu,ZHANG Tianxian,SHI Qiao,et al.LPI Radar Waveform Design with Desired Cyclic Spectrum and Pulse Compression Properties[J].IEEE Trans on Vehicular Technology,2023,72(5):1-6.
[18]陈洪猛,李明,李响.一种高效快速的二相码旁瓣抑制算法[J].雷达科学与技术,2012,10(1):48-53.




