0 引言
航天器外测测轨数据［1-2］是一类重要的飞行跟踪数据，在很多任务的轨道确定计算中是不可缺少的测量量。
随着航天器发射及在轨数量的日益增多，地面测控系统对大数据量、多星并行下的强实时［3］、自动化外测数据处理的要求不断提高。
航天器飞行过程中用于轨道测量的外测数据主要包含以下几类:1）地面雷达及微波统一测控系统［4-5］的测量数据:测量元素主要有测距、测角（方位角、仰角）、距离变化率（有时又称测速）等多类参数，以及深空设备［6］的距离和、距离和变化率等数据；2）光学设备测角数据；3）中继卫星四程测距［7］数据；4）甚长基线干涉测量数据［8］（Very Long Baseline Interferometry，VLBI）；5）星间外测测量数据等。
这些不同类别的外测数据在实际的传输格式（测量设备与处理中心之间的传输规定）、测量量等方面均存在着较大差异。合理地设计外测数据处理软件的架构，并进行并行化处理等就成为多任务、大数据量下外测处理软件设计的重要内容。同时，由于外测数据的实时处理过程有着明显区别于事后处理的一些特点，因而需要建立与实时处理要求相适应的各类算法。
针对这些问题，本文建立了一种强实时性的处理框架，并对其关键处理算法进行了阐述。
1 外测数据实时处理特点与内容
航天器外测数据实时处理软件需要对火箭发射、轨道转移与在轨运行、再入返回或天体着陆等多种不同场景下的各种类型外测测量数据进行处理，这就对外测实时处理软件的设计与实现提出了较高要求。
1.1 外测实时处理软件特点
航天器外测数据实时处理软件具有以下特点:
1）强实时性:出于对航天器飞行状态监视的需要，外测实时处理软件需要在短时间内快速完成观测数据的处理工作。
2）高可靠性:外测实时处理软件必须有强可靠性［9］，不能因某些数据的异常等问题导致软件的非正常退出，从而影响其他数据的处理。
3）大数据量:软件可能同时要处理多个航天器、多台设备的1 s多帧的测量数据，必须具备大数据量处理能力。
4）长期自动化运行:外测数据实时处理软件常常需要服务于航天器整个寿命过程，需要其具有较高的适应能力和自动化运行能力。
5）数据处理差异性:外测数据包含测距、测角、测速，及其他多种类型的测量元素，这些元素的处理要求有着较大差异。
1.2 数据处理内容
航天器外测数据实时处理的主要内容有:
1）数据接收与解算:实时接收各种类型外测测量数据，按照对应数据的传输格式及处理方法进行数值解算。
2）数据检择:主要进行数据的设备状态码检验、合理性检验［10］与野值剔除［11］等。
3）测距解模糊:当跟踪目标距离超出设备的最大无模糊距离时，需要利用卫星星历或轨道数据等对距离量进行解模糊［12］处理，以得到正确的值。
4）数据修正:完成地面设备距离零值修正、测角轴系误差修正、卫星应答机零值修正等。
5）时标修正:根据测量数据时标对应的时刻对测距、测角、测速进行空间传播时延修正，测速数据还包含积分时间修正，以及深空三向测距的钟差［13］修正等。
6）电波折射修正:电波在目标和测控站之间传播时，由于穿过大气层的不均匀介质，使电波传播路径发生弯曲，而且是非匀速的传播，使得观测量出现折射误差。大气折射效应对无线电波的角度、距离、速度等测量值都会带来误差，电波折射修正主要完成此类修正处理，它包含了对流层［14］、电离层［15］等多类型的修正处理。
7）数据平滑处理:测量数据帧频较大时，有时需要利用多帧数据平滑处理出单帧数据，达到减少数据量的目的。
8）拼帧处理:有些应用场合需要将测距、测角、测速等不在同一帧的数据拼接成一帧数据（例如有的定位算法需要将火箭跟踪的测距与测角数据一起使用来计算出其位置信息）。
9）数据记录与发送:将处理后的结果按规定接口发送给其他软件，并完成必要的数据记录。
2 并行处理设计
外测数据实时处理软件具有数据量大、类型复杂、实时性及可靠性要求高等特点，同时不同类型的数据在处理内容上有较大差异，为此本文将综合采用多线程与多进程相结合的方式实现并行化的设计与处理。
2.1 软件架构设计
为简化软件开发，以及方便后期的维护和扩展，将处理软件划分为公共服务层、基础实现层、处理部件层、应用层等多个不同层级，如图1所示。
图1 外测软件的层次结构设计
公共服务层主要实现一些底层的公用服务，包括消息通信、日志服务、线程、数据及轨道动力学算法等，该层部件以动态链接库的形式提供给上层软件调用。其中，数据及轨道动力学算法库实现了各类坐标系的转换、轨道外推计算、时间转换、测站观测量计算、轨道摄动力计算、矢量及矩阵运算、插值算法、积分算法、方程组求解方法、数据拟合算法、数值统计算法等。
在公共服务层基础上，外测处理基础实现层完成了各类型外测数据的主要处理过程实现。由于不同地基设备、天基测量、移动测量设备的数据传输类型不一致、所包含的测量量不尽相同、处理要求不同，因而需要实现不同的处理过程。本基础实现层即对每种不同类型的数据分别提供不同的算法及处理线程实现，以供外测处理部件层的各软件调用。
处理部件层为实际的可执行软件层。外测数据处理软件系统在逻辑结构上划分为数据分类处理软件、数据补充处理软件、VLBI 处理软件、深空外测处理软件等多个可执行部件。可根据处理需要为不同的航天器创建不同的部件执行映像，实现各航天器数据的并行处理。
数据分类处理软件实时接收各类外测原始数据、航天器时间信息等，根据配置信息设置为各设备信源及数据类型的组合动态创建处理对象（各对象为一个处理线程，如图2所示），并将外测原始数据分发给相应的处理对象进行分类处理。该软件同时接收航时等公用信息，维护一个公用信息共享内存，以加锁的方式供各处理线程并发访问。
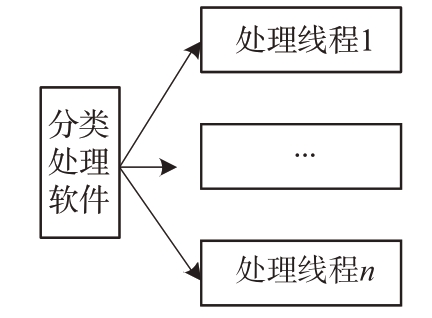
图2 分类处理软件线程示意图
数据补充处理软件实时接收测元不在同一帧的部分分类处理结果数据（有的数据类型处理完后可直接打包发送），进行拼帧处理及电波折射等修正后，将结果数据打包发送出去。
雷达及统一测控系统等普通类型外测观测数据在各软部件间的流动如图3所示。
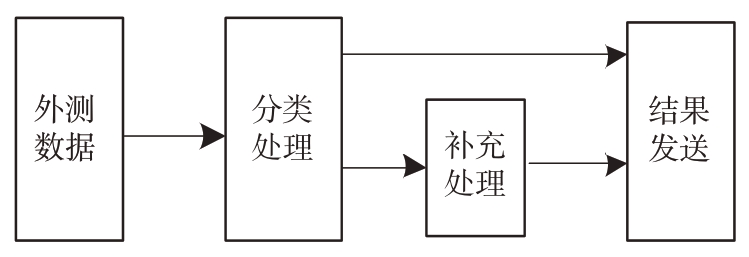
图3 雷达数据处理流程
VLBI 处理、深空数据处理等其他类复杂类型数据的处理部件主要完成一些专用类型数据的处理工作。
应用层主要是各类外测数据实时处理结果的应用计算软件，例如各类定位计算等。
2.2 分类处理及数据映射
对各类测量数据的处理方法库实现了指定类型数据的解析、处理流程、打包发送、线程创建与运行等方法。同一类的或相似的测量数据只需设计一种处理方法库，在调用软件的配置信息中设置有各类测量数据与处理方法库的映射关系，如其中一个记录{type1,lib1.so;}就表示了类型type1与处理方法库lib1.so之间的映射。
各种处理方法库从统一的处理方法基类继承，并重载必需的处理函数。
2.3 数据帧结构设计
为了满足不同的应用场合，软件对雷达与统一测控设备的处理结果设计了两类结果帧格式，一类是非拼帧格式，另一类是拼帧结果格式。
拼帧格式的结果帧包含的数据内容有:测量设备编码、数据类型编码、测距、方位角、仰角、测距变化率值、收端时标、数据时标、数据有效位、站址坐标等信息。
其中，使用了1 个字节的8 个比特位表示各个测量元素的有效性，如图4所示。
图4 比特位示意图
定义B0 位表示测距有效性；B1 位表示方位角有效性；B2 位表示仰角有效性；B3 位表示测距变化率的有效性；B4 位表示测距类型:单程测距、双程测距等；B5 位表示测速类型:测距变化率、距离和变化率等；B6～B7位用于扩展其他测量元素的表示。B1～B3 比特位初始化赋值为0，当同时满足下列条件时在处理结果中将对应比特位的值置为1（代表相应值有效）:1）一帧测量数据中有相应的测量元素；2）测量元素的值在事先给定的值域范围内；3）设备状态码校验有效。
相对拼帧格式，非拼帧格式的结果中仅包含一种或几种测量元素（测角帧一般同时包含方位角、仰角）。
中继星四程距离和数据、VLBI时延、时延率，赤经、赤纬等其他类外测数据采用单独的帧格式传输。
2.4 信息维护
软件以加锁的方式维护了包括航天器的名称、状态信息、精密轨道等各类公用信息。
软件单独使用一个线程外推出每秒钟的卫星星历数据，并保存到缓冲区中，供各设备的处理线程解模糊时使用。当维护线程检测到定轨结果更新时，清除缓冲区，重新存储星历数据。
2.5 特殊类型数据的处理
深空数据处理部件需要适应距离和数据、双向测量、三向测量等不同测距类型，适应单向、双向、三向等深空测速数据，并完成必要的修正处理和拼帧处理等。
为便于应用层软件使用，软件内部定义了统一的深空数据输出帧格式，其在主要测元量基础上，增加了信号发端站坐标、发端时间、信号收端站坐标、收端时间，以及测元类型等信息。信号收端和发端的时标可通过迭代算法计算得出［10］。当收端站与发端站一致时，三向测量［10］即变为双向测量。
同样中继四程测距处理软件除必须的修正处理外，也需要加上跟踪站坐标、中继星当前瞬时坐标（经纬高等，由中继星轨道外推获得当前帧历元处的坐标数据）等，同时利用各个中继星的轨道外推结果完成测距的解模糊处理。VLBI测量数据处理软件除必要的处理外，也需要增加其基线两端站的瞬时坐标等。
2.6 常驻运行模式
外测实时处理软件调度执行的一种传统方式是通过测控计划进行启停管理，但由于一些近地卫星运行圈次和测站跟踪计划切换较为频繁，而且多任务并行处理时各任务跟踪测控方式也不尽相同，采用这种方式会为操作带来诸多不便，且启停时可能造成数据处理的中断。
为解决这一问题，此处设计了“常驻运行”模式，即外测实时处理软件启动后将持续运行；同时软件将卫星中与具体跟踪弧段和测控事件有关的参数分离出来，通过共享内存方式来实时监视这些参数的变化，进而确定跟踪弧段和跟踪计划是否变化。一旦发生变化，实时处理软件执行相应的初始化操作，更新相关参数，创建有关设备测量数据的处理对象。
考虑到不同时段可能使用不同的设备进行航天器的跟踪测量，故采用常驻模式运行时如果不能合理管理所生成的处理线程，可能造成某些线程成为“僵尸”线程。为此软件在检索到某个处理线程已经长时间不处理数据，会将其销毁，以释放相应的资源。
此种常驻运行模式支持跟踪弧段和测控计划的无缝切换，满足了数据处理的连续性要求，在该模式下可实现处理软件的“自动运行、无人职守”。
它的优点主要体现在以下几个方面:
实现了卫星跟踪测控中外测数据实时处理软件的不间断运行，在跟踪弧段和跟踪计划切换时，数据实时处理工作不受影响，从而实现了“无缝”的切换，有效地避免了数据丢失等问题的发生。
该模式能够保证在各类情况下实时数据处理的连续性，为事后采集数据进行轨道确定和各类飞控计算带来了较大方便。
使用该模式后，软件只在卫星环境建立过程中启动一次，整个生命期间将持续运行，工作时不再需要受跟踪计划和跟踪弧段约束。这在很大程度上简化了相关的操作，显著地提高了工作效率。
在该模式下，可根据环境需要进行灵活配置，满足不同类型航天器的跟踪测控需求，具有很强的适应性和灵活性。
3 实时处理关键算法
3.1 一种基于增量累加的新型解模糊算法
测控设备的测量距离与其信号发射频率是相关的。受精度限制，测控设备的可测距离（即最大无模糊距离）是有限的，当跟踪目标超越最大无模糊距离时，就会产生一个求解真实距离的问题，此过程称作测距解模糊。
设t 时刻测距值为Rt，设备最大无模糊距离为Rmax，计算的模糊整周数为Nt，则解模糊后的测距值
应为
整周数Nt 计算时需要采用轨道或星历数据外推出测量设备的理论测量值Rc，Nt的计算方法为:
当
时，Nt取为int(Rc/Rmax)；
当
且
时，Nt取为int(Rc/Rmax)-1；
当
且
时，Nt取为
。
其中，mod 表示取余数运算，int（）表示取整运算。
考虑到长时间大范围机动过程中，采用轨道外推整周数方法进行实时解模糊处理时，有时可能出现整周数计算错误的情况，为此，本文同时提供了另一种实时解模糊算法，即增量累加算法。
设t0,t1,…,tn 时刻的设备距离数值依次为R0,R1,…,Rn（0 < Ri < Rmax，i=0,1,2,…,n）。
定义各点的增量值为
考虑到整周数的变化，将上述增量在此基础上修订为
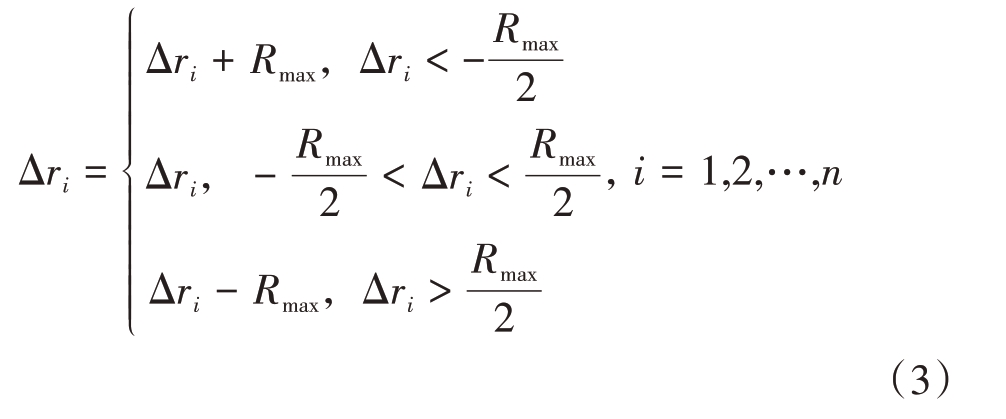
定义增量累加值为
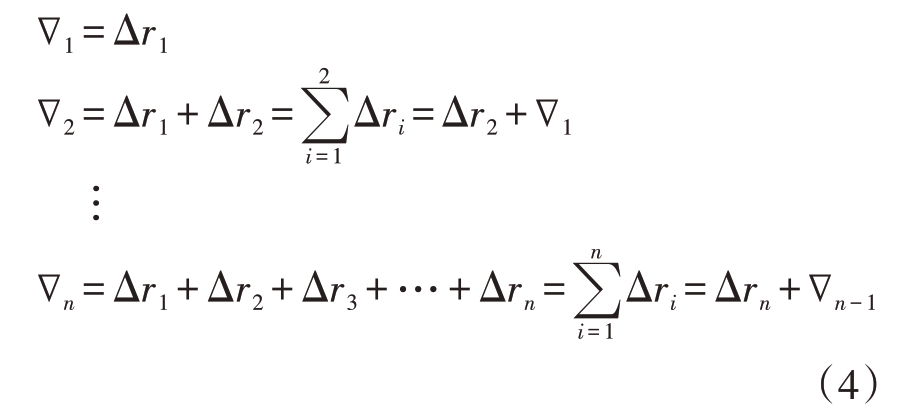
则采用增量累加法解模糊处理后的实测距离
依次为
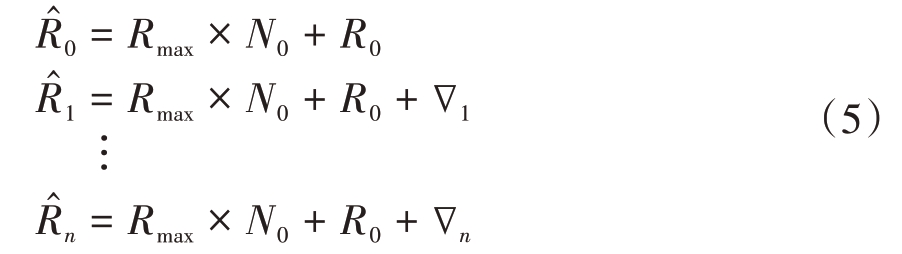
该方法受异常数据干扰后，仅影响当前数据的解模糊计算，而不会影响到后面的数据，因而稳定性较好。
增量累加法初始化时，先采用传统方法连续计算几点（如取10 点）的整周数，如果判断出这些点的整周数相同，则选定该值为初始整周数，增量累加算法转入正常运行状态。
当数据中断后，增量累加法需恢复初始状态。
3.2 基于三次多项式及三角函数转换的插值算法
外测数据的测距、测角、测速等数据由于采集及预处理等方面的原因，其数据时标常常存在差异，实时处理中经常需要进行时标的插值对齐操作，工程上多采用多项式插值［17］、滤波平滑等方法进行时标的对齐处理。
插值处理时，需注意以下几点:1）时标的跨天处理；2）方位角“过北”［17］的处理；3）角度插值的精度问题，如图5所示“过顶”附近的插值，本软件的解决方法之一是采用三角函数转换测量后进行插值计算［17］。
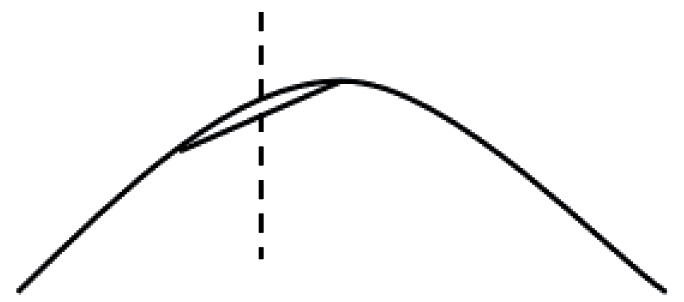
图5 “过顶”现象及插值误差示意
方位角的“过北”和角度插值精度问题本质上都是由于测量角度在数值上的不连续性造成，为此，本软件的解决方法是采用三角函数转换测量后进行插值计算，最后反解出角度的方法。
如对某类角度序列{t1,a1}、{t2,a2}、{t3,a3}…，要插值t 时刻的值，可利用角度的正弦函数与余弦函数的连续性来解决。具体地，先对{t1,sin（a1）}、{t2,sin（a2）}、{t3,sin（a3）}…序列插值出t时刻的值y1，再对{t1,cos（a1）}、{t2,cos（a2）}、{t3,cos（a3）}…序列插值出t时刻的值y2，则可计算出t时刻的角度值为y（t）=atan2（y1,y2），说明一下，此处的atan2 为C++语言中的反正切函数，表示值域在［-π，π］之间的反正切计算。
对某一类型数据的插值计算可采用多项式拟合的方法进行，为了达到较好的插值精度，本软件计算时使用三次或二次多项式进行插值处理。
3.3 时间实时性和数据完整性优先准则下的多缓冲搜索拼帧算法
由于有些应用层计算软件需要将测距、测角、测速等不同测量元素放在同一帧中，形成测元完备［16］的观测数据，此时往往需要将各种不同类型数据拼接成测元完备的数据帧，此即拼帧处理。
拼帧处理可采用两种合成准则:
1）数据完整性优先合成准则，即将几种数据收集完成后，再拼帧输出，优点是每帧数据都包含完整信息，缺点在于某一类数据中断或延迟会导致整帧的中断或延迟，实时性较差。
2）数据实时性优先合成原则，将实时性作为首要考虑因素，可直接将一种或几种数据合成一帧，此方法的缺点是有些帧的信息可能不完整。
本软件采用兼顾两类合成准则的超时合成策略，预先设置一定的时间限制，在限定时间内采用数据完整性合成准则，超时时采用实时性优先合成准则。
拼帧时的处理算法为:为同一设备的每一类数据设置一个单独的缓冲区（如图6所示），当新数据到来后，先按时间顺序插入相应的缓冲区中，然后遍历一次缓冲区，查找时标相同的数据，拼帧完成后将相应数据弹出缓冲区。
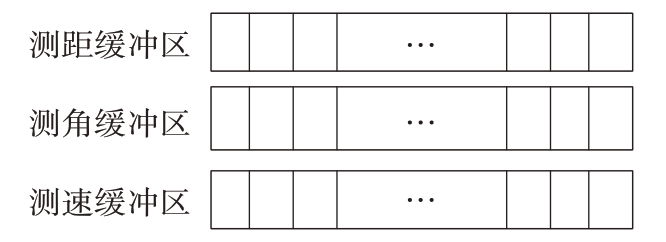
图6 数据拼接缓冲区示意图
为防止缓冲区无限制增大及影响处理效率，软件对各缓冲区的最大长度进行了限制（如最大保存10 s的数据）。
3.4 电波折射修正算法
电磁波通过对流层时传播速度将发生变化，路径也将产生弯曲，此现象称作对流层折射效应。在天顶方向，对流层引起的距离折射误差可达2～3 m，在3°仰角时，可达30～40 m。对流层延迟包括干燥大气附加延迟、湿润大气或水蒸气效应影响等。
软件提供了映射函数法［14］、球面分层模型［14］等算法来实现对流层折射效应的修正。
电磁波穿越电离层时，信号的路径会发生弯曲，传播速度变化，由此产生的偏差称作电离层折射误差［18-19］。电离层电子密度是求解电波路径延迟的关键，它与地理位置、地方时、太阳辐射强度、季节等因素有关。电离层具有散射性、互补性、瞬息万变等特点。
本软件提供了基于电离层格网模型［18-19］、Klobuchar模型［18-19］等的电离层修正算法。
3.5 基于最小二乘的多点数据平滑算法
外测数据的测量帧频可能较大，为了剔除数据中的野值或减少数据量，有时需要使用多点数据平滑算法计算出一点数据。此处采用基于多项式拟合和最小二乘估计的方法来实现多点平滑处理。
具体做法为，对多点测量数据序列yi,（i=1,…,m），使用
多项式进行拟合（一般取二次或三次多项式），采用最小二乘［20］算法计算出拟合系数ak,（k=0,…,n），使得yi- f(ti)的平方和最小即可，这样就可得到一次处理后的多项式拟合值。
然后可继续对样本序列点的均值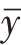
和方差σy进行统计，定义每一点的拟合残差为εi=yi-f(ti)，当
时可认为该点在本次迭代计算中为不合理值，予以舍弃。进而使用余下的点重新进行多项式最小二乘拟合，然后再次对所有点进行3σ野值剔除（有些点在不同的多项式下可能不一定当成野值）。这样经过多次反复迭代后，即可得到多点数据中心平滑后的值。
4 结束语
本文介绍了一种外测数据实时并行处理软件的设计思路及其实时处理的关键算法，该软件的主要特点如下:
1）联合采用多进程加多线程的方式进行了并行化处理实现，便于多任务大数据量下的并行处理；
2）采用常驻模式实现了全过程自动化运行；
3）采用了多种强实时性算法适应各种不同场景下的数据处理需求；
4）所提出的基于增量累加的新型解模糊算法解决了大范围机动过程中的解模糊难题。
应该看到，实时性要求下的外测数据处理软件及处理算法有很多不同于事后处理的地方，下一步还需在精细化处理等方面进行不断完善。
［1］涂国勇，刘利军，朱时银，等.外测数据融合准则及最优权值计算方法［J］.测控技术，2020，39（11）:39-44.
［2］朱丹，秦刚.一种提高外测数字引导准确性的系统工程方法［J］.遥测遥控，2019，40（2）:57-62.
［3］吴金美，侯亚威，李永刚，等.船载外测数据的实时检择方法［J］.电讯技术，2017，57（12）:1457-1463.
［4］石启亮，李强，曾俊康.船载统一载波测控系统基带实时可视化综合监视系统软件设计［J］.计算机测量与控制，2020，28（4）:7-10.
［5］何谦，刘洋，戴超，等.S 频段统一测控雷达健康故障诊断系统的设计［J］.计算机测量与控制，2019，27（4）:60-63.
［6］柯影，李大鹏，曹灿，等.深空探测网自动化运行管理研究［J］.无线电工程，2021，51（7）:573-579.
［7］王重阳，李心怡，熊亮，等.月球四程中继测量模式定轨定位方法研究［J］.深空探测学报（中英文），2022，9（6）:589-595.
［8］孙焱，张波，舒逢春.地球卫星VLBI 观测研究进展［J］.天文学进展，2019，37（1）:45-60.
［9］朱丹，孙君亮，童艳.高可靠飞行器外测实时处理软件关键技术研究［J］.遥测遥控，2018，39（5）:21-26.
［10］淡鹏，李恒年，李志军.应用三向测量数据的深空探测器实时滤波定位算法［J］.航天器工程，2015，24（2）:21-26.
［11］曹俊武，胡志群.多普勒天气雷达与风廓线雷达测风比较［J］.雷达科学与技术，2013，11（6）:605-610.
［12］李坤坤，曹锐，胡亚雄.一种弹道外测数据的野值处理方法［J］.火力与指挥控制，2021，46（6）:145-148.
［13］秦万治.相位干涉仪解模糊测量算法优选分析［J］.电子信息对抗技术，2019，34（4）:17-22.
［14］王丹，淡鹏.对流层经验映射函数模型精度分析［J］.无线电工程，2020，50（8）:666-671.
［15］杨超如，陈建文，鲍拯.天波雷达电离层相位污染模式认知与分析［J］.雷达科学与技术，2019，17（1）:37-43.
［16］淡鹏，李恒年，张定波，等.基于多元非完备信息的实时滤波定轨方法［J］.飞行力学，2014，32（3）:283-288.
［17］淡鹏，王丹.基于多项式插值的外测数据拼帧及平滑问题研究［J］.无线电工程，2017，47（7）:20-24.
［18］于耕，郝俊，赵龙.基于分片线性插值的北斗格网电离层延迟问题［J］.科学技术与工程，2018，18（26）:141-146.
［19］薛凯敏，刘瑞华，王剑.基于北斗GEO 的电离层延迟修正方法比较与分析［J］.全球定位系统，2018，43（2）:33-39.
［20］刘洪志，刘莉鑫.非线性最小二乘在工程测量坐标系统转换中的应用［J］.测绘与空间地理信息，2023，46（4）:186-188.
