0 引言
车载毫米波雷达具有探测距离远、测速精度高以及可实现穿透检测等特点。与激光雷达、摄像头等车载传感器相比，其在光线环境较差和风沙雨雪恶劣天气下表现出更可靠的感知水平，是车载辅助系统重要的传感器之一。现有的雷达体制有合成孔径雷达（SAR）、多发多收（MIMO）雷达以及多发多收-合成孔径雷达（MIMO-SAR）［1-3］。SAR 利用合成孔径原理，可以实现高分辨的微波成像。MIMO 雷达利用多发多收的波形分集特性联合处理多通道回波数据，可以虚拟出更大的虚拟孔径，从而实现高分辨测角［4-7］。MIMO 雷达与SAR 相结合，从而形成MIMO-SAR。本文使用MIMO 雷达通过时分复用（TDM）的方式发射和接收信号，然后进行一系列信号处理，得到目标的距离、速度和角度三维点云像。为了获得三维点云像，需要进行距离像估计、多普勒像估计和角度像估计。距离像和多普勒像的估计一般使用传统的快速傅里叶变换（FFT）方法，角度像的估计需要使用高分辨的测角方法才能区分角度相近的目标。因此，为了得到目标的高分辨成像，就需要结合高分辨的测角方法。
文献［8］提出一种结合渐近最小方差稀疏迭代的高分辨点云成像方法。该方法根据AMV 准则，利用采样数据协方差矩阵与真实协方差矩阵的差异，对网格功率进行多次迭代，从而提高角度分辨率［8］。然而，该方法需要迭代次数较高，计算量大，并且需要大量的数据快照，在数据快照较少的时候角度分辨性能急剧下降，不适合于车载场景。文献［9］使用基于加权协方差拟合准则的稀疏迭代协方差估计方法进行角度估计。该方法能够提供较高的角度分辨率和低旁瓣电平，但是其功率谱估计值与真实值之间存在一定的偏差，在得到功率谱估计初值之后还需要进一步进行迭代矫正，计算量大。文献［10］提出一种迭代自适应方法（IAA）用于MIMO 雷达成像。由于没有迭代更新噪声功率，因此角度分辨率有限。文献［11］提出一种基于奇异值分解的正则化IAA 方法（RIAA）来提高机载前视雷达成像分辨率。RIAA 通过去除小奇异值提高了噪声抑制性能，与传统的IAA相比，该方法角度分辨率有所提高。文献［12］利用GS因子分解计算IAA的数据协方差矩阵和其逆矩阵，提出了一种快速迭代自适应方法（FIAA）应用于车载平台。然而，该方法仅从降低计算量的角度考虑，角度分辨率依然有限。文献［13］使用迭代最小化稀疏学习（SLIM）方法用于MIMO 雷达成像。SLIM 在迭代过程中不断更新噪声估计值和信号功率估计值，因此具有良好的角度分辨率。SLIM 的迭代次数较少，一般不超过10 次就达到收敛条件，计算量适中。
上述高分辨测角方法都是基于网格划分来估计角度方向，角度估计结果只在划分好的网格点上。然而，在车载场景中，目标点不一定出现在划分好的网格点上，当目标点出现在网格点之外的角度时，估计的角度值与实际角度方向存在误差，这种误差称为离网误差，离网误差会导致估计精度下降。当前方目标距离较近的时候，精度下降不会对定位产生较大影响；但随着目标距离的加大，精度下降产生的定位不准确问题对后续的聚类、跟踪等信号处理带来巨大影响，因此必须解决离网误差问题。为了获得更加精准的目标来波方向，往往是通过将网格间距化分得更小来实现。然而过于密集的网格划分不仅会增强传感器阵列之间的相干性从而不满足有限等距性质条件，而且将大大增加方法的运算量［14］。为了获得更加精准的目标来波方向，同时避免密集网格划分带来的阵列相干性和运算量大的问题，本文利用ML 准则的统计特性，提出了一种SLIM 和ML 估计相结合的高精度测角方法用于点云成像。首先使用SLIM 方法对多个虚拟接收阵元的数据进行角度估计，然后最小化ML 成本函数来细化方向网格，经过较少次数的循环迭代，解决了离网误差问题，从而获得高分辨、高精度的测角结果。通过将本文提出的高精度测角方法用于角度像的估计，能够获得高精度的点云像，角度精度能够达到0.1°。
1 信号模型
假设MIMO 雷达系统具有I 个发射阵元和J 个接收阵元，每个发射阵元分时发射，J 个接收阵元同时接收。发射阵元水平间隔为
，接收阵元水平间隔
，这里的λ为信号波长。该系统通过TDM 发射方式，构成I× J 个虚拟阵元。考虑如图1所示，2发4收的MIMO 雷达系统，Tx1和Tx2为水平发射阵元，Rx1、Rx2、Rx3和Rx4为水平接收阵元，θh为第h个目标的来波方向，w=2πd sin θh/λ为相邻接收阵元相位差。
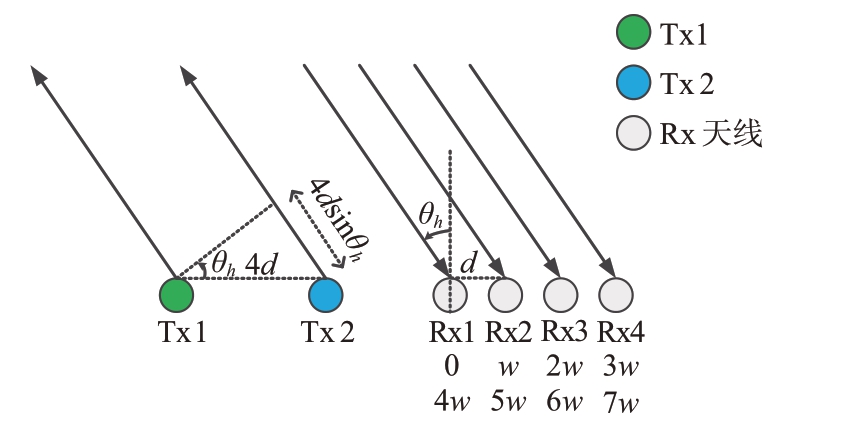
图1 MIMO雷达阵元分布
两个发射天线的间距是4d，以第一个Rx1 为参考，则各个接收阵元会出现[0 w 2w 3w]的相位延时，Tx2发射的信号相较Tx1要多经过4d sin θh的路程，因此各个接收阵元会出现[4w 5w 6w 7w]的相位延时。通过TDM 发射方式，共构成8 个等效虚拟阵元，虚拟阵元如图2所示。
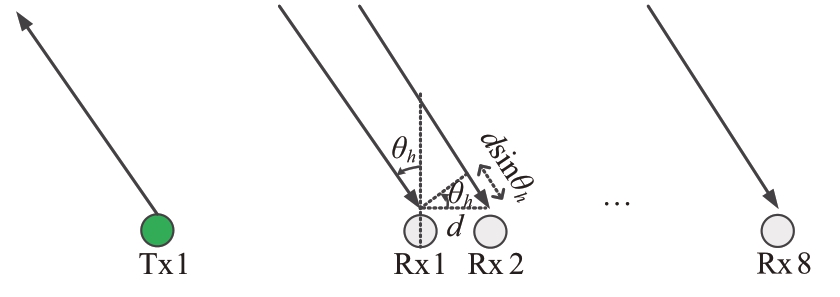
图2 等效虚拟阵元分布
假设t时刻第i个发射阵元的发射信号为
式中，f0为起始频率，
为调频斜率，B为信号带宽，T为每个调频信号Chirp的持续时间。
假设雷达照射区域内存在H 个目标，则第j 个接收阵元接收第i 个发射阵元所发射信号到目标并返回的回波信号表达式为
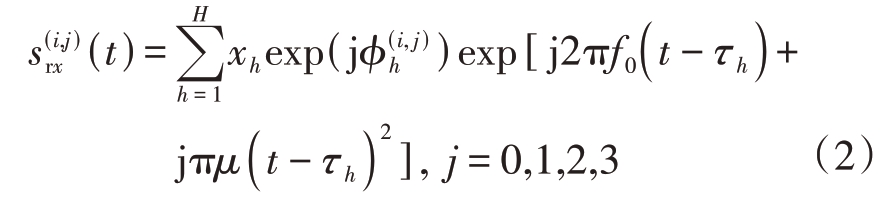
式中，
为第(4i+ j)个虚拟阵元相对参考阵元的相位延时，xh 表示第h 个目标的散射系数，τh表示第h个目标到参考阵元的信号传播时延，表示为
式中，c 代表光速，vh 代表速度，rh 代表距离。将回波信号与发射信号进行混频并经过低通滤波器进行滤波，得到的中频信号表达式为
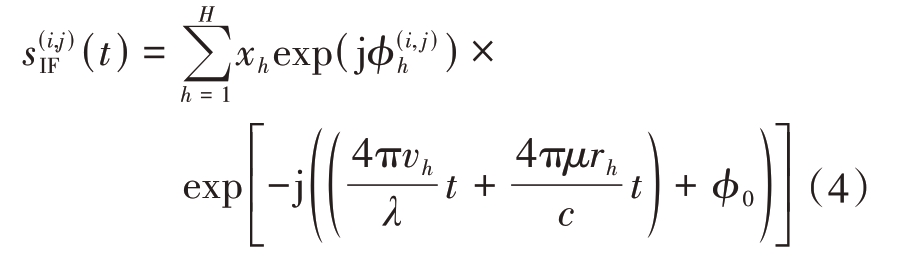
式中，
为信号波长，
为中频信号的初相，
为多普勒频率项。由于多普勒频率对中频信号频率的影响非常小，对目标的距离估计基本不会产生影响，故可将其忽略，则式（4）变为
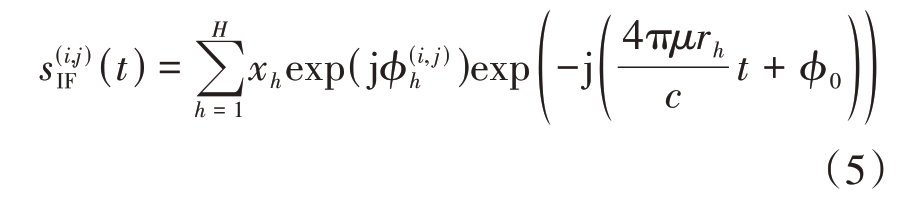
对中频信号以采样频率fs 进行K 点采样得到离散采样序列，其表达式为
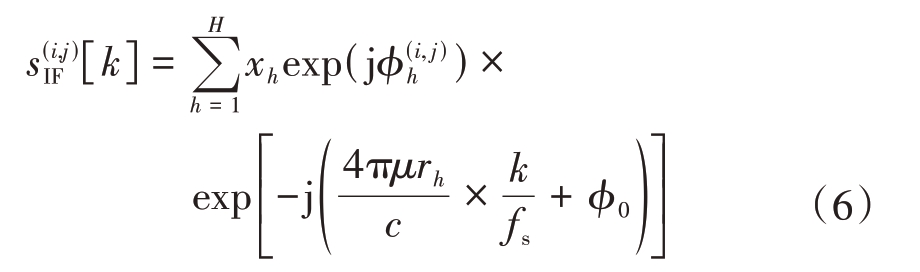
式中，k=0,1,2,…,K-1为采样频点。
2 方法描述
2.1 距离像估计
对离散采样序列信号
进行N 点FFT 得到一维距离像，表达式为
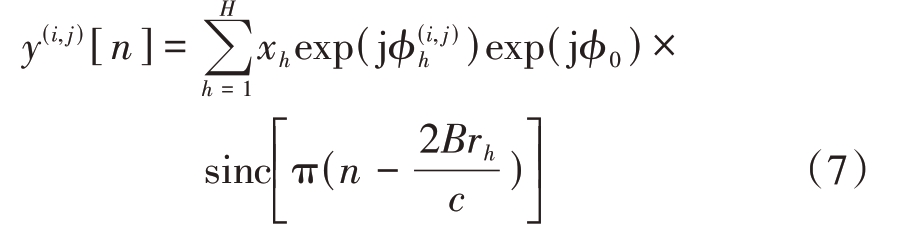
式中，n=0,1,2,…,N-1 为距离索引点。经过距离维FFT，可以获得目标距离像。
2.2 多普勒像估计
相邻周期的Chirp在距离维FFT谱中的峰值位置几乎没有发生变化，但是目标在Chirp 间的微小距离变化会引起中频信号的初相的变化。由傅里叶变换特性可知，信号的初相体现在峰值处对应的相位，因此计算相邻周期Chirp 相位差，即可得到目标的速度。相邻周期Chirp 相位差可以通过FFT 获取，这个过程称为多普勒维FFT［4］。相邻周期Chirp的相位差表达式为
式中，Δr= vhT 是目标在相邻Chirp 间的微小距离变化。对相同距离频点下的M 个Chirp 进行M 点FFT，则式（7）变为
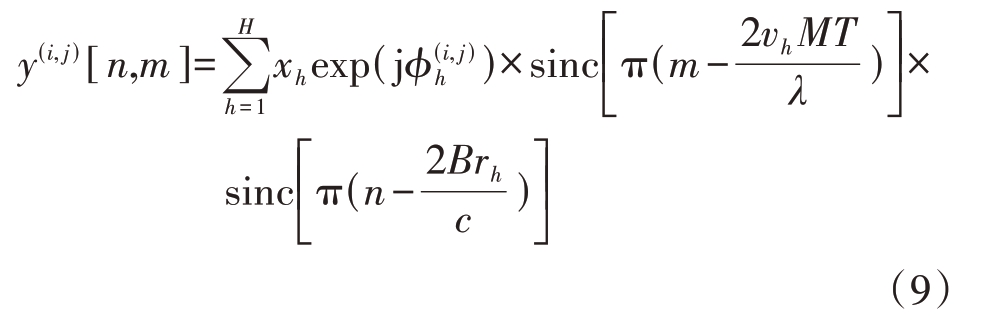
式中，m=0,1,2,…,M-1 为多普勒频率索引点。经过多普勒维FFT，可以获得目标多普勒像。
2.3 CFAR目标检测器
CFAR 目标检测器能够根据雷达杂波数据动态调整检测门限，在虚警概率保持不变的情况下实现目标检测概率最大化，CFAR 目标检测器如图3所示。
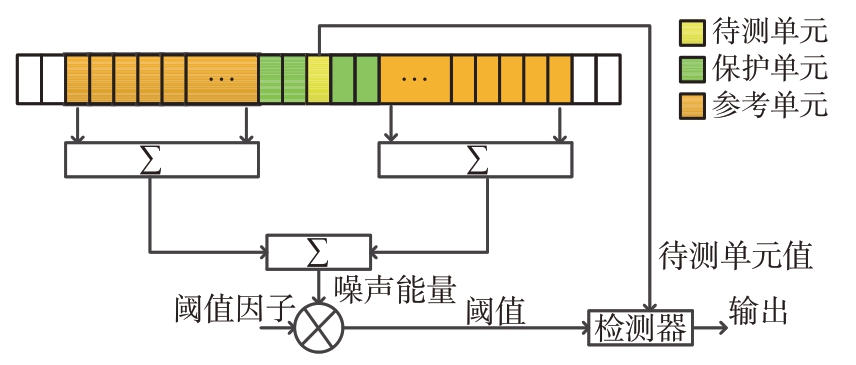
图3 CFAR目标检测器
经过距离FFT和多普勒FFT之后，可以获得距离-多普勒热图。将距离-多普勒热图先执行距离维CFAR，找到目标距离索引点r，再对距离索引点对应的多个Chirp 数据执行多普勒维CFAR，找到目标多普勒索引点v，从而得到目标的距离-多普勒索引点(v,r)。由sinc 函数的性质可知，当
时，
函数值为1，此时距离rh=
函数值为1，此时速度
因此式（9）表示为
将
代入式（10），则式（10）变为
2.4 相位矫正
目标的运动会产生多普勒相偏，这会导致无法正确进行角度估计，因此必须对目标运动引起的相位变化进行补偿矫正［15］。根据文献［15］提出的相位补偿方法进行补偿之后的信号表达式变为
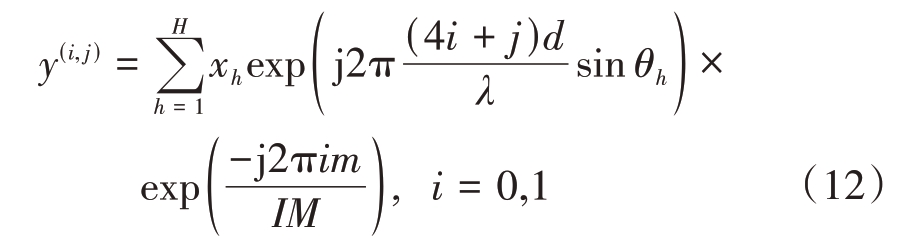
式中，I为发射阵元个数，M为多普勒频率索引点个数，m为多普勒频率索引点。由于I和M已知，m经过多普勒维FFT 并执行CFAR 之后也已知，所以
项为常数，将其归一化到xh 中，则式（12）变为
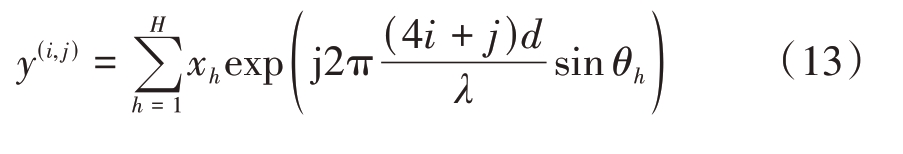
2.5 角度估计
为了产生稀疏性，将来波方向进行网格划分，将式（13）改写为
式中，K为划分的网格数，且K ≫H。
进一步，将多个虚拟阵元的数据进行堆叠，上式写成矩阵形式:
式中，
为测量数据向量，L=I*J 为等效虚拟接收阵元数，
为散射系数向量，
为导向矩阵，
为导向矢量，
为独立同分布的高斯白噪声向量，σ2为噪声值。
测量数据y的理论协方差矩阵表示为
其中，
pk 代表θk 方向未知的信号功率，I 为L 阶的单位矩阵。
在实际中，理论协方差矩阵通常是通过样本协方差矩阵进行估计:
根据文献［13］，考虑以下用于稀疏信号恢复的正则化最小化方法:
其中，
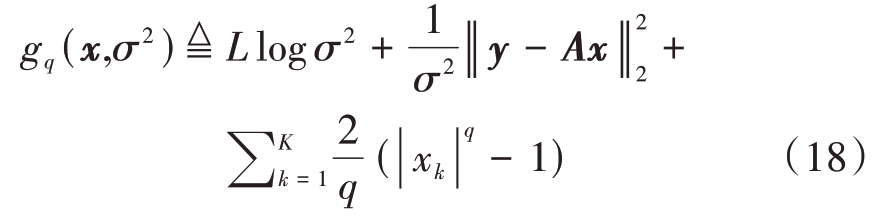
x 和σ2 的初始估计值通过延时求和（DAS）方法进行初始化，结合循环优化迭代，可以得到x 和σ2的新估计值。迭代过程分为两部分，估计x的时候保持σ2 不变，估计σ2 的时候保持x 不变。SLIM的迭代更新公式求解如下:
1）假设x和σ2的第i次迭代值为x(i)和σ2(i)，那么为了最小化关于x的函数gq(x,σ2)，令
gq(x,σ2)=0求解x(i+1)，得到以下非线性方程:
式中，
令
其中
那么式（19）变为
然后式（20）的解为
那么，第（i+1）次的迭代表达式为
2）最小化关于σ2的函数gq(x(i),σ2)。令
gq(x(i),σ2)=0 求解σ2(i+1)，可得第（i+1）次的迭代表达式为
如图4所示，假设方向网格的间隔为1°，在距离均为100 m、角度分别为1°和2°的两个网格点的横向距离x1和x2分别为1.74 m 和3.48 m，格点间的横向距离误差能够达到1.74 m，这样的离网误差会导致目标定位出现巨大偏差，如果不加以纠正，提供给ADAS 系统的点云数据将是不可靠、不准确的，无法与其他传感器数据进行融合，因此必须解决离网误差问题。
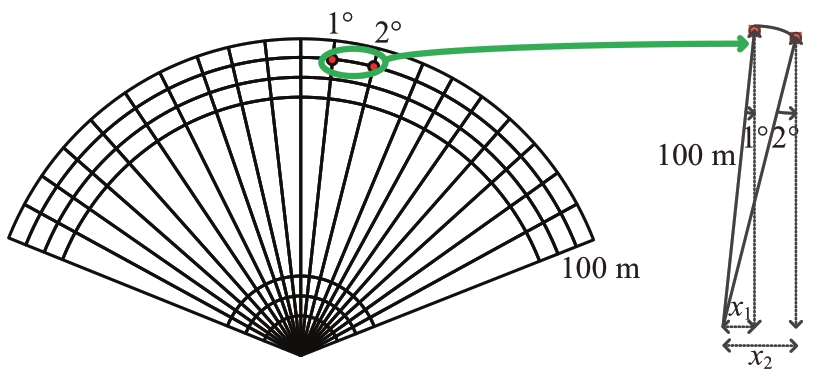
图4 离网误差示意图
为了解决离网误差问题，我们利用ML 准则的统计特性，将SLIM 方法的角度估计结果通过最小化ML 成本函数来细化方向网格，使得细化的方向网格与实际来波方向不断接近，以此来消除网格误差。
根据文献［16］，x 的随机负对数似然函数可以表示为
定义干扰协方差矩阵为
将矩阵求逆引理(A+ BCD)-1= A-1- A-1B·(C-1+ DA-1B)-1DA-1应用于式（24），可得
令
，则式（25）可写为
将式（26）代入
，可得
将代数恒等式
可得
将式（27）和式（28）代入式（23）得到
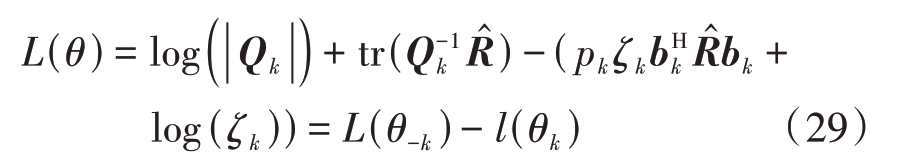
式中，
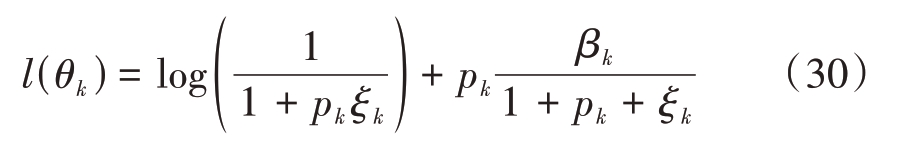
其中，
。
ML 代价函数分解为两部分:不包含θk 的边缘似然函数L(θ-k)和与θk有关的函数l(θk)。因此，关于θk 的ML 代价函数的最小化问题与关于θk 的函数l(θk)的最小化问题等价，所以θk 的细化过程可以通过最小化式（30）得到。在本文中，l(θk)的最小化问题使用Nelder-Mead 算法求解，在MATLAB中使用的是“fminsearch”函数。
本节提出的高精度测角方法的流程总结如表1所示。
表1 方法流程
初始化:由SLIM方法得到初始值pk(0)和σ2(0)，由CFAR目标检测器得到初始估计角度{ }θ̂k N k= 1，迭代次数为i。重复:步骤1:根据式（16）计算R(i)；步骤2:根据式（24）计算Qk(i)；步骤3:根据式（21）更新x(i+1)；步骤4:根据式（22）更新σ2(i+1)；步骤5:最小化式（30）中关于θk的ML代价函数得到细化后的估计角度{ }θ̂k N k= 1；步骤6:更新方向网格，根据细化后的方向网格更新导向矢量ak；步骤7:判断收敛条件是否满足‖‖pk(i+1)-pk(i) /‖‖pk(i)<10-5，如果是，则停止迭代，否则i= i+1，跳到步骤1；直至收敛
从前面的分析可以知道，本节提出的测角方法主要包含SLIM 和ML两部分。SLIM 的主要计算量来自于矩阵R 的求逆，其复杂度为O(L2K)。ML的主要计算量来自于矩阵Qk 的求逆和ML 代价函数最小化的求解，计算量分别为O(L2K)和O(K3)，因此本节方法的计算复杂度为O(2L2K+ K3)。可以看出，本节方法是在牺牲一定计算量的情况下对测角的精度进行提升。
2.6 点云成像信号处理流程
综上，基于本文提出的高精度测角方法的点云成像信号处理流程如图5所示。
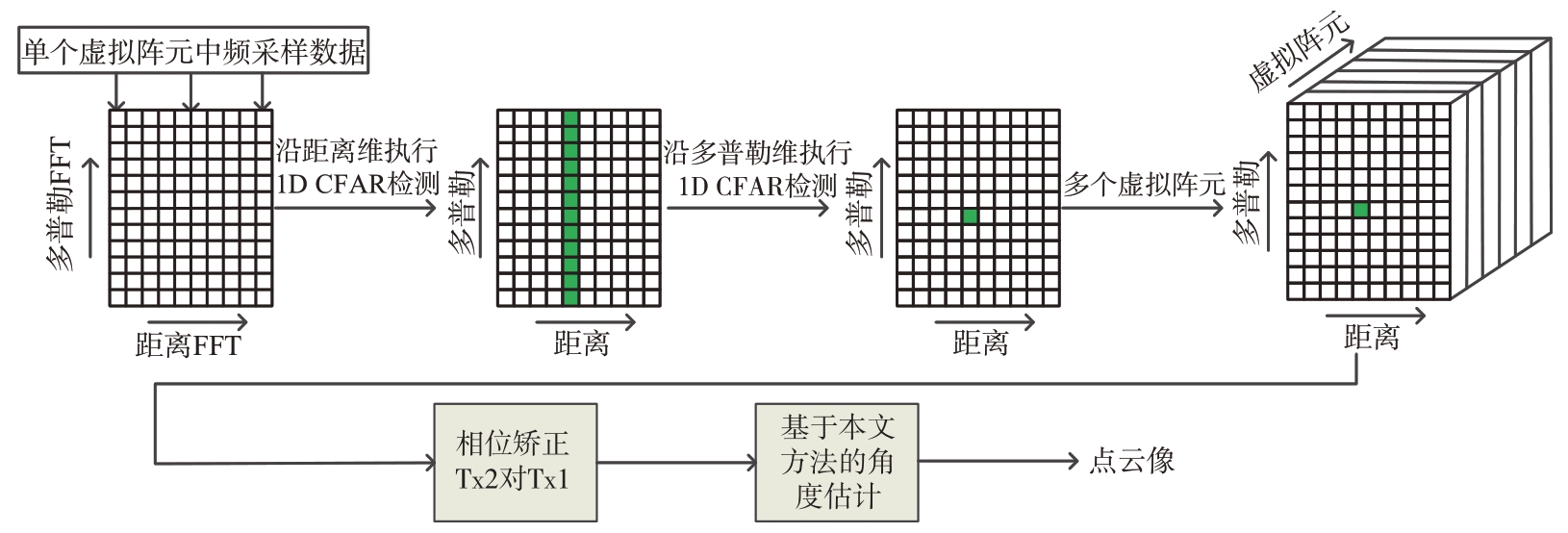
图5 本文成像方法的信号处理流程框图
3 仿真和实验结果分析
3.1 仿真数据处理结果分析
本文仿真的运行平台为联想笔记本电脑Y7000P，CPU 型号为i5-12500H，仿真软件为MATLAB2020a。根据控制变量法思想，我们设置点目标的距离和速度相同、角度不同，从而验证基于不同测角方法的成像性能。仿真系统参数设置如表2所示，目标参数设置如表3所示。
表2 系统参数
参数载波频率/GHz阵元个数采样点数/距离单元数Chirp数/速度单元数方位角网格划分/（°）角度范围/（°）参数值77 2T×4R 256 64 1-60～60
表3 目标参数
目标距离/m 速度/（m·s-1）1 2 8 8 5 5角度/（°）-2.5 2.5
图6 为经过距离FFT 和多普勒FFT 之后生成的距离-多普勒图，图中红色圆圈为经过CFAR 目标检测器之后的目标检测点，检测到的距离为8.02 m，速度为5.07 m/s，与实际设置参数基本一致。因此，使用FFT 方法进行距离像和多普勒像估计，经过CFAR 目标检测器，能够得到正确的目标点距离和速度。
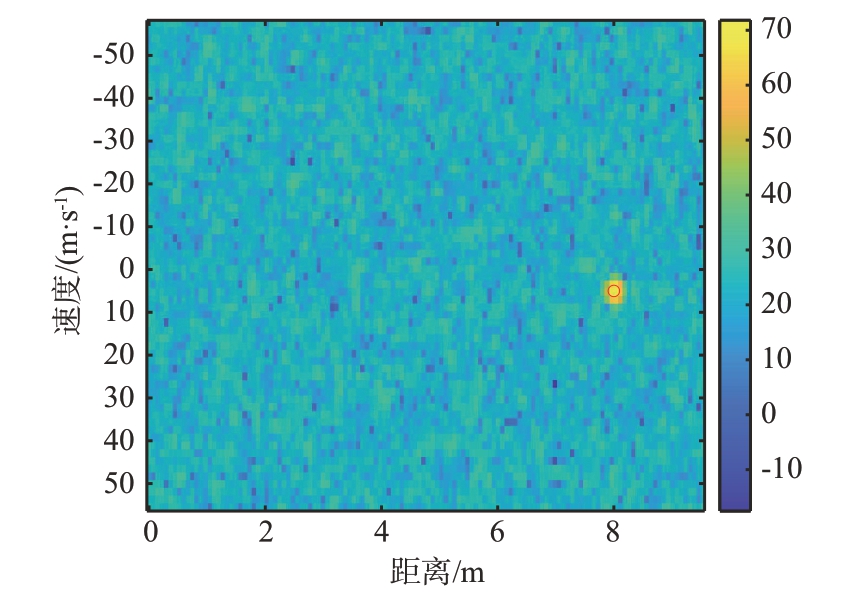
图6 距离-多普勒图生成及目标检测结果
为了验证本文的成像方法具有高精度的特点，接下来，我们利用目标索引点对应的多个虚拟阵元数据使用不同测角方法进行距离-角度二维点云成像，这些测角方法包括文献［11］提出的RIAA方法、文献［13］提出的SLIM 方法以及本文提出的方法。图7 给出了基于不同测角方法的点云成像图，图中相邻虚线网格间隔为1°。可以看出文献［11］提出的方法分辨率较低，无法分辨角度相近的两个目标，经过CFAR 目标检测器之后会产生虚假目标点。文献［13］提出的方法可以有效抑制功率泄露，能够分辨角度相近的两个目标，相比文献［11］提出的方法，其分辨率更高，旁瓣更低，经过CFAR 目标检测器之后没有产生虚假目标点。因为我们设定的点目标其方位向并不在划分的网格点上面，所以我们发现基于这些测角方法的成像结果都存在离网误差，只有本文提出的成像方法能够准确估计目标来波方向，消除了离网误差，精度达到了0.1°。
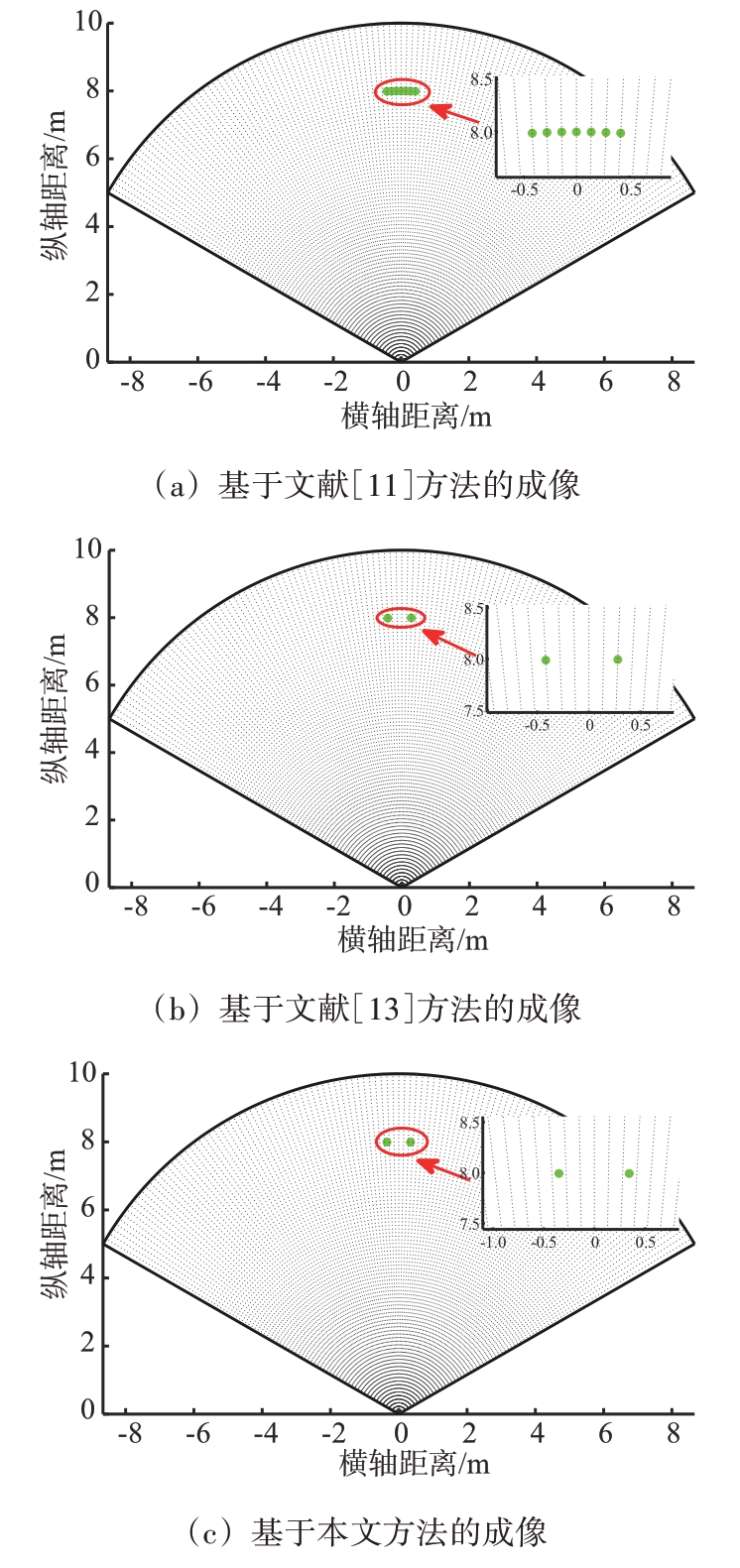
图7 距离-角度二维点云成像
为了进一步说明本文方法的测角精度性能，我们进行了500 次的蒙特卡洛实验。定义均方根误差（RMSE）为
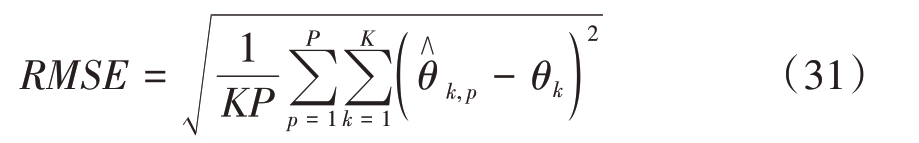
式中，
为第p次蒙特卡洛实验中第k个信源的估计值，θk为第k个信源的精确值，P为蒙特卡洛实验的次数。设定实验次数P=500。RMSE 曲线如图8所示。
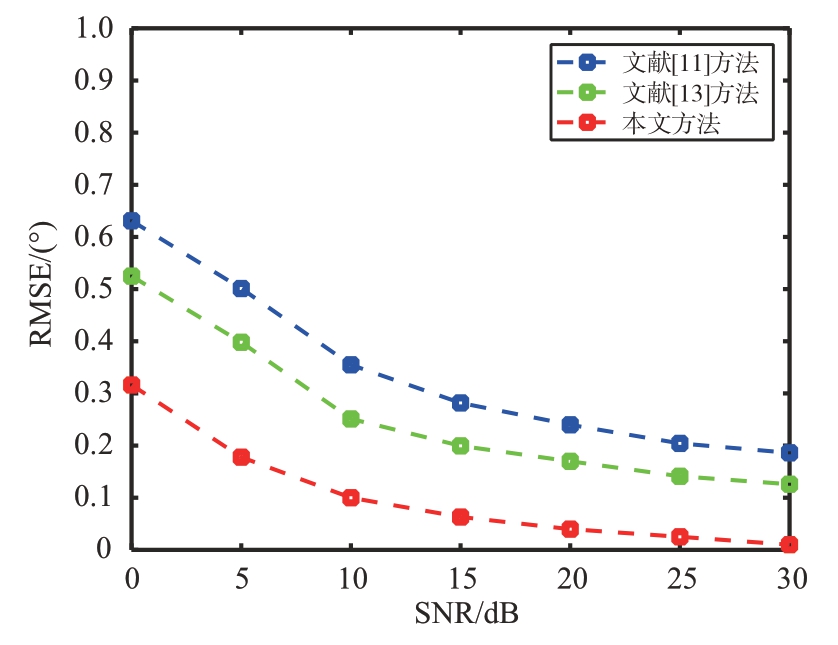
图8 不同测角方法的RMSE随SNR变化曲线
从图8 可以看出，所有测角方法的RMSE 均随着信噪比的增加而减小，其中本文提出的高精度测角方法的RMSE 始终保持在一个较低的值。因此，根据RMSE 曲线可知，本文方法估计值更接近信源的真实值，算法更加稳健。
随着信噪比的进一步下降，对文献［11］方法的影响最大，因为在信噪比较低时小奇异值会与大奇异值相当，从而导致该方法的噪声抑制性能变弱，角度分辨率进一步降低，最终的成像结果会出现更多的杂波点。文献［13］方法由于是基于上一次的值进行更新迭代噪声值，所以噪声抑制性能相比来说更强，成像结果会出现更少的杂波点。本文方法是在文献［13］方法的基础上增加了ML 估计，因此噪声抑制性能相对来说没有损失，并且在最小化ML 成本函数的过程中依然不断更新迭代噪声值，所以在提高噪声抑制性能的同时能够进一步提高测角精度，从成像结果来看仍然能够使得点云出现在偏离网格点的位置。
3.2 实测数据处理结果分析
为了测试本文方法在实际场景中的表现，本文设计了两个不同的场景分别对静止目标和运动目标进行成像。静态场景是为了验证不同测角方法在实际场景中的角度分辨率，动态场景是为了验证不同成像方法在实际动态场景中的成像效果。
实验所使用雷达系统由德州仪器公司的汽车雷达传感器评估模块AWR1843 和数据采集卡DCA1000 组成。通过配套的mmWave Studio 软件对AWR1843 的发射波形参数进行配置并启动发射信号，数据采集卡DCA1000 将AWR1843 处理后的中频数据进行打包并通过网口将数据传输给PC机，在PC机上面对中频数据进行信号处理。
3.2.1 静态场景
静态实验场景如图9所示。在雷达正前方的13 m 左右的地方静止站立两个人体目标，两目标的间隔角度大约5°。
图9 静态场景
图10 为距离-多普勒图，图中红色圆圈为经过CFAR 目标检测器之后的目标检测点。从图中可以看出检测到速度相同、距离相同的一个点目标。该点目标的距离为12.83 m、速度为0 m/s，和实际目标参数一致。
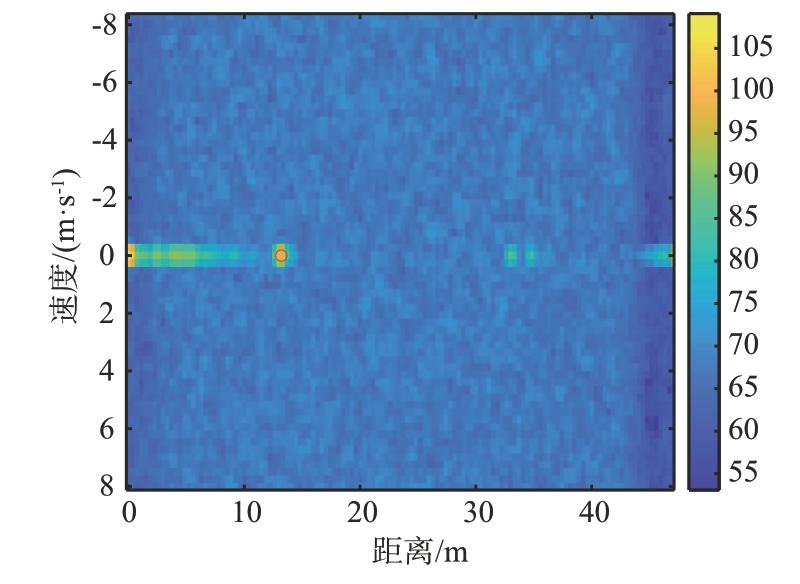
图10 距离-多普勒图生成及目标检测结果
图11 给出了基于不同测角方法的点云成像图，图中相邻虚线网格间隔为1°。与仿真结果一样，文献［11］方法由于分辨率较低无法分辨角度相近的两个目标，产生了许多虚假目标点。文献［13］方法相比文献［11］方法，其分辨率更高、旁瓣更低，经过CFAR 目标检测器之后没有产生虚假目标点。我们可以看出，基于这些方法产生的点云都出现在固定角度网格上面，但是本文提出的成像方法能够使得点云出现在偏离网格点的位置，更加准确地估计目标方向，得到更加精准的点云数据，这为后面的聚类、跟踪等信号处理提供了精准、可靠的点云数据。
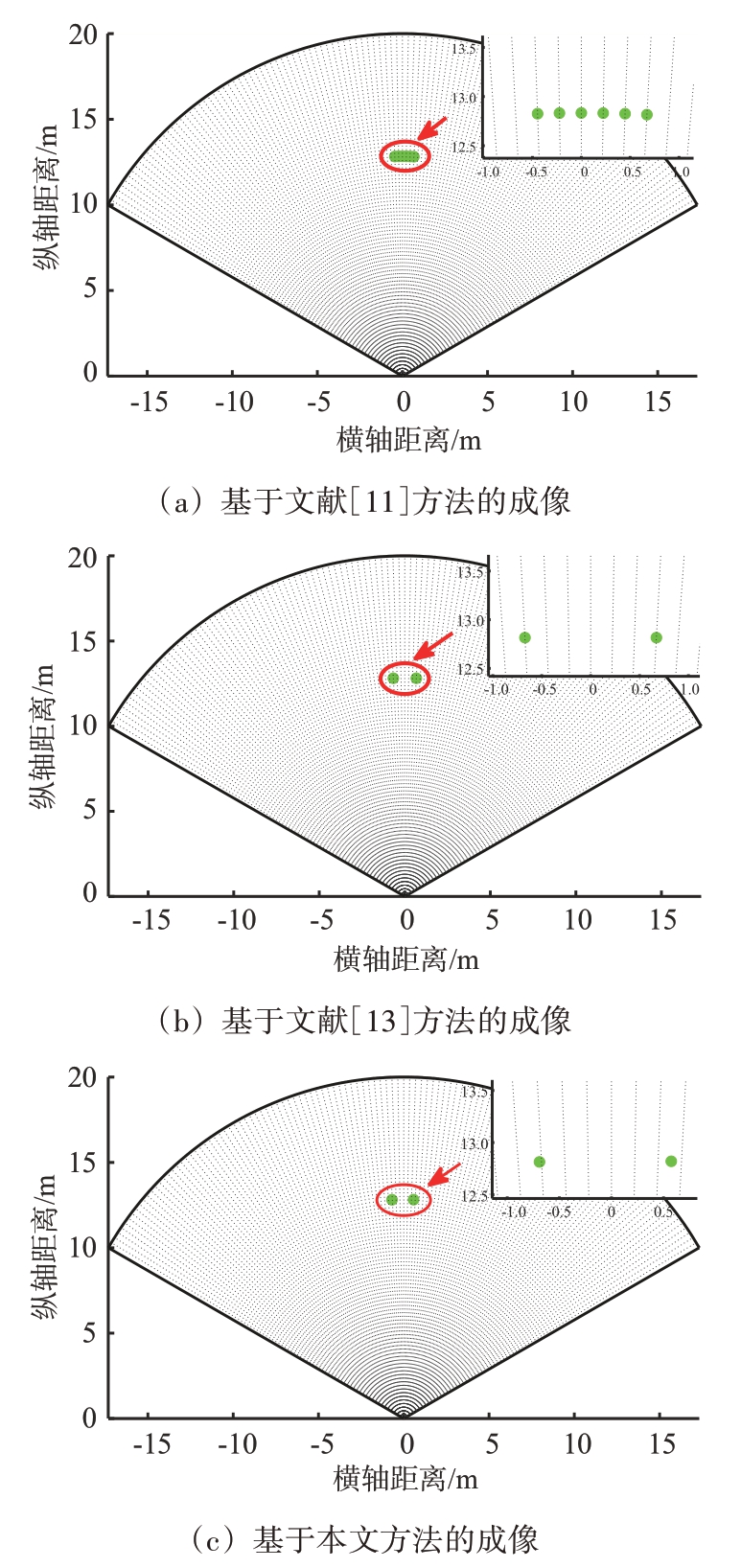
图11 静态场景实测成像
3.2.2 动态场景
动态实验场景如图12所示。在雷达的左前方有一个人体目标在远离雷达方向运动，右前方有一辆电动车也在远离雷达方向运动。
图12 动态场景
图13 为距离-多普勒图，图中红色圆圈为经过CFAR 目标检测器之后的目标检测点。从图中可以看出根据距离-多普勒图能够检测出运动的人体和车辆目标。通过数据比对，发现检测到的距离和速度参数与实际运动参数一致。
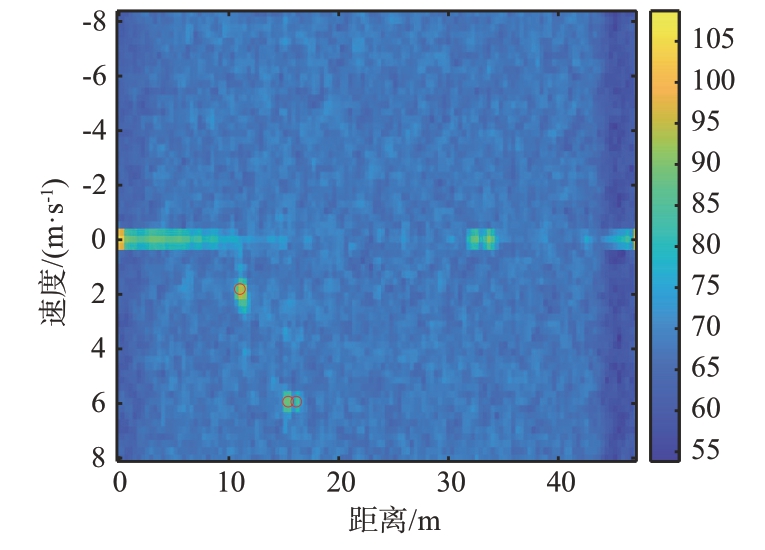
图13 距离-多普勒图生成及目标检测结果
图14给出了基于不同测角方法的点云成像图，图中相邻虚线网格间隔为1°。我们将电动车的点云像进行局部放大，可以发现，和静态成像场景类似，只有本文提出的成像方法产生的点云会出现在偏离固定角度网格的位置，得到更加精准的点云数据。
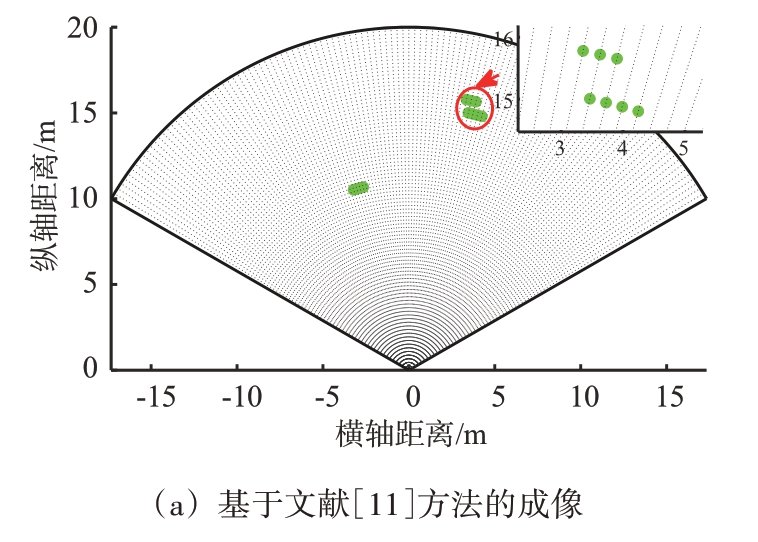
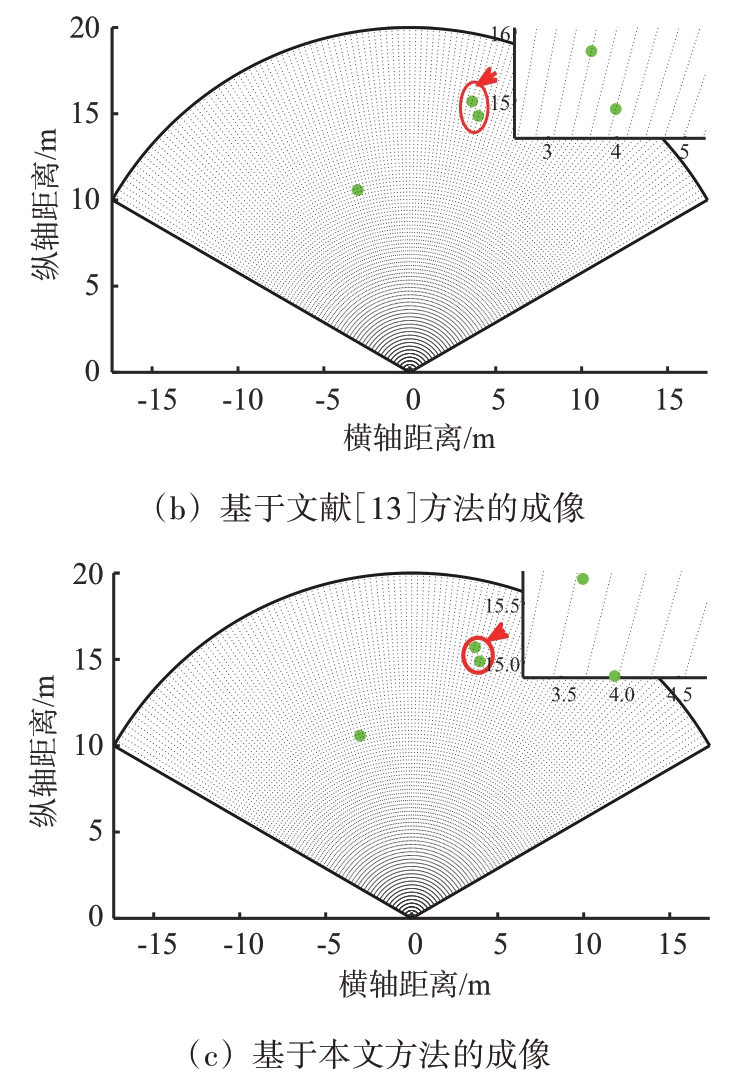
图14 动态场景实测成像
经过静态场景和动态场景的实验，验证了本文提出的成像方法不管对静止目标还是动态目标进行成像，都能够得到更加精准的点云数据。
4 结束语
针对现有的车载毫米波雷达高分辨成像方法因存在离网误差导致精度低的问题，通过利用ML准则的统计特性，本文提出了一种SLIM 和ML 估计相结合的高精度测角方法用于点云成像。仿真和实验结果表明:相比于其他成像方法，本文提出的成像方法得到的点云像在角度维精度更高，精度能够达到0.1°，具有高精度的特点，解决了由于离网误差导致目标定位出现巨大偏差的问题。将本文提出的成像方法用于车载场景中，能够为ADAS系统提供精准、可靠的点云数据。
［1］冯利鹏，王辉，郑世超，等.FMCW 体制毫米波SAR 实时信号处理方法研究［J］.上海航天，2022，39（3）:116-121.
［2］刘健，钱莹晶，张仁民.毫米波大规模MIMO 系统混合波束赋形技术综述［J］.吉首大学学报，2022，43（1）:43-52.
［3］杨军，周芳.分布式小卫星MIMO-SAR 超高分辨成像方法［J］.西安电子科技大学学报，2021，48（2）:99-108.
［4］PATOLE S M,TORLAK M,WANG Dan,et al.Automotive Radars:A Review of Signal Processing Techniques［J］.IEEE Signal Processing Magazine,2017,34（2）:22-35.
［5］SUN Shunqiao,PETROPULU A P,POOR H V.MIMO Radar for Advanced Driver-Assistance Systems and Autonomous Driving:Advantages and Challenges［J］.IEEE Signal Processing Magazine,2020,37（4）:98-117.
［6］GENNARELLI G,NOVIELLO C,LUDENO G,et al.24GHz FMCW MIMO Radar for Marine Target Localization:A Feasibility Study［J］.IEEE Access,2022,10（6）:68240-68256.
［7］LI Xinrong,WANG Xiaodong,YANG Qing,et al.Signal Processing for TDM MIMO FMCW Millimeter Wave Radar Sensors［J］.IEEE Access,2021,9（12）:167959-167971.
［8］晋良念，王燃.毫米波FMCW MIMO 雷达三维点云成像方法［J］.雷达科学与技术，2022，20（5）:497-506.
［9］STOICA P,BABU P,LI J.SPICE:A Sparse Covariance Based Estimation Method for Array Processing［J］.IEEE Trans on Signal Processing,2011,59（2）:629-638.
［10］ROBERTS W,STOICA P,LI Jian,et al.Iterative Adaptive Approaches to MIMO Radar Imaging［J］.IEEE Journal of Selected Topics in Signal Process,2010,4（1）:5-20.
［11］ZHANG Yongwei,LI Jie,ZHANG Yongchao,et al.A Regularized Iterative Adaptive Approach Based for Radar Forward-Looking Imaging［C］//2021 IEEE International Geoscience and Remote Sensing Symposium,Brussels,Belgium:IEEE,2021:5151-5154.
［12］黄以兰，晋良念，刘庆华.一种车载毫米波FMCW MIMO 雷达快速成像方法［J］.雷达科学与技术，2022，20（2）:128-135.
［13］TAN Xing,ROBERTS W,LI Jian,et al.Sparse Learning via Iterative Minimization with Application to MIMO Radar Imaging［J］.IEEE Trans on Signal Processing,2011,59（3）:1088-1101.
［14］YANG Zai,XIE Lihua,ZHANG Cishen.A Discretization-Free Sparse and Parametric Approach for Linear Array Signal Processing［J］.IEEE Trans on Signal Processing,2014,62（19）:4959-4973.
［15］蒋留兵，温和鑫，车俐，等.一种TDM-MIMO 雷达的运动目标相位补偿方法［J］.太赫兹科学与电子信息学报,2020,18（4）:575-580.
［16］YANG Zai,LI Jian,STOICA P,et al.Sparse Methods for Direction-of-Arrival Estimation［J］.arXiv,2016,https://doi.org/10.48550/arXiv.1609.09596.
