0 引 言
波形设计是雷达系统设计和信号处理研究中的重要内容［1-3］。从雷达实际应用角度来看，雷达波形可以分为两大类［4-5］：一类是脉冲压缩波形，包括线性调频信号、相位编码信号、非线性调频信号等，这类波形通过相位调制的方式避免了单脉冲波形时间带宽积为1 的限制，扩展了发射脉宽，相位调制的过程就是脉冲压缩；另一类是脉冲串波形，它利用多普勒效应测量目标到雷达的径向速度，并能区分运动和固定目标（一般为杂波），脉冲串波形包括动目标显示［6］（Moving Target Indication, MTI）、动目标检测［7］（Moving Target Detection,MTD）和脉冲多普勒［8］（Pulse Doppler,PD）波形，但从滤波器响应看，MTI 是通过宽响应频带传递目标，可以抑制零速目标，但不能给出目标速度，MTD 和PD 则是形成滤波器组传递目标，可以给出目标速度。
线性调频信号是应用最广泛的一种脉冲压缩波形［9-10］，它的突出优点是匹配滤波器对回波信号的多普勒频移不敏感，这极大简化了后续信号处理系统，但是，它会带来与多普勒频移成正比的附加时延，产生多普勒-距离耦合误差，此外，其匹配滤波输出响应旁瓣高，需加权处理降低旁瓣，这会带来信噪比损失。
相位编码信号具有距离和多普勒两维分辨率，当回波信号的多普勒频率与匹配滤波器失配时，滤波器将无法起到脉冲压缩作用［11-13］。因此，其信号处理系统需按多普勒分辨单元分别匹配不同的多普勒频率，匹配滤波器较为复杂，一般应用于目标速度变化范围较窄的场合。但相位编码具有同时测距、测速的优点，在码元长度较长时（大的脉压比），其脉压副瓣低，无加权处理损失。
对空间目标探测而言，其雷达功率孔径积巨大，降低处理损失、提高测量精度是该类雷达设计追求的目标［14-16］。空间目标具有速度快、回波动态变化大等特点，采用线性调频信号，虽然易于做到大时宽，但处理损失、距离-多普勒耦合带来的测距误差会对系统性能产生不利影响。本文讨论用于空间目标探测的相位编码信号波形处理问题，分析速度/加速度限制、遮蔽影响、精度和处理损失等性能，为工程应用提供参考。
1 目标模型
空间目标的运动轨迹符合开普勒定律，其运动速度与轨道高度相关，原则上说，轨道越低，速度越高，另外目标速度还与轨道偏心率相关，不同轨道高度的目标速度和加速度分布如图1所示。
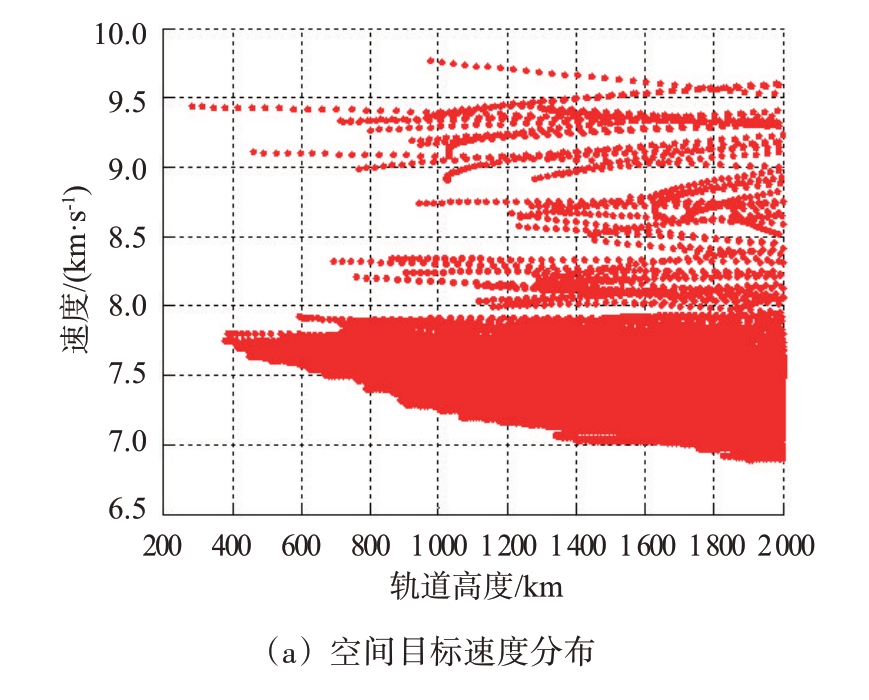
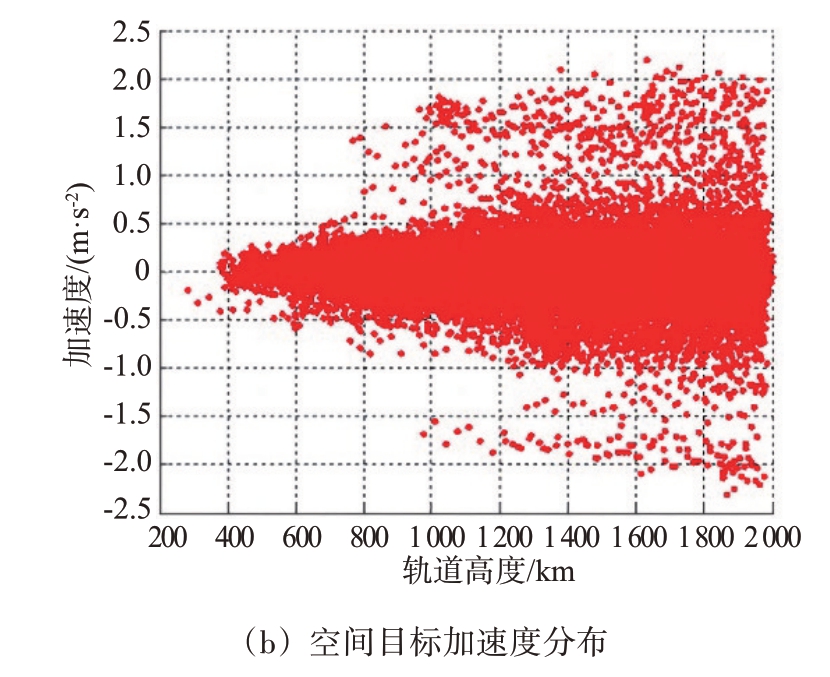
图1 空间目标运动特性
由图1 可知，空间目标的运动速度很大，但加速度很小，最大值约为2 m/s2。对雷达探测而言，更关注的是目标相对于雷达的径向速度和径向加速度。这里假设雷达的探测仰角与水平面夹角为30°，此时空间目标相对雷达的径向速度和径向加速度分布如图2所示。可以看出，其径向速度和径向加速度的变化范围都极大扩展，径向速度的范围从接近0 m/s到7.9 km/s，径向加速度的范围最大到100 m/s2。
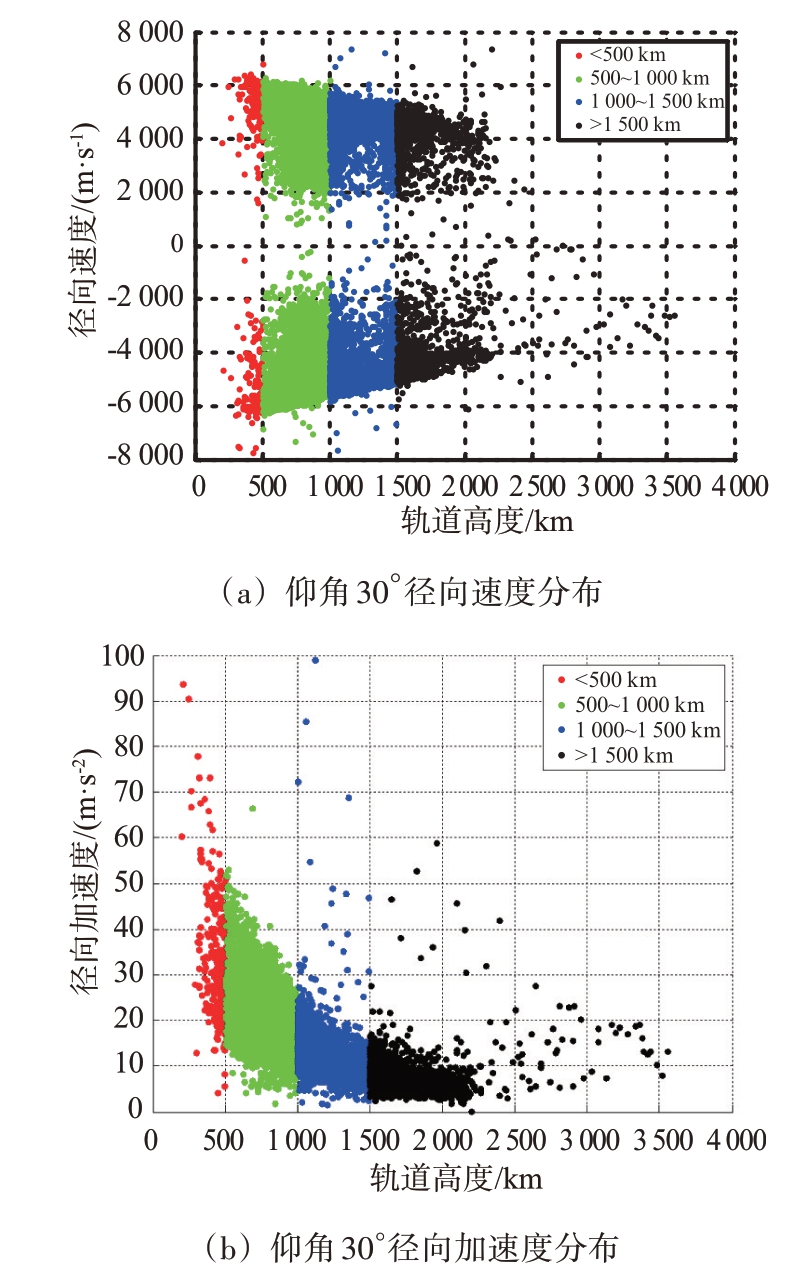
图2 空间目标相对雷达仰角30°时的运动特性
本文后续章节就以上述运动模型为基础分析波形设计和相关处理性能。
2 相位编码信号处理方法
设相位编码回波信号为
式中，τ 为子码宽度，N 为码长，则信号总时长T=Nτ，fd 为回波多普勒频率，a(n)=0,1 为子码中的发射调制相位值，这里以二相码为例说明相位编码的处理过程。
相位编码信号为多普勒敏感信号，其用于脉冲压缩的匹配滤波器必须与目标速度匹配，否则无法脉压出回波峰值。对总时长为T的脉冲，其多普勒分辨率为
，匹配滤波器的速度补偿需以多普勒分辨率Δfd 为间隔。以S 波段为例，空间目标对应的多普勒范围为±158 kHz，若雷达发射时宽T=10 ms，则需补偿的滤波器组的数量为3 160个，硬件实现的规模非常大。
仔细观察式（1），其相位项分为两部分，第一部分为回波调制产生的多普勒频移，系未知项，也是信号处理需要测量的参数，第二部分为相位编码调制项，该部分系已知项，如果我们对相位编码调制项先作解调处理，将发射波形的相位调制关系去除，即按子码元对应进行反相处理，形成下式的结果：
由式（2）可知，若要实现回波检测，需要对多普勒频率进行补偿，由于有N 个子码，从多普勒处理的角度看，可以形成N 个频道的输出，频率分辨率为
，第k个频道的输出为
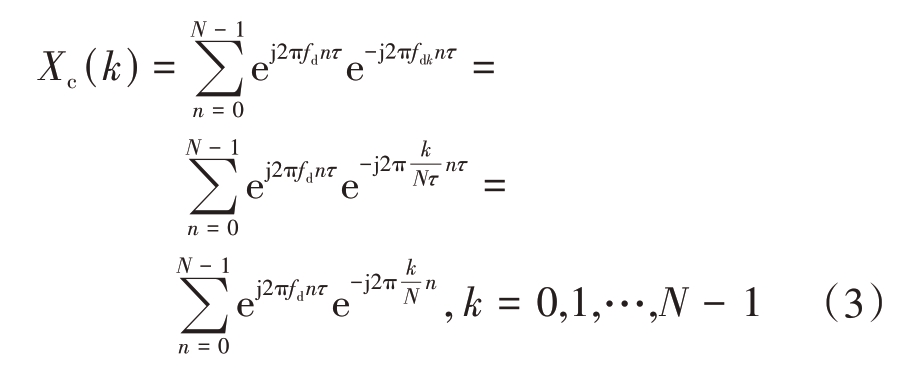
在实际处理时，按距离单元先用发射相位编码信号对回波进行共扼相乘，该过程称为相位解调，使其变成仅包含回波多普勒的信号，再利用FFT 方法进行分频道输出，检测到目标后，可以同时给出目标的距离和速度结果。需注意的是，其对目标多普勒频率的采样是以信号带宽进行的，信号带宽取决于子码元宽度，考虑到测距精度要求，信号带宽一般在MHz 量级，因此，该方法不存在多普勒模糊的问题。其处理过程见图3。该处理方法需按每个被检测的距离单元分别进行N 点（子码元长度）FFT处理，实际系统需结合待处理的距离单元数和子码元长度，分配计算资源。
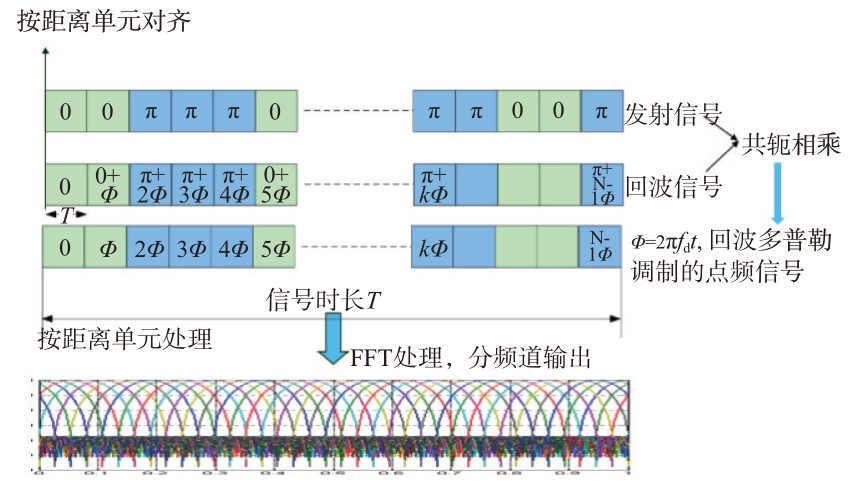
图3 相位编码信号处理过程
3 相位编码信号处理性能分析
空间目标相对雷达观测视角的高速、高加速度的特点，对相位编码信号波形的参数设计和处理性能有较大影响，本节分析相关限制因素。
3.1 速度限制
对大时宽带宽信号，目标速度会引起回波在积累时间内产生距离走动，对相位编码信号而言，当子码元因距离走动产生错位后，脉压会形成失配，图4 给出了回波距离跨越与失配损失的关系，可以看出若脉内距离跨越超过半个距离单元，则会产生较大的失配损失。因此，不产生脉内距离跨越的条件为
（不跨越半个距离单元），其中V 为目标速度，T 为脉宽
为信号带宽决定的距离单元。对于空间目标探测，目标速度很高，为了提高平均功率，发射脉宽往往也很大，这就造成VT 值较大，以目标速度7.9 km/s，脉宽10 ms 为例，其VT=79 m，为避免距离跨越效应，距离分辨单元不宜超过150 m。
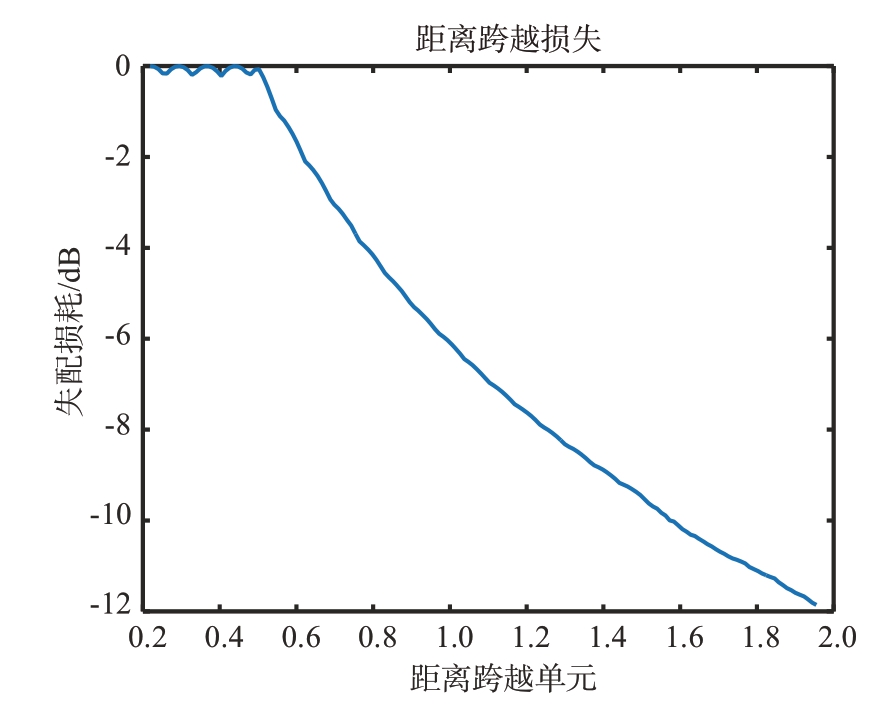
图4 距离跨越与失配损失的关系曲线
3.2 加速度限制
相位编码的处理过程为相参积累，目标加速度会造成回波谱展宽，当谱展宽量级超过多普勒分辨单元时，相参积累的效率将受到较大影响。与距离跨越类似，脉内加速度带来的谱扩展不超过半个多普勒分辨单元，即
，式中a为加速度，λ 为波长。以S 波段，10 ms 脉宽为例，图5 给出了加速度与失配损失的关系曲线，可以看出，在100 m/s2加速度内，失配损失很小，由于空间目标本身的加速度很小，相对雷达的视线加速度也在100 m/s2内，因此，采用相位编码信号探测空间目标可以忽略加速度的影响。
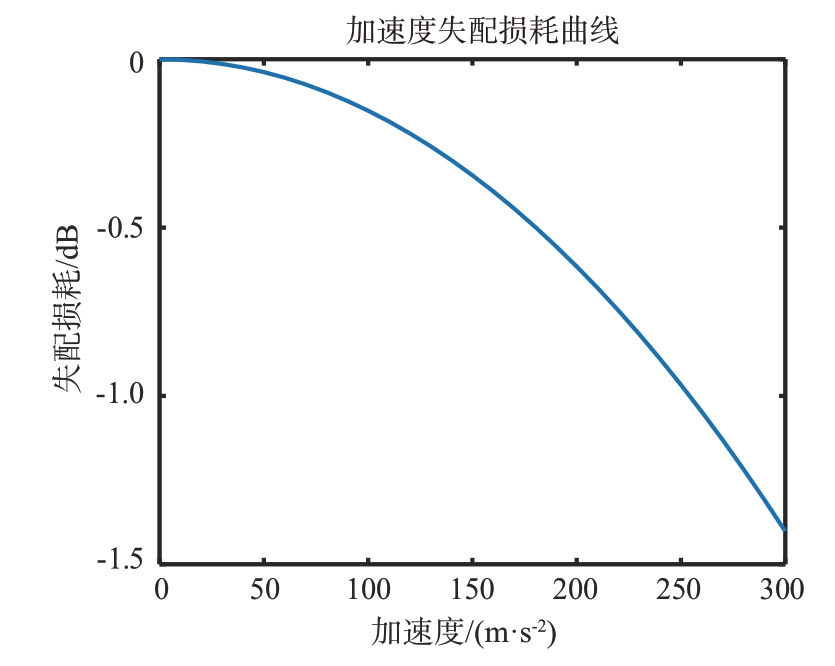
图5 加速度与失配损失的关系曲线
3.3 目标遮蔽
相位编码处理采用发射信号模板按距离单元与回波共扼相乘后，再进行FFT 处理后从频域进行检测。当发射模板与目标回波完全在同一窗口时，将在相应频道形成脉压峰，只要错开一个距离单元，将不能产生峰值，回波成为噪声，此时为失配状态，失配比为脉压比。在发射脉宽较长的情况下，在多目标（或杂波）时，不同回波在时域上重叠，由于匹配距离窗口不可能同时对所有目标回波进行相关，失配的目标能量将变成噪声，在强弱目标同时存在时，失配的强目标回波会抬高噪底，对弱目标造成遮蔽。
目标遮蔽的物理概念描述如下（参见图6）：相位编码信号具有互相关为零的特点，其码元必须完全匹配才能自相关出峰值，多目标时，由于目标在距离上是错开的，进入匹配距离单元的部分码元的脉压结果将成为噪声，完全匹配时的检测因子为S/N，失配后的输出检测因子为
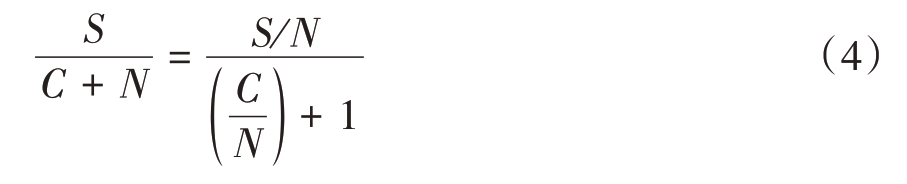
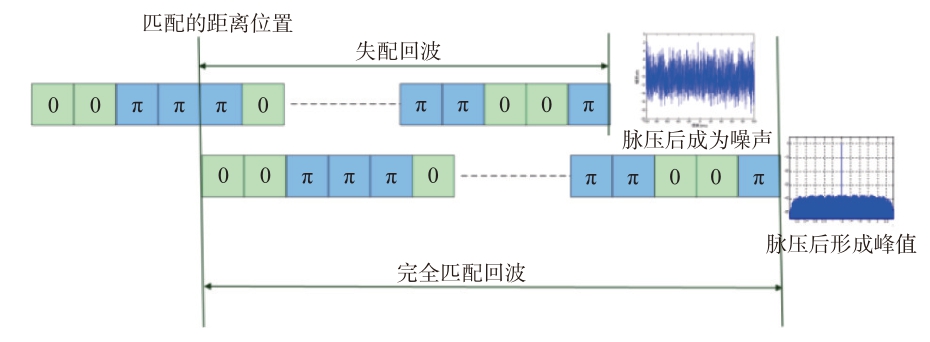
图6 多目标遮蔽时间关系
式中C为失配剩余。从式中可以看出，信噪比的下降因子与失配剩余相关，若
，则输出信噪比下降3 dB。图7 给出了强弱目标相差20，30，40和60 dB情况下的脉压输出和噪底变化情况，从仿真结果可见，当强弱目标信号强度差超过30 dB时，噪底将明显抬升，弱目标检测将受影响。仿真条件为：弱目标SNR=13.2 dB，脉压比为40 dB，目标速度为6 000 m/s，强目标与弱目标重叠N/2个距离单元。在实际场景中，若信号脉宽对应的距离范围内存在多个回波强度差异很大的目标，有可能会发生强目标遮蔽弱目标的现象。
图7 目标遮蔽仿真
3.4 处理损耗
处理损耗产生的原因是由于回波多普勒不在频道输出的最大值上，每个频道的多普勒残差为σfd，σfd的范围为
为多普勒分辨单元，相邻码元之间的相差为
，最大相差为
，最小相差为0。处理损耗为
滤波器组的处理损耗曲线见图8，最大损失为3.6 dB，考虑到目标速度是变化的，平均处理损耗为1.2 dB。
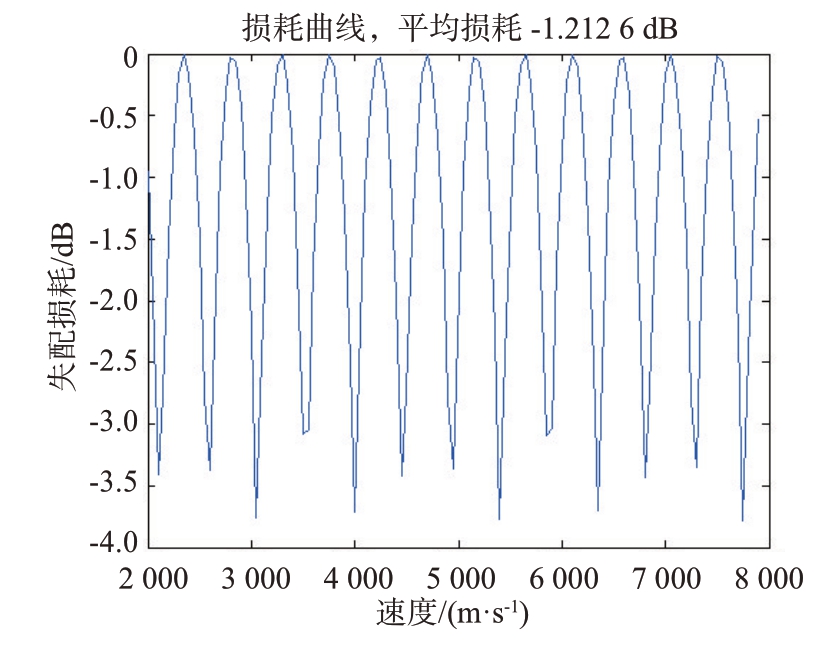
图8 滤波器组处理损耗
3.5 测速精度
相位编码信号是多普勒敏感信号，要实现匹配脉压，必须对回波速度进行补偿，其补偿结果就是测速测量值。从相位编码信号处理方法中可以看出，它具有单脉冲测速的特点，不模糊速度范围由信号带宽决定，由多普勒滤波器组给出测速结果，多普勒分辨率（对应为速度分辨率）为发射时宽倒数。在多普勒（测速）误差项的组成上，与多普勒分辨单元直接相关的误差项有热噪声误差和频域采样误差，对13 dB 信噪比，热噪声误差大约是多普勒带宽的十分之一，频域采样误差表达式为
，为多普勒带宽的三分之一，远大于热噪声误差。从误差理论可知，极限误差是由Cramér-Rao限决定的热噪声误差（由分辨单元和信噪比决定），实际系统为获得接近Cramér-Rao 限的精度，必须降低频域采样误差。从相位编码处理过程可知，其多普勒输出为频域离散采样输出，要降低频域采样误差，需要提高多普勒滤波器谱密度，即保证多普勒滤波器的输出采样尽可能接近目标谱的最大值。为实现此目标，在实际FFT 处理时，可以采用补零的方式提高多普勒频道的谱密度，从而极大降低频域采样误差。
4 结束语
本文针对空间目标探测需要的大发射时宽、高测量精度的波形设计需求，提出了在单个脉冲就具备同时测距、测速能力的相位编码信号，分析了同时实现测距、测速的原理，给出了实现过程和方法，详细分析了目标速度、加速度对信号波形设计的限制和目标遮蔽效应、处理损耗、测速精度等性能，并给出了相应的仿真结果，相关结果对相位编码波形在空间目标探测方面的工程应用具有一定的指导作用。
［1］黄磊，柳艾飞，高才才.集中式MIMO 雷达研究进展：正交波形设计与信号处理［J］.雷达科学与技术，2023，21（1）:1-15.
［2］JIANG Wei,ALEXANDERI M H,OSVALDO S.Joint Design of Radar Waveform and Detector via End-to-End Learning with Waveform Constraints［J］. IEEE Trans on Aerospace and Electronic Systems,2022,58（1）:552-567.
［3］TANG Zejia, BAO Qinglong, PAN Jiameng, et al. Noncooperative Bistatic Radar Countermeasures Based on the Joint Design of Radar Waveforms and Mismatched Filters［J］. IEEE Geoscience and Remote Sensing Letters, 2023,20:1-5.
［4］BARTON D. 雷达系统分析与建模［M］.南京电子技术研究所，译.北京：电子工业出版社，2007.
［5］SONG Yuxiao,WANG Yu, XIE Jingyang, et al. Ultra-Low Sidelobe Waveforms Design for LPI Radar Based on Joint Complementary Phase-Coding and Optimized Discrete Frequency-Coding［J］.Remote Sensing,2022,14（11）:2592.
［6］SONG Chong, WANG Bingnan, XIANG Maosheng, et al.A General Framework for Slow and Weak Range-Spread Ground Moving Target Indication Using Airborne Multichannel High-Resolution Radar［J］. IEEE Trans on Geoscience and Remote Sensing,2022,60:1-16.
［7］HUANG Peihui, XIA Xianggen, WANG Lingyu, et al. A Coherent Integration Method for Moving Target Detection in a Parameter Jittering Radar System Based on Signum Coding［J］. IEEE Signal Processing Letters, 2022, 29:2313-2317.
［8］BELTRAO G, PRALON L, BARRETO A, et al. Subpulse Processing for Unambiguous Doppler Estimation in Pulse-Doppler Noise Radars［J］. IEEE Trans on Aerospace and Electronic Systems,2021,57（6）:3813-3826.
［9］PARK J H, PARK S C. Complex Range Resolution Model of Point Scatterers in LFM Chirp Pulse Radar［J］. IEEE Trans on Instrumentation and Measurement,2022,71:1-12.
［10］YUAN Hongwei, DAI Keren, LI Qingyu, et al. A Low-Complexity Parameter Estimation Algorithm for an Integrated Radar-Communication Waveform with Cross-Mode Interference［J］.IEEE Communications Letters,2021,25（11）:3679-3683.
［11］BAI Wenlin,ZOU Xihua,LI Peixuan,et al.Photonic Millimeter-Wave Joint Radar Communication System Using Spectrum-Spreading Phase-Coding［J］. IEEE Trans on Microwave Theory and Techniques, 2022, 70（3）:1552-1561.
［12］赵晶晶.相位编码OFDM 新体制雷达信号设计与处理研究［D］.长沙：国防科学技术大学，2018.
［13］葛优，刘景萍，赵惠昌，等.基于正交相位编码信号的MIMO 雷达测速测距算法［J］.探测与控制学报，2016，38（6）:80-83.
［14］高梅国，付佗.空间目标监视和测量雷达技术［M］.北京：国防工业出版社，2017.
［15］谭贤四.临近空间高超声速目标预警探测若干研究进展［J］.雷达科学与技术，2021，19（6）:625-639.
［16］罗健.雷达探测临近空间高超声速目标关键技术研究［J］.雷达科学与技术，2021，19（6）:640-650.
