0 引 言
波达方向（Direction of Arrival,DOA）估计在军事与民用领域的应用十分广泛［1-2］，因而一直是阵列信号处理的研究热点。其中子空间类算法的典型多重信号分类算法［3］（Multiple Signal Classification,MUSIC）因为能对多目标进行突破瑞利限的角度分辨，所以得到了广泛关注与应用，但它需要已知信源数目，且需要多快拍采样数据才能处理非相干信号源，一旦上述条件有任何一条不满足就会导致其估计性能下降甚至失效。
近年来得益于压缩感知理论及其相关应用的发展，产生了一系列基于压缩感知理论的DOA 估计算法［4-6］，如正交匹配追踪［7］（Orthogonal Matching Persuit, OMP）和稀疏贝叶斯学习［8-10］（Sparse Bayesian Learning, SBL）等在网格类算法，这一类算法需要提前在预期的空域上建立字典集，也就是划分网格点。当目标方位准确落在网格点上时，这一类算法可以在少快拍和信源相干等条件下实现高精度DOA 估计。但实际情况中，目标的实际方位并不会准确落在既定的网格点上，这就会引起这一类算法无法避免的网格失配问题［11］，从而导致其估计误差增大。
针对这一问题，一种连续域上的无网格DOA估计方法［12］被提出。该方法利用均匀阵列的阵列流形矩阵具有范德蒙德结构这一特点，基于原子范数最小化（Atomic Norm Minimization,ANM）将原本难以求解的NP 问题凸松弛转化为一个基于拓普利兹（Toeplitz）矩阵的半正定规划（Semi-Definite Programming, SDP）问题，最后通过范德蒙德分解获得阵列流形矩阵，从而实现DOA 估计［13-14］。相比于在网格类压缩感知算法，该算法做到了在连续空域上进行DOA 估计，从而避免了网格失配问题。但由Caratheodory 分析得到，在高维情况下Toeplitz 矩阵无法正确进行范德蒙德分解，因此上述的ANM 原理不能直接应用于二维DOA 估计中。所以现有的常规ANM应用一般都针对均匀线阵做DOA 估计，或针对某特殊阵列结构如文献［15］基于L 型阵列实现了二维DOA 估计。然而实际应用中有需求用到不满足范德蒙德结构的非均匀阵，如非均匀圆阵［16］等，为使ANM 能够应用于非均匀圆阵，本文基于虚拟阵列变换提出了一种改进的原子范数最小化二维DOA估计算法。
1 虚拟阵列变换
虚拟阵列变换［17］即是通过构造一个变换矩阵使得实际获得的原始数据矩阵转换为预期的数据形式。首先要确定一个来波方向的预期范围，针对这一预定的角度范围，构造原始阵列与预期阵列的流形矩阵。再利用两个流形矩阵计算变换矩阵，从而获得预期阵列的拟接收数据。
本文以某非均匀圆阵作为原始阵列，如图1所示，以阵元间距为半波长d=0.5λ 的均匀L 型阵列作为预期虚拟阵列，如图2 所示，以此为例说明虚拟阵列变化方法。
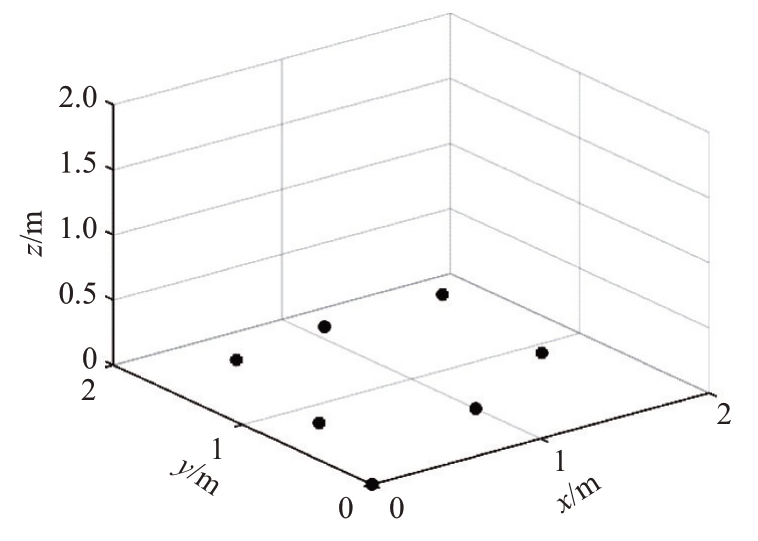
图1 非均匀圆型阵列
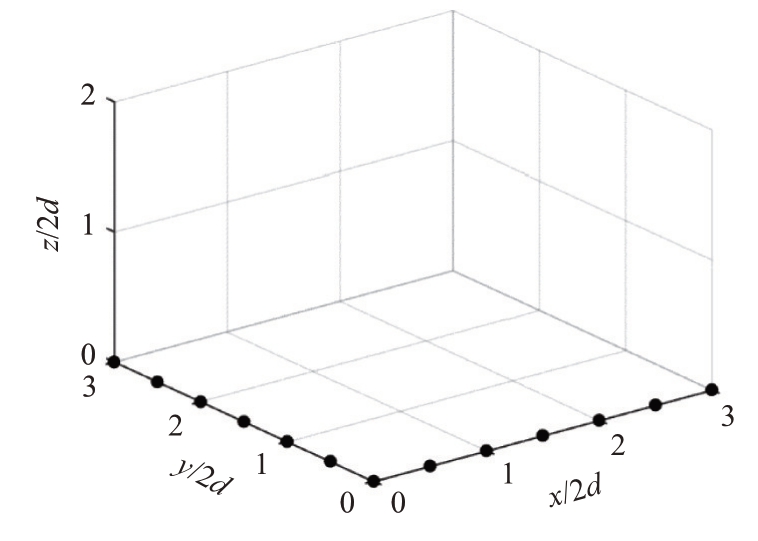
图2 均匀L型阵列
图1 中共M=7 个阵元，第一个阵元位于原点，定义第k 个阵元坐标为rk=(xk,yk,zk)，则来自方向(θn,βn)的信号的导向矢量为
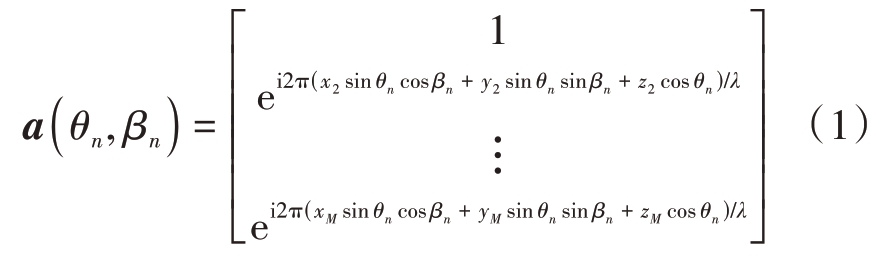
预定的信号源角度范围设为：俯仰角El=[θmin,θmax]，方位角Az=[ βmin,βmax]。以Δθ 和Δβ 为间隔分别划分俯仰角区间和方位角区间为ElΔ=[θmin,θmin+Δθ,…,θmax-Δθ,θmax]和AzΔ=[βmin,βmin+Δβ,…,βmax-Δβ,βmax]。那么原始阵列的流形矩阵为
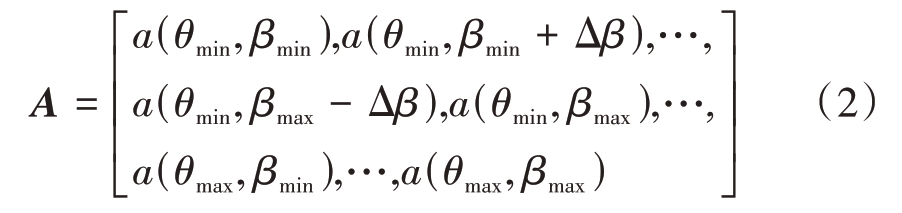
预期的阵列结构为由阵元数为M 的两条均匀线阵x轴和y轴组成的L型阵列，阵元间隔为d，预期阵列的导向矢量与流形矩阵分为x轴和y轴两部分。
x轴的导向矢量ax和流形矩阵Ax为
纵轴y的导向矢量ay和流形矩阵Ay为
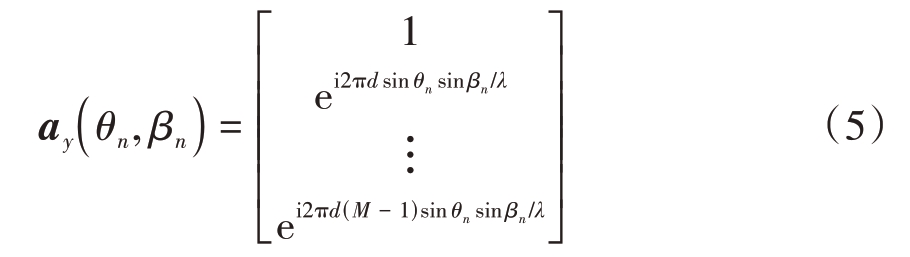
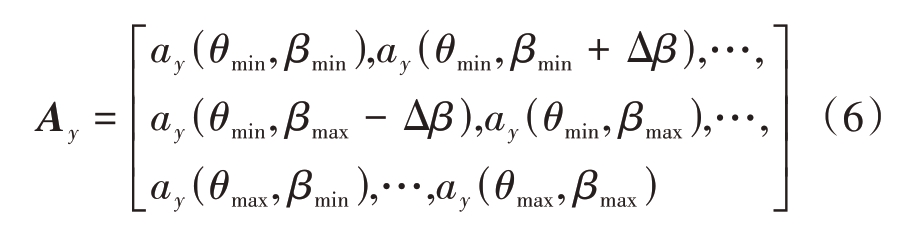
通过原始阵列与预期阵列的导向矢量构造两阵列间的变换矩阵，下面以x 轴为例，推导变换矩阵Bx。
式中，Bx 为原始阵列向L 型阵x 轴的变换矩阵。不可避免地，由变换矩阵得到的流形矩阵总是与预期阵列的理想流形矩阵之间存在误差：
式中，||·||F 表示Frobenius 模。以式（7）为目标，式（8）为约束，求得变换矩阵Bx：
受限于预定角度区间及其划分间隔等因素，误差不可避免，此时的变换误差定义为
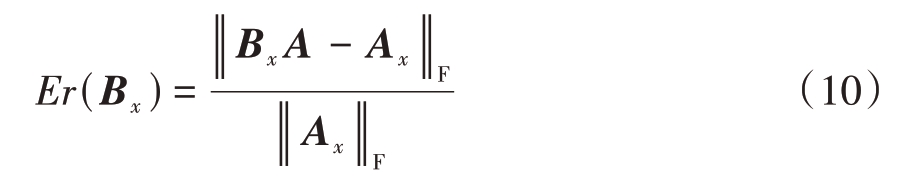
而这一误差的主要来源之一是预定角度与实际角度间存在差距，这一差距越大DOA 估计误差也就越大。最简单的解决办法就是减小划分预定角区间的划分间隔Δθ 和Δβ，然而在一定的角区间上一味减小间隔并不会有明显效果。因此先用较大的划分间隔进行初步DOA 估计，再在此基础上缩小预定角区间同时减小划分间隔后进行二次DOA估计，从而减小误差。
和Bx 同理得到原始阵列向L 型阵纵轴y 的变换矩阵By：
通过变换矩阵Bx和By即可获得预期的L 型阵的流形矩阵Ax和Ay，从而进行下一步的DOA估计。
2 基于ANM的DOA估计
针对如图1所示阵列结构的接收数据，通过虚拟阵列变换得到虚拟L型阵接收数据，最后利用基于原子范数最小化的DOA 估计算法和L 型阵二维几何关系得到俯仰角与方位角。
本文假设在远场条件下，以图1所示阵列接收来自方向{(θ1,β1),(θ2,β2),…,(θK,βK)}的K 个频率为f 的信号s1(t),s2(t),…,sK(t)，则原始阵列接收信号表示为
式中S(t)=[s1(t),s2(t),…,sK(t)]T，N(t) 表示阵列接收噪声矩阵。
通过式（9）和（11）得到的变换矩阵Bx和By，获得虚拟阵列的接收信号，分为x轴和y轴两部分：
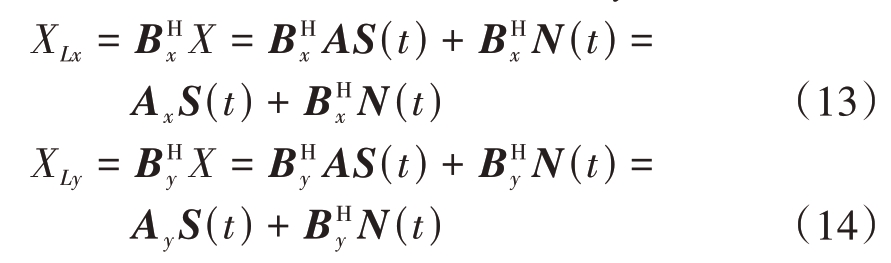
至此原本基于非均匀圆阵的DOA 估计问题转化为两个简单的均匀线阵上的DOA 估计问题，接下来以XLx 为例介绍均匀线阵上的ANM-DOA 估计算法，XLx 即为x 轴这一均匀线阵的接收信号。原子a( f,ϕ)和原子集Â参考式（13）的信号形式定义为
由式（13）和式（15）可以看出，虚拟阵列接收信号XLx 可以通过原子集Â中的原子线性组合构成，且所用原子数最少的一种对应着DOA 估计目标，类似于通过冗余字典中的原子来表示稀疏接收信号，区别在于冗余字典建立在离散域而原子集建立在连续域，这就避免了网格失配问题。
设x=AxS(t)，其l1-原子范数||·||A,1定义为
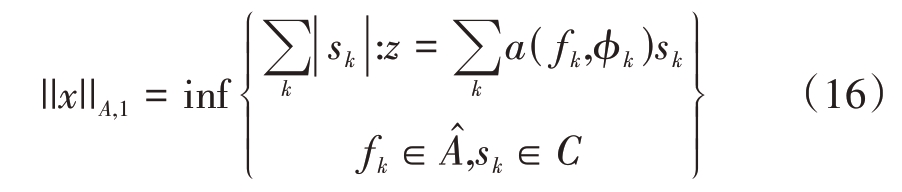
基于原子范数最小化的去噪问题模型［18］，式（13）可以表示为
进一步将式（17）转化为一个半正定规划问题进行求解：
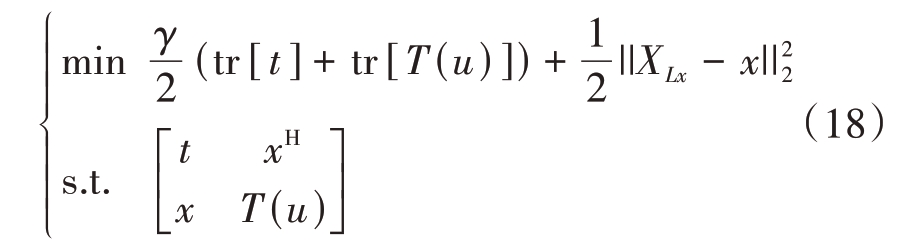
式中
为数据拟合项，γ为非负正则系数，t为自由变量，T(u)为半正定Toeplitz矩阵，x和u为待求解变量。
利用CVX 工具包求解式（18）所述半正定规划问题，获得重构出的T(u)，对其进行范德蒙德分解如下：
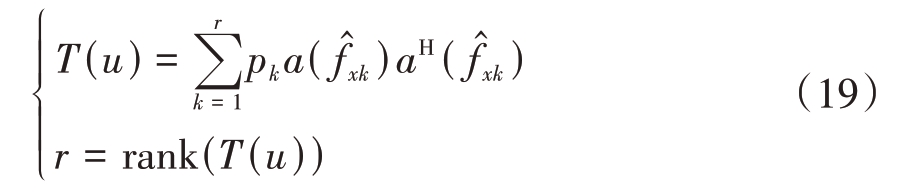
式中pk 为自然系数，a(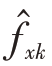
)来自于原子集
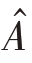̂。可以发现ANM 算法要求接收信号的导向矢量a( f)必须满足范德蒙德结构，才能在这一步进行范德蒙德分解，而本文所用非均匀圆阵并不满足这一条件，所以需要通过式（13）和式（14）将原接收信号转变为满足范德蒙德结构的虚拟阵列接收信号。
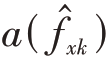对应着接收信号的导向矢量如式（3）所示，通过MUSIC方法进行频率检索，获得
：
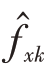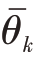和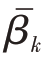
为待估计俯仰角与方位角。
同理，代入XLy，得到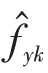
：
联立式（20）和式（21）可以解得方位角：
将方位角信息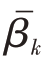
带入式（20），计算得到俯仰角
：
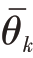本文算法适用于解决远场的DOA 估计问题，可以处理相干信源，且对样本数要求较低，基本步骤如下算法1所示。
算法1：
输入输出步骤1步骤2步骤3步骤4接收的回波信号X方位角β和俯仰角θ根据原始阵列与虚拟阵列在预定角区间的阵列流形矩阵，计算虚拟变换矩阵Bx和By对接收信号X 进行虚拟阵列变换处理，获得虚拟L型阵的x轴接收信号XLx和y轴接收信号XLy分别用基于ANM 的DOA 估计算法处理XLx 和XLy，获得f̂xk和f̂yk根据二维角度关系，由式（22）和式（23）估计得到俯仰角θˉk和方位角βˉk
算法复杂度分析：因本文算法所用的变换矩阵Bx和By在阵列结构固定的情况下是可以提前计算得到的常量矩阵，所以并不会增加算法的计算复杂度。而原ANM-DOA 估计算法的时间复杂度由半正定规划问题求解过程决定为O(n3.5)，所以改进本文算法的时间复杂度也是O(n3.5)。
3 仿真与实验分析
本节将通过仿真与实测实验验证所提算法的可行性与性能。以文献［16］的块稀疏贝叶斯学习算法和经典的二维多重信号分类（2D-MUSIC）算法作为对比算法。仿真以图1 所示的非均匀圆阵为原始接收矩阵，本文算法所用虚拟阵列如图2 所示。均方根误差定义为
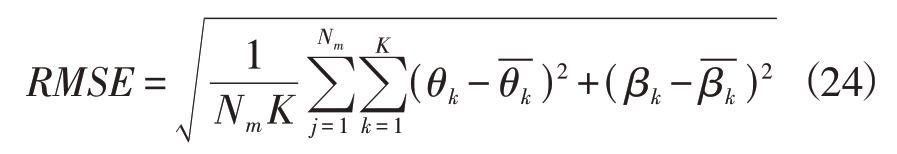
式中：Nm表示蒙特卡罗仿真的次数，K 是信源数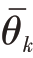；和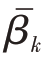为估计出的俯仰角和方位角。
3.1 对相干信号的估计性能分析
假设两目标的俯仰角和方位角分别为：(20°,20°) ，(40°,40°) 。蒙特卡罗仿真的次数Nm=100。在信号相干和非相干情况下分别研究不同算法的均方根误差随信噪比变化的情况，如图3所示。
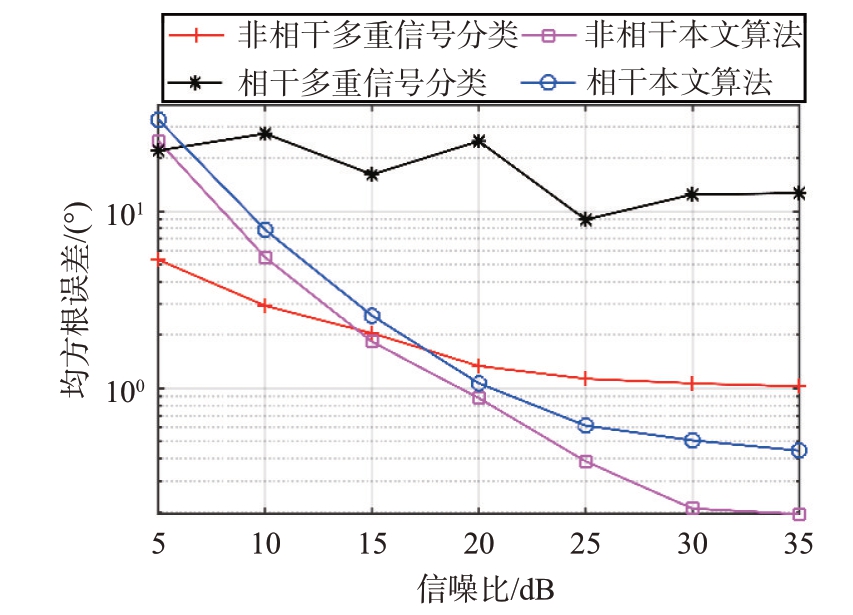
图3 对相干信号的估计性能分析
图3 描述了在信号相干与非相干两种情况下均方根误差随着信噪比变化的情况，快拍数设为N=100。在信号不相干的情况下，当信噪比较低时，MUSIC 算法有较好的估计性能，但随着信噪比的增加，本文所提算法的性能逐渐超过MUSIC 算法。当信号相干时，接收信号的协方差矩阵存在秩亏损问题，这会导致MUSIC 算法无法正常进行DOA 估计，但本文所提算法不涉及协方差矩阵估计，依然具有较好的精度。由此可见，本文算法可以实现对相干信号的DOA估计。
3.2 信噪比与快拍数对测角的影响
假设两目标的俯仰角和方位角分别为：(20°,20°) ，(60°,60°) 。蒙特卡罗仿真的次数Nm=100。不同算法的均方根误差随信噪比和快拍数变化的情况如图4和图5所示。
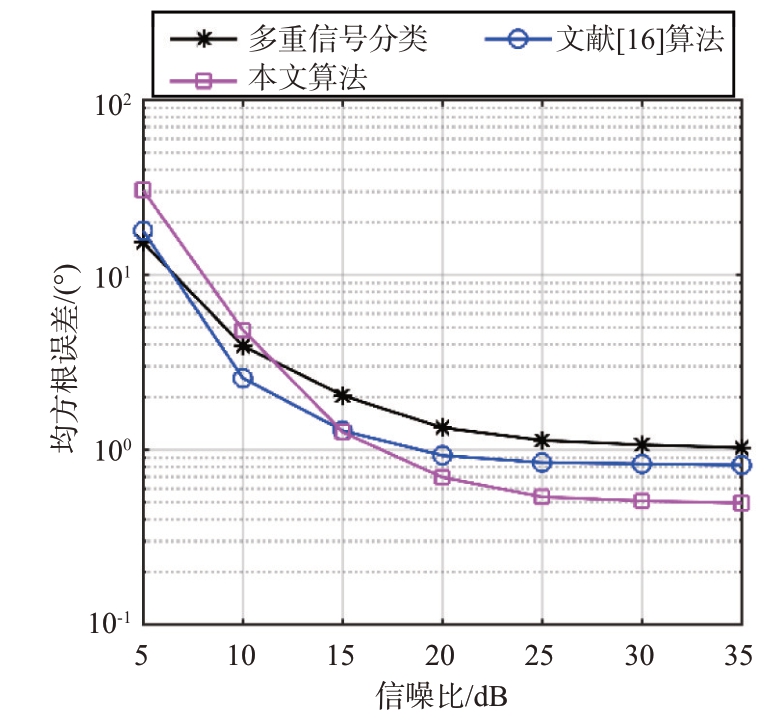
图4 均方根误差随信噪比变化
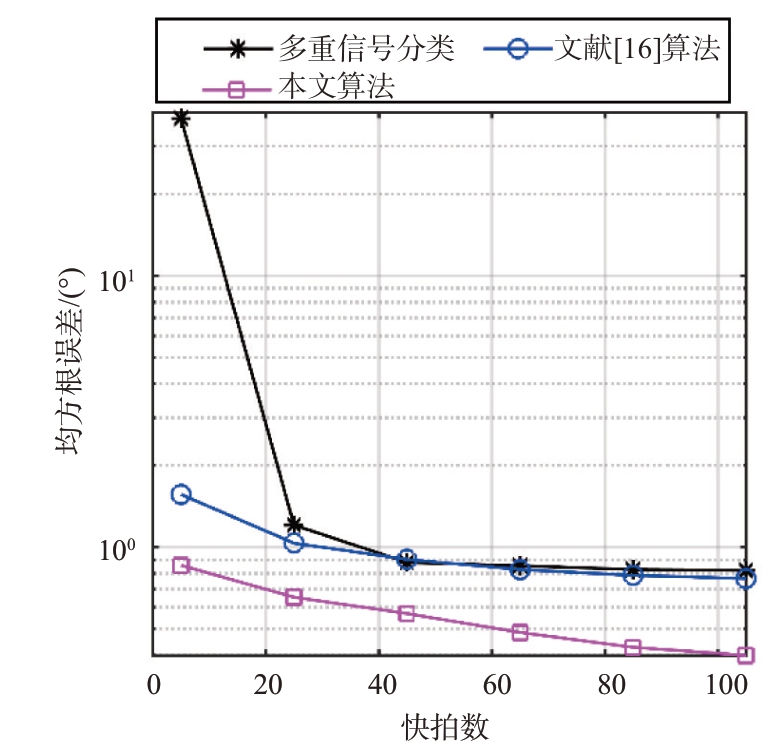
图5 均方根误差随快拍数变化
图4描述了在目标分散分布情况下，均方根误差随信噪比的变化情况，此时快拍数设为N=100。当信噪比大于15 dB 时，本文算法具有最好的估计性能，并且随着信噪比增加这种优势增加。MUSIC 和BSBL 算法受限于网格失配问题，导致在信噪比较高情况下依然具有一个无法避免的较高误差。而本文算法因虚拟阵列变换，导致对噪声较敏感，在信噪比较低情况下均方根误差较大。
图5描述了在目标分散分布情况下，均方根误差随快拍数的变化情况，此时信噪比设为SNR=20 dB。同快拍数下本文算法具有更好的估计性能，且当快拍数较小时依然有很好的估计精度，具有实时性。而MUSIC 算法因需要估计接收信号协方差矩阵，少快拍时会因为协方差矩阵估计不准而导致测角精度较低。BSBL算法虽然同样可以完成少快拍DOA 估计，但因网格失配问题，导致测角精度受限。
3.3 信源数对估计性能的影响
假设目标的俯仰角和方位角分别为：(20°,20°) ，(40°,40°) ，(60°,60°) ，(80°,80°) 。蒙特卡罗仿真的次数Nm=100。研究本文算法在单信源、双信源、三信源和四信源的情况下，均方根误差的变化情况如图6和图7所示。
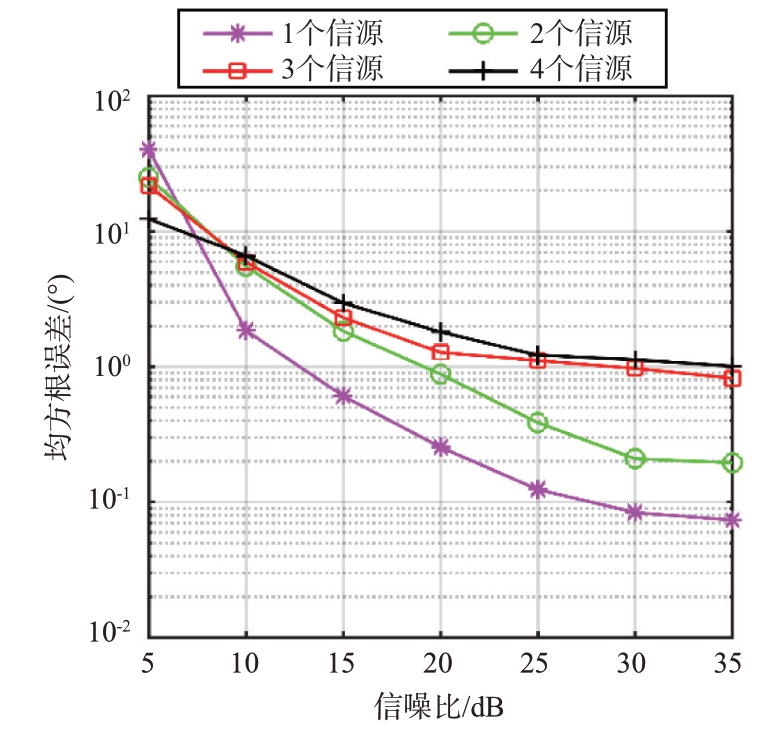
图6 信源数对估计性能的影响
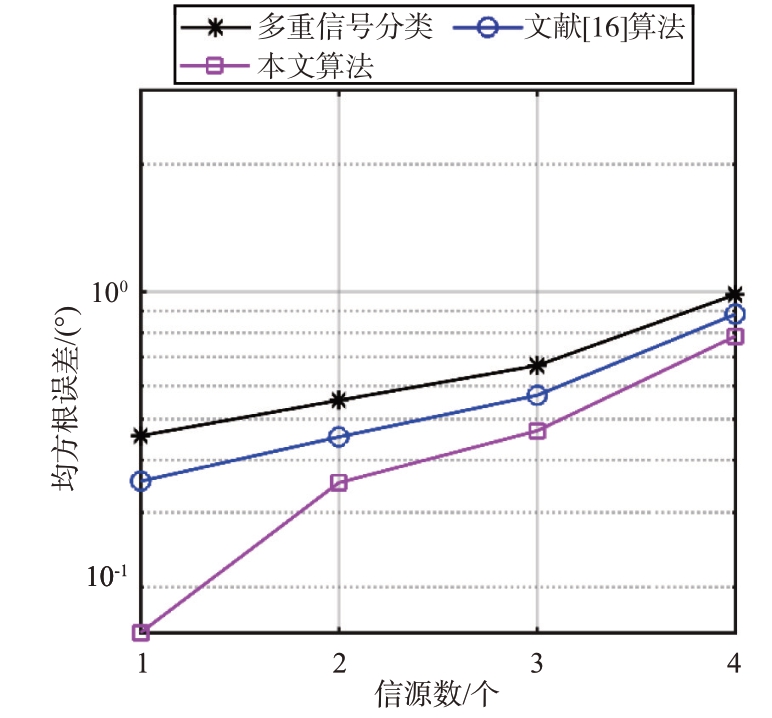
图7 不同算法受信源数的影响
图6 描述了本文算法在不同信源数下的测角均方根误差随信噪比的变化情况。随着信源数增加，均方根误差越来越大。图7描述了不同算法的测角均方根误差随信噪比的变化情况，可以看出各算法都有信源数越多估计误差越大的趋势，但因为可以避免网格失配问题，所以本文算法性能要优于其他算法。
3.4 虚拟阵列变换误差的影响
虚拟阵列变换误差主要来自于预定角与实际角之间的误差，假设两目标的俯仰角和方位角分别为：(20°,20°) ，(40°,40°) 。蒙特卡罗仿真的次数Nm=100。在预定角误差分别为0°,0.2°,0.4°时，本文算法的均方根误差随信噪比变化的情况如图8所示。
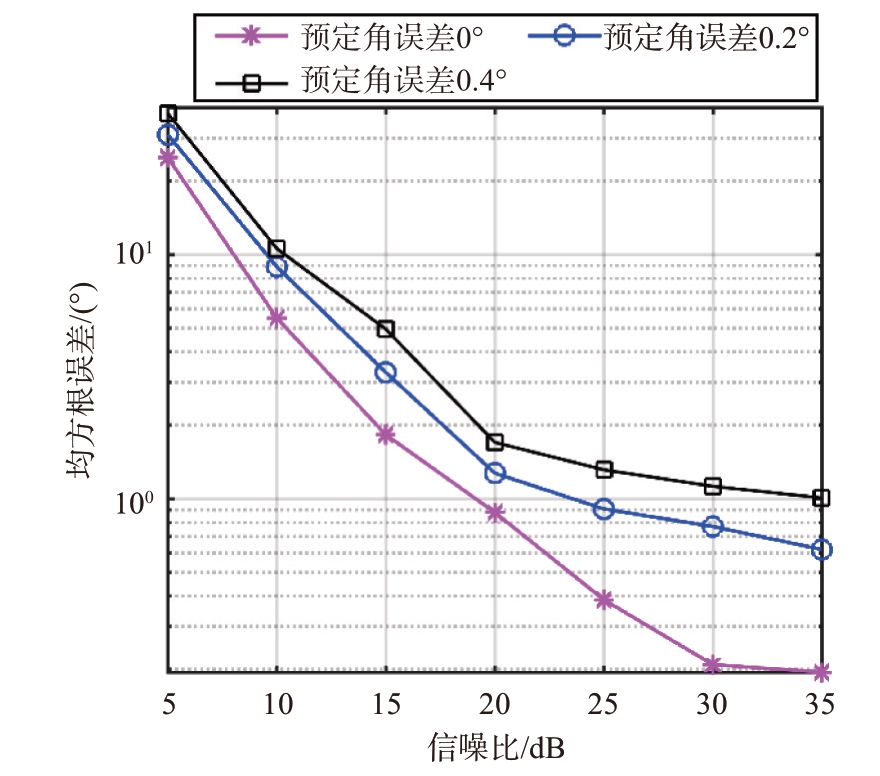
图8 预定角误差对估计性能的影响
图8 描述了本文算法在不同预定角误差下的测角均方根误差随信噪比的变化情况。随着预定角误差增加，均方根误差越来越大。这就要求把划分角度间隔控制在0.1°以下，而且因为变换矩阵都是可以预先计算的固定值，因此不会因为提高划分精度而影响计算效率。
3.5 实测实验
实测场景和条件：实验采用基于弹载7阵元非均匀圆阵阵列天线接收辐射源信号，信号包括1个辐射源和3个有源干扰。初始阶段，导弹与目标距离较远，4 个信号源之间空间角度差较小，随着导弹接近，角度差逐渐变大，如图9所示。
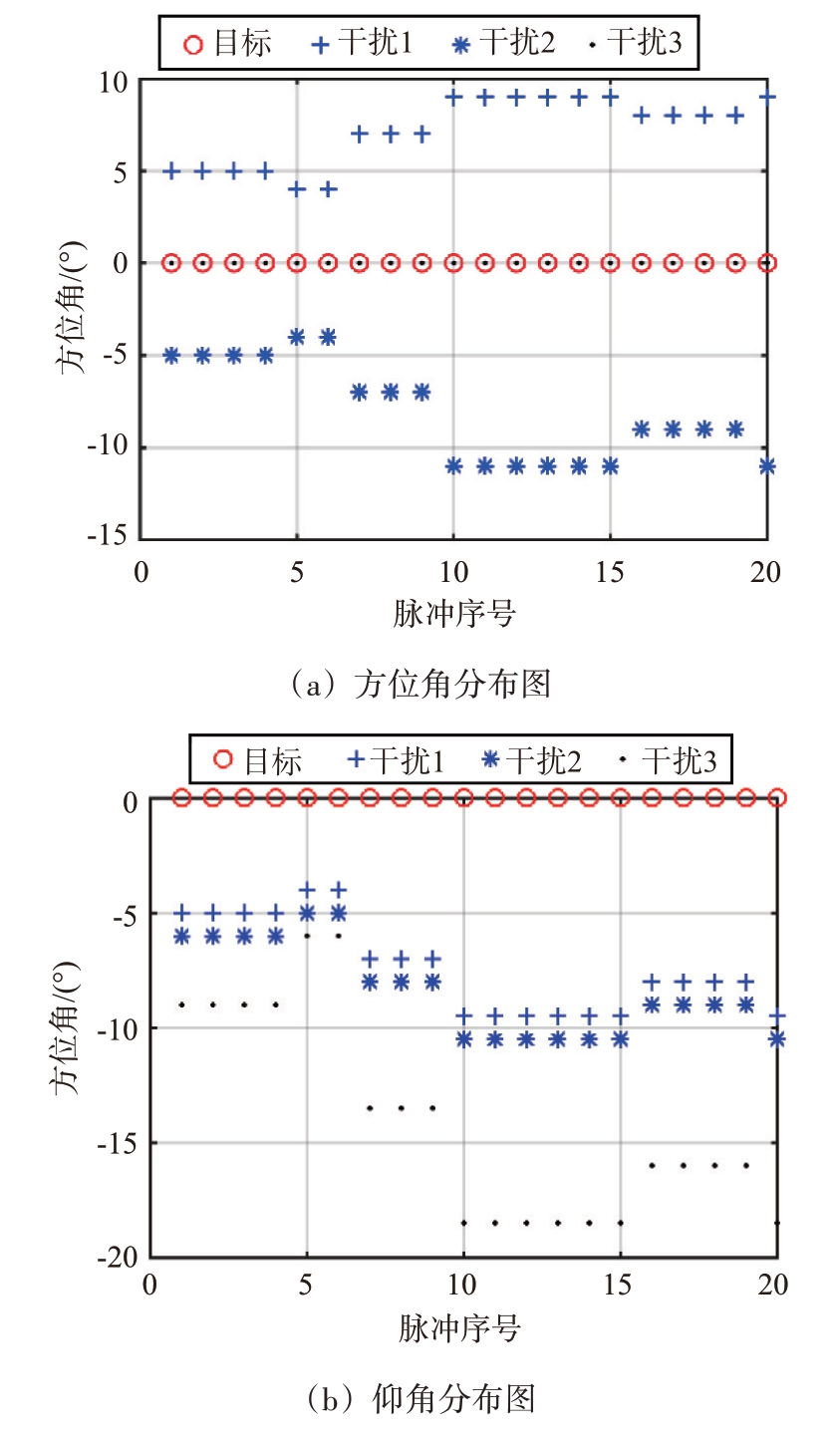
图9 方位角和仰角分布图
经过与文献［16］相同的预处理之后，分别用多重分类算法、文献［16］算法与本文算法进行处理，得到不同脉冲下各自的估计结果如图10所示。
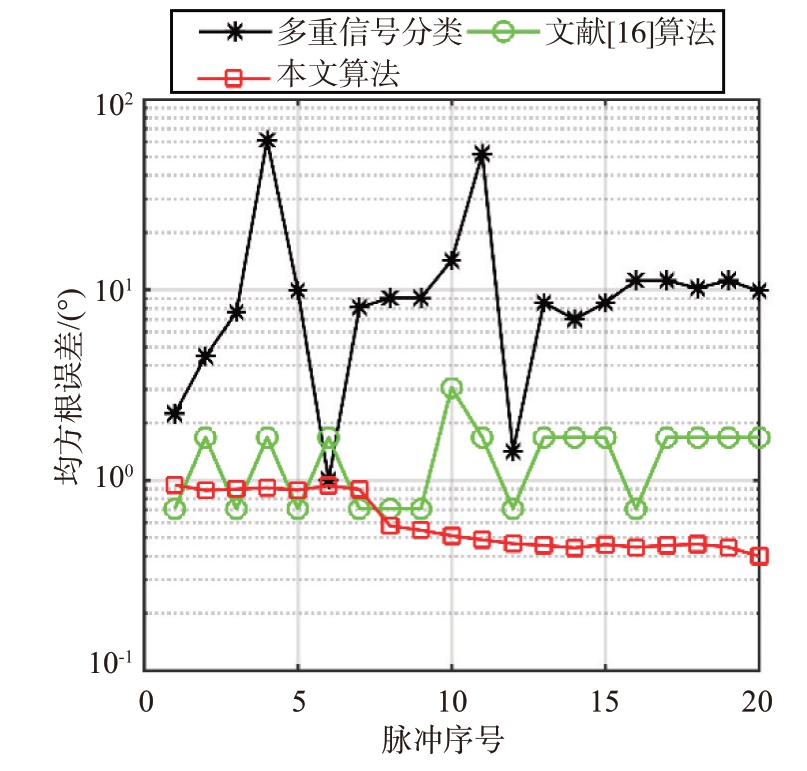
图10 实测数据测角均方根误差图
图10 描述了3 种不同算法对同一组实测数据的处理结果。由于单脉冲内采样数较少，无法稳定正确估计接收信号的协方差矩阵，所以MUSIC的估计结果较差。文献［16］的算法可以实现少样本估计，结果较好，但可以发现在某些信源方向没有落在网格点上的时刻，会有一个比较大的误差，也就是发生了网格失配问题。而本文算法可以在少样本的情况下实现无网格的DOA 估计，估计精度不会受到网格限制，估计精度较高。
4 结束语
针对传统的基于ANM 的DOA 估计算法无法直接应用于不满足范德蒙德结构的非均匀圆阵这一问题，本文基于虚拟阵列变换提出了一种改进算法。以某非均匀圆阵作原始阵列为例，通过虚拟阵列变换构建ANM 算法可以处理的虚拟L 型阵列接收信号，利用其二维角度关系进行DOA 估计。相比于常规ANM 算法，本文算法可以推广应用于非均匀阵列结构，同时拥有较好的DOA估计精度。
［1］CHEN Zhang, WU Hao, LIU Yongxiang. A Novel ULADifference-Coarray-Based DOA Estimation Method for General Coherent Signals［J］. Mathematical Problems in Engineering,2020（11）:1-13.
［2］王宁，吕晓德，李苗苗.低信噪比下非冗余阵列的无网格DOA 估计［J］.系统工程与电子技术，2023，45（2）:352-359.
［3］黎昕婷，钟舜聪，钟剑锋.基于改进MUSIC 算法的宽带信号DOA估计［J］.计算机工程，2022，48（11）:201-206.
［4］左罗，王俊，陈刚,等.基于TLS-CS的外辐射源雷达超分辨DOA 估计方法［J］.系统工程与电子技术，2020，42（1）:61-66.
［5］刘尚，蒋金华，段海洋，等.基于CS-MVDR 的多目标方位估计新方法［J］.雷达与对抗，2023，43（1）:26-30.
［6］高卫港,王鼎,张钺洋,等.基于贝叶斯压缩感知的子空间拟合离格DOA估计［J］.电讯技术,2023,63（2）:158-164.
［7］张骄，王敏.基于正交匹配追踪算法的虚拟内插空间平滑DOA估计［J］.测试技术学报，2022，36（5）:369-375.
［8］YANG Jie, YANG Yixin, LIAO Guisheng, et al. A Super-Resolution Direction of Arrival Estimation Algorithm for Coprime Array via Sparse Bayesian Learning Inference［J］.Circuits,Systems,and Signal Processing,2018,37（5）:1907-1934.
［9］YANG Jie,YANG Yixin,LU Jieyi.A Variational Bayesian Strategy for Solving the DOA Estimation Problem in Sparse Array［J］.Digital Signal Processing,2019,90:28-35.
［10］张俊，张新禹，姜卫东，等.基于广义近似消息传递的快速DOA 估计方法［J］.系统工程与电子技术,2022,44（10）:2995-3002.
［11］FENG Weike,GUO Yiduo,ZHANG Yongshun,et al.Airborne Radar Space Time Adaptive Processing Based on Atomic Norm Minimization［J］. Signal Processing, 2018,148:31-40.
［12］BHASKAR B N, TANG Gongguo, RECHT B. Atomic Norm Denoising with Applications to Line Spectral Estimation［J］. IEEE Trans on Signal Processing,2013,61（23）:5987-5999.
［13］石娟，张群飞，毛琳琳，等.基于联合子带ANM 的小快拍宽带DOA 估计方法［J］.系统工程与电子技术，2020，42（4）:733-739.
［14］YANG Zai, XIE Lihua, STOICA P P. Vandermonde Decomposition of Multilevel Toeplitz Matrices with Application to Multidimensional Super-Resolution［J］. IEEE Trans on Information Theory,2016,62（6）:3685-3701.
［15］ZHANG Yu, SUN Yinan, ZHANG Gong, et al. Crosscorrelation and DOA Estimation for L-Shaped Array via Decoupled Atomic Norm Minimization［J］. Wireless Communications and Mobile Computing,2021（1）:1-11.
［16］王珊珊，刘峥，谢荣，等.有源欺骗干扰环境下的DOA估计［J］.电子与信息学报，2019，41（5）:1040-1046.
［17］庞桐桐.基于双弧阵的反卷积波束形成［J］.无线电通信技术,2021,47（4）:424-431.
［18］YANG Zai, LI Jian, STOICA P. Sparse Methods for Direction-of-Arrival Estimation［M］. Amsterdam:Elsevier,2018:509-581.
