0 引 言
相较于传统的相控阵雷达，MIMO 雷达利用波形分集技术形成大孔径虚拟阵列，具有更强的抗干扰能力以及更优的参数估计性能［1-7］。角度估计是MIMO 雷达系统探测目标信息的核心研究内容之一。众多学者先后提出Capon 算法［8］、MUSIC算法［9］、ESPRIT 算法［10］等多种方法应用于双基地MIMO 雷达的目标波离角（Direction of Departure,DOD）和波达角（Direction of Arrival, DOA）估计。然而，在实际大规模雷达阵列系统中，由于工作环境恶劣、元器件老化以及愈发复杂的雷达系统等因素的影响，增加了MIMO雷达系统中阵元的受损概率［11-13］。部分阵列天线的损坏会造成阵列采样数据的丢失，产生较差的角度估计性能［14］。因此，在MIMO雷达中，有效地应对阵元故障对目标角度估计带来的不利影响具有重要的意义。
当阵列中存在故障阵元时，阵列接收数据会出现大量的丢失［15-17］。为解决阵元失效导致的角度估计算法性能下降的问题，文献［18］将深度神经网络（Deep Neural Network,DNN）应用于阵元缺损时的DOA 估计问题，联合利用去噪自动编码器（Denoising Autoencoder, DAE）和并行网络实现受损数据的分类和重建，但该方法需要大量的训练样本来提高DNN 的DOA 估计性能。文献［19］对存在故障阵元的协方差矩阵进行差分处理，构造虚拟差分阵列，利用正常的冗余虚拟阵元数据来填充故障阵元的缺失数据，进而获得完整的协方差矩阵，实现目标DOA 的估计。文献［20］将该方法拓展应用于阵元故障下单基地MIMO 雷达DOA估计问题中［20］，为了保证MIMO雷达的协方差矩阵具有Toeplitz 结构，要求发射阵元间距为接收阵元间距的N 倍，其中N 为接收阵元数，因此该方法的应用具有较大的局限性。文献［21］提出一种结构化的MC（Matrix Completion）算法，该方法首先将虚拟阵列协方差矩阵构造为不存在整行整列元素缺失的四重Hankel矩阵，然后利用低秩MC算法恢复出缺失数据。然而，该方法需利用Vandermonde 分解等方法实现角度的精确估计，且四重Hankel 矩阵操作造成了巨大的矩阵维度扩张问题，导致该算法运算时间变长。
在双基地MIMO 雷达中，为更好地解决因阵元缺损而导致的丢失数据恢复问题，并改善阵元缺损时的角度估计性能，提出一种基于不完整矩阵因子重构的MIMO 雷达角度估计方法。先使用奇异值分解方法从不完整的协方差矩阵中提取出维度较低的矩阵因子，并将协方差矩阵缺失数据恢复问题转换为不完整矩阵因子重构问题。然后，利用矩阵因子行和列间的结构特性，将不完整矩阵因子变换为块Hankel 矩阵，并对其施加核范数约束从而建立不完整矩阵因子重构模型。此外，为避免核范数求解中运算量较大的奇异值分解操作，利用Hankel 矩阵可分解性质，重新表征了核范数约束问题。最后，采用ADMM 算法求解上述矩阵因子重构模型。仿真实验表明本文方法可以有效地恢复MIMO 雷达不完整矩阵因子中的缺失数据，在阵元故障时仍获得较高精度的角度估计，并具有较低的计算复杂度。
1 阵元失效MIMO雷达信号模型
双基地MIMO 雷达系统具有M 个发射阵元和N 个接收阵元，发射和接收阵元间隔分别为dt 和dr，且收发阵列均为半波长间距的均匀线阵。发射阵列发射M个正交信号
且该信号满足
其中，K 为每个脉冲周期内的采样个数
表示转置运算
表示共轭转置运算。在空间远场内若存在P 个非相干目标，第
个目标位于
其中θp 为波离方向角，φp 为波达方向角。则在第
个脉冲周期的接收信号Xq表示为
式中
为接收阵列导向矩阵，其中
为发射阵列导向矩阵，其中
表示由向量sq 构成的对角矩阵，其中
和fdp 分别为第p 个目标的反射系数和多普勒频率，fs 为脉冲重复频率；Zq ∈ℂM×K为高斯白噪声矩阵。利用发射信号之间的正交特性，用
右乘式（1），则经匹配滤波后的输出为
式中：Yq=XqWH/K 表示经匹配滤波后的接收信号矩阵；
表示匹配滤波后的噪声矩阵。将Yq=XqWH/K按列表示MN × 1维列矢量，即
式中
表示向量化处理；⊙表示Khatri-Rao 积。Q 个脉冲周期下的虚拟阵列输出矩阵Y为
式中
则Q 个脉冲周期下的协方差矩阵R可估计为
式中
为信号协方差矩阵，RZ=
为噪声协方差矩阵。对于非相干目标，
在实际应用中，由于恶劣的外界环境和日益复杂的雷达系统等因素影响，天线阵列中出现部分阵元失效的概率增加，导致阵列采样信号的丢失。令ΩT 和ΩR 分别为发射和接收阵列中故障阵元的位置集合，由于失效阵元的存在，因此发射和接收导向矩阵中的一些行元素全为零，可表示为
式中，ct ∈ℝM×1 和cr ∈ℝN×1 均为由0 和1 构成的向量。 若第m(m ∈ΩT)个发射阵元故障，则
表示向量ct 中第m 个元素；若第
个接收阵元故障，则
表示向量cr 中第n 个元素。阵元正常时，向量ct 和cr中所有元素都为1。阵元失效下虚拟阵列输出信号矩阵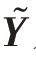
͂及其协方差矩阵
͂分别表示为
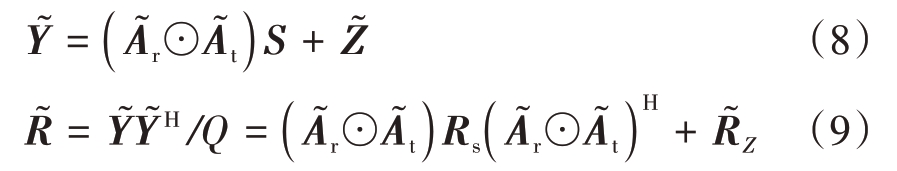
式中
为阵元失效下的噪声矩阵，其中，◦表示Hadamard积，⊗表示Kronecker积
为阵元失效下的噪声协方差矩阵。
2 基于不完整矩阵因子重构的MIMO雷达角度估计
传统矩阵填充方法是依据矩阵的低秩特性来约束待重建矩阵，当缺失项随机分布在待重建矩阵内，可以精确地重建出完整矩阵［22］。然而，在双基地MIMO 雷达中，由于失效阵元的存在，协方差矩阵中存在一些整行和整列中无观测数据的情况，这些缺失数据的位置不符合随机分布，这类数据缺失模式被称为结构性缺失［22］。此时，传统矩阵填充方法中的秩最小化不足以在恢复结构性缺失数据时产生足够的约束，例如对矩阵中整列缺失的元素直接填充零元素仍然将使得矩阵的秩最小，因此导致现有的矩阵填充算法无法恢复结构性缺失数据［22］。
2.1 不完整矩阵因子的重构模型
为解决协方差矩阵中结构性缺失数据重建问题，首先分析协方差矩阵的分解特性，根据式（5），阵元正常情况下完整的协方差矩阵R可表示为
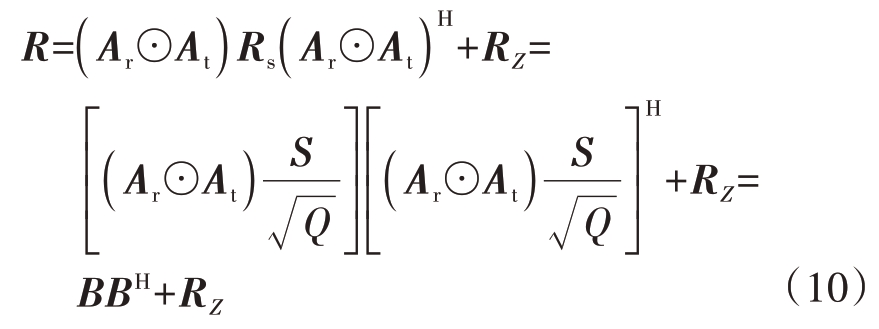
式中，
为矩阵因子。当阵元出现故障时，协方差矩阵分解出的矩阵因子
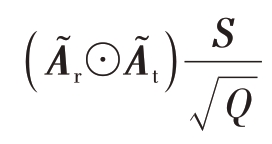中会出现整行的缺失数据，此时无法直接通过MC 算法恢复这些结构性的缺失数据。本文引入块Hankel 矩阵操作对矩阵因子
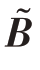͂进行变换，建立如下矩阵因子重构模型：
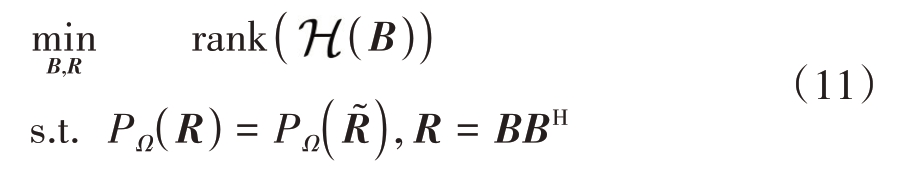
式中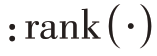
表示矩阵的秩函数；R 为待恢复的完整协方差矩阵；
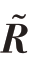为阵元故障下的协方差矩阵；B ∈ℂMN×P 为待重建矩阵因子；Ω 为R 中已知非零元素的索引集
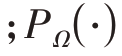表示矩阵在索引集Ω 上的投影
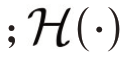为块Hankel矩阵操作。
矩阵B ∈ℂMN×P 可由P 个列向量
构成，即
其中，bp表示矩阵B的第p列元素组成的向量。列向量bp可由N个子列向量
构成，即
，其中，子列向
表示
中第m个元素。
将向量映射到Hankel矩阵的变换操作ℱ(·)定义为
式中
为向下取整运算。以子列向量
中的元素构造Hankel矩阵
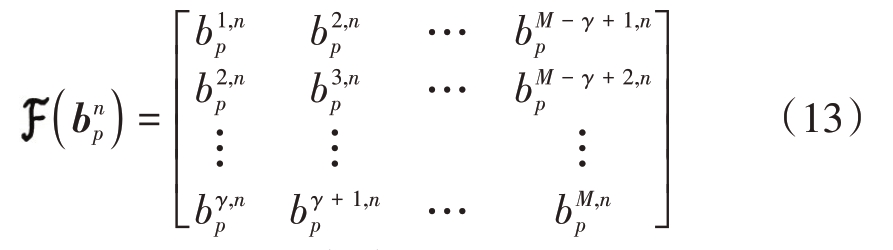
以Hankel矩阵
为子块矩阵，将N个子块矩阵
排列为矩阵
定义矩阵映射到块Hankel矩阵的操作
为
式中，
。以矩阵Hp 构造的块Hankel 矩阵
可表示为
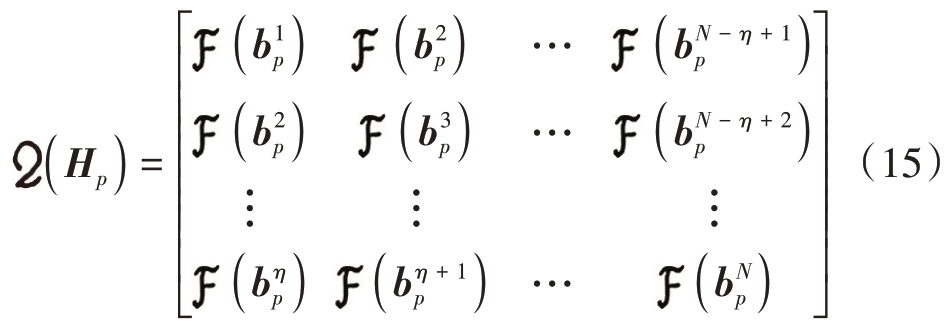
以块Hankel 矩阵
为子块，将P 个子块
构造为矩阵D=
为了分析方便，本文用块Hankel 矩阵操作
表示由矩阵因子B 经过变换获得块Hankel 矩阵D 的操作，即
若收发阵元数分别为M=5，N=3，目标个数为P=3，对虚拟阵列协方差矩阵分解后可得到矩阵因子B ∈ℂ15×3，由矩阵因子B 构造块Hankel 矩阵的操作过程如图1所示。
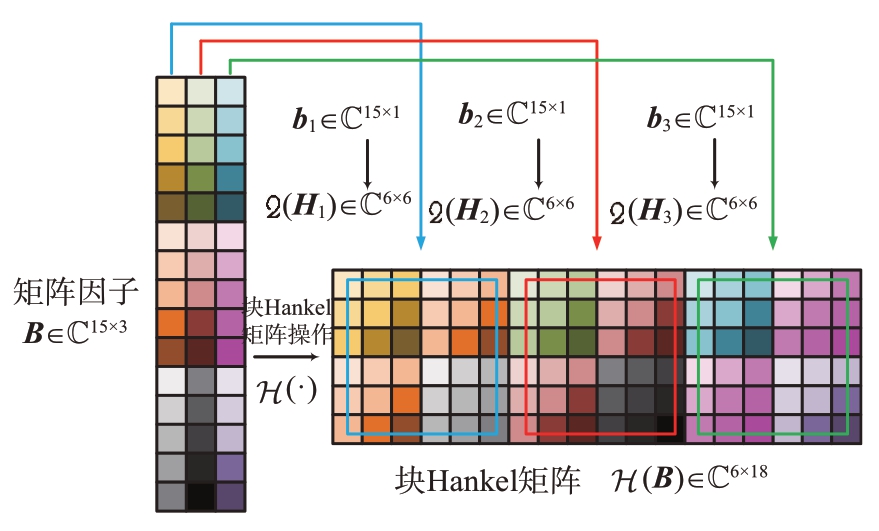
图1 块Hankel矩阵的操作过程示意图
由于式（11）中秩的求解为非凸问题，常用核范数
替代矩阵的秩函数，因此将式（11）转换为如下核范数最小化模型：
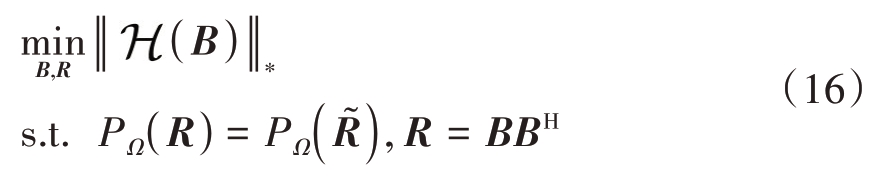
2.2 优化算法
在求解式（16）时，需引入矩阵的SVD（Singular Value Decomposition）运算［23］。对一个维度为M × N的矩阵进行SVD运算时，一般其计算复杂度为
由于本文引入了块Hankel矩阵操作，使得矩阵因子B 的维度从MN × P 扩大为
这样在采用SVD运算时会产生较高的计算复杂度。
为有效降低计算复杂度，将块Hankel 矩阵等价表达为两个矩阵的乘积形式［24］，表示如下：
式中
称为结构化的Hankel 矩阵分解［25］，因此核范数可等价表示为
式中
为Frobenius范数。
根据式（18），将式（16）转换为如下所示的不完整矩阵因子的重构模型：
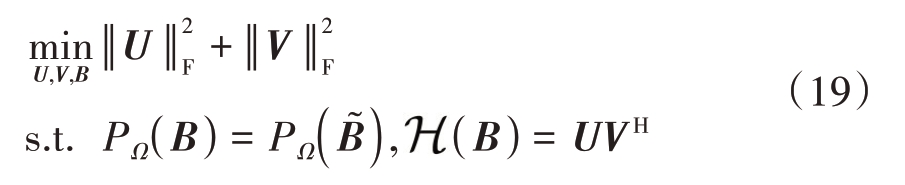
式中，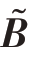
͂为不完整矩阵因子，由阵元失效下协方差矩阵
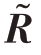͂分解所得。可以根据式R=BBH 从恢复出的完整矩阵因子B估计出完整的协方差矩阵R。
由于噪声的影响，完整矩阵B与不完整B͂之间会存在误差，在式（19）模型中加入噪声约束项。此外，式（19）中的等式约束项
在实际情况中也为近似相等，因此引入
最小二乘约束项使得
逼近UVH。最终建立以下不完整矩阵因子填充的模型：
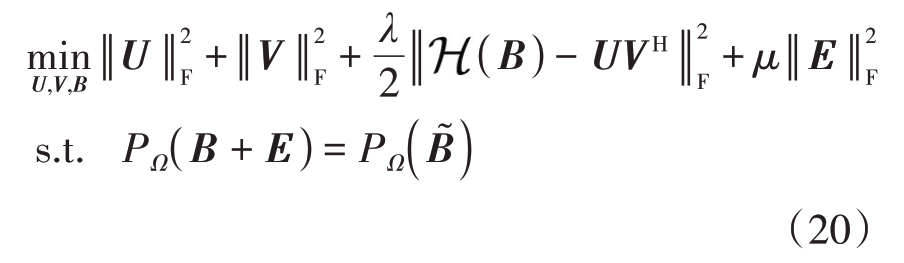
式中：λ 为正则化参数；μ 为权重参数；E 为高斯白噪声矩阵
为Frobenius 范数约束的噪声项。将式（20）转化为无约束项的优化问题，则其增广拉格朗日函数可定义为
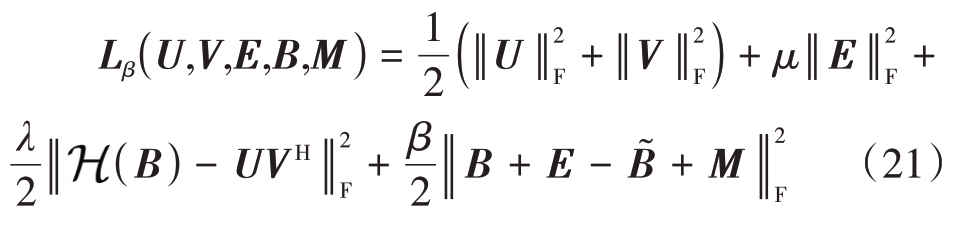
式中，M 为拉格朗日乘子矩阵，β 为惩罚系数。在ADMM 的框架下，通过固定多个变量的值，迭代更新一个变量的值来依次更新变量U,V,E,B 和M。在第k次迭代中，各个变量的更新函数为
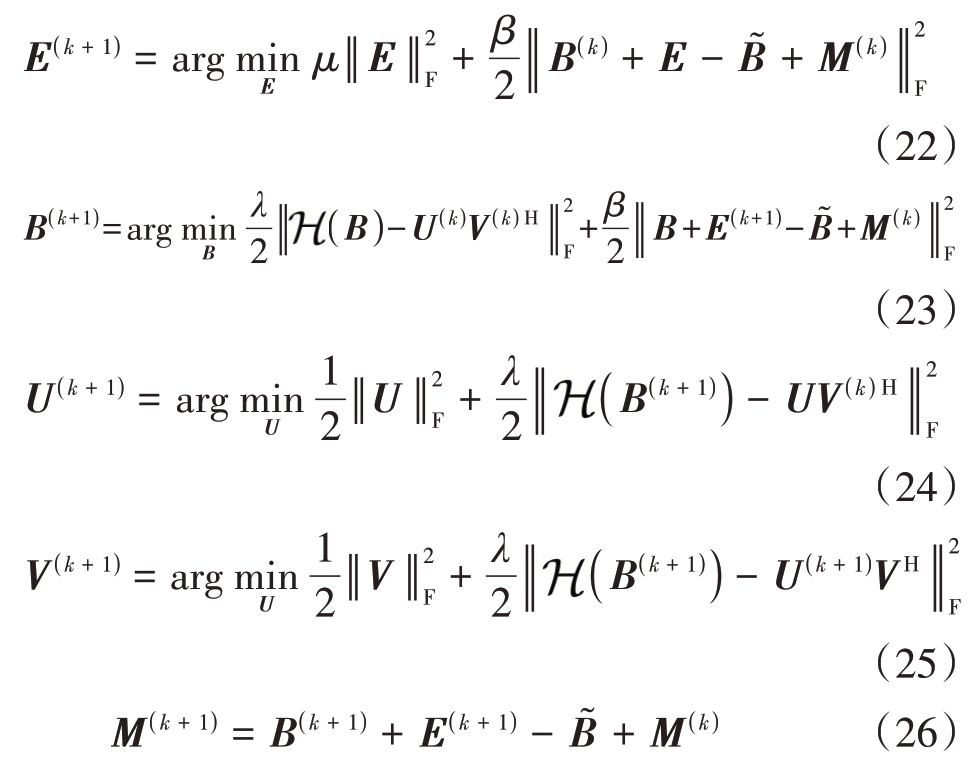
通过求解式（22），更新E的迭代解为
利用最小二乘法求解式（23），可得到更新B的迭代解为
式中
为块Hankel矩阵操作
的逆变换，对于任意一个矩阵X，均有
在变量U和V的子问题求解时，对式（24）中的矩阵U求偏导数得
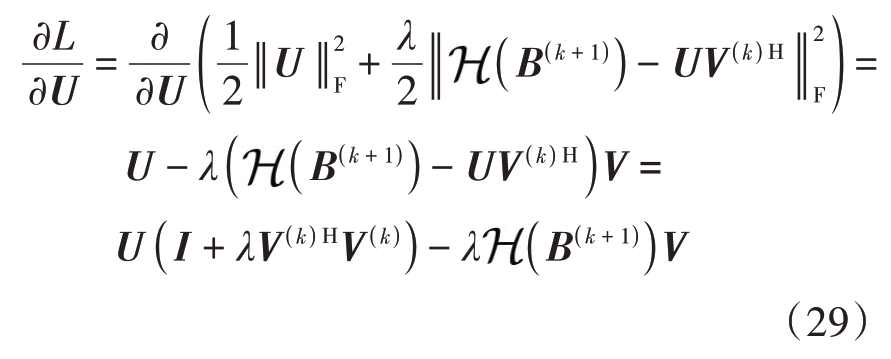
显然，使
，就可得到子问题U 的最优迭代解。类似地，子问题V的闭式解也可以通过类似方式得到，因此变量U和V的更新迭代解分别为
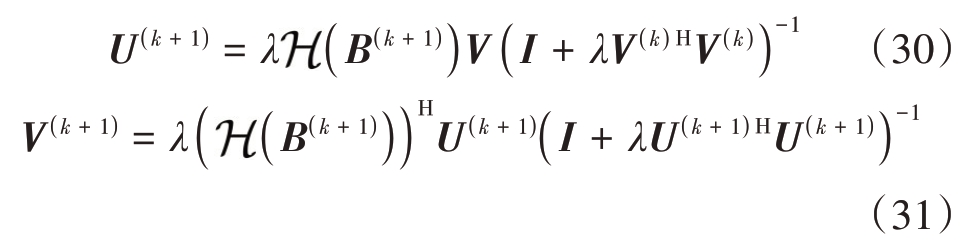
拉格朗日乘子矩阵M的更新迭代解为
综上所述，式（20）所表示的优化模型求解如表1所示。
表1 式（20）所示的优化模型求解算法
算法1:ADMM算法求解式（20）的优化模型Input:不完整协方差矩阵R͂∈ℂMN×MN 及其采样索引集Ω以及迭代次数K 1）对R͂进行奇异值分解获得不完整的矩阵因子初始值B͂∈ℂMN×P，k=ΔB=1；2）初始化U ∈ℂγη×P，V ∈ℂ()M-γ + 1 ()N-η + 1 P × P；while not converged do 3）通过求解式（27）更新E;4）通过求解式（28）更新B;5）通过求解式（30）更新U;6）通过求解式（31）更新V;7）通过求解式（32）更新M;8）ΔB=‖‖B-Blast F/‖ ‖Blast F;9）Blast ←B;end while Output: 重建结果:完整的矩阵因子B
在算法1 中，当迭代条件满足ΔB ≤ε 或达到最大迭代次数K 时，迭代停止，其中ε 为较小的正数。此外，本文利用了协方差矩阵的SVD 分解进行矩阵因子初始化，有效地加快了算法收敛速度。当迭代停止时，可得到完整的矩阵因子B，然后基于完整矩阵因子进行目标角度估计。
2.3 算法复杂度分析
文献［20］的计算复杂度集中在构造完整协方差矩阵上，需对MN 个子矩阵进行取平均操作，其计算复杂度约为
；本文算法的计算复杂度主要集中在式（30）和式（31）中的矩阵相乘和求逆运算，其计算复杂度约为
其中K1 为迭代次数；文献［21］方法对由协方差矩阵构造的四重Hankel矩阵进行核范数最小化求解，需要对复杂度较高的四重Hankel 矩阵进行SVD 分解，其复杂度为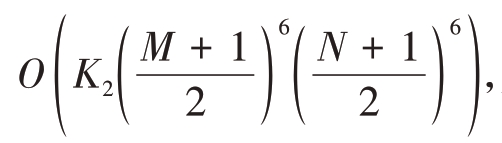
其中K2为迭代次数。
3 仿真与分析
为保证各算法对比的公平性，统一采用ESPRIT 算法［10］对本文方法（记为IMFR-MC）、文献［20］方法（记为DC-MC）和文献［21］方法（记为FFH-MC）恢复出的完整协方差矩阵进行目标角度估计，并以基于完整协方差矩阵直接进行ESPRIT算法估计的目标角度性能进行对比。在仿真实验中，设置收发阵元数分别为M=5，N=15。假设有P=3 个远场目标，其角度分别为
第m 个发射阵元发射的波形信号为wm=
其中，wm为W的第m行，hm表示维度为256×256的Hadamard矩阵的第m行。信噪比定义为
均方根误差定
MT 为蒙特卡洛实验次数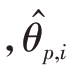
和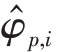
分别为第p 个目标在第i 次蒙特卡洛实验中的DOD 和DOA 估计值。
仿真实验1:设置MIMO 雷达故障阵元位置集合为
，信噪比为-5 dB，快拍数Q=100，MT=100。图2（a）和（b）分别为阵元故障时ESPRIT 算法和IMFR-MC 算法的角度估计结果星座图。图中符号“*”表示目标角度估计值，符号“+”表示目标角度真实值。由图2可知，由于故障阵元缺失数据未填补，阵元失效时直接采用ESPRIT 算法估计出的目标角度值与真实值相差较大，而IMFR-MC 算法充分利用矩阵因子的结构特性对故障阵元的缺失数据进行了有效填补，其目标角度估计值与真实值接近。
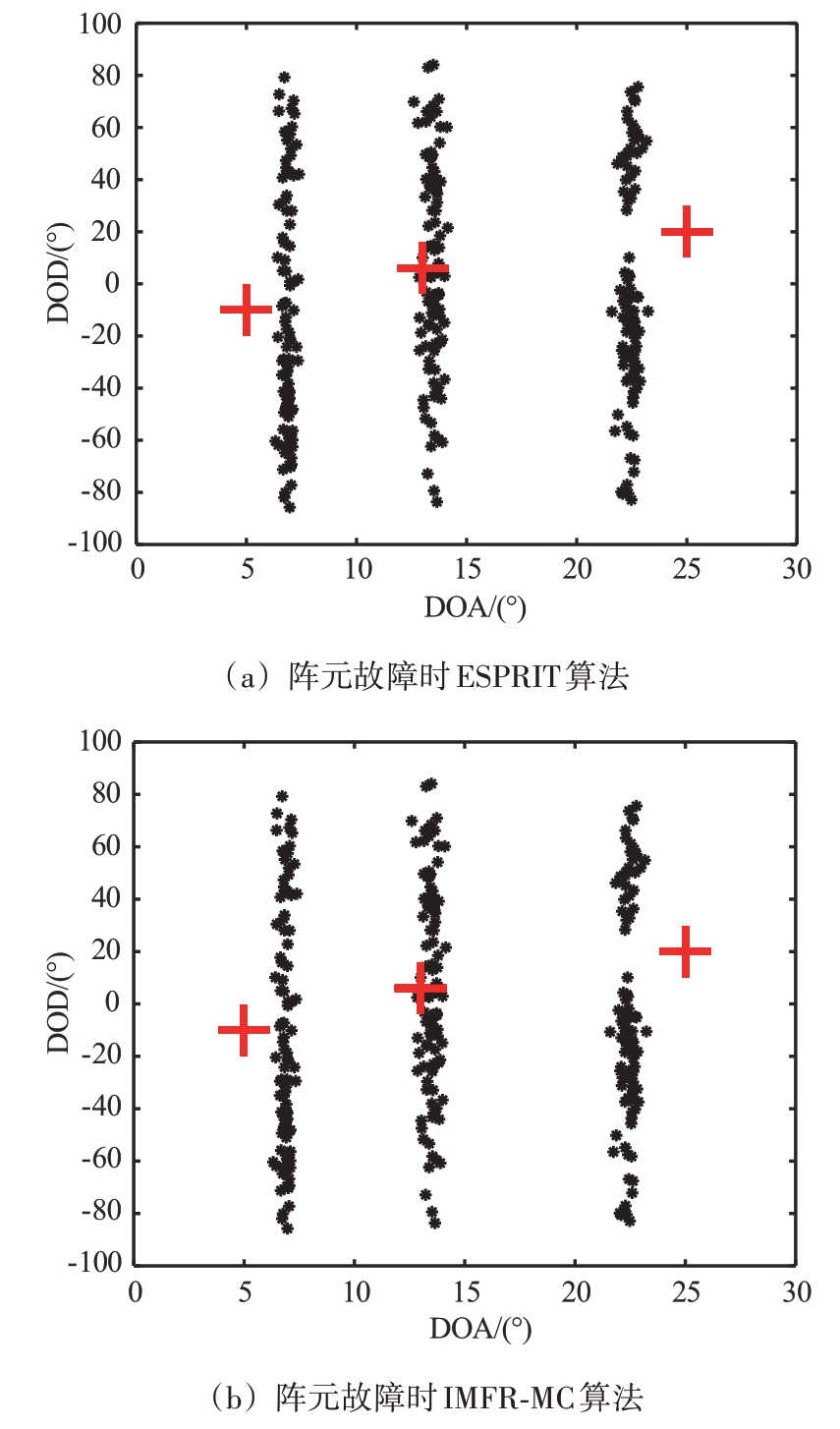
图2 目标角度估计星座图
仿真实验2：阵列故障阵元位置设置与仿真实验1 相同，Q=100，MT=100。图3 为不同方法的RMSE 随SNR 变化的曲线图。由图3 可知，故障阵元会导致阵列接收数据缺失，致使协方差矩阵的完整结构遭到破坏，此时直接使用ESPRIT 算法估计出的目标角度精度非常差，从而无法有效地估计目标的角度。此外，由于目标的DOD 和DOA 不同，MIMO 雷达协方差矩阵具有块Toeplitz 特性而非Toeplitz 特性，因此采用差分处理技术的DC-MC算法无法填补故障阵元缺失数据，其目标角度估计误差较大。FFH-MC 算法和IMFR-MC 算法对故障阵元的缺失数据进行了有效填补，在低信噪比区域两者几乎具有相同的性能，而在高信噪比区域IMFR-MC 算法的角度估计精度优于FFH-MC算法。
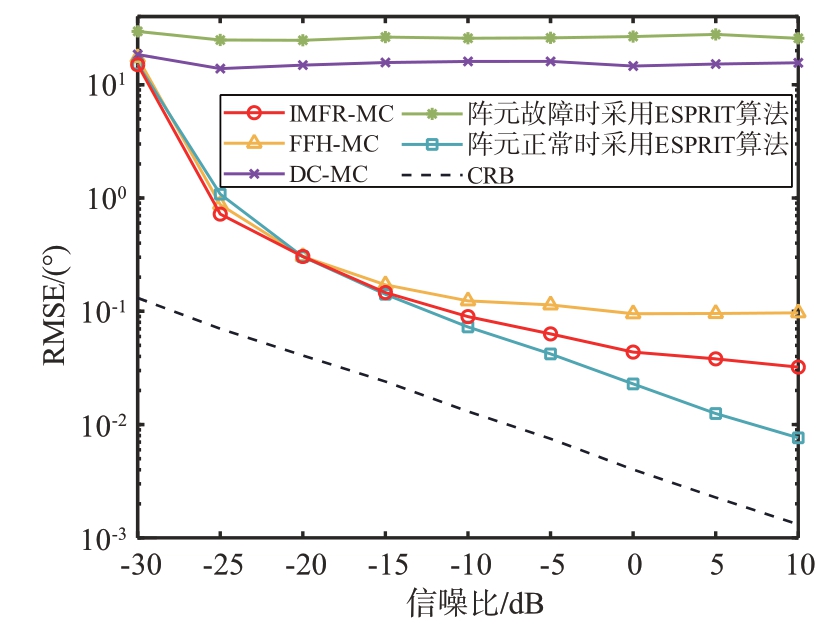
图3 不同方法的RMSE随SNR的变化曲线图
仿真实验3：设置信噪比为-5 dB，发射阵列和接收阵列的故障阵元位置设置与仿真实验1 中相同，MT=100。图4 为RMSE 随快拍数变化的曲线图，图中除DC-MC 算法的目标角度估计精度较差以外，其余方法随着快拍数的增多，角度估计精度均有所提升，但IMFR-MC 算法明显优于FFH-MC算法。
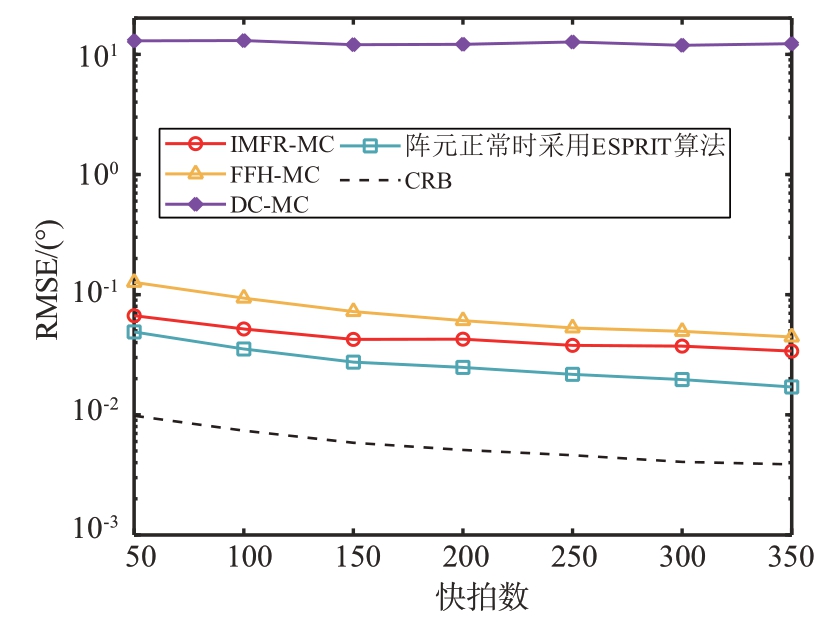
图4 不同方法的RMSE随快拍数变化曲线图
仿真实验4：假设失效接收阵元的数量从0 至8 递增，对应的接收阵列的故障率为0%～53%，其中故障率为0%表示接收阵列中故障阵元个数为0。在每次独立实验中，故障接收阵元的位置随机选取，而发射阵列中第3个发射阵元故障。设置信噪比为-5 dB，快拍数为Q=100，MT=100。图5为不同方法的RMSE 随接收阵列故障率变化的曲线图，除DC-MC 算法的角度估计性能普遍较差以外，FFH-MC 算法与IMFR-MC 算法的RMSE 随着接收阵元故障率的增加均有不同程度的增大，但IMFR-MC 算法总体上比FFH-MC 算法具有更低的RMSE值。
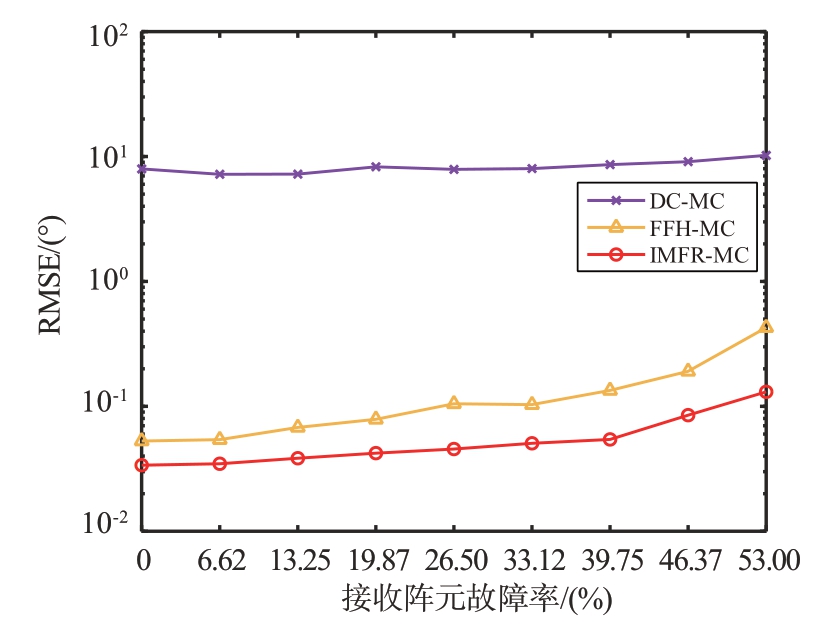
图5 不同方法的RMSE随接收阵列故障率变化曲线图
仿真实验5：本仿真实验参数设置与仿真实验1 相同。实验仿真软件为MATLAB2018a，CPU 为Intel Core i5-4570，内存为8 GB。由表2 可知，DCMC 算法的运算时间最短，但角度估计误差较大；FFH-MC 算法和IMFR-MC 算法均能实现目标角度的有效估计，相较于FFH-MC 算法，IMFR-MC 算法的运行时间更短、角度估计精度更高。
表2 不同角度估计方法的运行时间
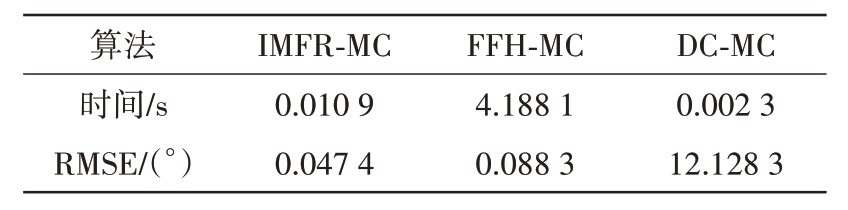
算法时间/s RMSE/（°）IMFR-MC 0.010 9 0.047 4 FFH-MC 4.188 1 0.088 3 DC-MC 0.002 3 12.128 3
4 结束语
双基地MIMO 雷达收发阵列中出现失效阵元时，其虚拟协方差矩阵中会产生大量结构性缺失数据，严重影响了传统角度估计算法的性能。为此，本文提出一种有效的不完整矩阵因子重构算法。基于矩阵SVD 分解从不完整协方差矩阵中提取出维度较低的矩阵因子，通过分析矩阵因子中行和列间相关性，将矩阵因子变换为块Hankel 矩阵，并对其施加核范数约束，从而建立不完整矩阵因子的重构模型。为了有效降低算法的运算时间，利用Hankel 矩阵分解性质，基于低秩矩阵拟合算法重新表征了核范数约束。基于ADMM 设计了不完整矩阵因子重构模型的求解算法，以获得完整的矩阵因子，从而能有效估计出目标角度。本文方法可以有效缓解因阵元失效而导致MIMO 雷达角度估计性能恶化的影响，实现高精度的角度估计。
［1］LI Jian, PETRE S. MIMO Radar with Colocated Antennas［J］. IEEE Trans on Signal Processing Magazine, 2007, 24（5）:106-114.
［2］HAN K, HONG S. High-Resolution Phased-Subarray MIMO Radar with Grating Lobe Cancellation Technique［J］.IEEE Trans on Microwave Theory Techniques,2022, 70（5）:2775-2785.
［3］SATYA G D, RATNAM V R. A Distributed MIMO Radar with Joint Optimal Transmit and Receive Signal Combining［J］.IEEE Trans on Aerospace and Electronic Systems,2021,57（1）:623-635.
［4］YU Zehua, LI Jun, GUO Qinghua,et al. Efficient Direct Target Localization for Distributed MIMO Radar with Expectation Propagation and Belief Propagation［J］. IEEE Trans on Signal Processing,2021,69:4055-4068.
［5］ZAHRA G, MOSTAFA D. Performance Analysis of the Matched Subspace Detector in the Presence of Signal-Dependent Interference for MIMO Radar［J］. Signal Processing,2020,176（1）:1-12.
［6］GAO Xiangyu,ROY S,XING Guanbin.MIMO-SAR:A Hierarchical High-Resolution Imaging Algorithm for mmWave FMCW Radar in Autonomous Driving［J］. IEEE Trans on Vehicular Technology,2021,70（8）:7322-7334.
［7］黄磊，柳艾飞，高才才.集中式MIMO 雷达研究进展：正交波形设计与信号处理［J］.雷达科学与技术，2023，21（1）:1-15.
［8］YAN Haidong,LI Jun,LIAO Guisheng.Multitarget Identification and Localization Using Bistatic MIMO Radar Systems［J］. Eurasip Journal on Advances in Signal Processing,2008（1）:1-8.
［9］ZHANG Xiaofei, XU Lingyun, XU Lei，et al. Direction of Departure（DOD）and Direction of Arrival（DOA）Estimation in MIMO Radar with Reduced-Dimension MUSIC［J］. IEEE Communications Letters, 2010, 14（12）:1161-1163.
［10］CHEN Jinli, GU Hong, SU Weimin. Angle Estimation Using ESPRIT without Pairing in MIMO Radar［J］.Electronics Letters,2008,44（24）:1422-1423.
［11］OM P,AMALENDU P.Antenna Array Failure Correction［J］.IEEE Antennas and Propagation Magazine,2017,59（6）:106-115.
［12］ZARDI F, OLIVERI G, SALUCCI M，et al. Minimum-Complexity Failure Correction in Linear Arrays via Compressive Processing［J］. IEEE Trans on Antennas and Propagation,2021,69（8）:4504-4516.
［13］GAO Sizhe,MA Hui,LIU Hongwei,et al.DOD and DOA Estimation from Incomplete Data Based on PARAFAC and Atomic Norm Minimization Method［J］. IEEE Trans on Geoscience and Remote Sensing,2023,61:1-14.
［14］JALAL B,ELNAHAS O,QUAN Zhi.Efficient DOA Estimation Under Partially Impaired Antenna Array Elements［J］. IEEE Trans on Vehicular Technology, 2022,71（7）:7991-7996.
［15］SETAYESH A, YAZDIAN E, MALEK M. Direction of Arrival Estimation with Missing Data via Matrix Completion［J］. Signal Image and Video Processing, 2019, 13:1451-1459.
［16］张永顺，葛启超，丁姗姗.阵元缺损下的波达方向估计算法［J］.电子科技大学学报，2017，46（4）:501-504.
［17］杨东，廖桂生，朱圣棋，等.阵列信号降采样低秩矩阵的恢复方法［J］.西安电子科技大学学报，2014，41（5）:30-35.
［18］JI Yuanjie, WEN Cai, YAN Huang, et al. Robust Direction-of-Arrival Estimation Approach Using Beamspace-Based Deep Neural Networks with Array Imperfections and Element Failure［J］. IET Radar, Sonar ＆Navigation,2022,16（11）:1761-1778.
［19］ZHU Chenglong, WANG Wenqin, CHEN Hui, et al. Impaired Sensor Diagnosis, Beamforming and DOA Estimation with Difference Co-Array Processing［J］. IEEE Sensors Journal,2015,15（7）:3773-3780.
［20］ZHANG Weiyu, VOROBYOV A, GUO Lianghao. DOA Estimation in MIMO Radar with Broken Sensors by Difference Co-Array Processing［C］//2015 IEEE 6th International Workshop on Computational Advances in Multi-Sensor Adaptive Processing（CAMSAP）,Cancun:IEEE,2015:321-324.
［21］CHEN Jinli,ZHANG Tingxiao,LI Jiangqiang,et al.Joint Sensor Failure Detection and Corrupted Covariance Matrix Recovery in Bistatic MIMO Radar with Impaired Arrays［J］. IEEE Sensors Journal, 2019, 19（14）:5834-5842.
［22］YANG Jingyu, YANG Xuemeng, YE Xinchen,et al. Reconstruction of Structurally-Incomplete Matrices with Reweighted Low-Rank and Sparsity Priors［J］. IEEE Trans on Image Processing,2017,26（3）:1158-1172.
［23］XIONG Wenxin, CHENG Ge, SCHINDELHAUER C, et al. Robust Matrix Completion for Elliptic Positioning in the Presence of Outliers and Missing Data［J］. IEEE Trans on Geoscience and Remote Sensing,2023,61:1.
［24］WANG Jianping,DING Min,YAROVOY A.Interference Mitigation for FMCW Radar with Sparse and Low-Rank Hankel Matrix Decomposition［J］. IEEE Trans on Signal Processing,2022,70:822-834.
［25］XU Gang, ZHANG Bangjie, CHEN Jianlai,et al. Sparse Inverse Synthetic Aperture Radar Imaging Using Structured Low-Rank Method［J］. IEEE Trans on Geoscience and Remote Sensing,2022,60:1-12.
