0 引 言
随着数字射频存储技术的不断革新，以间歇采样转发式干扰（Interrupted Sampling Repeater Jamming,ISRJ）为典型代表的相参干扰兼具压制和欺骗的干扰效果，在电子对抗领域受到广泛关注［1-3］。ISRJ 利用欠采样的原理，巧妙地对发射的雷达信号进行切片采样、分段转发，能够在雷达接收机中产生高逼真的假目标群，具有高效性、强相干和高度可控的特点，严重威胁到雷达系统的目标检测和跟踪性能［4-6］。传统的空域干扰对抗技术在处理ISRJ 时，由于难以获得精确的干扰协方差矩阵且易引起合成波束的主瓣畸变，导致滤波性能大打折扣［7-8］。因此，研究抗ISRJ 技术对提高雷达抗干扰能力具有重要的理论意义和军事价值。
目前针对ISRJ的抑制有3类主流的方法，包括发射波形设计、接收信号处理以及联合波形和滤波器设计。在波形域，通过诸如线性调频信号（Linear Frequency Modulation, LFM）、相位编码信号的正交波形［9-12］以及稀疏多普勒敏感波形［13-14］设计，有效识别和抑制间歇采样转发式干扰。在信号处理方面，ISRJ 在时频域上的不连续性成为了雷达对抗的窗口。文献［15］采用时频分析手段对ISRJ 进行识别与重构；文献［16］在时频分析的基础上设计多个带通滤波器，实现干扰抑制；盖季妤等［17］另辟蹊径，利用目标和干扰在差分域上的差异，有效进行干扰辨识。然而上述方法存在着提高时频分辨率和差分窗的选择两大难点。为联合发射端和接收端信号处理的优势，文献［18-20］提出了联合波形设计和接收滤波器设计的抗ISRJ 方法，并从控制脉冲压缩峰值增益和降低算法计算复杂度着手，进一步优化设计方法。但是以上方法引入复杂的波形优化，难以实时应对复杂干扰场景的变化；同时普遍利用单通道进行信号处理，忽略了多通道技术在抗干扰中的应用潜力。
极化表征着电磁波的矢量特征，拓宽了雷达干扰对抗的信息维度。全极化雷达能够更好地利用干扰场景中的自由度，提升雷达目标检测和抗干扰能力［21-22］。鉴于此，本文在全极化雷达体制下，研究抗间歇采样转发式干扰的非匹配滤波方法。首先分析了典型ISRJ 样式的产生原理，并以脉内正交LFM 信号为发射波形，建立起雷达目标+干扰+噪声的回波模型；其次，以抑制脉冲压缩后信号的旁瓣能量和干扰积分能量为目标，引入惩罚因子对四路极化通道脉压输出峰值进行控制，建立抗ISRJ 多目标优化模型；然后通过帕累托参数的组合加权，将模型进一步转化为多线性约束下最小积分能量输出的目标函数，以此设计非匹配滤波器；最后，对滤波器关键参数、可行性和抗干扰性能进行分析与评估，验证所提方法的有效性。
1 信号模型
1.1 发射信号模型
线性调频（LFM）信号利用非线性相位调制来实现宽时带宽积，具有峰值功率低、较不敏感于多普勒频移且易于工程实现等特点，是雷达最常用的信号形式。假设全极化雷达通过正交极化通道（H：水平极化，V：垂直极化）发射正负斜率的LFM信号:
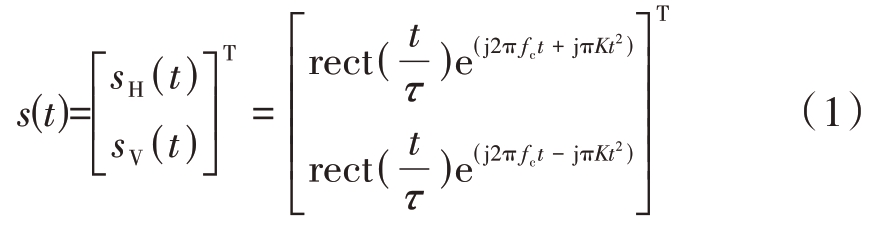
式中，rect（·）表示门函数，τ 表示信号的脉宽，fc为信号的载频，K为信号的调斜率。
1.2 干扰信号模型
设在距雷达R处的空间中存在敌方干扰机，对信号进行间歇采样转发。典型的干扰方式包括直接转发、重复转发和循环转发。不同干扰方式的差异源于对采样信号转发的次数和时序，其工作原理如图1所示。
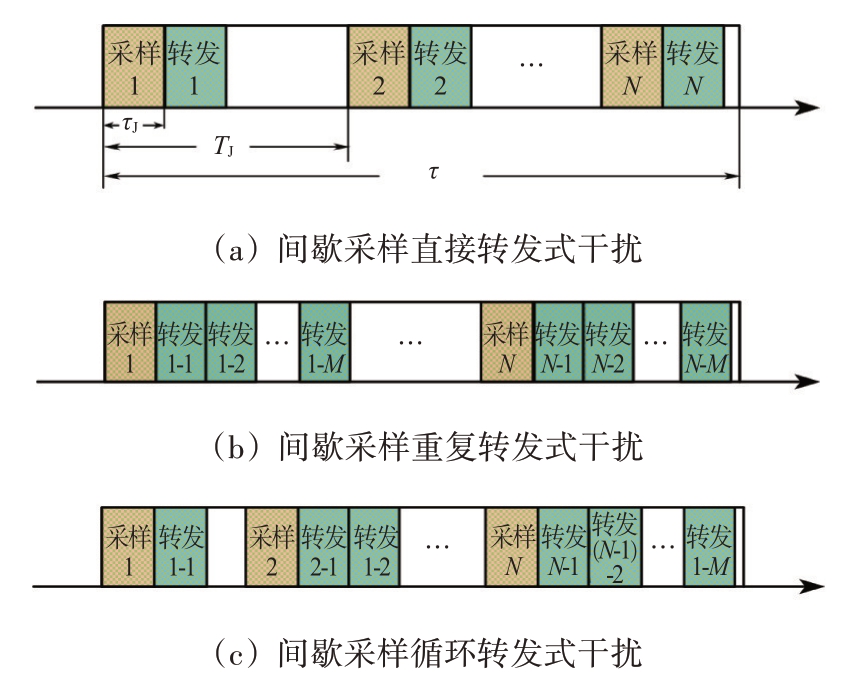
图1 间歇采样转发式干扰工作原理图
进一步假设干扰机对一个脉冲内的雷达信号进行N次采样，干扰切片周期为TJ，脉宽为τJ。
由图1（a）可知，直接转发式干扰是在一个采样周期内，对截取信号进行一次转发，直到完成对一个脉冲的全部采样。相应的干扰模型可表示为
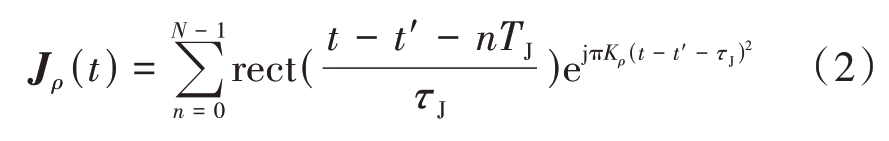
式中，p=H,V 表示信号的极化状态，t'=R/c 表示由雷达到干扰机距离产生的时延，Kp=±K 对应不同极化通道发射信号的斜率。
重复转发式干扰则是对一个采样周期内的信号进行多次转发，如图1（b）所示。相应的干扰模型可表示为
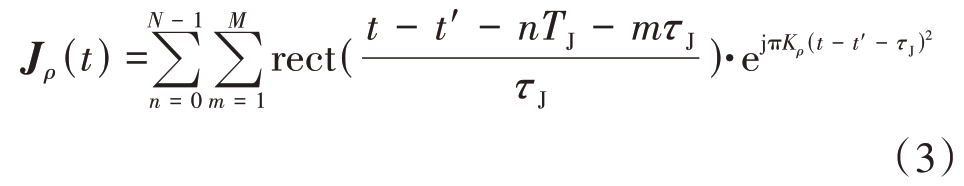
式中，M表示干扰切片的转发次数。
与上述两种干扰方式不同，循环转发式干扰在转发时序上做文章。所谓“循环”，是对当前采样切片的直接转发，同时转发之前的采样信号，直到完成一个脉冲内的所有采样。其干扰模型可表示为
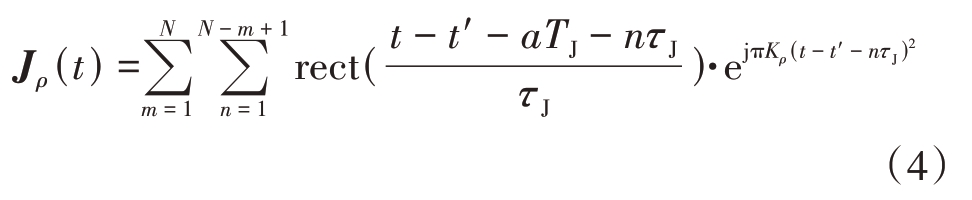
式中，a=m=n-2 代表每个干扰切片转发周期的系数。
1.3 接收信号模型
对于相对静止的点目标，全极化雷达接收的信号x(t)可表示为
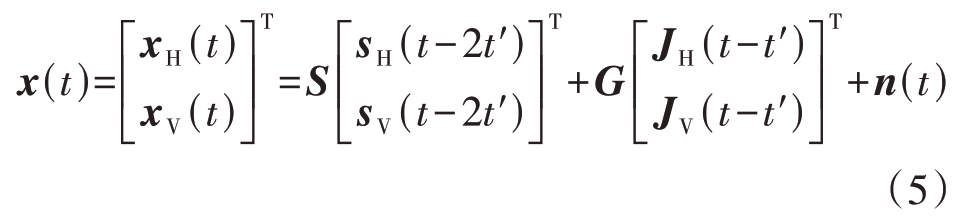
式中，n(t)表示噪声矢量，S 和G 分别表示目标和干扰机的极化散射矩阵：
式中:Spq的角标表示以q 为极化方向的入射波和以p 为极化方向的散射波，p,q=H,V；α 表示干扰机的增益因子；EJt，EJr分别表示干扰机的发射和接收极化Jones矢量。
2 非匹配滤波器优化设计方法
本节在全极化雷达体制下，将抗间歇采样转发式干扰的多目标优化问题转化为多线性约束下最小化输出积分能量问题，建立了抗干扰的优化模型，推导出非匹配滤波器设计的解析表达式，实现非匹配滤波器的设计。
2.1 抗ISRJ问题描述
为了测量极化散射矩阵并进行后续的信号处理，需要对正交极化通道的回波信号进行脉冲压缩。定义非匹配滤波器
经脉压处理后，得到四路极化通道的相关矩阵
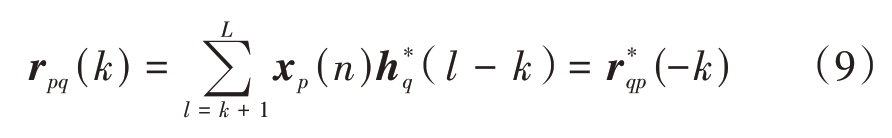
式中，l=0,1,…,L-1 表示离散采样序列标号。非匹配滤波器和回波的脉冲压缩实际上是hp,q（t）和sp,q（t）的时域卷积。
以H 极化通道为例，我们希望hH(t)不仅要与sH(t)具有良好的脉冲压缩性能，还需要与交叉极化通道sV(t)和间歇采样干扰信号JH(t)、JV(t)保持正交。这种多目标的优化对滤波器的设计提出了更高的要求。为此，本文以最小化发射信号脉压输出的旁瓣能量和干扰信号非匹配滤波输出的积分能量为代价函数，建立抗ISRJ多目标优化模型。
2.2 多目标优化模型构建
为了以矩阵形式描述脉冲压缩的过程，定义发射信号矩阵
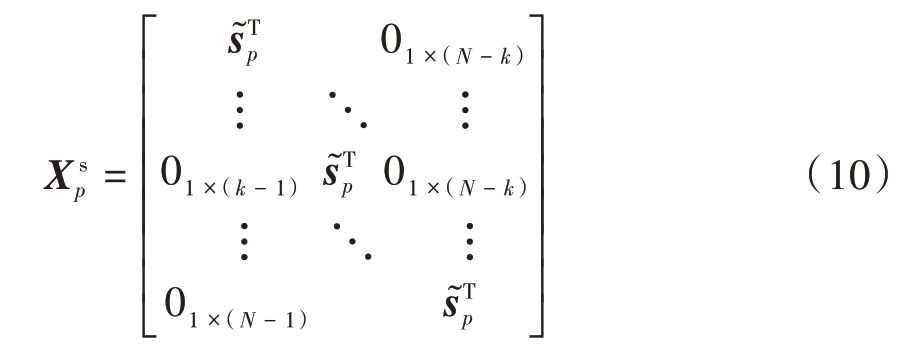
式中，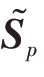
表示对发射信号sp 进行L 点采样后的逆序排列矢量。因此，由式（9）定义的非匹配滤波输出可进一步表示为
对于主极化通道而言，发射信号脉冲压缩积分旁瓣能量具体为
式中，Ω 为2N-1 维的对角矩阵，除第L 个主对角线元素为0 外，其余位置均为1。该对角阵的引入目的是为了消除脉压零时延处的主瓣能量的影响。此外，考虑到脉冲压缩过程中峰值的损耗，引入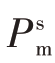
约束输出的主瓣能量，约束的程度是由罚因子
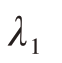决定。则发射信号脉压积分旁瓣抑制模型可表示为
对于交叉极化通道而言，非匹配滤波器和发射信号的脉压积分能量为
经脉冲压缩后信号在零时延处易出现尖峰，这破坏了交叉极化通道的正交性，因此需要引入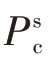
约束该峰值。基于此，发射信号非匹配滤波积分能量抑制模型可由下式定义：
以上是针对发射信号的滤波优化模型。下面对抗间歇采样转发式干扰的代价函数进行分析。
同理于式（12），干扰信号与非匹配滤波器的脉冲压缩输出的积分能量为
式中，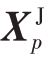
表示干扰信号矩阵:
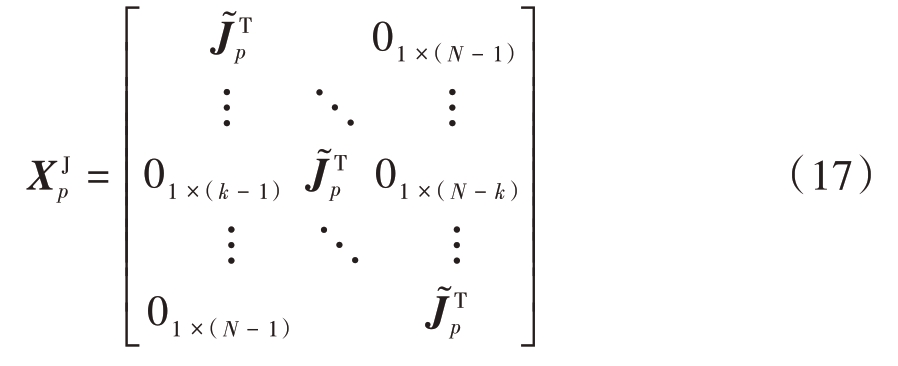
因此，干扰信号非匹配滤波积分能量抑制模型可表示为
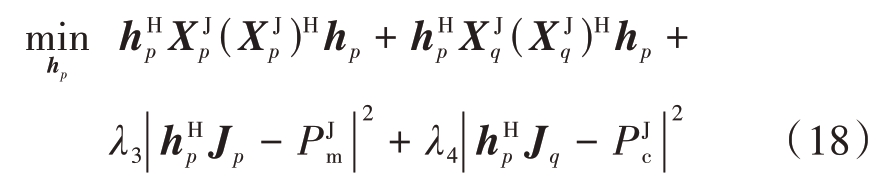
式中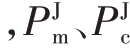
表示干扰信号经过非匹配滤波后在两路极化通道零时延处所被允许的预设峰值，并通过罚因子λ3、λ4实现非匹配滤波峰值的控制。引入此约束是考虑到间歇采样转发式干扰本质上是发射信号的部分采样，与非匹配滤波器仍保持良好的脉压性能。
2.3 非匹配滤波器优化设计
在式（13）、式（15）和式（18）所组成的抗ISRJ多目标优化模型中，每个独立的目标函数之间往往互有冲突。因此，本文引入帕累托参数ω=
对多目标模型进行线性加权，使之联合成为一个整体的损失函数。多线性约束非匹配滤波模型可构建为
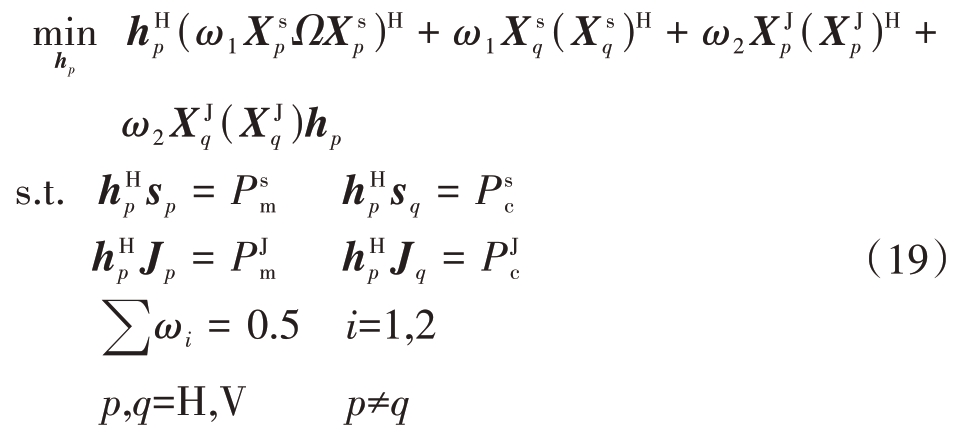
上式综合考虑了发射信号和干扰信号非匹配滤波四路极化通道的影响，通过控制ω的值来获得期望的滤波效果。当希望滤波器有更好的旁瓣抑制能力，此时可设置较大的ω1；当希望滤波器有更好的干扰抑制性能，可设置较大的ω2 加以实现。此外，滤波器的脉冲压缩峰值通过预设的P=
进行控制。预设值的大小与发射信号的脉宽τ、干扰切片个数N 和干扰切片的脉宽τJ 相关。干扰切片个数和切片脉宽是通过干扰参数估计技术实现的，此不作为本文研究的重点，现假设干扰参数已准确获取。定义信号干扰脉宽比
在最小化积分输出能量的目标函数下，脉宽比越大，意味着干扰和信号的相参性越强，经匹配滤波后信号的能量损耗越多，导致信号脉压后的理论峰值越小，干扰脉压后的理论峰值越大，反之亦然。因此，在设置脉冲压缩峰值参数时，需充分考虑脉宽比对非匹配滤波性能的影响。
在合理设置帕累托参数ω 和脉冲压缩预设峰值P 的情况下，根据模型（19），非匹配滤波器的设计是基于多线性约束下的凸优化函数，因此，可以采用拉格朗日乘数法进行模型求解，其解析表达式为
其中，
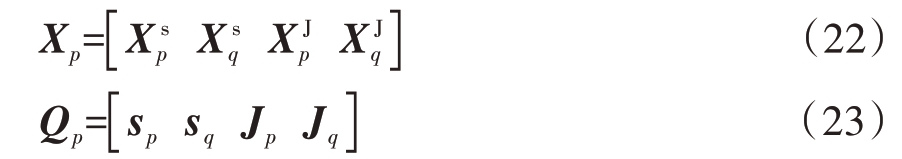
2.4 计算复杂度分析
由式（21）可知，设计的非匹配滤波器计算复杂度来源于矩阵与矩阵的乘法和矩阵与向量的乘法。其中，计算协方差矩阵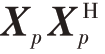
的计算复杂度为O(L3)，L代表矩阵的维度/采样点的个数；计算矩阵Qp 与
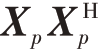相乘的计算复杂度为O(4L)；计算帕累托参数ω 对非匹配滤波器进行线性加权的计算复杂度为O(L)。因此，算法总体计算复杂度为O(L3 + 5L)。
3 仿真与分析
为了验证所提非匹配滤波器的有效性，本文设计了5 组仿真实验。首先对非匹配滤波器的关键参数进行仿真分析；其次验证滤波器的可行性，并评估其性能；最后，通过与传统的匹配滤波和非匹配滤波进行对比分析，评估所提方法的抗干扰能力。仿真以MATLAB 2019a为实验平台展开，部分使用参数如表1所示。
表1 部分仿真参数设置表
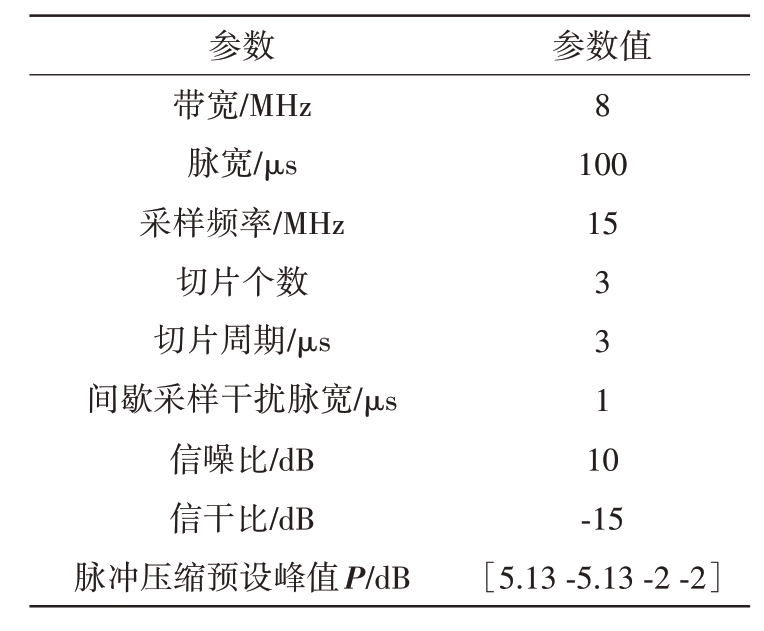
参数带宽/MHz脉宽/µs采样频率/MHz切片个数切片周期/µs间歇采样干扰脉宽/µs信噪比/dB信干比/dB脉冲压缩预设峰值P/dB参数值8 100 15 3311 0-15［5.13-5.13-2-2］
3.1 关键参数分析
仿真1：以间歇采样直接转发式干扰为例，以非匹配滤波输出的积分旁瓣比和积分能量比为指标，定量描述帕累托参数对滤波性能的影响。仿真中，假设空间内存在1 个目标信号和1 个干扰信号，目标位于距雷达10 km 处，目标的极化散射矩阵为
干扰机位于距目标2.2 km 处，其发射/接收极化矢量为
图2（a）展示的是经非匹配滤波后四路极化通道输出的积分旁瓣能量随帕累托参数变化曲线。从图中可以看出，随着帕累托参数的增加，四路极化通道的信号积分旁瓣比总体呈现下降趋势。究其原因，帕累托参数ω1 反映的是对旁瓣能量的抑制能力。当ω1 越大时，说明非匹配滤波目标函数中抑制积分旁瓣能力所占的权重越大，抑制性能越好。此外，在交叉极化通道中，有部分ω1所对应的积分旁瓣不符合整体变化趋势，可能的原因是在文章给定的参数设置下，经非匹配滤波后，信号的主瓣宽度匹配点数过少，进而使积分旁瓣比变大。
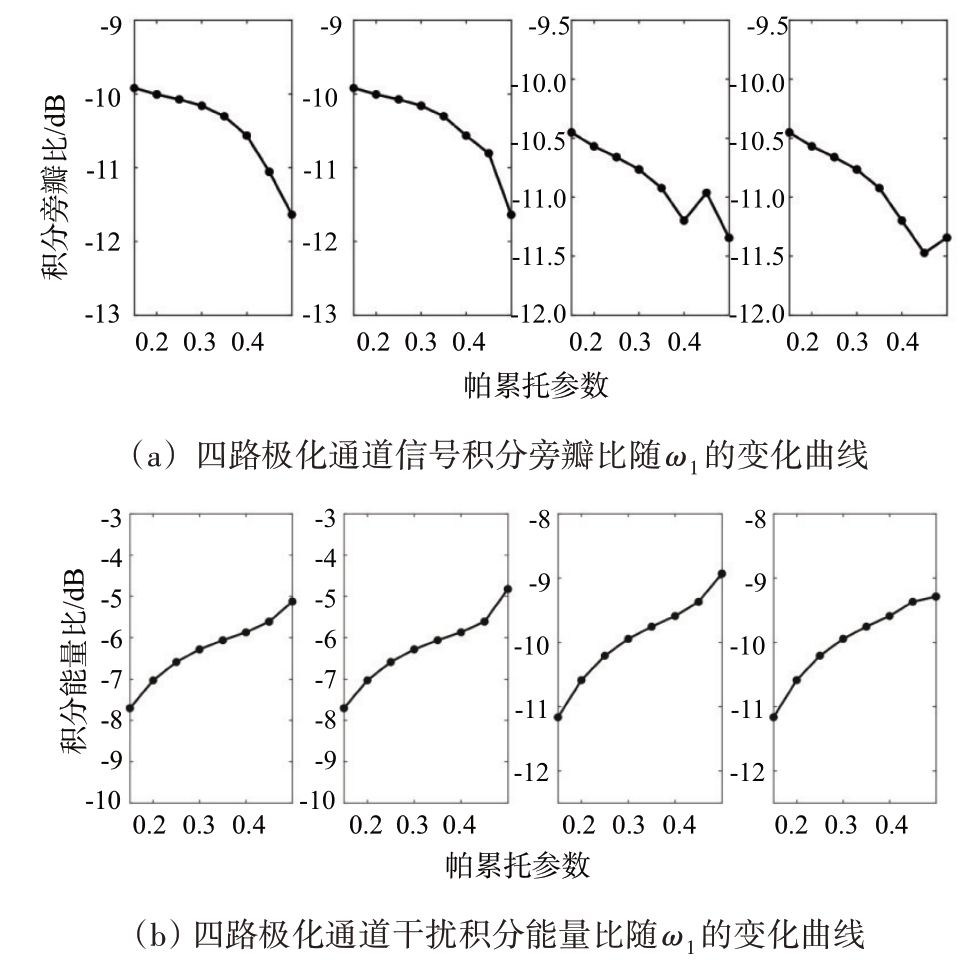
图2 积分旁瓣比和积分能量比随帕累托参数ω1变化曲线
图2（b）反映的是经非匹配滤波后四路极化通道干扰输出的积分能量比随帕累托参数变化曲线。当ω1逐渐增加时，ω2逐渐减小，对干扰的积分能量抑制性能逐渐下降，输出的积分能量比就越大，因此，变化曲线总体呈现出上升趋势。
综合比较分析，随着ω 的变化，信号的积分旁瓣能量和干扰的积分能量存在此消彼长的变化过程，难以同时取得良好的能量抑制效果。为了平衡二者的关系，本文设置ω1=ω2=0.25。
仿真2：从前面的分析可知，信号干扰脉宽比作为连接脉压预设峰值和非匹配滤波性能的关键参数，影响着脉冲压缩后信号及干扰的理论峰值，从而影响滤波性能。由式（20）所定义的脉宽比与干扰切片数、干扰切片的脉宽和信号的脉宽有关。仿真中，脉冲压缩预设值、信号脉宽由表1所定义，通过改变干扰切片数和干扰切片脉宽改变脉宽比。图3是以间歇采样直接转发式干扰为例，考察脉宽比（PWR）对输出干扰峰值的影响。可以看到，本文所设脉冲压缩预设值能在脉宽比为3%的条件下，取得良好的脉压结果，主极化通道干扰脉压峰值在-15 dB 以下，交叉极化通道干扰脉压峰值在-10 dB 以下。此外，从图中可以看出，随着脉宽比的增大，脉冲压缩后输出的干扰峰值逐渐增大，当脉宽比接近50%时，此时转发式干扰与目标信号具有较高的相似度，导致非匹配滤波器性能变差，因此，需要改变脉冲压缩预设峰值实现对输出干扰峰值的控制，提升滤波性能。
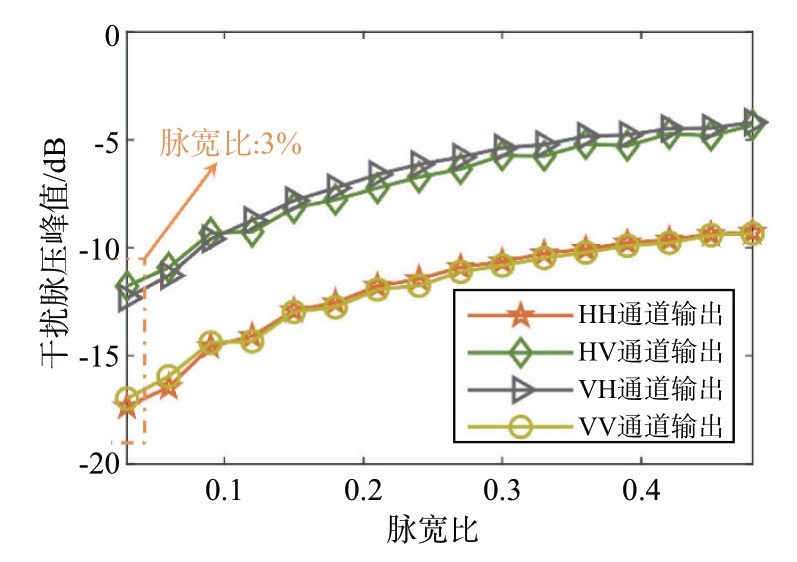
图3 干扰非匹配滤波输出峰值随脉宽比变化曲线
3.2 算法性能分析
本节主要分析在典型的间歇采样转发式干扰样式下非匹配滤波器的性能。仿真场景设置如下：考虑空间中存在3 个目标和2 个干扰机，目标分别位于距雷达10，12 和15 km 处，其极化散射矩阵分别设置为
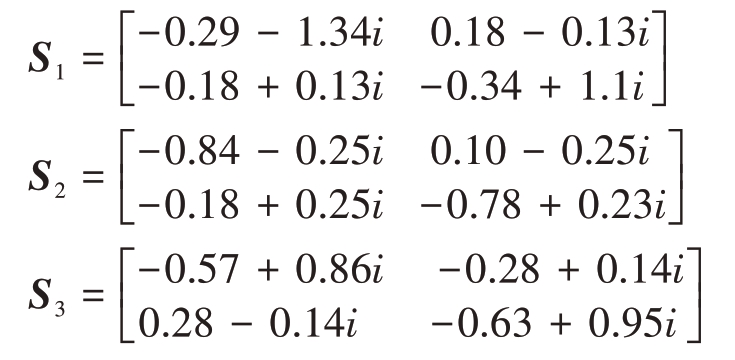
干扰机对雷达信号间歇采样转发，不同转发干扰样式参数均与表1所设参数保持一致，其中重复转发式干扰的转发次数设置为3 次。两个干扰机分别位于距雷达12.2 km 和14 km 处。干扰的极化幅角γ为45°和30°，极化相位差η为70°和60°。
仿真3：图4～图6 展示的是在不同间歇采样转发式干扰样式下利用设计的滤波器进行脉冲压缩后的结果。由于两路主极化通道和两路交叉极化通道的滤波效果相当，因此，仅展示两路极化通道的脉压结果图。从图中可以看出，本文设计的滤波器在全极化雷达体制下能对间歇采样转发式干扰产生有效抑制。经脉冲压缩后，在主极化通道中，目标的峰值高于旁瓣峰值，其幅度之差约为10 dB；在交叉极化通道中，目标峰值与旁瓣峰值相差7 dB左右。此外，由图6可知，经脉冲压缩后，目标在距离维上形成尖峰，但却具有较明显的动态起伏。这是由于本文的目标函数是基于最小化旁瓣能量准则设计的，对于在目标主瓣内的干扰能量无法实现完全抑制。因此，在目标距离维处的输出能量是包含目标和干扰的混合能量。
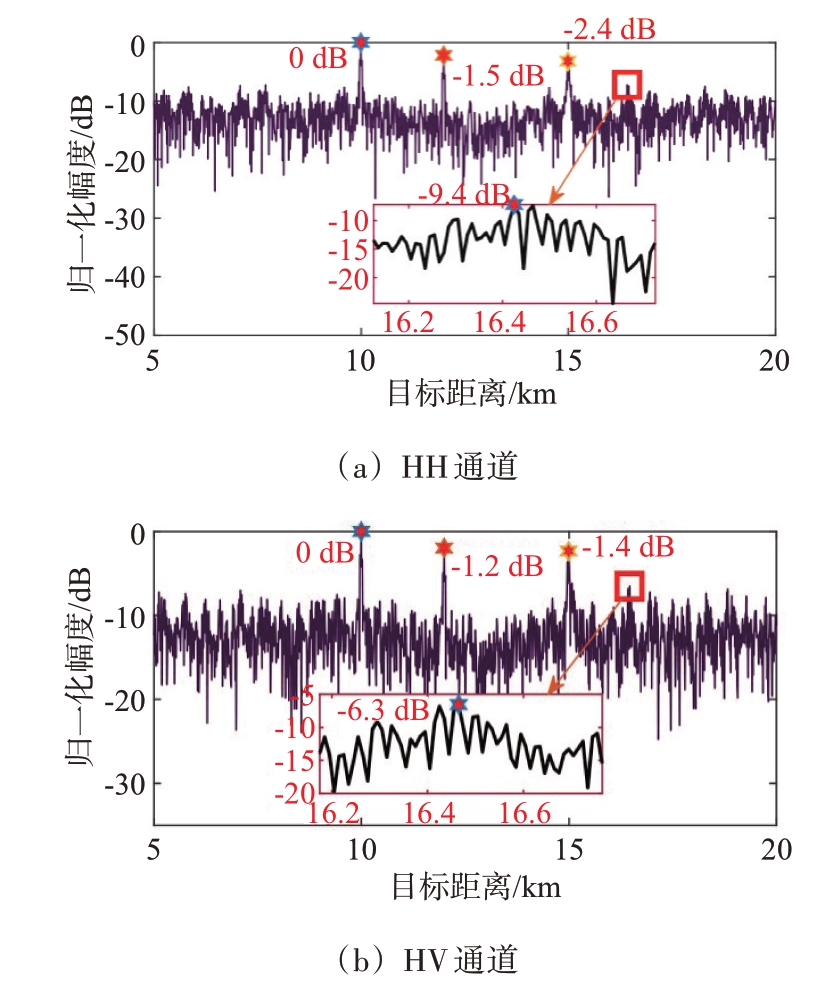
图4 抗间歇采样直接转发式干扰非匹配滤波输出
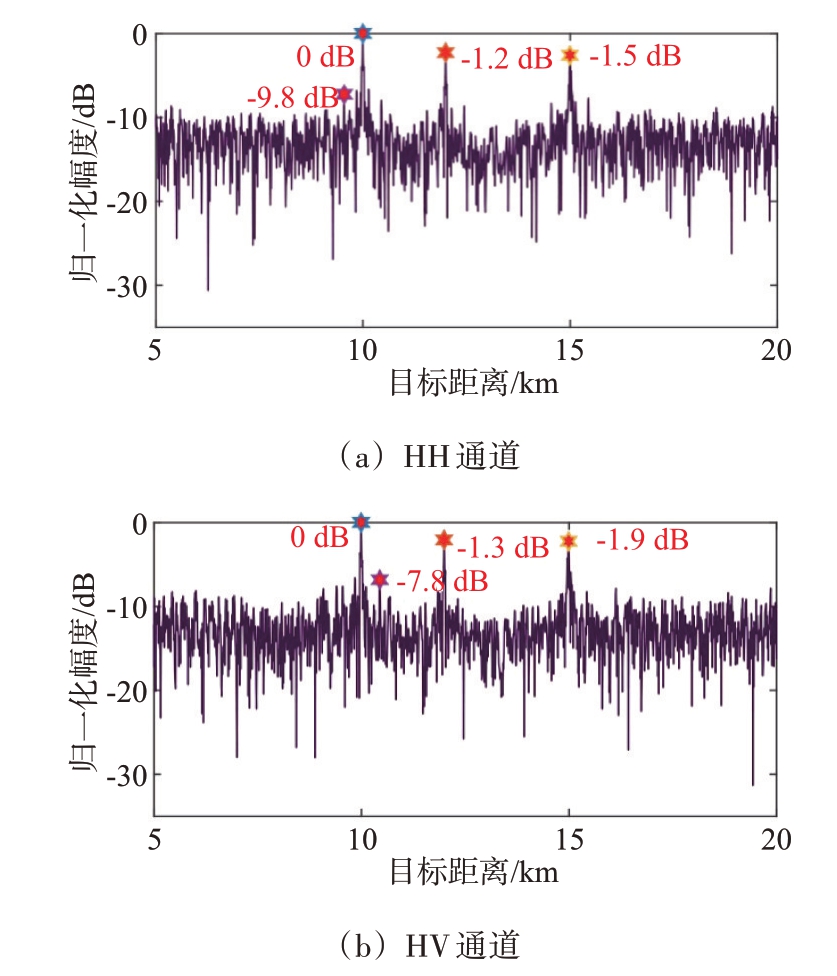
图5 抗间歇采样重复转发式干扰非匹配滤波输出
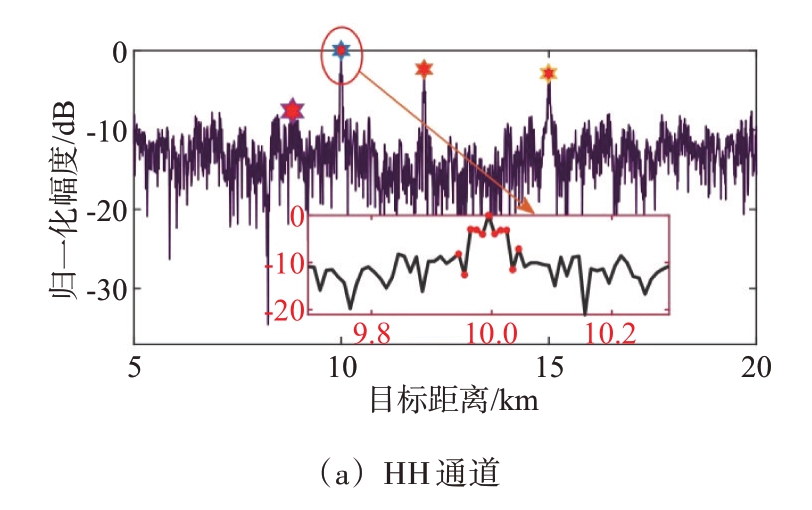
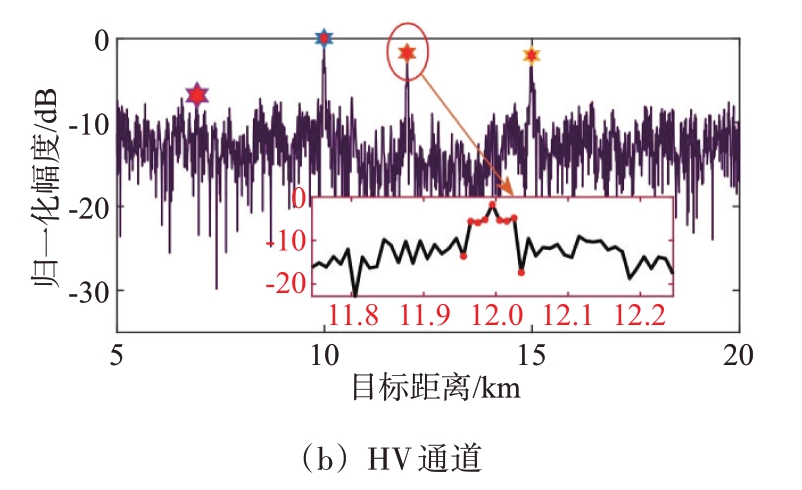
图6 抗间歇采样循环转发式干扰非匹配滤波输出
仿真4：表2 展示的是回波信号采样点数与算法运行时间的关系，以此验证所提方法的复杂度。仿真中，参数设置均与仿真3 保持一致，并进行了100 次的蒙卡模拟，计算平均运行时间。从表中可以看出，当回波采样点数增加1 倍时，算法的运行时间约增加6倍，大致符合本文算法的总体复杂度O(L3 + 5L)。
表2 算法运行时间
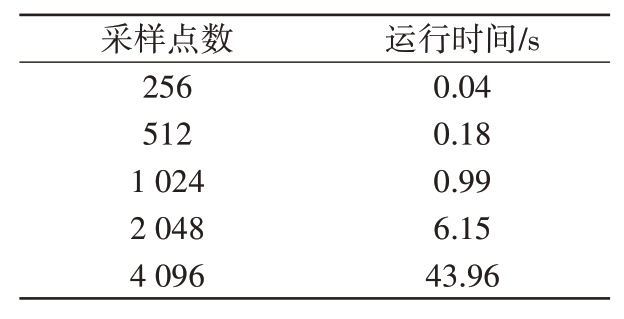
采样点数256 512 1 024 2 048 4 096运行时间/s 0.04 0.18 0.99 6.15 43.96
进一步考察不同采样点数下的信号经非匹配滤波后脉压旁瓣峰值的变化情况，以此评估采样点数对算法滤波性能的影响，如图7所示。
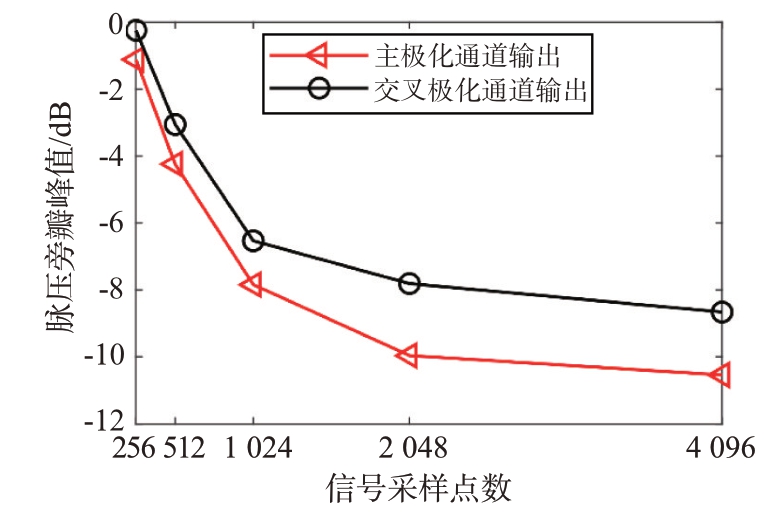
图7 脉压旁瓣峰值随采样点数的变化曲线
仿真参数与前文保持一致，从图7 可以看出，主极化和交叉极化通道中，脉压旁瓣峰值随着采样点数的增大呈现出较大的动态变化。究其原因，采样点数越大，回波信号的细节信息会被更加准确地捕捉到，从而提高信号的表示精度。此外，设计的非匹配滤波器也会有更多的信息进行滤波处理，从而提高算法性能。但是需要注意的是，采集和处理大量的采样点会占用更多的存储空间和计算资源。因此，需根据实际应用需求进行权衡，以达到最优性能和资源利用效率之间的平衡。
3.3 抗干扰能力评估
仿真5：为了评估设计的非匹配滤波器抗干扰性能，以间歇采样重复转发式干扰为例，在同等发射波形和参数设置条件下，与传统的匹配滤波和传统的非匹配滤波器进行对比，结果如图8、图9所示。图8（a）、图9（a）为回波信号与发射信号匹配滤波的结果，可以看到，间歇采样转发式干扰在主极化通道和交叉极化通道的距离维上形成密集假目标压制，无法分辨出真实目标位置。在信号接收端，采用传统非匹配滤波体制对回波进行脉冲压缩，非匹配滤波器定义为发射信号和干扰信号的差值［23］。图8（b）、图9（b）中黑色曲线代表匹配滤波输出，红色曲线为非匹配滤波的结果，可以看到，在两路极化通道内，干扰信号的峰值得到一定程度的抑制，但目标信号仍淹没在密集的干扰中。相比与黑色曲线所代表的匹配滤波输出，图8（c）、图9（c）中的红色曲线是利用本文设计的非匹配滤波器进行脉冲压缩的结果，从图中可以看出，3 个目标信号在距离向上形成尖峰，而干扰信号得到有效抑制。
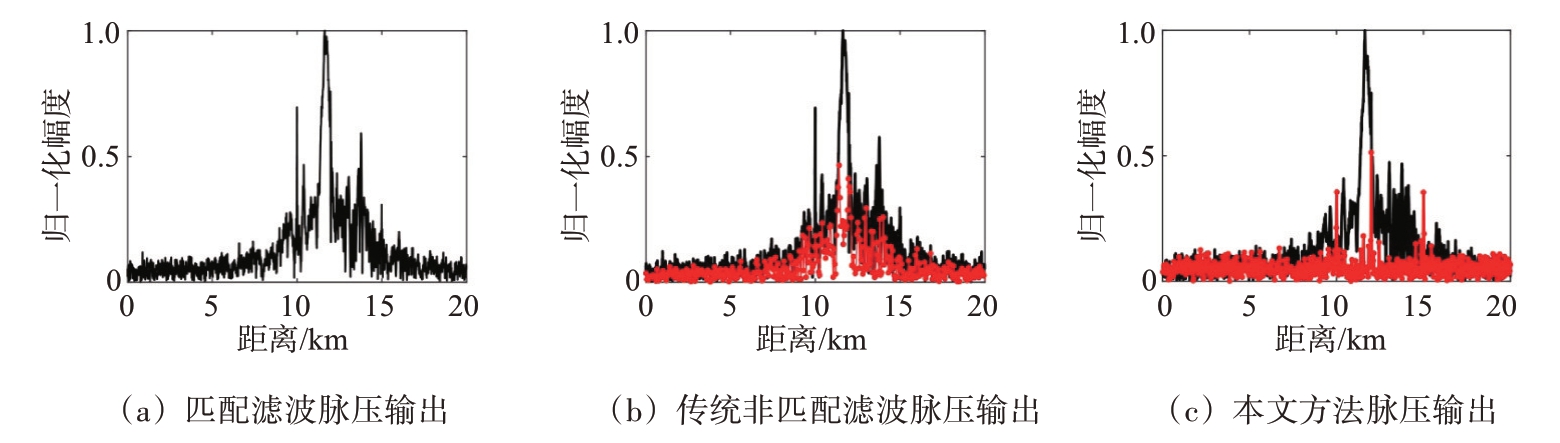
图8 抗间歇采样重复转发式干扰脉冲压缩结果（主极化通道）
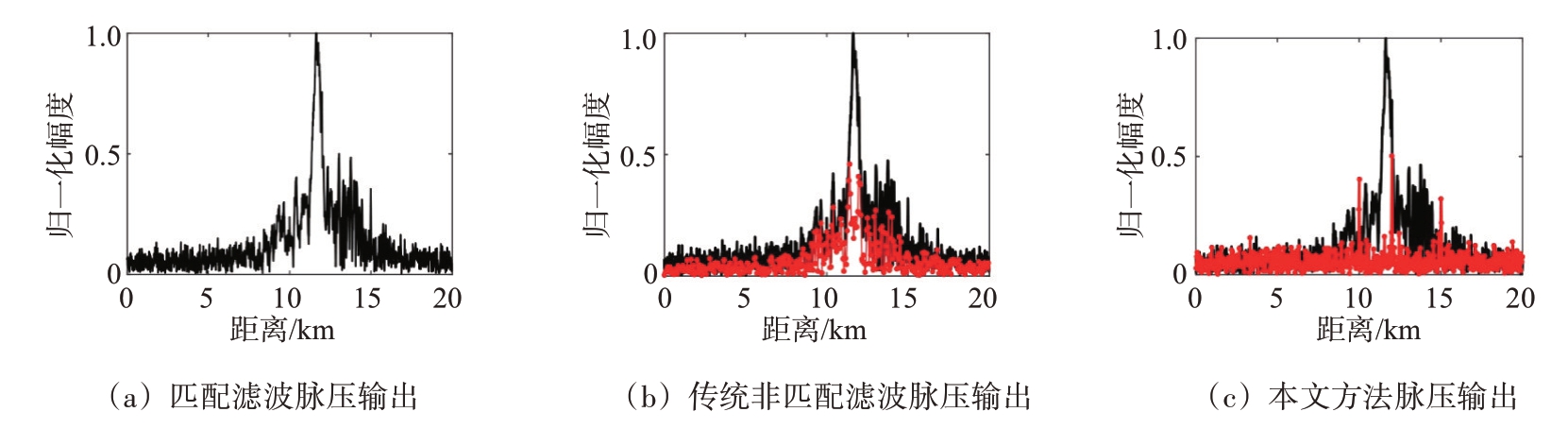
图9 抗间歇采样重复转发式干扰脉冲压缩结果（交叉极化通道）
4 结束语
本文针对现有抗ISRJ 方法未考虑多通道系统带来的高自由度优势，在全极化雷达体制下，以脉内正交的线性调频信号为发射波形，提出了一种抗ISRJ 的非匹配滤波方法。仿真结果表明，所提方法能够有效抑制不同样式的间歇采样转发式干扰，对提高相参干扰场景下雷达系统的抗干扰能力具有一定的应用价值。值得注意的是，脉冲压缩预设峰值和信噪比的大小影响着非匹配滤波器的性能。下一步，如何规范化地设置脉压预设峰值以及提高算法在低信噪比下适应性将是工作研究的重点。
［1］SOUMEKH M.SAR-ECCM Using Phase-Perturbed LFM Chirp Signals and DRFM Repeat Jammer Penalization［J］.IEEE Trans on Aerospace and Electronic Systems, 2006,42（1）:191-205.
［2］王雪松，刘建成，张文明，等.间歇采样转发干扰的数学原理［J］.中国科学E辑:信息科学，2006，36（8）:891-901.
［3］尚东东，张劲东，胡婉婉，等.基于ADMM 的间歇采样转发式干扰的参数估计［J］.雷达科学与技术，2021,19（4）:417-422.
［4］FENG Dejun,XU Letao,PAN Xiaoyi,et al.Jamming Wideband Radar Using Interrupted-Sampling Repeater［J］.IEEE Trans on Aerospace and Electronic Systems, 2017,53（3）:1341-1354.
［5］WU Qihua,ZHAO Feng,AI Xiaofeng,et al. Two-Dimensional Blanket Jamming Against ISAR Using Nonperio-dic ISRJ［J］.IEEE Sensors Journal,2019,19（11）:4031-4038.
［6］杨沛，庄俊.间歇采样重复转发干扰效果分析［J］.舰船电子对抗，2023，46（1）:33-37.
［7］OLIVIER K,CILLIERS J M,DU PLESSIS M. Design and Performance of Wideband DRFM for Radar Test and Evaluation［J］.Electronics Letters,2011,47（14）:824-825.
［8］周超.雷达抗间歇采样转发式干扰的时/频域方法研究［D］.北京：北京理工大学，2018.
［9］张建中，穆贺强，文树梁，等.基于脉内步进LFM波形的抗间歇采样转发干扰方法［J］.系统工程与电子技术，2019，41（5）:1013-1020.
［10］张建中，穆贺强，文树梁，等.基于LFM 分段脉冲压缩的抗间歇采样转发干扰方法［J］.电子与信息学报，2019，41（7）:1712-1720.
［11］周畅，汤子跃，余方利，等.基于脉内正交的抗间歇采样转发干扰方法［J］.系统工程与电子技术，2017，39（2）:269-276.
［12］ZHENG Hao,JIU Bo,LIU Hongwei.Waveform Design Based ECCM Scheme Against Interrupted Sampling Repeater Jamming for Wideband MIMO Radar in Multiple Targets Scenario［J］.IEEE Sensors Journal,2022,22（2）:1652-1669.
［13］ZHANG Yang,WEI Yinsheng, YU Lei.Interrupted Sampling Repeater Jamming Recognition and Suppression Based on Phase-Coded Signal Processing［J］.Signal Processing,2022,198:108596.
［14］周畅，汤子跃，朱振波，等.抗间歇采样转发干扰的波形设计方法［J］.电子与信息学报，2018，40（9）:2198-2205.
［15］ZHOU Chao,LIU Quanhua,CHEN Xinliang.Parameter Estimation and Suppression for DRFM-Based Interrupted Sampling Repeater Jammer［J］.IET Radar,Sonar&Navigation,2018,12（1）:56-63.
［16］ CHEN Jian,WU Wenzhen,XU Shiyou,et al.Band Pass Filter Design Against Interrupted-Sampling Repeater Jamming Based on Time-Frequency Analysis［J］.IET Radar,Sonar&Navigation,2019,13（10）:1646-1654.
［17］盖季妤，姜维，张凯翔，等.基于差分特征的间歇采样转发干扰辨识与抑制方法［J］.雷达学报，2023，12（1）:186-196.
［18］XU Cheng,AUBRY A,CIUONZO D,et al.Robust Waveform and Filter Bank Design of Polarimetric Radar［J］.IEEE Trans on Aerospace and Electronic Systems, 2017,53（1）:370-384.
［19］ZHOU Kai,LI Dexin,SU Yi,et al.Joint Design of Transmit Waveform and Mismatch Filter in the Presence of Interrupted Sampling Repeater Jamming［J］.IEEE Signal Processing Letters,2020,27:1610-1614.
［20］王福来，庞晨，黄大通，等.一种同时全极化雷达发射波形和接收滤波器联合设计的抗间歇采样转发干扰方法［J］.中国科学:信息科学，2022，52（7）:1333-1348.
［21］HE Yaomin, YANG Jian. Polarization Estimation with a Single Vector Sensor for Radar Detection［J］. Remote Sensing,2022,14（5）:1137.
［22］HE Yaomin, ZHANG Tao, HE Huafeng, et al. Polarization Anti-Jamming Interference Analysis with Pulse Accumulation［J］. IEEE Trans on Signal Processing, 2022,70:4772-4787.
［23］GONG Shixian, WEI Xizhang, LI Xiang. ECCM Scheme Against Interrupted Sampling Repeater Jammer Based on Time-Frequency Analysis［J］. Journal of Systems Engineering and Electronics,2014,25（6）:996-1003.
