0 引 言
我国海洋疆域广阔，资源丰富，海上目标种类繁多，分布广泛。尤其是近海岸与重要航道，船只密集分布，姿态各异，交织在一起，增加雷达对目标精准检测的难度［1-3］。
针对不同的目标，雷达收到的目标回波特征是有区别的。相同的目标的姿态、距离、相对雷达角度等众多条件的不同，目标回波的特征也不尽相同。对于SAR 雷达来说，其图像具有很强的姿态角敏感特性［4］。文献［5］提出基于稀疏表示分类的方法对原始图像与方位角灵敏图像进行分类，提高了分类准确率。文献［4］根据SAR 图像姿态角敏感特性，利用稀疏表示的方法提高分类的准确率。雷达目标的姿态角变化对一维距离像极其敏感。文献［6］研究发现，当目标的宽度和高度系数较小时，方位姿态变化对一维距离像更为敏感。文献［7］研究表明，若探测目标和雷达的相对方位姿态改变，目标散射中心在雷达视线上的投影也会发生改变。文献［8］研究表明，在一定范围内一维距离像的变化情况相似，在增大雷达带宽的情况下载频变化对高分辨距离像姿态敏感度不大。
复杂的海洋环境使得海上目标检测面临诸多挑战，已有的海面目标检测方面的研究根据检测机理不同，可以分为两大类：基于海杂波分布模型的统计检测方法和基于海杂波与目标回波差异分析的特征检测方法。第一种检测方法根据海杂波的复合高斯模型，研究其时空相关性；第二类检测方法是通过统计分布特性分析，寻找两者之间在不同变换域上的特征差异性。但海上目标姿态各异，统计特征是否具有差异性还鲜有报道。为此，从海上目标探测研究需求出发，利用X 波段固态全相参雷达，在2级海况条件下开展海上目标探测试验，获取同一目标不同姿态回波数据，分别从相关性和幅度统计特性两方面进行系统研究。在相关性方面，分析其时间相关性、空间相关性；在幅度统计特性方面，重点从时域、频域以及时频域分析其变化趋势和适用性，为后续海上目标数据采集试验以及目标检测提供支撑。
1 海上多姿态目标实测数据
多姿态海上目标数据采集试验［9-10］，主要是利用烟台港附近船只作为试验目标，根据目标运动姿态的不同，雷达工作于凝视模式，采用HH 极化天线观测模式，将雷达波束全覆盖目标，采集目标雷达回波数据。
试验期间，雷达（如图1所示）架设地点为烟台第一海水浴场试验点，架高约为80 m，试验地点示意图如图2 所示，雷达采集数据时，采样频率为60 MHz，发射带宽为20 MHz，采集时间约为180 s，雷达技术参数如表1所示。
图1 试验雷达天线
图2 试验地点示意图
表1 X波段固态试验雷达技术参数表
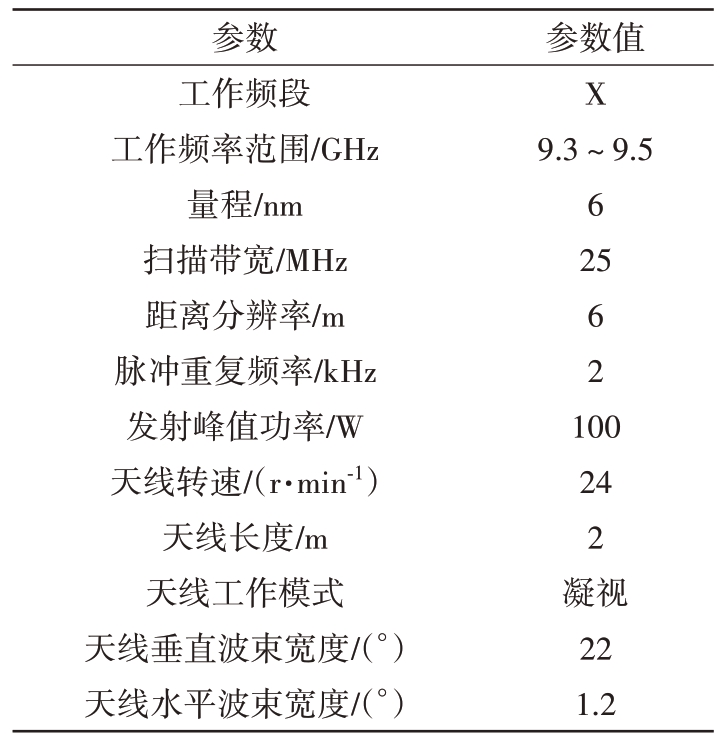
参数工作频段工作频率范围/GHz量程/nm扫描带宽/MHz距离分辨率/m脉冲重复频率/kHz发射峰值功率/W天线转速/（r·min-1）天线长度/m天线工作模式天线垂直波束宽度/（°）天线水平波束宽度/（°）参数值X 9.3～9.5 6 25 6 2 100 24 2凝视22 1.2
为说明数据的有效性，对比不同姿态目标的时空相关性与数据统计特征，本节从实测数据集中选取4 组不同姿态目标的典型数据（DATA_I，I为数据编号），数据概括见表2，图3 给出4 种不同姿态下目标试验场景，图4 为4 种姿态目标的一维距离像，其具有明显的差异。每组数据分别从时空相关性、时域、频域以及时频域上，提取与分析其特征差异。
图3 4种姿态目标实验场景图
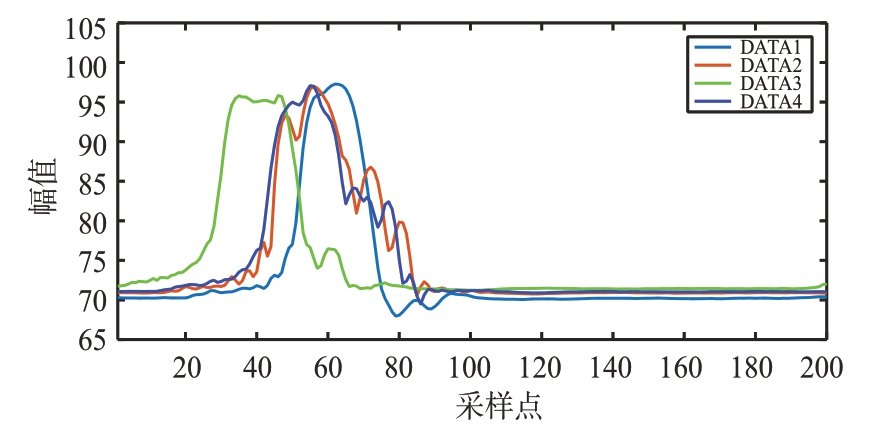
图4 多姿态目标一维距离像
表2 目标典型数据示例
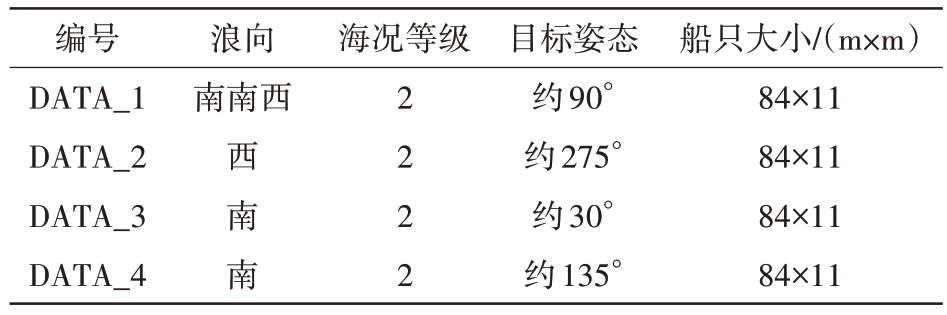
注：①雷达波向与目标船首之间的夹角确定目标姿态角度；②试验海域有效浪高约为0.5 m，综合判定为2级海况。
编号DATA_1 DATA_2 DATA_3 DATA_4船只大小/（m×m）84×11 84×11 84×11 84×11浪向南南西海况等级西南南2 2 2 2目标姿态约90°约275°约30°约135°
2 时空相关性分析
基于海杂波分析建模的统计检测是指将海杂波拟合为特定分布模型，结合统计检测理论进行海面目标检测［11］。随着研究的发现，雷达回波在时间维度与空间维度上蕴含着丰富的海洋与目标有关的信息，如在时间维度的相关性反映了同一个雷达距离单元上回波信号在时间测量上表现出的相似性。通过分析目标与海杂波强度的自相关函数获得两者的时间相关性；海杂波纹理分量的空间相关性反映了海面散射在距离维度上的均匀度，目标回波在距离维度上分散和泄露使得多个距离单元都能提供目标的散射信息［12］。本节对4组不同姿态目标实测数据的时空相关性进行分析。
2.1 时间相关性分析
时间相关性可以反映不同姿态目标的强相关时间差异，强相关时间是以1/e 作为参考门限，即时间相关系数第一次与1/e 相交所对应的相关时间为强相关时间［13-14］。图5展示了4种姿态下大目标的时间相关性曲线。
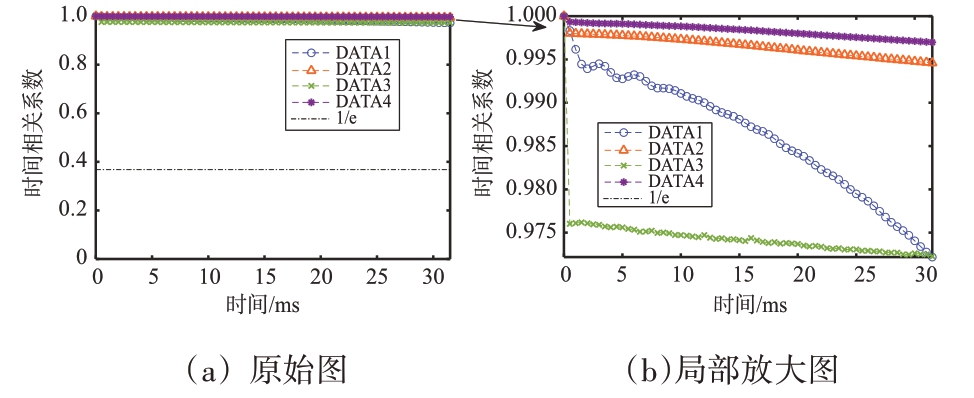
图5 目标时间相关性
由图5可知：单一姿态目标的时间相关系数下降趋势极其缓慢，甚至可以忽略不计。4 种姿态目标的时间相关性变化趋势极其相似，为观察4 种姿态时间相关性的具体变化趋势，将其放大如图5（b）所示。在时间延迟为30 ms 时，各姿态目标的时间相关系数均高于0.9，基本可以认为完全相关。因此，不同姿态目标的协方差矩阵在相邻时间单元之间可以认为近似相同。
2.2 空间相关性分析
空间相关性分析可以反映不同姿态目标的强相关距离差异，强相关距离是以1/e 作为参考门限，即空间相关系数第一次与1/e 相交所对应的相关距离为强相关时间［15］。图6 为4 种姿态下目标的空间相关性曲线。
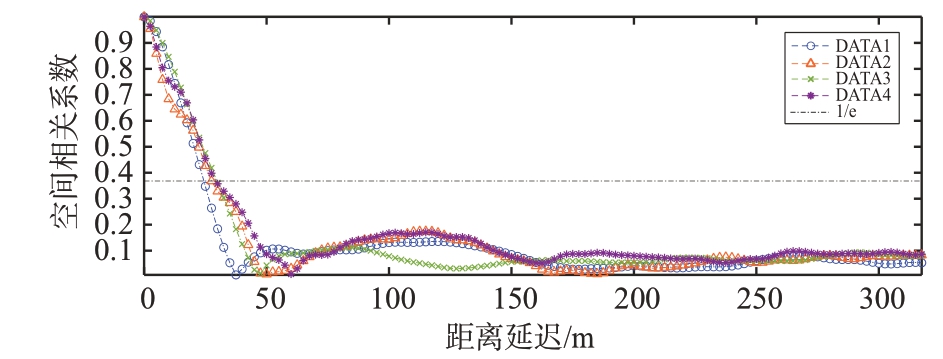
图6 目标空间相关性
由图6可知：单一姿态目标的空间相关在经历一个快速的下降期后，出现周期性的衰减过程，这种周期性与涌浪的调制作用有关。4种姿态的空间相关性变化趋势极其相似。在距离延迟为30 m 时（约5 个距离分辨单元），4 种姿态的空间相关系数均高于1/e。在距离延迟为10 m左右时（约2个距离分辨单元），4种姿态的空间相关系数均高于0.9，基本可以认为完全相关，因此，不同姿态目标的协方差矩阵在相邻距离单元之间可以认为近似相同。
3 时域特征分析
本节从时域角度提取不同姿态目标与海杂波的特征。信号时域反映了信号波形随着时间变化情况，一定程度上可以展现出目标与海杂波能量的大小，利用时域能量信息可作为区分海杂波与目标的标志［16-19］。图7为4种姿态目标时域图像。相对平均幅度（RAA）、相对峰值峰高（RPH）、时域熵值均值（TEM）分别在时域上表示不同的物理含义，利用不同姿态目标的实测数据，对海杂波与目标进行特征提取与分析，可以分析时域特征之间的差异性。
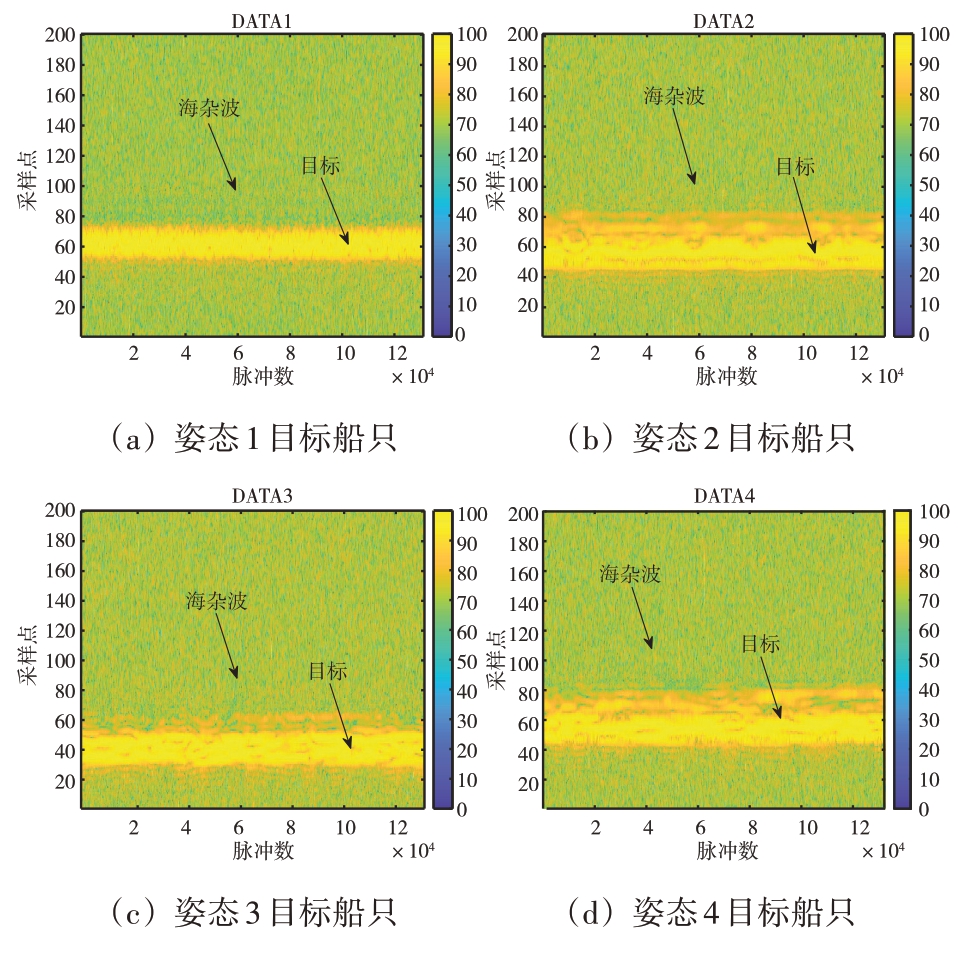
图7 多姿态目标时域回波图
3.1 相对平均幅度分析
图8 展示4 种姿态目标与海杂波的相对平均幅度特征值对比图。相对平均幅度定义为待测单元与参考单元平均幅度的比值，可以用来衡量待测单元与参考单元的幅度差异。
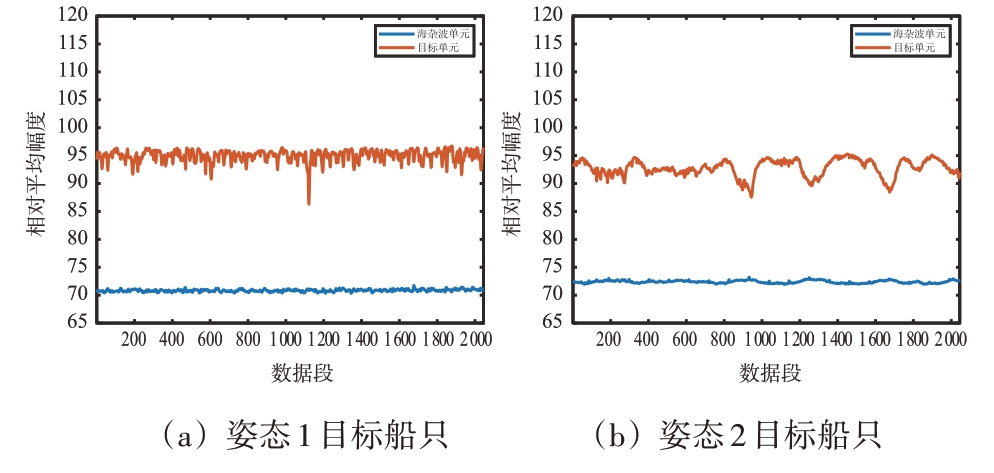
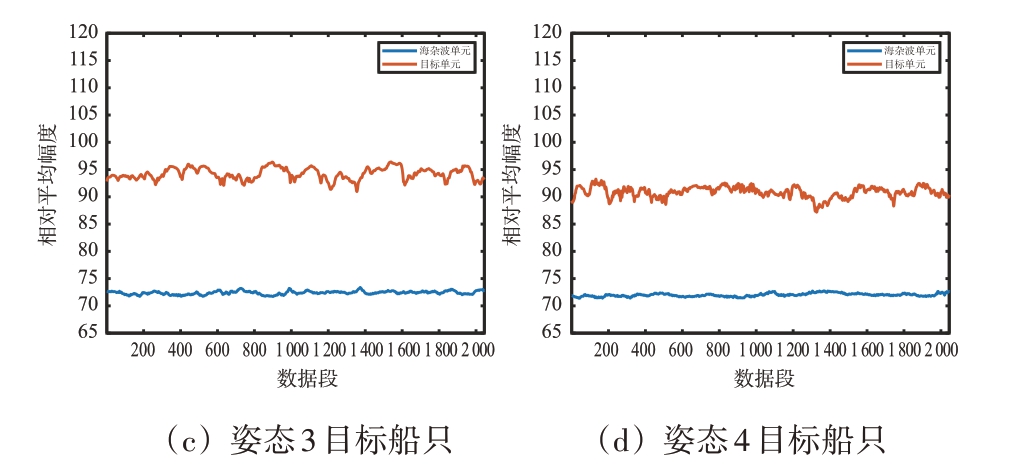
图8 多姿态目标相对平均幅度对比图
由图8 可知：不同姿态目标的RAA 大于海杂波；单一姿态目标的RAA 时序波形较为平稳，数值主要集中在90～95 之间，海杂波的RAA 时序波形也较为稳定，数值主要集中在70～75 之间；对于不同姿态的目标，其RAA数值较为接近，无较大差异。
目标船只体积较大，雷达散射截面积（RCS）大于海杂波，又因雷达工作于凝视状态，导致目标RAA 数值大于目标姿态变化并未影响雷达采集的强散射点，使得雷达采集目标信号幅度并未有较大差异。
3.2 相对峰值峰高分析
图9 展示4 种姿态目标与海杂波的相对峰值峰高特征值对比图。相对峰值峰高定义为待测单元时域波峰值与参考单元平均幅度的比值，可以用来衡量目标与海杂波信号峰值大小所占比重以及峰值起伏程度的差异。
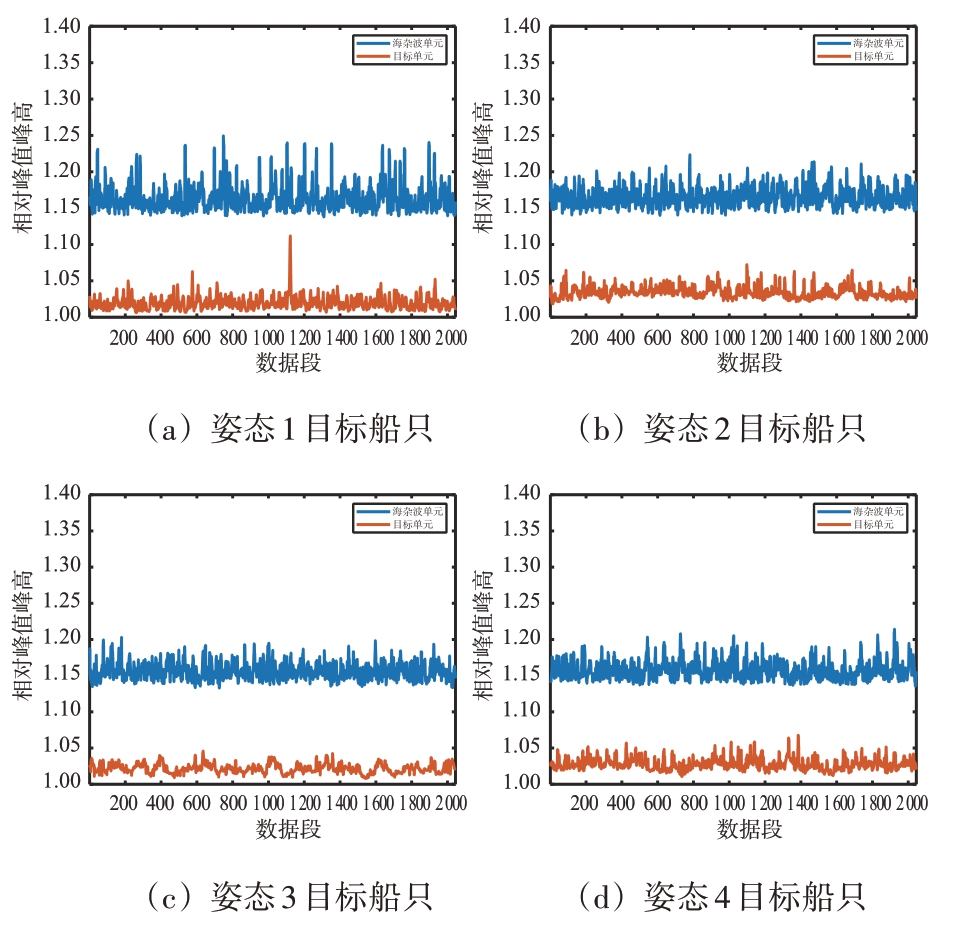
图9 多姿态目标相对峰值峰高对比图
由图9 可知：不同姿态目标的RPH 小于海杂波；单一姿态目标的RPH 时序波形起伏程度较小，数值主要集中在1.00～1.05 之间，海杂波的RPH 时序波形起伏较大，数值主要集中在1.15～1.25之间；对于不同姿态的目标，其RPH 波形起伏程度与数值都极其相似，无较大差异。
海面碎浪的存在，海杂波中会出现一些海尖峰，尖峰能量可能高于目标能量，目标相对于海杂波，RCS 较为稳定，目标回波信号尖峰相对于相邻单元平均值相差较小，不同时刻之间目标回波信号峰值波形变化程度相比海杂波并不明显，导致RPH 小于海杂波。目标姿态变化未影响雷达采集目标的信号幅度，因此不同姿态目标的RPH 无较大差异。
3.3 时域熵值均值分析
图10 展示4 种姿态目标与海杂波的时域熵值均值特征值对比图。时域熵值均值定义为待测单元时域信息熵的平均数值，可以用来衡量目标信号与海杂波信号的混乱程度。
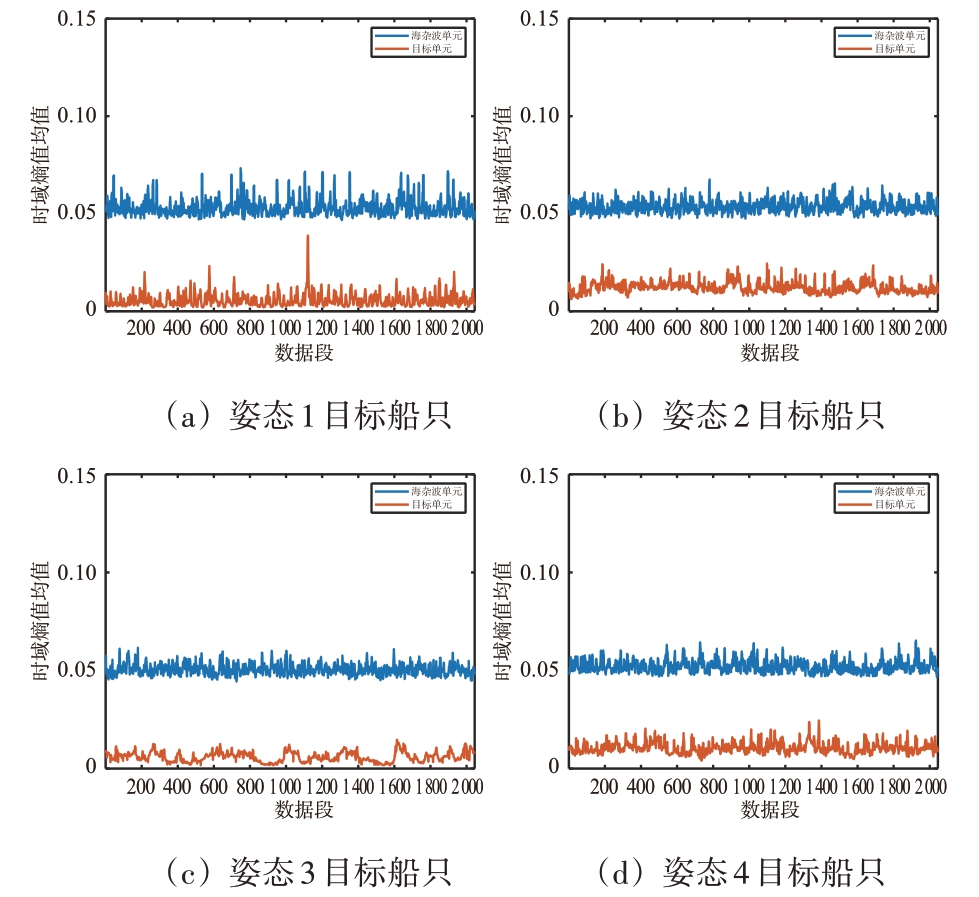
图10 多姿态目标时域熵值均值对比图
由图10 可知：海杂波的TEM 大于不同姿态目标；单一姿态目标与海杂波的TEM 时序波形起伏程度均较小，目标TEM 数值主要集中在0.05～0.07之间，海杂波TEM 数值主要集中在0.01～0.02 之间；对于不同姿态目标，TEM 波形起伏程度与数值无较大差异。
目标具有稳定的RCS，体积质量都较大，雷达采集目标波形较稳定，信号回波起伏较小，而海杂波RCS 极不稳定，信号回波序列起伏剧烈，相比之下，目标信号回波混乱程度更低，但其混乱程度变化较大，所以数值小于大于海杂波；目标姿态变化并未影响雷达采集目标强散射点的数据，因此TEM并无较大差异。
4 频域特征分析
本节从频域角度提取不同姿态目标与海杂波的特征。信号的频域信息反映信号波形随频率变化情况，一定程度上可以展现出海杂波与目标的信号能量在各个频点上的分布情况，可以利用频域信息的差异作为区分海杂波与目标的标志［20］。图11 为4 种姿态目标的时频变换的图像。多普勒峰高（RDPH）、相对多普勒向量熵（RVE）、频域熵值二阶矩（SOFE），分别在频域上表示不同的物理含义，利用4 组不同姿态目标的实测数据，对海杂波与目标进行特征提取与分析，可以分析频域特征之间的差异性。
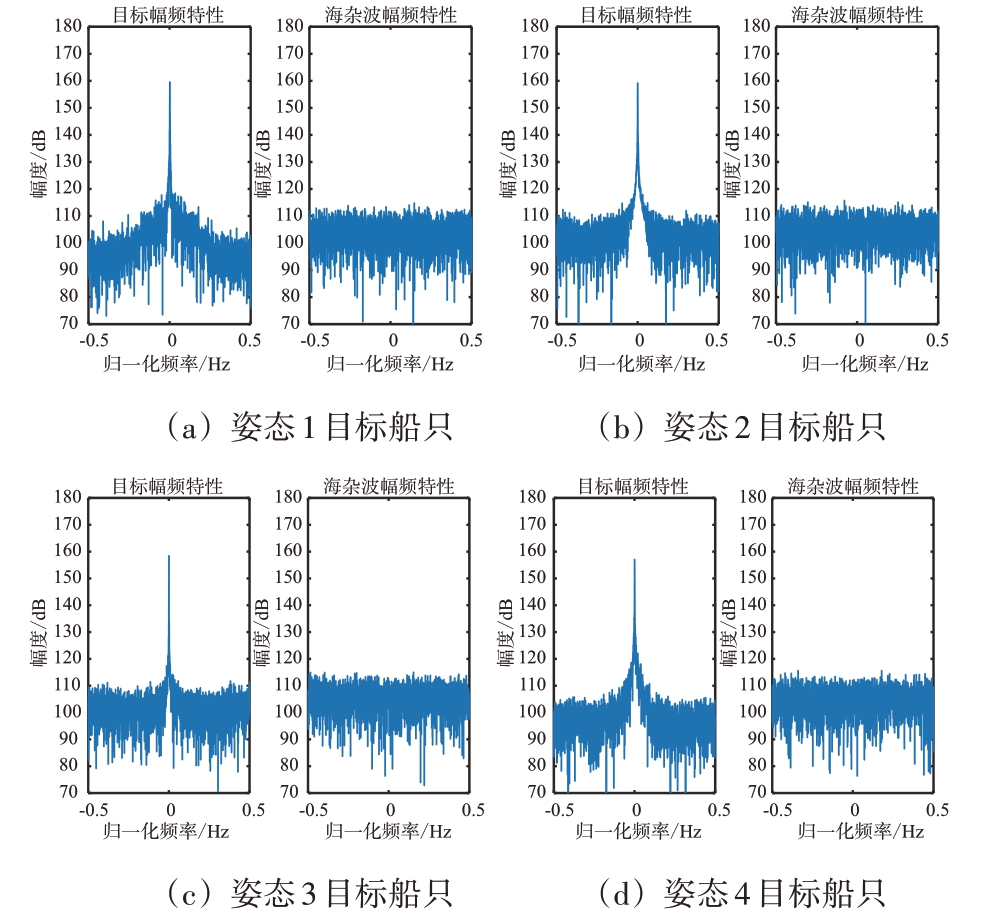
图11 多姿态目标频谱图
4.1 相对多普勒峰高分析
图12 展示4 种姿态目标与海杂波的相对多普勒峰高特征值对比图。相对多普勒峰高定义为待测单元的多普勒峰值与参考单元的平均多普勒峰值的比值，可以用来衡量目标与海杂波在多普勒谱上峰值突变程度的差异。
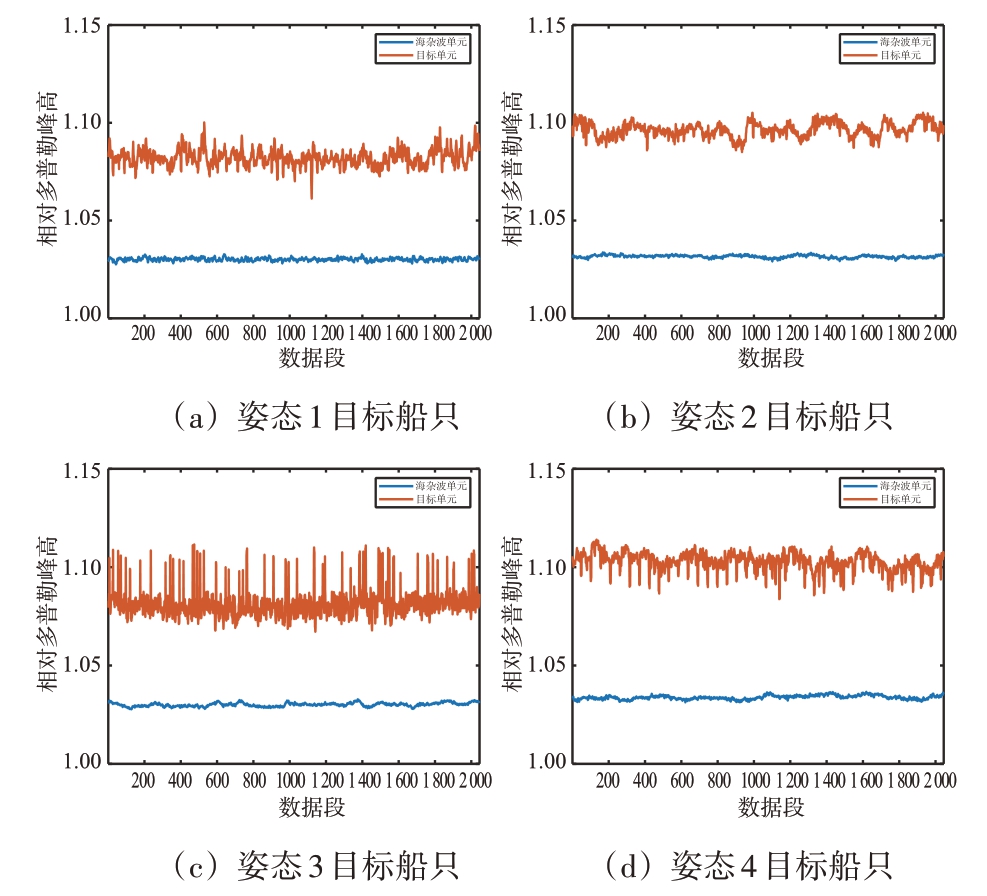
图12 多姿态目标相对多普勒峰高对比图
由图12 可知：目标RDPH 大于海杂波；单一姿态目标RDPH时序波形起伏程度较大，数值主要集中在1.07～1.10 之间，海杂波RDPH 时序波形起伏较小，数值主要集中在0.03 附近；对于不同姿态目标，RDPH波形起伏程度与数值无较大差异。
由于目标是运动状态，在雷达径向存在非匀速运动，则多普勒频移是时变的，在频谱上存在频谱展宽；而低海况下海面较为平静，在频谱上不存在频谱展宽，如图11所示，且目标频率对应的幅度大于海杂波，使得目标RDPH大于海杂波。
4.2 相对多普勒向量熵分析
图13 展示4 种姿态目标与海杂波的相对多普勒向量熵特征值对比图。相对多普勒向量熵定义为待测单元多普勒信息熵与参考单元多普勒信息熵的比值，可以用来衡量目标与海杂波在多普勒谱上回波序列混乱程度的差异。
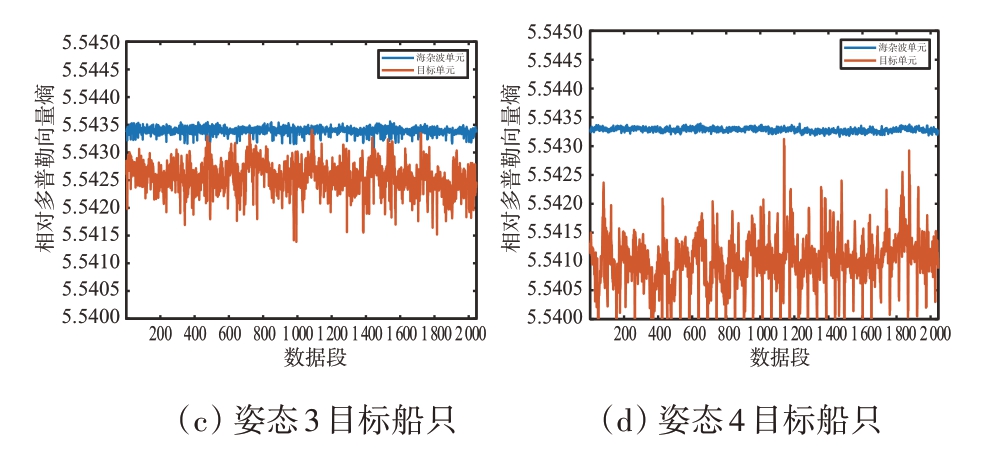
图13 多姿态目标相对多普勒向量熵对比图
由图13 可知：目标的RVE 小于海杂波；单一姿态目标的RVE 时序波形起伏程度较大，数值主要集中在5.540～5.543 之间，而海杂波的RVE 时序波形起伏较小，数值主要集中在5.543 5～5.544 0之间；对于不同姿态的目标，其RVE 波形起伏程度与数值无较大差异。
相比较于海杂波，目标RVE 偏小，其原因是雷达目标的多普勒谱回波序列比海杂波更加有序，其多普勒混乱程度相对较低。目标姿态变化缓慢，转动速度忽略不计，雷达采集目标的强散射点数据，目标姿态变化对多普勒谱幅度影响极小，如图11所示，因此4种RVE无较大差异。
4.3 频域熵值二阶矩分析
图14 展示4 种姿态目标与海杂波的频域熵值二阶矩特征值对比图。频域熵值二阶矩定义为待测单元在频域上信息熵值的方差，可以用来衡量目标与海杂波在多普勒谱上回波序列熵值离散程度。
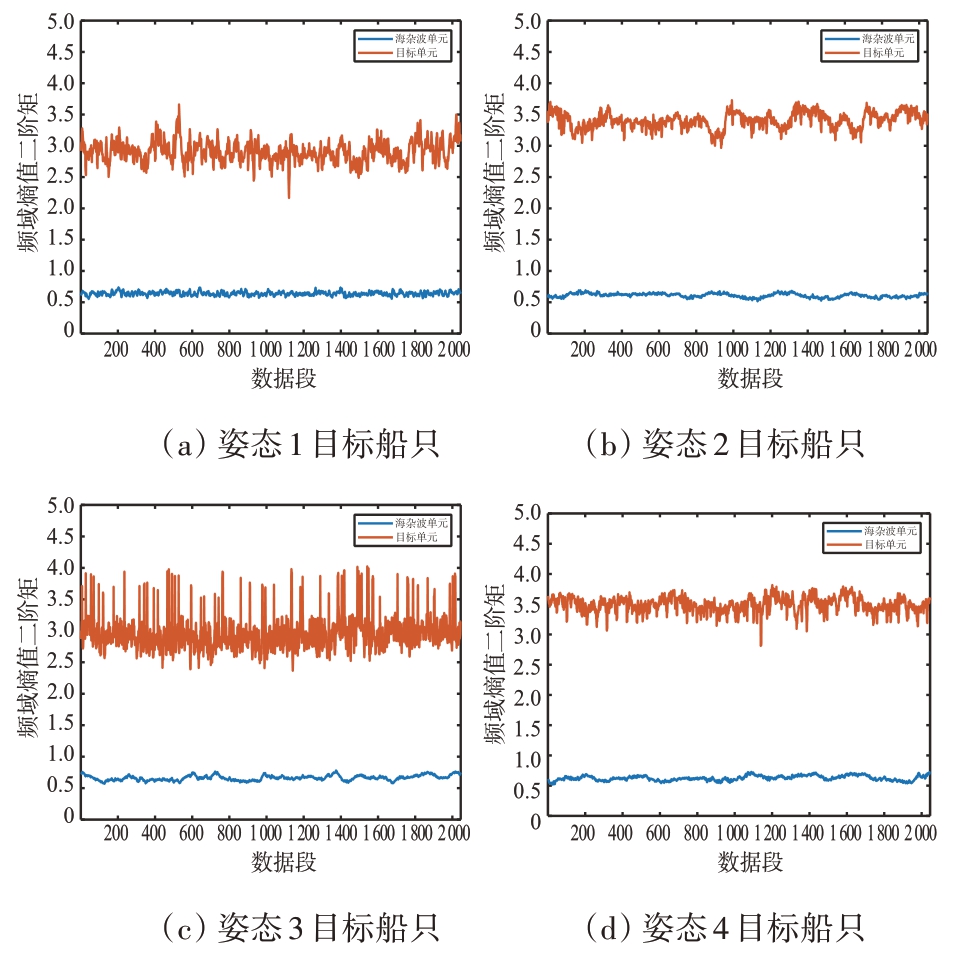
图14 多姿态目标频域熵值二阶矩对比图
由图14可知：目标SOFE大于海杂波；单一姿态目标的SOFE时序波形起伏程度较大，数值主要集中在2.5～3.5之间，而海杂波的SOFE时序波形起伏较小，数值主要集中在0.5～0.7之间；对于不同姿态的目标，其SOFE波形起伏程度与数值无较大差异。
相比较于海杂波，目标SOFE 偏小，其原因是雷达目标频域向量熵波形起伏较大，海杂波频域向量熵波形起伏较小，导致两者方差有较大差异。目标姿态变化缓慢未影响频域向量熵，因此姿态差异对SOFE无影响。
5 时频域特征分析
本节从时频域角度提取不同姿态下目标与海杂波的特征。时频分析利用时域与频域进行联合表示组成信号的时频谱对信号进行分析，可以采用平滑的伪魏格纳-维利分布（Smoothed Pseudo Wigner-Ville Distributions,SPWVD）计算归一化时频分布（Normalized Time-Frequencecy Distribution,NTFD），可以利用海杂波与目标在NTFD 上表现出不同的特性作为区分两者的标志［21-22］。图15 为4种姿态目标的SPWVD 时频变换域图像。时频脊累积量（RI）、连通区域个数（NR）在时频域上表示不同的物理含义，利用4组不同姿态目标的实测数据，对海杂波与目标进行特征提取与分析，可以分析时频域特征之间的差异性。
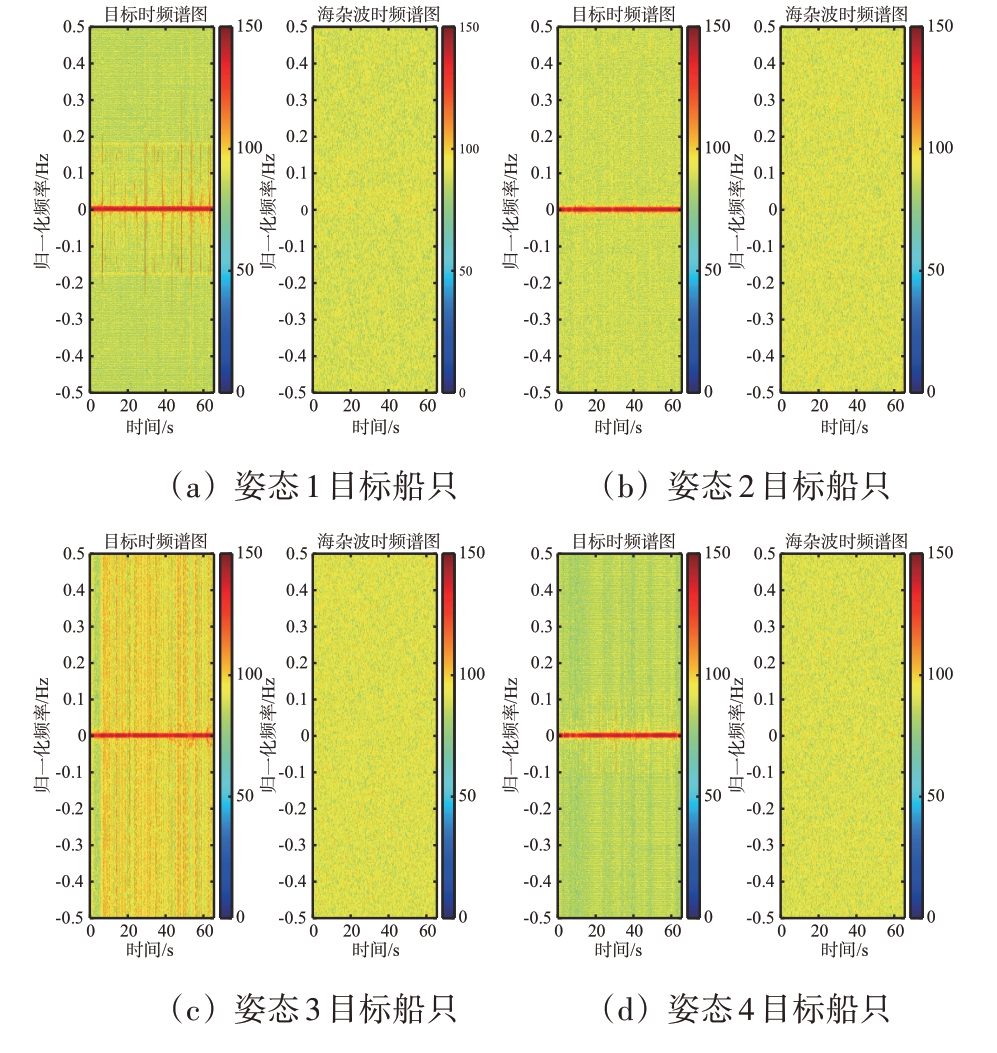
图15 多姿态目标时频谱图
5.1 时频脊累积量分析
图16 展示4 种姿态目标与海杂波的时频脊累积量特征值对比图。时频脊累积量定义为待测单元在时频图像上的时频脊累积量，时频脊是时频谱中不同时刻频率维的一系列极值，可以用来衡量目标与海杂波时频脊能量的强度。
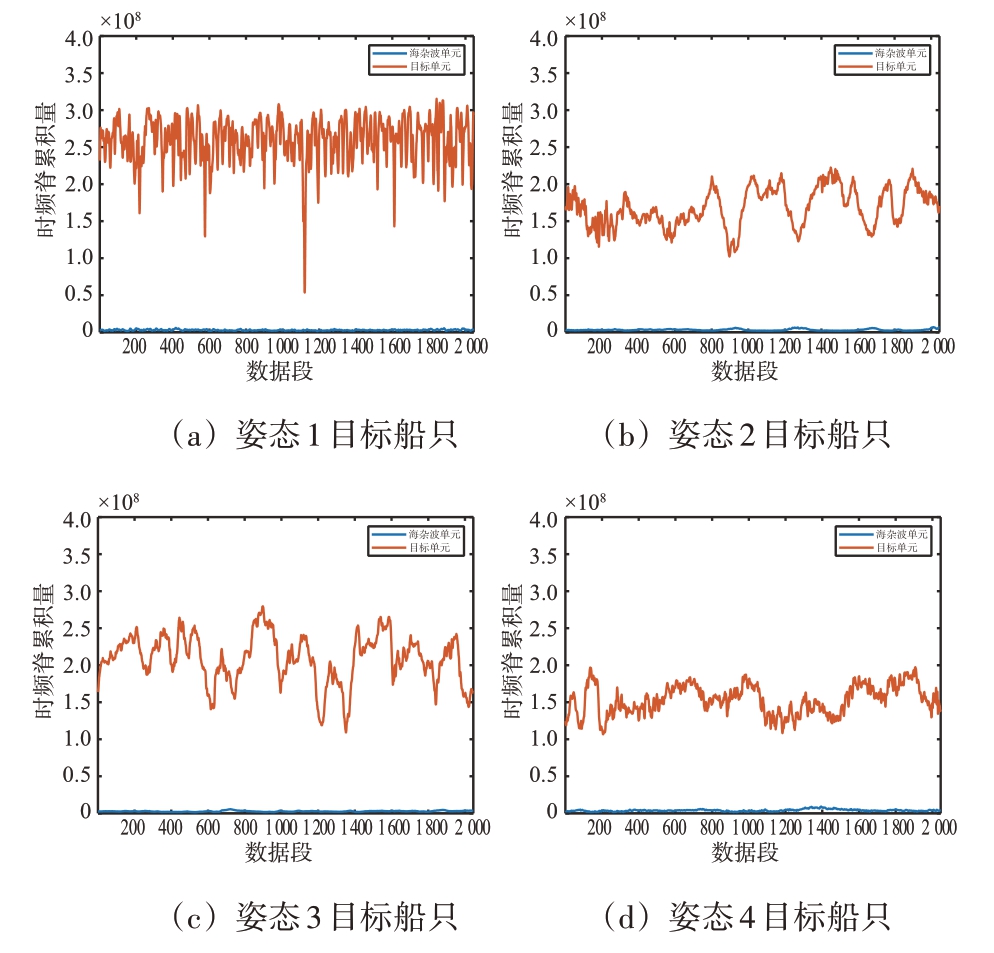
图16 多姿态目标时频脊累积量对比图
由图16 可知：目标RI 大于海杂波；单一姿态目标的RI 时序波形起伏程度较大，数值主要集中在1.0～3.0 之间，而海杂波的RI 时序波形起伏较小，数值主要集中在0.1 附近；对于不同姿态的目标，其RI 波形起伏程度与数值大小无较大差异。
相比较于海杂波，目标RI偏大，其原因是雷达凝视模式采集目标数据，由于海杂波随机性较强，具有非高斯性特点，导致海杂波在时频谱图像上连通区域较多，连续性较差；目标时频谱图像较为集中，连续性较强，基本成为一整片连通区域。
5.2 连通区域个数分析
图17 展示了4 种姿态目标与海杂波的连通区域个数特征值对比图。连通区域个数定义为待测信号单元在时频脊图像中的连通区域的数目，可以用来衡量目标与海杂波在时频脊能量上的离散程度。
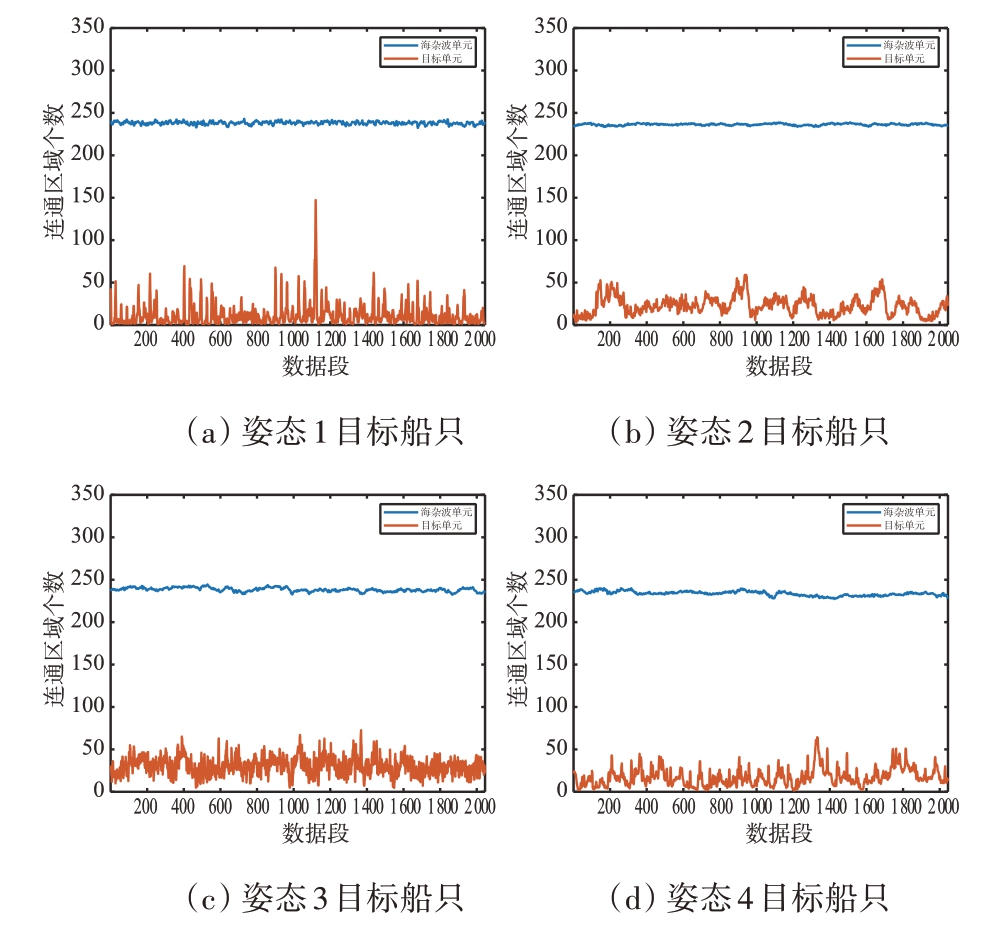
图17 多姿态目标连通区域个数对比图
由图17 可知：目标NR 小于海杂波；单一姿态目标的NR 时序波形起伏程度较大，数值主要集中在0～50 之间，而海杂波的NR 时序波形起伏较小，数值主要集中在240 附近；对于不同姿态的目标，其NR 波形起伏程度与数值大小无较大差异。
目标时频谱图像较为集中，其连通区域数值较小，海杂波时频谱图像较为分散，其连通区域数值较大。
6 实验结果分析
由图8 至图17 可以发现，海杂波具有的统计特征与含目标回波的统计特征有明显差异。而且，两者的统计特征时序图曲线离得越远，表明两者的可分性越大。不同姿态目标之间统计特性的差异较小。为了定量描述不同姿态目标回波统计特性之间的差异，定义差异系数D：
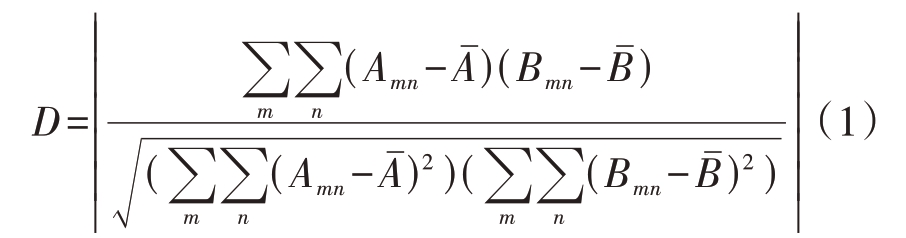
式中，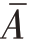
表示待测目标数据均值，
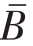表示参考目标数据均值，m 为数据的行数，n 为数据的列数，差异系数数值越大，特征越接近。
选取姿态1目标为参考数据，分别对姿态2、姿态3 和姿态4 目标船只统计特征数据进行差异系数计算与对比，图18 为8 种统计特征的差异系数统计图。
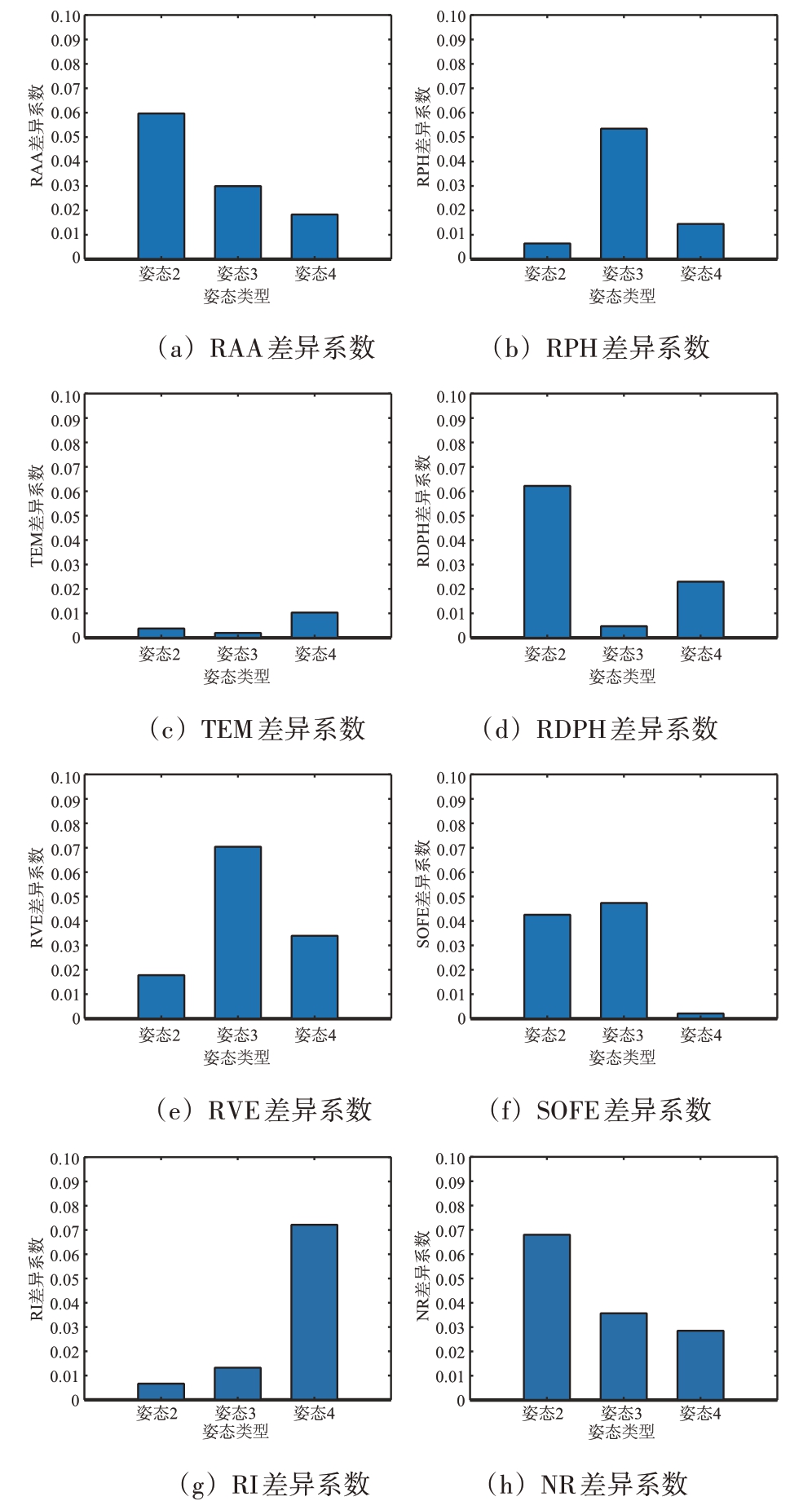
图18 特征差异对比图
按照差异系数的数值，在0.8～1.0 之间具有较强差异性，在0.6～0.8 之间具有强差异性，在0.4～0.6 之间具有中等差异性，在0.2～0.4 之间具有弱差异性，在0～0.2 之间具有极弱差异性。在图18中，不同姿态目标之间8 种统计特征的差异系数均在0～0.1 之间，具有较强的相似性，由此认为不同姿态目标实测数据，同一种统计特征具备相似性。
7 结束语
本文利用X 波段雷达凝视不同姿态目标船只实测数据，根据目标对雷达信号的散射特性，分析了不同姿态目标在时空维度上表现出来的相关性；同时利用统计方法对不同姿态目标进行时域、频域、时频域上的特征提取与分析。
目标体积较大，RCS 因姿态变化影响甚微，雷达采集目标强散射点信号幅度值无较大差异，在目标最典型数据上进行时空相关性，其4种姿态目标回波数据的时间相关系数均在0.9 之上，空间相关系数均在30 m 附近强相关，且相关性曲线变化趋势一致；为描述统计特征之间差异性，定义差异系数，4 种姿态目标回波的统计特征之间差异系数均在0～0.7 之间，可认为近似一致；上述结论为后续海上目标数据采集试验以及目标特性分析与识别等工作奠定基础。
［1］汪金波，张顺生.基于两步法的海上目标智能检测方法［J］.现代雷达，2023，45（1）:35-40.
［2］关键.雷达海上目标特性综述［J］.雷达学报，2020，9（4）:674-683.
［3］许述文，白晓惠，郭子薰，等.海杂波背景下雷达目标特征检测方法的现状与展望［J］.雷达学报，2020，9（4）:684-714.
［4］李家强，胡张燕，杨广乐，等.基于多姿态角模型的SAR图像分类方法［J］.现代雷达，2022，44（12）:63-69.
［5］DING Baiyuan, WEN Gongjian, HUANG Xiaohong, et al.Target Recognition in SAR Images by Exploiting the Azimuth Sensitivity［J］. Remote Sensing Letters, 2017,8（9）:821-830.
［6］LI H J, YANG Songhan. Using Range Profiles as Feature Vectors to Identify Aerospace Objects［J］. IEEE Trans on Antennas and Propagation,1993,41（3）:261-268.
［7］HUDSON S, PSALTIS D. Correlation Filters for Aircraft Identification from Radar Range Profiles［J］.IEEE Trans on Aerospace and Electronic Systems,1993,29（3）:741-748.
［8］孙昭峰.复杂背景的海上目标雷达信号特性研究［J］.舰船科学技术，2016，38（16）:100-102.
［9］刘宁波，丁昊，黄勇，等.X 波段雷达对海探测试验与数据获取年度进展［J］.雷达学报，2021，10（1）:173-182.
［10］关键，刘宁波，王国庆，等.雷达对海探测试验与目标特性数据获取——海上目标双极化多海况散射特性数据集［J］.雷达学报，2023，12（2）:456-469.
［11］王童，童创明，许光飞，等.基于电磁模型的宽带雷达海杂波信号建模与分析［J］.电子与信息学报，2022，44（4）:1358-1365.
［12］罗泽峰.基于海杂波相关性估计的弱目标检测方法研究［D］.重庆:重庆大学，2022.
［13］刘宁波，董云龙，于家伟，等.基于实测数据的海杂波时空相关性分析［J］.海军航空工程学院学报，2017，32（2）:199-204.
［14］刘照标，张友益，陈翰.舰载近程搜索雷达时空二维海杂波建模与仿真［J］.舰船电子对抗，2023，46（3）:70-74.
［15］关键，丁昊，黄勇，等.实测海杂波数据空间相关性研究［J］.电波科学学报，2012，27（5）:943-953.
［16］许述文，茹宏涛.基于标签传播算法的海面漂浮小目标检测方法［J］.电子与信息学报，2022，44（6）:2119-2126.
［17］关键，伍僖杰，丁昊，等.基于三维凹包学习算法的海面小目标检测方法［J］.电子与信息学报，2023，45（5）:1602-1610.
［18］SHUI Penglang, LI Dongchen, XU Shuwen. Tri-Feature-Based Detection of Floating Small Targets in Sea Clutter［J］. IEEE Trans on Aerospace and Electronic Systems,2014,50（2）:1416-1430.
［19］LI Yuzhou, XIE Pengcheng, TANG Zeshen, et al. SVMBased Sea-Surface Small Target Detection: A False-Alarm-Rate-Controllable Approach［J］.IEEE Geoscience and Remote Sensing Letters,2019,16（8）:1225-1229.
［20］许述文，焦银萍，白晓惠，等.基于频域多通道图特征感知的海面小目标检测［J］.电子与信息学报，2023，45（5）:1567-1574.
［21］SHI Sainan，SHUI Penglang. Sea-Surface Floating Small Target Detection by One-Class Classifier in Time-Frequency Feature Space［J］. IEEE Trans on Geoscience and Remote Sensing,2018,56（11）:6395-6411.
［22］伍僖杰，丁昊，刘宁波，等.基于时频脊-Radon变换的海面小目标检测方法［J］.信号处理，2021，37（9）:1599-1611.