0 引 言
长期以来，随着散射中心概念与模型在雷达目标识别等技术中的广泛应用［1-8］，研究者们更多地采用非线性参数估计的手段，依靠目标的雷达特性数据（测量或仿真获得）来反演或提取目标散射中心［9-14］。在限定条件下，往往都能确保由散射中心所重构的目标特性是有效的，例如，各向同性的理想点散射中心模型，衰减指数表征的散射中心模型［15］，由GTD 构造的散射中心模型［16］，以及当前被广泛认可的属性散射中心模型［17］。尽管提取或者反演散射中心存在着多解或不确定性，但都可在各自适用条件下重构有效的目标特性。上述事实，使得人们加深了对目标散射中心作为等效散射源的认识，这种认识或许并不全面和准确。
正向散射中心参数化建模是一种针对复杂环境中目标识别应用的快速重建雷达回波方法［18-21］,它能够重构出目标的特性，并且能够唯一确定散射中心的位置参数。确定散射中心位置的过程，实际上是将目标表面不同区域的感应电流等效折合为某个空间位置“点”的感应电流贡献。由于面片上的感应电流分布复杂，导致这个过程存在困难。同时，考虑到多种机理形成的感应电流混合在一起的情况，将其等效为单一散射中心时，散射中心所具有的物理意义会受到限制，很难超越等效源的抽象概念。对于由复杂多次散射产生的散射中心［22-23］，目前的建模和分析研究相对有限，由于多次散射形成的射线路径通常不限于一个平面，其在三维空间内展开并呈复杂的折叠结构。这样形成的散射中心往往远离目标区域，导致其位置参数难以准确预测。
为了构造可以清晰反映目标散射特征，具有明确的物理含义属性的散射中心模型，本文从散射中心位置属性的角度入手进行探讨，改善人们将散射中心作为等效源的认识，为目标识别提供更精准的位置信息。本文结构安排如下：首先，从朱兰成方程出发，基于电磁散射物理过程，论述了散射中心三维位置是目标结构在电磁散射情形下固有属性的观点。其次，结合雷达成像条件，将目标投影至二维成像面上进行分析，由射线光程直接给出散射中心距离向位置；分析射线光程在合成孔径期间的变化量，建立了多次射线光程变化与多普勒频率之间的联系。最后，以目标的几何光学场为依据，构建了目标镜面反射散射场的雷达回波信号数学表达式，并用其表征了目标单站雷达图像，验证了散射中心位置的准确性。最终通过对直二面角、直三面角、规则矩形腔、Slicy 等算例的散射中心位置正向推导与分析，为散射中心的形成过程提供了理论基础。
1 散射中心建模与位置分析
雷达图像中散射中心横向位置的固有属性，来自于目标散射中心三维空间位置的固有属性，本节首先以朱兰成（Stratton-Chu）方程为出发点，阐述了散射中心三维位置具备物理属性的概念。随后，借助高频射线理论及转台成像方法，从射线光程的计算和目标几何光学场的求解两个角度对目标散射回波的初始相位进行了分析，得出了散射中心的二维投影位置以及目标的雷达图像表征，并进一步比对验证了一致性。散射中心位置参数的分析流程如图1所示。
图1 散射中心位置参数分析流程图
1.1 散射中心三维位置属性分析
由朱兰成积分给出的高频区散射远场近似式为
式中，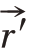
为曲面上任意一点P 的空间位置矢量，
分别为P 点的感应电磁流矢量，R 为雷达距离，s'为物体表面的照亮区集合。式（1）不要求积分区间是闭合曲面，因此可以将散射部件细分为若干三角面元计算，将被照亮面元的独立散射相干叠加，获取部件的散射场。对于PEC 材质的物体有
某时刻雷达照射姿态如图2所示，根据雷达距离关系可知，
，其中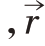
是场点，代表了任意点P 到雷达的距离。在远场我们可以认为R =r + r'cos Ω。
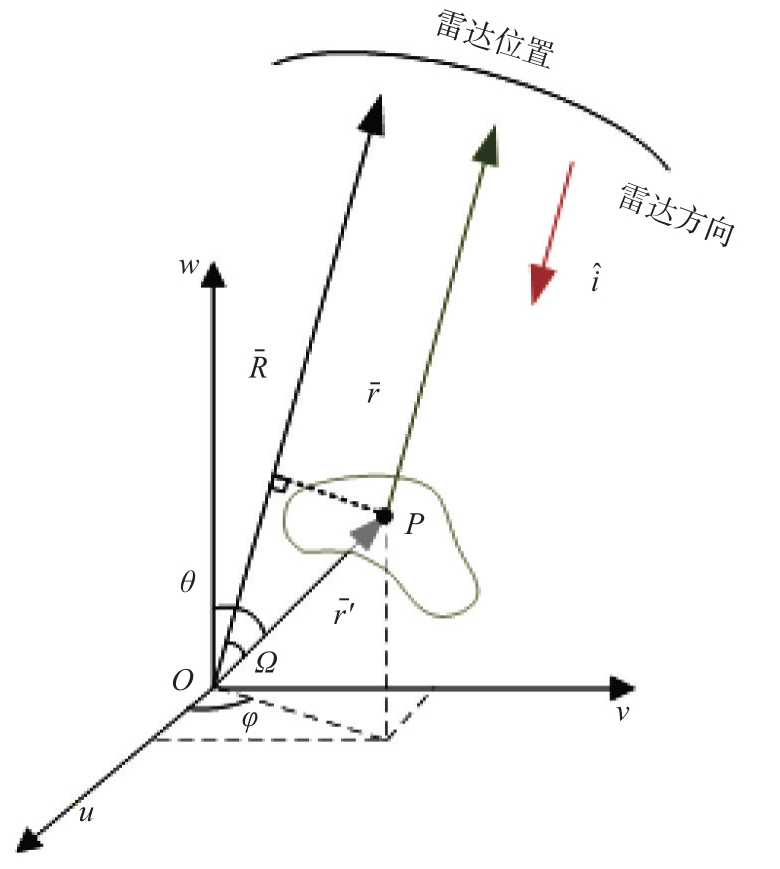
图2 雷达照射姿态示意图
那么PEC 材质目标的散射远场就可以进一步表示为
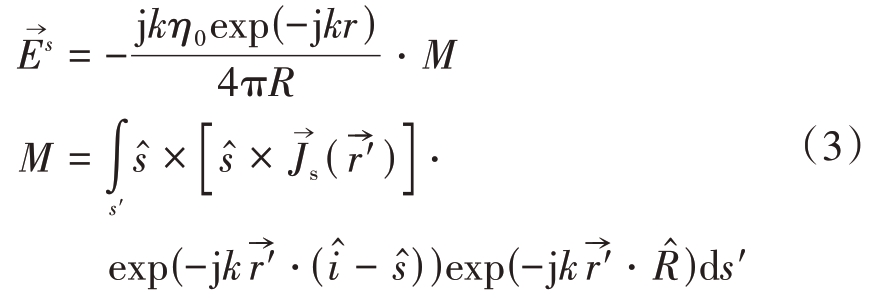
式（3）中，由M 确定的是初始相位，是由入射波照射到目标所产生的电磁流信息。固定姿态的前提下，在电磁波向外辐射的过程中该项相位是不发生变化的，可认为是一个常复数。因此，初始相位具备稳定性，等价于目标相位中心的概念。在单站远场条件下
，此时M可以化简为
式中，i为被照亮面元的序号。该式表明，目标任一局部几何结构（部件）产生的雷达散射贡献，是该部件上所有分布感应电磁流相干散射的合成。在计算后向散射时，面片上的感应电流又可以按照散射机理分解为不同阶次的感应电流，
为射线在目标表面作用n次后形成的感应电流，分别对应着不同反射次数下的高频散射机理。若将多种机理形成的感应电流混在一起，等效为单一散射中心来确定散射中心的位置参数，将使散射中心所具有的物理意义受到限制。
进行朱兰成积分的计算过程中，我们观察到来自目标曲面上的驻相点或镜面反射点的散射主导了该局部的散射贡献。因此，将产生镜面反射的射线作用点作为局部部件级散射中心三维空间位置参考点是合理的。将积分曲面集合替换为目标表面镜面反射点的集合s1'，并将面元上由不同机理形成的电磁流区分开，同种机理形成的镜面散射电磁流大小一致，可视为常数An（n 为射线作用次数），该式可以进一步表示为
因此，在目标几何模型给定并满足高频远场观测条件的前提下，目标的相位中心可由镜面散射点分布情况给定，其三维位置具备稳定性，对散射中心空间三维位置物理属性的定量探讨是具备理论基础的。
1.2 雷达图像中散射中心位置分析
散射中心三维位置已具备固有属性的概念，再加以雷达观测参数的限制条件，散射中心在雷达图像上的二维位置是三维空间在低维图像上的映射，同样具备固有属性的意义。为了从物理层面表征目标图像，需结合转台成像过程具体分析。
转台成像模型的示意图如图3所示，假设目标自身三维空间坐标系为uvw，将目标放置转台上，使三维坐标系原点o 与转台原点O 重合。记某时刻雷达视线方向（观察角）与w 向的夹角为俯仰角θw，与u向的夹角为方位角φu。
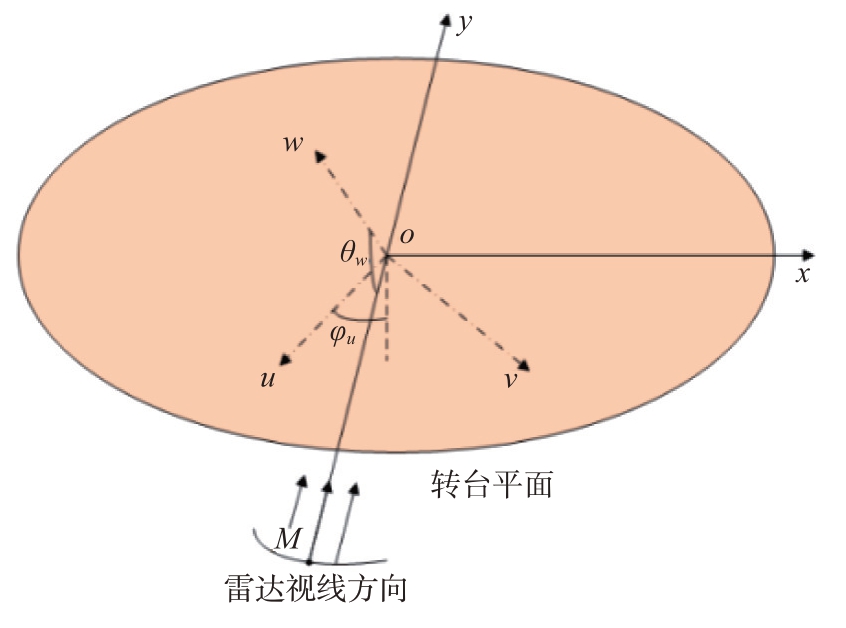
图3 转台成像模型示意图
在该观察角下，三维空间中目标表面被照亮的一点P(u0,v0,w0 )与其在转台平面中的投影位置P( x0,y0 )满足投影矩阵的关系：
利用式（6），将坐标系转换至成像的二维平面内，如图4 所示。此时MO 为雷达视线方向，场景相位中心O 至雷达的距离为R0。记沿雷达视线方向为距离向y 轴，垂直于雷达视线方向为方位向x轴。
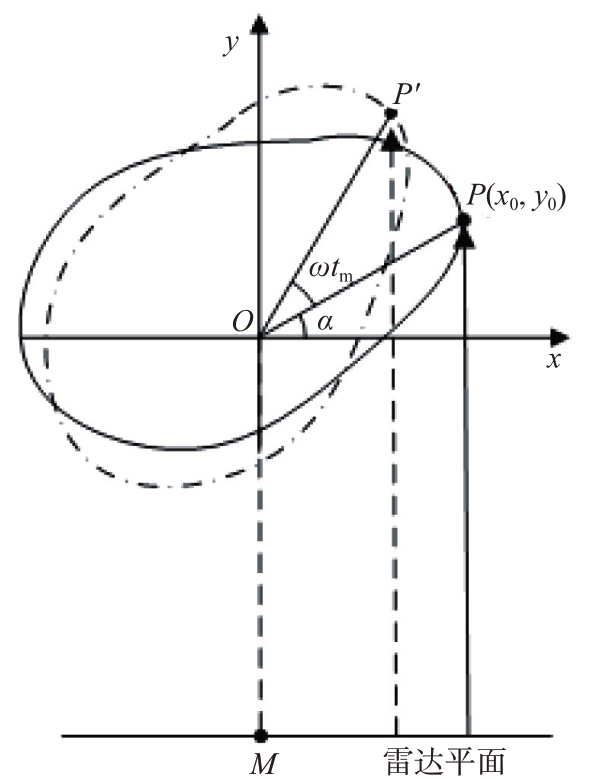
图4 任意时刻目标点与雷达距离
若合成孔径期间转台以恒定角速度ω旋转，在慢时域tm 时，原目标表面与O 点相距r 处的某点P(x0,y0)已随转台旋转至P'处。由于R0 ≫r，P'到雷达的双程距离（射线光程）可近似表示为到雷达平面的距离：
不考虑其他因素的影响，只研究回波相位与雷达位置、工作频率的关系，不妨将雷达发射信号简单视为一组单频连续波信号ejK→R·R→。结合式（7），在与基频信号混频后，接收的雷达回波可表示为
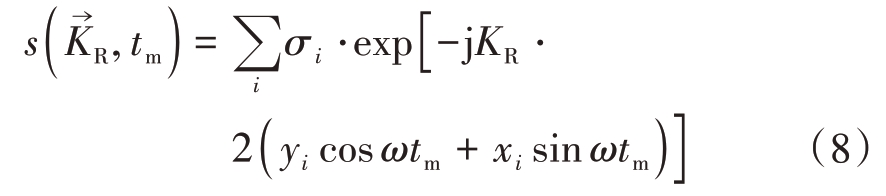
这里σi 为第i 个散射点的强度，( xi,yi )为其位置。此时
是空间分布信号的形式，可以理解为当观察角（tm 为常量）和雷达工作波长确定时（f 为常量），该式是与时间无关的复常量，但波数向量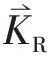
的指向随着雷达和目标的径向指向改变而变化。当雷达工作在聚束SAR（或ISAR）模式时，会用到很窄的波束，此时波数向量
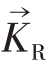的指向可以采用波束指向R 近似代替，向量点乘
就退化为了式（8）中标量相乘的形式。
与时间信号变换至频域分析过程相类似，空域信号可变换至波数域进行分析。以波数标量k = 2π f/c 来表征雷达工作频率，以φ = ωtm 表征雷达观察角度，采用波数分析法，将空域信号变换到波数域。利用小角度近似cos φ ≈1，sin φ ≈φ，回波表达式可进一步表示为
式中，sD( x,y )是雷达图像，可以理解为雷达观测到的二维散射密度函数，也是空间三维散射密度函数s(u,v,w )在二维成像面上的投影。可以看出，散射密度函数与接收到的雷达回波信号之间满足傅里叶变换对的关系。
另一方面，研究者们更习惯于用多普勒频率来表征散射中心横向位置，而多普勒频率与射线双程距离（回波相位项）有关，利用式（7）可以求得多普勒频率fd：
在合成孔径时，应将转角控制在小角度范围内，避免散射点出现越距离单元徙动，此时x0 cos ωtm ≫y0 sin ωtm，多普勒频率可近似表达为
由此看出，产生的多普勒频率大小与散射点所处横向位置x0 有关，不同横向位置的散射点对应不同大小的多普勒，因此可将目标横向位置区分出来。结合式（11）和式（12），可以建立射线双程距离和散射中心横向位置之间的联系，由射线双程距离随观察角度的变化率直接推算散射中心横向位置：
在工程应用中，可采用增量的形式近似替代求导。因此，获得目标同一作用点（或微三角面元）在微动前后的射线双程距离差（或相位差）及微动的角度后，可以正向推导出该射线对应散射中心的横向位置。对于多次作用路径的射线，例如形成多次散射的角反和腔体结构，同样可以采用这种方式来推导其横向位置。同时，避免了求解多次散射问题采用的寻找等效源的传统方法所带来的不确定性。后文给出具体算例分析。
散射中心纵向位置可以由射线半程距离直接给出：
因此，不依赖于给定的成像条件和雷达参数，可直接由目标几何模型出发，借助光学区射线理论得到目标散射中心的位置信息。
2 多次散射中心位置分析
为了更加简洁地揭示目标散射中心位置在雷达图像上的映射关系，本节引入直二面角、直三面角、规则矩形腔体等算例进行定性分析，探讨射线多次作用情形下，目标镜面反射点分布情况与雷达回波相位特性的关系。借助高频射线场，直观正向地揭示光学区目标散射中心位置和部件几何结构之间的联系。
2.1 直二面角
散射源分布一致（呈线状、面状等）的目标在雷达图像中的映射仍具有差异性，这是由于目标摆放姿态不同，导致方位向数据录入的维度不同所产生的。具体以直二面角为例，在不同摆放姿态下正向推算其散射中心位置。
2.1.1 局部型散射中心二面角
将直二面角垂直于成像面xoy 摆放，棱点放置于(r cos α,r sin α)处，如图5 所示。图5（b）是自由空间二面角图5（a）在成像面上的投影。利用NQ为直角三角形斜边上的中线，得到直二面角的射线双程距离满足以下几何性质：任意角度下照射至直二面角并按严格后向散射被雷达接收的射线双程距离与雷达接收平面至直二面角棱点的双程距离相同。
图5 垂直于成像面摆放的直二面角射线路径
以相同入射面元作为射线编号基准，正向计算的所有射线微动前射线双程距离均为
微动后，直二面角绕原点旋转小角度φ，同样采用相同入射面元作为射线编号，此时射线双程距离均变为
可以求得射线对应的散射中心位置坐标：
由此看出，所有射线产生的点散射中心位置坐标均位于(r cos α,r sin α) 处，在雷达图像上将叠加形成一个局部型散射中心。
在波数域进一步分析其在雷达图像上的表征，将射线光程视为随雷达观察角度φ 变化的函数，假设该角度下棱点坐标为P(a,b)，某射线第一次作用（入射）面元坐标为P1(x1,y1)，二次作用（出射）面元坐标为P2(x2,y2)，两点间距为l，利用直二面角的几何性质，结合式（8），回波表达式可表示为
通过二维逆傅里叶变换可得到雷达图像（散射密度函数）：
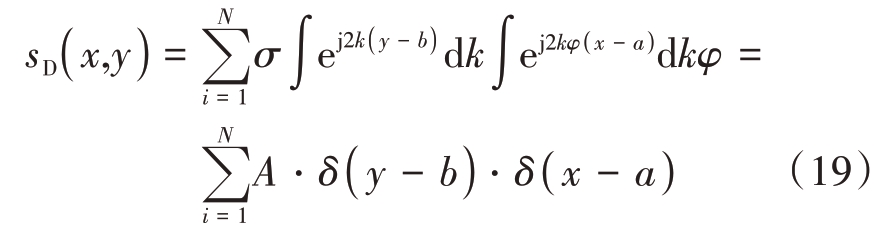
由此看出，雷达图像上将在二面角棱点位置处出现一个局部型散射中心，与采用射线理论正向推导的位置相同。
2.1.2 分布型散射中心二面角
另将直二面角棱边平行于成像面x轴摆放，如图6 所示。棱边中点位于P( a,b) 处，宽边棱长为2l。
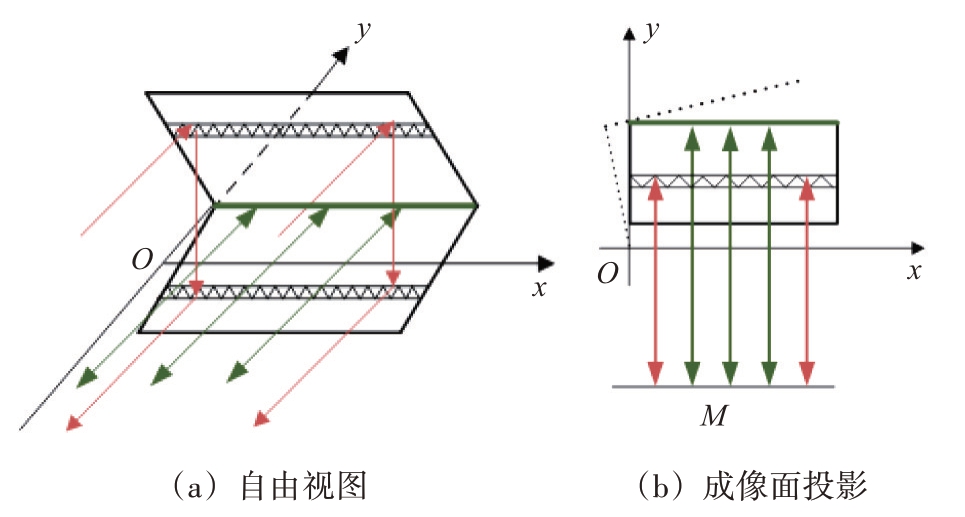
图6 平行于成像面摆放的直二面角射线路径
正向计算入射面元位置Pi( xi,yi )处的射线光程为
微动后，相同射线编号的射线双程距离变为
可以求得射线对应的散射中心位置坐标
由此看出，当面元剖分足够细腻时，不同横向位置空间射线形成的点散射中心将在成像面上沿方位向均匀致密排布，由于xi ∈[a - l,a + l]，表征为在该区域内的线状形式，为分布型散射中心。
在波数域进行推导分析，回波表达式可表示为
改写成对目标区域进行积分，并提出中心相位项：
由这些致密排布的点散射中心所产生的场是sinc函数的形式。对回波进行二维逆傅里叶变换：
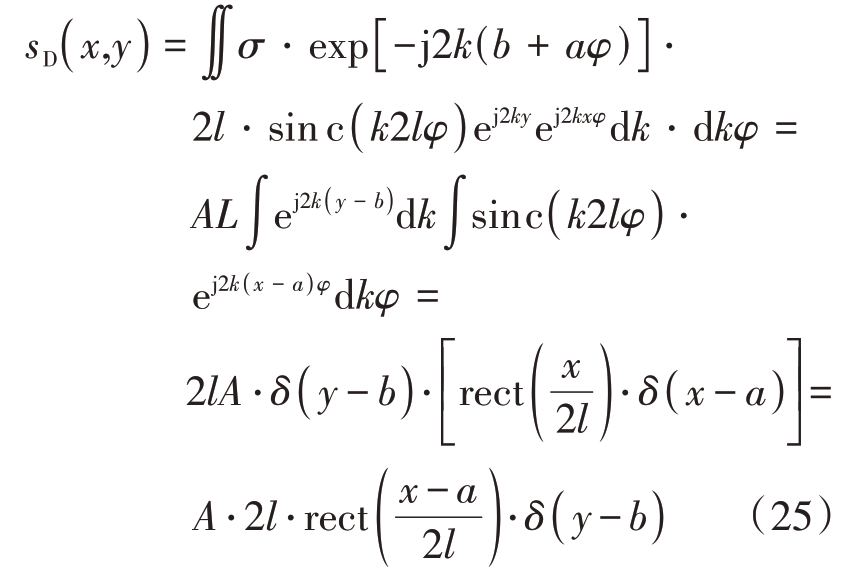
由此看出，散射中心纵向排布是位于同一处，横向排布是窗函数的形式，分布在长2l 的区域内。故二维雷达图像是线状的形式，为分布型散射中心。
2.2 直三面角
以三面角自身坐标系为例，直三面角射线路径在底面的投影是一个入射二面角的问题，且底面仅改变射线向量的w 向分量，路径投影如图7 所示。经研究，直三面角射线路径具有以下几何性质：任意角度下，入射直三面角并按严格后向散射被雷达接收的射线，其双程距离与雷达平面至直三面角角点的双程距离相同。
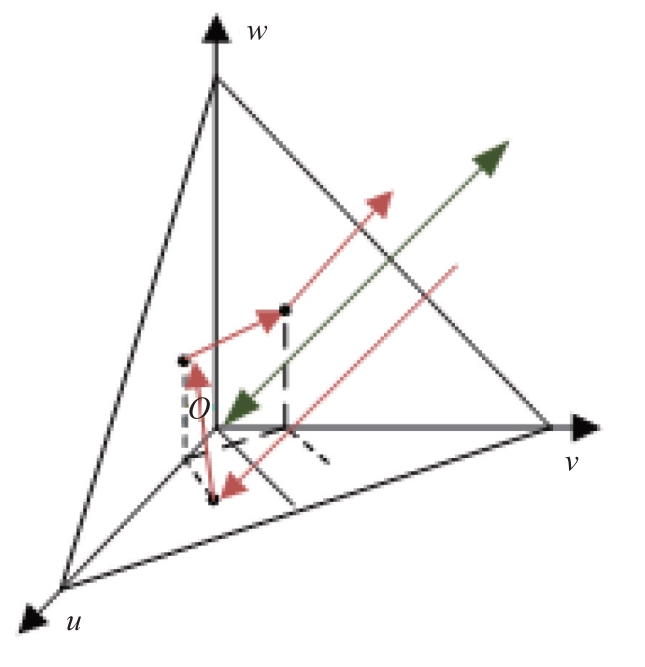
图7 射线入射直三面角在底面的投影图
另将直角边长为m 的三面角以口面垂直朝向雷达方向摆放，角点位于xoy 成像面上的坐标P(r cos α,r sin α )处，如图8所示。
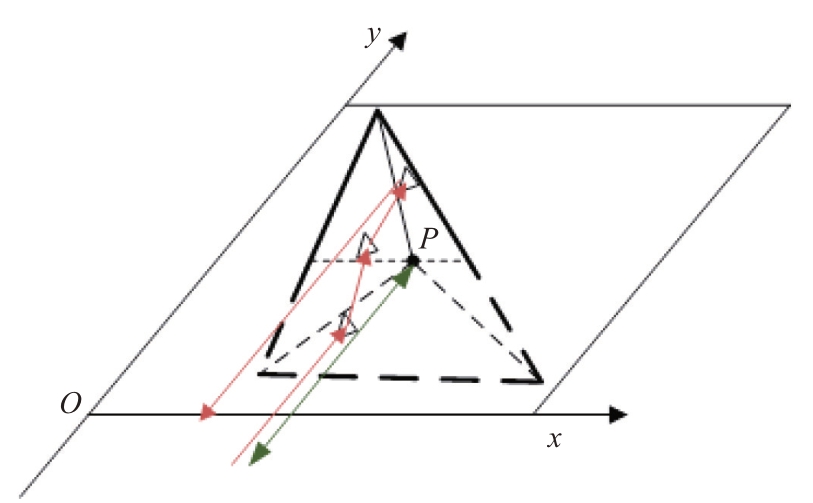
图8 口面朝向雷达的三面角
利用直三面角的几何特性，微动前所有入射射线双程距离可表示为
微动后，相同射线编号的射线双程距离变为
由于射线双程距离在微动前后与垂直摆放的直二面角情形完全一致，采用相同的分析过程，直三面角将在()r cos α,r sin α 处叠加形成一个局部型散射中心。
2.3 规则矩形腔
以内腔长度为6 m，宽为3 m，高为2 m 的矩形腔体为例研究射线多次散射情况。规则矩形腔模型三视图如图9所示。
图9 规则矩形腔模型三视图
将内腔壁底部右侧角点置于坐标系原点O，在俯仰角90°，方位角53°（夹角α =37°）的情况下，正向推算矩形腔体的散射中心空间位置参数。此时成像面与底面uov 平行，将模型投影至成像面分析，射线传播过程的路径俯视图如图10所示。
图10 成像面上腔体射线路径示意图
在该姿态角下，射线平行面入射，矩形腔体各面法向均不与射线入射方向反向，因此不存在一次作用后被雷达接收的情况。射线入射到矩形内腔侧面，第二次、第三次和第四次作用相当于连续与两个直角二面角作用，且两个直角二面角有一边重合。所以，经过四次作用的射线严格满足后向回波散射条件。
记入射点与出射点连线的中点为B，经计算，任意经过四次反射的射线双程距离均与过B 点并入射到内腔角点处的射线距离相同。利用OB 为BCN 的角平分线，可以求得所有射线在微动前的双程距离：
微动后，腔体绕坐标原点旋转了φ，此时所有射线双程距离变为
可以正向推导散射中心位置：
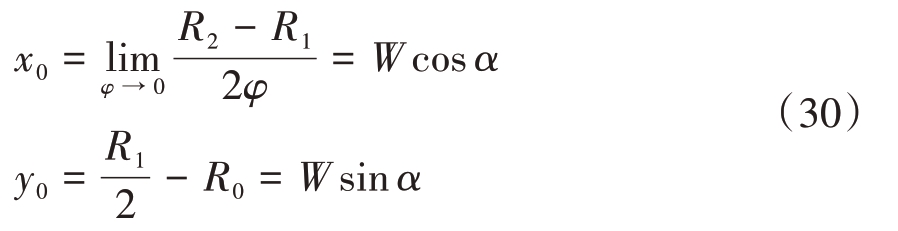
与局部型散射中心的形成过程类似，所有射线贡献的散射点将在该处叠加，在雷达图像上形成一个亮点。
接下来进行定量分析。假设没有发生越距离单元走动，采用几何光学计算所有射线的回波表达式，并对所有射线进行高度维的累加：
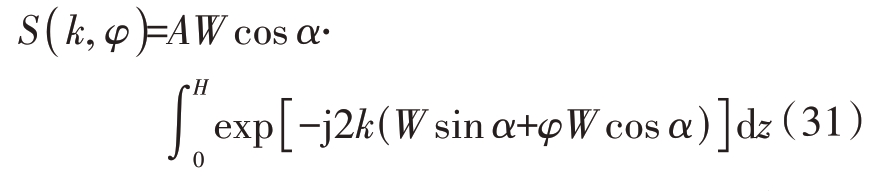
式中l 和H 分别为内腔壁照亮区域长度及高度。对其进行二维逆傅里叶变换可获得散射密度函数（雷达图像）表达式：
经理论推导，其在雷达图像上表现为一个位置在(W cos α,W sin α )处的亮点。
3 仿真与讨论
为验证推导过程的准确性，对直二面角两种摆放姿态、直三面角、矩形腔分别进行仿真成像。雷达参数设置如下：中心频率15 GHz，带宽1.5 GHz，频率步进25 MHz，俯仰角90°，中心方位角0°，角宽6.033 9°，角度步进0.100 57°，图像分辨率0.1 m×0.1 m，场景大小6 m×6 m，极化方式HH。
直二面角宽边为2 m，窄边为1 m，棱点放置于xoy 成像平面的P( 1,1) 处，如图11、图12 所示呈垂直和水平两种不同摆放姿态。均在棱点在成像面上的投影处分别表现为局部型和分布型散射中心，分布型长度与宽边相同，与式（19）、式（25）的推导一致。
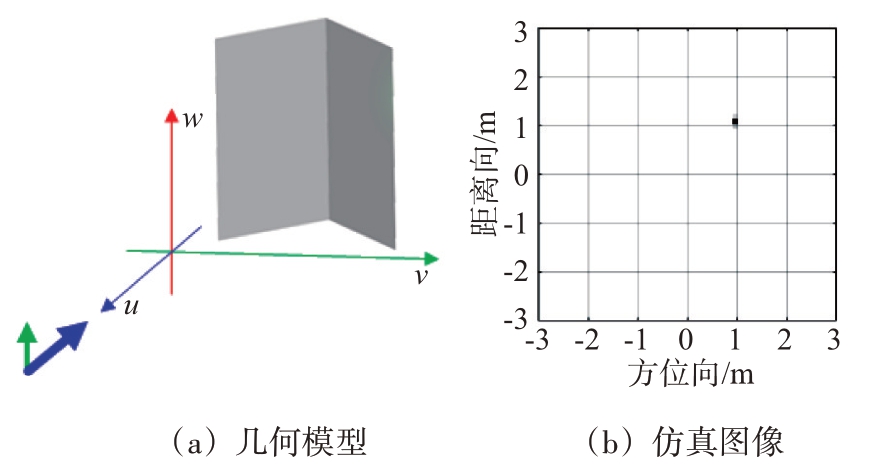
图11 垂直摆放直二面角仿真SAR图像
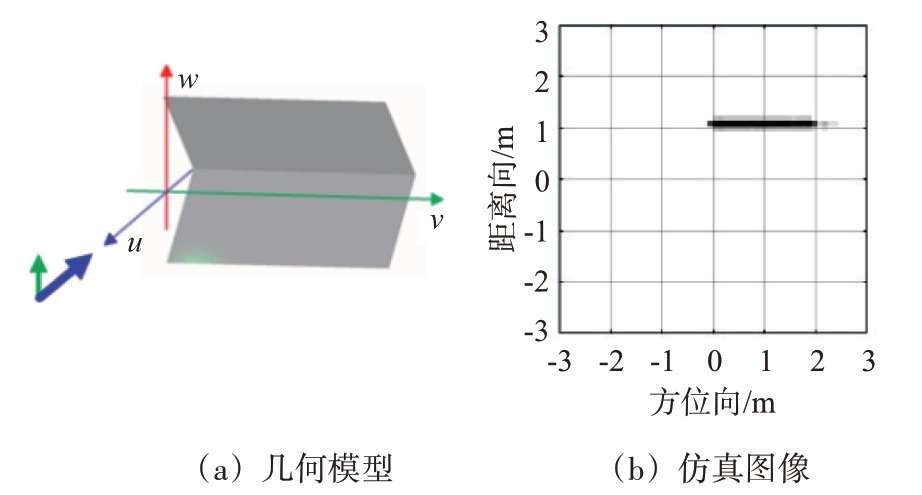
图12 水平摆放直二面角仿真SAR图像
直三面角直角边长2 m，角点放置于xoy 成像平面的P( 2,2) 处，如图13 所示。图像上在角点位置处出现一个局部型散射中心，与上节分析一致。
图13 直三面角仿真SAR图像
规则矩形腔体模型与仿真图像如图14 所示。在(W cos α,W sin α )即(2.4,1.8 )处附近出现一个亮点，与式（32）推导一致。
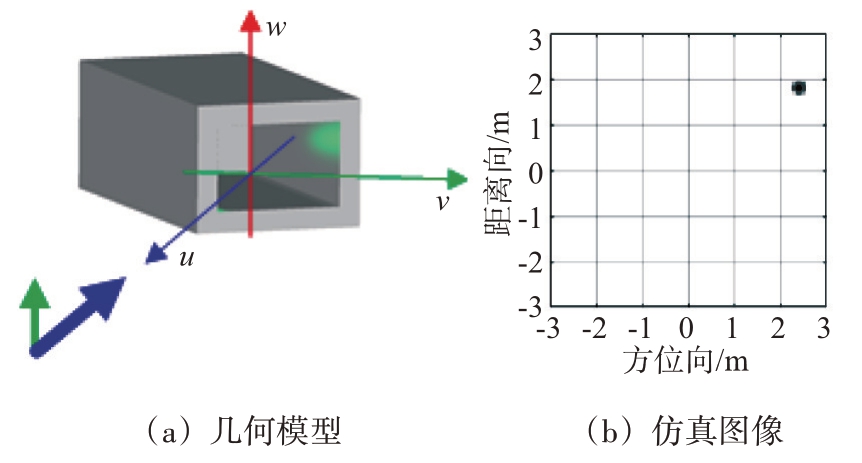
图14 规则矩形腔仿真SAR图像
Slicy模型按照射线作用机理被分为6个区域，分别对应二面角、圆柱母线镜面反射、三面角、顶帽结构这些主要贡献。模型分区如图15（a）所示。
图15 Slicy仿真SAR图像
将雷达成像参数设置为：中心频率9.6 GHz，带宽0.75 GHz，频率步进37.5 MHz，俯仰角60°，中心方位角0°，角宽5.380 3°，角度步进0.269 02°，图像分辨率0.2 m×0.2 m，场景大小6 m×6 m，极化方式HH。得到仿真图像，如图15（b）所示。
在观测角俯仰角60°，方位角0°时，由方位角微动3°时（俯仰角60°方位角3°）的射线光程变化量ΔR 正向推导散射中心位置参数，并在仿真图像上标注出来，如表1所示。
表1 Slicy模型光程变化量及散射中心位置推算
区域1 2 3 4 5 6机理二次一次二次三次二次二次ΔR/m-0.071 0.025 0.094 0.035-0.055 0.066推算位置/m（-0.68，-0.61）（0.24，-0.91）（0.90，-0.61）（0.33，0.12）（-0.52，0.14）（0.63，0.14）
仿真图像中的散射中心与通过正向推算射线光程变化量得出的散射中心位置相一致。
4 结束语
本文从电磁散射物理过程出发，正向演绎论证了散射中心的位置属性，导出了目标镜面反射散射场表达式，并用其表征了目标单站雷达图像；另一方面，借助射线双程距离正向导出了散射中心二维位置，揭示了散射中心横向位置与多普勒频率之间的联系。进一步以直二面角、直三面角、规则矩形腔等对象为例，讨论了多次散射机理下目标散射中心的形成原因和位置特性。
为恰当反映散射中心的物理意义，必须弱化其等效散射源的角色与意义，不能仅以能重构目标散射特性为目的来看待散射中心，以免陷入过于倚重散射中心的等效散射源意义而忽略其应当承载的物理属性与内涵，这对目标散射中心概念的各种应用尤为重要。关于单站雷达位置属性的探讨可以为散射中心在雷达识别中的应用提供更加有针对性的理论基础，也为目标特性的利用提供新思路。
［1］POTTER L C, MOSES R L. Attributed Scattering Centers for SAR ATR［J］. IEEE Trans on Image Processing, 1997,6（1）:79-91.
［2］CHIANG H C, MOSES R L, POTTER L C. Model-Based Classification of Radar Images［J］. IEEE Trans on Information Theory,2000,46（5）:1842-1854.
［3］El-DARYMLI K, GILL E W, MCGUIRE P, et al. Automatic Target Recognition in Synthetic Aperture Radar Imagery: A State-of-the-Art Review［J］. IEEE Access, 2016,4:6014-6058.
［4］DING Baiyuan, WEN Gongjian, HUANG Xiaohong, et al.Data Augmentation by Multilevel Reconstruction Using Attributed Scattering Center for SAR Target Recognition［J］. IEEE Geoscience and Remote Sensing Letters, 2017,14（6）:979-983.
［5］ZHOU Jianxiong, SHI Zhiguang, CHENG Xiao, et al. Automatic Target Recognition of SAR Images Based on Global Scattering Center Model［J］.IEEE Trans on Geoscience and Remote Sensing,2011,49（10）:3713-3729.
［6］DING Baiyuan, WEN Gongjian, HUANG Xiaohong, et al.Target Recognition in Synthetic Aperture Radar Images via Matching of Attributed Scattering Centers［J］. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing,2017,10（7）:3334-3347.
［7］许延龙，潘昊，丁柏圆.基于深度信念网络的属性散射中心匹配及在SAR 图像目标识别中的应用［J］.液晶与显示2023，38（11）：1511-1520.
［8］孙圣凯，何姿，管灵，等.基于散射中心模型的目标电磁特性智能生成网络研究［J］.电波科学学报，2023，38（5）：835-844.
［9］ODENDAAL J W,BARNARD E,PISTORIUS C W I.Two-Dimensional Superresolution Radar Imaging Using the MUSIC Algorithm［J］. IEEE Trans on Antennas and Propagation,1994,42（10）:1386-1391.
［10］BHALLA R, MOORE J, LING H. A Global Scattering Center Representation of Complex Targets Using the Shooting and Bouncing Ray Technique［J］. IEEE Trans on Antennas and Propagation,1997,45（12）:1850-1856.
［11］ZHOU Jianxiong, ZHAO Hongzhong, SHI Zhiguang, et al. Global Scattering Center Model Extraction of Radar Targets Based on Wideband Measurements［J］. IEEE Trans on Antennas and Propagation, 2008, 56（7）:2051-2060.
［12］ZHOU Jianxiong, SHI Zhiguang, FU Qiang. Three-Dimensional Scattering Center Extraction Based on Wide Aperture Data at a Single Elevation［J］. IEEE Trans on Geoscience and Remote Sensing, 2014, 53（3）:1638-1655.
［13］XIE Yiyuan, XING Mengdao, GAO Yuexin, et al. Attributed Scattering Center Extraction Method for Microwave Photonic Signals Using DSM-PMM-Regularized Optimization［J］. IEEE Trans on Geoscience and Remote Sensing,2022,60（1）:1-16.
［14］罗宇航，陈彦锡，郭琨毅，等.基于神经网络和散射中心模型的目标参数提取［J］.系统工程与电子技术，2023，45（1）：9-14.
［15］HURST M, MITTRA R. Scattering Center Analysis via Prony's Method［J］.IEEE Trans on Antennas and Propagation,1987,35（8）:986-988.
［16］POTTER L C, CHIANG D M, CARRIERE R, et al. A GTD-Based Parametric Model for Radar Scattering［J］.IEEE Trans on Antennas and Propagation,1995,43（10）:1058-1067.
［17］GERRY M J,POTTER L C,GUPTA I J,et al.A Parametric Model for Synthetic Aperture Radar Measurements［J］. IEEE Trans on Antennas and Propagation, 1999, 47（7）:1179-1188.
［18］HE Yang,HE Siyuan,ZHANG Yunhua,et al.A Forward Approach to Establish Parametric Scattering Center Models for Known Complex Radar Targets Applied to SAR ATR［J］. IEEE Trans on Antennas and Propagation,2014,62（12）:6192-6205.
［19］LIU Jin, HE Siyuan, ZHANG Lei, et al. An Automatic and Forward Method to Establish 3-D Parametric Scattering Center Models of Complex Targets for Target Recognition［J］. IEEE Trans on Geoscience and Remote Sensing,2020,58（12）:8701-8716.
［20］HUANG Kai, HE Siyuan, ZHANG Yunhua, et al. Composite Scattering Analysis of the Ship on a Rough Surface Based on the Forward Parametric Scattering Center Modeling Method［J］. IEEE Antennas and Wireless Propagation Letters,2019,18（12）:2493-2497.
［21］HE Siyuan, HUA Mengbo, ZHANG Yunhua, et al. Forward Modeling of Scattering Centers from Coated Target on Rough Ground for Remote Sensing Target Recognition Applications［J］.IEEE Trans on Geoscience and Remote Sensing,2023,62:1-17.
［22］CLAEYS X, HIPTMAIR R. Multi-Trace Boundary Integral Formulation for Acoustic Scattering by Composite Structures［J］. Communications on Pure and Applied Mathematics,2013,66（8）:1163-1201.
［23］PENG Zhen.A Novel Multitrace Boundary Integral Equation Formulation for Electromagnetic Cavity Scattering Problems［J］. IEEE Trans on Antennas and Propagation,2015,63（10）:4446-4457.