0 引 言
逆合成孔径雷达（Inverse Synthetic Aperture Radar, ISAR）旨在解决非合作运动目标的成像问题，被用于获得飞机、舰船、空间目标等的高分辨率图像［1-2］。随着技术的不断发展，应用中对高分辨ISAR 图像的需求也越来越高，如当前航天领域中的热点，空间目标态势感知，其更关注航天器部件级的识别，因此高分辨ISAR 空间目标成像越来越受关注。
由ISAR 成像原理可知，成像积累转角越大，方位向分辨率越高，但是大转角给成像处理带来的影响，必须予以考虑和解决：1）越分辨单元走动现象（Migration Through Resolution Cell, MTRC）；2）平动与转动之间的耦合增强，转动造成的MTRC对平动补偿精度产生影响［3-4］。
针对大转角成像中的散射点越距离单元走动问题，已经有一些解决方法：Keystone 变换被广泛用于散射点越距离单元走动的校正［5-6］，但是，当目标转角进一步增大而使散射点的回波包络产生弯曲时，该方法将不再适用。为此，学者们提出了极坐标格式算法［7-8］（PFA）,该算法根据中心切片定理，在目标回波的波数域将目标的扇型波数谱支撑区插值为矩形，进而采用二维逆傅里叶变换对目标图像进行重建。由于该算法允许散射点的回波包络以及多普勒产生弯曲，因此该算法适用的转角范围大于Keystone算法。除此之外，子孔径算法（SA）、卷积反投影（BP）算法等［9-10］也被提出用来解决大转角成像中的MTRC问题。
上述算法中，PFA操作简单、运算效率高，已被证实为一种可靠的大转角成像算法。但其算法效果受估计的转动参数准确性影响，这就需要先对目标的运动参数进行准确的估计。针对参数估计问题，注意到文献［11-12］在进行目标测速时运用相关处理操作，对不同时刻的距离像进行共轭相乘处理，充分利用了距离像中各个散射点的信息，具有目标回波相关系数大，噪声和杂波相关系数小的特性，并且具有强抗干扰能力。我们简称该处理为TDCM处理，考虑到雷达回波信号具有二维相干性，在本文中对ISAR 相邻回波信号进行TDCM 处理，结合最小二乘拟合，对平动参数进行估计。并且为解决大转角场景下平动与转动MTRC的耦合，在TDCM 处理的基础上进行改进，将其与PFA结合以消除大转角带来的耦合问题。
1 大转角ISAR信号模型
目标运动示意图如图1所示，目标的运动可分为平动与转动两个部分，平动过程中各散射点产生的多普勒变化相同，对成像没有贡献且会导致最终图像的散焦，需要对此分量进行补偿；转动过程则会导致散射点产生不同的多普勒变化，这也是ISAR获取方位向分辨的基础［13］。
图1 ISAR目标运动示意图
以卫星运动轨迹与雷达相位中心所在的平面为坐标平面，雷达天线相位中心为坐标原点，坐标原点至合成孔径中心点的连线为Y 轴，垂直于Y 轴方向为X 轴。用(x0(ta),y0(ta))表示ta 时刻目标中心相对于雷达的坐标，而目标上的散射点相对于其中心点的坐标表示为(xm,ym)，R0(ta)和Rm(ta)（下文简写为Rt和Rm）分别为卫星中心和卫星上任一点到雷达天线相位中心的瞬时距离值，可由下式计算得到：
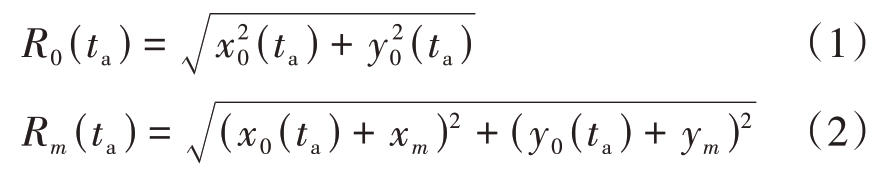
雷达发射宽带LFM 信号；假设散射点个数为M，解调后得到的二维回波信号为
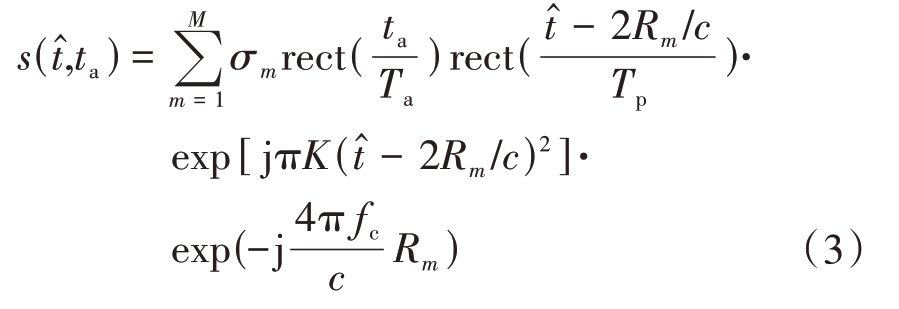
式中，σm为散射点m的后向散射系数，ta为慢时间，Ta 为合成孔径时间，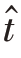
为快时间，Tp 为脉冲持续时间，Rm 为散射点m 至雷达距离，c 为光速，K 为信号调频率，fc 为信号载频。利用驻留相位定理，对式（3）作距离向脉冲压缩后得到
式中fr 为距离频率，Rr = xm sin θ(ta)+ ym cos θ(ta)表示转动分量（为便于公式推导，下文中θ(ta)写作θ，其表示转角与时间的对应关系）。理论上，在计算出平动分量RT后，即可构造平动补偿函数：
与式（4）相乘以补偿平动的影响；在小转角情况下，转动造成的MTRC（由式（4）中的分量
引起）小于距离分辨单元，Rr造成的影响可以忽略，此时直接对平动补偿后的信号进行二维傅里叶变换即可得到聚焦的图像。而在大转角运动场景下，即转角θ 较大时，
中的转动分量Rr 就需要予以考虑了，因此，为了降低转动的影响，引入PFA 算法对转动参数进行估计。
2 基于TDCM的平动补偿
2.1 TDCM 原理
在平动补偿部分，我们利用TDCM 对回波信号中的平动参数进行估计。对式（4）中不同方位脉冲时间的信号进行共轭相乘得到
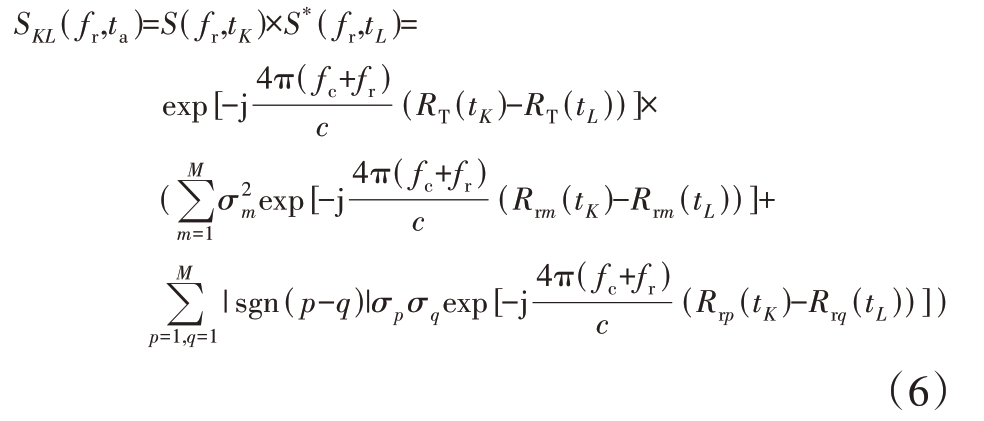
式中，tK = ta + Kτ,tL = ta + Lτ分别表示其与初始方位时间相差K、L 个脉冲（τ=1/PRF,PRF 表示脉冲重复频率），Rrm(tK)表示散射点m 在tK 时刻的转动分量。为了方便推导，假设L = 1，K = 0。式（6）中第一项代表方位时间K、L 之间的平动分量差分，故称其为平动差分项，若将目标的运动设为三次多项式形式，则其表达式如式（7）所示，其中的v、a、a1 分别表示目标径向速度、加速度、加加速度；第二项代表同一散射点在方位时间K 与L 处的转动差分，称其为自身项；第三项代表不同散射点之间的转动差分，称其为交叉项。上述两者的表达式如式（8）、式（9）所示。
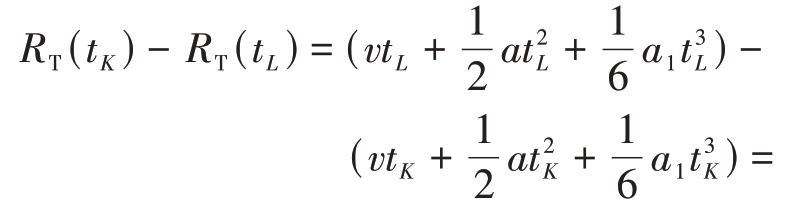
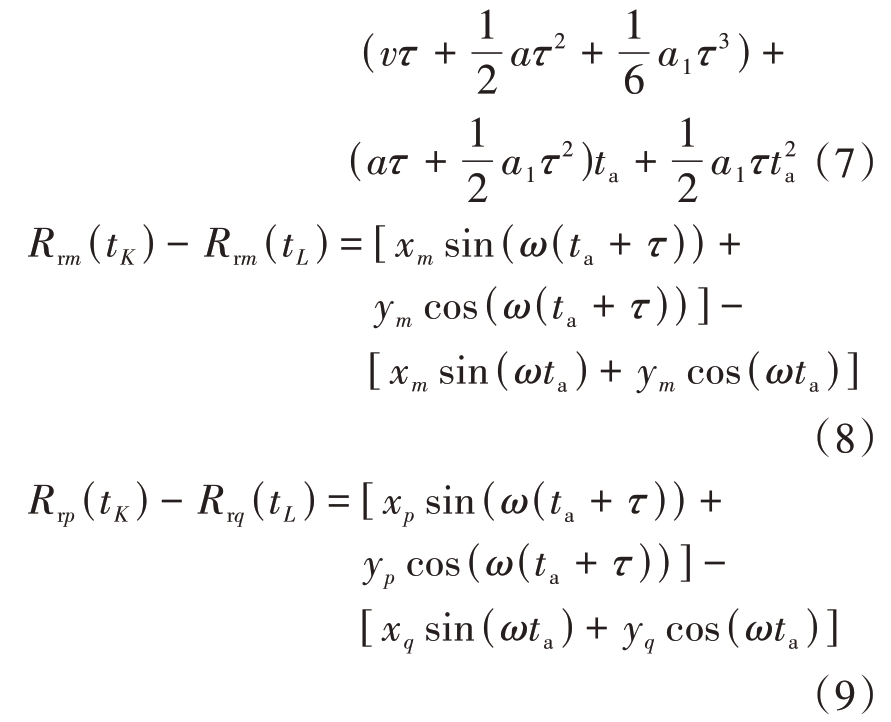
观察上式可以发现，由于一般ISAR 的脉冲间隔很小，导致式（8）的计算结果接近于0，将其代入式（6）的结果就是自身项的指数项值接近1，在信号中可将其理解为幅度为
的直流信号。而交叉项的分布则没有固定规律。此时交叉项的存在对最终平动差分项的提取会造成干扰，应当进行抑制。
对式（6）作二维傅里叶变换，将信号转换至距离-多普勒域，可看出自身项分布在频域零点位置，而交叉项则分布在整个平面上，此时只需将信号通过低通滤波器即可消除交叉项。需要注意的是，从式（8）、式（9）可以看到，对于强散射点密集的区域，位置接近的散射点数量较多，此时式（6）中交叉项的指数接近0的项增多，导致此位置的交叉项值增大，变换至频域后会使得零频附近的信号幅度增大，从整体来看就是零频位置处的信号既包含自身项又包含交叉项，通过滤波操作难以准确地将自身项与交叉项进行分离，此时可以考虑使用通带更窄的低通滤波器进行滤波以去除一部分零频附近的交叉项。
2.2 基于TDCM 的平动估计
基于TDCM的平动参数估计流程如图2所示。
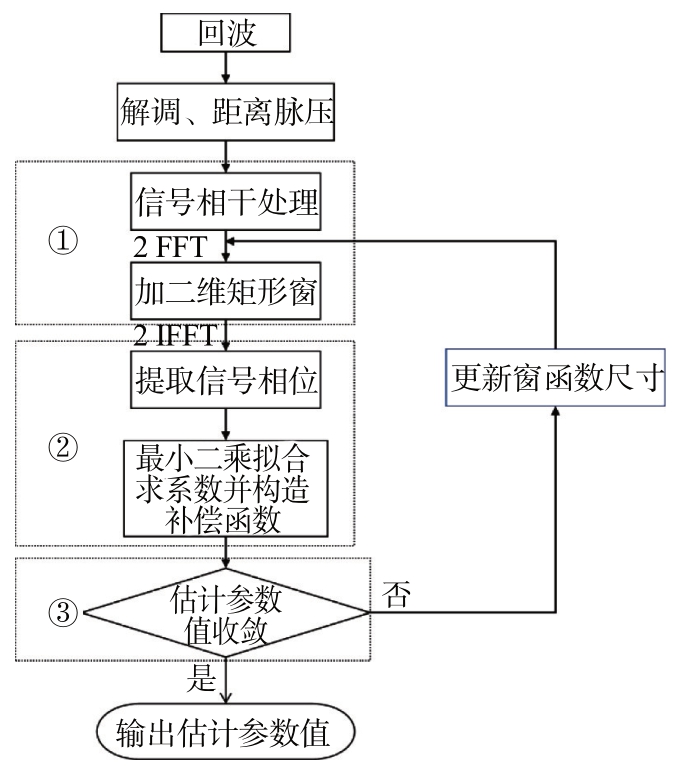
图2 算法流程图
步骤1 TDCM处理和交叉项抑制
对TDCM 处理后的信号作二维傅里叶变换得到其在距离-多普勒域的信号SRD，对信号SRD 采用二维矩形窗进行滤波，以去除交叉项的影响。
步骤2 提取包含运动参数的相位
将加窗后的信号作二维逆傅里叶变换，信号可表示为
可以看出，在方位时间维，信号为ta的二次函数，为了降低误差，可先将信号在同一距离点处进行叠加再进行系数估计。对于式（10），其相位中与时间ta 相关的一次和二次项系数可以通过函数拟合得到，据此可计算出速度a 与加速度a1；但其常数项
因存在相位缠绕问题无法直接得到［14-15］，为此需要先对式（10）做方位向FFT，得到其表达式为
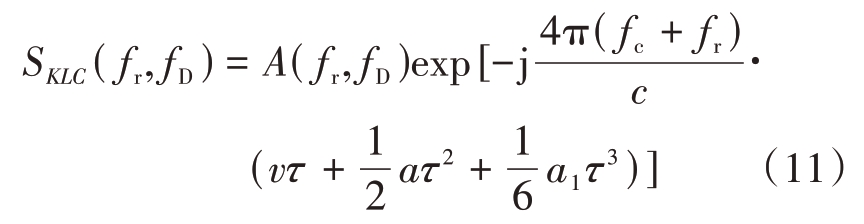
式中
为实信号，此时信号相位中的(vτ +
与距离频率成线性关系，同样使用函数拟合的方法即可求得其斜率值，结合以上计算得到的加速度和加加速度值，已可估计出目标的平动参数，因为此时并未考虑大转角情况下转动引起MTRC的影响，此时估计得到的参数值并不精确。
步骤3 估计参数值收敛
通过以上两步操作，可得到估计的目标平动参数(v,a,a1)的初步估计，然后通过迭代，逐步优化窗函数，相应优化对平动参数的估计，直至收敛。
3 联合TDCM与PFA的ISAR成像算法
第2 节对本文所用的平动补偿方法进行了阐述，由于在整体算法中涉及到的平动、转动解耦操作先于转动参数估计部分，即首次使用PFA 插值时目标的转动参数是未知的，为此，下面首先对转速失配时PFA 算法的有效性进行讨论；之后结合实际的大转角成像场景对算法整体流程进行说明。
3.1 转速失配时的PFA算法有效性分析
当前关于大转角下校正MTRC 与进行转动估计的方法有很多，如PFA、BP、SA算法，本文选择其中运算效率高、操作简单的PFA 算法。但需要注意的是，使用PFA 算法时，要消除方位二次以上相位对成像的影响，必须准确知道目标的转动参数。
下面首先介绍在转动参数未知时，仍然使用PFA 算法对结果造成的影响。假设信号进行PFA插值前已进行平动粗补偿，即此时式（4）可写为
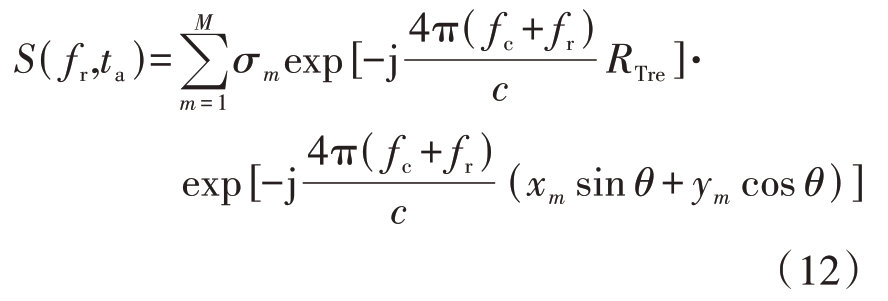
式中RTre表示补偿后的剩余平动分量。
假设转角真实值θ = aθe +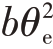 
，θe 为均匀变化的估计转角，即估计值与真实值之间为二次函数关系 ，令 Kx = Kr sin θe，Ky = Kr cos θe，Kr =
，则式（12）的第二个指数项进行泰勒展开可写为
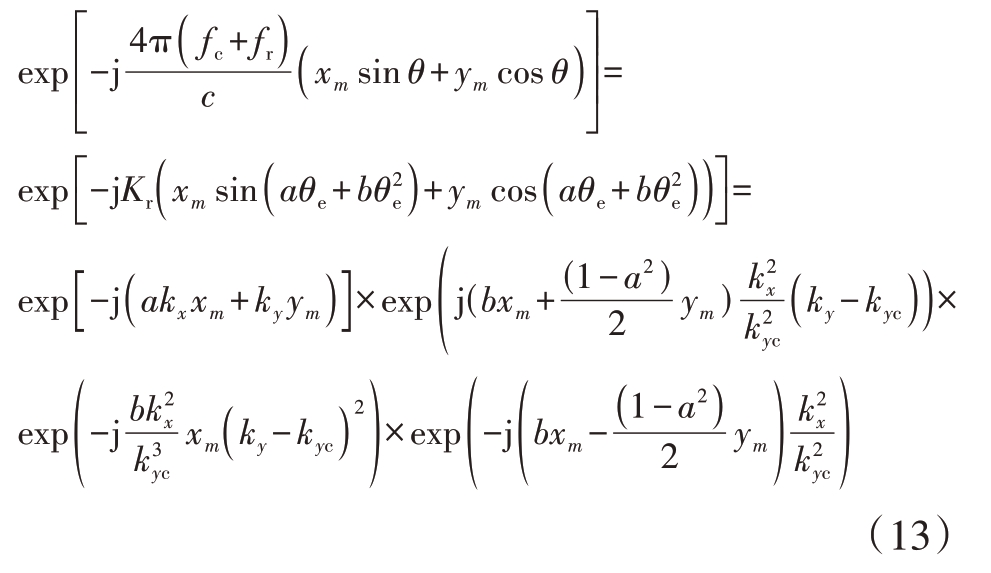
式中，kyc 为距离向波束中心。式（13）中第一个指数项表示散射点的聚焦位置项，第二个指数项表示用估计转角进行插值后的二次距离弯曲项，第三个指数项表示转动校正不完全引起的距离向散焦项，第四个指数项表示方位二次相位项。由式（13）可见，在转动参数未知时，转动引起的线性徙动仍可以被校正,一定程度上降低了平动与转动之间的耦合，但由于高次项的存在，剩余的转动分量仍会对成像结果造成影响。
大转角成像场景中，对目标进行平动补偿时，转动分量Rr = xm sin θ(ta)+ ym cos θ(ta)随着转角θ的增加，其造成的MTRC 不可忽略，使用TDCM 进行平动补偿时估计的平动分量包含转动造成的MTRC，平动补偿精度降低，式（12）中的剩余平动项不再等效为1。但即使存在剩余平动的影响，PFA仍然可以校正大部分的转动，因此本文提出先通过PFA 降低二者的耦合，在后续的迭代中逐步提高运动补偿精度，并进一步提高MTRC 校正精度。
3.2 TDCM-PFA联合成像算法
算法整体流程如图3所示，下面对其中几个关键步骤进行说明。
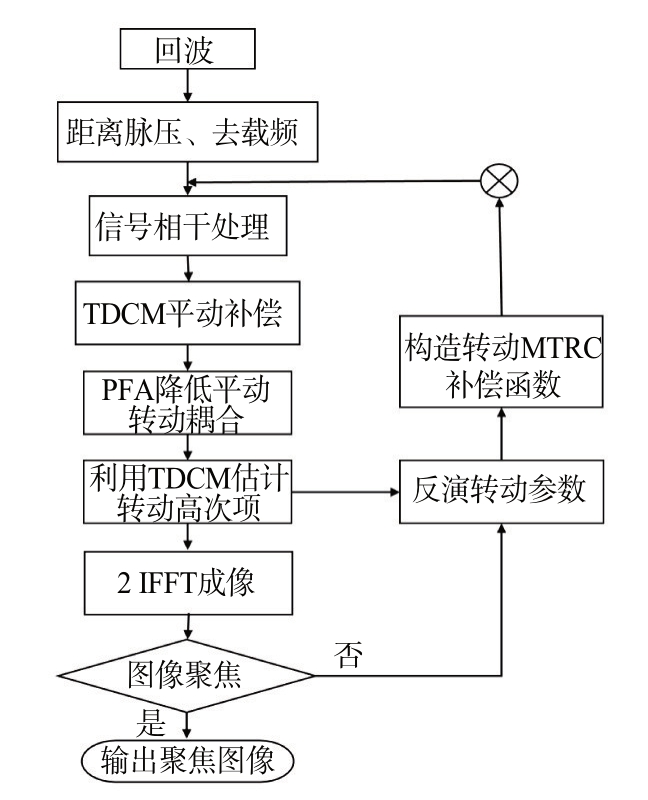
图3 TDCM-PFA大转角ISAR成像算法流程图
1）平动估计：对应迭代开始阶段的TDCM 平动补偿，随着迭代的进行，估计的平动参数会逐渐接近准确值。
2）转动估计：观察式（13），结合实际情况，对空间目标而言，其运动状态相对平稳，故可假设目标匀速转动，即插值使用的估计转角θe 与真实值θ 之间的关系变为线性关系，此时式（13）可表示为
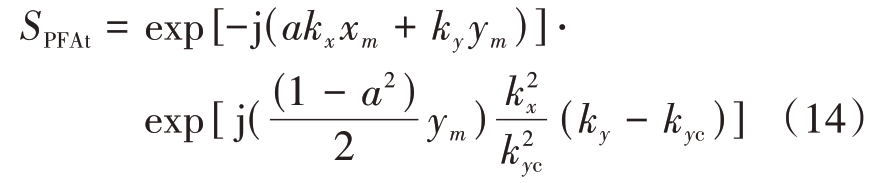
对距离向做FFT得到
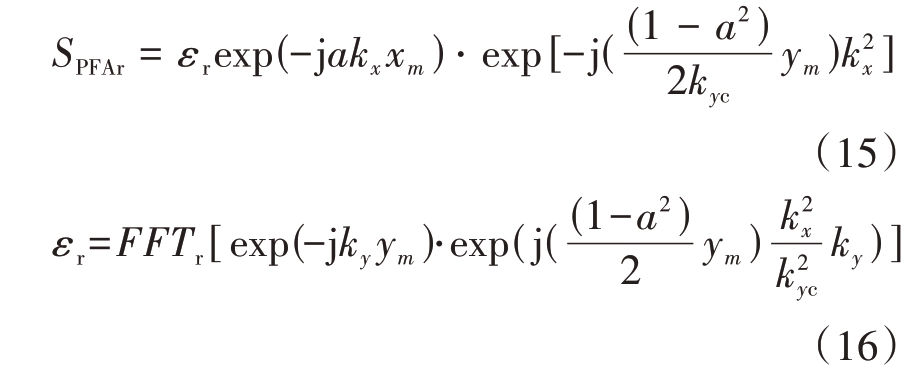
对式（15）作TDCM 处理可求得方位调频率值
，进而可利用θe 与θ 的对应关系估计转动参数：假设式（12）中第k个距离单元对应的方位调频率为γk，为使结果更加准确，对每个距离单元对应的参数求均值得
由此可得到转角θ的粗估计值。
3）迭代成像直至聚焦：上述两步分别对平动和转动分量进行了粗估计，随着迭代的进行，目标的转动参数估计值逐步收敛，此时可认为图像随着参数估计值的收敛达到聚焦条件，转动引起的MTRC 已得到良好校正，同时平动补偿的精度也随着迭代得到提高。
4 实验验证
本节对前文提到的算法进行实验验证，包括转速失配时PFA 有效性、TDCM 在平动补偿中的有效性及TDCM-PFA 成像算法验证，具体实验安排如下。
4.1 转速失配时PFA成像性能分析
为验证3.1 节中关于转速失配时使用PFA 进行插值仍然具有有效性的结论，本节在转速失配的条件下设置了以下仿真实验：其中雷达仿真参数如表1 所示，图4（a）为散射点模型，图4（b）为仿真过程中目标的运动轨迹，图4（c）为原始信号脉冲压缩处理后的结果，图4（d）为在PFA 插值操作前进行运动补偿后的信号脉压线，图4（e）和图4（f）分别为真实值插值与转角未知时使用估计值进行插值得到的结果，可以看到后者中由转动引起的MTRC 也在一定程度上被校正，由此可以验证3.1节中结论的正确性。
表1 雷达仿真参数
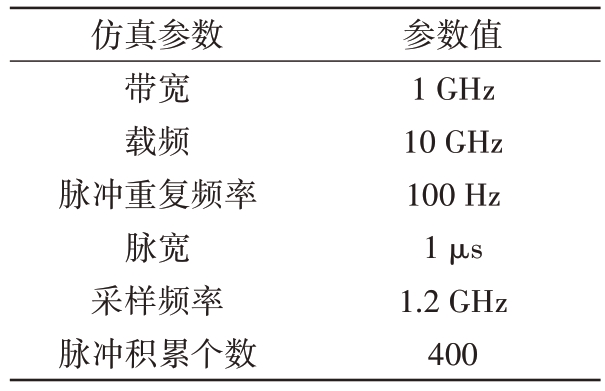
仿真参数带宽载频脉冲重复频率脉宽采样频率脉冲积累个数参数值1 GHz 10 GHz 100 Hz 1 μs 1.2 GHz 400
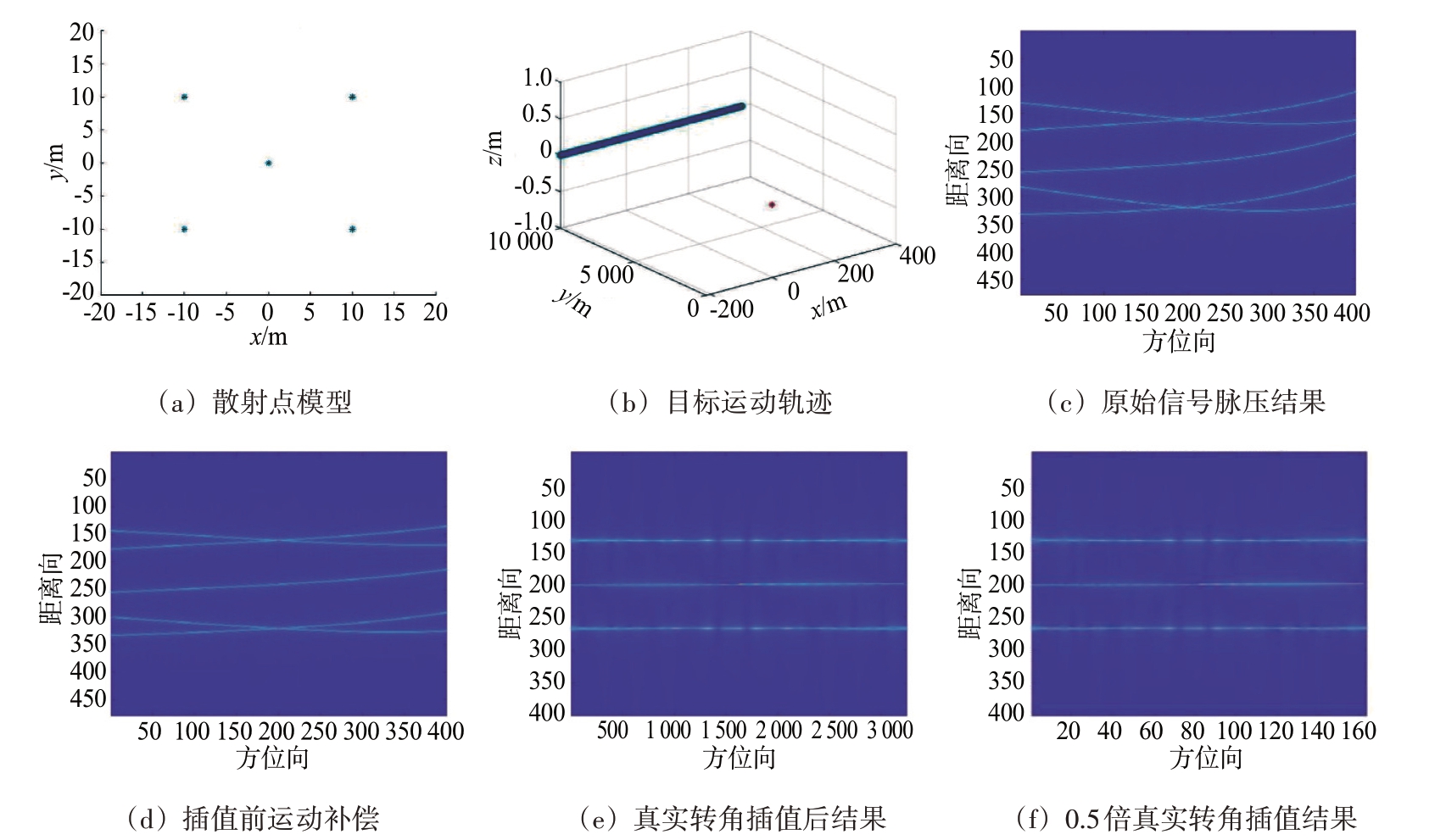
图4 转速失配时极坐标格式插值算法效果
4.2 TDCM 平动补偿处理结果与分析
本节为对TDCM方法有效性与正确性的验证，仿真仍使用表1 的雷达仿真参数，图5（a）和图5（b）为TDCM 操作后信号的平动差分项、自身项与交叉项在RD 平面上的分布情况，可以看出，由于交叉项的影响，平动差分项无法被直接提取；图5（c）为通过TDCM 处理后对该项进行拟合得到的平动差分值与理论值对比，可以看出，二者之间的差距较小并且其函数曲线与上文中推导的其为二次函数的结论相符；据此可估计出目标的平动参数并拟合出其径向运动曲线如图5（d）所示；图5（e）中显示了理论值与拟合值之间的残差；图5（f）为平动补偿后的脉压线，可以看出在转动不大的情况下，此时的平动分量已基本被校正，剩余误差主要是由转动引起的线性距离徙动及高次项。
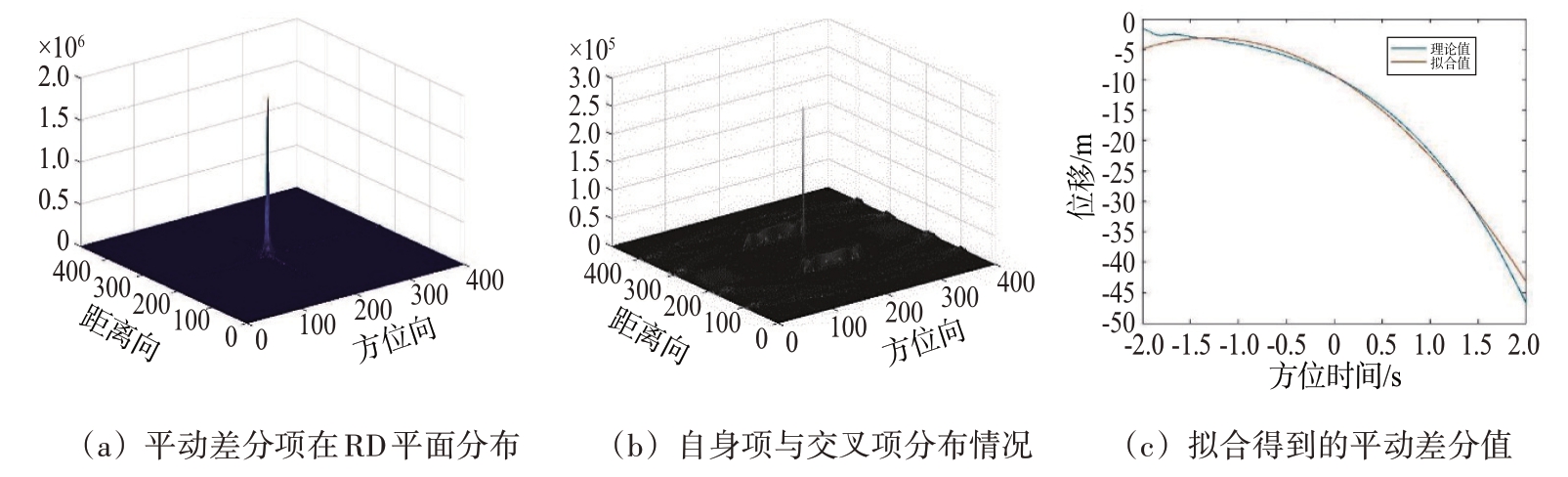
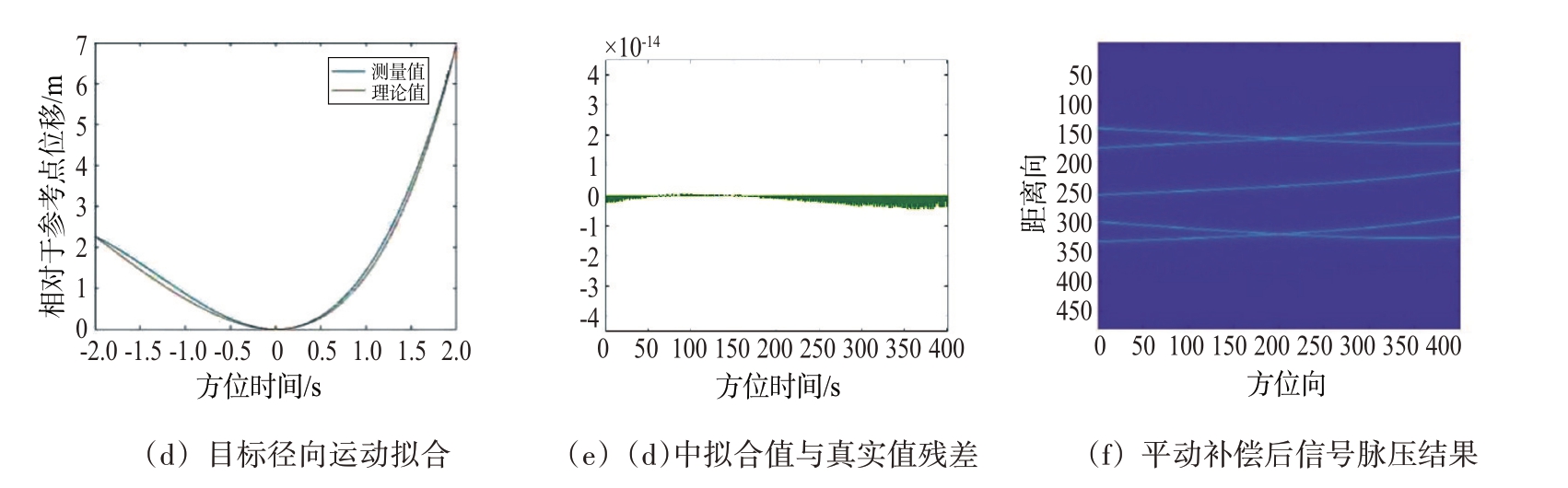
图5 时域信号共轭相乘方法仿真实验
4.3 TDCM-PFA成像算法验证
下面通过实验验证TDCM-PFA 成像算法的有效性。设置卫星的散射点模型如图6（a）所示，帆板宽度设置为1.16 m（X轴方向上散射点间隔0.29 m），长度设置为10 m（Y轴方向帆板部位散射点间隔为1 m，卫星主体部位散射点间隔为0.5 m）；雷达参数设置如表2所示，设置目标转动速度为0.1 rad/s，使用STK 软件在J2000 坐标系下设置目标与雷达的轨道参数如表3所示。
表2 雷达仿真参数
仿真参数带宽载频脉冲重复频率采样频率脉冲积累个数参数值3 GHz 10 GHz 100 Hz 3.6 GHz 8 192
表3 轨道参数设置
轨道参数目标星雷达初始位置/km（3 718.7,41 832.2,0）（3 434.72,41 659.2,0）飞行速度/（km·s-1）（-3.042 09,0.275 137,0）（-3.044 66,0.282 143,0）
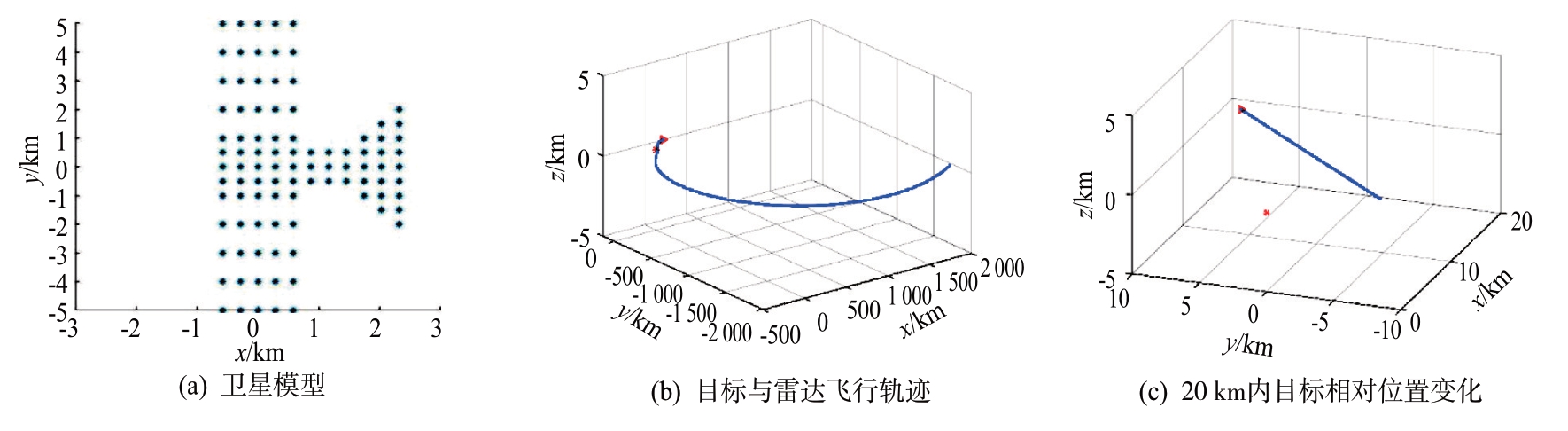
图6 TDCM-PFA联合成像算法仿真结果
在目标可见时间段内相对运动轨迹如图6（b）所示，为适应成像需求，图6（c）选取20 km 内二者间的相对位置变化；图6（d）为使用传统PFA大转角成像算法得到的成像结果；图6（e）～（g）分别表示迭代1、3、5 次后得到的图像并定标的结果，在三次迭代中，估计的目标转速分别为0.086，0.094 和0.105 rad/s，第5 次迭代之后，估计的转动参数值收敛，故可以认为第5 次估计到的转动参数值即为最终估计结果，其误差为0.005；在成像所需时间上，直接使用PFA 成像方法所用时间为2.151 s，三次迭代成像所用时间分别为2.512，3.164 和4.223 s，可以看出，即使需要另外进行转动估计，算法所用时间也和传统PFA 方法在一个数量级。为比较迭代过程中散焦的校正情况，图6（h）为本文算法第一、第三、第五次迭代以及传统PFA 算法成像结果中相同帆板位置（即图6（e）红色边框位置）的成像效果对比，可以看出，即使在第一次迭代中，本文提出算法的效果也要优于传统算法，并且随着迭代的进行，目标转动引起的MTRC 逐步被校正，对其进行量化：使用图像熵作为衡量图像聚焦性的标准，一般而言，图像熵值越小，图像聚焦效果越好，相对于传统方法成像6.556 的图像熵值，三次迭代中得到的图像熵值分别为6.541，6.210 和6.121，也可以验证方法的有效性。
5 结束语
针对大转角ISAR 成像过程中的平动转动耦合问题，本文提出了一种基于TDCM与PFA结合的迭代补偿成像算法。文章对两种基本算法的原理进行了解释与散射点仿真实验，结果验证了二者在补偿平动和校正转动时的有效性，得出PFA 在转速失配的情况下仍可一定程度上校正转动的结论，且通过推导发现PFA 插值后的剩余转动分量可以通过TDCM处理估计并由此计算出转动角度。基于此，文章在之后部分提出了利用TDCM 和PFA通过迭代的方式逐步估计出目标的准确平动与转动参数，并且通过仿真实验说明了该方法的可行性。
［1］ANGER S, JIROUSEK M, DILL S, et al. ISAR Imaging of Space Objects Using Large Observation Angles［C］//2021 21st International Radar Symposium, Berlin, Germany:IEEE,2021:1-7.
［2］DING Zegang, LIU Siyuan, LI Yinchuan, et al. Parametric Translational Compensation for ISAR Imaging Based on Cascaded Subaperture Integration with Application to Asteroid Imaging［J］. IEEE Trans on Geoscience and Remote Sensing,2020,60:1-17.
［3］LIU Lei, ZHOU Feng, TAO Mingliang, et al. Adaptive Translational Motion Compensation Method for ISAR Imaging Under Low SNR Based on Particle Swarm Optimization［J］.IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2015, 8（11）:5146-5157.
［4］侯颖妮，谢洁.稀疏采样数据大转角高分辨ISAR 成像技术研究［J］.雷达科学与技术，2021，19（5）：604-609.
［5］PERRY R P, DIPIETRO R C, FANTE R L. SAR Imaging of Moving Targets［J］.IEEE Trans on Aerospace and Electronic Systems,1999,35（1）:188-200.
［6］SAKIN A O, SONGUR A C, ONAT E. Combining Genetic Algorithm Based Joint Time-Frequency Analysis and Keystone Transform for ISAR Image Enhancement［C］// 14th European Conference on Synthetic Aperture Radar,Leipzig,Germany:VDE,2022:1-6.
［7］GONG Rui, WANG Ling, ZHU Daiyin. High Resolution 3D InISAR Imaging of Space Targets Based on PFA Algorithm with Single Baseline［C］//2023 24th International Radar Symposium,Berlin,Germany:IEEE,2023:1-10.
［8］SONG Yue, HAI Yu, WU Junjie, et al. An Efficient PFA Subaperture Algorithm for Video SAR Imaging［C］//2021 IEEE International Geoscience and Remote Sensing Symposium,Brussels,Belgium:IEEE,2021:5179-5182.
［9］CHEN Jiajia, WANG Duo, WANG Kaizhi. Sensor-Based Motion Compensation Methods of Back Projection Algorithm in SAR［C］// 2023 IEEE International Geoscience and Remote Sensing Symposium,Pasadena,CA,USA:IEEE,2023:4395-4398.
［10］HE Chi, DENG Yuhui, SUN Guangcai, et al. Multi-Subaperture Interference for SAR Autofocusing［C］// 2023 IEEE International Geoscience and Remote Sensing Symposium,Pasadena,CA,USA:IEEE,2023:4536-4539.
［11］包云霞，毛二可，何佩琨.基于一维高分辨距离像的相关测速补偿算法［J］.北京理工大学学报，2008，28（2）:160-163.
［12］李民.基于压缩感知的雷达高分辨成像技术研究［D］.哈尔滨：哈尔滨工业大学，2014.
［13］保铮，邢孟道，王彤.雷达成像技术［M］.北京：电子工业出版社，2005.
［14］XIAO Mingxi, WANG H, WU Sili, et al. Interferometric SAR Phase Unwrapping Method Based on Improved Markov Energy Model［C］//2022 3rd China International SAR Symposium,Shanghai,China:IEEE,2022:1-5.
［15］LI Yuhe, CHEN Yanxiang, TONG Xiaolei, et al. Phase Unwrapping by K-Means Clustering in Three-Dimensional Measurement［C］//2013 Third International Conference on Instrumentation, Measurement, Computer, Communication and Control,Shenyang,China:IEEE,2013:65-69.