0 引 言
近年来，随着我国基础建设的不断发展，对城市地下空间进行了一系列的改造，在各种社会行为和自然因素的影响下，导致城市地下空洞的滋生。地下空洞往往会引发路面塌陷等病害发生，对工程施工及城市交通安全构成极大的威胁。除此之外，由于这些空洞具有极高的隐蔽性、较大的危害性等特点，因此，在城市道路施工前准确地检测和识别这些空洞显得尤为重要［1-2］。探地雷达是一种重要的地下管道和空洞探测手段，在勘探中往往会遇到成像不清的问题，对其进行精细化的成像分析十分重要。
探地雷达（GPR）是一种利用天线发射和接收电磁波来研究介质内部物理性质和分布规律的地球物理勘探方法。通过软件对接收到的电磁回波进行分析，从而能够精确地判断出地下目标体的几何形态及空间位置［3-5］。国内外学者针对雷达扫描图像展开了深入的研究，张鹏等［6］利用双曲线模型对三点定圆管径计算方法的可靠性进行了实证检验，结果表明管径的准确性与GPR 图像的成像质量密切相关；杨军等［7］采用室内管线模型实验研究了地下管线的雷达波传播规律及特征，结果表明金属管线的反射波能量最强，含水管线会引起多次波；Sagnard 等［8］和Ahmadi 等［9］通过模板匹配技术实现了管道双曲线的准确定位，验证表明检测效果良好；Li 等［10］通过利用双曲线模型的相对角度特性，精确地计算出了管道的半径和埋深；周黎明等［11］采用探地雷达对道路地下异常体进行正演模拟和时频特征提取，结果表明地下空洞顶界面的反射波呈弧形，空洞区域的中心频率集中在低频区间；刘洋洋等［12］采用GprMax 软件模拟管道的雷达正演图谱，研究管道雷达图谱的波形特征，得到管道与雷达图谱的对应关系；李世念等［13］基于GprMax 软件研究不同填充空洞参数对探地雷达的正演模拟的影响，得到了不同填充空洞的判别依据；韩俊涛［14］对路基病害模型进行正演模拟，结果表明矩形空洞边界呈现一段水平弧段，两端为双曲线特征。
综上所述，目前国内外研究人员主要是以管线特征和双曲线模型为研究基础，对异常体扫描曲线的精细化分析并不多见。本文拟以地下矩形空洞为研究对象，通过对雷达贴地运动过程中电磁回波收发特性的研究，建立雷达移动距离与成像曲线厚度的对应关系，并深入研究不同大小的矩形空洞的电磁波传播特性，并以探测实例对其成像曲线厚度规律进行验证。
1 地下矩形空洞成像曲线厚度计算
1.1 地下矩形空洞成像原理
探地雷达在某一位置向地下发射高频电磁波，这种波在地下传播时，遇到不同介质会发生反射，并被天线接收，从而得到回波信号。随着地质雷达运行至下一位置，天线接收到新的回波信号。最后通过图像处理软件，把接收到的所有信号转换成空洞的探测曲线［15-16］。
如图1所示，探地雷达勘探过程中，当在位置1进行扫描时，其扫描范围为一扇形，因此可以检测到B 点的空洞，该空洞的反射特征点在剖面图中A处显示；当探地雷达在位置2 处时，就进行垂直探测，反射特征点在剖面图中B 处显示；当探地雷达移至位置3 时，在剖面图C 处显示空洞反射特征点［17-18］。
图1 地下空洞扫描成像原理图
1.2 地下空洞成像分析模型
当探地雷达贴近地表探测时，假定发射器与接收装置处于同一位置，电磁波在地下均匀介质中传输，电磁波信号接触空洞后，立即反射回接收天线。
如图2 所示，矩形空洞ABCD 上顶边中点E 在雷达地表探测线上的投影点为x0；雷达在x0 位置探测时有效信号区域如图中阴影部分所示；其回波延时为
，并且
为雷达在x0 位置探测时接收到的第一个回波延时，
是雷达探测接收到信号时的最短距离，即为空洞埋深，
为雷达在x0 位置探测时接收到的最后一个回波延时，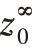
是雷达探测收到信号时的最长距离；其余雷达水平位置是xi；相应地回声延时是
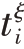；矩形空洞的顶边长度为2a；侧边长为b；假定天线发出的电磁波波束角是2θ，地下介质为均匀介质，那么波速v 将保持不变。
图2 矩形空洞扫描曲线分析图
1.3 矩形空洞成像曲线阶段方程
以雷达在地表探测时的x0 位置为原点，雷达水平运动方向为横轴，向右为正；电磁波回波延时为纵轴，向下为正，构建坐标系如图3 所示。由于空洞为关于纵轴t 对称的图形，因此分析对称轴右侧图像即可。
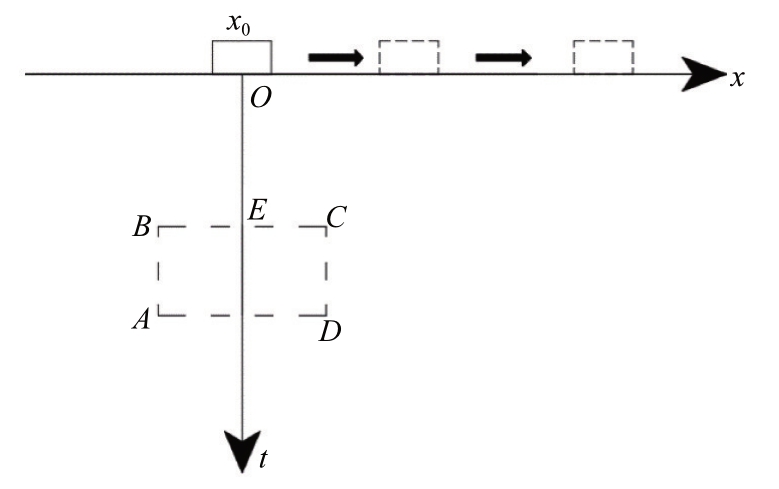
图3 矩形空洞扫描曲线坐标系图
由文献［19］可知，该文以雷达接收到的第一个信号的回波延时与水平距离建立矩形空洞成像曲线方程，且曲线方程划分为三个阶段，各阶段划分图如图4所示，阶段方程如式（1）、式（2）、式（3）所示。
图4 矩形空洞扫描曲线阶段划分图
式（1）～（3）中水平距离x为自变量，回波延时t为因变量，其余均为常数，此时公式中的回波延时t 应是雷达在x处扫描时收到的第一个回波延时t1。
现以水平距离x 与雷达接收的最后一个回波延时t∞建立各阶段曲线方程，各阶段划分如图5所示。矩形空洞成像曲线第一阶段方程是指空洞E点正上方x0 处到雷达发射波的最大波束角扫描到空洞左下顶点A时对应的x1位置；第二阶段是指x1到雷达发射信号最大扇形面半径扫描到矩形右下顶点D时相对应的x2处。
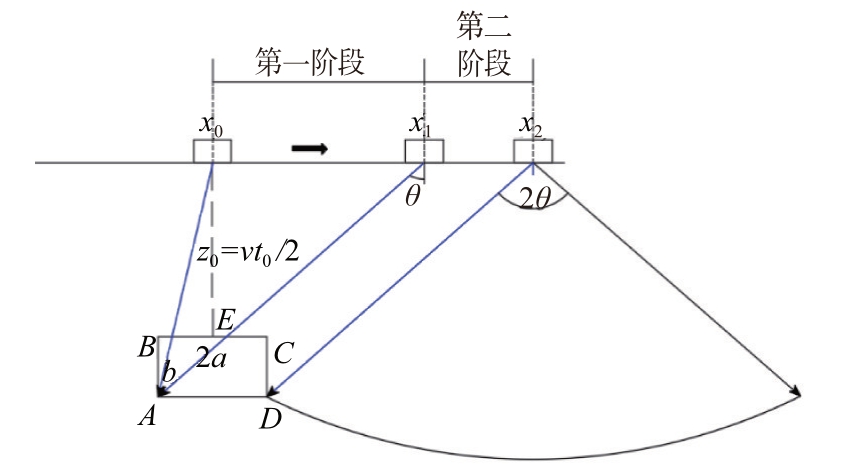
图5 矩形空洞扫描曲线阶段划分图
以雷达距x0 位置的水平距离为自变量、最后一个回波延时为因变量，雷达扫描矩形空洞建立的第一阶段如图6所示。
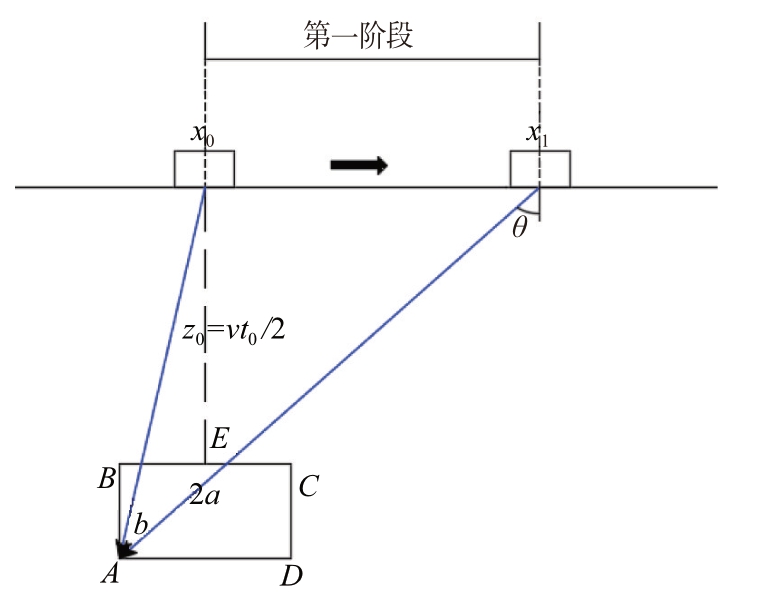
图6 矩形空洞扫描曲线第一阶段图
依据三角形勾股定律，可以得出如下等式：
把z0 = vt0/2，z = vt/2 代入式（4）可得第一阶段曲线方程：
式（5）是以水平距离x 为自变量，最后一个回波延时t为因变量的双曲线方程。
以最后一个回波延时计算时，雷达扫描矩形空洞第二阶段如图7所示。
图7 矩形空洞扫描曲线第二阶段图
根据平行四边形法则可得
化简得
式（7）是以水平距离x 为自变量，最后一个回波延时t为因变量的水平直线方程。
1.4 矩形空洞成像曲线厚度方程
各阶段曲线厚度划分如图8所示，曲线厚度方程为雷达在任一处时所接收的最后一个回波延时减去第一个回波延时，即曲线厚度方程为δ = t∞-t1。
图8 矩形空洞扫描曲线厚度阶段划分图
由图8可知，第一阶段曲线厚度方程为最后一个回波延时t∞的第一阶段方程减去第一个回波延时t1的第一阶段方程,即式（5）减去式（1）：
第二阶段曲线厚度方程为最后一个回波延时t∞的第一阶段方程减去第一个回波延时t1 的第二阶段方程,即式（5）减去式（2）：
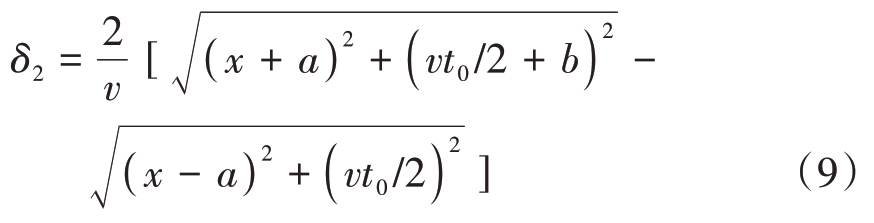
由于雷达电磁波的波束角为2θ，那么第三阶段曲线厚度方程与矩形空洞的大小有关，当2a/b ＞tan θ 时，第三阶段曲线厚度方程为最后一个回波延时t∞的第二阶段方程减去第一个回波延时t1 的第二阶段方程；当2a/b ＜tan θ 时，第三阶段曲线厚度方程为最后一个回波延时t∞的第一阶段方程减去第一个回波延时t1的第二阶段方程，则第三阶段曲线厚度方程为
第四阶段曲线厚度方程为最后一个回波延时t∞的第二阶段方程减去第一个回波延时t1 的第三阶段方程，即式（7）减去式（3）：
综上所述：当雷达发射信号最大扇形面半径恰好穿过矩形空洞对角线时，即空洞大小满足2a/b = tan θ，此时矩形空洞曲线厚度方程划分为三个阶段，各阶段厚度方程分别为式（8）、式（9）、式（11）；当雷达发射信号最大扇形面半径未穿过矩形空洞对角线时，即空洞大小不满足2a/b = tan θ，此时矩形空洞曲线厚度方程划分为四个阶段，各阶段厚度方程分别为式（8）、式（9）、式（10）、式（11）。
2 矩形空洞成像曲线厚度因素分析
2.1 雷达运行时矩形空洞成像厚度分析
当探地雷达从x0处沿x轴正方向扫描时，那么各阶段方程中x 一直在增加，此时水平距离x 为自变量，厚度δ为因变量。
对式（8）中x求导有
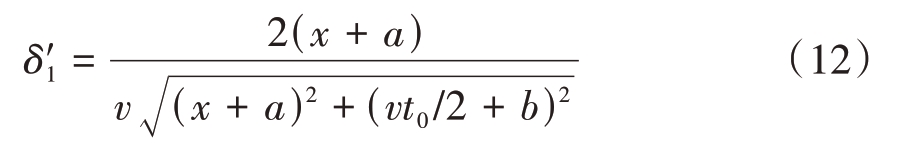
对式（9）中x求导有
对式（10）中x求导有
对式（11）中x求导有
当探地雷达在原点从左往右运行时，那么各阶段方程中x 一直在增加，根据式（12）和（13）可知厚度δ 对x 的一阶导数大于零，函数为增函数，因此第一和第二阶段曲线厚度随x 增加而增大；根据式（14）和（15）可知δ 对x 的一阶导数小于零，函数为减函数，因此第三和第四阶段曲线厚度随x 增加而减小。综上分析当雷达在x0 处从左往右扫描时，图像曲线厚度先增加至最大后减小至零，实际矩形空洞对角线附近为图像曲线厚度最大处。
2.2 矩形空洞大小对成像厚度影响分析
矩形空洞在地层中的大小信息具有重要意义，矩形空洞大小的变化必然会引起探地雷达成像特征形态上的变化。通过对各阶段成像曲线厚度的具体变化进行分析，从而得到不同大小的矩形空洞成像上的差异。当探地雷达在不同阶段进行点测相同埋深不同大小矩形空洞时，此时x为定值，a或b为自变量，δ为因变量。
当矩形空间的顶边增加时，代表各公式中a值变大，此时自变量为a。对式（8）中a求导有
对式（9）中a求导有
对式（10）中a求导有
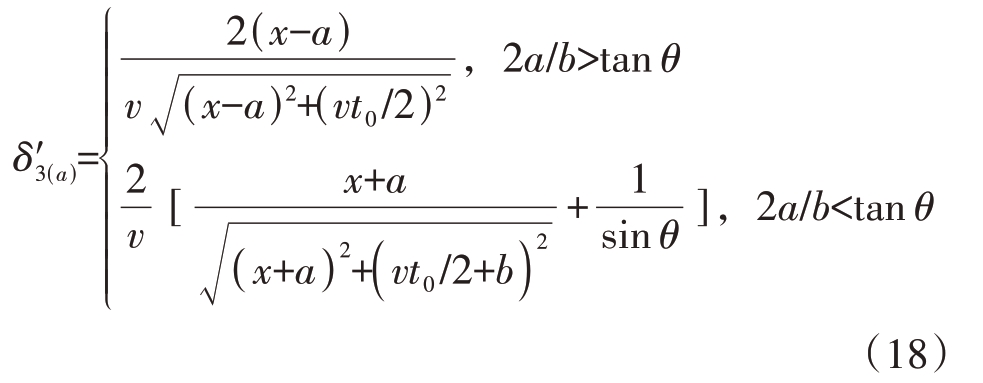
对式（11）中a求导有
当探地雷达在不同阶段进行点测时，根据公式（16）～（19）可知厚度δ 对x 的一阶导数均大于零，函数为增函数，因此各阶段曲线厚度随顶边长增加而增大。
当矩形空间的侧边长b 增加时，此时自变量为b，分别对式（8）、式（9）、式（10）、式（11）中b 求导有
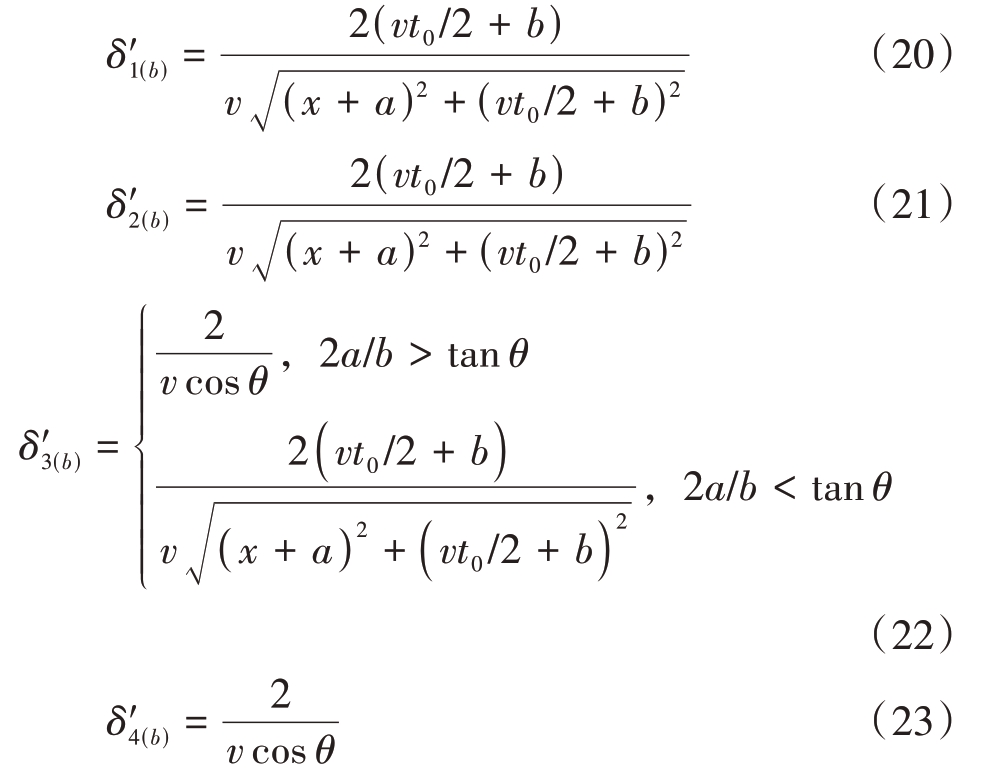
当探地雷达在不同阶段进行点测时，根据公式（20）～（23）可知厚度δ 对b 的一阶导数均大于零，函数为增函数，因此各阶段曲线厚度随侧边长b增加而增大。
综上可得各阶段曲线厚度对矩形空洞大小参数的一阶导数均大于零，因此当仅考虑矩形空洞大小参数变化时，雷达成像曲线厚度随矩形空洞变大而增加，即同一条件下的空洞越大图像成像曲线线条越粗。
3 试验验证
本次室内试验探测模型箱尺寸为2 m×2.5 m×1.2 m，矩形空洞尺寸分别为300 mm×250 mm×200 mm（1 号）和180 mm×180 mm×180 mm（2 号），如图9所示。
图9 矩形空洞图
本次试验仪器采用GSSI美国劳雷地质雷达，使用3207A型探测天线，天线频率为400 MHz，其空洞上覆土层深度为10 cm，探测深度为0.8 m，其探测过程如图10 所示。图11 和图12 分别为采用地质雷达探测模型箱内1 号和2 号矩形空洞的扫描图，结合埋置深度和测线布置情况将空洞长高剖面图实际位置绘制如上。
图10 雷达探测图
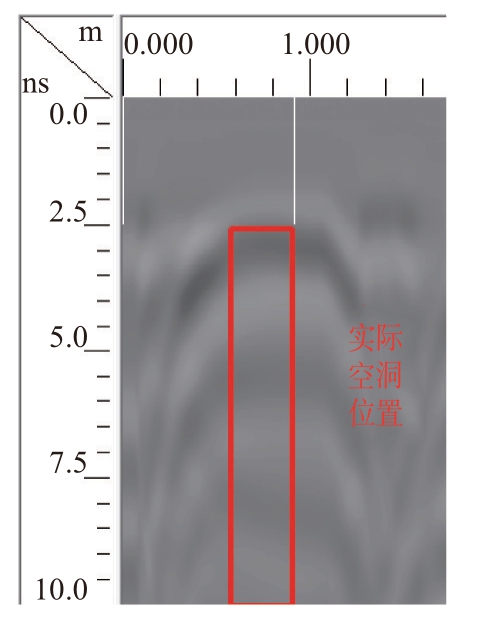
图11 1号矩形空洞雷达实测图
图12 2号矩形空洞雷达实测图
由图11 和图12 可知空洞顶点均在2.5 ns 处，整体曲线厚度基本都符合先从零增加至最大后减小的对称曲线，其曲线厚度最大处均在图像水平弧段两端，在实际空洞对角线附近；对比图11和图12 可知，图11 成像曲线线条厚度略大于图12 且在曲线中部时较明显，前文理论分析与实际矩形空洞成像曲线厚度变化规律基本吻合。
4 结束语
本文通过时域有限差分法，对矩形空洞的成像机制进行深入研究，并对其成像厚度规律进行分析与总结。其结论如下：1）在以水平运动方向为横轴、回波延时为纵轴的坐标系中，成像曲线厚度应为最后一个回波延时减去第一个回波延时，其厚度方程划分与矩形大小有关，一般为可划分为四个阶段且各阶段方程均为曲线方程。2）当雷达在空洞中心正上方从左往右扫描过程中，成像曲线厚度在第一、第二阶段内逐渐增加，且厚度最大处在矩形空洞对角线附近，在第三、第四阶段内逐渐减小，最后减小至零。当仅考虑矩形空洞大小变化时，图像曲线厚度随空洞变大而增大，即矩形空洞越大时，在雷达图像上表现为曲线线条越来越粗。3）本文推导的图像曲线厚度变化方程具有一定的局限性，在地质雷达探测分析时将空洞简化为矩形空洞，未考虑空洞形状、雷达参数等。
［1］郭士礼，段建先，张建锋，等.探地雷达在城市道路塌陷隐患探测中的应用［J］.地球物理学进展，2019，34（4）:1609-1613.
［2］刘国超，彭卫平，杨水华，等.地质雷达+三维测量内窥镜的城市道路病害检测与应用［J］.测绘通报，2022（7）:134-137.
［3］刘澜波，钱荣毅.探地雷达:浅表地球物理科学技术中的重要工具［J］.地球物理学报，2015，58（8）:2606-2617.
［4］张宏萄，张智慧，许强.地质雷达技术在地铁整体道床病害检测中的应用［J］.工程地球物理学报，2021，18（5）:709-715.
［5］蔡勤波，田学军，穆建强，等.探地雷达在城市道路病害探测中的应用［J］.勘察科学技术，2023（5）:56-59.
［6］张鹏，董韬，马彬，等.基于探地雷达的地下管线管径探测与判识方法［J］.地下空间与工程学报，2015，11（4）:1023-1032.
［7］杨军，李婷，袁忠明，等.管线模型的探地雷达物理模拟实验［J］.地球物理学进展，2023，38（2）:912-927.
［8］SAGNARD F, TAREL J P. Template-Matching Based Detection of Hyperbolas in Ground-Penetrating Radargrams for Buried Utilities［J］. Journal of Geophysics and Engineering,2016,13（4）:491-504.
［9］AHMADI R, FATHIANPOUR N. Estimating Geometrical Parameters of Cylindrical Targets Detected by Ground-Penetrating Radar Using Template Matching Algorithm［J］.Arabian Journal of Geosciences,2017,10（6）:1-13.
［10］LI Shuai, CAI Hubo, ABRAHAM D M, et al. Estimating Features of Underground Utilities: Hybrid GPR/GPS Approach［J］. Journal of Computing in Civil Engineering,2016,30（1）:1-12.
［11］周黎明，张杨，付代光，等.道路地下空洞探地雷达波场和时频特性［J］.同济大学学报（自然科学版），2024，52（1）:77-85.
［12］刘洋洋，尹奇峰，倪圣军，等.地质雷达正演模拟及其在地下管道探测中的应用［J］.给水排水，2022，58（S2）:532-536.
［13］李世念，王秀荣，林恬，等.基于GprMax 的道路空洞三维探地雷达正演数值模拟［J］.中国地质灾害与防治学报，2020，31（3）:132-138.
［14］韩俊涛.铁路路基病害的地质雷达正演模拟与探测方法研究［D］.北京：北京交通大学，2019.
［15］彭建，杨泽帆，白洁，等.基于探地雷达的地下管线埋深估计方法［J］.雷达科学与技术，2022，20（1）:79-86.
［16］程江洲，陈秋航，卞九洲，等.探地雷达技术在变电站地层隐蔽管线探测中的应用［J］.现代雷达，2021，43（2）:82-88.
［17］韩佳明，李冠兵，马鑫，等.地下三角形空洞地质雷达成像机理研究［J］.雷达科学与技术，2023，21（2）:175-183.
［18］吕高.黄土填方介电参数特性及地质雷达回波的正演与解译研究［D］.西安:西安理工大学，2016.
［19］韩佳明，牛宇凯，刘明明，等.地下方形空洞地质雷达成像机理研究［J］.物探与化探，2022，46（3）:685-692.