0 引 言
随着数字技术不断进步、处理能力的不断提高,数字阵列以其扫描波束多、设计灵活性高等特点,已经逐步取代模拟阵列天线,成为通信、对抗、雷达等电子信息技术领域主要的研究方向[1-3]。数字阵列通常采用超外差中频采样接收机(包括多级模拟下变频与滤波、A/D 中频采样和数字下变频等)将各个阵列天线的接收射频模拟信号变换为基带数字信号。
相比于超外差中频采样接收机,零中频接收机具有电路结构简单、功耗低、易于集成、体积小、成本低等优点。由多通道零中频接收构建的数字阵列具有低成本、低功耗、高集成等特点,是当前数字阵列发展的一个重要方向[4-5]。在实际工程中,由于当前器件工艺水平的限制,零中频接收芯片中同相(I支路)和正交(Q支路)支路使用的正交本振频率源无法保证绝对正交,各支路的混频器、低通滤波器等模拟器件的幅频响应也无法保证完全一致,这将同相和正交支路之间存在一定的幅相误差(通常称为I/Q 不平衡误差)。当I/Q 不平衡误差过大时,数字阵列各通道接收均会出现镜像信号,这将极大影响接收阵列波束形成的性能指标。因此,研究零中频接收阵列波束形成的镜像抑制性能具有非常高的实用价值。
目前,关于单通道零中频接收机的I/Q 不平衡补偿方法和镜像抑制能力的研究文献非常多[6-11]。零中频接收机在数字阵列中应用的研究主要集中在多通道I/Q 不平衡误差补偿、多通道I/Q 不平衡误差标校、宽线性波束形成等方面。例如文献[12]给出了一种零中频窄带接收和发射数字阵列的通道间幅相误差、通道内I/Q 不平衡误差的测量与补偿方法,文献[13]提出了一种在多天线系统中利用最小二乘准则对通道内I/Q 不平衡误差进行补偿的方法,并用MQAM 信号验证了所提补偿方法的有效性。文献[14]讨论了一种适用于毫米波相控阵天线的低复杂度标校与补偿方法,并在暗室实测验证了所提方法的可行性。文献[15]对宽线性波束形成技术进行了综述,当阵列接收圆信号,受零中频接收阵列各通道I/Q 不平衡影响,各通道接收基带信号具有非圆特性,此时可使用宽线性波束形成技术。文献[16]研究了数字阵列雷达系统中,I/Q 不平衡误差对数字阵列雷达检测性能的影响,并给出了数字阵列系统中I/Q 不平衡误差补偿的三种方案。关于零中频接收阵列波束合成镜像抑制性能分析,无需I/Q 不平衡误差测量的镜像抑制方法的文献鲜有报道。
为分析零中频接收阵列波束合成的镜像抑制性能,本文首先推导了零中频接收数字阵列的数学模型,然后以此模型为基础,对同时存在通道间幅相误差、通道内I/Q 不平衡误差时的阵列方向图、波束形成镜像抑制性能进行理论分析。根据分析结果,提出了一种基于随机辅助相位的阵列波束合成镜像抑制方法,该方法无需进行各通道的I/Q 不平衡误差。仿真实验验证了本文对零中频接收数字阵列波束合成的镜像抑制比的理论分析的正确性。同时验证了本文所提镜像抑制方法的有效性。
1 单通道零中频接收模型
单通道零中频接收机的原理框图如图1所示。假设模拟正交混频的角频率为ΩLO,同相支路(I路)的余弦本振无误差,而正交支路(Q 路)的正弦本振存在幅度误差ε 和相位误差φ。HBP( ω )和hBP( t )分别为同相(I)和正交(Q)支路分路之前的通道频率响应和冲激响应,具有带通特性,即
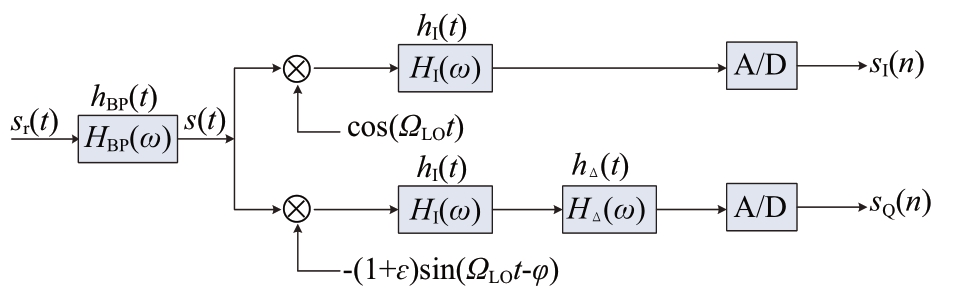
图1 单通道零中频接收机的原理框图
式中,hL( t )为hBP( t )的低通等效冲激响应。HI( ω)和hI( t )分别为同相支路(I 路)的通道频率响应和冲激响应,HΔ( ω )和hΔ( t )分别为正交支路(Q路)相对于同相支路(I 路)的通道频率响应和冲激响应,故正交支路(Q 路)的通道频率响应HQ( ω )和冲激响应hQ( t )分别为
式中,符号⊗代表线性卷积。
在该模型中,单通道零中频接收机的输入信号为sr( t ),可表示为
式中, ( t )为接收信号sr( t )的复包络,Ωc 为接收信号的射频载波模拟角频率。将接收信号sr( t )通过hBP( t )后,其输出信号s( t )可表示为
( t )为接收信号sr( t )的复包络,Ωc 为接收信号的射频载波模拟角频率。将接收信号sr( t )通过hBP( t )后,其输出信号s( t )可表示为
为方便后续推导,令
则有
式中,A( t )为幅度调制信息,ϕ( t )为相位调制信息。若A/D 的采样频率为1/Ts,定义数字角频率ωd =(Ωc - ΩLO )Ts,经模拟正交混频、I/Q 支路低通滤波和A/D采样后,有

根据I 和Q 信号,构造复信号s( n )= sI( n )+jsQ( n ),有

令

则单通道零中频接收信号可表示为

2 零中频接收阵列模型
假设数字阵列包括M 个阵元,每个阵元对应一个零中频接收通道。对于第i 个通道,类似于上一节单通道模型的定义,模拟正交混频的角频率为ΩLO,正交支路(Q 路)相对于同相支路的幅度误差ε(i )和相位误差φ( i)。 (t)为同相(I)和正交(Q)支路分路之前的通道冲激响应,
(t)为同相(I)和正交(Q)支路分路之前的通道冲激响应,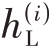 ( t )为
( t )为 ( t )的低通等效冲激响应。
( t )的低通等效冲激响应。 ( t )分别为同相支路(I 路)的通道冲激响应,
( t )分别为同相支路(I 路)的通道冲激响应, ( t )为正交支路(Q 路)相对于同相支路(I路)的通道冲激响应。
( t )为正交支路(Q 路)相对于同相支路(I路)的通道冲激响应。
设第i个阵元接收信号 ( t )为
( t )为
其复包络为
式中,τi 为由第i 个阵元位置和信号入射方向决定的空间时延差。因此,类似于单通道模型的推导,经零中频接收采样后,第i个阵元的基带信号为
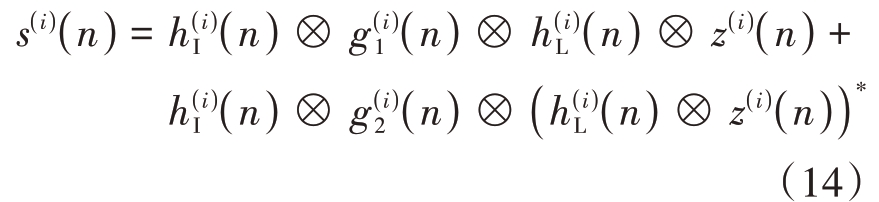
式中,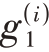 ( n )和
( n )和 ( n )分别可表示为
( n )分别可表示为
z( i)( n )可表示为
由第i 个阵元的基带信号表达式可知,当阵元接收信号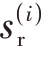 ( t ),若希望相应基带信号为
( t ),若希望相应基带信号为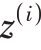 ( n ),则必须对各通道误差
( n ),则必须对各通道误差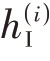 ( n )和
( n )和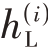 ( n ),I/Q 不平衡误差
( n ),I/Q 不平衡误差 ( n )和
( n )和 ( n )进行补偿。由此可得,零中频接收阵列模型的示意图如图2所示。
( n )进行补偿。由此可得,零中频接收阵列模型的示意图如图2所示。
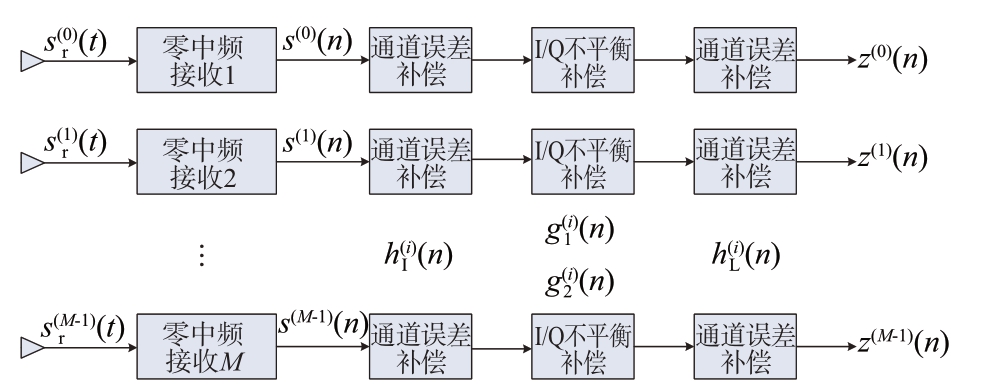
图2 零中频接收阵列模型示意图
若利用上述零中频接收阵列模型进行波束合成,除需要补偿各通道误差 ( n )和
( n )和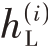 ( n ),I/Q 不平衡误差
( n ),I/Q 不平衡误差 ( n )和
( n )和 ( n )外,还需对波束的幅相加权系数、空间时延进行补偿。波束合成的示意图如图3所示。
( n )外,还需对波束的幅相加权系数、空间时延进行补偿。波束合成的示意图如图3所示。
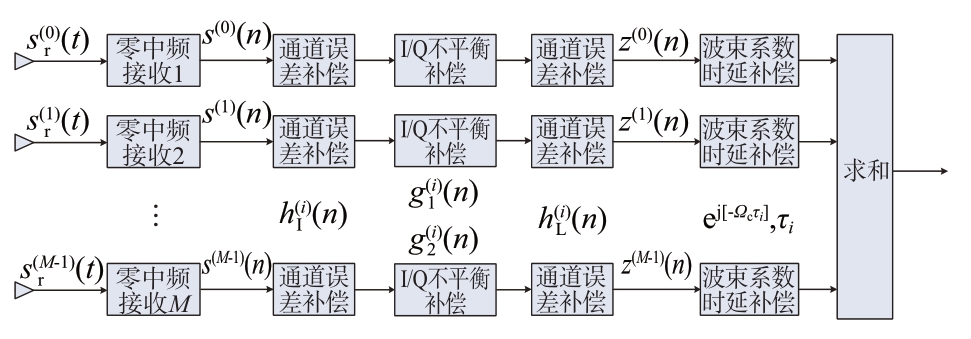
图3 零中频接收阵列的波束合成示意图
上述模型为零中频接收阵列的通用模型,可适用于宽带和窄带接收数字阵列。假设I 路的冲激响应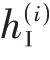 ( n )= δ( n ),Q 路相对于I 路的冲激响应hΔ( n )= δ( n ),第i 个零中频接收通道的本振I/Q 不平衡幅度误差gi = 1 + ε( i),相位误差θi = φ( i)。I/Q分路之前的冲激响应
( n )= δ( n ),Q 路相对于I 路的冲激响应hΔ( n )= δ( n ),第i 个零中频接收通道的本振I/Q 不平衡幅度误差gi = 1 + ε( i),相位误差θi = φ( i)。I/Q分路之前的冲激响应 ( n )= Aiejφi,Ai 为通道间幅度误差,φi为通道间相位误差,此时有
( n )= Aiejφi,Ai 为通道间幅度误差,φi为通道间相位误差,此时有

由此可得,窄带零中频接收阵列模型的基带信号可表示为

其中,阵列接收信号的复包络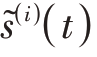 使用了如下窄带假设:
使用了如下窄带假设:

即
由上述窄带模型可知,窄带零中频接收阵列的波束合成示意图如图4所示。

图4 窄带零中频接收阵列的波束合成示意图
3 零中频接收阵列的镜像抑制
本节基于前述窄带零中频接收阵列模型,首先讨论在通道间幅相误差和通道内I/Q 不平衡同时存在时的阵列波束图,然后分析仅补偿通道间幅相误差,通道内I/Q 不平衡误差对波束合成输出信号的影响。
3.1 阵列波束图
在推导阵列波束图之前,将I/Q 不平衡幅度误差gi和相位误差θi分别表示为
式中:g0 和θ0 为阵列I/Q 不平衡的确定幅相误差,它是由阵列各通道使用的相参本振带来公共误差;gri 和θri 为各阵元的I/Q 不平衡随机幅相误差,它是由不同通道间本振信号传输、温漂等因素带来的。
对于任意几何结构的数字阵列,若阵列包含M个阵元,每个阵元在()X,Y,Z 直角坐标系下的坐标为(xi,yi,zi )。若目标入射方向对应的方向余弦(入射方向在直角坐标系下归一化直角坐标)为(u0,v0,w0 ),则由第i个阵元位置和信号入射方向决定的空间时延差τi可表示为
式中,c为光速。
当I/Q 不平衡误差和通道误差存在时,由前述窄带零中频接收阵列模型可得,在射频角频率Ω处的阵列方向图为
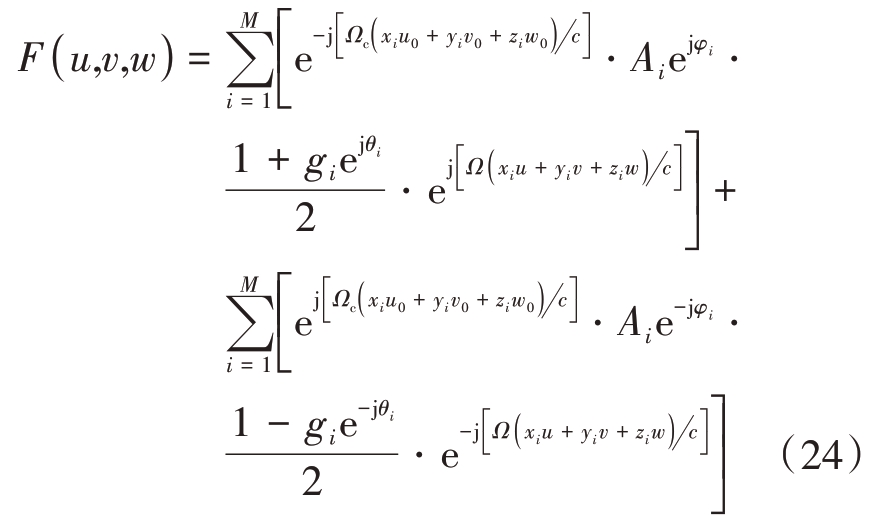
将gi = g0 · gri,θi = θ0 + θri代入上式,经整理,可得

式中,参数κ1和κ2是由空间时延差、通道间幅相误差、I/Q不平衡随机误差共同决定的,分别表示为

FT(u,v,w )为目标方向图,FI(u,v,w )为由镜像带来的方向图,称作镜像方向图,分别表示为

由以上推导可知,当存在I/Q 不平衡误差时,阵列方向图由两部分组成,即第一项是期望得到的目标方向图FT(u,v,w )·(1 + κ1 · g0ejθ0 )/2,第二项是由I/Q 不平衡误差带来的镜像方向图FI(u,v,w )·(1 - κ2 · g0e-jθ0 )/2。
3.2 阵列波束合成
由上一节讨论可知,通道内I/Q 不平衡误差导致阵列方向图中出现了空间镜像分量,这将严重影响阵列波束合成的性能。为了抑制通道内I/Q不平衡误差,可考虑首先对每一通道的I/Q 不平衡误差进行测量,然后对每一通道进行误差补偿。从已有文献来看,若要获得较高的单通道镜像抑制比,单通道必须采集大量测量数据。例如文献[11]所提I/Q 不平衡测量与补偿方法在信噪比为20 dB时,利用3 × 106个测量数据,可获得70.57 dB的镜像抑制比。文献[17]所提I/Q 不平衡测量与补偿方法在信噪比20 dB时,利用3 × 106个测量数据,可获得70.89 dB 的镜像抑制比。因此,当数字阵列规模较小时,可以对每一通道进行I/Q 不平衡误差测量与补偿。但当数字阵列规模较大时,单通道的I/Q 不平衡误差测量与补偿将会带来非常大的计算量。
本节针对大规模数字阵列,假设仅对通道间的幅相误差进行补偿,讨论I/Q 不平衡误差对波束合成输出信号的影响。
由窄带零中频接收数字阵列模型可知,若事先不对I/Q 不平衡误差进行处理,每一通道接收基带信号都会同时受到通道间幅相误差和通道内I/Q不平衡误差的影响,故第i 个通道幅相误差的实际估计值Ei 由两部分组成:第一部分是I/Q 不平衡误差估计值 和
和 ,第二部分是真实通道间幅相误差估计值
,第二部分是真实通道间幅相误差估计值 和
和 。因此,第i 个通道幅相误差的实际估计值Ei可表示为
。因此,第i 个通道幅相误差的实际估计值Ei可表示为
若波束指向对应的方向余弦为![]() ,则射频角频率Ωc处的波束合成的幅相加权可表示为
,则射频角频率Ωc处的波束合成的幅相加权可表示为

因此,M个阵元的波束合成输出为

上式中第二项为镜像信号的波束合成。当 = gi,
= gi,![]() 且波束正好对准目标时,目标信号被完全同相叠加,此时有
且波束正好对准目标时,目标信号被完全同相叠加,此时有

因此,阵列波束合成输出的镜像抑制比为

故阵列波束合成输出的镜像抑制比满足

式中,IIRi 为第i 个通道的I/Q 不平衡镜像抑制比,表示为

上式表明,当波束对准目标,且准确补偿目标频率处的实际通道误差时,波束合成输出的镜像抑制比下限仅取决于各通道的I/Q 不平衡误差。阵列中镜像抑制比越小的通道,对波束合成输出镜像抑制比下限影响越大。
为进一步分析方便,不考虑I/Q 不平衡随机误差的影响(griejθri = 1) 。关于存在I/Q 不平衡随机误差的情况,将结合仿真实验进行分析。阵列波束合成输出的镜像抑制比可重新表示为
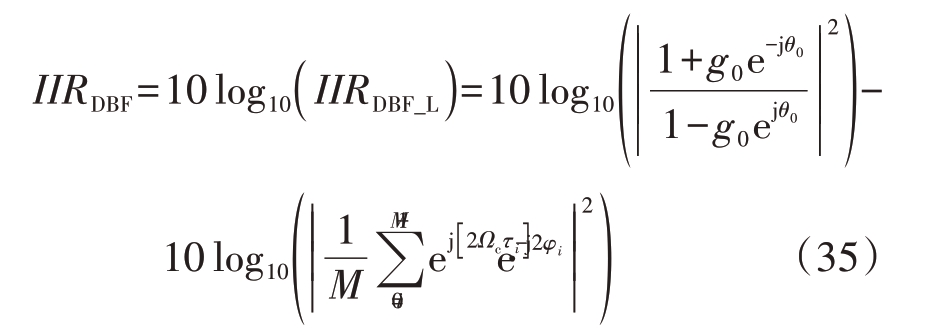
当不存在通道间相位误差(ejφi = 1) 时,阵列波束合成输出的镜像抑制比为

当目标从法向入射时,ej[2Ωcτi ]= 1,此时阵列波束合成输出的镜像抑制比为
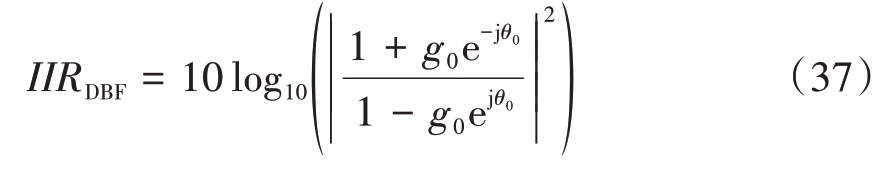
即法向的波束合成未带来任何镜像抑制比得益。对于间距d的均匀线阵,若目标入射方向为ϕ,则第i个阵元的空间时延差τi = di sin ϕ0/c,此时有

由此可知,阵列波束合成输出镜像抑制能力与目标入射方向有关,当目标远离法向时,可获得更高的阵列波束合成输出镜像抑制比。
当通道间相位误差波动较小(ejφi ≈1) 时,此时阵列波束合成输出的镜像抑制比仍可近似表示为
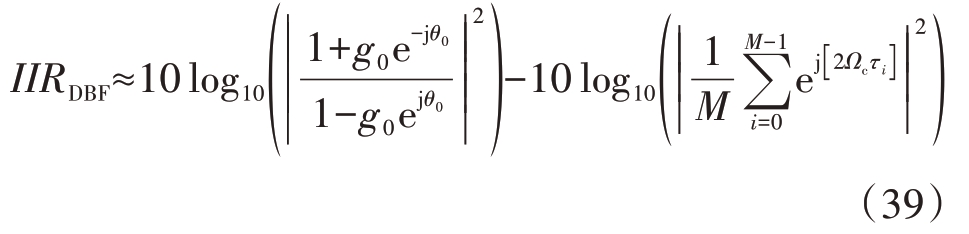
即在通道间相位误差波动较小时,法向的波束合成未带来任何镜像抑制比得益,当目标远离法向时,可获得更高的阵列波束合成输出镜像抑制比。
当通道间相位误差波动很大时,阵列波束合成输出的镜像抑制比受波束指向和通道间相位误差的共同影响。法向波束的镜像抑制比也具有一定得益。阵列波束合成带来的镜像抑制得益取决于通道间相位误差的分布情况。若通道间相位误差的分布恰好使得
此时可获得最大的波束合成镜像抑制比,即IIRDBF ≈+∞。
基于以上分析,可获得一种改善阵列波束合成输出镜像抑制比的方法,本文称为随机辅助相位法。该方法在系统的各通道I/Q 分路之前引入辅助相位αi,则由式(19)给出的第i 个通道的窄带零中频接收基带信号可重新表示为
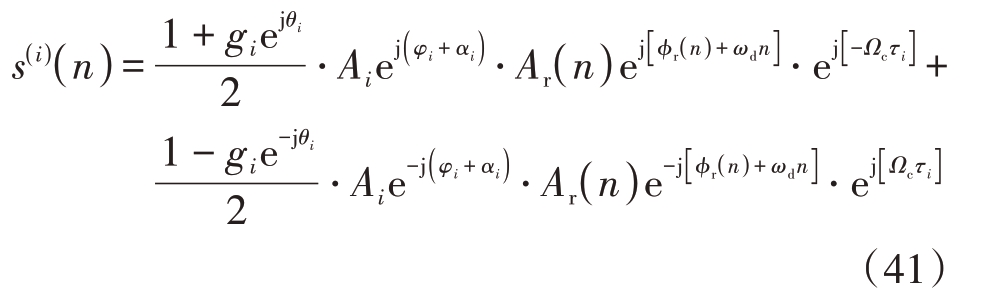
利用式(41)对目标频率处幅相误差进行估计,可获得如式(28)所示的实际估计值Ei,此时Ei中的 是通道相位误差αi + φi 的估计值。采用与式(29)到式(35)相同的处理,可得阵列波束合成输出的镜像抑制比为
是通道相位误差αi + φi 的估计值。采用与式(29)到式(35)相同的处理,可得阵列波束合成输出的镜像抑制比为

在实际应用中,式(42)中Ωcτi 取决于阵列波束扫描角度,通道间相位误差φi 未知,选取在[ 0,π ]内服从均匀分布随机辅助相位αi,可使得M 个相位值2(Ωcτi - φi - αi )尽可能均匀分布在[0,2π ]范围内,式(42)中第二项的求和部分尽可能小,达到波束合成镜像抑制的效果。所提方法即使在通道间相位误差φi 波动较小时,法向(Ωcτi = 0)波束合成仍可获得一定的镜像抑制比得益,且随着阵列规模的增加,波束合成镜像抑制效果越来越好。下面将结合仿真实验说明上述分析的正确性。
4 仿真实验分析
本节以均匀线阵为例,首先通过仿真实验验证前述理论分析的正确性,然后对所提随机辅助相位法的有效性进行仿真分析。
实验1:考虑均匀线阵,阵元个数64,射频工作频率为8 GHz,阵元间距为11 mm。波束可在-90°到90°的空域范围内进行扫描。均匀线阵的各阵元采用-30 dB的泰勒加权,用于降低副瓣电平。
设I 和Q 路数据分路之前的通道间幅度误差为0.5 dB,通道间相位误差为10°或90°。通道内I/Q不平衡幅度确定误差为1 dB,幅度随机误差为0.5°,相位确定误差为5°,相位随机误差为5°。上述通道内I/Q 不平衡误差,使得阵列中各通道镜像抑制比的平均值为22.8 dB。
同时考虑上述误差,当通道间相位误差为5°时,波束指向为0°时的阵列波束图如图5所示。图中理想波束图为不存在任何误差时的波束图。相比于理想波束图,存在误差时的阵列方向图(误差方向图)对副瓣电平有影响。
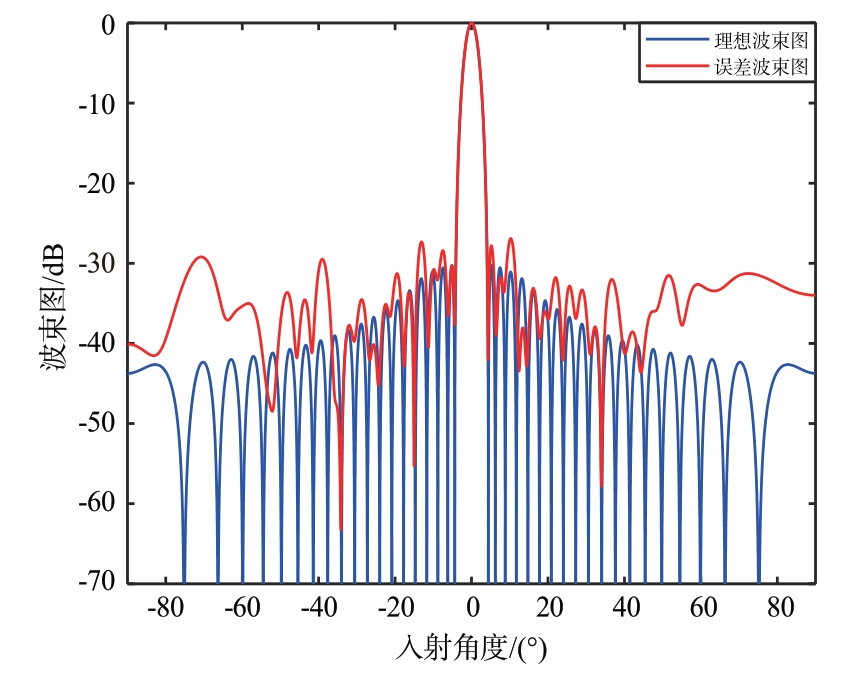
图5 加权30 dB存在误差的方向图
如果将目标波束图和镜像波束图分别计算,其阵列方向图如图6 所示。由图可知,对于主瓣,镜像波束图是目标波束图的向下平移,法向波束在3 dB 波束宽度内的镜像抑制为23 dB,近似无镜像抑制比得益。误差波束图的副瓣电平略有失真。
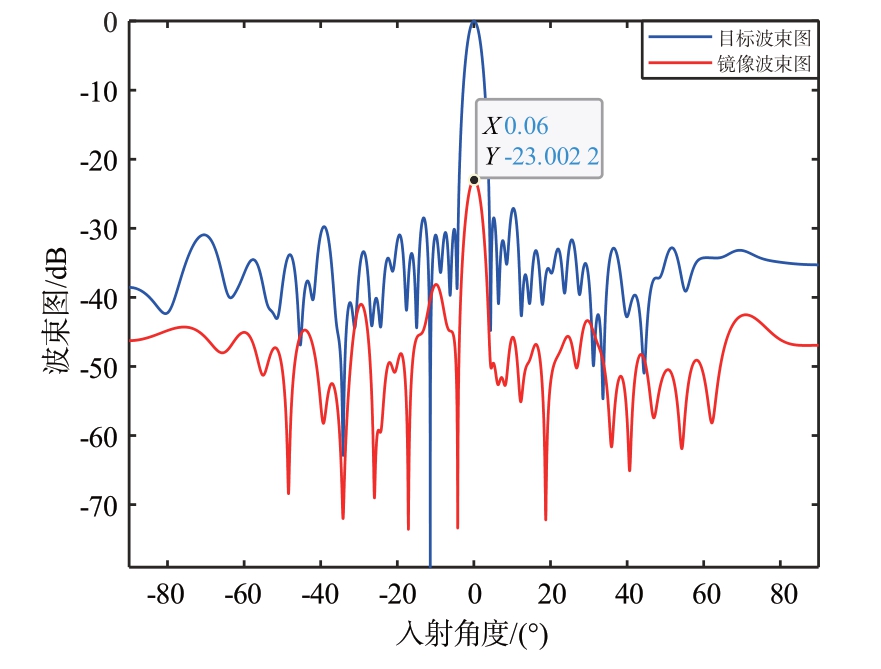
图6 加权30 dB目标方向图和镜像方向图
当通道相位误差为90°时,阵列波束图如图7所示。相比于理想波束图,通道相位误差非常大,若不对幅相误差进行补偿,目标波束图和镜像波束均不能合成,最终法向波束将无法正常合成。

图7 加权30 dB存在误差的方向图
若将目标方向图中通道间幅相误差补偿,可得到通道误差补偿方向图、目标方向图和镜像方向图,如图8 和图9 所示。相比于理想方向图,补偿方向图的副瓣电平略有恶化。经通道误差补偿后,目标方向图可以正常合成波束,镜像方向图进一步得到抑制,目标波束主瓣的镜像位置不存在镜像波束。这是因为目标方向图中Aiejφi 补偿后,将使得镜像方向图中Aie-jφi 变为Aie-j2φi,通道幅相误差在未补偿前已非常大,目标的通道误差补偿后,导致镜像方向图中通道幅相误差加倍,镜像抑制比从-23 dB 降低到-35 dB。目标波束可正常合成,镜像波束图无法合成,最终波束图可正常合成,仅是副瓣电平略有失真。
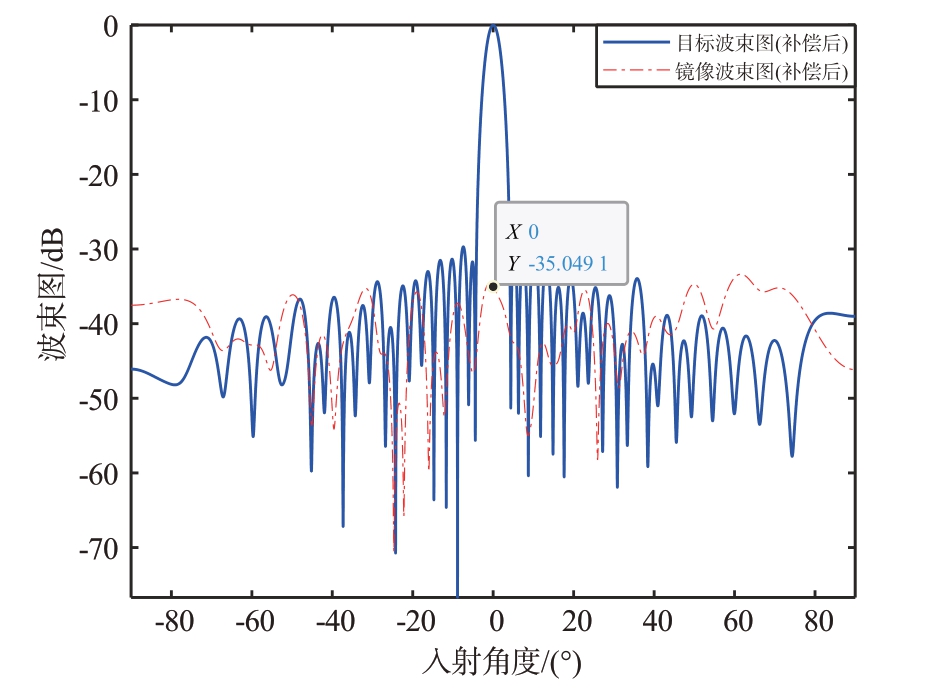
图8 加权30 dB通道误差补偿后目标和镜像方向图
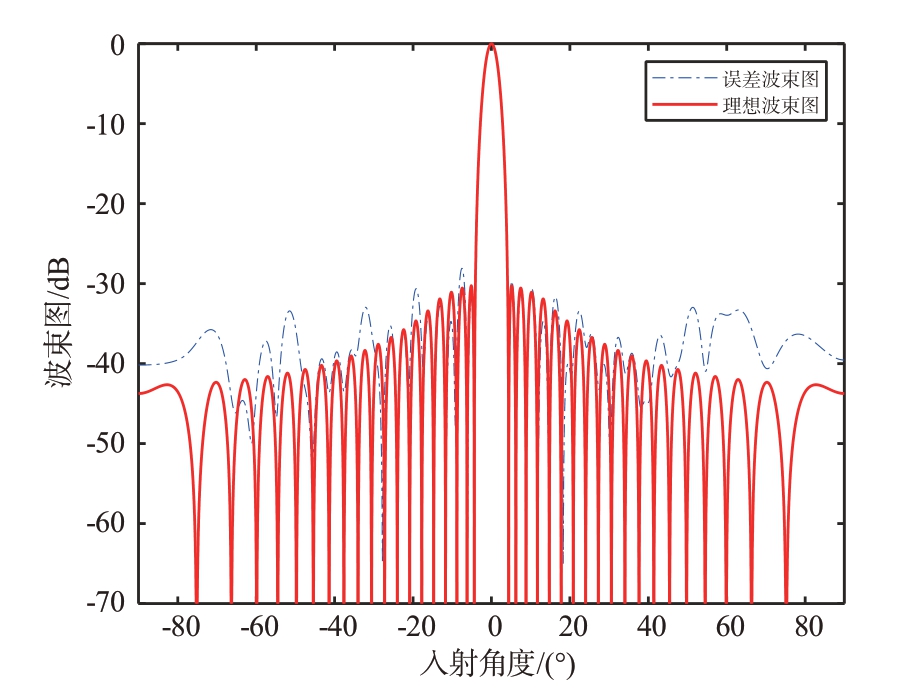
图9 加权30 dB通道误差补偿后的方向图
实验2:除将波束指向设为60°,其他仿真条件同实验1。
当通道相位误差为5°时,波束指向为60°时的阵列波束图如图10 所示。相比于理想波束图,存在误差时的阵列方向图(误差方向图)对副瓣电平有影响,且在目标波束指向的镜像指向处存在明显峰值,该峰值约为-24.2 dB。
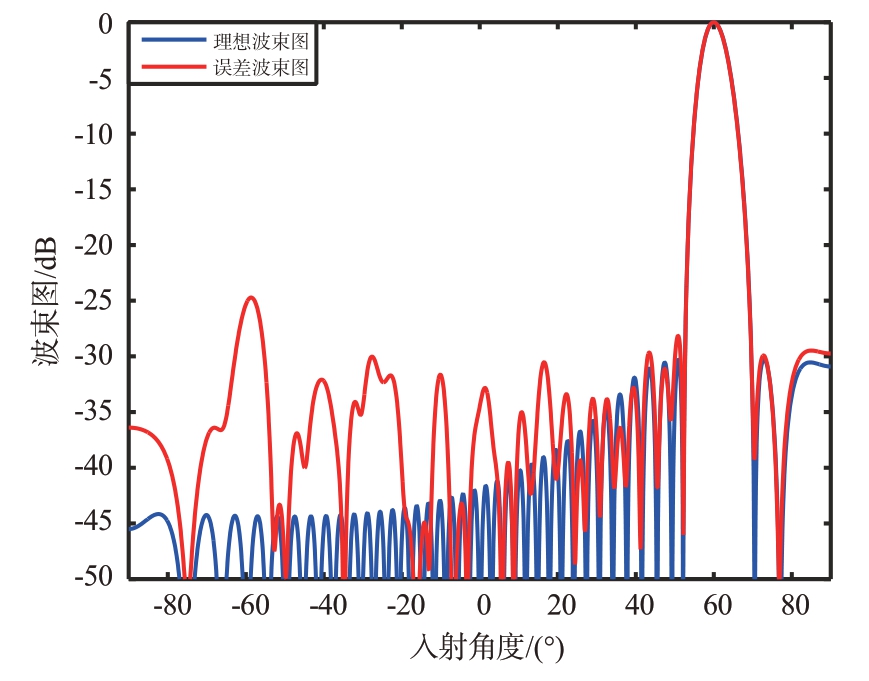
图10 加权30 dB存在误差的阵列方向图
如果将目标波束图和镜像波束图分别计算,其阵列方向图如图11 所示。由图可知,由于通道误差和I/Q 不平衡误差的存在,镜像波束在目标波束指向处并未合成,但在波束指向镜像处存在受到抑制的镜像主瓣。

图11 加权30 dB目标和镜像方向图
当通道相位误差为90°时,阵列波束图如图12 所示。相比于理想波束图,通道相位误差非常大,若不对幅相误差进行补偿,目标波束图和镜像波束均不能合成,最终波束将无法正常合成。

图12 加权30 dB存在误差的方向图
若将目标方向图中通道间幅相误差补偿,可得到通道误差补偿方向图、目标方向图和镜像方向图,如图13 和图14 所示。相比于理想方向图,补偿方向图的副瓣电平略有恶化。经通道误差补偿后,目标方向图可以正常合成波束,镜像方向图进一步得到抑制,镜像抑制比从-23 dB 降低到-42.5 dB,目标波束主瓣的镜像位置不存在镜像波束。
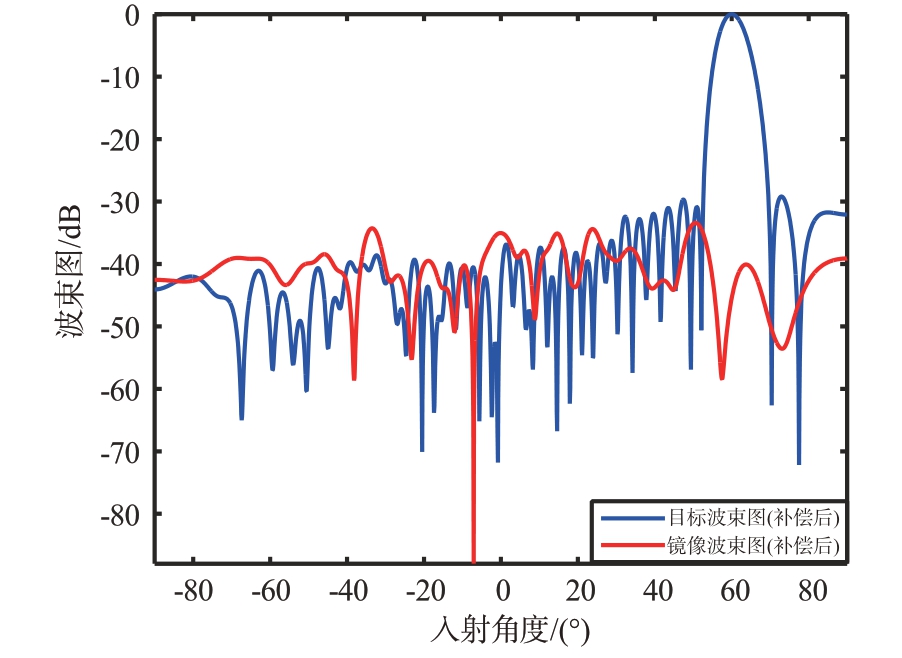
图13 加权30 dB通道误差补偿后目标和镜像方向图
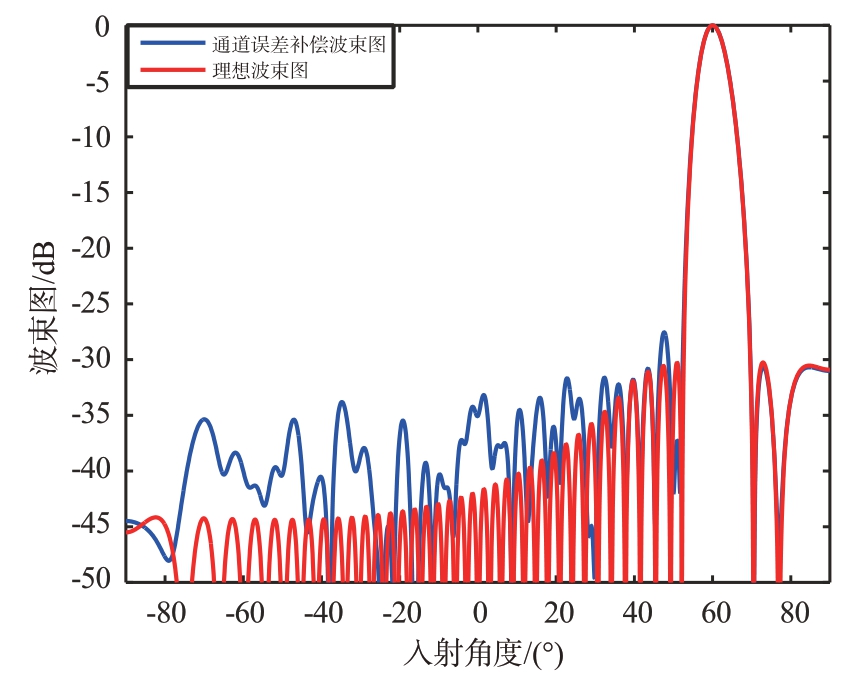
图14 加权30 dB通道误差补偿后的方向图
实验3:考虑均匀线阵,阵元个数在16~2 048之间取值,射频工作频率为8 GHz,阵元间距为11 mm。波束可在-90°~90°的空域范围内进行扫描。均匀线阵的各阵元采用-30 dB 的泰勒加权,用于降低副瓣电平。
设I 和Q 路数据分路之前的通道间幅度误差为0.5 dB,通道间相位误差为10°。通道内I/Q 不平衡幅度确定误差为1 dB,幅度随机误差为0.5°,相位确定误差为5°,相位随机误差为5°。上述通道内I/Q 不平衡误差,使得阵列中各通道镜像抑制比的平均值为22.8 dB。
本实验采用随机辅助相位方法,在系统的各通道I/Q 分路之前引入[]0,π 内服从均匀分布随机相位。
不考虑噪声,模拟目标运动与波束切换对波束合成输出I/Q 不平衡误差的影响。目标从-60°运动到60°,步进0.1°。接收波束按0.5倍波束宽度的步进切换。当阵元个数为64 时,不同目标角度位置下,目标和镜像波束形成输出幅度值如图15所示。目标幅度的平均值为36.15 dB,镜像幅度的平均值为-6.76 dB,波束合成输出的平均镜像抑制比为42.91 dB,扣除各通道的平均镜像抑制比,波束合成带来的平均镜像抑制比为20.11 dB。

图15 阵元数64目标与镜像波束输出幅度值
当阵元个数为256时,不同目标角度位置下,目标和镜像波束形成输出幅度值如图16所示。目标幅度的平均值为48.63 dB,镜像幅度的平均值为0.41dB,波束合成输出的平均镜像抑制比为48.22 dB,扣除各通道的平均镜像抑制比,波束合成带来的平均镜像抑制比为25.42 dB。
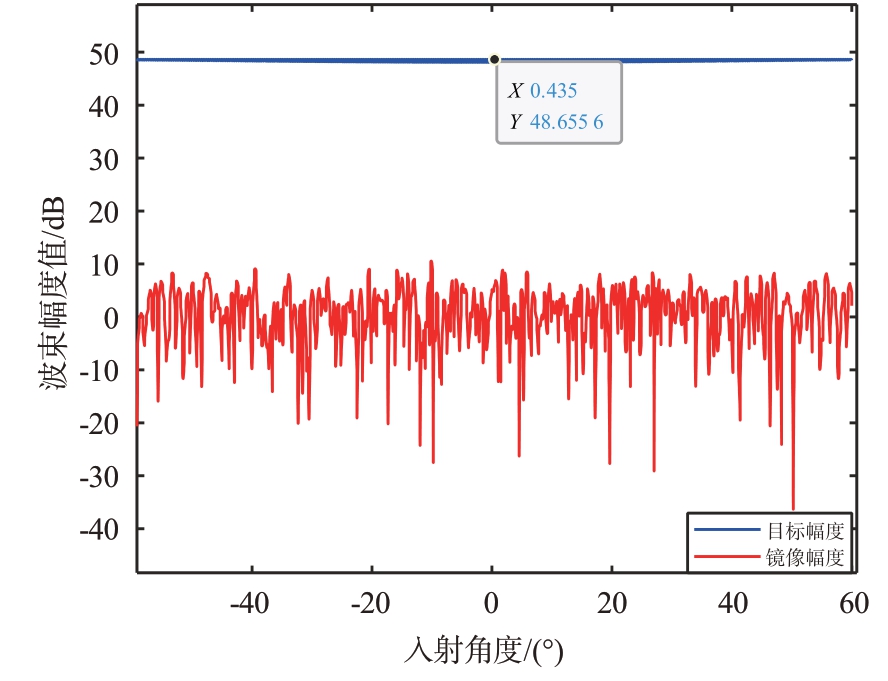
图16 阵元数256目标与镜像波束输出幅度值
当阵元个数为1 024 时,不同目标角度位置下,目标和镜像波束形成输出幅度值如图17所示。目标幅度的平均值为60.01 dB,镜像幅度的平均值为5.94 dB,波束合成输出的平均镜像抑制比为54.07 dB,扣除各通道的平均镜像抑制比,波束合成带来的平均镜像抑制比为31.27 dB。
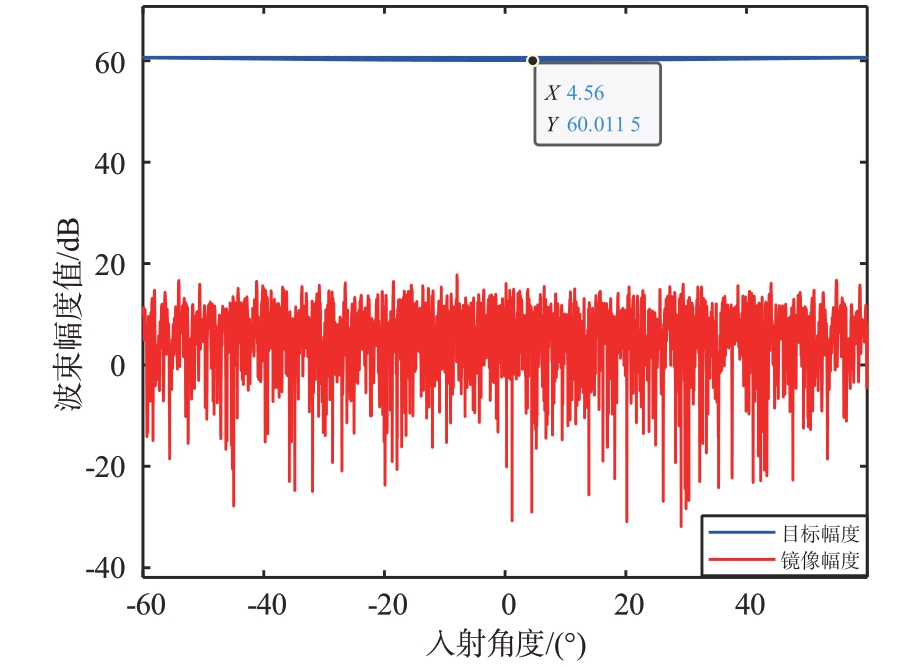
图17 阵元数1 024目标与镜像波束输出幅度值
当阵元个数从16变化到2 048时,利用不同目标角度位置下的目标和镜像波束形成输出平均幅度值、各通道的平均镜像抑制比可计算出波束合成带来的平均镜像抑制比,其变化曲线如图18 所示。所提方法获得的平均镜像抑制比随着阵元个数增加而增加,阵元个数每增加一倍,平均镜像抑制比近似提高3 dB。

图18 平均镜像抑制比随阵元个数的变化曲线
由图15~图18 可知,各阵元对通道幅相误差进行补偿后,整个观测空域内,镜像抑制水平在某个平均值附近随机波动。阵元个数增加,提高了观测空域内的平均镜像抑制比。目标和波束的相对空间位置略微改变,将会使镜像抑制比变化较大。目标在观测空域内角度连续变化时,I/Q 不平衡带来的镜像分量会有明显波动。
前述3 个仿真实验分析与本文所述的理论分析结论是相同的,这进一步验证了本文对零中频接收数字阵列波束合成镜像抑制比的理论分析的正确性。同时,仿真实验也验证了本文所提基于随机辅助相位的波束合成镜像抑制方法的有效性。
5 结束语
为了提高零中频接收阵列波束合成的镜像抑制能力,本文在讨论零中频接收数字阵列数学模型的基础上,对阵列波束图和波束合成输出镜像抑制比进行理论分析,提出了一种基于随机辅助相位的波束合成镜像抑制方法。所提方法随着阵元个数的增加,可明显改善波束形成输出的镜像抑制比,特别适合于大规模数字阵列,且不需要测量各通道的I/Q 不平衡误差。当采用本文所提方法获得的波束合成输出镜像抑制比仍无法满足系统性能要求时,需要在波束合成输出进一步提升镜像抑制比,这将是下一步重点研究的内容。
[1]吴曼青,赵逸超,何峰,等.计算阵列——计算赋能的数字阵列技术[J].中国科学,2022,52(12):2270-2289.
[2]鲁加国.数字阵列雷达发射多波束的若干关键技术[J].雷达科学与技术,2021,19(3):233-240.
[3]李圣衍,黄海波,江涛,等.基于数字阵列的干扰机架构研究[J].现代雷达,2022,44(10):72-77.
[4]HAKKARAINEN A, WERNER J, RENFORS M,et al.Transceiver I/Q Imbalance and Widely-Linear Spatial Processing in Large Antenna Systems[C]//2015 International Symposium on Wireless Communication Systems, Brussels,Belgium:IEEE,2015:651-655.
[5]MAHENDRA R,MOHAMMED S K,MALLIK R.Compensation of Transmitter IQ Imbalance in Multi-User Hybrid Beamforming Systems[J]. IEEE Access, 2021, 9(7):98231-98248.
[6]陶毅,丁丽.利用共轭对称性的数字IQ 频域校准方法[J].西安电子科技大学学报,2021,48(2):181-189.
[7]唐婷.基于盲均衡技术的宽带IQ 不平衡补偿设计与实现[J].电子技术应用,2023,49(2):72-75.
[8]曹钰琛,万建,陶加祥.基于统计特征的IQ 不平衡高效校正算法[J].电子器件,2022,45(2):468-473.
[9]马雅男,徐卫,刘道煦,等.一种新型的宽带接收机IQ矫正结构[J].测控技术,2021,40(2):118-122.
[10]孟婕,王厚军,叶芃.一种I/Q 失衡误差的估计和补偿方法[J].电子科技大学学报,2022,51(2):227-233.
[11]CHEN Chun, SU Xiaomin, LI Chunhua. Widely Linear Estimation Technique Based on Circularity for I/Q Imbalance Compensation in Low-IF Receivers[C]// 2014 IEEE Workshop on Advanced Research and Technology in Industry Applications, Ottawa, ON, Canada: IEEE,2014:1047-1050.
[12]PARK H G, PARK C,OH H,et al. RF Gain/Phase and I/Q Imbalance Error Correction Technique for Multi-channel Array Antenna Systems[C]//IEEE VST 53rd Vehicular Technology Conference, Rhodes, Greece:IEEE, 2001:175-179.
[13]HE Dongmei,WANG Longping.Compensation of I/Q Imbalance in M-QAM Transceiver with Multi-Antennas[C]// 2012 2nd International Conference on Consumer Electronics, Communications and Networks, Yichang,China:IEEE,2012:3140-3143.
[14]SALEHI M,NEZHAD-AHMADI M R,SAFAVI-NAEINI S.A Low Complexity Approach for Calibration and Characterization of a Millimeter Wave Phased-Array Transceiver-Antenna Module[C]// 50th European Microwave Conference,Utrecht Netherlands:IEEE,2021:1043-1046.
[15]叶中付,徐东阳,曹圣红.宽线性波束形成技术综述[J].数据采集与处理,2012,29(3):333-340.
[16]HODKIN J E,SOMERLOCK O F,SHARP M D,et al.IQ Imbalance Decorrelation in Digital Array Radars[C]//2016 IEEE Aerospace Conference, Big Sky, MT, USA:IEEE,2016:1-8.
[17]CHURCHILL F E, OGAR G W, THOMPSON B J. The Correction of I and Q Errors in a Coherent Processor[J].IEEE Trans on Aerospace and Electronic Systems, 1981,17(1):131-137.