0 引 言
随着城市的不断发展,越来越多的公路和道路由于年久失修或遭受到自然灾害破坏,逐渐产生脱空、裂缝等病害,这些问题严重影响人类生活。因此,有必要对公路病害等地下病害进行检测和养护。在公路养护领域,探地雷达由于其无损、高效和高分辨率等卓越特性,正被逐渐推广开来[1]。
在探地雷达(Ground Penetrating Radar, GPR)的信号体制中,超宽带无载波窄脉冲和宽带步进频连续波(Stepped-Frequency Continuous Wave,SFCW)是两种常用的波形。相比于超宽带窄脉冲信号,SFCW 通过瞬时带宽合成超宽带信号,既降低信号产生和接收的硬件要求,减小了系统复杂度,又能增加接收机灵敏度,同时实现信号带宽的灵活控制。为了提升收发共址GPR(单测线)的作业速度,引入多发多收的MIMO(Multi-Input Multi-Output, MIMO)体制,即MIMO-GPR。MIMO-GPR通过形成虚拟孔径来合成多测线,达到使用较少的天线数量就可以实现整个车道横向的密集采集[2]。但是,目前MIMO-GPR 大都采用时分MIMO体制。为了进一步提升MIMO-GPR 的作业速度,采用MIMO正交波形设计,通过各个发射天线同时辐射正交波形,所有接收天线同时匹配接收。而对于SFCW 的MIMO-GPR 系统而言,往往使用随机步进频信号作为正交波形[3]。当MIMO-GPR 用于公路病害探测时,公路介质层间距小,且上层间的多次反射波会掩盖下层中被衰减的微弱回波信号,因此MIMO-GPR 需要研究低旁瓣的高分辨距离像。
现阶段随机跳频信号的距离旁瓣抑制研究中,研究者主要从设计低旁瓣波形和抑制回波的距离旁瓣两方面进行。关于低旁瓣波形设计,文献[4]通过将量子遗传算法和遗传算法结合,有效地降低了信号之间的互相干扰;文献[5]将混沌序列与遗传算法结合,对MIMO-GPR 发射波形集频率编码进行设计,得到了具有较低互相关的正交离散频率编码信号。上述方法虽然可以得到较低旁瓣的发射波形,但是这种方法对回波信号的距离旁瓣抑制能力有限。因此目前主要使用失配滤波器对随机步进频信号进行旁瓣抑制。文献[6]利用二阶锥规划(Second-Order Cone Programming,SOCP)对失配滤波器进行设计,并且取得了良好的效果。这些基于凸优化设计的滤波器主要使用CVX 及Sedumi求解,当设计的信号码长较长时,直接使用CVX 会导致内存溢出,陷入死解;利用Sedumi求解凸优化则需要将失配滤波器问题转化为严格的约束形式,且Sedumi 求解速度也远小于最新的Yalmip 模型。文献[7]利用线性规划(LP)对频率编码进行旁瓣抑制,实验结果证明LP 属于凸优化问题,可以对频率编码进行旁瓣抑制。除此之外还有神经网络[8]、最小迭代二乘[9]等优化算法用于失配滤波器设计。神经网络求解大带宽的信号则会占用太多资源;最小迭代二乘等智能算法需要通过多次迭代寻找最优解,迭代过程的时间长短往往与门限条件的设置有较大关系,如若是门限设置较大,不容易找到最优解。
本文基于上述分析,提出一种适合随机步进频信号旁瓣抑制方法。通过将随机步进频信号旁瓣抑制问题表示成二阶锥规划[10](SOCP)问题,然后求解滤波系数,并且给出Yalmip 求解SOCP 问题的方法。本文方法更适合长码随机步进频信号处理,可以有效抑制随机分布的旁瓣,且迭代速度更快。
1 公路层环境下随机步进频信号模型及处理分析
1.1 探地雷达信号模型
电磁波在层状介质中传播时,当电磁波到达第一层时会发生反射与折射,折射的能量继续向下传播。反射后的能量经过再次折射传播到空气中,这部分折射能量没有损耗,直接被接收机接收。接收机最终接收到的回波信号则由地面强反射和层间折射波和目标折射波组成。具体传播示意如图1所示。

图1 GPR原理
在图1 中,εi,σi 分别为介电常数和磁导率,N为公路层数;s1,s2,s3,s4 分别为第一层分界面反射波、第二层分界面反射波、第三层分界面反射波和目标回波。根据文献[11],层间分界面的反射系数Qi和折射系数Pi分别为
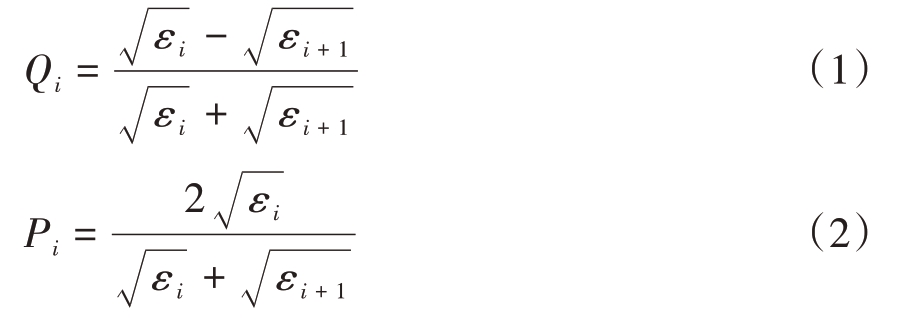
由此,我们可以得到接收到的第n 层目标回波为[12]

式中,第一项为地面直达波,第二项为第i 层分界面折射回波,以此类推第i 项为第i 层分界面回波或病害目标回波。
公路路面主要由面层、基层、底基层构成,这三层结构的建造材料分别为沥青混凝土、碎石及水泥混合碎石。假设病害目标在第3 层。以第m个接收天线为例,按照预先设置的随机步进顺序某一发射天线依次发送L个脉冲,同时按照固定方向等间隔采样,则根据式(3)得到第一层分界面(地面强反射回波)的信号可以表示为
第二层分界面的信号为
第三层分界面的信号为

病害目标回波为

将式(4)至式(7)相加并结合GPR 信号模型[13],推导出MIMO-GPR 第m 个天线接收到的回波信号模型为
式中,o 为天线间的互耦直达波,g 为各种杂波,ni为第i层介质的噪声干扰。
1.2 随机步进频回波信号模型
设随机步进频信号子脉冲宽度为τ,载频为f0,频率跳变点数为L,脉冲重复周期为Tr,第m 根天线发射L个脉冲,发射信号模型为
式中,0 <t <LTr,rect(t)为矩形脉冲,fl 为第l 个子脉冲的频率,表达式为
c( l )是频率跳变序列,Δ f是频率间隔。
令探地雷达径向距离R处有一病害目标,则回波信号表示为

相参本振信号为
混频后得到中频回波信号为
这里t0为双程延时,其等于2R/c。在公路层之间传播时,需要考虑公路层之间不同介质的影响,因此可以得到目标距离与速度之间的关系,具体为
式中,z 为探地雷达探测剖面的横向坐标值的大小,x 为纵向坐标值的大小,v 为电磁波传播速度。由层状介质的二维传播式,得到速度与介电常数的关系[14]:

将式(15)代入式(14)得到目标距离和介电常数的关系式,具体为
利用式(16)推出双程延时为
1.3 随机步进频信号预处理
将式(13)表示的连续信号进行采样,得到长度为H 的复采样序列,然后依次对采样数据进行零偏移处理、脉冲压缩和离散傅里叶变换(IDFT)得到一维距离像,流程如图2所示。
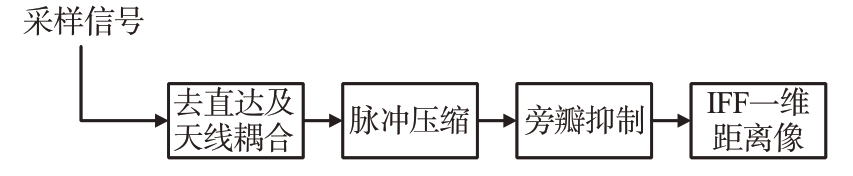
图2 MIMO-GPR信号处理流程
根据上述可知,采样后的回波序列为
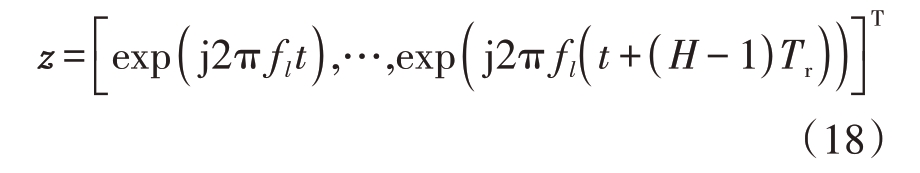
利用平均对消法去除直耦波和直达波,即

设参考距离为Rα,参考时延为tα,参考信号为
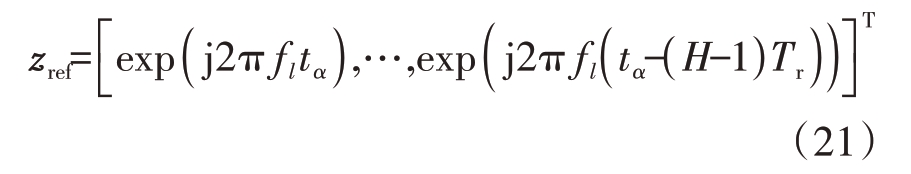
将zo与zref互相关,得到脉压输出m为

这里的Nm 为脉冲压缩输出序列长度。令Δt =![]() ,则式(22)表示为
,则式(22)表示为
继续对式(23)作频域失配加权就可以在频域对其进行旁瓣抑制。
2 随机步进频信号旁瓣抑制方法
随机步进频信号的旁瓣抑制主要是匹配滤波器级联失配滤波器的方法。目前对于失配滤波器设计的方法主要考虑对旁瓣的抑制能力而没有同时考虑主峰损失与综合旁瓣电平的抑制。除此之外,大部分方法仅仅考虑信号的旁瓣抑制能力,没有考虑失配滤波器对大规模码长信号的适应能力,也缺少实测数据分析。本文基于目前的失配滤波器方法进行设计,主要改进的地方如下:1)基于峰值旁瓣最小[15](Peak Sidelobe Level,PSL)和积分旁瓣比(Integrated Sidelobe Level Ratio, ISLR)最优进行设计失配滤波器,同时约束峰值旁瓣电平与综合旁瓣电平;2)在较低信噪比损失条件下,实现信号旁瓣抑制;3)约束旁瓣的同时约束滤波器输出信号的主瓣宽度,降低主瓣展宽,提高分辨率;4)对失配滤波器在不同码长条件下,以及探地雷达系统参数下旁瓣抑制能力进行分析,并使用实测数据验证失配滤波旁瓣抑制能力。
2.1 失配滤波器问题分析
失配滤波器设计的目的是使得滤波之后回波信号旁瓣得到抑制,失配滤波器系数一般通过对频域信号加权求信号旁瓣电平最小值得到。
设失配滤波器阶数为M,M ≥Nm,失配滤波系数向量为w,将脉冲压缩输出序列m 右端补q 个信号向量x,x为M × 1阶向量,w和x分别表示为

将x 与失配滤波器频域w 相乘,得到失配脉压输出为
式中,k1 = max{0,n - M + 1},k2 = min{n,M - 1}。为了方便设计,将式(26)转化为矩阵形式,首先定义信号约束矩阵为
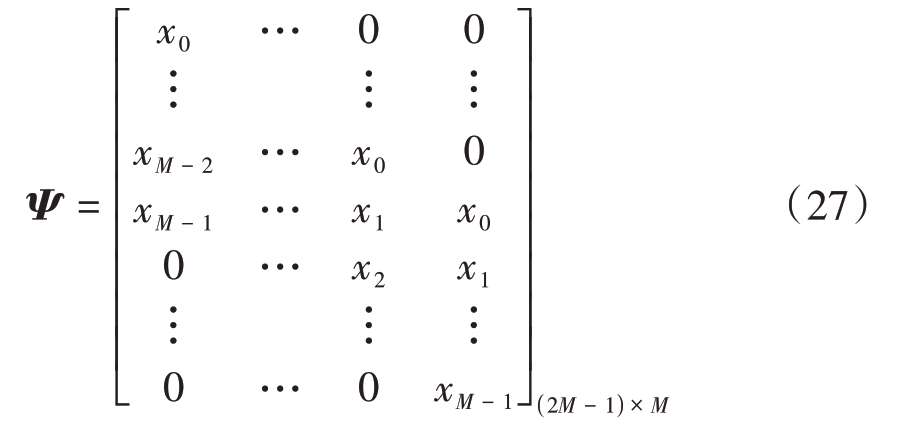
式(26)用向量表示为

式中y0为主瓣。设去掉主瓣后旁瓣矩阵u为
接下来对信号主瓣成分与旁瓣进行分析,设计合适的滤波器。
2.2 失配滤波器设计方法
目前,随机步进频信号的旁瓣抑制滤波设计主要使用PSL准则。但是,由于MIMO-GPR雷达具有多发多收特性,导致其旁瓣出现位置不固定,因此MIMO-GPR 探地雷达中随机步进频信号的旁瓣抑制可根据ISLR建立约束。具体约束如下:
1)通过优化使得旁瓣抑制滤波器的PSL 最小即可实现回波信号距离旁瓣电平最小,利用信号旁瓣矢量u建立PSL,即
式中-M ≤i ≤M,且i ≠0。
此外,失配滤波器还要实现综合旁瓣电平的抑制,用u来表示积分旁瓣,可得

令ISLR最小化,得到失配滤波器最优权系数:
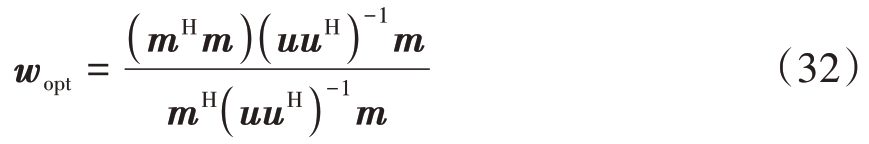
令wopt = w,并对式(32)进行化简得到
式(33)是使得ISLR 最优的滤波器,而PSL 不是最优,因此基于两者之间平衡建立失配滤波器二阶锥规划问题如下:

式中i = 0,1,…,2M - 1,且i ≠M。
2)根据失配滤波器损失[16](Mismatch Filter Loss,MMFL)表达式,对m归一化后得到限制失配滤波器损失(信噪比损失)在损耗值σ 之内,得到第二个约束条件:
通常情况下,σ越小,代表滤波器损失越大,距离旁瓣电平越低,距离旁瓣抑制能力越强;反之σ越大,距离旁瓣电平越高,距离旁瓣抑制能力越弱。
3)通常情况下,峰值旁瓣的降低是以主瓣的展宽为代价实现的。主瓣的展宽引起分辨率的降低会导致探地雷达系统性能的下降,因此接下来对失配滤波器的主瓣宽度进行约束。设约束主瓣宽度向量为p =(p-l,…,p-1,p0,p1,…,pl)T,l 为主瓣内点数的一半。将主瓣输出限制在一定范围内,得到对主瓣宽度的约束如下:
式中i ≤l,q =(M - H )/2,ΨH + q + i 代表矩阵Ψ 的H+q+i行。
结合上述的3 个约束与1.3 节中的分析,失配滤波器优化问题表示为二阶锥规划问题的形式:

求出满足式(38)要求的失配滤波器系数,就可得到符合随机步进频信号特性的最佳失配滤波器。
2.3 基于Yalmip的二阶锥规划求解失配滤波器权值
由于yi = 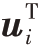 wi,则式(38)的目标函数可以表示为
wi,则式(38)的目标函数可以表示为
为求解式(38),需要w 作为未知量,结合式(39)将式(38)化简为
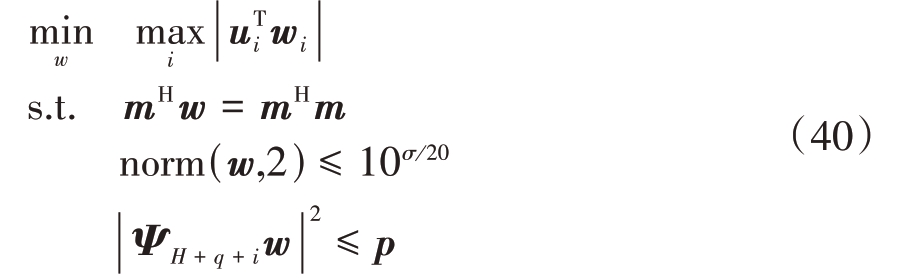
接下来利用Yalmip 求解二阶锥问题,首先一般问题表示为
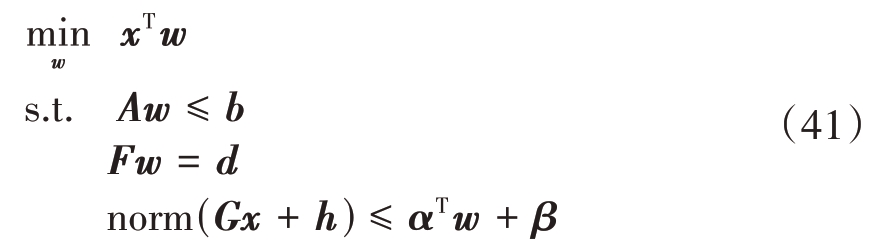
式中w 为要求解的未知向量,x为代价函数的系数向量,A、F、G 为常数矩阵,b、d、h、α 和β 为已知向量。
最后将w、u、m、Ψ、σ、p对照式(41)输入,利用Mosek 求解器中的Yalmip 即可按照设置好的约束条件不断迭代寻优找出w。
3 仿真与实测结果分析
3.1 仿真分析
仿真实验1 公路层环境下随机步进频信号失配滤波器性能分析
为验证本文失配滤波器对MIMO-GPR 随机步进频信号旁瓣抑制的有效性,使用GPRMAX3.0 进行三层介质公路层仿真实验,实验参数设置为步进频探地雷达系统参数。仿真实验设置存在一个大小为20 cm × 60 cm 的长方体空洞,频率间隔为2 MHz,频率跳变点数为150,失配滤波器损耗为0.2 dB,带宽设为1.8 GHz。公路层设置上面层为沥青混凝土,中面层为碎石及水泥混合碎石,下面层为土基,具体参数见表1。
表1 公路结构参数

参数厚度/cm相对介电常数电导率磁导率上面层0.4 11.12 0.001 0中面层0.6 7.80 0.001 0下面层2.0 6.56 0.001 0
公路层结构仿真图如图3 所示,病害为空洞,位于土基层。图4 给出了仿真数据处理结果,图4(a)为全局结果图,图4(b)为其中的局部放大图。可以看出,图4(a)中由于随机分布旁瓣,目标已经被掩盖在较高的旁瓣之中;图4(b)信号的地面反射波和耦合波的电场强度远大于层间反射波和病害目标回波。

图3 公路层环境仿真示意图

图4 公路层仿真回波数据处理结果
利用本文失配滤波器处理之后得到图5结果。由图5 可以看出,失配滤波之后,地面强反射和直达波得到一定抑制,强目标回波得到良好的抑制。电磁波经过不同介质层时产生1 个目标回波和2个层间反射回波。两个层间反射回波分别出现在0.4 m附近和0.8 m附近,这与设置的公路模型基本一致。病害目标回波出现在1.3 m 附近,且目标信号附近距离旁瓣得到抑制,整体不均匀的距离旁瓣降至-40 dB 左右,说明了本文失配滤波器在公路场景下可以对随机步进频信号进行良好的旁瓣抑制。
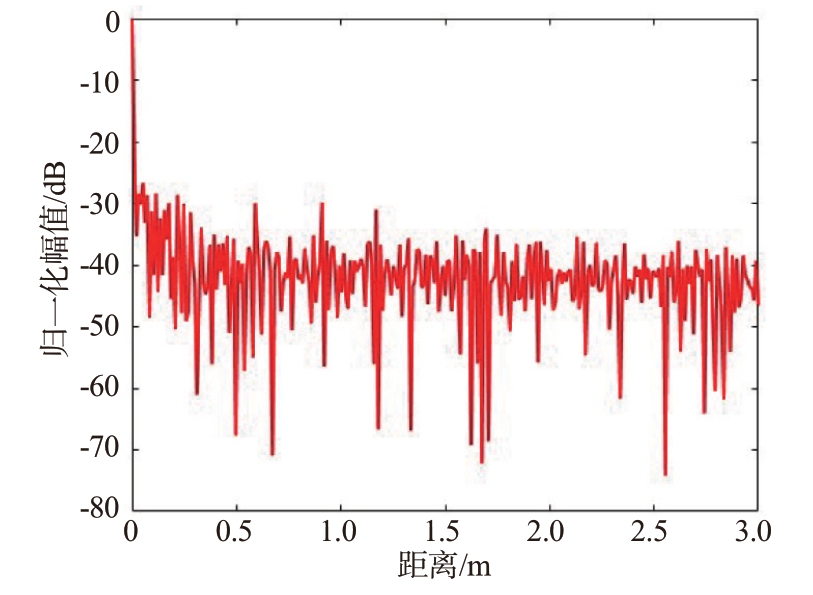
图5 公路层回波信号旁瓣抑制结果
仿真实验2 不同失配滤波器性能分析
对码长为128 时的随机步进频信号进行100次蒙特卡洛失配滤波仿真实验,然后与文献[7]、文献[16]和文献[17]进行对比,分别计算峰值旁瓣和积分旁瓣。
从表2 可以看出,本文结果要优于文献[7]和文献[17]。在同样的增益损失条件下,本文结果与文献[16]的结果相比,在峰值旁瓣抑制这方面相差不大,但本文的积分旁瓣电平最优,滤波器阶数也更短,积分旁瓣电平比文献[16]低6.42 dB。说明了本文失配滤波器对峰值旁瓣和综合旁瓣抑制的有效性。
表2 不同滤波器性能比较
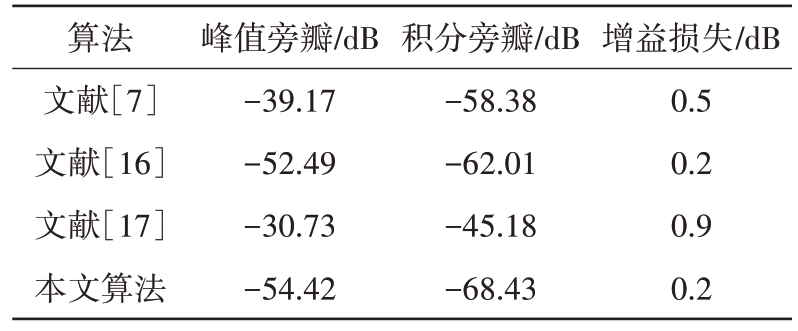
算法文献[7]文献[16]文献[17]本文算法峰值旁瓣/dB-39.17-52.49-30.73-54.42积分旁瓣/dB-58.38-62.01-45.18-68.43增益损失/dB 0.5 0.2 0.9 0.2
仿真实验3 失配滤波器不同长度性能分析
采用本文方法对32, 64, 128 位随机步进频信号设计旁瓣抑制滤波器,失配滤波器阶数均与匹配滤波输出长度相等,并与文献[7]和文献[16]的结果进行对比。
从图6(a)到图6(c)可以看出,随着码长的增加,滤波器阶数也相应增加,传统峰值旁瓣抑制滤波的旁瓣抑制能力有所下降。传统峰值旁瓣滤波器在码长为64 和128 时,旁瓣电平几乎相等,均在-40 dB 左右。分析基于二阶锥的PSL 滤波器和本文的失配滤波器可知,随着码长增加,两者都能将旁瓣抑制得更低,在码长为128 时,分析图6(c)可知,本文失配滤波器比文献[7]的二阶锥PSL 滤波器的综合旁瓣电平更低,约6.5 dB,PSL约2.2 dB。这表明本文失配滤波器在较低的信噪比损失情况下,对综合旁瓣电平抑制能力更好,码长越长,旁瓣抑制能力越好,具有更好的适应性。
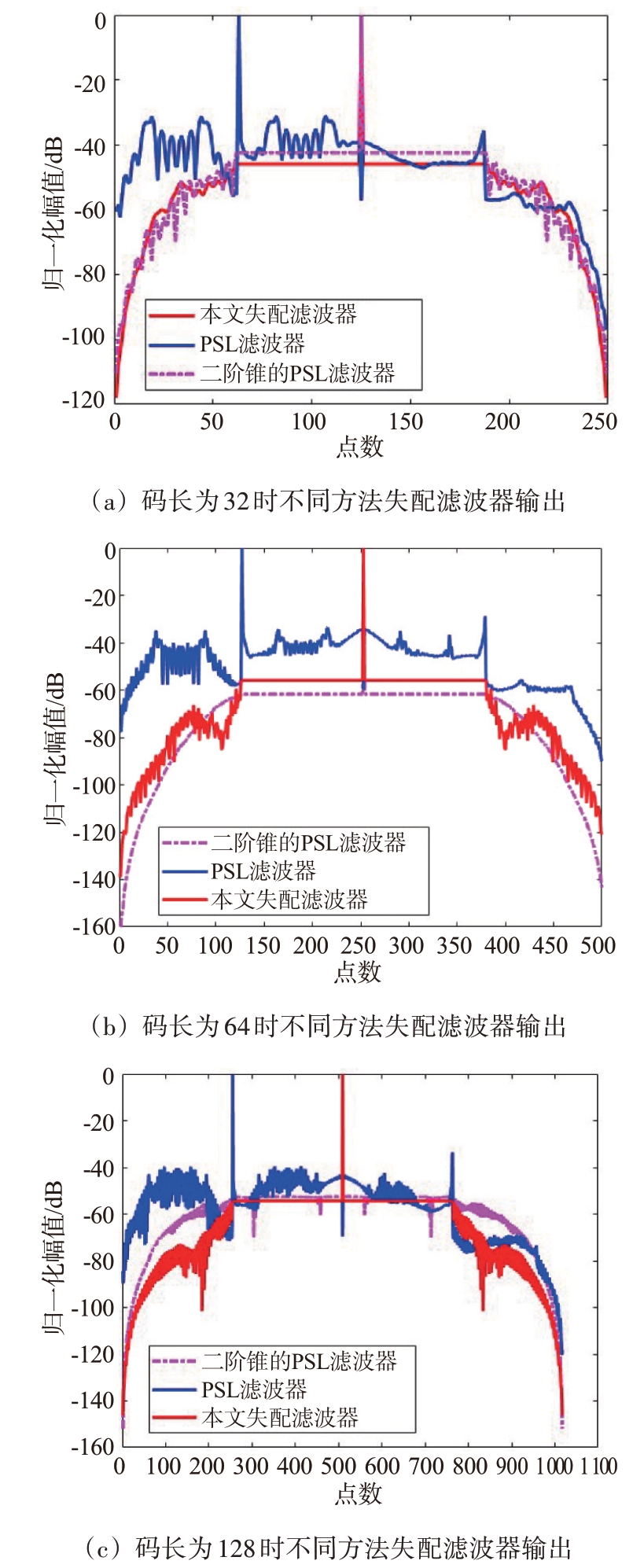
图6 不同码长的输出结果对比
仿真实验4 不同带宽不同失配滤波器性能分析
为分析失配滤波器用于MIMO-GPR 时,不同带宽对旁瓣抑制能力的影响,实验4 对码长相同,滤波器阶数相同,带宽为128 MHz~1.8 GHz 之间的多组信号进行分析。
图7是滤波器阶数(255阶)与增益损失(0.2 dB)都相同的情况下,带宽与峰值旁瓣的关系。当带宽较少时,本文失配滤波与文献[16]的基于二阶锥的失配滤波都有较好的抑制效果,文献[7]抑制能力较弱;而当带宽逐渐增大,三者的抑制能力都有下降。但本文设计的失配滤波器,当PSL下降到一定范围时保持不变,这是因为滤波器的阶数限制了PSL 的进一步下降。所以本文的失配滤波器对带宽的适应性更强。
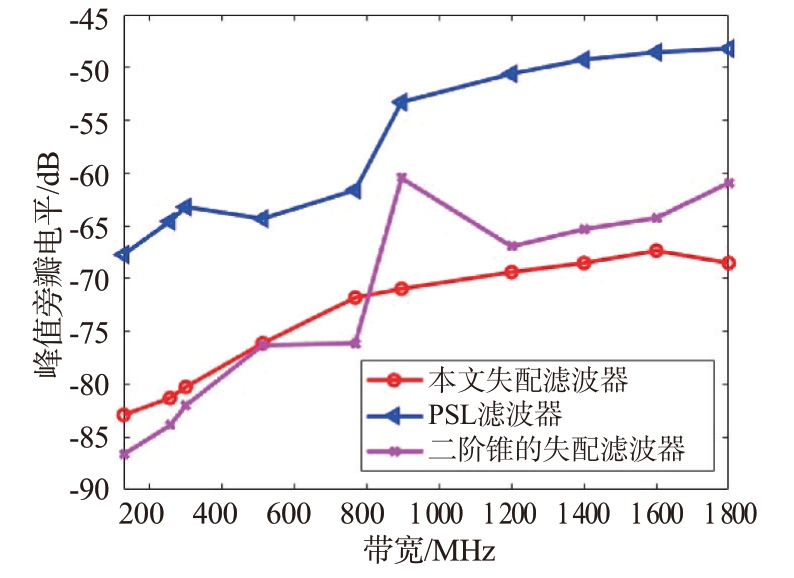
图7 不同带宽下失配滤波器PSL对比
3.2 实测数据分析
实测数据采用Keysight Technologies 公司的N9918A 手持微波分析外接Vivaldi 单发单收空耦天线。实验采样点数601,频率范围为370 MHz~2 GHz,采样率为两倍带宽。实验场景为一塌陷公路路面下水道,下水道中有少量水分,公路层介质为混凝土,介电常数为8~12。
实测数据处理结果如图8 所示。从图8(a)可以看出,本文的失配滤波器将信号的峰值旁瓣抑制到了-20 dB 左右。从图8(b)可以看出公路层有3层反射回波,目标位于2 m左右,这与实际情况相符合。综上所述,本文的旁瓣抑制滤波器可以用MIMO-GPR中的随机步进频信号处理,符合实际雷达旁瓣抑制要求。


图8 实测数据处理结果
4 结束语
本文结合MIMO-GPR 应用需求,讨论了随机步进频信号失配滤波的设计问题。针对随机跳频信号距离旁瓣较高的问题,首先通过分析公路层环境下的信号处理流程和原理给出了失配滤波器设计的问题描述,然后将随机步进频信号旁瓣抑制问题转化为二阶锥规划问题。最后利用Yalmip求解二阶锥规划问题,对公路层环境下的回波信号及不同码长、不同带宽的随机步进频信号进行仿真,同时将设计的滤波器应用于实测数据分析。仿真和实测数据分析结果表明,设计的失配滤波器不仅十分适合MIMO-GPR 中随机步进频信号的旁瓣抑制,而且对MIMO-GPR 中不同带宽、不同码长的信号都有很好的旁瓣抑制表现。
[1]安维乐.阵列式探地雷达滤波去噪技术的研究与实现[D].哈尔滨:哈尔滨工业大学,2019.
[2]CHENG Weixia,TAN Haihai,KANG Li,et al.Estimating the Diameter of Reinforcing Bars Using an Ultra-Wideband MIMO GPR Array[J]. Construction and Building Materials,2022,10(5):1099-1124.
[3]ZHANG Liao, XU Yan, XU Hua.Waveform Design for Random Stepped Frequency Radars to Achieve the Ultra-Low Side-Lobes in High Resolution Range Profile[C]//2021 CIE International Conference on Radar, Haikou,China:IEEE,2021:1809-1812.
[4]郝昭昕,孙进平.基于量子遗传算法的MIMO 雷达正交信号波形设计[J].信号处理,2019,35(6):1064-1071.
[5]李春辉,马健,杨永建,等.多载波混沌频率编码雷达信号设计与分析[J].现代雷达,2022,44(3):41-45.
[6]LI Jin, JING Wang, YANG Zhong, et al.Optimal Mismatched Filter Design by Combining Convex Optimization with Circular Algorithm[J]. IEEE Access, 2020, 10(7):56763-56772.
[7]鞠振飞,杨华.一种基于线性规划的频率编码旁瓣抑制方法[J].海军航空工程学院学报,2020,35(2):176-180.
[8]谭覃燕,宋耀良.基于神经网络的混沌调频信号旁瓣抑制算法[J].兵工学报,2010,31(2):177-183.
[9]周骏,王冬华,沈洋,等.脉冲压缩距离副瓣抑制研究[J].雷达与对抗,2022,42(3):25-27.
[10]LIU Junhao, GAO Liang, LI Yinwei, et al. Sidelobe Suppression for Random Stepped Frequency Signal Based on Interpolation and Extrapolation[C]//International Conference on Radar Systems,Belfast:IET,2017:1-4.
[11]尹德,叶盛波,张经纬,等.公路结构和介电特性对探地雷达反射回波的影响研究[J].电子测量技术,2018,41(5):51-56.
[12]张明昊.基于探地雷达的地下管线智能辨识技术研究[D].哈尔滨:哈尔滨工业大学,2022.
[13]顾伟立,赵新铭,陆俊.基于GprMax 的沥青混凝土心墙空洞探地雷达正演模拟[J].水利科技与经济,2023,29(4):27-33.
[14]黄磊,柳艾飞,高才才.集中式MIMO 雷达研究进展:正交波形设计与信号处理[J].雷达科学与技术,2023,21(1):1-15.
[15]何子述,程子扬,李军,等.集中式MIMO 雷达研究综述[J].雷达学报,2022,11(5):805-829.
[16]位寅生,杨思亮.基于二阶锥规划的跳频脉冲信号旁瓣抑制方法研究[J].电子学报,2011,39(11):2686-2691.
[17]单文童,栾晓明.基于鲸鱼优化算法的失配滤波器设计[J].无线电工程,2021,51(6):453-457.