0 引 言
机载多输入多输出（Multiple-Input Multiple-Output，MIMO）雷达采用波形分集技术，通过在空域维虚拟出更多信号处理通道，获得较单输入多输出（Single-Input Multiple-Output，SIMO）雷达更多系统自由度（Degree of Freedom，DOF），在运动目标检测和参数估计方面受到广泛关注［1］。空时自适应处理（Space Time Adaptive Processing，STAP）技术通过空域和时域自由度的联合处理可以有效滤除地杂波，该技术依赖于准确估计待检测距离单元杂波协方差矩阵（Clutter Covariance Matrix，CCM）［2］。根据RMB（Reed-Mallett-Brennan）准则，要使估计CCM 的信干噪比损失小于3 dB，至少需要系统自由度2 倍的独立同分布（Independent Identically Distributed，IID）样本数。在实际场景中，受限于非均匀杂波环境和天线阵列配置方式的影响，用于估计CCM 的IID 训练样本数很难满足条件［3-4］。在MIMO 雷达中，系统自由度的增加也使得所需IID训练样本数急剧增大。因此，如何利用少量IID 训练样本精确估计CCM 是机载MIMO 雷达STAP 技术面临的关键问题。
近年来，稀疏恢复技术在机载SIMO 雷达STAP 中得到快速发展［5-8］，该技术也逐渐从SIMO雷达拓展到MIMO雷达中［9-11］。稀疏恢复STAP（SRSTAP）技术利用杂波谱在角度-多普勒域上固有的稀疏性，可在单样本或少量样本情况下提高CCM的估计精度。字典网格的划分对稀疏恢复技术尤为关键，然而当前稀疏恢复技术构造的离散字典还存在格点失配问题，若直接将该技术应用到机载MIMO 雷达STAP 中，稀疏恢复性能将会下降。针对格点失配问题，众多学者提出许多离网（Off-Grid）稀疏恢复方法。文献［12］提出了基于参数搜索正交匹配追踪（Parameter-Searched Orthogonal Matching Pursuit，PSOMP）的稀疏恢复方法，补偿了稀疏恢复中的格点失配误差。文献［13］提出了基于杂波脊先验知识的稀疏恢复方法，实现了字典网格间距的自适应调整。文献［14］通过建立格点失配误差校正模型，提出了基于离网稀疏贝叶斯推理（Off-Grid Sparse Bayesian Inference，OGSBI）的稀疏恢复方法。然而，上述针对格点失配问题提出的稀疏恢复方法都是基于离散字典实现的，不能从根本上避免格点失配问题的产生。
为彻底解决格点失配问题，Candes 等［15］提出了全变分范数，实现了在连续参数空间上恢复稀疏信号。文献［16］在此基础上将l0 范数凸松弛为l1范数，提出了原子范数最小化（Atomic Norm Minimization，ANM）的半正定规划（Semi-Definite Programming，SDP）求解方法，同时将恢复信号的空间分辨率提高到4/DOF。文献［17］对原子范数最小化的半正定规划求解模型进行了推广，解决了高维信号（d ≥2）的稀疏恢复问题。文献［18］将原子范数理论应用到机载雷达STAP 处理中，提出了基于二维ANM 的机载雷达SR-STAP 方法，然而该方法只能在空-时二维参数空间上估计杂波子空间，若应用到机载MIMO 雷达STAP 中，将会出现系统自由度的损失。但如果能直接在发射-接收-时域三维参数空间上对MIMO 雷达杂波信号进行ANM稀疏恢复，就可以充分利用MIMO雷达的系统自由度，获得较二维ANM方法更优的估计性能。因此，本文在文献［18］的基础上，推导了适用于机载MIMO雷达的ANM 求解模型，提出了基于三维原子范数的机载MIMO 雷达STAP 算法，解决了机载MIMO雷达SR-STAP 中的格点失配问题，实现了杂波空时谱的高分辨率估计，有效提高了机载MIMO雷达STAP 杂波抑制性能。仿真结果表明，本文方法在存在格点失配情况下的STAP处理性能优于已有的基于字典网格的稀疏恢复方法和二维ANM方法。
1 MIMO雷达信号模型
图1 为机载MIMO 雷达均匀线阵几何模型，其中发射阵元数为M，阵元间距为dt，接收阵元数为N，阵元间距为dr，载机平台沿x 轴放置，飞行速度为v，速度方向与阵列轴线的夹角（即偏航角）为ϕ，当ϕ = 0°时为正侧视阵，当ϕ ≠0°时为非正侧视阵，H 为载机高度，θ、φ 为对应杂波块的方位角和俯仰角。雷达工作波长为λ，在恒定脉冲频率fr 的相干处理间隔（Coherent Processing Interval，CPI）内发射K个脉冲。
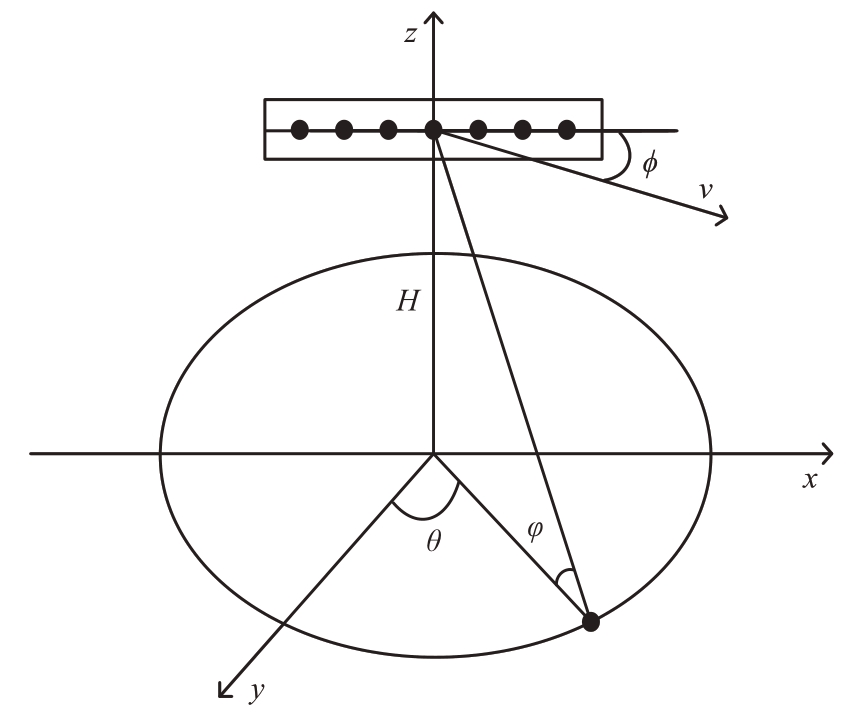
图1 机载MIMO雷达均匀线阵几何模型
机载MIMO雷达发射正交信号，在接收端通过匹配滤波将接收信号分离出M个发射阵元信号，从而实现虚拟阵列。定义各杂波块的空域发射导向矢量at( fs)∈ℂM × 1、空域接收导向矢量ar( fs)∈ℂN × 1分别为
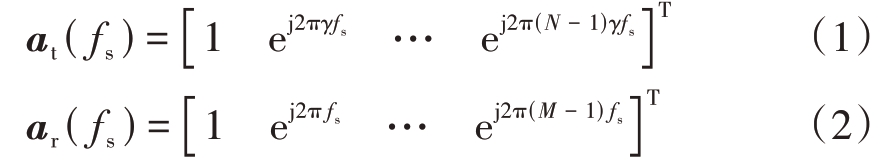
式中，fs为杂波块的归一化空间频率，γ = dt/dr为发射阵元和接收阵元的间距比，ℂ表示复数空间。
时域导向矢量ad( fd) ∈ℂK × 1为
式中，fd为杂波块的归一化多普勒频率。
设φl 为第l 个距离单元的俯仰角，θp 为第p 个杂波块的方位角，则第p个杂波块的归一化空间频率fs,p = dr sin(θp)cos(φl)/λ，第p个杂波块的归一化多普勒频率fd,p = 2v sin(θp + ϕ)cos(φl)/(λ fr)。
当天线阵采取正侧视配置方式，即偏航角ϕ =0°时，杂波的fd,p 和fs,p 在空时二维平面上满足线性关系，即fd,p = βfs,p，其中β = 2v/( frdr)为杂波脊斜率。当天线阵采取非正侧视配置方式，即偏航角ϕ ≠0°时，杂波的fd,p 和fs,p 在空时二维平面上满足椭圆曲线关系。
第l 个距离单元的空时快拍数据经匹配滤波后，输出MNK维的信号矢量xl ∈ℂMNK × 1，即
式中，n 为噪声信号，xc,l 为杂波信号。xc,l 可以表示为Nc个杂波块的空时信号的叠加，即
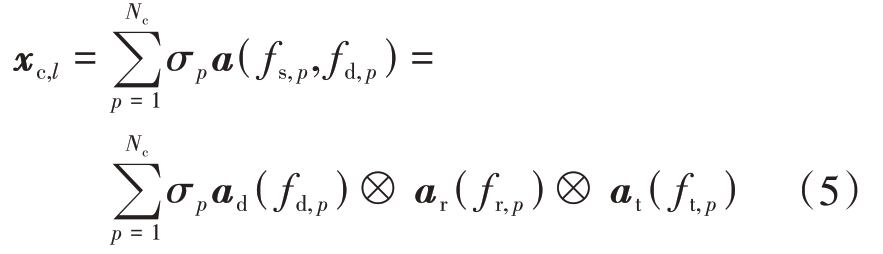
式中，Nc 为杂波块的个数，σp 为第p 个杂波块的复幅度，a( fs,p,fd,p)为第p 个杂波块的空时导向矢量，⊗表示Kronecker积。
则L 个距离单元的空时快拍数据经匹配滤波后的数据X ∈ℂMNK × L可以表示为
式中，Xc=[xc,1, xc,2, …, xc,L ]为杂波分量，N =[n1, n2, …, nL ]为噪声分量。
2 MIMO雷达SR-STAP算法及格点失配问题
2.1 MIMO雷达SR-STAP原理
MIMO 雷达SR-STAP 方法利用杂波谱在空时二维平面上固有的稀疏性，通常将整个空时平面进行等间隔网格划分，然后将网格点对应的空时导向矢量看作基向量并构造空时导向矢量字典。设网格点大小为Q = Ns × Nd，其中Ns = ρsMN，Nd = ρdK，ρs ＞1，ρd ＞1 分别表示空域和时域的网格疏密标度，空时导向矢量字典Ψ ∈ℂMNK × NsNd可以表示为
式中，fs,i(i = 1,2,…,Ns)和fd,j(j = 1,2,…,Nd)分别表示空域第i 个网格点对应的空间频率和时域第j个网格点对应的多普勒频率。
经匹配滤波后的空时多快拍样本X 可以由空时导向矢量字典Ψ表示为
式中，S ∈ℂMNK × L 为杂波在角度-多普勒域上的像，其每个非零行表示对应的网格点上存在杂波分量。
多快拍训练样本的MIMO 雷达杂波空时谱稀疏恢复模型可以表示为
式中‖· ‖2,0 表示ℓ2,0 混合范数，‖ · ‖F 表示Frobenius 范数，ε 为允许误差容限。通过求解杂波的角度-多普勒像S，可以获得MIMO雷达杂波协方差矩阵为
式中，
,k = 1,2,…,NsNd 为第k 个基向量的平均功率。
由于ℓ2,0 范数很难优化求解，属于非确定性多项式难题（Non-deterministic Polynomial-hard，NPhard），可以通过其松弛方法求解。
2.2 格点失配问题
SR-STAP 技术假设杂波脊正好落在构造字典的离散网格点上，然而，这一假设通常并不成立。对于正侧视阵，杂波脊线在空时平面上呈斜对角线分布，在构造空时导向矢量字典时，很难保证Ns/Nd 比值为整数倍的杂波脊斜率，导致杂波脊线和离散化的网格点不能完全对准，产生格点失配问题。对于非正侧视阵，杂波脊线沿椭圆分布，杂波脊线和离散网格点存在明显偏移，只有少量离散网格点和杂波脊线完全对准，格点失配问题更加严重。格点失配问题一旦产生，估计的杂波谱将会展宽，导致杂波抑制性能下降。虽然缩小网格间隔可以在一定程度上增加杂波脊线对准离散网格点的概率，但是空时导向矢量字典中相邻基向量的相关性会随之增强，不仅导致稀疏恢复性能下降，而且计算复杂度也会增加。
图2 是MIMO 雷达在不同阵列配置方式下杂波谱在空时平面上的分布图，图2（a）和2（b）分别对应正侧视阵（偏航角ϕ = 0°，β = 1.2）和非正侧视阵（偏航角ϕ = 90°）情况，这两种情况均存在格点失配问题。
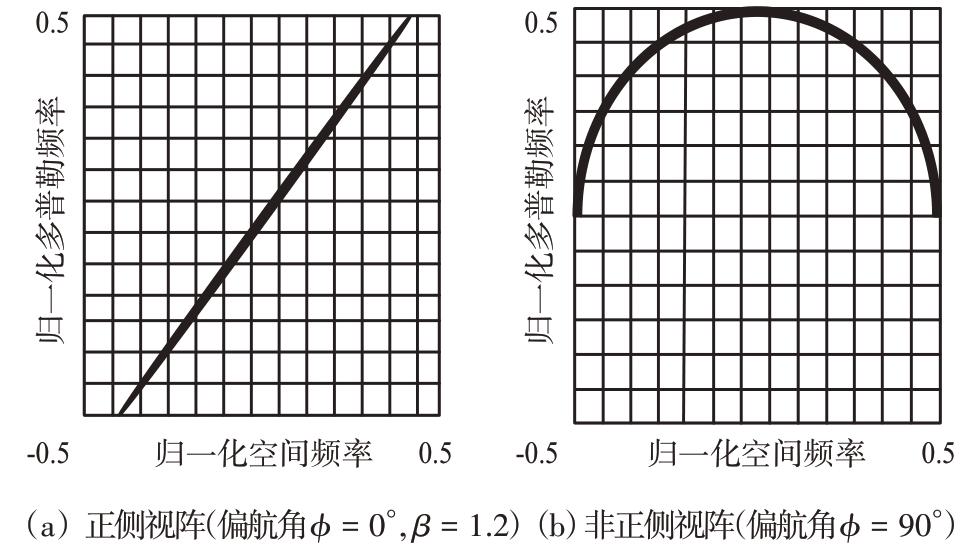
图2 MIMO雷达在不同阵列配置方式下的杂波谱
3 基于三维原子范数的机载MIMO雷达STAP算法
与离散域上的稀疏恢复技术不同，原子范数理论是直接在连续域中进行稀疏恢复，通过在连续域中使用最少的原子来表征稀疏信号，避免了网格化方法构造离散字典带来的格点失配问题。针对机载MIMO 雷达SR-STAP 方法中杂波脊线存在的格点失配问题，本文提出一种基于三维原子范数的机载MIMO雷达STAP算法。
为构造基于三维连续原子集的MIMO 雷达杂波信号稀疏恢复模型，令fr,p = fs,p 为接收阵归一化空间频率，ft,p = γfs,p 为发射阵归一化空间频率，则MIMO 雷达杂波空时导向矢量可以写成关于三维频率的范德蒙德向量形式，即
假设连续空时平面上的所有杂波空时导向矢量表示的集合为三维原子集A，即
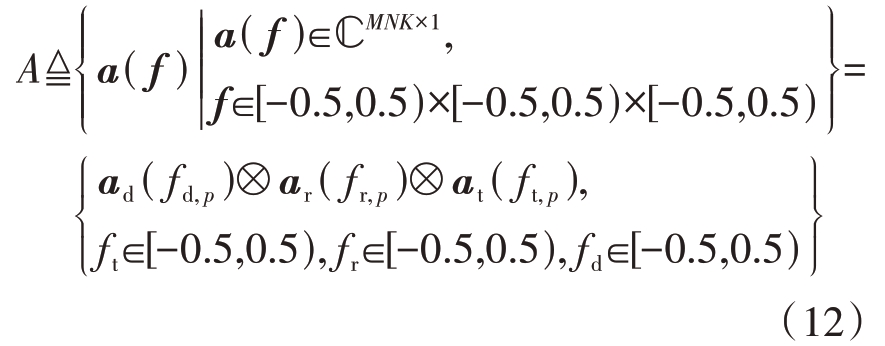
式中，f 为杂波的发射阵、接收阵归一化空间频率和归一化多普勒频率ft，fr和fd组成的三维频率，即f =( ft,fr,fd)。
此时，基于式（12）可以得到杂波信号Xc 的ℓ0范数，表示形式为
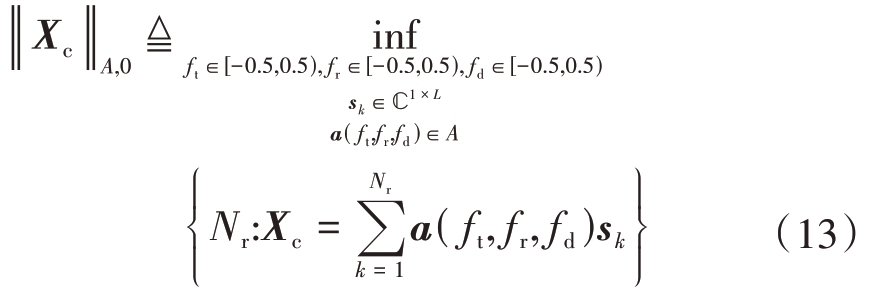
式中，Nr 为原子的个数，即杂波秩。Xc 可以通过求解下式的原子ℓ0范数最小化获得，即
式中，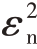
为噪声水平。由‖ ‖Xc A,0 = rank(Rc)= Nr可知，Xc 和杂波子空间T(B)可以通过求解秩最小化优化问题估计得到，即
式中，rank(·)表示矩阵的秩。由于秩最小化优化问题是NP-hard 难题，通过对秩约束进行凸松弛，式（15）可以转化为原子范数最小化问题，即
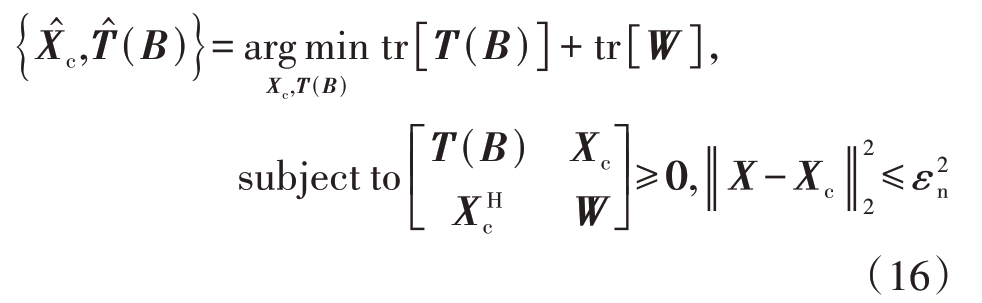
式中，tr[·]为迹运算，T(B)为MNK × MNK 的三重块Topelitz矩阵，即
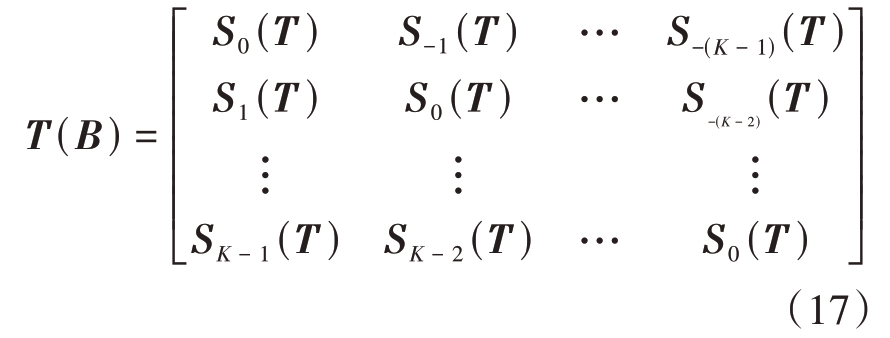
式中，Si(T)(1 - K ≤i ≤K - 1) 为MN × MN 的块Topelitz矩阵，即
式中，Ti,j(1 - M ≤j ≤M - 1)为N × N 的Topelitz 矩阵，即
通常求解式（16）的对偶问题来获取原始问题的解，即
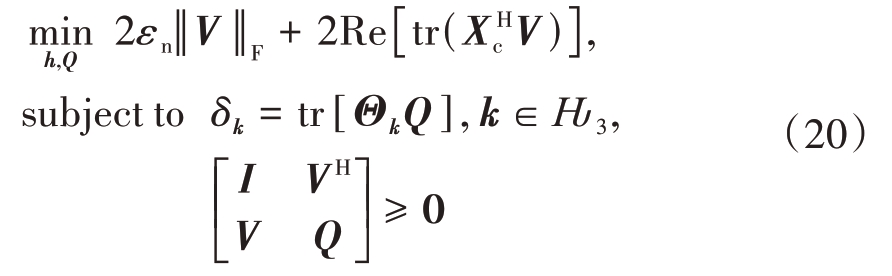
式中，Re[·]为取实部运算，V ∈ℂMNK × L 为Xc 的对偶变量，Θk = Θk1 ⊗Θk2 ⊗Θk3，Θk1，Θk2，Θk3分别为格拉姆矩阵，Q ∈ℂMNK × MNK为具有低秩及三重Topelitz矩阵结构特性的半正定埃尔米特矩阵［18］，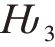
表示半空间，k=(k1,k2,k3), -M ≤k1 ≤M, -N ≤k2 ≤N,-K ≤k3 ≤K，δk的取值为
通过求解式（20）可以获得杂波子空间和杂波分量的估计值
，对
进行特征值分解，进而得到杂波协方差矩阵的估计值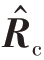
，即
其中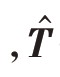
(B) = U∑U-1表示特征值分解。
则待检测距离单元的CCM 估计值
和MIMO雷达空时滤波器的自适应权向量ω 可以分别表示为
其中，at( ft, fr, fd)为待检测距离单元的空时导向矢量，IMNK 为MNK × MNK 的单位向量，σ2 为噪声功率。
本文算法的具体操作步骤如下：
步骤1：根据式（16）对多快拍训练样本数据X进行稀疏恢复，获得杂波子空间的估计值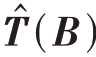
；
步骤2：根据式（22）对杂波子空间估计值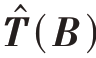
进行特征值分解，得到杂波协方差矩阵的估计值
；
步骤3：由式（23）估计待检测距离单元的杂波加噪声协方差矩阵的估计值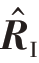
；
步骤4：由式（24）计算MIMO 雷达空时滤波器的自适应权向量ω。
4 仿真实验分析
本节利用仿真实验评估所提出的基于三维原子范数的机载MIMO 雷达STAP 算法的性能，使用3 个空时快拍作为训练样本，分别仿真格点失配问题产生时，本文方法、文献［14］中的OGSBI 方法及文献［18］中的二维ANM 方法等3 种离网方法和文献［5］中的FOCUSS 方法及文献［6］中的SBL 方法等2种方法的杂波谱和信干噪比损失，信干噪比损失中各曲线均是进行100 次蒙特卡罗仿真实验所得。机载MIMO雷达系统参数设置如表1所示。
表1 机载MIMO雷达系统参数
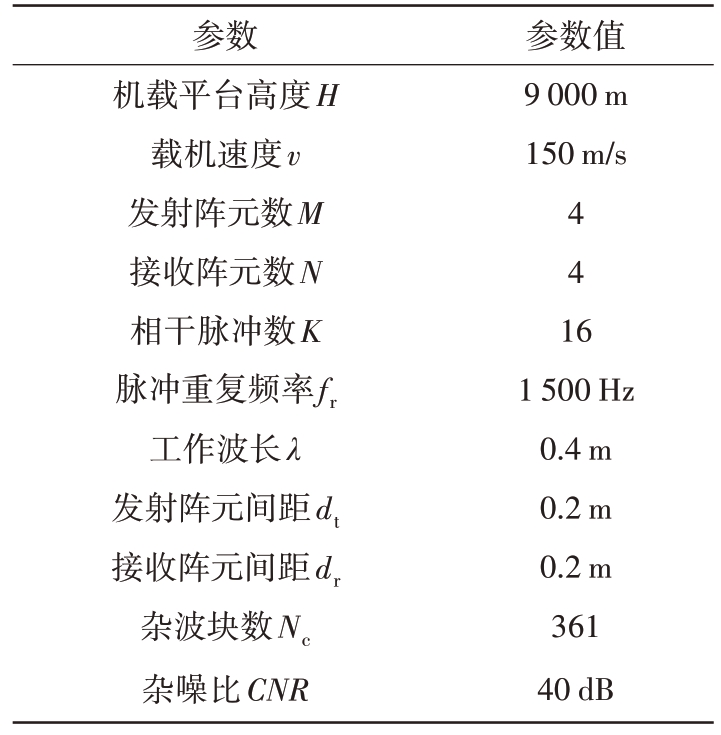
参数机载平台高度H载机速度v发射阵元数M接收阵元数N相干脉冲数K脉冲重复频率fr工作波长λ发射阵元间距dt接收阵元间距dr杂波块数Nc杂噪比CNR参数值9 000 m 150 m/s 4 4 16 1 500 Hz 0.4 m 0.2 m 0.2 m 361 40 dB
此外，仿真实验中各算法参数设置：OGSBI 方法的网格分辨率设置为0.02，迭代终止条件为tol =10-4，最大迭代次数为2 000，FOCUSS 方法和SBL方法的网格离散化系数ρs = ρd = 4，FOCUSS 方法的正则化参数为λ = 10-2，采用l0.8范数，SBL方法的正则化参数初始值为λ0 = 10-2，超参数修剪阈值为γ = 10-4，FOCUSS方法和SBL方法的最大迭代次数分别为800和2 000。
4.1 杂波谱估计对比
为了分析格点失配情况下5 种方法的杂波谱估计性能，MIMO 雷达阵列分别配置为正侧视阵（偏航角ϕ = 0°，β = 1.2）和非正侧视阵（偏航角ϕ = 90°）两种方式，采用Capon 谱（最小方差谱）对杂波谱进行描述，Capon 谱是用于分析杂波谱的高分辨谱，Capon谱定义为
图3为正侧视阵存在格点失配（偏航角ϕ = 0°,β = 1.2）情况下的杂波Capon 谱估计结果。从图中可以看出，FOCUSS 方法和SBL 方法估计的杂波谱均有明显展宽，且分辨率不高，这是因为这两种方法都是基于固定离散字典实现的，在构造字典时由于无法准确获取杂波脊斜率，杂波脊线和离散化的网格点不能完全对准，导致格点失配问题产生，其估计结果只能落在划分好的离散网格点上，字典网格的疏密影响估计性能。OGSBI方法动态解决了格点失配误差，其估计结果好于FOCUSS 方法和SBL 方法，然而模型近似引入的误差限制了其估计性能的提升。二维ANM 方法虽然避免了网格化方法因构造离散字典而带来的格点失配问题，但系统自由度的损失限制了其估计精度的提高。而本文方法充分利用了系统自由度，其估计的杂波谱集中分布在真实杂波脊线附近，且十分接近真实杂波谱，验证了本文方法在正侧视阵存在格点失配情况下的杂波谱估计性能优于基于字典网格的稀疏恢复方法和二维ANM 方法。
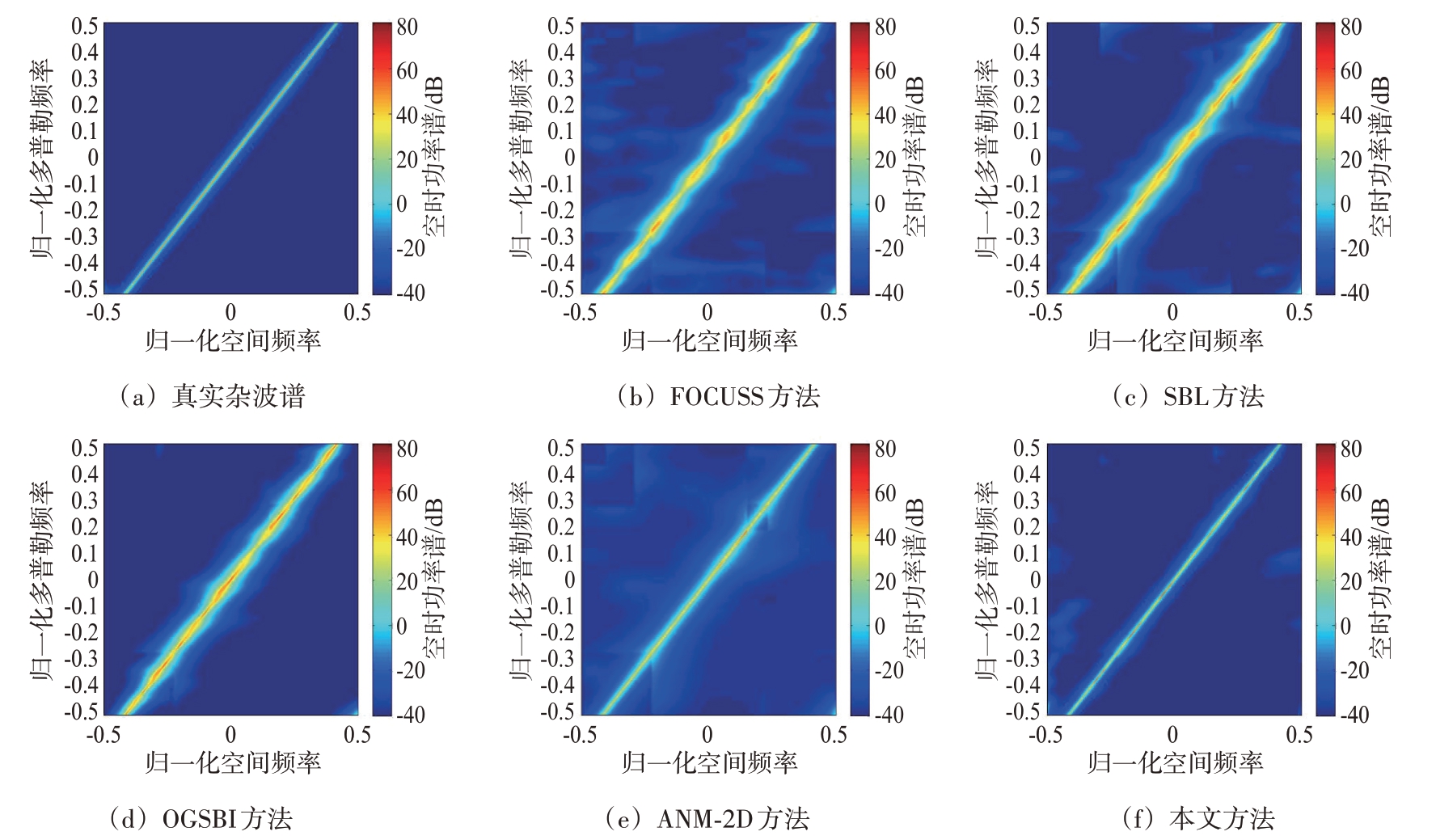
图3 正侧视阵存在格点失配（偏航角ϕ = 0°,β = 1.2）情况下的杂波Capon谱估计
图4 为非正侧视阵（偏航角ϕ = 90°）情况下的杂波Capon谱估计仿真图。从图中可以看出，在非正侧视阵情况下，FOCUSS 方法、SBL 方法、OGSBI方法估计的杂波谱均较正侧视阵存在格点失配情况更为模糊，展宽十分严重，这是由于在非正侧视阵情况下的杂波脊线沿椭圆分布，杂波脊线和离散化的网格点存在明显偏移，只有少量离散网格点和杂波脊线完全对准，格点失配问题更加严重，二维ANM 方法虽然不受格点失配问题的影响，但系统自由度的损失限制了其估计性能的提升，而本文方法依然能够获得较为清晰的杂波谱，且无明显展宽，验证了本文方法在非正侧视阵情况下的杂波谱估计性能优于基于字典网格的稀疏恢复方法和二维ANM方法。
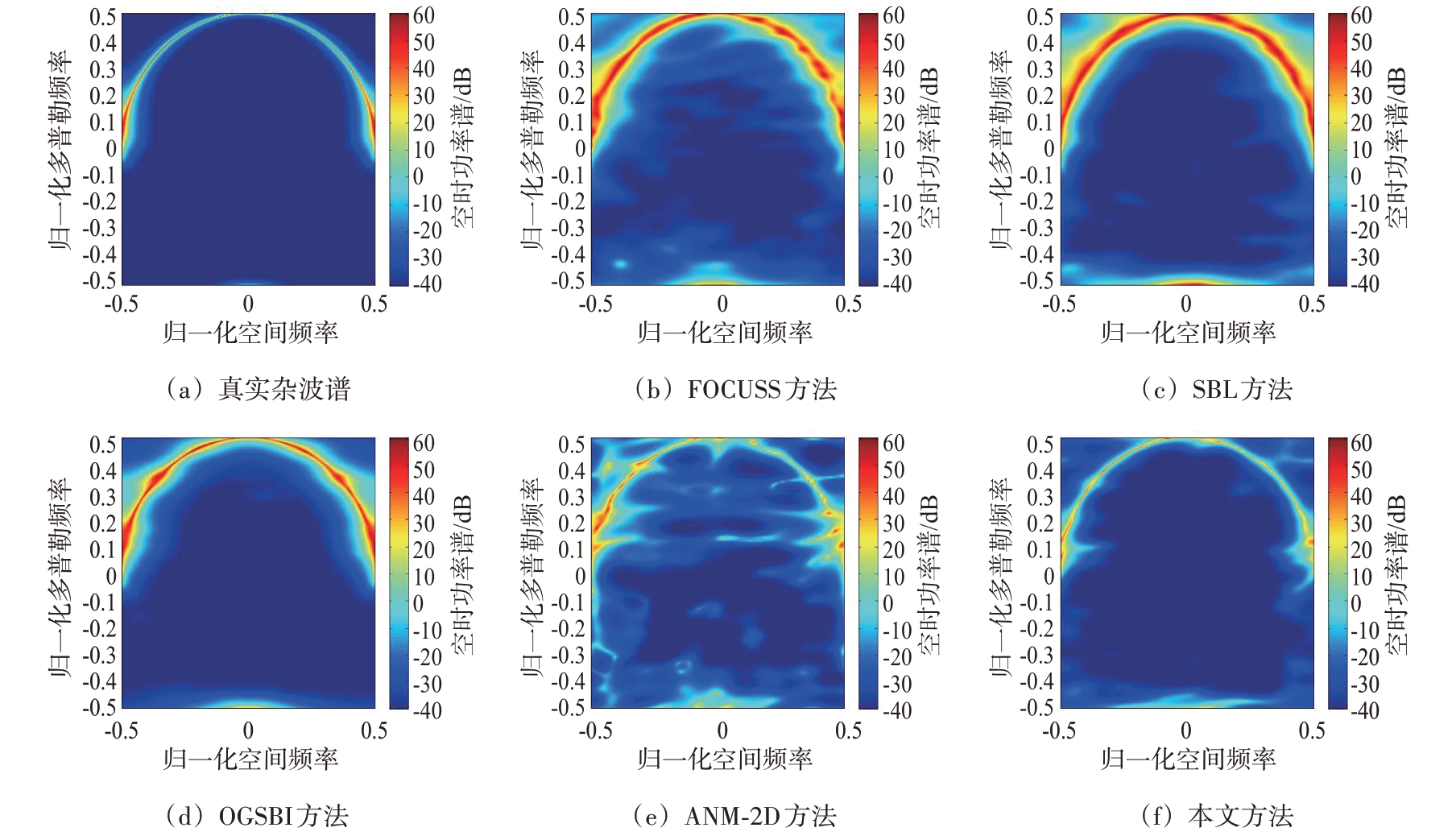
图4 非正侧视阵（偏航角ϕ = 90°）情况下的杂波Capon谱估计
4.2 信干噪比损失对比
本实验采用信干噪比损失（Signal-to-Interference-plus-Noise Ratio Loss，LSINR）评价指标作为5 种方法的杂波抑制性能衡量标准，SINR 损失LSINR 定义为空时滤波器输出SINR 与仅有白噪声的输出SINR的比值，即
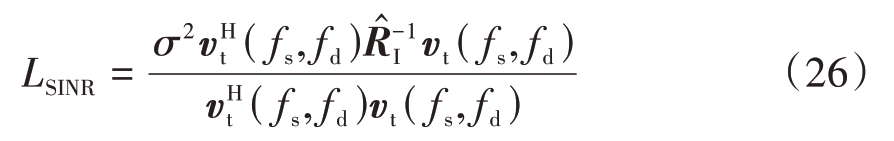
式中，vt( fs,fd)为目标信号导向矢量，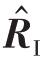
为各方法获取的CCM估计值。
图5为格点失配情况下的信干噪比损失曲线。其中，图5（a）是正侧视阵存在格点失配情况（偏航角ϕ = 0°,β = 1.2）下的信干噪比损失曲线，图5（b）是非正侧视阵情况（偏航角ϕ = 90°）下的信干噪比损失曲线。从图5（a）可以看出，对于正侧视阵，FOCUSS 方法、SBL 方法和OGSBI 方法由于构造的离散字典中未能有足够多的网格点与杂波脊线对准，存在格点失配问题，其主杂波区的凹口会有展宽，而本文方法和二维ANM 方法在主杂波区无明显展宽，但本文方法得到的SINR 损失曲线最接近最优滤波器的SINR 损失曲线。从图5（b）可以看出，对于非正侧视阵，由于存在更为严重的格点失配问题，FOCUSS 方法、SBL 方法、OGSBI 方法估计的杂波子空间和真实杂波子空间出现较大偏差，导致其主杂波区的凹口展宽非常严重，而本文方法和二维ANM 方法在该区仍可形成较窄的零陷，但在其他区域的SINR 损失曲线较二维ANM 方法更接近最优滤波器的SINR 损失曲线，具有较好的杂波抑制性能和慢速运动目标检测能力。
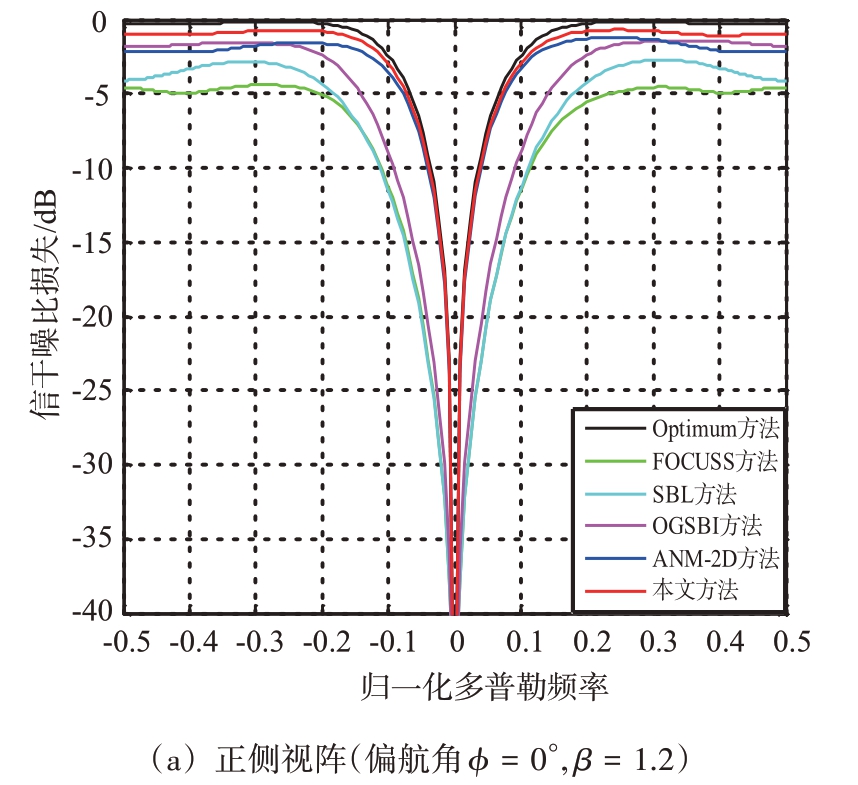
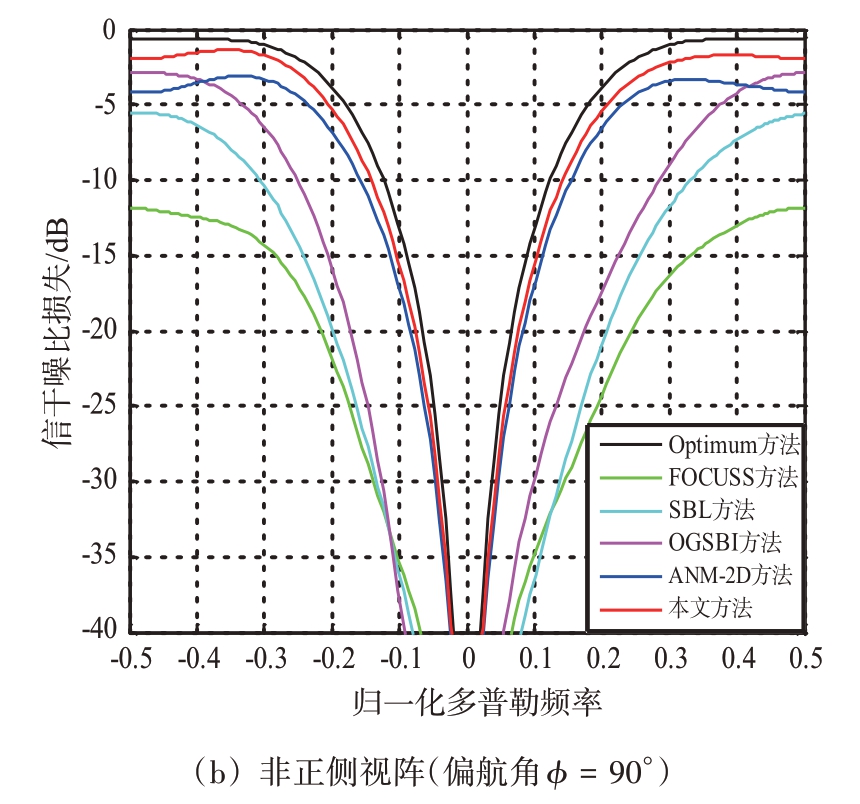
图5 格点失配情况下的信干噪比损失曲线
5 结束语
本文提出了一种基于三维原子范数的机载MIMO 雷达空时自适应处理算法。该方法利用杂波谱在空时二维平面上固有的稀疏性，根据低秩矩阵恢复理论构造了基于三维连续原子集的MIMO 雷达杂波信号稀疏恢复模型，实现了ANM 的半正定规划求解方法，获得了高分辨率估计的杂波空时谱。仿真实验结果表明，在格点失配情况下本文方法获得杂波空时谱的分辨率和SINR 损失性能优于对比的4种方法，体现了本文方法的优越性。
［1］何子述，程子扬，李军，等.集中式MIMO 雷达研究综述［J］.雷达学报，2022，11（5）:805-829.
［2］ XIONG Yuanyi, XIE Wenchong, WANG Yongliang.Space Time Adaptive Processing for Airborne MIMO Radar Based on Space Time Sampling Matrix［J］.Signal Processing,2023,211:109119.
［3］史靖希.机载非均匀阵列雷达空时自适应处理算法研究［D］.成都：电子科技大学，2023.
［4］SUN Guohao,LI Ming,TONG Jun,et al.Structured Clutter Covariance Matrix Estimation for Airborne MIMO Radar with Limited Training Data［J］. IEEE Geoscience and Remote Sensing Letters,2022,19:1-5.
［5］阳召成，黎湘，王宏强.基于空时功率谱稀疏性的空时自适应处理技术研究进展［J］.电子学报，2014，42（6）:1194-1204.
［6］DUAN Keqing,WANG Zetao,XIE Wenchong,et al.Sparsity-Based STAP Algorithm with Multiple Measurement Vectors via Sparse Bayesian Learning Strategy for Airborne Radar［J］.IET Signal Processing,2017,11（5）:544-553.
［7］徐文先，高志奇，徐伟，等.基于迭代自适应的字典校正空时自适应处理算法［J］.信号处理，2021，37（11）:2216-2226.
［8］高志奇，王雪香，黄平平，等.一种改进的稀疏恢复直接数据域STAP方法［J］.信号处理，2023，39（6）:1060-1069.
［9］CUI Ning, XING Kun, DUAN Keqing, et al. Knowledge-Aided Block Sparse Bayesian Learning STAP for Phased-Array MIMO Airborne Radar［J］.IET Radar Sonar&Navigation,2021,15（12）:1628-1642.
［10］YIN Qiuyue, YI Jinwang, TANG Jun, et al. A Novel Orthogonal Matching Pursuit Algorithm Based on Reduced-Dimension Dictionary for Airborne MIMO Radar［C］//2021 2nd International Symposium on Computer Engineering and Intelligent Communications, Nanjing, China:IEEE,2021:202-206.
［11］MCMULLEN B, KIM S J. Performance of Compressed Sensing MIMO Radar Based on Low-Rank Matrix Recovery［C］// 2022 IEEE Military Communications Conference,Rockville,MD,USA:IEEE,2022:330-335.
［12］BAI Gatai, TAO Ran, ZHAO Juan, et al. Parameter-Searched OMP Method for Eliminating Basis Mismatch in Space-Time Spectrum Estimation［J］. Signal Process,2017,138:11-15.
［13］DUAN Keqing, LIU Weijian, DUAN Guangqing, et al.Off-Grid Effects Mitigation Exploiting Knowledge of the Clutter Ridge for Sparse Recovery STAP［J］. IET Radar Sonar&Navigation,2018,12（5）:557-564.
［14］YANG Zai, XIE Lihua, ZHANG Cishen. Off-Grid Direction of Arrival Estimation Using Sparse Bayesian Inference［J］.IEEE Trans on Signal Processing,2013,61（1）:38-43.
［15］CANDÈS E J, FERNANDEZ-GRANDA C. Towards a Mathematical Theory of Super-Resolution［J］. Communications on Pure and Applied Mathematics, 2014, 67（6）:906-956.
［16］TANG Gongguo, BHASKAR B N, SHAH P, et al. Compressed Sensing off the Grid［J］.IEEE Trans on Information Theory,2013,59（11）:7465-7490.
［17］XU Weiyu, CAI Jianfeng, MISHRA V K, et al. Precise Semidefinite Programming Formulation of Atomic Norm Minimization for Recovering D-Dimensional（D≥2）Offthe-Grid Frequencies［C］//2014 Information Theory and Applications Workshop, San Diego, CA, USA: IEEE,2014:1-4.
［18］FENG Weike,GUO Yiduo,ZHANG Yongshun,et al.Airborne Radar Space Time Adaptive Processing Based on Atomic Norm Minimization［J］. Signal Processing, 2018,148:31-40.