0 引 言
螺栓连接作为工程结构中最常采用的连接形式,具有强度高、可拆卸等优点,在结构服役过程中承担着载荷传递的关键作用[1-2]。然而螺栓所处的机械结合面处受力形式往往较为复杂,一方面存在着螺栓预紧而产生的预应力,另一方面也承受着外部机械载荷。在航空结构中,随机振动作为一种常见的载荷工况,对机载设备的寿命及可靠性有着至关重要的影响[3-4],因此螺栓连接在振动载荷下的疲劳失效便成为设计中所必须考虑的问题。
受限于振动疲劳问题的复杂性和随机性,目前工程中最为可靠的研究方法仍以试验为主,试验中对振动载荷的模拟由早期的正弦载荷等效[5]发展为基于功率谱密度曲线控制的随机加载。近年来,学者们基于PSB 拟牛顿算法[6]及自适应逆控制与滑模控制组成的复合控制策略[7]以较高的精度实现了功率谱密度曲线的复现。在测量方法上,Rathish 等[8]提出了一种在试验中对结构损伤的原位监测手段,可以对结构的危险点进行预判。另一方面,计算技术的发展也使得仿真计算在振动疲劳研究中的作用愈发重要,马雅丽等[9]基于有限元方法改进了螺栓连接刚度模型;华一畅等[10]基于应力严重系数法研究了螺栓孔在振动疲劳载荷下的疲劳寿命;朱光宇等[11]利用有限元分析对螺栓在随机振动载荷下预紧力的松弛进行了预测。
在机载设备的设计过程中,频繁采用试验的方法校核螺栓的疲劳强度势必带来成本与设计周期的极大提高。本文基于Abaqus软件对某型机载雷达随机响应进行仿真分析,提取该过程中关键部位连接螺栓的载荷,并基于最小应力法理论公式对比了两种螺栓的疲劳安全系数,为最终连接螺栓的选型及机载雷达结构的安全性设计提供参考。
1 随机振动中螺栓疲劳强度分析方法
本文中所研究的螺栓位于机载雷达基座和负载的连接处,在载荷传递中起主导作用,因此对于其在振动疲劳载荷下的安全性有很高要求。螺栓本身作为一个包含螺帽、螺牙、螺杆等结构的零件,其疲劳强度受到几何形式、母材性能、加工工艺、表面处理等多方面因素的影响,很难从疲劳理论出发推导螺栓疲劳的解析解,因此在工程上多采用经验公式进行研究。由于螺栓自身存在预紧力,其所经受的疲劳载荷往往是非对称的,此时基于最小应力法可以估算螺栓的疲劳安全系数ns,其表达式为[12]
式中[n]为许用安全系数,本文中取为1.2,σ-1为材料对称循环拉压疲劳强度,σmin为循环过程中螺栓的最小应力,σa为螺栓应力幅,Kσ和Ψσ为试件材料常数,其中Ψσ为平均应力的折算系数,对于合金钢取0.2~0.3,而Kσ为疲劳极限综合影响系数,其表达式为
式中kσ为有效应力集中系数,εσ为尺寸系数,βσ与βq分别为螺栓的表面质量系数以及表面强化系数。本文比较了HB1-101 以及PH13-8Mo 两种M5 摩擦型航标螺栓,两种螺栓采用了不同的合金体系,并在表面处理手段上有所差异。表1 列出了两种航标螺栓的材料参数。
表1 螺栓材料参数表

材料参数σ-1 kσ εσ βσ βq ψσ HB1-101 367 2.61 1 0.8 1 0.3 PH13-8Mo 605 2.9 1 0.75 1 0.25
公式(1)表明,计算疲劳螺栓的安全系数ns关键在于获取振动过程中的应力幅σa以及最小应力σmin。在理想随机过程中,螺栓载荷服从高斯分布,设其均方根为σ,则载荷分布在[-3σ,3σ]区间内的概率达到99.73%,因此可以忽略[-3σ,3σ]区间以外应力对于结构疲劳的影响[13]。此外,文献[14]中结果表明摩擦型螺栓结合面处的剪切载荷仅有5%~10%通过螺栓承担,其余由预紧力带来的结合面摩擦力承担,因此本文中忽略螺栓剪切载荷的影响,仅考虑由轴向载荷引起的螺栓疲劳。设随机振动中螺栓载荷均方根值为Frms,则螺栓受到的最大轴向载荷Fmax与最小轴向载荷Fmin可以表示为

式中F0为螺栓预紧力,本文取7 500 N,Cb为螺栓刚度,Cm为被连接件刚度,本文根据螺栓与被连接件之间的几何及材料关系取Cm=8Cb,由此可以计算螺栓实际轴向载荷,则螺栓的σa与σmin可以表示为

式中d 为螺栓的小径。将式(2)、(4)和(5)带入式(1)后即可得到螺栓在振动疲劳载荷下的安全系数。
2 有限元分析模型
为获取随机振动过程中螺栓力均方根值Frms,在Abaqus软件中建立某型机载雷达有限元模型如图1所示,模型中的关键连接点为负载与基座间的8 颗连接螺栓,如图1 中虚线框所示。仿真前对模型的重心位置进行了调节,确保重心与实际结构一致。模型共包含764 793 个单元,其中基座以及安装板均采用实体单元(C3D8R),其他部件采用壳单元。模型中基座与转接板材料为TC4 钛合金,密度为4 430 kg/m3,弹性模量为116 GPa,泊松比为0.31。螺栓连接采用Abaqus 软件中的连接器单元(CONN3D2)进行等效,考虑到实际结构中预紧力使得结合面间紧密接触,仿真中将连接器单元设置为刚性连接。仿真模型的约束点设置在基座外缘的螺栓孔处,该处在实际结构中与载机平台相连。仿真中的随机振动载荷通过功率谱密度函数进行控制,频率范围为0~500 Hz,X,Y 和Z 方向振动的功率谱密度曲线一致,如图2所示。

图1 机载雷达有限元模型及关键螺栓分布
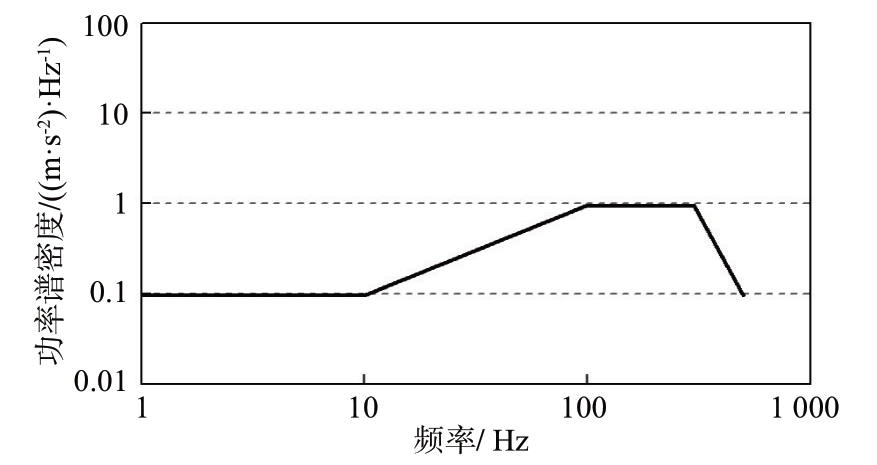
图2 随机振动激励的功率谱密度曲线
3 基于模态叠加法的随机响应分析
3.1 模态分析
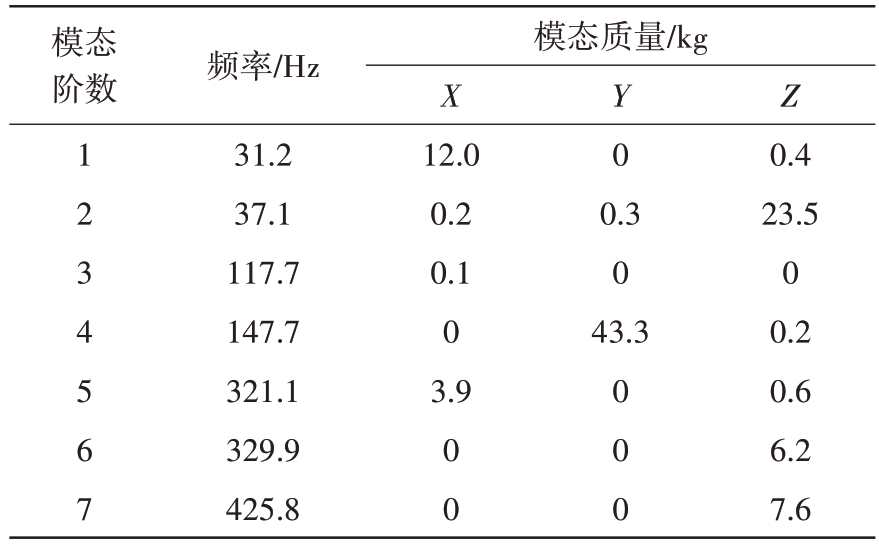
在进行结构随机响应分析前首先对结构进行模态分析以确定结构的固有频率及振型,结构在0~500 Hz内的固有频率及模态质量如表2所示(表中忽略小于0.1 kg 的模态质量),其中前4 阶模态的振型图如图3所示。

图3 0~500 Hz内结构响应的前4阶模态振型
表2 0~500 Hz内结构各阶模态及模态质量
模态阶数模态质量/kg 频率/Hz 31.2 37.1 117.7 147.7 321.1 329.9 425.8 Z 1 2 3 4 5 6 7 X 12.0 0.2 0.1 0 3.9 Y0 0.3 0 43.3 0 0 0 0 0 0.4 23.5 0 0.2 0.6 6.2 7.6
从表2 可以看出,结构在500 Hz 以内共存在7阶振动模态。三向振动的模态质量之和分别占总质量的34%(X向),91%(Y向)以及81%(Z向)。结合图3 中的振型云图,可以看出系统第一阶模态(31.2 Hz)为X 向摆动,是系统在X 方向的主振模态。Y 向的主振模态为第四阶(147.7 Hz),即系统上下摆动。Z向的主振模态为第二阶(37.1 Hz),表现为系统前后摆动。在这些频点附近的载荷激励将显著影响结构的整体响应。
3.2 随机振动响应分析
按照图2 中所示的功率谱密度基于模态叠加法对结构在三向随机振动下的响应进行仿真分析,并提取8颗连接螺栓轴向力均方根值随频率的变化曲线,结果如图4 至图6 所示。图中的螺栓编号与图1一致。

图4 X向激励下螺栓轴向力均方根随频率变化

图5 Y向激励下螺栓轴向力均方根随频率变化
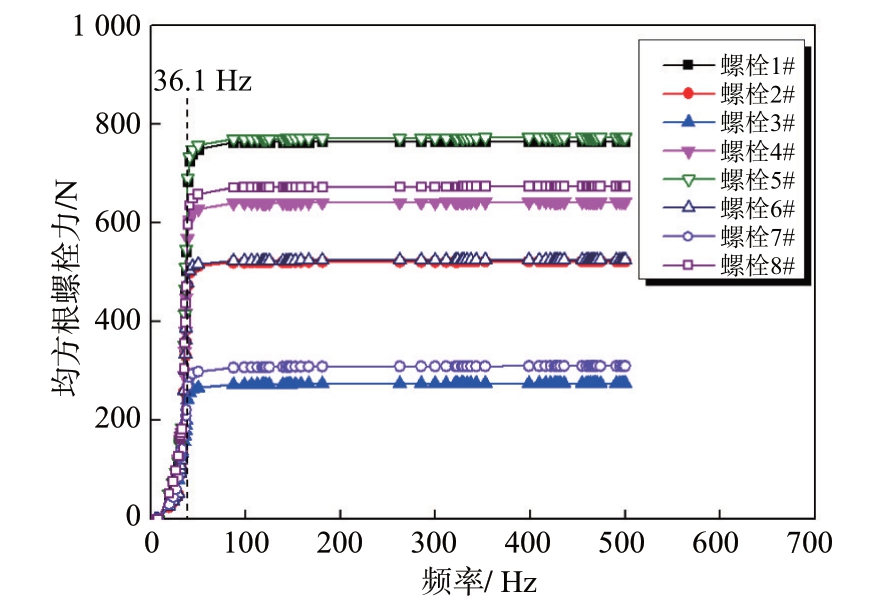
图6 Z向激励下螺栓轴向力均方根随频率变化
从图中可以看出,均方根螺栓力随频率的变化曲线存在明显的阶跃行为,表明该频点附近的载荷激励使得螺栓力明显增加,对比上一节中的模态分析结果,可以发现X方向和Z方向的随机振动中螺栓力发生阶跃的频率均为该方向上的主振频率,而Y 向振动时螺栓力的响应则较为复杂,存在两次明显的阶跃,其中第一次发生在结构X向主振频率上,这是由Y 向激励在X 向所引起结构耦合响应导致的,而第二次阶跃则发生在结构的Y向主振频率上。此外在图中也可以看出处于不同位置的螺栓在不同方向激励下的响应也表现出明显差异,为更直观体现这种影响,将三向随机振动下均方根螺栓力统计如表3所示。
表3 三向随机振动下均方根螺栓力统计

螺栓编号均方根螺栓力/N 1#2#3#4#5#6#7#8#X向振动210 642 690 311 211 634 704 320 Y向振动224 537 479 187 270 574 496 174 Z向振动765 522 276 642 773 525 310 674
从表3 结果可以看出,在X 向激励下,2#,3#,6#和7#螺栓的均方根螺栓力明显更大,对比图1中的螺栓位置关系,可以发现这4 颗螺栓在X 方向处于离圆心较远的位置,因而在下方负载沿X向摆动过程中,这4 颗螺栓的力臂较长,在载荷传递过程中起主导作用。而在Z 向振动中则表现出相反的趋势。另一方面,当负载的重心完全与螺栓分度圆圆心完全重合时,结构在Y向激励下的螺栓力应当趋于一致,但由于实际重心存在一定偏心,Y 向激励会引起X 向的耦合响应,因此,2#,3#,6#和7#螺栓载荷显著增加。这种振动模式将对结构的整体疲劳安全性带来不利影响。
3.3 连接螺栓强度校核
利用公式(1)到公式(5)并结合表3中的结果,可以计算螺栓在三向随机振动中的疲劳安全系数(各向振动中均取最大螺栓力进行校核)结果,如表4所示。
表4 三向随机振动下螺栓疲劳安全系数

安全系数螺栓类型HB1-101 PH13-8Mo X向振动1.14 1.39 Y向振动1.16 1.41 Z向振动1.13 1.38
计算结果表明HB1-101 螺栓在随机振动疲劳载荷下的安全系数仅为1.13,不满足安全系数1.2的设计要求,当改为PH13-8Mo 后,安全系数达到1.38,考虑到该处为结构关键连接处,应当选择PH13-8Mo 螺栓。在实际结构中应用PH13-8Mo后,雷达整机顺利通过振动测试。
4 结束语
本文采用螺栓疲劳经验公式结合有限元仿真计算对某型机载雷达关键连接处所采用的两款螺钉进行了校核,可以得到以下结论:1)通过有限元仿真结合工程经验公式,可以对连接螺栓的疲劳安全系数进行预估,有利于在设计阶段识别风险,保障结构在振动疲劳载荷下的安全性;2)螺栓力主要受到该方向激励下结构主振型的影响,因此设计时应当尽量将结构的三向主振频率与激励载荷能量较高的频段隔离;3)当结构重心存在偏心时,偏心力矩的存在会引起结构的耦合模态并加大螺栓载荷,在设计时应当通过配平的方式予以修正。
[1]LIAO Jingping,ZHANG Jianfu,FENG Pingfa,et al.Interface Contact Pressure-Based Virtual Gradient Material Model for the Dynamic Analysis of the Bolted Joint in Machine Tools[J]. Journal of Mechanical Science and Technology,2016,30(10):4511-4521.
[2]丁振东,赵振华,罗刚,等.摩擦型螺栓连接冲击载荷传递特性试验[J].航空发动机,2023,49(3):105-111.
[3]谭贵红,张志毅,宋志行,等.机载雷达吊舱的结构设计[J].雷达科学与技术,2010,8(3):284-288.
[4]瞿绍奇,孙英超,邬亨贵,等.飞行器径向连接螺栓振动断裂分析[J].航空学报,2021,42(5):358-363.
[5]孙宁,李瑰贤.随机振动信号的一种简单模拟计算方法[J].振动与冲击,2000,19(2):50-53.
[6]廖洋,范大莽,张博鑫,等.电液振动台加速度随机振动控制[J].液压与气动,2021,45(12):45-50.
[7]王志超,关广丰,熊伟,等.两自由度电液振动台随机波形复现控制[J].组合机床与自动化加工技术,2023(12):113-116.
[8]RATHISH P K, OSHIMA T, MIKAMI S, et al. Damage Identification in a Lightly Reinforced Concrete Beam Based on Changes in the Power Spectral Density[J].Structure and Infrastructure Engineering,2012,8(8):715-727.
[9]马雅丽,刘国超,危家勇,等.基于有限元法改进螺栓连接刚度模型[J].组合机床与自动化加工技术,2021(3):45-48.
[10]华一畅,姚卫星,黄杰.连接件振动疲劳寿命分析的应力严重系数法[J].振动、测试与诊断,2023,43(2):349-354.
[11]朱光宇,郑保仲.随机振动螺栓松动数值仿真分析[J].机械设计与制造,2018(1):233-235.
[12]机械工程师手册第二版编辑委员会.机械工程师手册[M].2版,北京:机械工业出版社,2004.
[13]关迪,范学领,肖滨,等.某型机载模块的随机振动疲劳分析[J].机械强度,2019,41(1):66-71.
[14]熊亮.高强摩擦型螺栓连接的节点板力学性能分析[D].北京:北京交通大学,2017.