0 引 言
针对未来机载雷达宽带与雷达内部电子战侦收一体化综合软硬件设计的发展趋势,以及雷达系统更高精度成像要求信号带宽能够达到1.8~3.6 GHz级甚至更高;电子战侦收系统[1]小型化与集成化设计要求单模块能够实现更大频带信号侦测,进而需要单个通道的处理带宽能够达到2 GHz级及以上,从而改变多个1 GHz级侦收带宽拼接带来的射频接收与数字采样硬件规模大的缺点。如此大带宽信号的数字中频采样,要求ADC 采样率要达到4~8 GS/s,而对数字中频信号的预处理要首先进行宽带数字下变频。工程应用上对于高速ADC 采样率大于500 MS/s 的数字接收信号预处理,通常基于并行多相滤波架构实现宽带数字下变频,即采用扩展数字中频解析信号并行度来换取FPGA 对数字信号合适的处理速度,但是代价是增加FPGA 乘法器的资源消耗。当数字中频信号解析和多相滤波的并行度随着ADC 采样率的不断增加而扩大时,采用传统并行多相滤波算法的宽带数字下变频预处理,必将导致FPGA 乘法器资源消耗成倍增加,从而限制FPGA 对大带宽数字中频信号的预处理能力。
对高采样率、大带宽信号的数字下变频预处理,部分研究文献[2-3]提供了一些解决措施:通过多级FIR 和HB 滤波器级联逐级降低处理速率、对传统并行多相滤波进行结构优化以降低资源,以及根据基带信号抽取倍数改进滤波架构等,这些方法能够缓解ADC 采样率不高时的FPGA 预处理压力,但很难灵活适用于并行度较高时,需要FPGA大量乘法器进行多相滤波运算的应用需求。
本文采用并行滤波的快速运算形式,在传统并行2相滤波基础上首先构建出其快速运算形式,然后再依据2 相快速滤波的构建过程得到快速滤波的4 相结构,依次类推最终构建出并行16 相快速滤波运算架构。基于并行16相快速滤波算法实现高速中频采样信号的数字下变频预处理,降低多相滤波的子滤波器并行度,进而大幅降低FPGA乘法器资源消耗,为机载雷达宽带接收或电子战大带宽侦收系统的采样信号预处理提供一种有效的工程实现解决方法。
1 并行16相快速滤波算法
1.1 快速滤波构建
设FIR 数字低通滤波器系数为H( z ),输入信号为X( z ),输出信号为Y( z ),那么数字下变频滤波过程可表示为
将式(1)按传统并行多相分解方式进行2相分解,得到
根据Winograd 短卷积算法,将式(2)构建为并行2相滤波的快速运算形式[4]:
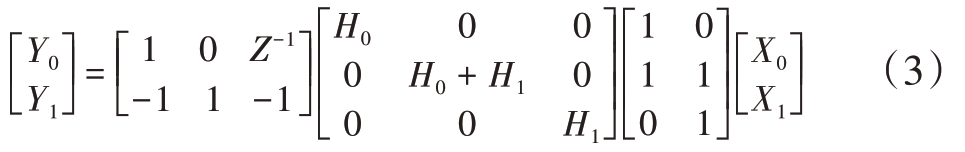
即

比较式(2)和式(4)的并行2 相滤波的传统方式和快速算法架构,其关键的滤波运算过程并行度由4 减少至3,即快速算法方式仅需要3 个并行支路滤波器运算,相比4个并行支路的传统方式能够节省FPGA乘法器资源25%。
并行4相快速滤波可通过由3组并行2相快速滤波构建而成,其实现架构如图1 所示[5]。由于每个2 相快速滤波包含3 个并行支路滤波器,那么并行4 相快速滤波算法的子滤波器并行度即为3 ×3 = 9。相比传统并行4 相滤波的子滤波器并行度为16,快速滤波算法的FPGA乘法器资源仅为传统方式的9 16。
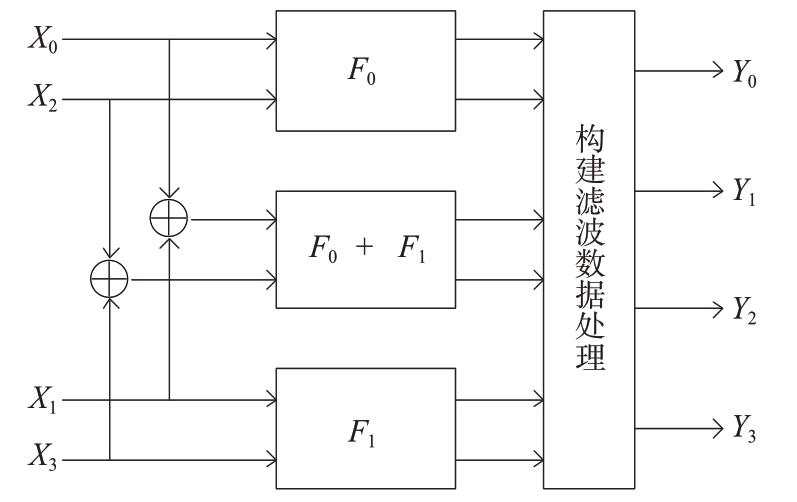
图1 并行4相快速滤波构建架构
依此类推,由3 组并行4 相快速滤波构建并行8 相快速滤波,其子滤波器运算并行度为3 × 9 =27;进而并行16相快速滤波通过3组并行8相快速滤波构建,其子滤波器运算并行度为3 × 27 = 81。而传统并行16相滤波的子滤波器运算并行度达到了16 × 16 = 256,由此得出采用快速滤波算法架构的FPGA乘法器资源仅为原来的81 256。
1.2 16相快速滤波
设Xi,Hi,Yi(i = 0,1,2,…,9,a,b,…,f )分别表示并行16 路输入信号、数字滤波器并行16 相分解系数以及并行16 路滤波输出信号。同时,令Y'表示81个子滤波器,且定义如下:

根据快速滤波的构建方法,得到并行16相快速滤波算法表达式:

根据上述16 相快速滤波计算公式,宽带数字下变频的并行16 支路低通滤波输出是对81 个子滤波器运算结果的再次组合,即其核心运算并行度只有81。相比传统并行滤波架构的256 个子滤波器及组合,快速滤波的运算复杂度与FPGA 资源消耗都明显降低,这是工程上能够基于FPGA 实现对高采样率信号预处理的重要前提。
2 信号与滤波系数预处理
2.1 信号解析与混频
对于采样率位于4~8 GS/s 的高速采样中频预处理,由于其支路信号并行度和数据率的双重增加,在进行数字中频信号解析和数字下变频过程中,FPGA 的处理速度和资源消耗同时面临较大压力。为尽可能降低FPGA处理复杂度,高速ADC采样率fs 与大带宽信号的载频fc 通常要符合带通采样定理,即fc =(2n + 1) fs/4(n = 0,1,2,…) 。符合这种特定关系的数字下变频的数字本振只有0 和±1三个常数,数字混频只需对信号进行加减运算,简化运算的同时也节省FPGA乘法器资源开销。
此外,由于数字本振中的常数0,使并行解析信号在数字混频的过程中也同时完成了2倍抽取。以将数字中频信号x 解析为并行度M 的多支路信号为例,即x = x0,x1,x2,…,xM - 1,数字本振实部为ni = 1,0, - 1,0,1,0,…,虚部为nq = 0,1,0, - 1,0,1,…,数字混频后基带复信号可表示为
将基带复信号实部与虚部值为0 的支路分别剔除掉,那么数字混频后的基带信号可进一步简化为
简化后的基带复信号并行度是数字中频解析信号的1 2,也相当于对数据实现了2倍抽取,这使得后续并行多相滤波的并行度也减半,降低数字下变频多相滤波运算的复杂度。
如果信号载频fc 与高速ADC 采样率fs 无法满足带通采样定理中的特定关系,则可以将fc拆解为两级:fc =(2n + 1) fs/4 + f0(n = 0,1,2,…) 。第一级载频按照本文数字混频及2倍抽取方法进行处理,然后在数字下变频后通过对基带IQ 信号进行频谱搬移的方式实现去除第二级载频f0,而不必增加多相滤波的并行度。
2.2 滤波器系数分解
数字下变频数字低通滤波实际上是时域信号与滤波器系数的线性卷积过程,设输入信号和输出信号分别为x( n )和y( n ),(N - 1) 阶FIR 滤波器为h( n ),则数字滤波计算表达式为
由于数字中频信号解析并行度M,采用基于并行多相滤波架构的数字下变频算法也需将滤波器系数分解为并行M 相[6]。多相分解后的第m 相滤波器系数可表示为

根据式(8)、式(9)和式(10)的中频信号预处理及滤波线性卷积实现过程,数字混频预处理后并行M 2 路I 信号滤波器系数为多相分解的M 2个偶数相分支,而并行M 2路Q信号滤波器系数则为M 2个奇数相分支,即
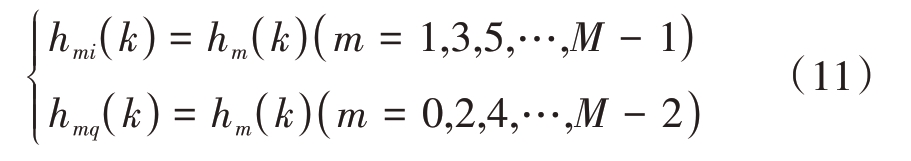
数字中频信号与滤波器系数预处理后,将并行M 路解析信号数字混频后简化为M 2 路基带复信号,滤波器系数配合这种简化方式将系数拆解为并行M 2相奇偶分支,进而可以基于并行M 2相快速滤波架构实现数字下变频低通滤波处理。
3 高采样信号预处理实现
3.1 数字下变频架构
在机载雷达或电子战系统基于FPGA 实现高速采样信号预处理,通常要确保FPGA 速率与资源的均衡。FPGA 的处理时钟不宜过高,适当速率的处理时钟有利于FPGA 在高低温环境下的时序稳定性;资源消耗也需预留足够的余量,保证FPGA工程编译可实现。FPGA 在实现多通道ADC 采样信号预处理功能,处理时钟一般不超过250 MHz,而当时钟达到300 MHz量级时,数字下变频算法等逻辑时序调试就较为困难,尤其是在-55~70 ℃的全温度工作范围内。基于此,可以将高速ADC采样率区间划分为500 MS/s~1 GS/s、1~2 GS/s、2~4 GS/s、4~8 GS/s等,中频信号数据解析并行度分别对应4、8、16 和32,这样解析后的并行支路速率基本上在250 MHz 内。不过在区间临界点则可根据工程实现需要选择适合的并行度,采样区间的划分与解析并行度并不是绝对不变的。
本文针对采样率在4~8 GS/s 区间的数字接收预处理,高速ADC采样中频信号在FPGA中解析为并行32支路,其单个支路的数据率在125~250 MS/s之间。由于中频信号解析预处理能够将并行32路信号混频及抽取至并行16 路基带复信号,进而与并行16相快速滤波算法架构结合实现数字下变频低通滤波,最终实现高速采样信号的预处理。以传统并行4 路LVDS 接口高速ADC 芯片为例,应用Xilinx FPGA 基于并行16 相快速滤波对高采样率信号进行数字下变频的实现架构如图2所示。

图2 并行16相快速滤波数字下变频架构
3.2 硬件实现与测试
由于高速ADC 采样率位于4~8 GS/s 的数字中频信号分解为32 相时,单支路的处理时钟都不大于250 MHz,位于此采样率范围内的数字中频信号预处理均可以采用本文的16 相快速滤波架构,只是不同采样率下的FPGA 处理时钟速率不同。TI公司的一款并行LVDS 接口的高速ADC 芯片ADC12DL3200,其模拟接收带宽7.8 GHz、单通道模式最大采样率为6.4 GS/s,适用于机载雷达大带宽信号或者电子战侦收系统的高速中频信号采样。本文选取某块搭载ADC12DL3200 采样芯片的数字中频接收模块、且硬件布线设计能够支持的5.6 GS/s 采样率(4~8 GS/s 之间的处理架构完全相同)为例,通过FPGA 仿真与硬件测试,验证基于16 相快速滤波架构的高采样率中频信号预处理实现过程。
采样率为5.6 GS/s 的数字中频信号如果解析为并行16 支路,则FPGA 处理时钟为350 MHz,可能会导致FPGA 对信号的后续处理在时序上很难实现;而按照本文方法解析为并行32支路、处理时钟降至175 MHz,尽管会导致多相滤波的并行度加倍、进而增加FPGA 乘法器资源数量,但资源与速率的合理均衡更符合FPGA 工程设计与应用规律。采样率fs 设置为5.6 GS/s,接收处理的信号带宽最大可达2.5 GHz,模拟信号载频设计为fc=3 fs/4=4 200 MHz符合带通采样定理。选择频率为4 209 MHz和5 450 MHz 的点频信号进行测试,中频信号解析后的频谱分析结果如图3所示。

图3 高速ADC采样中频信号频谱
数字下变频数字低通滤波器以63 阶为例,按照式(11)系数分解方法和图2 数字下变频实现架构,即N = 64,M = 32,则I 路(或Q 路)信号滤波器组的子滤波器系数个数为L = N/M = 2。根据前文分析的并行16相传统滤波和快速滤波的滤波器组并行度分别为256 和81,对I 路(或Q 路)信号分别采用一组滤波器组进行滤波,FPGA 乘法器资源比较如表1所示。
表1 并行16相传统滤波与快速滤波资源比较

滤波方式传统滤波快速滤波FPGA乘法器(DSP48E1)数量256 · L · 2 = 1 024 81 · L · 2 = 324
应用16 相快速滤波算法对频率为4 209 MHz和5 450 MHz 点频信号进行数字下变频预处理,基带信号频谱如图4所示。
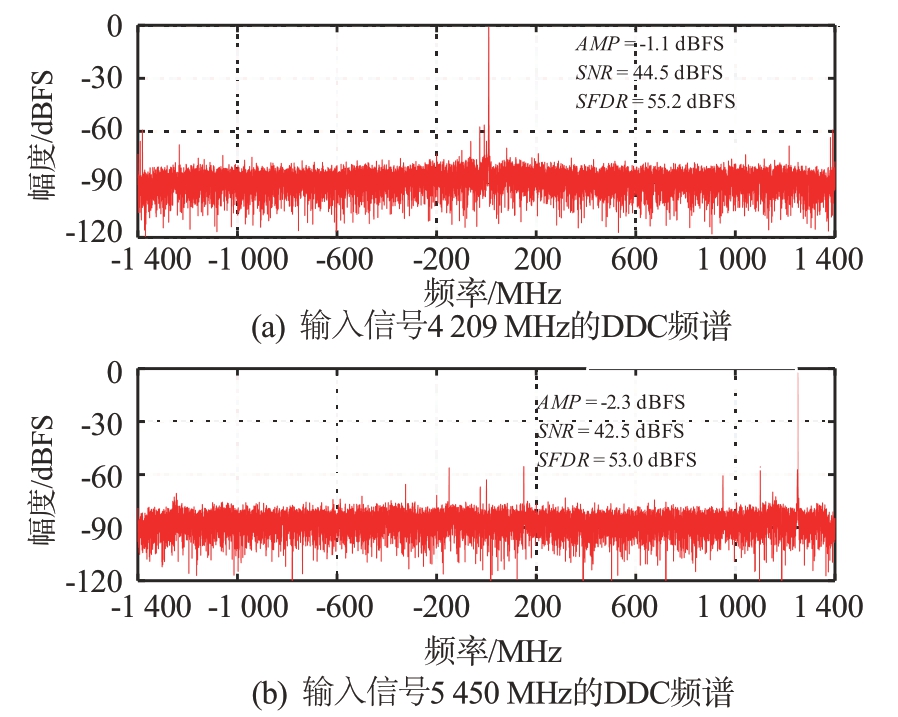
图4 快速滤波数字下变频基带信号频谱
3.3 不同滤波架构对比
对高速采样信号的数字下变频多相滤波处理,不同实现方式[7-8]的优缺点比较如表2所示。
表2 多相滤波不同架构比较
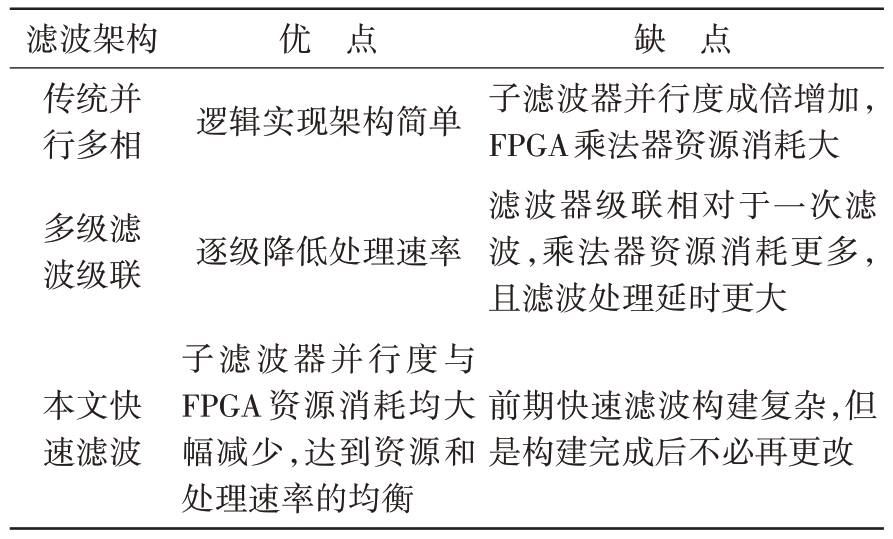
滤波架构传统并行多相多级滤波级联优 点逻辑实现架构简单逐级降低处理速率缺 点子滤波器并行度成倍增加,FPGA乘法器资源消耗大滤波器级联相对于一次滤波,乘法器资源消耗更多,且滤波处理延时更大本文快速滤波子滤波器并行度与FPGA 资源消耗均大幅减少,达到资源和处理速率的均衡前期快速滤波构建复杂,但是构建完成后不必再更改
不过部分高速ADC 芯片有内置DDC 功能,并可以进行低通滤波后输出基带信号,进而将ADC原始采样中频信号的并行度降低一倍,达到本文对中频信号数字混频过程中的2 倍抽取相同的效果,同时滤波在ADC芯片中实现能够节省FPGA处理资源。但是,并不是所有的高速ADC 芯片都支持DDC 功能,当模块硬件设计阶段对芯片选型无法确保能够采用此类ADC 芯片时,本文基于FPGA实现大带宽信号的数字下变频则提供了一种解决方案,并具有相应的应用价值。
4 结束语
通过构建并行多相滤波的快速运算形式,以及对高速采样信号解析与滤波器系数分解的优化设计,实现了基于16相快速滤波算法架构对4~8 GS/s高采样率中频信号数字下变频预处理。快速滤波运算架构的应用,极大地降低了多相滤波运算对FPGA 乘法器资源消耗,提升FPGA 对大带宽信号的预处理能力。
[1]曹兰英,郭明明,罗美方.雷达与电子战的认知博弈[J].雷达科学与技术,2021,19(5):552-557.
[2]吴晓晔,胡志伟,白晓远.基于高速采样的实时DDC 架构技术[J].计算机测量与控制,2020,28(1):255-260.
[3]戴曜泽,张棋,徐小淇.基于FPGA的高速高效率数字下变频[J].航天电子对抗,2021,37(2):47-51.
[4]李凯勇.基于FPGA 的高效FIR 滤波器设计[J].青海大学学报,2017,35(6):56-60.
[5]孙田雨.并行FIR 滤波器系数设计及结构优化[D].杭州:浙江大学,2017.
[6]赵飞,杨建.多相分解的高速并行FIR 滤波器的FPGA实现[J].电子信息对抗技术,2022,37(5):105-109.
[7]田波,程云鹏,罗庆驰.短波宽带数字下变频设计与仿真[J].通信技术,2022,55(8):977-983.
[8]李来轩.多通道采集与处理的若干关键技术研究[D].杭州:浙江大学,2022.