0 引言
雷达干扰一体化可实现雷达系统与电子对抗干扰系统的资源整合、缩减平台电子设备体积和能量开支、提高平台的电磁兼容性能，是近年来信息化作战系统研究的一大热点。OFDM 架构的雷达干扰一体化波形从信号层面实现探测与干扰一体，该类波形通过OFDM 时频复用的方式同时保证了波形探测的稳定性和干扰的机动性，是雷达干扰一体化实现的有效途径。然而，OFDM 时频复用体制决定了该类雷达干扰一体化波形在时域上易形成峰均比较大的性能短板，造成波形的功率线性放大成本较高、功率饱和放大失真较大等问题，因此解决峰均比问题是该类波形运用到工程实践的关键一步。
近年来，国内外学者围绕OFDM 波形的峰均比抑制问题开展了大量研究，总体来说，形成了三大类峰均比抑制技术：预畸变类技术［1-2］、预编码类技术［3-5］、概率类技术。其中，概率类技术通过符号映射、子载波随机分组等方式产生多个OFDM 波形，进而选取其中峰均比最小的波形作为传输波形，从而完成对波形峰均比进行抑制的效果，是近年来国内外研究较多的一类峰均比抑制技术。典型的概率类峰均比抑制算法包含选择型映射算法［3,6］（Selected Mapping,SLM）、部分序列传输算法［7-8］（Partial Transmit Sequences,PTS）、预留子载波算法［9-14］（Tone Reservation,TR）三种。SLM 算法对子载波调制序列进行多种排列，选取其中对应时域峰均比最小的排列方式，从而得到峰均比相对较小的波形。该算法实现过程中需对不同排列方式的每组子载波符号进行OFDM 调制，开展大量的IDFT 运算，因此该算法实现复杂、运算量大。PTS 算法将需要调制的载波符号划分为若干个互不重叠的子序列，通过对子序列进行加权实现峰均比的抑制。PTS算法与SLM算法相同，需要生成多组权值序列对子序列符号进行调制，从中选取峰均比最小所对应的权值序列，同样存在算法实现复杂、运算量大的缺点。
TR算法是一种利用预留子载波进行峰值抑制的峰均比优化算法［9］。该算法利用除信息子载波以外的子载波来生成峰值削减波形（PCS）、进而对信息子载波调制产生的峰值进行抑制。该算法的特点是：峰均比抑制效果较好，采取对波形峰值进行不断削减的方式、可以获得较为理想的峰均比抑制效果，且不会造成信息子载波上调制序列的失真；但该算法需要利用除信息子载波外的子载波完成峰值削减，因此其波形子载波的信息传输效率有所下降。文献［10］提出了一种基于峰值加窗残余噪声的算法。该算法对残余噪声进行滤波以满足TR 约束，并使用确定的缩放因子进行缩放以最小化范围外功率生成PCS，在一定程度上降低了TR 算法的计算量。文献［11］提出一种利用时域核矩阵生成PCS 的算法。该算法利用在时域核仅生成一次或离线生成的情况下、在峰值降低迭代中不需要IDFT 运算的特性，从减少单次迭代中IDFT 运算的角度较大地降低了TR 算法的计算量。文献［12］提出了一种分组载波峰值窗口TR 算法，该算法基于一种新的内核定义，一次消除多个波形峰值，从减少TR 算法迭代次数的角度较大地降低了TR 算法的计算量。文献［13］提出了一种使用预先生成PCS的改进TR算法。该算法在预处理中生成并保存PCS、以便在运行时直接使用它们，从调整TR 算法中PCS 生成顺序的角度降低了TR算法的计算量。文献［14］提出了一种基于误差适量幅度约束的TR 算法，该算法将传统的预留子载波扩展至信息子载波生成PCS，进而获得比传统TR 算法更优的峰均比抑制效果，该算法峰均比抑制效果提升的同时也带来了信息子载波数据的扰乱。
综上所述，现有的峰均比抑制技术和算法各有优缺点，根据OFDM 架构雷达干扰一体化波形的结构特点，其干扰部分子载波本身不承载任何有用信息、仅由随机序列调制而成，因此利用TR算法对OFDM 架构雷达干扰一体化波形进行峰均比抑制可以将干扰部分子载波作为预留子载波进行使用，这样就避免了TR 算法中子载波利用率下降的问题。本文提出一种针对OFDM 架构雷达干扰一体化波形的峰均比抑制算法，该算法减少了TR 算法的迭代次数、提高了TR 算法的运算效率，同时也克服了TR算法子载波利用率不高的缺点。
1 OFDM架构的雷达干扰一体化波形模型
OFDM架构的雷达干扰一体化波形通过OFDM调制实现在波形频域分别定义探测子载波和干扰子载波进而完成探测和干扰功能。图1所示为OFDM架构的雷达干扰一体化波形子载波调制示意图。
图1 一体化波形子载波调制示意图
OFDM 架构的雷达干扰一体化波形的中频信号数学模型可统一表示为
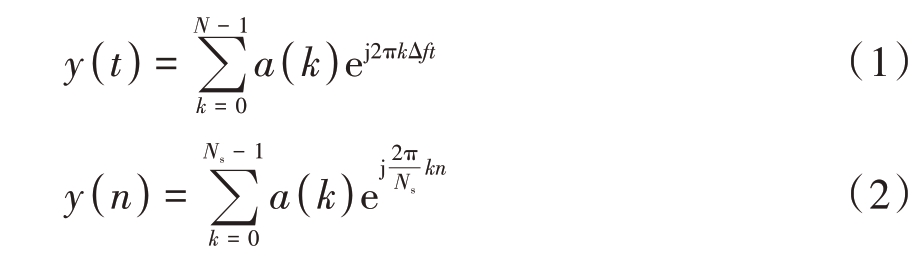
式（1）中，a(k)为由探测序列和干扰序列联合构成的波形频域调制序列，Δf为子载波频率间隔，Ns 为子载波总数。式（2）为经过中频采样后的一体化波形的数学模型。a(k)的数学表达式为
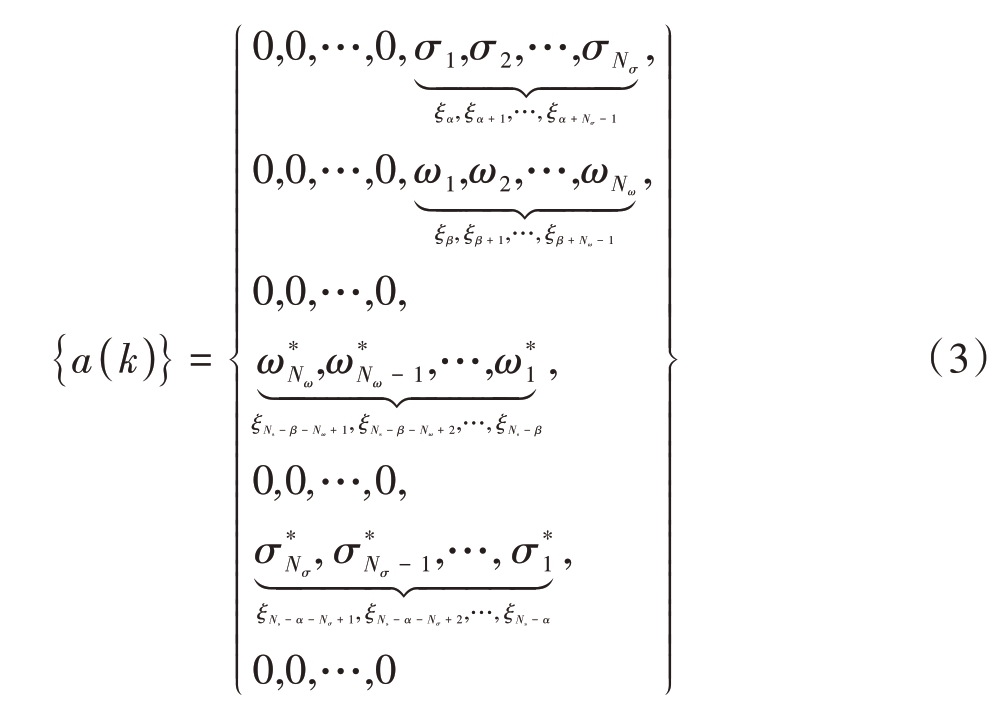
式中：*为共轭符号，{σ}为探测序列，该序列调制一体化波形的探测子载波以完成雷达探测功能，Nσ 为探测子载波个数；{ω}为干扰序列，该序列调制一体化波形的干扰子载波以完成电子对抗干扰功能，Nω 为干扰子载波个数；ξc 为子载波位置序列，由于中频信号的正负频率呈现共轭对称的特性，因此式（3）子载波调制序列关于Ns/2对称。图2 为OFDM 架构的雷达干扰一体化波形的中频信号频域子载波调制示意图。如图3 所示，OFDM 架构的雷达干扰一体化波形探测子载波保持稳定、干扰子载波根据目标雷达信号频率灵活机动的波形架构，使得一体化波形同时具备探测所需的频率稳定性和干扰所需的频率机动性。
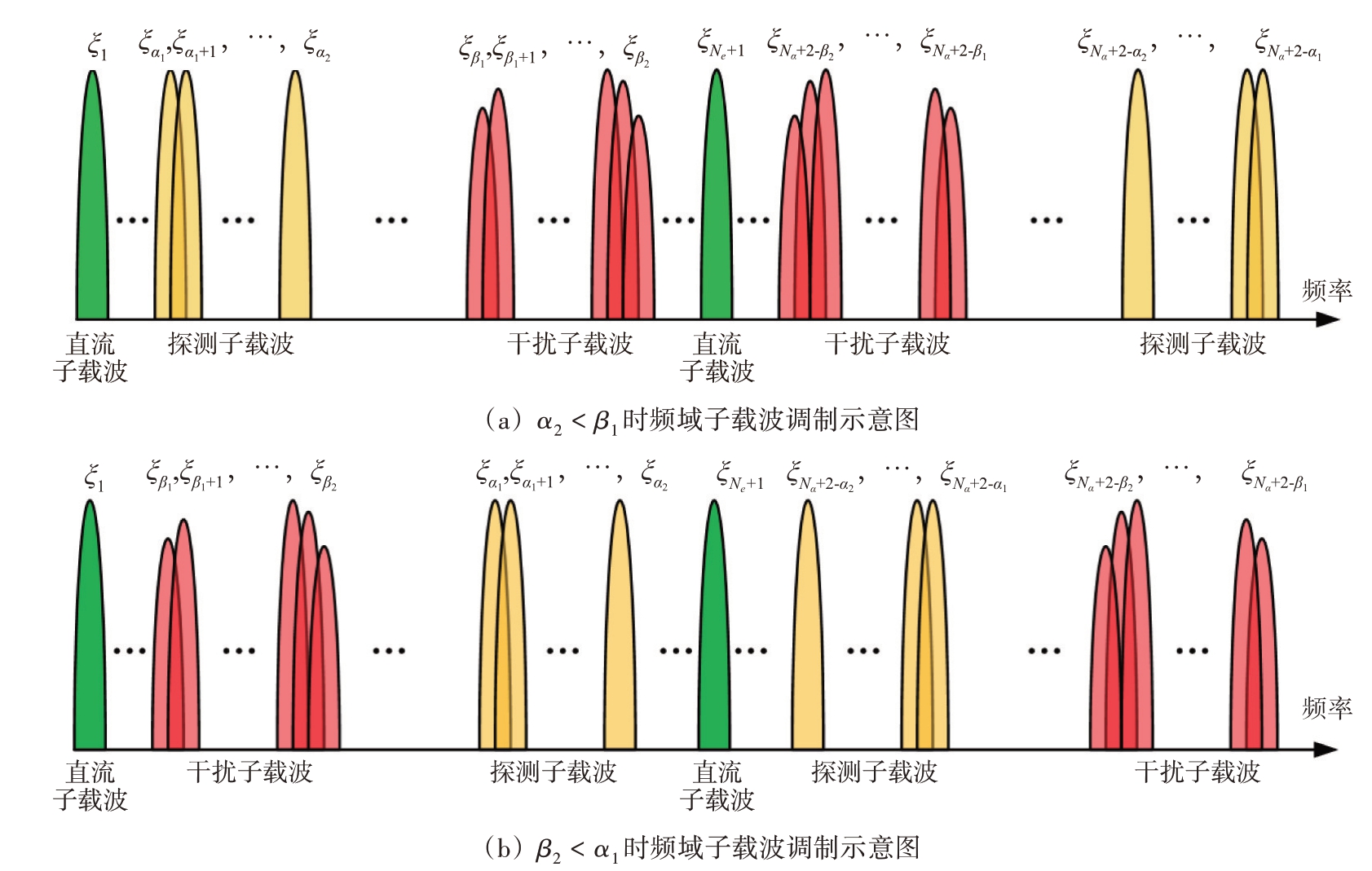
图2 OFDM架构的雷达干扰一体化中频波形频域子载波调制
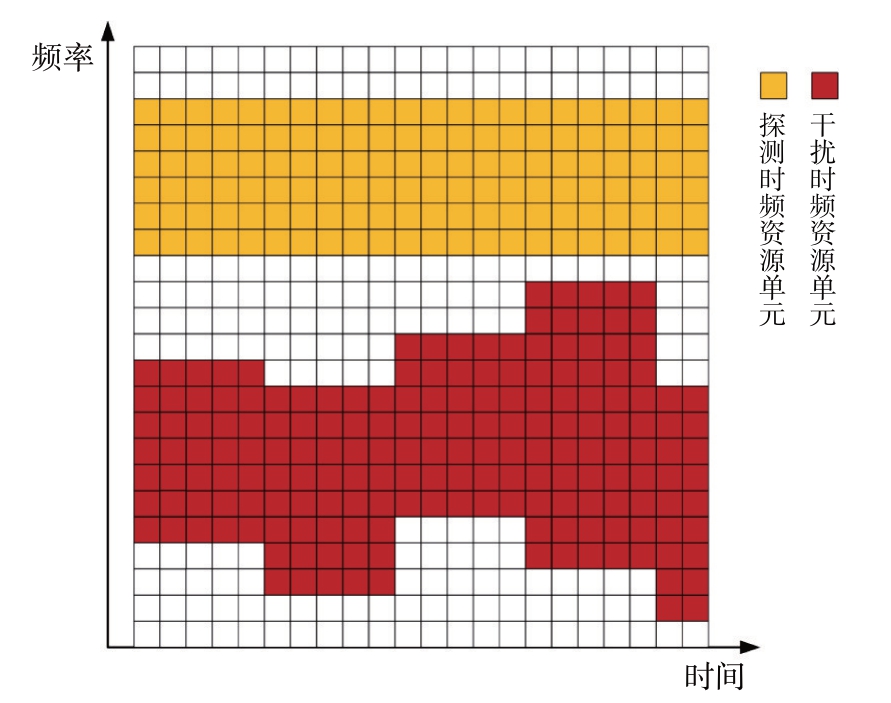
图3 根据探测和干扰要求对不同时频资源进行赋能
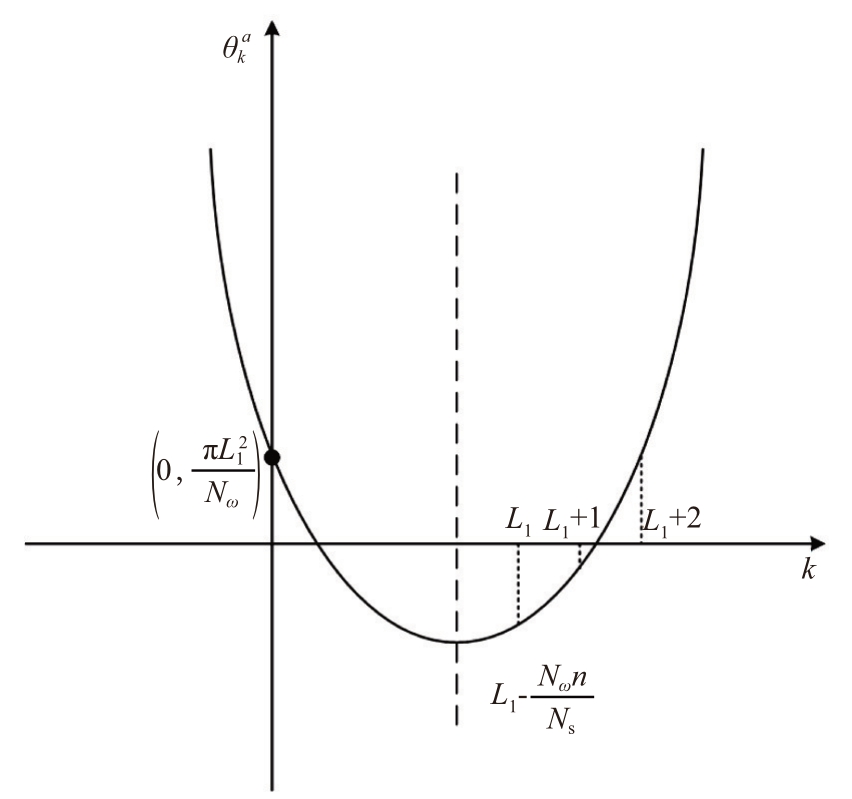
图4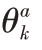 
～k函数关系图
2 预编码-TR联合峰均比抑制算法
OFDM 架构的雷达干扰一体化波形的峰均比可定义为［15］
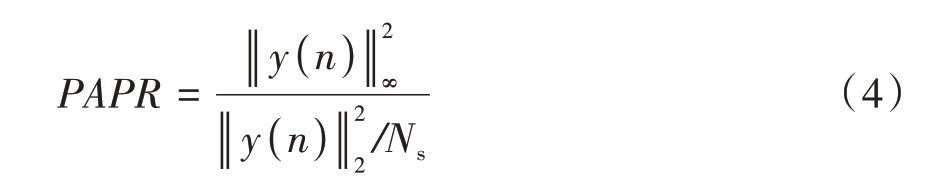
式中，‖·‖∞为无穷范数，‖·‖2 为2 范数。从峰均比的定义可知，波形的峰均比大小反映了波形时域的起伏变化程度，若波形的峰均比大，则波形时域存在突出峰值，若波形峰均比小，则波形时域能量分布均匀。根据OFDM 调制的线性关系，式（1）又可写成
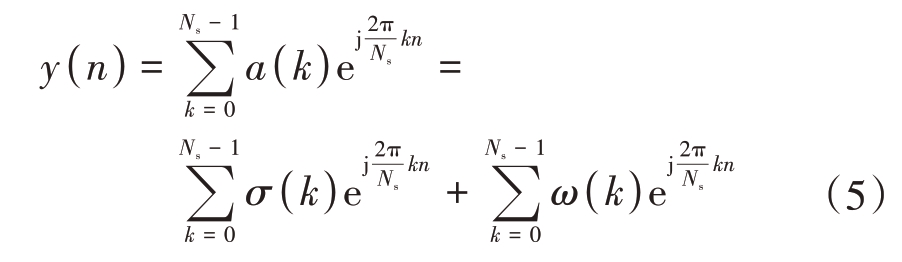
式中：σ(k)由一体化波形频域序列中探测部分序列构成，其定义如式（6）所示；ω(k)由一体化波形频域序列中干扰部分序列构成，其定义如式（7）所示；σ(k)和ω(k)满足a(k)= σ(k)+ ω(k)。
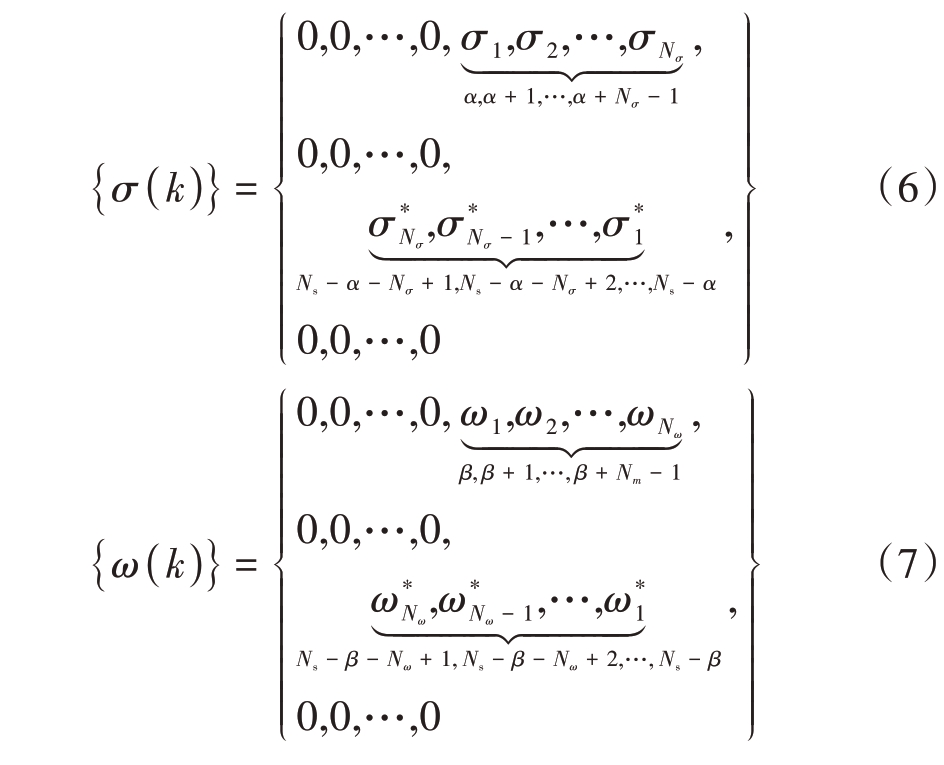
令
为一体化波形时域的探测部分影响分子
为一体化波形时域的干扰部分影响分子，有
yω(n)。由OFD M 架构雷达干扰一体化波形的特点可知，该波形的频域子载波调制序列是由探测序列和干扰序列以及零值序列共同构成。零值序列调制的子载波能量为0，因此不会对波形的峰均比情况有任何影响；探测部分子载波由固定探测序列调制，此部分的序列值和子载波位置是稳定值，即探测部分影响分子yσ(n)对波形峰均比的影响是恒定的；干扰部分子载波由干扰序列调制，序列的相位角和幅值具备随机性特点，由此，干扰部分影响分子yω(n)是影响一体化波形峰均比的主要因素，因此对一体化波形的峰均比抑制可转化为对干扰部分影响因子yω(n)的峰均比抑制。预编码-TR 联合峰均比抑制算法首先通过对干扰部分子载波进行预编码的方式获得具备低峰均比特性的一体化波形。
2.1 基于一体化波形的预编码算法
由文献［16］可知，OFDM 波形形成较大峰均比的主要原因是频域子载波在调制时在某一时刻点的相位角相等或相近、形成的能量叠加。具体来讲，在某一时刻点n0，OFDM 波形的频域子载波调制序列{xk}中有大量的调制符号
与其对应的IDFT 蝶形算子
结合后的相位角保持一致，导致此时刻{υ1,υ2,…,υM}位置的频域子载波的能量叠加，从而形成了波形在此时刻较大的幅值。通过一体化波形架构特点可知，波形的干扰性能主要由干扰子载波的能量分布决定，而干扰子载波部分子载波的相位角不影响干扰子载波的能量分布，因此，可通过预编码的方式使得一体化波形频域子载波调制序列的相位角分散分布的方式避免因相位角相同而导致子载波能量累加情况的发生。
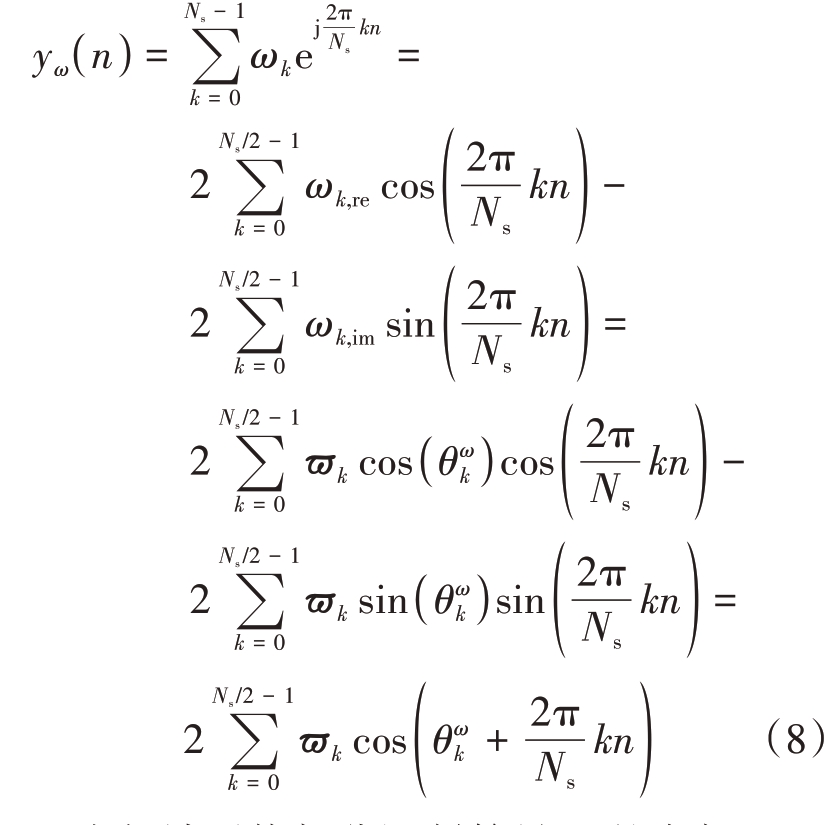
式中，ωk,re为频域干扰部分调制符号ωk的实部，ωk,im为ωk 的虚部，ϖk 为ωk 的幅度，
为ωk 的相位角。此时，根据文献［17］可知，在n取[0,1,…,Ns-1]中任意值时，当干扰部分子载波相位角和IDFT 蝶形算子结合后的相位角
均在[0,2π]区间上分散分布时不会造成子载波能量累加的情况发生，波形具有低峰均比特性。由此，若令干扰部分子载波相位角
式中此时有
OFDM 架构的雷达干扰一体化波形具有低峰均比特性，此时干扰部分子载波的随机性由子载波的幅度ϖk表征。
2.2 基于一体化波形的TR算法
预编码算法使得一体化波形具有低峰均比特性，但不能按照要求将波形峰均比约束到指定指标之内，本文进一步结合TR 算法，提出一种基于峰值对消的一体化波形TR 抑制算法。该算法可在预编码算法的基础上对一体化波形的峰均比进一步抑制，使波形的峰均比约束到指定指标之内。
若将OFDM 波形y(n)的频域子载波序列分为由数据子载波组成的频域序列{s(k)}和预留子载波组成的频域序列{r(k)}，两者满足
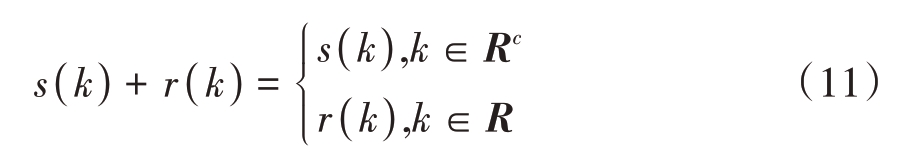
式中R为预留子载波在频域序列中的位置序列号。则OFDM波形y(n)可表示为
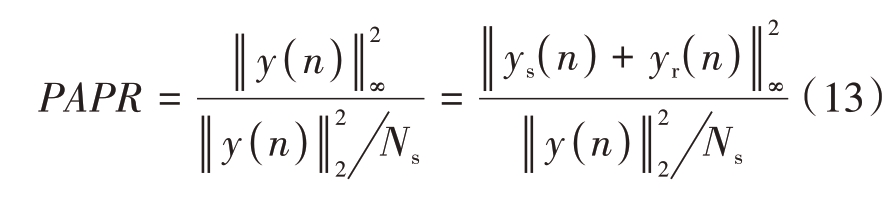
式中
为波形能量，当波形能量恒定时，是一恒值，因此可以看出TR 算法的基本原理是通过波形中预留子载波对消数据子载波造成的幅值起伏的方式实现峰均比抑制。由式（3）、式（6）、式（7）可知，对于OFDM 架构的雷达干扰一体化波形y(n)，其干扰部分的子载波由干扰序列调制，具有随机性，因此预编码-TR 联合峰均比抑制算法在对干扰部分子载波符号相位角进行预编码的基础上进一步地又利用干扰部分子载波作为预留子载波，通过干扰部分子载波来对消波形中的峰值以达到峰均比抑制的目的。图5所示为算法示意图，算法将预编码处理后得到的一体化波形y(n)与由预留子载波得到的对消函数yr(n)进行峰值对消；对消后得到的波形y′(n)频域保持探测部分子载波符号不变，干扰部分子载波符号为原子载波符号与对消函数子载波符号叠加的结果。
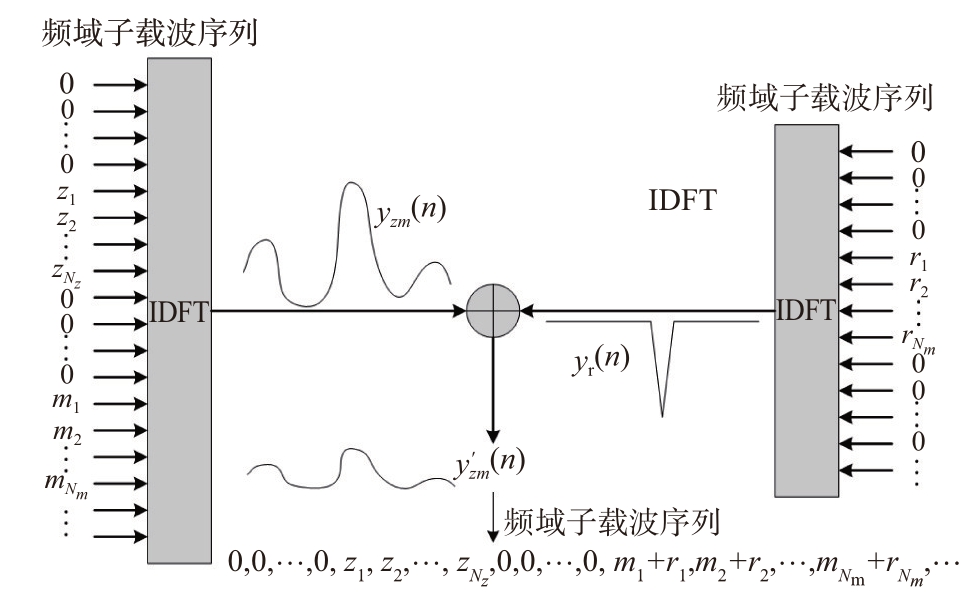
图5 预留子载波对消抑制峰均比示意图
一体化波形的TR 算法首先在干扰部分子载波上构造峰值对消函数。通过TR 算法的基本原理可知，峰值对消函数的基本条件是波形的频域能量约束在有限的带宽范围之内。根据此条件，常见的峰值对消函数包括sin 函数和sinc 函数，为了获得较高的峰值对消效率，本算法选择sinc函数作为峰值对消函数，sinc 函数的时频如图6 所示。由图6 可以看出sinc 函数的时域峰值突出，在进行峰值对消的同时引起第二峰值累加而形成新峰值的可能性较小；同时，sinc 函数的频域能量仅约束在有限的带宽范围之内，符合TR 算法有限预留子载波的要求。
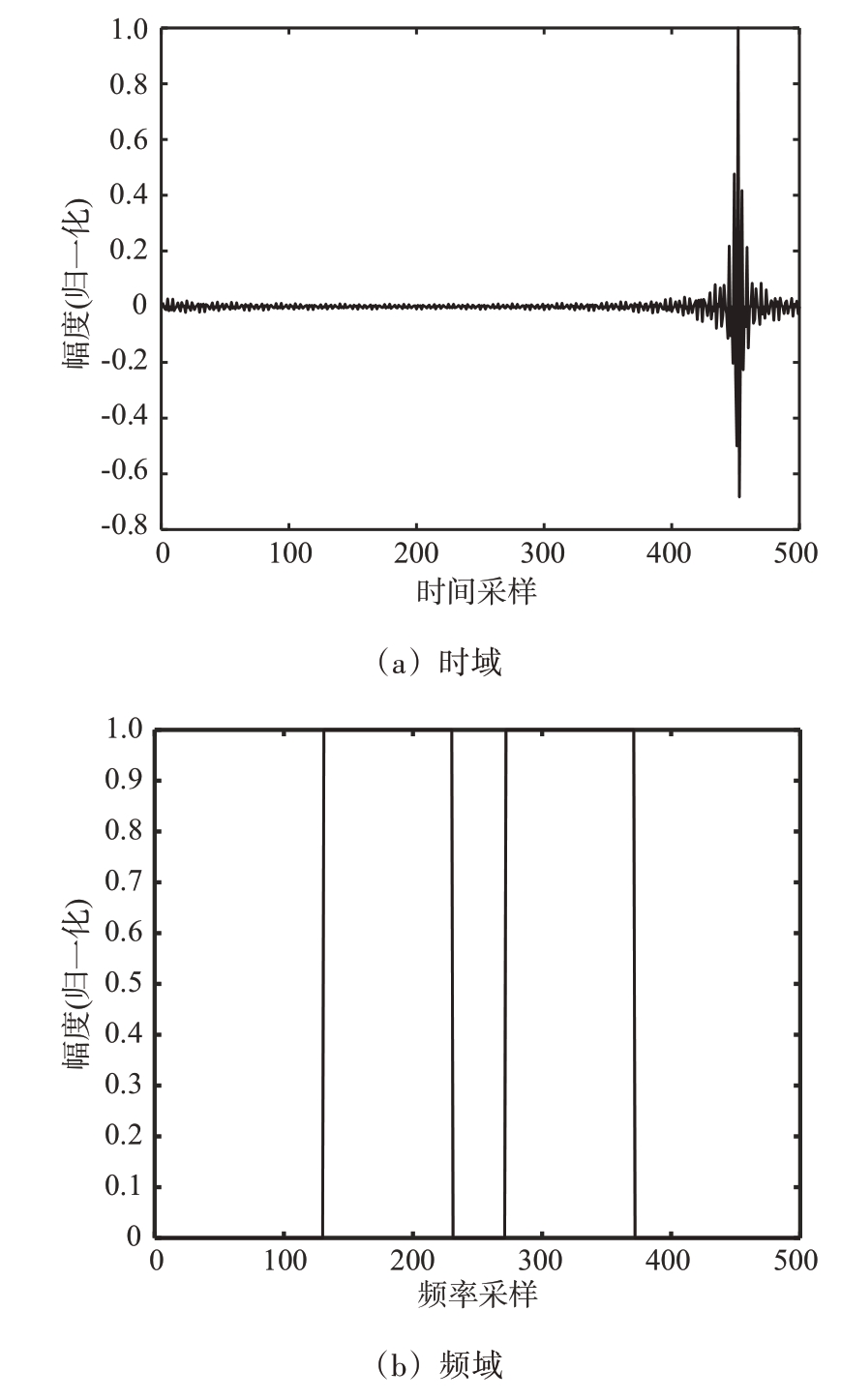
图6 sinc函数时频示例图
基于sinc函数的对消函数ysinc(n)可表示为
式中，r(k)为对消函数的子载波调制基本序列、决定对消函数的基本形状，n0 为对消函数的峰值平移因子、决定对消函数峰值的位置，ξ 为对消函数的归一化幅度控制因子、使对消函数的峰值幅度保持为1。r(k)可表示为
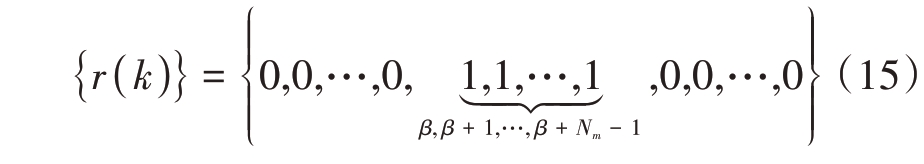
经ysinc(n)对消后的一体化波形y′(n)表示为
式中，α 为对消步进因子，该因子由一体化波形y(n)的峰值和功率决定，有
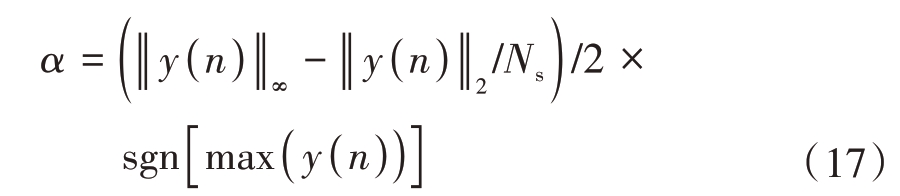
式中，sgn(·) 为符号函数。
由此可得到预编码-TR 联合峰均比抑制算法的算法流程为：
1）初始化：设置峰均比门限PAPR0；
2）根据式（9）对干扰部分子载波相位角
进行预编码；
3）根据式（5）调制得到低峰均比一体化波形y(n)；
4）计算y(n)的峰值‖y(n)‖∞、功率‖y(n)‖2、峰均比PAPR，以及对应的峰值位置n0；
5）如果PAPR′≤PAPR0 则算法结束，如果PAPR＞PAPR0则执行步骤6）～10）；
6）根据式（14）得到对消函数ysinc(n)；
7）根据式（17）得到对消步进因子α；
8）根据式（16）得到对消后的一体化波形y′(n)；
9）按照步骤4）更新峰值‖y′(n)‖∞、功率‖y′(n)‖2、峰均比PAPR′，以及对应的峰值位置
10）门限判定：
若PAPR′≤PAPR0则算法结束，
若PAPR＞PAPR0则重复步骤6）～10）。
ZC-OFDM 雷达干扰一体化波形是OFDM 架构雷达干扰一体化波形的一种，该波形利用Zadoff-Chu 序列良好的探测特性和Mersenne-Twister 序列良好的随机特性，使得波形即拥有类似于线性调频波形的探测性能又拥有机动灵活的干扰性能。ZC-OFDM雷达干扰一体化波形可定义为
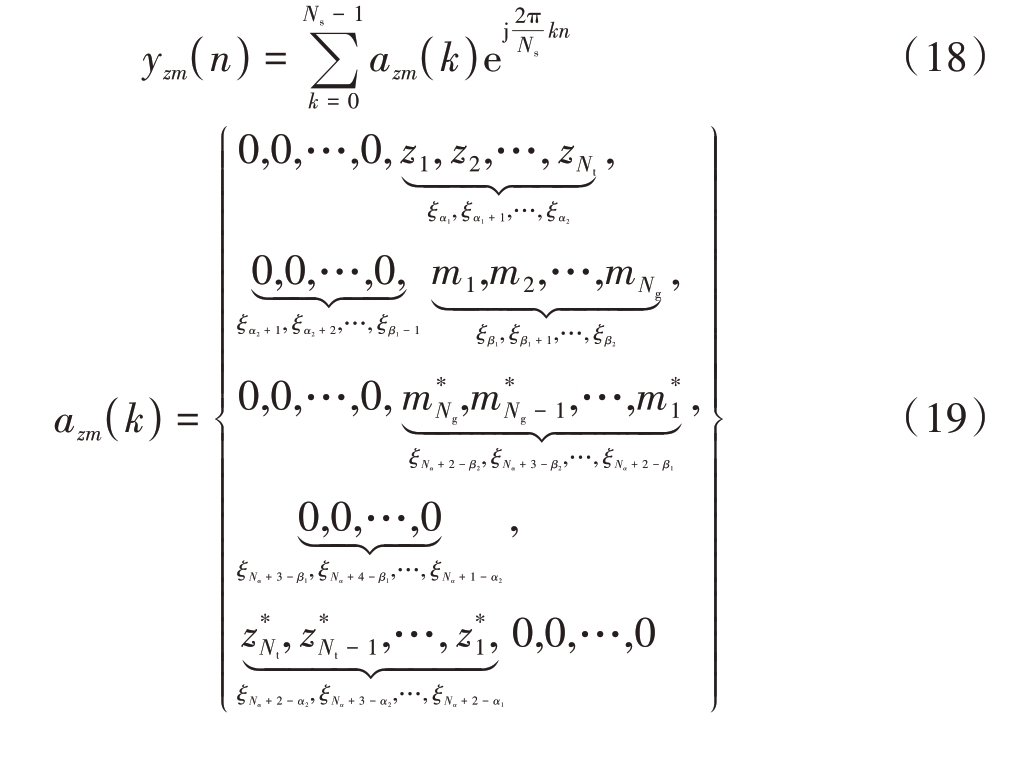
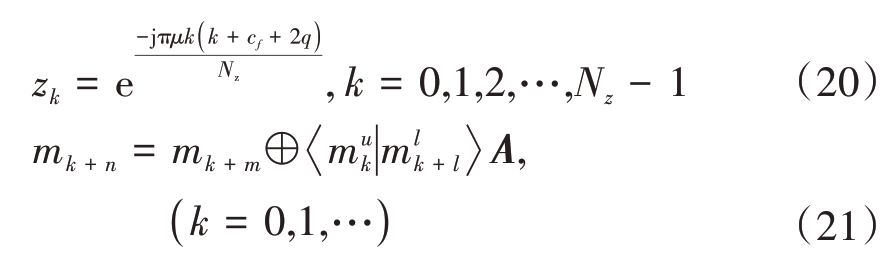
式（19）为一体化波形频域子载波调制序列，该序列由探测子载波序列和干扰子载波序列构成，且关于中心点呈共轭堆成分布。其中，Nt 为探测子载波个数，Ng为干扰子载波个数。式（20）为Zadoff-Chu 序列数学表达式，式中Nz 为序列长度，μ ∈Z+为序列根值，Nz 和μ 满足约束关系gcd(μ,Nz)=1，cf= Nzmod2，q ∈N 为序列参数［18］。参数μ、cf 和q的取值不影响一体化波形的功能特性，不妨设μ=1，cf= q=0。式（21）为Mersenne-Twister 序列数学表达式，式中整数n 为递推式的维数，整数m 满足1≤m≤n，A为F2域上w×w阶常数矩阵。若给出X0,X1,…,Xn-1 作为初始点，则当k=0 时，Xn 由式（21）递推式产生，⊕为mod2 加法，或称为异运算［17］。本文以ZC-OFDM 雷达干扰一体化波形为例验证OFDM 架构的雷达干扰一体化波形的峰均比抑制算法，不失一般性。
3 仿真实验
本文设计仿真实验对所提出的预编码-TR 联合峰均比抑制算法的峰均比抑制性能进行验证。以ZC-OFDM 雷达干扰一体化波形为例，仿真实验参数设置：ZC-OFDM 雷达干扰一体化中频波形采样率fs=600 MHz，时长t=10 μs,则波形子载波数为Ns= fs×t=6 000 个；探测部分中心频率fz=100 MHz，带宽Bz=10 MHz，则探测部分子载波数为Nz= Bz×t=100 个；干扰部分中心频率为fm=150 MHz，带宽Bm=50 MHz，则干扰部分子载波数为Nm= Bm×t=500，峰均比门限值为PAPR0=6 dB。
图7（a）、（b）分别给出了经预编码-TR 联合峰均比抑制算法前后的ZC-OFDM 雷达干扰一体化波形时频域仿真结果。从时域图中可以看出，原始一体化波形的时域起伏较大，经预编码-TR 联合峰均比抑制算法抑制后一体化波形时域起伏较大的情况得到了明显的抑制，峰均比得到明显抑制；从频域图中可以看出，初始一体化波形探测子载波能量分布呈规则状、干扰子载波能量分布呈随机状，经预编码-TR 联合峰均比抑制算法抑制后波形的探测子载波能量分布依然呈规则状、干扰子载波能量依然呈随机状，且探测和干扰子载波分布的位置保持不变。图7（a）、（b）对比表明预编码-TR联合峰均比抑制算法能够较好地对一体化波形的峰均比进行抑制，且在进行峰均比抑制的同时能够保持一体化波形的整体波形架构，使得一体化波形的探测特性和干扰特性不会遭到破坏。
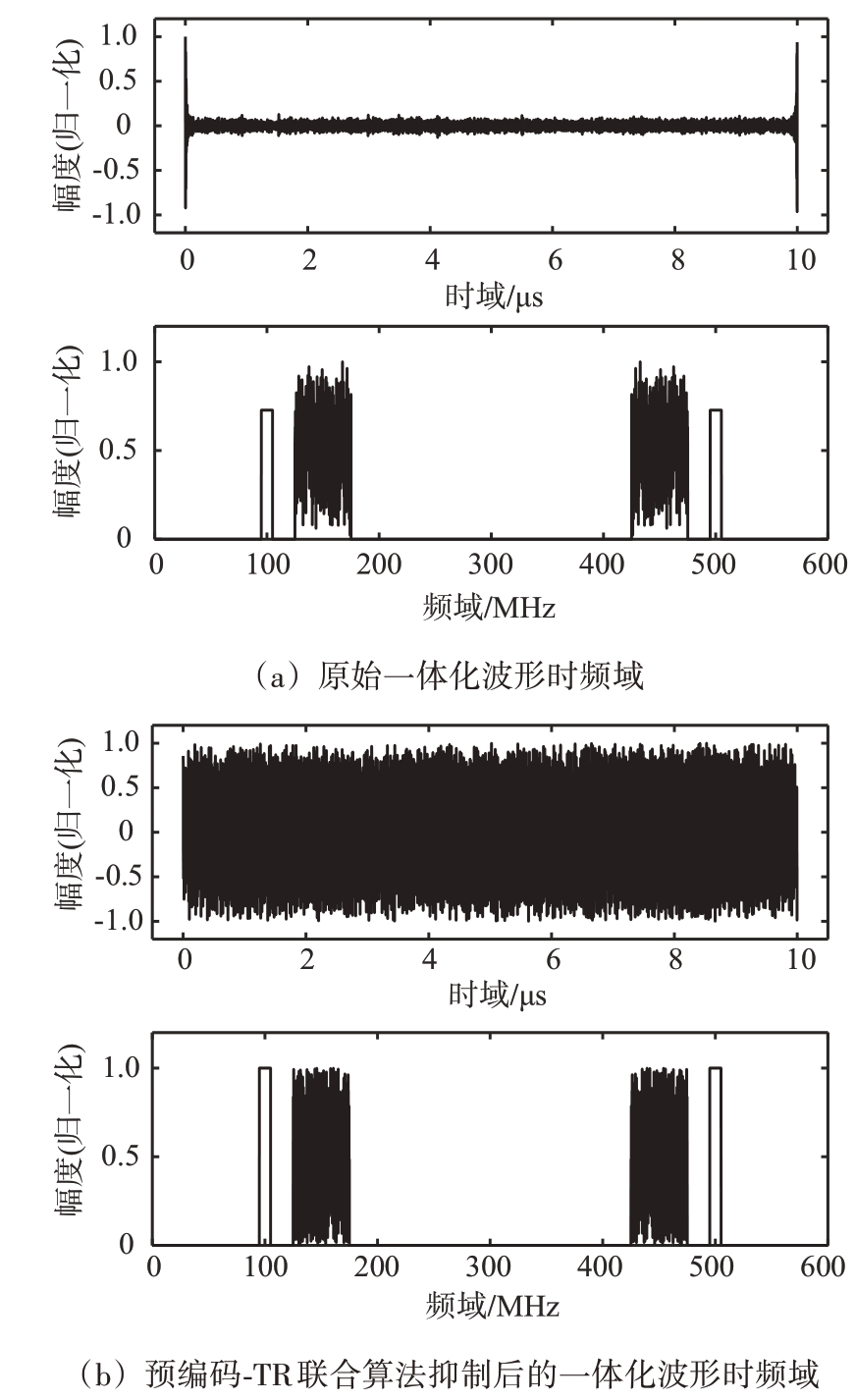
图7 预编码-TR联合峰均比抑制算法峰均比抑制效果
图8 给出了原始状态、仅预编码算法抑制、仅TR 算法抑制、100 次迭代预编码-TR 联合算法抑制、200 次迭代预编码-TR 联合算法抑制下的一体化波形的CCDF 曲线仿真结果。对比5 根CCDF 曲线可以得出，原始状态下一体化波形的峰均比分布在11～14 dB区间内，预编码-TR联合算法抑制后的一体化波形获得最优的峰均比抑制效果，具备近6 dB 的强峰均比抑制能力，且随着迭代次数的增加，预编码-TR 联合算法的峰均比抑制能力越强，400 次迭代能够将一体化波形的峰均比抑制到6 dB 以内。仅预编码的峰均比抑制算法与100 次迭代的TR 峰均比抑制算法的峰均比抑制能力相似，能够对一体化波形产生近2 dB 的峰均比抑制效果，均弱于预编码-TR 联合峰均比抑制算法的抑制能力。4 种峰均比抑制算法的峰均比抑制能力如表1所示。
表1 4种算法的峰均比抑制能力对比表 dB
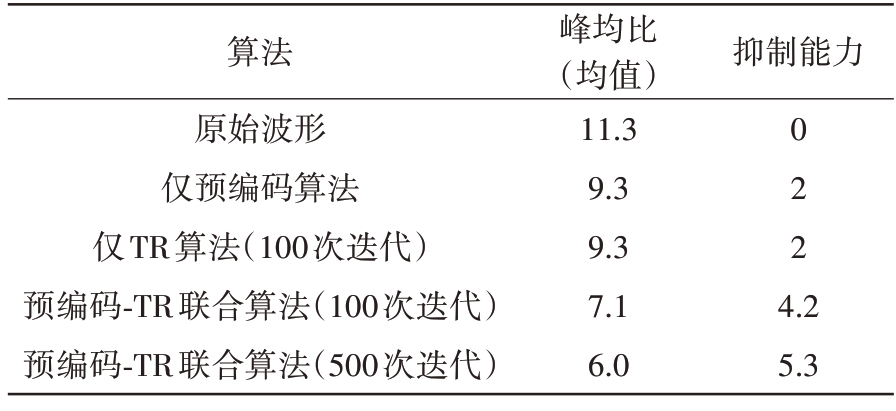
图8 4种峰均比抑制算法抑制能力对比
图9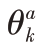 
在[0,2π]区间上的分布情况
图10对2.2节结论进行了仿真验证，给出了以sin 函数为对消函数的预编码-TR 联合峰均比抑制算法和以sinc 函数为对消函数的预编码-TR 联合峰均比抑制算法的峰均比抑制过程对比仿真。通过仿真可以看出，以sin 函数和以sinc 函数为对消函数的预编码-TR 联合峰均比抑制算法的抑制效果都是收敛的，以sinc 函数为对消函数的预编码-TR联合峰均比抑制算法在一体化波形峰均比达到6 dB 以后继续优化会出现一定的峰均比振荡反弹的现象，但总体来说随着迭代次数的增加，一体化波形的峰均比逐渐减小；同时，以sin 函数和以sinc函数为对消函数的预编码-TR 联合峰均比抑制算法均有较好的峰均比抑制效果，以sinc函数为对消函数的算法能将一体化波形的峰均比抑制到6 dB以内、需要约500 次迭代，同等条件下以sin 函数为对消函数的算法仅能将一体化波形的峰均比抑制到7.5 dB，以sinc 函数为对消函数的峰均比抑制能力和抑制效率明显高于以sin 函数为对消函数的峰均比抑制效率，这是由于sinc 函数比sin 函数更突出的峰值特性导致的。该结果表明2.2 节的理论分析结论是正确的。
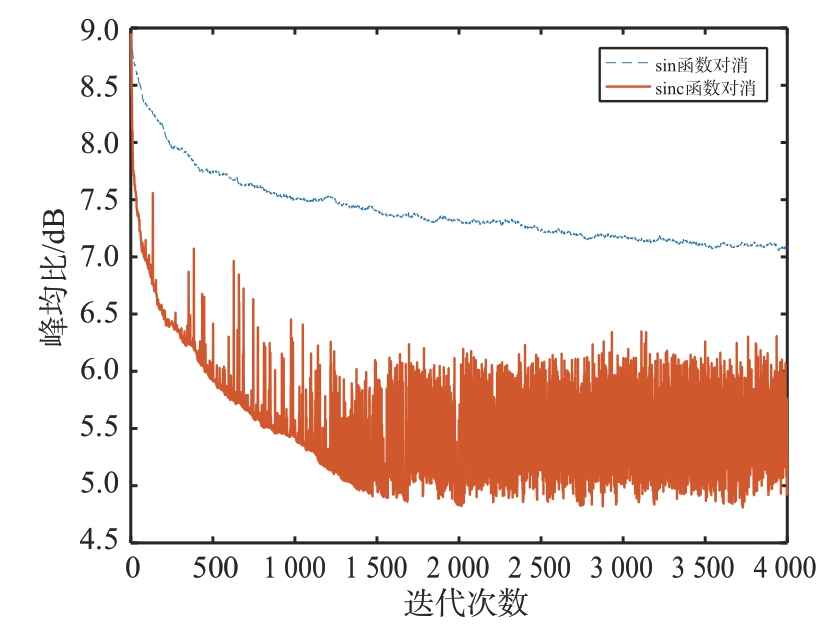
图10 sinc函数和sin函数作为对消函数的算法峰均比抑制能力对比
图11 给出了预编码-TR 联合峰均比抑制算法对不同探测子载波个数和不同干扰子载波个数一体化波形的峰均比抑制结果仿真。如图所示，在一体化波形的探测子载波从100 个变为200 个的情况下，预编码-TR 联合峰均比抑制算法的峰均比抑制效果基本没有波动；在一体化波形的干扰子载波从500 个变为800 个、再变为1 000 个的情况下，预编码-TR 联合峰均比抑制算法的峰均比抑制效果亦基本没有波动。由此表明，预编码-TR 联合峰均比抑制算法的峰均比抑制性能不受探测和干扰子载波数目的影响，即在一体化波形子载波间隔一定的条件下，预编码-TR 联合峰均比抑制算法的峰均比抑制性能不受探测和干扰带宽大小的影响。
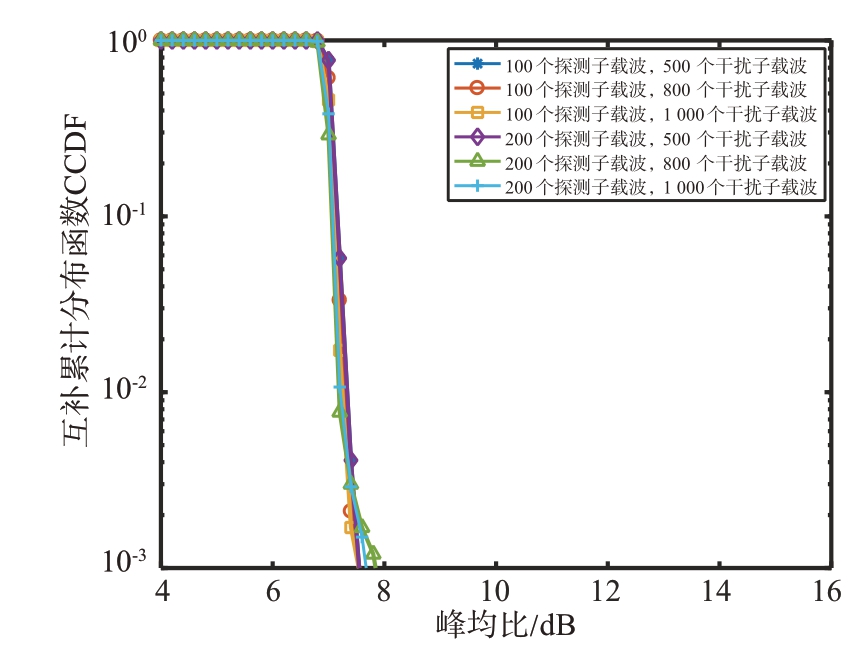
图11 算法对不同探测子载波个数和干扰子载波个数的峰均比抑制效果
4 结束语
本文提出了一种针对OFDM 架构雷达干扰一体化波形的预编码-TR 联合峰均比抑制算法，该算法针对一体化波形探测与干扰子载波时同频分的波形架构，将传统的预编码峰均比抑制算法原理和TR 峰均比抑制算法原理进行结合，在较大程度上提高了算法的峰均比抑制能力和效率。仿真实验表明，该算法能够将一体化波形的峰均比抑制到6 dB 以下，且在进行峰均比抑制的同时能够保持波形探测子载波和干扰子载波的架构，进而保证波形的探测和干扰性能。与传统的仅预编码峰均比抑制算法和仅TR 峰均比抑制算法相比，该算法有近3 dB 的峰均比抑制能力提高，且其峰均比抑制能力不受一体化波形探测子载波个数和干扰子载波个数的变化而波动。
［1］AZURDIA-MEZA C A,LEE K,LEE K.PAPR Reduction in SC-FDMA by Pulse Shaping Using Parametric Linear Combination Pulses［J］.IEEE Communications Letters,2012,16（12）:2008-2011.
［2］丁亚青，吕建鸿，王中鹏.一种降低OFDM 系统PAPR的改进限幅噪声压缩方法［J］.电讯技术，2022，62（11）:1691-1696.
［3］SUDHA V,KUMAR D S.Low Complexity PAPR Reduction in SLM-OFDM System Using Time Domain Sequence Separation［J］.Alexandria Engineering Journal,2018,57（4）:3111-3115.
［4］赵辉，王薇，莫谨荣，等.基于星座符号序列局部相位旋转的低峰均功率比滤波器组多载波结构优化［J］.电子与信息学报，2022，44（2）:668-676.
［5］鲁信金，雷菁，李为，等.一种基于酉矩阵变换的低峰均比正交时频空安全传输方法［J］.电子与信息学报，2023，45（7）:2395-2405.
［6］NIWAREEBA R,COX M A,CHENG L.PAPR Reduction in Optical OFDM Using Lexicographical Permutations with Low Complexity［J］.IEEE Access,2022,10:1706-1713.
［7］赵辉，王薇，莫谨荣，等.滤波器组多载波系统中基于双层优化的峰均比抑制算法［J］.电子与信息学报，2021,43（6）:1742-1749.
［8］秦雪莲，杨永立，邹鸿洋.一种降低FBMC-OQAM 系统PAPR 的ASSABC-PTS 算法［J］.电讯技术，2023，63（2）:260-266.
［9］KRONGOLD B S,JONES D L.A New Tone Reservation Method for Complex-Baseband PAR Reduction in OFDM Systems［C］//2002 IEEE International Conference on Acoustics,Speech,and Signal Processing,Orlando,FL,USA:IEEE,2002:2321-2324.
［10］HOU Jun,GE Jianhua,GONG Fengkui.Tone Reservation Technique Based on Peak-Windowing Residual Noise for PAPR Reduction in OFDM Systems［J］.IEEE Trans on Vehicular Technology,2015,64（11）:5373-5378.
［11］YU Pingyuan,JIN Shubo.A Low Complexity Tone Reservation Scheme Based on Time-Domain Kernel Matrix for PAPR Reduction in OFDM Systems［J］.IEEE Trans on Broadcasting,2015,61（4）:710-716.
［12］LAHBABI N,BULUSU S S K C,HELARD J F,et al.Very Efficient Tone Reservation PAPR Reduction Fully Compatible with ATSC 3.0 Standard: Performance and Practical Implementation Analysis［J］.IEEE Access,2018,6:58355-58372.
［13］LI Hao,WEI Jidong,JIN Ningde.Low-Complexity Tone Reservation Scheme Using Pre-Generated Peak-Canceling Signals［J］.IEEE Communications Letters,2019,23（9）:1586-1589.
［14］杨奎，刘志祥，刘旺，等.基于EVM 约束的预留子载波峰均比抑制［J］.电讯技术，2022，62（7）:966-970.
［15］韩康祺，钱骅，裴旭明，等.降低多用户MIMO 系统PAPR 的广义SLM 算法［J］.系统工程与电子技术，2021，43（6）:1673-1678.
［16］SLIMANE S B.Reducing the Peak-to-Average Power Ratio of OFDM Signals Through Precoding［J］.IEEE Trans on Vehicular Technology,2007,56（2）:686-695.
［17］MACHICAO J,NGO Q Q,MOLCHANOV V,et al.A Visual Analysis Method of Randomness for Classifying and Ranking Pseudo-Random Number Generators［J］.Information Sciences,2021（3）:1-20.
［18］WANG Y Y,YANG S J.Estimation of Carrier Frequency Offset and Channel State Information of Generalize Frequency Division Multiplexing Systems by Using a Zadoff-Chu Sequence［J］.Journal of the Franklin Institute,2022（1）:637-652.