0 引言
低空风切变是飞机在起飞降落阶段可能遇到的航空危险气象之一,它是指飞机进入风场时,风速风向在垂直或水平方向剧烈变化导致飞行升力的变化,极大影响飞行效率以及安全[1]。在突遇低空风切变情况时,飞行员往往难以及时调整飞机状态,从而导致严重飞行事故发生。因此,对低空风切变进行检测及预警成为了航空部门的一项重要任务,而对风场风速进行精确估计是检测低空风切变的前提,故而正确进行风速估计成为不可忽视的重要部分[2]。
机载气象雷达已成为保障民航飞机飞行安全的重要电子设备[3],能够最大程度帮助飞机免受危险气象的影响。随着航空技术的发展以及对于告警机制需求的提高,机载气象雷达的性能、功能也在不断发展,机载双极化相控阵气象雷达逐步进入人们的视野。机载双极化气象雷达与传统单极化机载气象雷达相比,可以借助发射的双极化波对气象目标回波进行检测;相控阵天线由于在空域、时域采样,因此具有灵活度高、节约扫描时间和雷达资源等优势[4]。机载双极化相控阵气象雷达将双极化和相控阵技术结合,获取到丰富的极化、空时域的信息,极大增强了对危险气象的探测能力[5]。因此,研究机载双极化相控阵气象雷达体制下的低空风切变风速估计方法,对于加强风切变环境下的气象保障具有重要意义。
在进行低空风切变检测时,由于机载双极化相控阵气象雷达处于下视工作模式,其接收到的回波信号往往掺杂着范围广、功率大的地杂波信号,进而导致所需要的低空风切变信号被地杂波信号覆盖,故而完成对低空风切变风速的估计前,有必要将地杂波的影响降至最低[6]。在实际情况中,由于地面情况复杂,杂波分布不均匀导致独立同分布(Independent Identically Distributed,IID)样本严重不足,进而影响杂波抑制的效果,使得风速无法被准确估计[7]。有关机载双极化相控阵气象雷达少IID 样本情况下的风速估计问题暂无相关文献报道,目前已有的研究集中在机载双极化气象雷达IID 样本数充足情况下的风速估计和机载单极化气象雷达IID 样本数不足情况下的风速估计两方面。针对机载双极化气象雷达IID 样本数充足情况下的低空风切变风速估计方法,文献[8]提出了一种基于机载双极化气象雷达的双极化通道融合低空风切变风速估计方法,该方法将双极化通道的数据进行融合,利用极化信息使杂波的协方差矩阵估计更精确,该方法在样本充足的情况下进行风速估计时效果较好,但在IID 样本数不足的情况下性能不佳。针对机载单极化气象雷达IID 样本不足情况下的低空风切变风速估计方法包括广义近似消息传递(GAMP)STAP方法[9]、同伦稀疏STAP[10]、知识稀疏迭代协方差STAP(Knowledge Aided Sparse Iterative Covariance-based Estimation STAP,KASPICE-STAP)[11]等,然而上述方法均未利用极化信息。
针对上述所提问题,本文提出了一种基于知识辅助的稀疏表示杂波零陷(Knowledge Aided Sparse Representation based Clutter Nulling,KA-SRCN)-pSTAP 的低空风切变风速估计方法。该方法在进行极化-空时域联合处理,提高抑制杂波能力的同时,结合SRCN 方法,利用先验信息极大减少了所需样本个数,提高了在IID 样本数不足情况下,低空风切变风速估计的准确性。该方法首先利用杂波脊的先验知识辅助构造极化空时稀疏字典,避免了网格失配和字典间相关性太强的问题。然后通过SRCN 算法对到杂波子空间补空间上的投影矩阵进行更新,从而得到pSTAP 权矢量,最后构造pSTAP 滤波器对地杂波进行抑制并积累低空风切变目标信号,最终得到风速的精准估计。同时,通过仿真分析,表明了本文方法能在少量IID样本的条件下,对地杂波实现抑制并准确完成在双极化相控阵气象雷达下的低空风切变风速估计。
1 信号模型
图1 为机载双极化相控阵气象雷达在前视阵下,探测低空风切变的示意图。假设飞机以高度H,飞行速度V沿X轴飞行,阵列天线由N个正交偶极子对沿Y轴排列,且每个正交偶极子对之间的间隔距离d=0.5λ,其中λ 代表波长。假设每个相干处理时间间隔为K 个脉冲,研究讨论L 个距离门,脉冲重复频率为fr,θ0 代表低空风切变目标的方位角,φl 代表其俯仰角,cos ψ0 代表空间锥角余弦,且有cos ψ0=cos θ0 cos φl。信号回波由风切变、地杂波以及噪声信号组成,以下分别进行介绍。
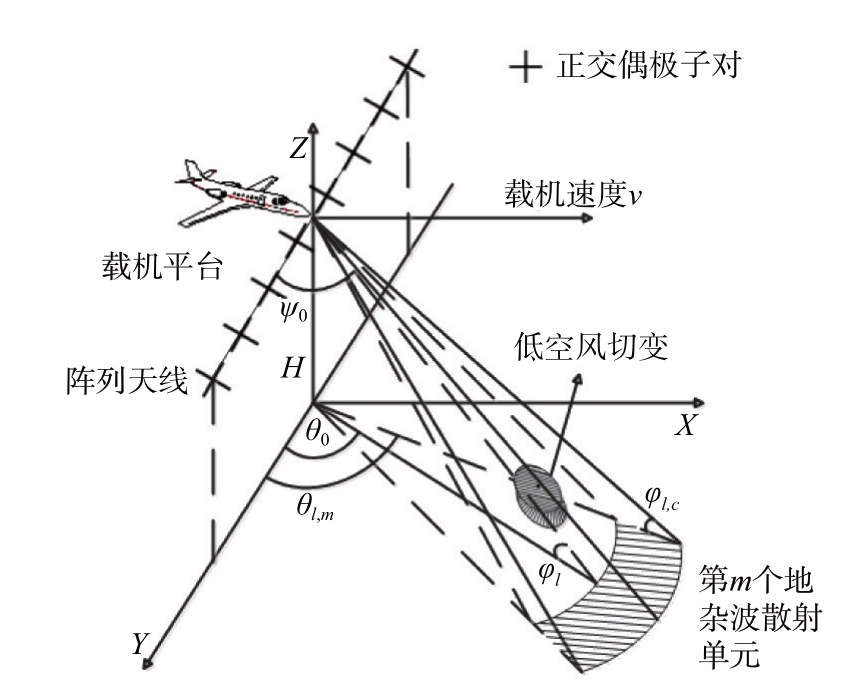
图1 机载双极化气象雷达前视阵下探测低空风切变示意图
1.1 低空风切变回波信号模型
第(ll=1,2,…,L)个待检测距离门内的低空风切变信号sl表示为
式中:⊗为Kronecker 积;po=![]() 为风切变信号的极化导向矢量,phh 与pvv 分别代表风切变回波信号HH与VV通道的幅度、相位等信息;ψ0代表其空间锥角,sd( fd)K×1 代表其时间导向矢量,ss(ψ0)N×1 为其空间导向矢量,fd 为机载双极化气象雷达前视阵模型中单个距离门下低空风切变目标归一化后的多普勒频率,具体表现形式为
为风切变信号的极化导向矢量,phh 与pvv 分别代表风切变回波信号HH与VV通道的幅度、相位等信息;ψ0代表其空间锥角,sd( fd)K×1 代表其时间导向矢量,ss(ψ0)N×1 为其空间导向矢量,fd 为机载双极化气象雷达前视阵模型中单个距离门下低空风切变目标归一化后的多普勒频率,具体表现形式为
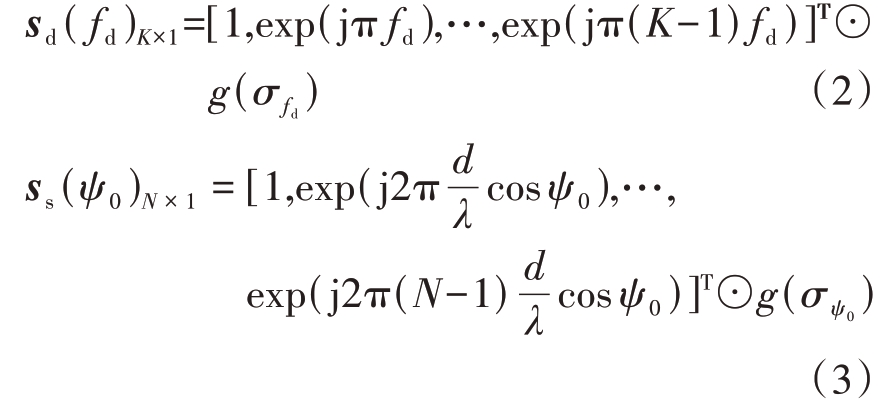
式中,⊙为Hadamard 积![]() 分别为该距离门内,风切变回波信号的频率、角度扩展函数,且
分别为该距离门内,风切变回波信号的频率、角度扩展函数,且
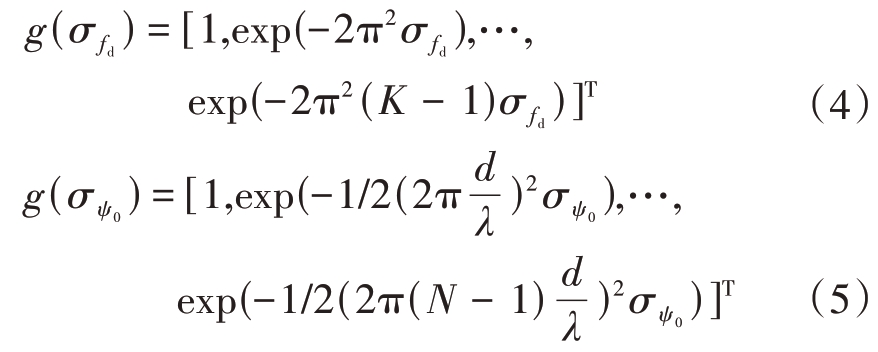
对于式中的![]() 有
有
式中![]() 表示θ0 在风场信号的方位角上的扩展,σφl表示φl在其俯仰角方向上的扩展[12]。
表示θ0 在风场信号的方位角上的扩展,σφl表示φl在其俯仰角方向上的扩展[12]。
1.2 地杂波回波信号模型
杂波通过使用Wald 模型进行建模,分别从方位角和距离维度将杂波分割为Nc 块,假设第m(m=1,2,…,Nc)个杂波水平上的方位角为θl,m,垂直上的俯仰角设为φl,c,因此其对应的归一化后多普勒频率fd,m和空间锥角ψs,m分别为
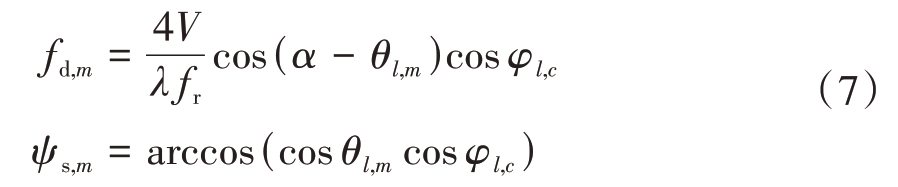
其中α为飞机飞行方向与天线阵列的夹角,因此可以进一步得到杂波信号的空间、时间导向矢量分别为
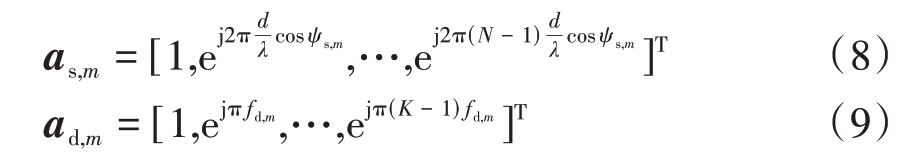
因此,杂波信号cl可以建模表示为
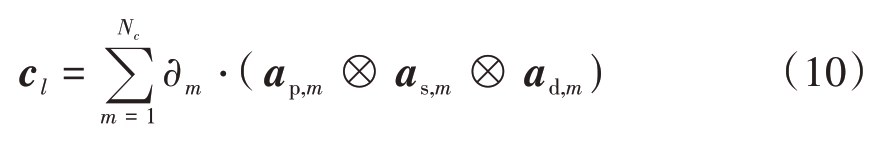
式中:∂m 代表每个杂波块回波信号的复幅度;as,m为第m 个杂波块的空间导向矢量;ad,m 为第m 个杂波块的时间导向矢量;ap,m 为各杂波块回波信号的极化散射矢量,其与杂波的极化协方差矩阵Rp 的关系为
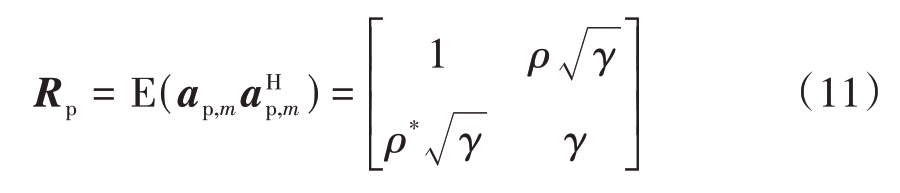
式中,ρ 为HH 与VV 两通道之间的互相关系数,γ为其功率比。因此各杂波块回波信号的极化散射矢量ap,m可由极化协方差矩阵Rp分解得到。
1.3 双极化相控阵气象雷达回波信号模型
双极化相控阵气象雷达第l 个距离门的接收数据为
式中:xhh 与xvv 分别表示HH 与VV 通道的接收数据;sl 表示第l 个待检测距离门内低空风切变目标的回波信号;cl 表示第l 个待检测距离门内的地杂波;nl表示第l个待测距离门内的加性高斯白噪声。
2 基于KA-SRCN-pSTAP的低空风切变风速估计
本节首先利用杂波脊先验知识构造极化空时稀疏字典,其次利用稀疏字典通过使用SRCN 算法估计到杂波线性子空间补空间的投影矩阵,然后利用其构建pSTAP 滤波器并对机载双极化相控阵气象雷达的回波信号进行处理,最终完成对低空风切变的风速估计。其中构造杂波极化空时稀疏字典、SRCN 算法估计到杂波线性子空间补空间上的投影矩阵、pSTAP权矢量的计算及进行风速估计为本文核心内容,本节分4部分进行具体说明。
2.1 知识辅助信息构造杂波极化空时稀疏字典
由第1 节机载双极化相控阵气象雷达接收回波数据模型可知,某距离单元的回波信号可看作由极化空时导向矢量线性叠加而成。将空时二维谱平面平均划分成许多网格,其中风切变以及噪声信号在空时二维谱中占比较大,功率较低,而地杂波信号占比较小且功率很强,因此地杂波信号在空时二维谱中具有稀疏性。本文利用杂波脊的先验知识辅助构造极化空时稀疏字典,以减小影响并提高恢复性能。
在机载双极化相控阵气象雷达前视阵下,由于机载平台的运动导致归一化多普勒频率与空间锥角余弦具有耦合关系[13],这种耦合关系确定的地杂波回波信号位置分布属于先验知识当中的一种。
如图2 所示,在低空风切变检测中,雷达回波信号中的地杂波回波信号在空时二维谱的空时耦合关系表示为
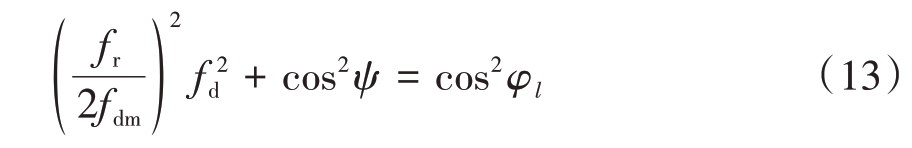
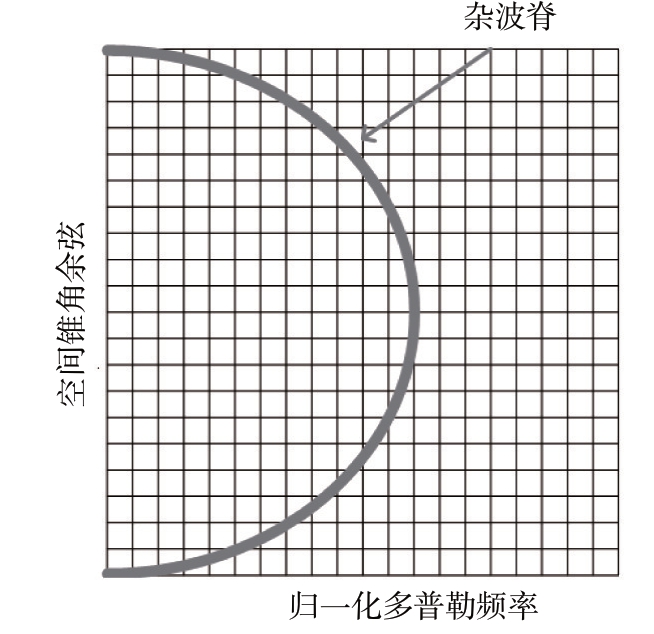
图2 地杂波信号在空时二维谱中的位置分布图
式中,fd 为归一化多普勒频率,fdm=2V/λ 为杂波最大多普勒频率。空间锥角的余弦值设为cos ψ=cos θ cos φl。
进行离散化时,从空间锥角方向均匀划分Na份。根据式(13)可得到相应的归一化多普勒频率为
式中,fd,u 为该网格归一化后的多普勒频率,cos ψs,u为该单元下空间锥角的余弦值。
由公式(10)与公式(11)可进一步推导:
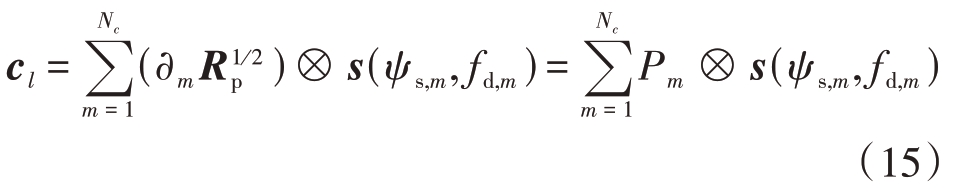
式中:Rp 为极化协方差矩阵;Pm 定义为Pm=![]() ,m=1,2,…,Nc 表示各杂波片的空时导向矢量,fd,m 为某杂波片的归一化多普勒频率,ψs,m为杂波的空间锥角。
,m=1,2,…,Nc 表示各杂波片的空时导向矢量,fd,m 为某杂波片的归一化多普勒频率,ψs,m为杂波的空间锥角。
对于双极化通道数据,根据式(15)进一步的地杂波可表示为
因此,将空时二维谱离散化后,接收的回波数据xl在第l个距离门下可表示为[14]

因此,杂波极化空时字典矩阵Ψ 为由HH通道与VV 通道各单元网格对应的空时导向矢量组成,可表示为
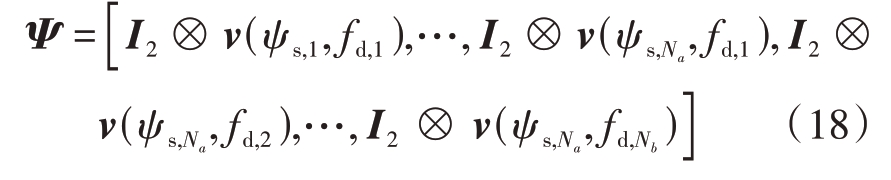
2.2 基于SRCN算法的到杂波子空间补空间的正交投影矩阵估计
通过2.1 节对样本数据进行稀疏表示后,可以使用SRCN 算法迭代地选取字典矩阵中的某些原子来构造杂波子空间[16]。该算法迭代过程中,每次均从字典中选取出一个原子,并估计到杂波线性子空间补空间上的投影矩阵。直到迭代停止后,杂波子空间由挑选出的所有原子构成,进而得到最终的到杂波线性子空间补空间上的投影矩阵。下面对某次迭代进行详细描述。
设D 表示集合{1,2,…,K},K 代表字典矩阵Ψ的列数;令Π 为每次迭代所选原子位置的集合,Γ设为K 中所有不属于Π 的集合,即Γ ∪Π= D;令ΨΓ和ΨΠ分别代表字典矩阵Ψ 中对应于集合Γ 和集合Π 的原子所构成的矩阵,其中ΨΠ为估计的杂波子空间。将Π 初始化为空集∅,Γ 为全集D;ΨΠ初始化为空集,ΨΓ为矩阵Ψ。

在一次迭代下,对字典矩阵Ψ 中的所有原子进行挑选时,要求待挑选的原子dk 到杂波子空间补空间的投影与样本空间的相关性最大。设

式中:Uc 为上一次迭代计算得到的到杂波线性子空间补空间上的投影矩阵,第一次迭代时,Uc 初始化为单位阵;分母代表dk与Uc的相关性[16],由于dk从可构成Uc的原子群中挑选,因此分母不会为零;k为当前迭代所选列的索引。
应挑选相关性最强的原子,使hk 最大的原子位置索引
将挑选出的原子及其索引分别纳入矩阵ΨΠ和集合Π 中,并将该原子及其索引分别从矩阵ΨΓ和集合Γ中去除,对ΨΓ和ΨΠ进行更新。
在此次迭代下,到杂波子空间的正交投影矩阵Un为

根据下式计算最终残差功率Er,判断是否满足迭代停止准则。Er 只由噪声功率决定,因此将噪声功率设为迭代停止的临界值,残差功率为[16]

当Er 大于噪声功率时,继续进行迭代并根据式(19)计算下一次迭代的hk 值;当Er 小于等于噪声功率时,迭代停止,此时的Uc即为最终的到杂波线性子空间补空间上的投影矩阵。
根据以上叙述,SRCN 算法估计到杂波子空间补空间的正交投影矩阵的完整步骤如下:
1)初始化参数:将Uc 初始化为2NK×2NK 的单位阵,Π 为空集,Γ 为全集D;同理,ΨΠ 初始化为空集,ΨΓ为矩阵Ψ。
2)根据式(19)计算矩阵ΨΓ 中所有原子对应的hk值,并由式(20)找出使hk最大的原子索引k′。
3)将索引k′从集合Γ 中去除并将其加入集合Π中,同时更新ΨΓ和ΨΠ。
4)根据式(21)计算到杂波子空间的正交投影矩阵Un。
5)根据式(22)计算到杂波线性子空间补空间上的投影矩阵Uc。
6)判断是否满足迭代停止准则,根据式(23)计算残差功率,当残差功率小于设置门限值,即![]() 时迭代停止,否则转至第2)步继续迭代。
时迭代停止,否则转至第2)步继续迭代。
7)输出到杂波线性子空间补空间上的投影矩阵Uc。
2.3 pSTAP权矢量的求解及风速估计
本节重点推导pSTAP 权矢量表达式。首先利用最大似然估计准则,对风切变信号的极化导向矢量p进行估计,接着推导出杂波协方差矩阵与到杂波线性子空间补空间的投影矩阵的关系,最后利用该关系对pSTAP 滤波器权矢量做进一步推导。
首先对极化导向矢量p 进行估计,由式(12)可得
设![]() 代表由含杂波加噪声数据估计得到的协方差矩阵,在杂波和噪声的高斯分布下有
代表由含杂波加噪声数据估计得到的协方差矩阵,在杂波和噪声的高斯分布下有
当研究目标为点目标时,用于估计杂波协方差矩阵的相邻距离门信号中仅含有杂波加噪声,但本文研究的风切变目标为分布式目标,相邻距离门信号中除杂波与噪声外还含有风切变信号。下面进行详细说明在毗邻距离单元下,杂波以及噪声所得杂波协方差矩阵 的估计,可由含风切变、杂波以及噪声的数据估计出的杂波协方差矩阵
的估计,可由含风切变、杂波以及噪声的数据估计出的杂波协方差矩阵 代替。
代替。
设在毗邻距离门下,由含杂波以及噪声信号得到的协方差矩阵的估计为 ,由包含风切变、杂波以及噪声信号估计得到的杂波协方差矩阵为
,由包含风切变、杂波以及噪声信号估计得到的杂波协方差矩阵为 。
。
第l 个距离门内,包含杂波以及噪声的信号el为
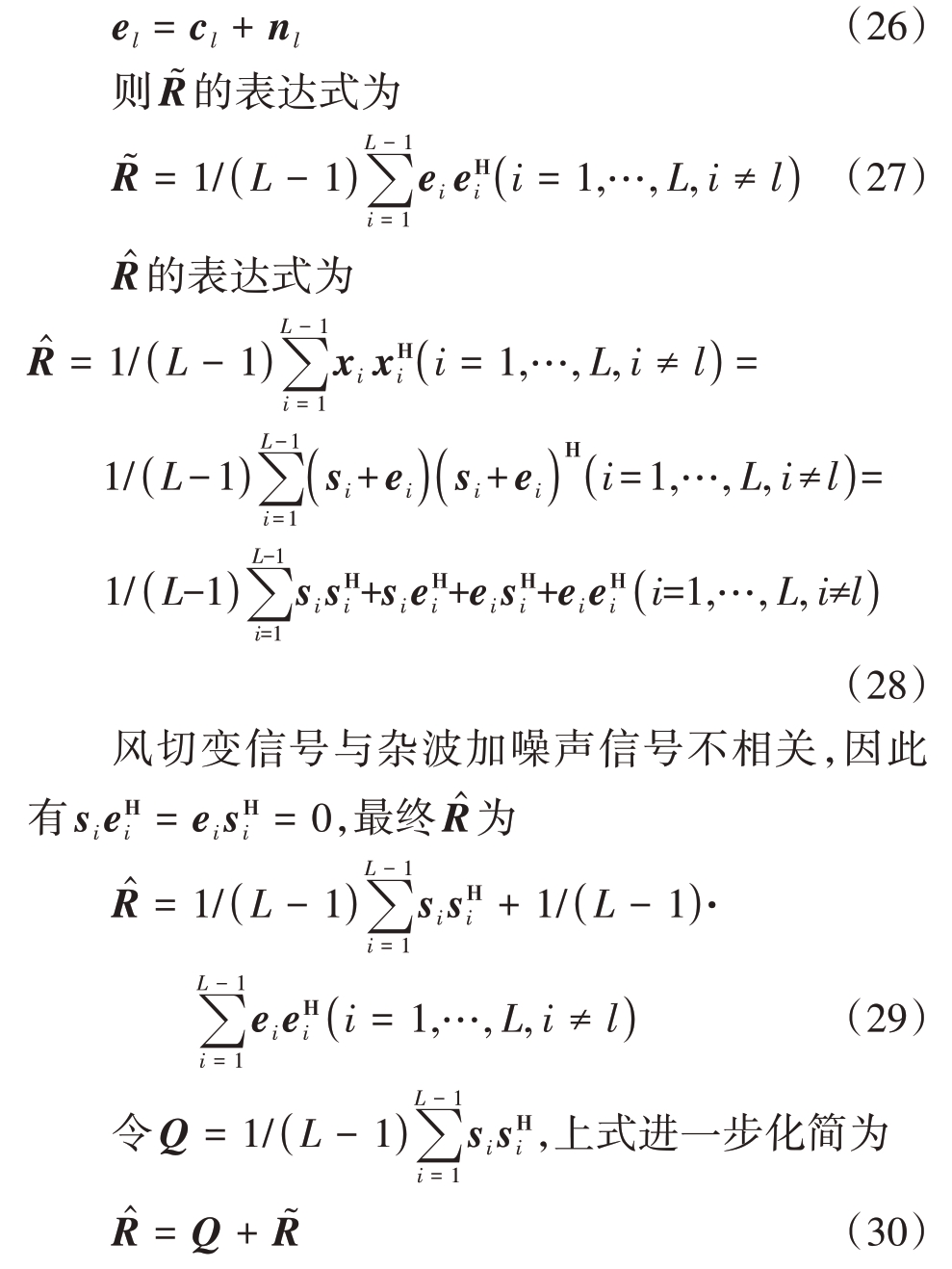
根据NASA测得的数据,实际机载气象雷达在进行风切变检测时,大部分情况下杂信比在30~60 dB区间[17],因此本文在40 dB 杂信比下仿真出回波数据,并分别计算Q和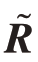 。
。
图3展示了40 dB 杂信比下Q 和 中各元素的模值,从图中可明显看出
中各元素的模值,从图中可明显看出 的模值远远大于Q的模值,因此式(30)中Q 可忽略不计,因此用
的模值远远大于Q的模值,因此式(30)中Q 可忽略不计,因此用 表示估计所得杂波的协方差矩阵进行计算。
表示估计所得杂波的协方差矩阵进行计算。
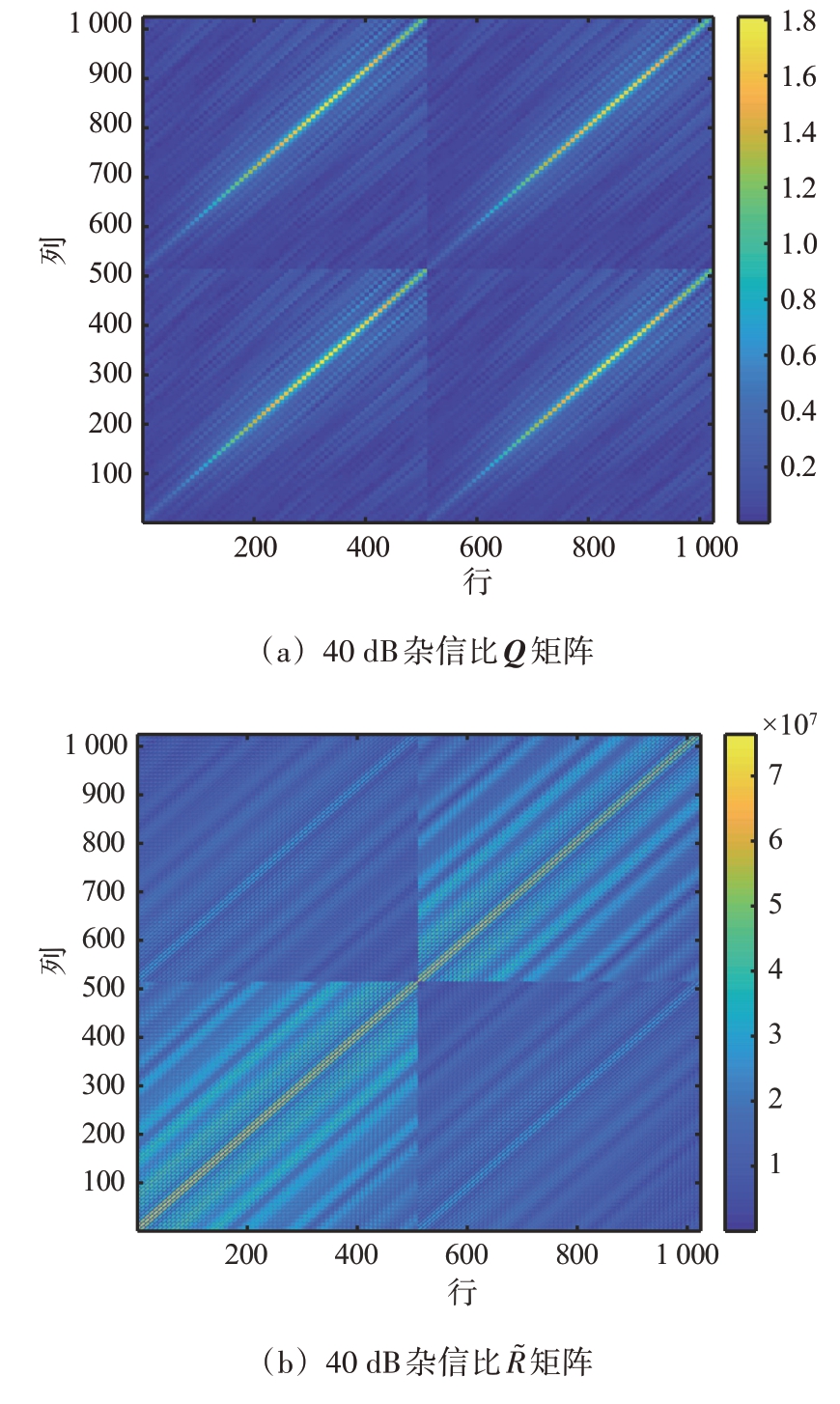
图3 40 dB杂信比下矩阵中各元素的模
确定协方差矩阵 后,定义式(24)中B=I2 ⊗Sst。因此,含风切变回波信号xl 的概率密度函数为
后,定义式(24)中B=I2 ⊗Sst。因此,含风切变回波信号xl 的概率密度函数为
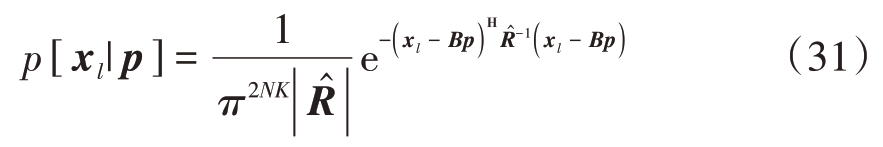
式中,p为待估计的极化导向矢量。
极化导向矢量p 由式(31)通过最大似然估计得到
使该式最大等效于使下式最小
等式两边同时对p求偏导,得到
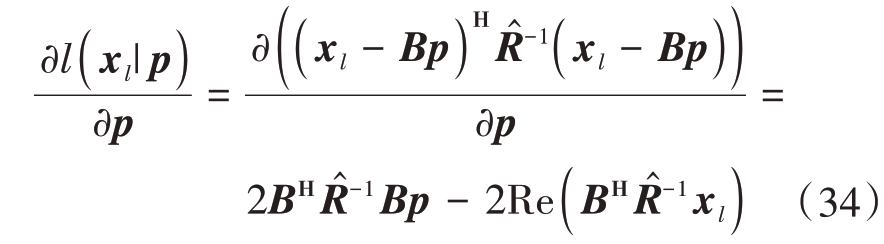
令上式等于0,因此可得到p的估计为

从上式可以看出,协方差矩阵的逆![]() 约等于Uc,因此利用该关系,用Uc替代
约等于Uc,因此利用该关系,用Uc替代![]() 进行计算,极化导向矢量p 和pSTAP 滤波器权矢量可以进行进一步推导。
进行计算,极化导向矢量p 和pSTAP 滤波器权矢量可以进行进一步推导。
将式(37)代入式(35)中,进一步得到
对于最优pSTAP滤波器,其加权矢量表示为
式中,μ 为常数,v0= p ⊗v(ψs,u,fd,j)为极化空时导向矢量。将上式中估计的极化导向矢量![]() 代入式(34)中,pSTAP权矢量可进一步表示为
代入式(34)中,pSTAP权矢量可进一步表示为
将通过SRCN 算法得到的Uc 代入式(40)得到pSTAP权矢量,为实现对地杂波的抑制和低空风切变目标信号的积累做准备。
利用式(40)求解得到pSTAP 滤波器权矢量,对待检测单元回波数据xl 进行处理。待检测距离单元中的地杂波信号被抑制后,低空风切变信号多普勒频率的估计可由使输出功率最大求解得![]() 到,如下式所示:
到,如下式所示:
进一步得到第l 个距离门下风场的速度估计为
2.4 方法流程
本文所提方法流程图如图4所示。
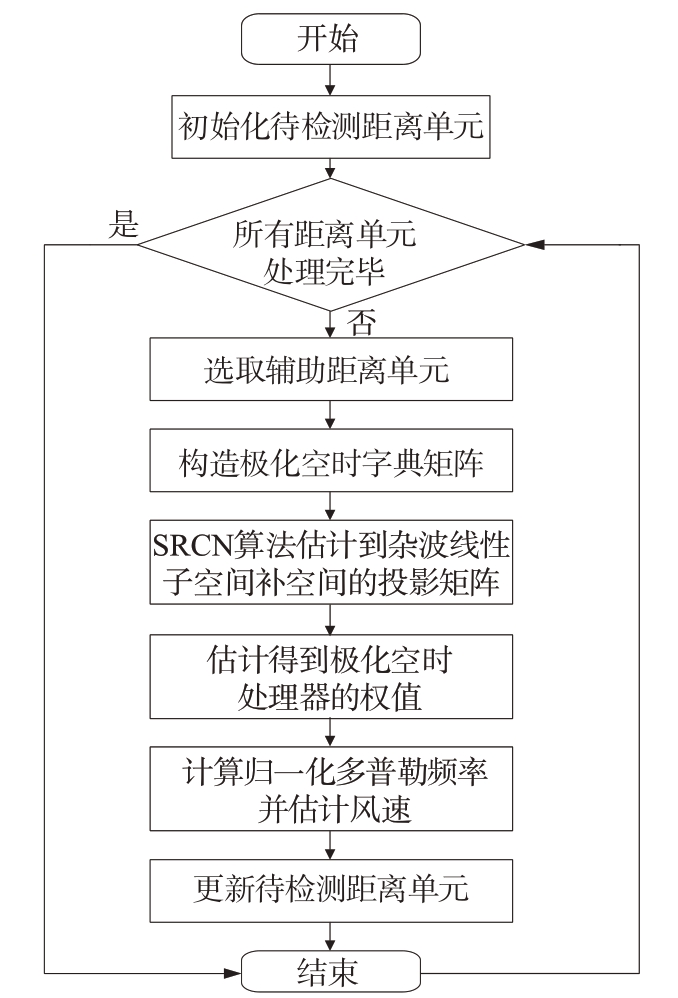
图4 基于KA-SRCN-pSTAP的低空风切变风速估计方法流程图
本文方法可以实现在IID 训练样本不足的情况下,对低空风切变风速进行精准估计,其步骤如下:
步骤1 通过回波信号得到不同距离单元的训练样本;
步骤2 利用地杂波回波信号在空时二维谱中位置分布先验信息构造待检测单元的杂波极化空时字典;
步骤3 利用SRCN算法估计待检测距离单元的到杂波线性子空间补空间的投影矩阵;
步骤4 利用到杂波线性子空间补空间的投影矩阵得到极化空时处理器的权矢量,并对地杂波进行抑制;
步骤5 得到待检测距离门下,估计的风切变目标信号多普勒频率![]() 及风速结果;
及风速结果;
步骤6 更新待检测距离门,对所有距离单元数据进行处理,输出最终估计风速结果。
3 仿真结果及分析
3.1 仿真条件设置
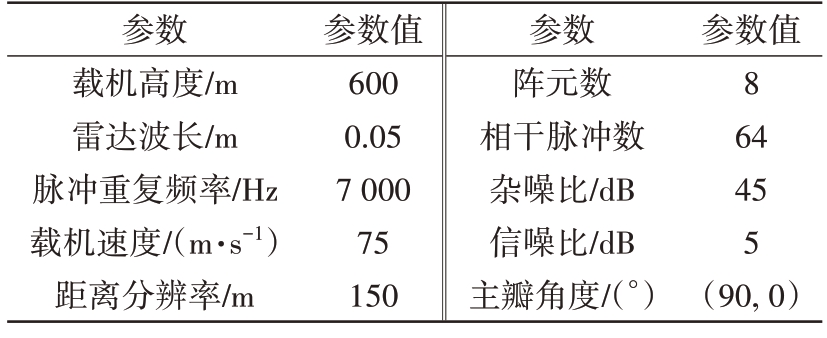
本文中假设低空风切变风场的位置在载机前方,距离载机8.5~16.5 km处。杂波的仿真参数为互相关系数ρ=0.52,功率比γ=1.03。雷达的仿真参数如表1所示。
表1 系统仿真参数
3.2 仿真结果分析
图5 分别展示了机载双极化相控阵气象雷达在前视阵情况下探测低空风切变目标信号时,HH、VV通道下回波信号的距离多普勒图。如图所示,杂波的多普勒信息愈接近零频强度愈大,低空风切变信号功率较弱,呈反“S”型淹没于杂波信号中。
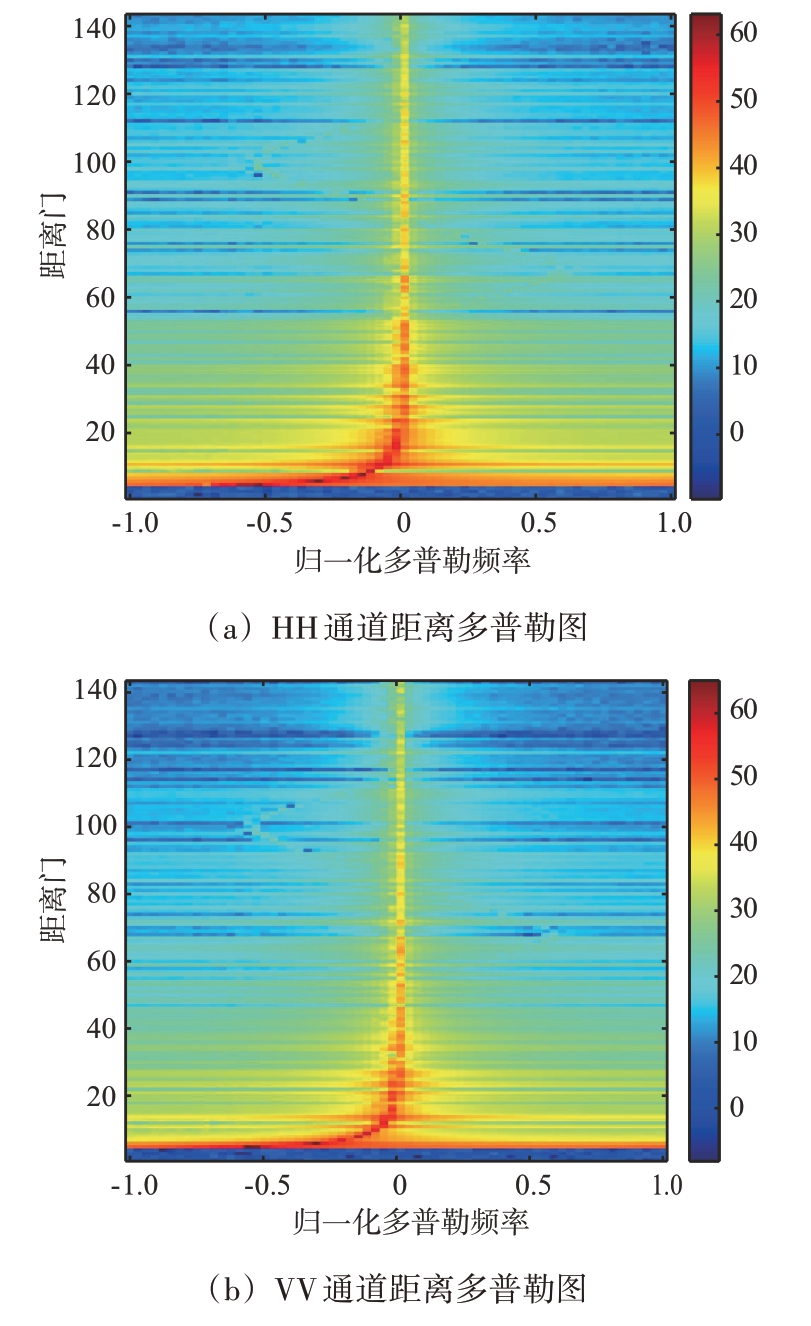
图5 前视阵下HH通道与VV通道回波信号距离多普勒图
图6 为机载双极化相控阵气象雷达在HH、VV通道的前视阵下,以风切变为目标的回波信号空时二维谱。在图中呈现一条窄带形式的为低空风切变信号,由于其为分布式目标,在空时域会出现展宽;与前文描述的地杂波在空时二维上的位置分布一致,地杂波的形状表现为半椭圆形。
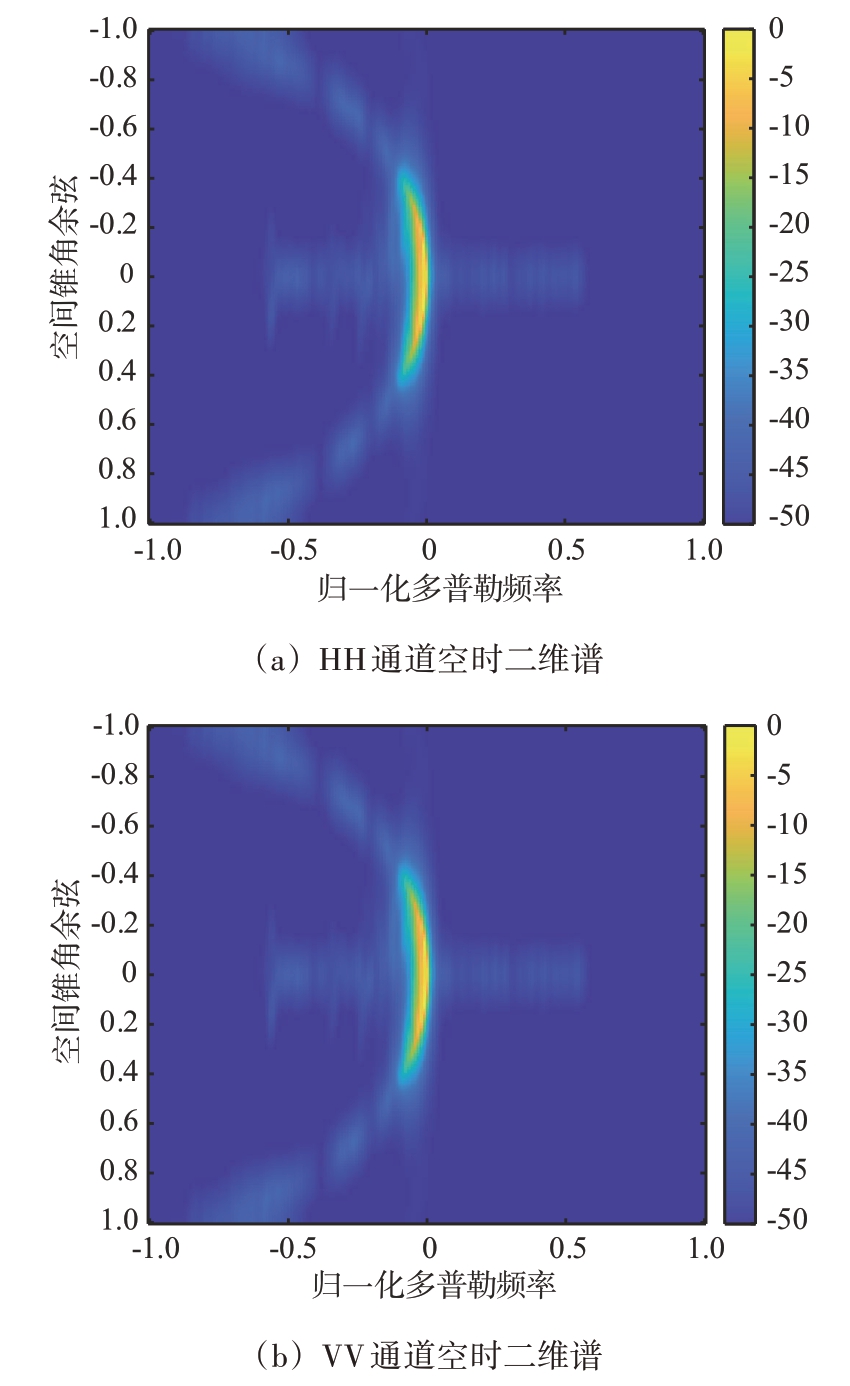
图6 前视阵下HH通道与VV通道回波信号空时二维谱图
从上述仿真结果及分析可知,低空风切变信号范围及功率远远小于地杂波,因此导致回波信号中低空风切变信号被掩盖在地杂波信号中,进而严重影响低空风切变风速估计效果。
图7 为以第57 距离门为例,本文所提方法、单通道(选取HH 通道)STAP、文献[6]所提CL-KASTAP 方法、文献[8]所提融合双极化通道数据STAP 方法、最优pSTAP 方法的改善因子对比图。文献[6]中CL-KA-STAP 方法与文献[8]中融合双极化通道数据STAP 方法分别在0.25 系统自由度和全样本情况下效果较好,但从图7 中可以观察到,在所选样本数为8的情况下,CL-KA-STAP方法由于未利用极化信息,杂波抑制性能下降。本文利用极化信息结合SRCN 算法,因此所提方法改善因子曲线在零频处更为窄,说明在样本数极少的情况下,本文方法相较于其他4种方法对于抑制杂波效果更佳,从而能得到更为准确的风速估计结果。
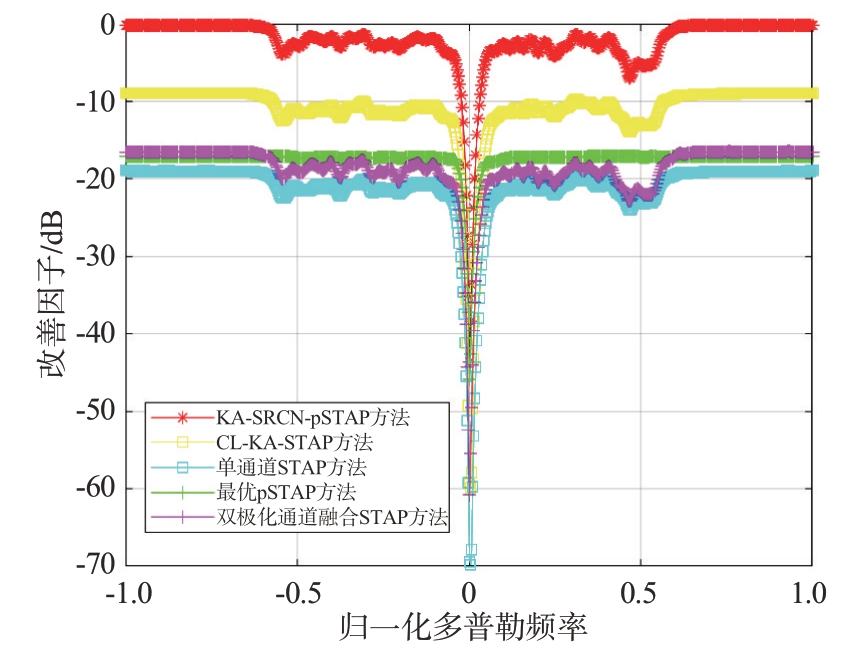
图7 各方法滤波后在第57距离门处的改善因子
图8 为本文所提方法、单通道(选取HH 通道)STAP、文献[6]所提CL-KA-STAP 方法、文献[8]所提融合双极化通道数据STAP 方法、最优pSTAP 方法的风速估计比较图。本文所提方法利用极化信息提高了杂波抑制性能,同时避免了估计pSTAP权矢量时对于样本数的严格要求。从图8 可以观察到,在所选样本为8的情况下,CL-KA-STAP方法由于未利用极化信息,估计风速结果有所偏差。本文方法在训练样本极少情况下仍然能准确估计风速,相较于其他4种方法更为准确。
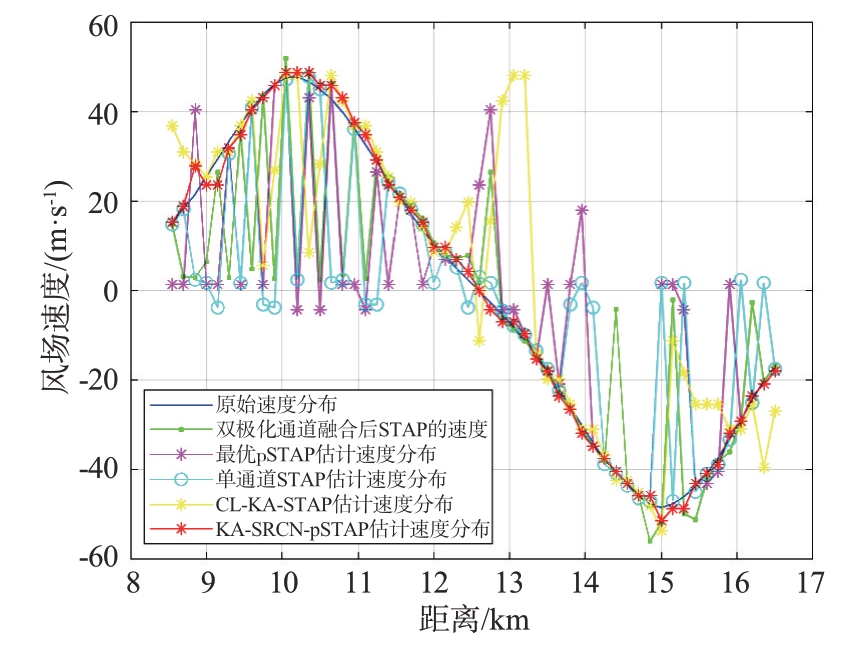
图8 各方法风速估计对比图
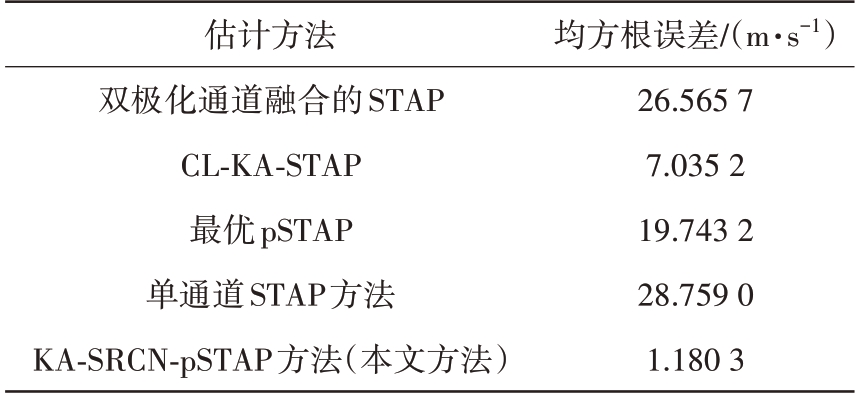
表2 为所提方法和其他4 种方法分别与原始风速计算所得均方根误差的对比。从表中数据可以直观地看到:本文所提方法与原始风速之间的均方根误差最小,从而证实在样本数较少的情况下,该方法对低空风切变进行风速估计更具有精确性。
表2 5种方法下风速估计计算均方根误差对比
4 结束语
本文针对机载双极化相控阵气象雷达对低空风切变进行探测时,由于IID 样本缺少所引起的无法精准对风速进行估计问题,提出一种基于KASRCN-pSTAP 的低空风切变风速估计方法。该方法将极化信息引入空时域,利用杂波脊的先验知识辅助构建极化空时稀疏字典,通过SRCN 算法挑选原子对到杂波子空间补空间的正交投影矩阵进行估计,仅使用少量样本数据求解pSTAP 权矢量,并构造pSTAP 滤波器实现地杂波的抑制,最终能够精准地估计低空风切变风速。仿真结果表明该方法在IID 样本较少的情况下能够精准地完成对低空风切变的风速估计,且该方法将SRCN 方法与pSTAP结合,不仅利用极化信息提高了杂波抑制性能,同时避免了估计pSTAP 权矢量时对于样本数的严格要求,因此该方法适用于机载双极化相控阵气象雷达体制下,样本数较少的情况。但由于该方法对字典矩阵中的所有原子进行挑选,复杂度略高、运行时间较长,因此需进一步研究小样本情况下的低复杂度pSTAP算法。
[1]LIN Caiyan,ZHANG Kaijun,CHEN Xintao.Overview of Low-Level Wind Shear Characteristics over Chinese Mainland[J].Atmosphere,2021,12(5):628.
[2]KHATTAK A,CHAN P W,CHEN F,et al.Interpretable Ensemble Imbalance Learning Strategies for the Risk Assessment of Severe-Low-Level Wind Shear Based on Li-DAR and PIREPs[J].Risk Analysis,2023(5):1084-1102.
[3]NIU Haotian,MA Cunbao,SHE Zhiyu,et al.A Hybrid Methodology for Knowledge Organization and Application of Chinese Civil Aviation Regulations from Mission Safety Support Perspective[J].Proceedings of the Institution of Mechanical Engineers,Part G:Journal of Aerospace Engineering,2023(15):3524-3559.
[4]Jackson D.Phased Array Antenna Handbook[Book Review][J].IEEE Antennas and Propagation Magazine,2018,60(6):124-128.
[5]杨通晓,袁招洪.多波段双偏振天气雷达识别降水类型的模拟研究[J].高原气象,2017,36(1):241-255.
[6]李海,谢伶莉,张志宁.复杂地形环境下基于CL-KASTAP 的低空风切变风速估计方法[J].电子与信息学报,2021,43(12):3647-3655.
[7]WANG Qiang,ZHANG Yani,LI Zhihui,et al.Fast Heterogeneous Clutter Suppression Method Based on Improved Sparse Bayesian Learning[J].Electronics,2023,12(2):343.
[8]李海,张志宁,周晔,等.基于双极化通道数据融合的低空风切变风速估计方法[J].火控雷达技术,2022,51(3):1-8.
[9]李海,谢瑞杰,谢伶莉,等.复杂地形环境下基于GAMPSTAP 的低空风切变风速估计方法[J].电子与信息学报,2023,45(2):576-584.
[10]李海,程伟杰,谢瑞杰.基于同伦稀疏STAP 的低空风切变风速估计[J].系统工程与电子技术,2022,44(4):1174-1181.
[11]LI Hai,CHEN Yutong,FENG Kaihong,et al.Low-Altitude Windshear Wind Speed Estimation Method Based on KASPICE-STAP[J].Sensors,2022,23(1):54.
[12]姚晖.分布式信号源参数估计技术研究[D].郑州:解放军信息工程大学,2013.
[13]RIEDL M,POTTER L C.Knowledge-Aided Bayesian Space-Time Adaptive Processing[J].IEEE Trans on Aerospace and Electronic Systems,2018,54(4):1850-1861.
[14]DUAN Keqing,LIU Weijian,DUAN Guangqing,et al.Off-Grid Effects Mitigation Exploiting Knowledge of the Clutter Ridge for Sparse Recovery STAP[J].IET Radar Sonar&Navigation,2018,12(5):557-564.
[15]ZHAO Kang,LIU Zhiwen,SHI Shuli,et al.Polarimetric Clutter Nulling Space-Time Adaptive Processing[C]//Proceedings of the 2020 4th International Conference on Digital Signal Processing,Chengdu China: Association for Computing Machinery,2020:331-335.
[16]王泽涛.基于稀疏表示的机载雷达STAP 技术研究[D].长沙:国防科学技术大学,2019.
[17]OU Jianping,ZHANG Jun,ZHAN Ronghui.Processing Technology Based on Radar Signal Design and Classification[J].International Journal of Aerospace Engineering,2020(1):4673763.