0 引言
无源定位是直接处理接收站收到的信号，自身不会主动发射信号，根据信号中蕴含的位置信息来确定辐射源的方位，又称为被动定位技术，因此其优势在于电磁隐蔽性高和定位距离远［1］。两步法则是传统无源定位中的代表方法：首要在于先针对位置参数进行估计，接收站接收到的观测数据中包含着如信号到不同接收站的时间（Time Difference of Arrival，TDOA）、方位角度［2］（Direction of Arrival，DOA）等位置信息，通过空间谱等方法对这些信息进行估计；第二步，建立定位参数和辐射源位置的方程并进行求解，从而实现定位。两步法虽然计算复杂度较低，但缺点也很明显，如在低信噪比下鲁棒性较差，无法处理多辐射源的参数关联、在同频信号上性能也表现较差等［3］。为了解决该问题，直接定位法［4］（Direct Position Determination,DPD）被提出并受到广泛研究，和两步法不同的是，DPD 并没有先估计定位参数这一中间步骤，改为对采样的原始信号进行直接处理，在构建目标函数上仅考虑与目标位置相关的因素，通过对感兴趣区域的完整搜索来估计辐射源的位置［5］。DPD 可利用多基站接收结构进一步提高定位性能，但由于直接处理原始信号，存在着难以获得辐射源位置解析解的问题，导致计算量相对较大。
压缩感知（Compressed Sensing,CS）在低信噪比、少快拍下较于传统信号处理模型具有更好的性能和鲁棒性。当目标信号具有稀疏特性时，便可以通过一欠定的线性方程利用稀疏重构算法将目标信号从高度欠采样的数据中重构出来［6］。CS算法发展至今大致可分为3类，分别为贪婪追踪算法［7］、以l1惩罚项为基础的凸优化/非凸优化算法［8］和以贝叶斯理论为基石的算法［9］。前两种算法需要人工设置参数，而这些参数又极大影响算法效能，缺乏科学的参数设置工具。为避免这一问题，贝叶斯类算法便脱颖而出，因其自动迭代信号参数，无须人工干预，使得恢复性能往往优于其他重构类算法［10］。Zhang等［11-12］利用信号元素的结构特性，改进了一种名为块稀疏贝叶斯学习（Block Sparse Bayesian Learning,BSBL）方法，通过探索信号块内相关性来达到增强算法恢复效果的目的。Babacan 等［13］通过赋予元素Laplace 先验来改进经典贝叶斯算法，其实质为LASSO 运用于贝叶斯理论的变形但存在变量未知则不能正确估计变量的缺陷。为避免这一固有缺陷，文献［14］给出了一种名为自适应LASSO 的算法，改变之处在于施加不同的权重于信号中的元素，并证明了LASSO 算法中Oracle 特性，弥补了普通LASSO 算法以及Laplace类算法的缺陷，显著增强了算法的恢复效果。文献［15-16］结合实际问题将自适应LASSO 理论成功运用在估计DOA 中。贝叶斯类算法在定位辐射源的需求上也得到了大量运用［17-18］，当同一个辐射源的信号发射到不同接收站上时，不同接收站字典中的稀疏性保持一致，可利用这种特性联合多字典进行信号恢复。文献［19］和文献［20］通过结合多基站的不同字典重组最终过完备字典，使得信号的观测角度增多，但存在着需要明确辐射源个数的缺陷。文献［21］为减少算法对辐射源的定位误差，进一步在块稀疏贝叶斯的基础上再结合了Laplace先验。但在上述文献中辐射源与接收基站的距离较小，受信道衰减和噪声的影响较小，而当辐射源位置较远时，在低信噪比下存在对该目标的定位精度下降的问题。
结合上述背景，对远距离定位精度下降的难题，本文给出了一种联合自适应LASSO 先验与块稀疏贝叶斯的直接定位方法，该方法的整体结构表现为多层形式，在利用信号的块结构的基础上，针对信号内的各元素施加独立自适应变化权重的LASSO 先验，同时利用存在于信号中的块内相关性，进一步提高了算法的稀疏恢复性能，并利用基站的不同字典联合构建过完备字典，有效地实现了远距离下辐射源位置估计。
1 信号模型
1.1 传统模型
若空间中存在H 个辐射源，有L 个基站来接收辐射源传输信号，其中每个基站都配备有M 个阵元组成的天线线性阵列。向量ph代表每个辐射源的位置，大小为D×1（D 表示维度）。则接收信号在时域上第l个接收站建模为
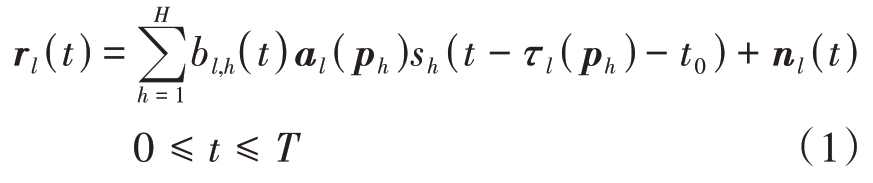
式中：rl(t)表示第l 个接收站的观测矢量，大小为M×1；bl,h 为未知复信道衰减存在于第l 个接收站接收第h 个辐射源信号；al(ph)=
为阵列响应，自h 号辐射源到l 号接收站，f0 为信号中的载波频率，d 为阵列中的阵元间距，θl,h为h号辐射源信号入射到l号接收站的角度，c 为电磁波在空间中的传播速度；sh(t-τl(ph)- t0)为h 号辐射源在t0 时刻发射的信号延时τl(ph)后到达l 号接收站的波形，持续收到辐射源信号时间为T；向量nl(t)为接收站接收信号中混杂的高斯白噪声且其均值为0。辐射源所处的传播环境影响着信道衰减的相位和幅度，因此信道衰减bl,h(t)与时间密切相关。当观测时间与相干时间比足够小时，信道衰减认为保持不变，即bl,h= bl,h(t)。随后利用式（1）进行离散傅里叶变换（Discrete Fourier Transform,DFT）转换至频域，则相应数据在第l号接收站的表现形式为
1.2 压缩感知模型
基础压缩感知建模为y= Φx+v，其中y ∈ℝZ×1表示观测矢量，Φ ∈ℝZ×N(Z ≪N)是已知的过完备字典矩阵并且任意Z 列线性不相关，x ∈ℝN×1 是待恢复的稀疏信号，v 是未知的噪声矢量。通常情况下稀疏信号x都具有块结构或者群结构，在这种结构下稀疏信号x可以被视为g个块的结合［11］，即
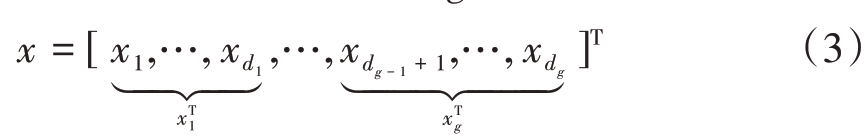
其中块大小di(∀i)并不一定相等，在这g 个块中只有z(z ≪g)个块是非0的，但位置未知，挖掘信号的块结构以及块内的相关性能使算法表现出更好的恢复性能［12］。在接收信号时，信道衰减总是混杂在观测数据中，导致幅度和相位在信号中发生不规则变化，因此将信道衰减和信号视为一个整体，定义
同时在多基站接收到的观测信号中引入块结构，从而式（2）推广至压缩感知形式为
式中，
其中，vec(·)表示重组矩阵的所有列为单一列矢量，⊗表示Kronecker 积，单位矩阵IK 大小为K×K，Q是针对感兴趣区域划分的网格数，也是字典的原子数中，diag {}表示将元素按矩阵主对角线排列，需要利用的辐射源相关方位信息则包含在阵列响应Al和信号延时τl(pq)中。
2 所提辐射源直接定位方法
2.1 自适应LASSO模型
假设任意一个块Sl,q服从零均值的高斯过程
其中，Sl,q的块稀疏性取决于γq，其含义为超参数并其值非负。若第q个块元素全为零，则γq=0，在参数更新的过程中，大多数γq 趋于零。Bq 是一个正定矩阵，表示Sl,q 块内相关性结构。当这些块不具备相关性时，Sl的先验概率为
利用式（7）和式（8）两层不同的贝叶斯先验共同构成了信号Sl 的LASSO 先验，为实现元素自适应变化LASSO 的权重，则需要施加独立的Gamma 分布于非负变量ξ，则有
联合式（9）和式（10）可推导出信号Sl关于变量γ的边缘分布为
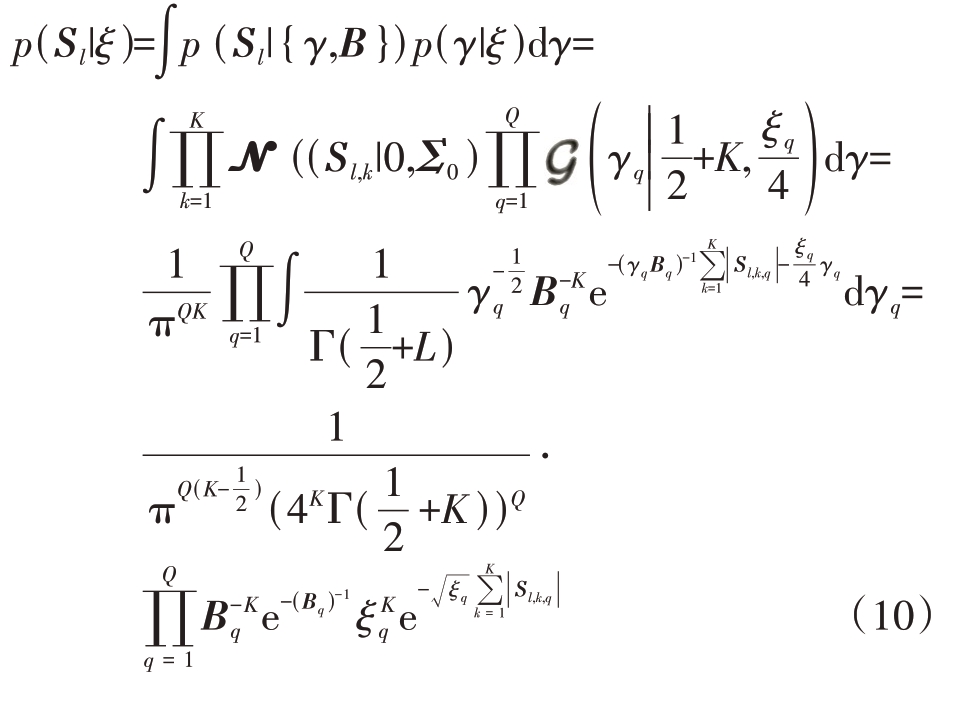
由式（10）可知，通过前后两层独立分布的形式得以为Sl 施加自适应LASSO 先验，从而表现出更好的稀疏性。图1 展示了本文提出的分层稀疏模型的详细组成，节点函数总结如下：
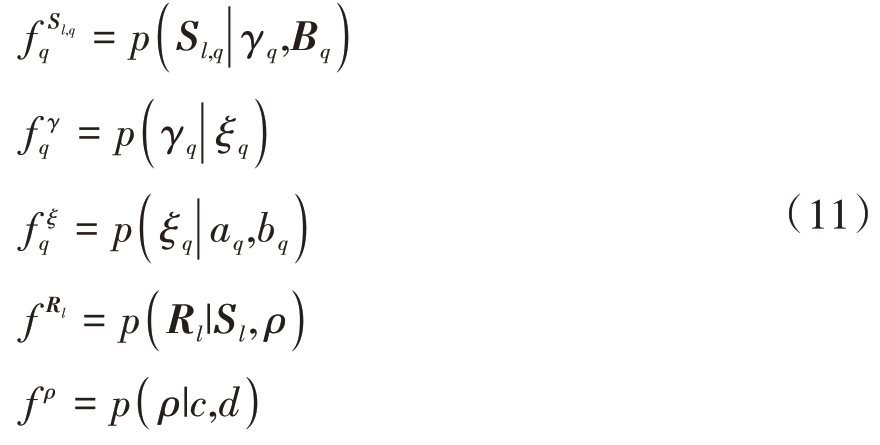
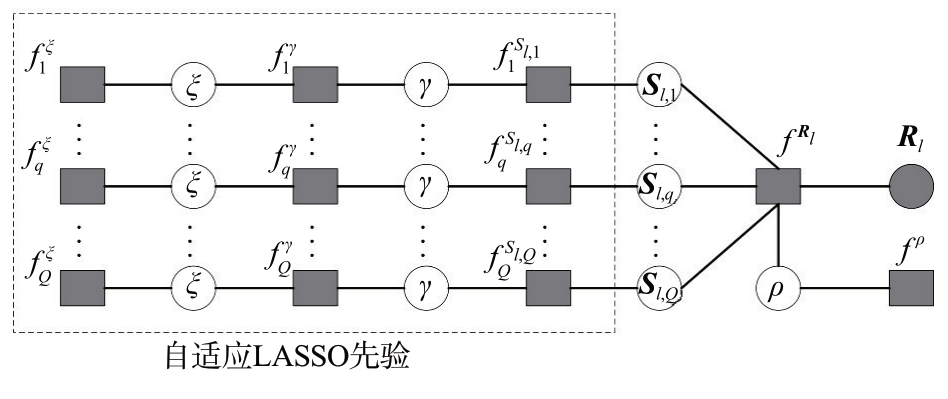
图1 以自适应LASSO先验为基础的分层稀疏贝叶斯模型
式中c，d为预设定的噪声模型参数。
2.2 噪声模型
2.3 贝叶斯推断
贝叶斯推断从后验概率开始，通过接收数据估计各参数的值。根据上文Sl的后验概率为
式中，
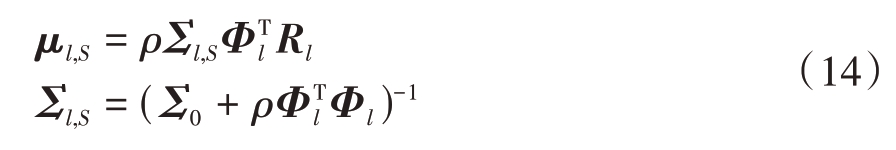
本文中有L 个接收基站，因此式（14）中有L 个不同的μl,S 和Σl,S 表达式，但本文中不同基站使用统一的Σ0和ρ，这是因为相同辐射源的信号被不同的基站接收，同一信号的稀疏结构和噪声方差并不随信道衰减的不同而变化，因此这些参数在不同观测站中保持一致。即认为不同Sl 中的第q 个块的块稀疏性受同一个参数γq 所控制，联合概率密度可经由链式法则得到
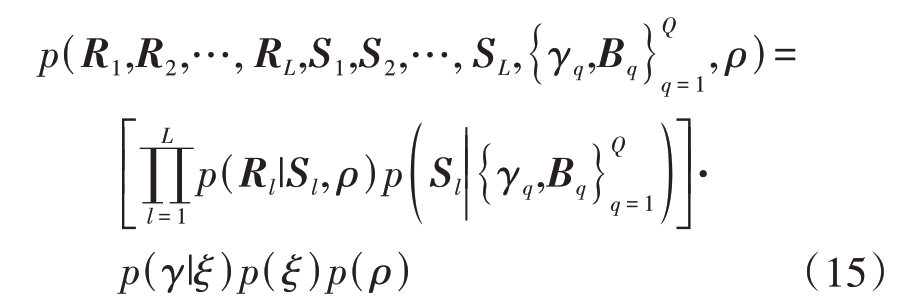
遵照第2类最大似然准则，由式（15）推出最终的代价函数为
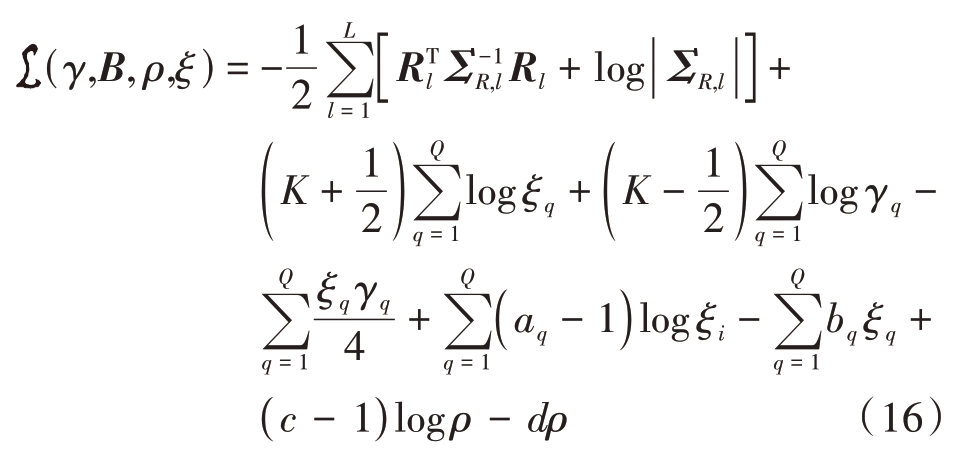
其中，|·|代表矩阵的行列式
式中已省略了常数项。文献［12］表明Bq仅仅影响局部收敛解，并不影响式（16）的全局最小解，而稀疏解往往在全局最小解处。如果不同块之间的Bq不同，则会导致过拟合，为避免过拟合的情况本文统一使用Bq 的平均值，即Bq= B(∀q)，因此Σ0=Γ ⊗B-1，其中Γ=
变量γ 的更新：根据稀疏贝叶斯推导过程，式（16）的第1项表示为
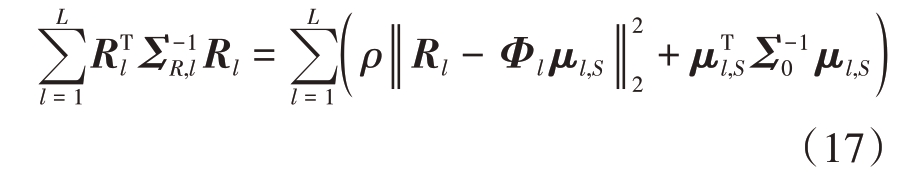
式中，‖·‖表示向量第二范数（或矩阵二范数）。文献［12］中BSBL-BO算法表明，式（16）的第2项的上界表示为
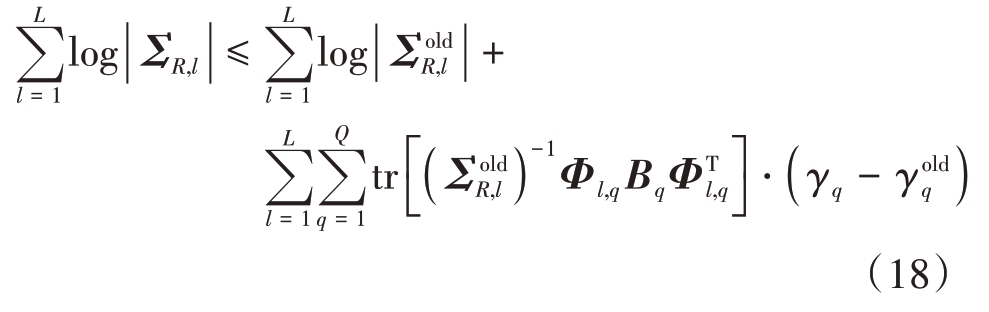
式中
，上标(·)old 代表前一次参数更新后的值，tr(·)为矩阵的迹。将式（18）和式（17）代入代价函数式（16），仅保留与γ相关的量后表示为
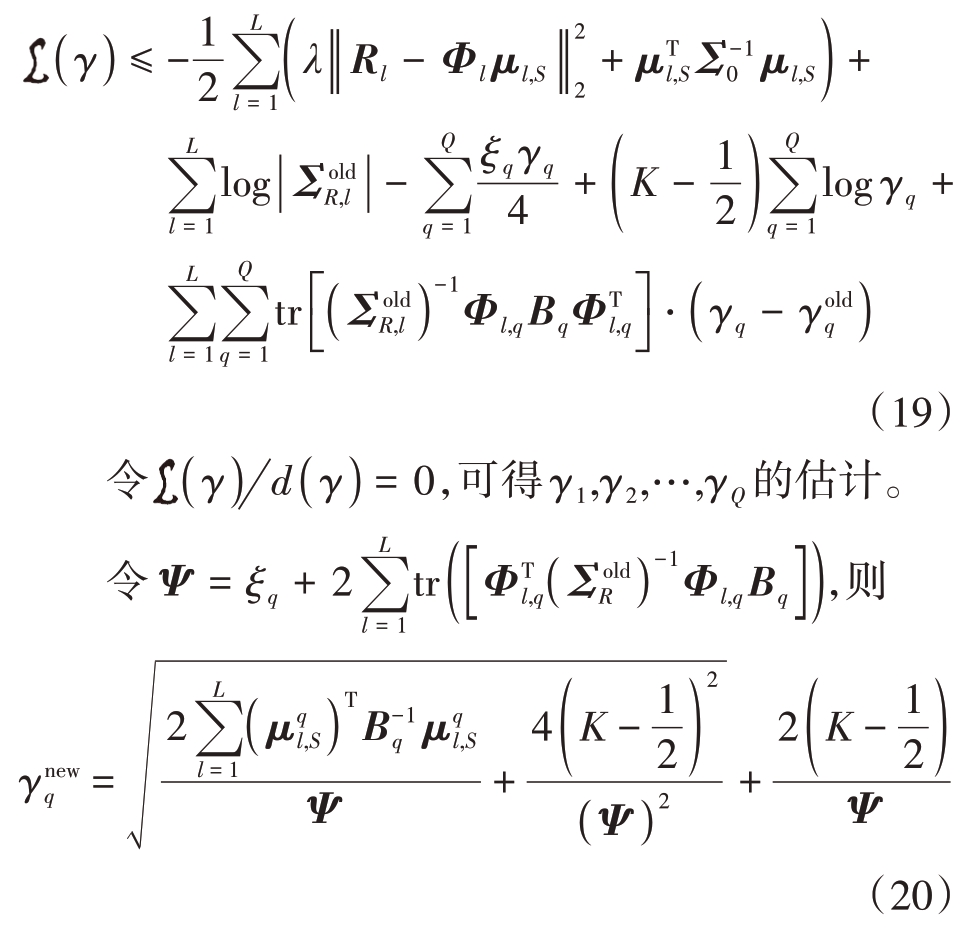
式中，上标(·)new表示本次参数更新后的值。
其他参数更新：求解过程和γ 相同，令
，其中Λ=(ξ,B,ρ)可得其他参数的更新方程为
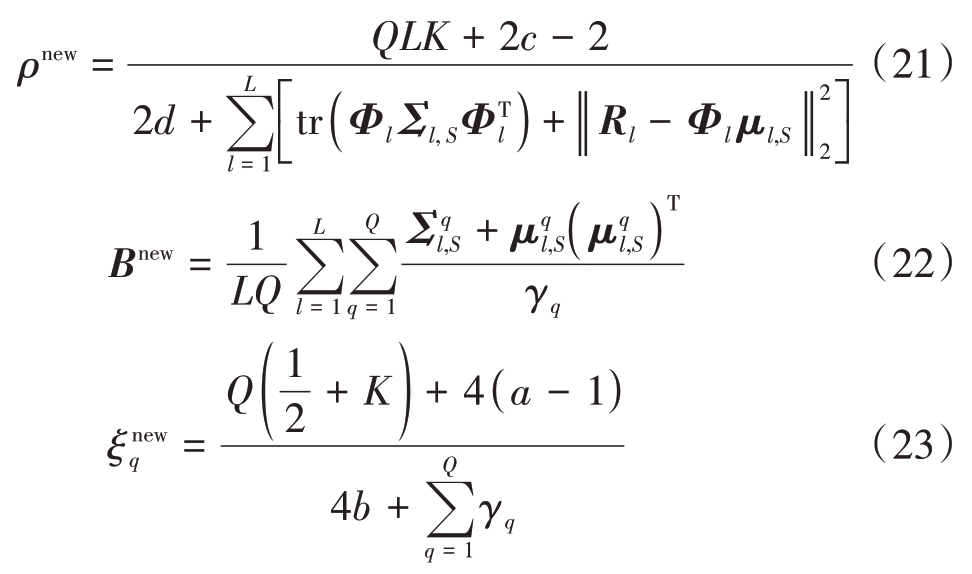
辐射源定位中接收数据为复数，而稀疏贝叶斯理论用于处理信号实数形式，为了推广至复数信号处理，需要将复数形式转换成实数形式［22］。
由上述分析，本文所提定位算法步骤实现如表1所示。
表1 自适应LASSO定位算法
3 算法分析
3.1 算法复杂度
由上可知，本文所提算法每次迭代更新的总时间复杂度为
。此外对本文所用的对比算法也进行了相关时间复杂度分析，为便于描述，时间复杂度只列出各自的最大量级，其结果如表2 所示，其中稀疏重构类算法复杂度明显高于传统MUSIC和MVDR算法。
表2 不同定位方法的时间复杂度分析
3.2 克拉美罗界限
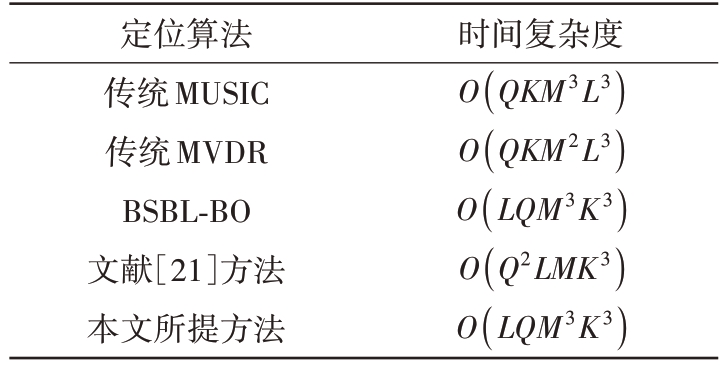
由于网格点数Q 远大于其他参数，使得算法的总运算量较大，但算法不断进行迭代更新，不满足门限的γq 的网格点会被清零，网格点数Q 也不断下降，从而使得算法的运算量降低。此外为了衡量算法的性能，本节推导了直接定位模型下辐射源位置误差的克拉美罗下界（Cramer Rao Lower Bound,CRLB），下式为其Fisher信息矩阵：
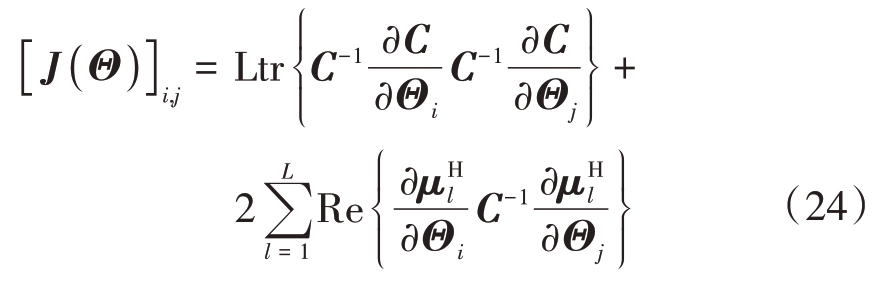
均值如式（25）所示和方差如式（26）：
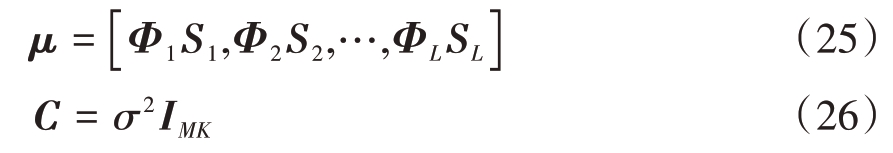
以下为模型中的未知参数向量：
水平向量和垂直向量构成了辐射源的最终位置向量，分别为px,py，信号内的幅度为Sl,q，σ2 表示噪声方差，将式（24）引入方差和均值后为
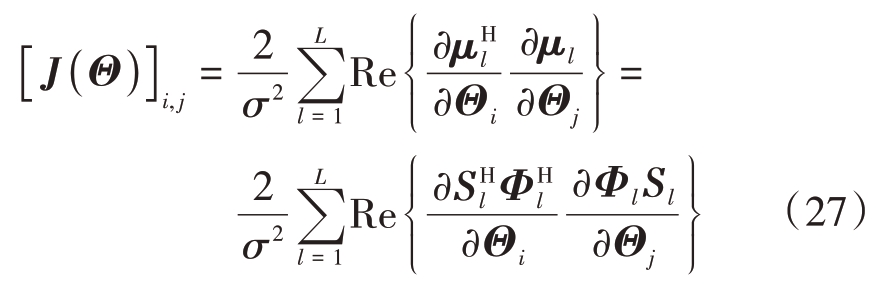
则下式为Fisher信息矩阵：
从而最终的关于辐射源位置估计的CRLB 表示为
4 仿真结果
为验证所提算法在远距离下的定位性能，对直接定位方法中的MUSIC、MVDR 和稀疏贝叶斯定位方法做了仿真实验并比较相关性能。当辐射源位置并没有位于预先对感兴趣区域划分的格子点上时，贝叶斯类算法会失效或产生离格误差，因此本文只考虑辐射源在对感兴趣区域划分的网格点上这一情况，具体离格的解决算法可通过查阅相关文献获知［17］。
在下文中4 个接收基站的位置分别为（0，0），（353，7 071），（0，7 071）和（7 071，7 071）（单位：m），基线长度为10 km。每个接收基站配备有一个均匀线性阵列（Uniform Linear Array,ULA），每个阵列的阵元数为M=10 个，阵元间距为d= λc/2，其中λc 为信号波长，路径损耗为bl=1+δl，其中δl为随机复高斯变量［23］，均值设定为0，同时方差值设定为0.1。
4.1 定位效果和谱分辨率
多辐射源位置的估计结果如图2（a）和图2（b）所示。本实验中SNR 为10 dB，快拍数为8，阵元数为10，两个辐射源位置分别为（110，140）和（140，132）（单位：km）。辐射源产生的信号都设定为未知二进制相移键控（Binary Phase Shift Keying,BPSK），且其带宽大小都设定为10 MHz，同时载频都设定为10 GHz。结果表明图中存在两个明显的尖峰，这两个尖峰所在网格中的位置就是算法估计的辐射源方位，其余的网格点在算法参数更新过程中因其γq 小于所设置的门限值而被剪切掉，结果表示算法能有效地估计出辐射源位置。
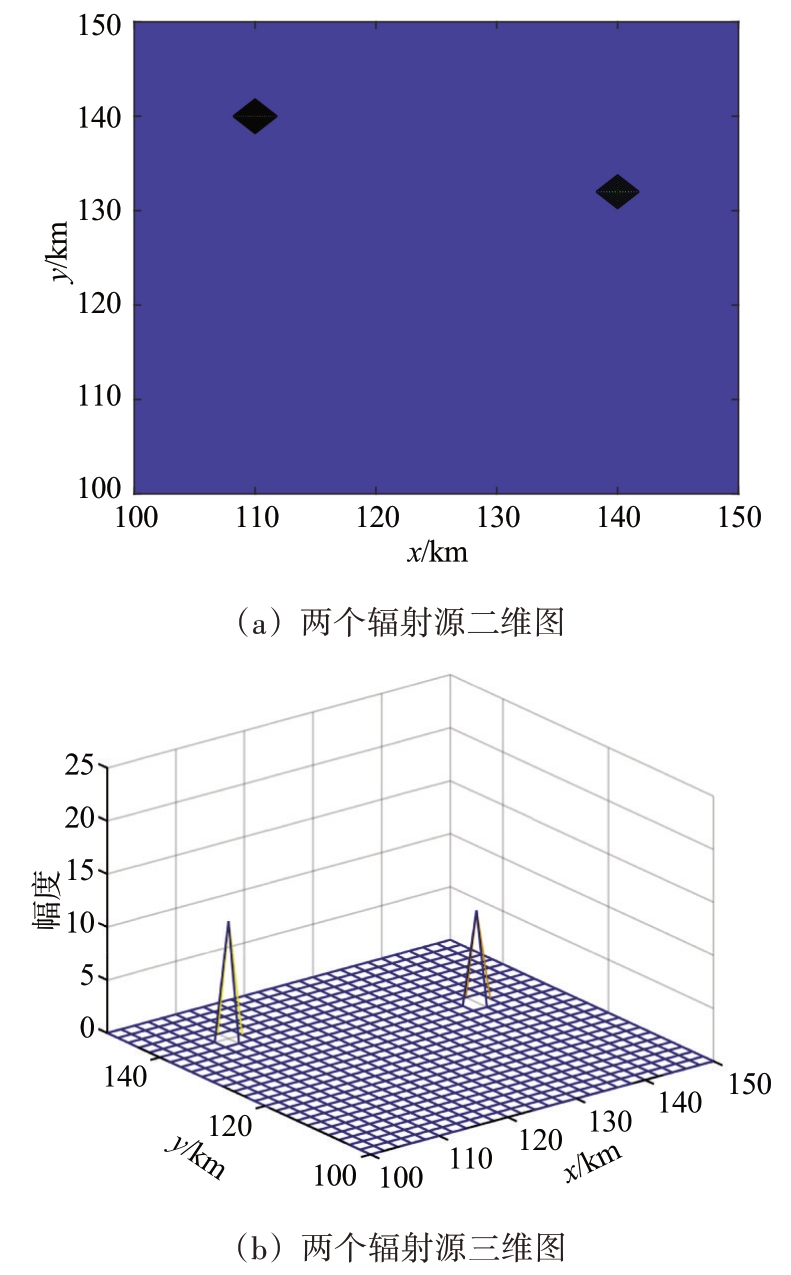
图2 两个辐射源时所提方法的定位结果
传统定位算法当多辐射源间距离较近时可能存在无法分辨辐射源的问题，而稀疏重构类算法根据辐射源在空间的稀疏特性，通过更准确的恢复稀疏信号，来提高多辐射源的谱分辨率。为验证本文所提算法的谱分辨率，本实验中设定辐射源2个，辐射源产生的信号都设定为BPSK，载频都设定为10 GHz，同时带宽一个设定是10 MHz，另一个为5 MHz，阵元数设定为10，快拍数为8，信噪比为10 dB。设置辐射源距离远近2 个场景，验证各算法的谱分辨率。
场景1：在本场景下验证辐射源距离间较近时谱分辨率性能。该场景下两辐射源位置设定为（110，140）和（116，138）（单位：km），辐射源间距离大约为6 km，各算法效果如图3 所示，本文所提算法虽然存在一些伪峰，但能量值较小，能够准确定位到2个辐射源，文献［21］算法和BSBL-BO算法虽然能识别出设定的2个辐射源，但还存在其他能量值较高的伪峰，从而导致位置误判，影响算法定位效果，而MUSIC、MVDR 两类算法由于快拍数设定较少，算法性能急剧恶化，导致无法分辨出两个辐射源位置。
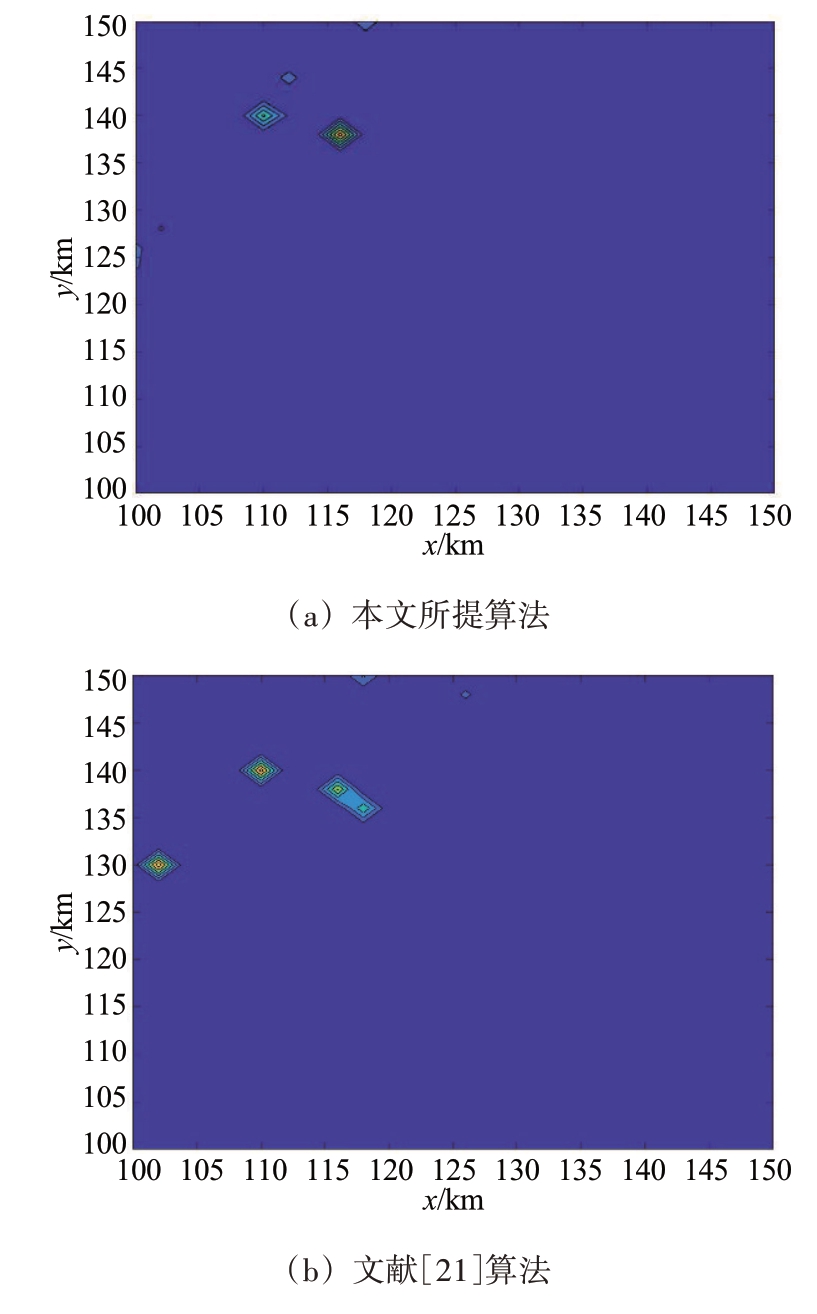
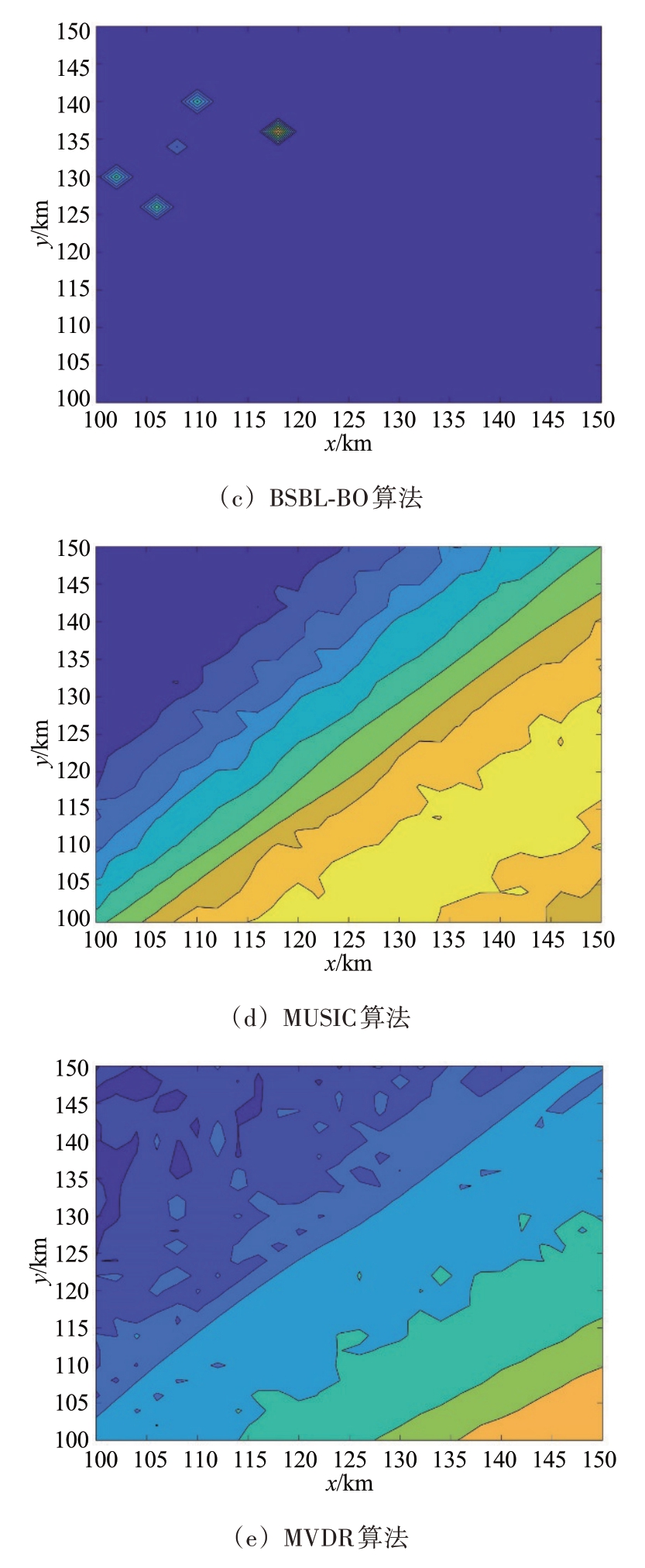
图3 近距离辐射源各算法谱分辨率图
场景2：在本场景下验证辐射源距离间较远时谱分辨率性能。设定两辐射源位置为（110，140）和（144，132）（单位：km），辐射源间距离大约为35 km。各算法谱分辨率效果如图4所示。在该场景下，本文所提算法展示的图中，存在一些零星伪峰，但总体能量值都较小，不影响定位效果，设定的辐射源位置能被准确定位，文献［21］算法和BSBL-BO 算法虽然能找到设定的辐射源，但存在能量值较高的伪峰，影响算法的定位效果，而MUSIC、MVDR由于快拍数太少，无法识别出辐射源的位置。
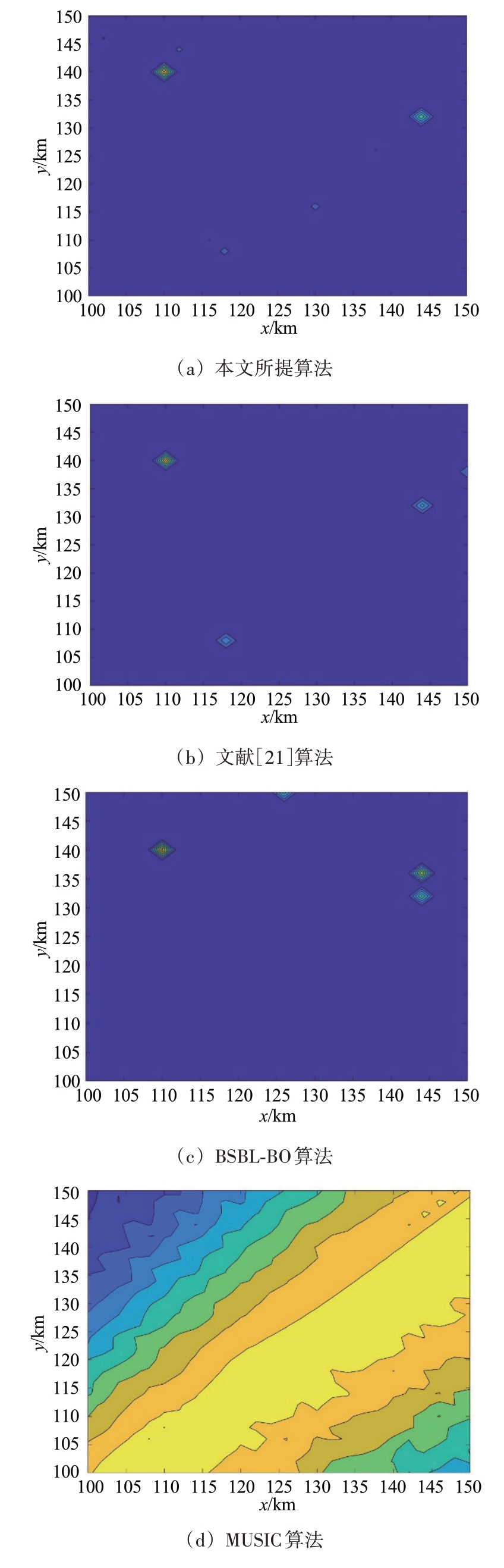
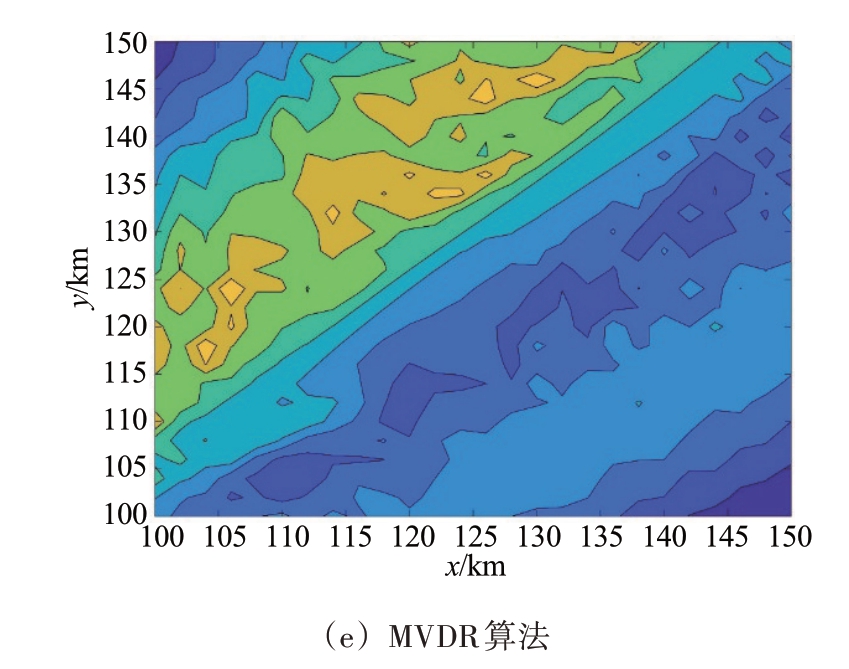
图4 远距离辐射源各算法谱分辨率图
4.2 算法对比结果
均方根误差是衡量算法性能的有效手段，其公式为
式中，pn 表示第n 次蒙特卡洛实验算法所得的辐射源方位估计，仿真时蒙特卡洛实验次数设置为N=500。辐射源初始位置位于（122，122）（单位：km），辐射源发射信号为BPSK，同时该信号的载频设定为10 GHz，其带宽设定为10 MHz，阵元数在每个接收基站内设定为10，快拍个数为8，意在获取本文所提算法在该场景下的定位效果，对BSBLBO［12］、文献［21］的方法和MUSIC［24］、MVDR［25］方法做了仿真实验并进行比较，各方法参数保持一致。
图5 则展示出了不同的定位方法和信噪比之间的关联性。可以发现在快拍数较少、信噪比较低的情况下，伴随着信噪比的不断增大，本文所提方法误差下降趋势更快，逐渐靠近CRLB，相比之下文献［21］算法和BSBL-BO 算法表现出的定位误差虽然都在不断减少，但变化趋势较慢，在-5 dB以后3种算法的定位误差趋势都趋于平缓，但本文所提算法仍表现出优于其他算法的性能，在该实验条件下接收基站和辐射源间平均距离（Dis）大约是170 km，初始时信噪比设定为-20 dB，此条件下本文提出的算法表现出的RMSE 精度为3.3%Dis，相较于BSBL-BO的RMSE表现，本算法误差降低了2%Dis，类比与文献［21］方法，本算法降低了1.2%Dis。而伴随着信噪比的不断增强，MUSIC 算法以及MVDR算法的RMSE也在减小，但由于快拍数较少，并不能有效地提高算法定位精度，和其他对比算法相比，其RMSE显著较低。在信噪比设定较低下，BSBL-BO、文献［21］方法以及传统MUSIC、MVDR算法的定位精度显著劣于本文所提算法。
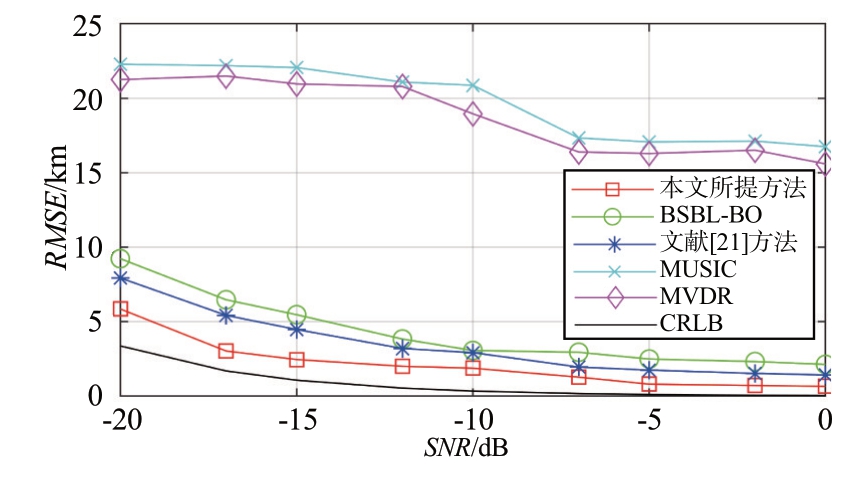
图5 SNR对不同定位算法的RMSE关联关系
4.3 快拍个数的影响
在算法关于辐射源的定位性能中快拍数产生了举足轻重的影响，快拍数过少会导致信号中有效信息不足以准确定位，过多则会信息冗余导致运算量过大，因此寻找合适的快拍数十分重要。当SNR 设置为0 dB 时，图6 则展示出了不同算法表现出的定位性能与快拍数之间的关联关系，由图可知，由于快拍数的不断增多，所有算法RMSE也会随之减少，而MUSIC 算法的RMSE 基本保持不变，这是因为快拍数过少，不能有效表现出信号特征。而对于稀疏重构类算法，在少快拍情况下就能表现出较好的性能，在快拍数设定为2 时，本文所提算法表现出的RMSE 约为5.8%Dis，与其他两种稀疏重构对比类算法差距不大，当快拍个数设定为3～7区间内时，所提算法的表现明显优于其他算法的表现，此外若快拍数设定为5，则本文算法表现出的RMSE 精度约为1.2% Dis，同时较于BSBL-BO 算法，本文算法降低了1.25%Dis、相比于文献［21］算法，本文算法降低了2.42%Dis，随着快拍数不断增大，3种算法性能也逐渐趋近相同。
图6 不同方法定位RMSE随快拍数变化关系
4.4 阵元个数的影响
合适的阵元个数不仅能降低构造成本，同时也能降低算法的运算量。设SNR 的值为0 dB，快拍数初始化为8时，阵元数对于不同定位方法定位性能的影响如图7 所示，不难看出，由于不断地增加阵元数，3 种稀疏重构类算法的性能也在不断降低，本文所提算法和文献［21］算法在阵元数达到5时，性能就趋于稳定，不再随着阵元数增加，性能有大幅度变好，BSBL-BO 在阵元数为8 时，算法性能才趋于稳定，而MUSIC 算法因为快拍数较少，定位误差基本没有变化。在阵元数为5时，本文所提算法RMSE 约为0.7% Dis，文献［21］算法和BSBLBO 算法和本文所提方法相比之下分别增加了1.4%Dis和5.6%Dis。
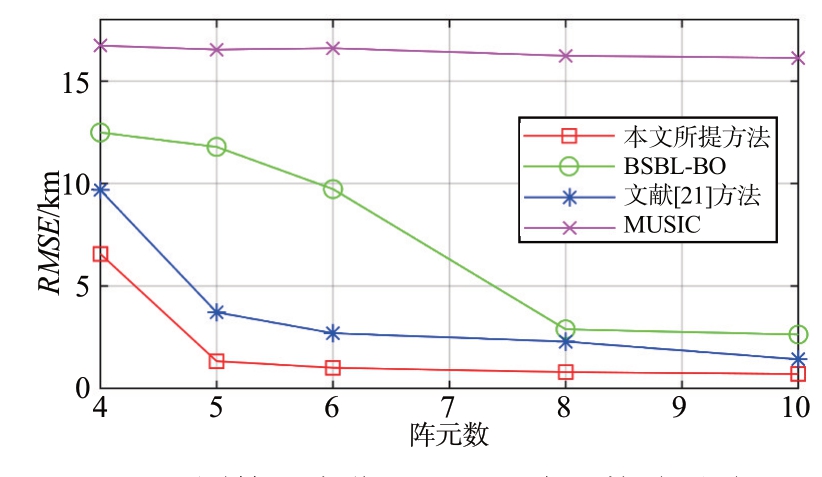
图7 不同算法定位RMSE和阵元数关联关系
5 结束语
本文针对远距离下辐射源位置定位性能下降的问题，给出了一种联合块稀疏贝叶斯框架与自适应LASSO 先验的直接定位方法，根据不同接收站的观测数据来自相同辐射源这一特性，利用多基站不同字典重建过完备字典，有效地估计辐射源的方位。在表现稀疏性层面上，传统的贝叶斯类算法、Laplace 类先验算法显著劣于先验设定为自适应LASSO 的分层稀疏结构。同时探索信号的块内相关性，进一步提升了算法恢复性能。仿真表明：在快拍数设定较少、信噪比设定较低的条件下，与传统MUSIC 和MVDR 算法、BSBL-BO 以及Laplace 类算法相比，本文提出的方法在定位精度上的表现更为优秀。
［1］张敏，张文俊，李曦，等.基于长基线干涉仪相位差的多站无源定位方法［J］.电子与信息学报，2023，45（11）:3868-3876.
［2］WANG Yubing,LIANG Xiaolong,ZHANG Jiaqiang,et al.Robust TDOA/FDOA Estimation from Emitter Signals for Hybrid Localization Using UAVs［J］.Defense Technology,2022,18（1）:81-93.
［3］吴癸周，郭福成，张敏.信号直接定位技术综述［J］.雷达学报，2020，9（6）:998-1013.
［4］WANG Cheng,WANG Ding,GAO Lu,et al.Direct Position Determination with Single Sensor Based on Signal Periodicity［J］.Mathematical Problems in Engineering,2021（5）:1-12.
［5］吴癸周，张源，张文俊，等.基于互质阵列的运动单站信号直接定位方法［J］.雷达学报，2022，11（4）:692-704.
［6］LI Lixiang,FANG Yuan,LIU Liwei,et al.Overview of Compressed Sensing:Sensing Model,Reconstruction Algorithm,and Its Applications［J］.Applied Sciences,2020,10（17）:5909.
［7］WEN Jinming,LI Haifeng.Binary Sparse Signal Recovery with Binary Matching Pursui［tJ］.Inverse Problems,2021,37（6）:065014.
［8］QIN Shun.Simple Algorithm for L1-Norm Regularisation-Based Compressed Sensing and Image Restoration［J］.IET Image Processing,2020,14（14）:3405-3413.
［9］王琦森，余华，李杰，等.基于稀疏贝叶斯学习的空间紧邻信号DOA 估计算法［J］.电子与信息学报，2021，43（3）:708-716.
［10］SEEGER M W,WIPF D P.Variational Bayesian Inference Techniques［J］.IEEE Signal Processing Magazine,2010,27（6）:81-91.
［11］ZHANG Zhilin,RAO B D.Sparse Signal Recovery with Temporally Correlated Source Vectors Using Sparse Bayesian Learning［J］.IEEE Journal of Selected Topics in Signal Processing,2011,5（5）:912-926.
［12］ZHANG Zhilin,RAO B D.Extension of SBL Algorithms for the Recovery of Block Sparse Signals with Intra-Block Correlation［J］.IEEE Trans on Signal Processing,2013,61（8）:2009-2015.
［13］BABACAN S D,MOLINA R,KATSAGGELOS A K.Bayesian Compressive Sensing Using Laplace Priors［J］.IEEE Trans on Image Processing,2010,19（1）:53-63.
［14］ZOU Hui.The Adaptive Lasso and Its Oracle Properties［J］.Journal of the American Statistical Association,2012（1）:1418-1429.
［15］白宗龙，师黎明，孙金玮.基于自适应LASSO先验的稀疏贝叶斯学习算法［J］.自动化学报，2022，48（5）:1193-1208.
［16］BAI Zonglong,JENSEN J R,SUN Jinwei,et al.A Sparse Bayesian Learning Based RIR Reconstruction Method for Acoustic Toa and DOA Estimation［C］//2019 IEEE Workshop on Applications of Signal Processing to Audio and Acoustics,New Paltz,NY,USA:IEEE,2019:393-397.
［17］曹仲康，李建峰，李潘，等.参数字典动态更新的SOMP离网格直接定位方法［J］.信号处理，2023，39（5）:807-816.
［18］NANNURU S,GEMBA K L,GERSTOFT P,et al.Sparse Bayesian Learning with Multiple Dictionaries［J］.Signal Processing,2019,159:159-170.
［19］SCHMITZ J,MATHAR R,DORSCH D.Compressed Time Difference of Arrival Based Emitter Localization［C］//2015 3rd International Workshop on Compressed Sensing Theory and Its Applications to Radar,Sonar and Remote Sensing,Pisa,Italy:IEEE,2015:263-267.
［20］HINCAPIE R,GOMEZ C,BETANCUR L,et al.Sparse Framework for Hybrid TDoA/DoA Multiple Emitter Localization［C］//2017 IEEE International Symposium on Signal Processing and Information Technology,Bilbao,Spain:IEEE,2017:174-179.
［21］叶泓臻，郭海召，关浩亮，等.基于多字典联合与分层块稀疏贝叶斯框架的多辐射源直接定位方法［J］.雷达学报，2022，11（3）:434-442.
［22］CARLIN M,ROCCA P,OLIVERI G.Directions-of-Arrival Estimation Through Bayesian Compressive Sensing Strategies［J］.IEEE Trans on Antennas and Propagation,2013,61（7）:3828-3838.
［23］WEISS A J.Direct Position Determination of Narrowband Radio Frequency Transmitters［J］.IEEE Signal Processing Letters,2004,11（5）:513-516.
［24］WEISS A J,AMAR A.Direct Position Determination of Multiple Radio Signals［J］.EURASIP Journal on Advances in Signal Processing,2005（1）:1-13.
［25］WANG Lu,YANG Yixin,LIU Xionghou.A Direct Position Determination Approach for Underwater Acoustic Sensor Network［sJ］.IEEE Trans on Vehicular Technology,2020,69（11）:13033-13044.