0 引言
卡尔曼滤波（Kalman Filtering，KF）［1］作为线性高斯条件下的最优状态估计算法，被广泛应用于目标定位、导航和自动控制等领域［2］。由于其本质上是噪声模型驱动的，算法性能依赖于噪声协方差矩阵的先验信息。实际应用场景中，噪声的统计特性通常未知且可能是时变的［3-4］。此时，KF 的状态估计性能将恶化甚至失效，极大影响了其在实际场景中的应用。因此，噪声协方差矩阵失配条件下的滤波问题引起了目标跟踪领域的学者们的广泛关注［5-6］。
为了解决噪声协方差矩阵未知或时变条件下的状态滤波问题，学者们相继提出了多种自适应卡尔曼滤波（Adaptive KF，AKF）方法，大致可分为：协方差匹配算法［7］、最大似然类算法［4-8］、贝叶斯类算法［9］等。其中，贝叶斯类算法由于可以估计系统状态和噪声协方差矩阵的联合后验分布被认为是最优的。然而，多参数的后验分布通常难以解析求解，实际中采用近似推理方法计算。近年来，基于变分贝叶斯（Variational Bayesian，VB）［10］近似推断的自适应卡尔曼滤波算法，由于具备贝叶斯性、数字稳定性、收敛性等优势，引起了学术界广泛关注，学者们相继提出了一系列AKF 算法。具体来说，通过选取噪声模型的共轭先验分布，该类算法可通过变分推断中的固定点迭代优化方法解析求解目标状态和未知噪声协方差的联合后验分布。文献［9］通过将未知噪声方差的先验分布建模为逆-伽马分布，提出了变分贝叶斯自适应卡尔曼滤波（Variational Bayesian-Adaptive Kalman Filtering，VB-AKF）算法。文献［11］进一步考虑了对量测协方差矩阵（Measurement Noise Covariance Matrix，MNCM）的估计，并用逆-威沙特分布作为其先验分布。由于该类方法具备的自适应特性，近年来VB-AKF 算法已被扩展至跳变马尔可夫系统［12］、非线性系统［13］、多目标跟踪［14］等方面。需要说明的是，上述算法仅适用于MNCM 未知或时变条件的自适应状态估计。
由于过程噪声协方差矩阵（Process Noise Covariance Matrix，PNCM）未知或时变条件对应的变分优化问题是非共轭的，其状态估计是个难题。为了解决这一问题，文献［15］提出利用预测误差协方差矩阵（Predicted Error Covariance Matrix，PECM）代替PNCM 进行变分推断，从而避免了模型非共轭的影响。然而，由于该方法在每一时刻均利用含有误差的PNCM 给出PECM 的初值，因此其无法利用历史估计信息提升状态估计性能。文献［16］通过仿真验证表明，该方法估计性能在特定条件下较KF 更差。文献［17］通过利用随机变分推断来解决上述非共轭变分推断问题，提出了黑箱变分贝叶斯-卡尔曼滤波（Black Box Variational Inference-AKF，BBVI-AKF）算法，性能优于文献［15］所提算法、传统的最大似然算法和启发式算法。然而，该方法通过蒙特卡罗方式实现状态估计，算法计算复杂度较高，限制了其在实际场景中的应用。总结现有研究现状可知，PNCM 未知条件下的自适应状态估计问题仍有提升和改进的空间。首先，精确的推理算法其复杂度较高，难以实际应用；而间接推断的方法并没有充分利用历史估计信息，使得其性能改善仍有提高空间。
本文针对PNCM 和MNCM 均未知条件下的自适应滤波问题，基于参数解耦推断的变分贝叶斯自适应卡尔曼滤波算法。首先，借鉴间接变分推断的思路并构造PECM 的马尔可夫演化模型，构造基于参数解耦的变分贝叶斯优化模型；其次，利用固定点迭代实现状态后验分布和PECM 后验分布的求解；最后，给出算法的收敛判别准则。仿真实验验证了算法的有效性。
1 问题描述
状态估计常用状态空间模型对目标演化和传感器量测进行建模表征，考虑线性状态空间模型：
从贝叶斯估计的角度，PNCM 和MNCM 未知条件下，自适应滤波算法需要估计目标状态xk、PNCM、MNCM 的联合后验分布。根据贝叶斯公式，联合后验分布可表示为
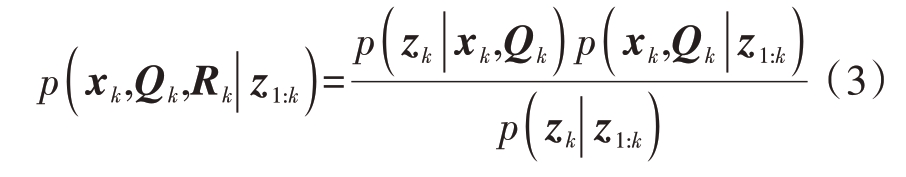
式中，z1:k表示直到第k时刻的量测数据集合。需要说明的是，公式（3）是非解析的，因此需要采用近似方法求解。VB 利用Kullback-Leibler 散度（Kullback-Leibler Divergence，KLD）最小化准则可实现多变量联合后验密度分布的近似求解。此时，公式（3）中后验分布的近似优化模型可表示为
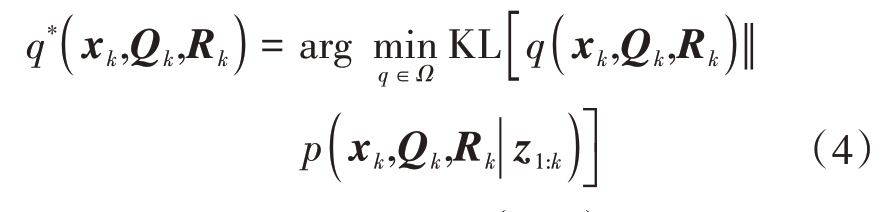
式中，Ω 表示可行的解集，KL(q‖p)表示概率密度分布q 对p 的散度。当q= p 时，KL(q‖p)=0。文献［17］指出，由于目标状态xk和Qk存在耦合性，公式（4）中的优化模型是非共轭的，传统VB 方法无法解析求解该优化问题。对此，文献［15］采用间接推断的方式，通过选取PECM 作为优化变量，构造了去耦合的变分优化模型：
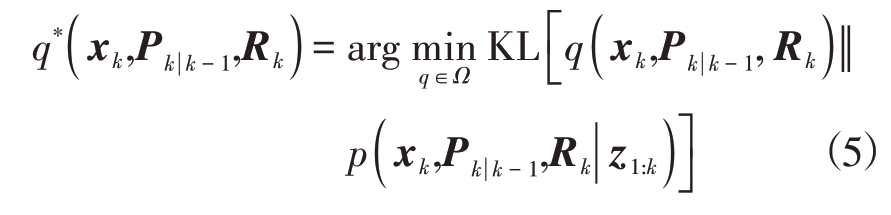
式中，Pk|k-1 表示第k 时刻的PECM。需要说明的是，文献［15］利用含有误差的Qk构造Pk|k-1的初始值时，并没有利用历史估计信息。
2 基于参数解耦的变分贝叶斯自适应卡尔曼滤波
本节提出了一种基于参数解耦的变分贝叶斯自适应卡尔曼滤波。首先，给出联合估计目标状态、PECM、MNCM 的分层概率图模型。该模型采用间接变分推断的方式，同时引入了PECM 的演化模型。其次，利用VB 理论，给出多参数迭代优化的求解方法。最后，给出了算法的收敛判断准则。
2.1 参数解耦的概率图模型
自适应状态估计问题可用分层概率图模型表征。借鉴文献［15］的思路，本文利用间接推断的方式，选取PECM 作为变分优化变量。同时为了充分利用历史估计信息，本文引入了PECM 的马尔可夫演化模型，参数解耦的概率图模型如图1 所示。具体来说，状态估计误差
的统计特性构建演化模型，即
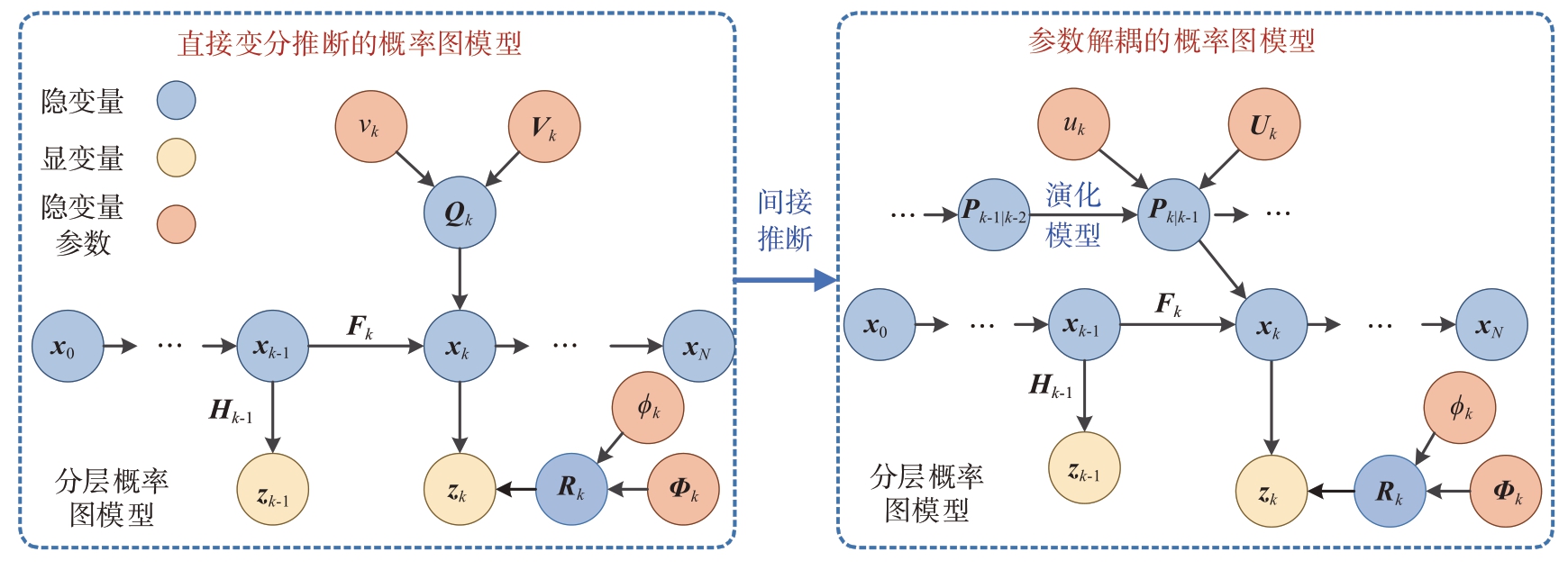
图1 参数解耦的概率图模型示意图
式中，Pk-1 表示第k-1 时刻的状态估计误差协方差矩阵。利用逆-威沙特分布建模可以给出第k-1时刻预测误差协方差矩阵的后验分布。在此基础上，利用Beta-Bartlett 概率演化模型［11］，可构造第k时刻预测误差协方差矩阵的马尔可夫演化概率模型，即
2.2 多变量的优化求解
在参数解耦的概率图模型基础上，本项目拟利用变分贝叶斯方法联合求解隐变量参数，同时设计自适应收敛准则。给定优化变量Ψk={xk,Pk|k-1,Rk}和参数化近似分布q(Ψk |λ)，公式（5）中的优化问题可表述为
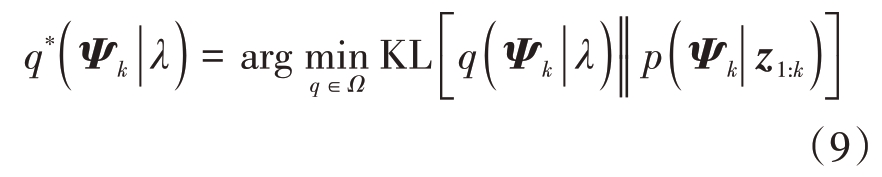
式中，λ 表示待优化参数。根据VB 理论，公式（9）可以通过平均场假设和固定点迭代优化求解［18］。此时，对于任一优化变量ωk ∈Ψk，其后验分布q(ωk)可通过如下公式迭代求解：
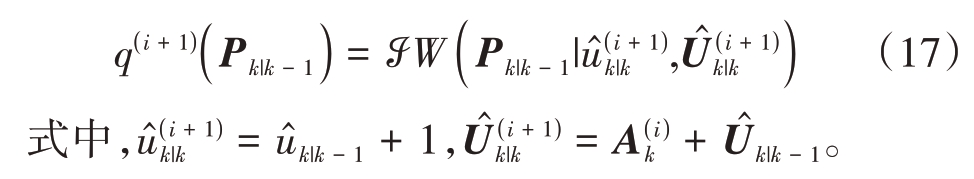
选取ωk= Rk 时，联合公式（9）至公式（14），可知第i+1次迭代时，后验分布q( i+1)(Rk)满足
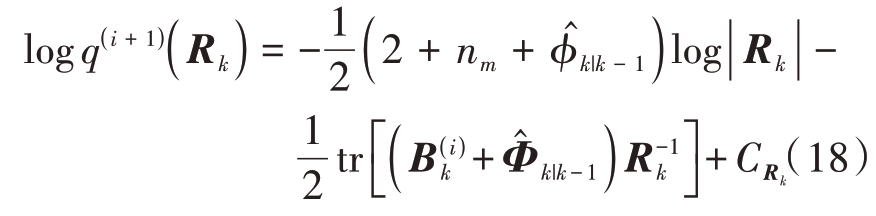
式中，
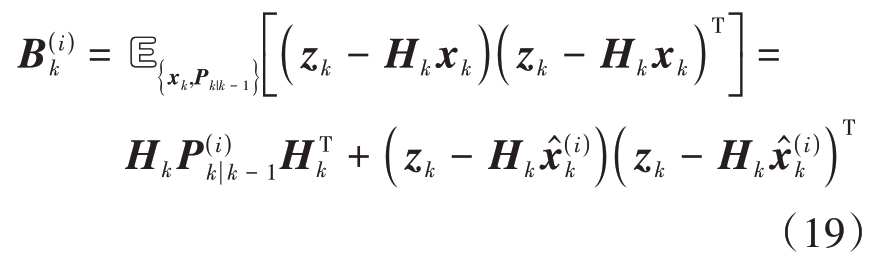
显然，由公式（18）可知，q( i+1)(Rk)满足
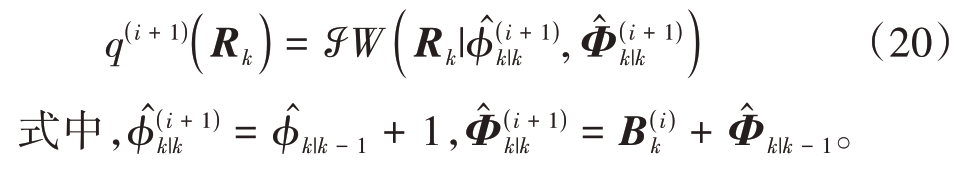
选取ωk= xk 时，联合公式（9）至公式（14），可知第i+1次迭代时，后验分布q(i+1)(xk)满足
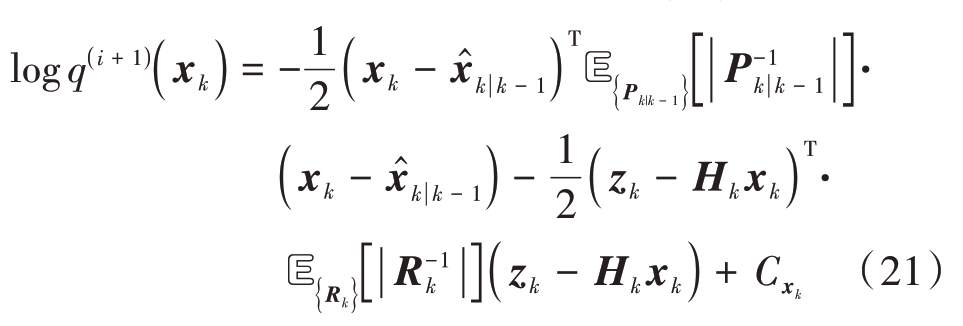
因此，
对于所提算法，本文有如下说明：1）为了便于引用，本文将所提算法简记为PD-VB-AKF；2）公式（15）、公式（18）和公式（21）的具体推导过程可参考文献［15］推导过程给出；3）本节给出了算法由第i次至第i+1次迭代的过程，算法后续迭代过程可按公式（15）至公式（22）递归进行。
2.3 算法收敛准则
在VB 方法中，变分证据下界（Evidence Lower Bound，ELBO）通常用来作为算法收敛性的判断准则，定义为
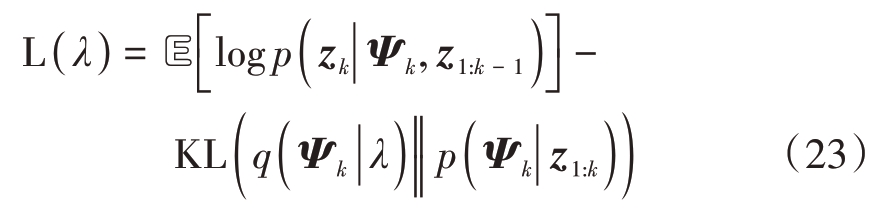
采用2.1 节中概率图模型，公式（23）可以解析求解。然而，求解ELBO 过程中涉及到多个复杂的矩阵运算，会额外增加算法的计算复杂度。根据固定点迭代的过程可知，随着迭代次数的增加，后验密度函数更接近理论的后验分布。为了简化算法的收敛准则的设计，本文考虑采用两次迭代过程中PECM 和MNCM 的矩阵欧氏距离作为收敛性判断准则，即
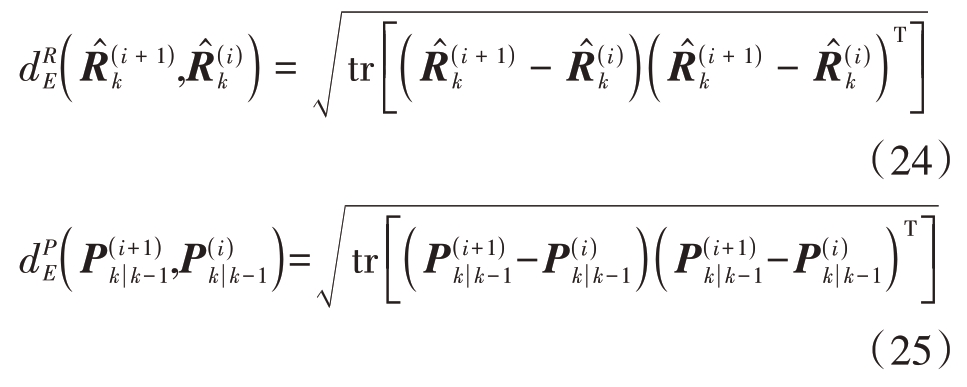
为了控制算法估计精度，可设置收敛阈值Tth作为算法的收敛门限。
3 仿真实验
本节通过仿真实验验证PD-VB-AKF 算法对目标的跟踪性能，并与现有的VB-AKF 算法进行了对比。仿真实验考虑目标在二维空间中作匀速直线运动，状态向量为
状态转移矩阵F 和观测矩阵H 可参考文献［19］给出。PNCM和MNCM可表示为
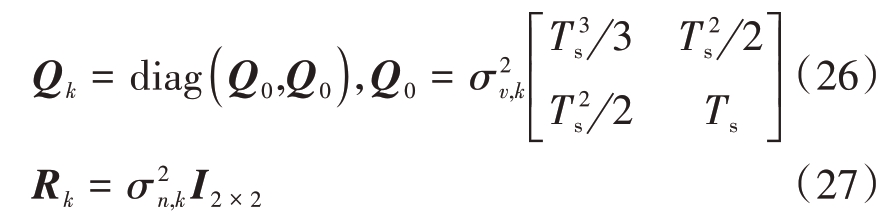
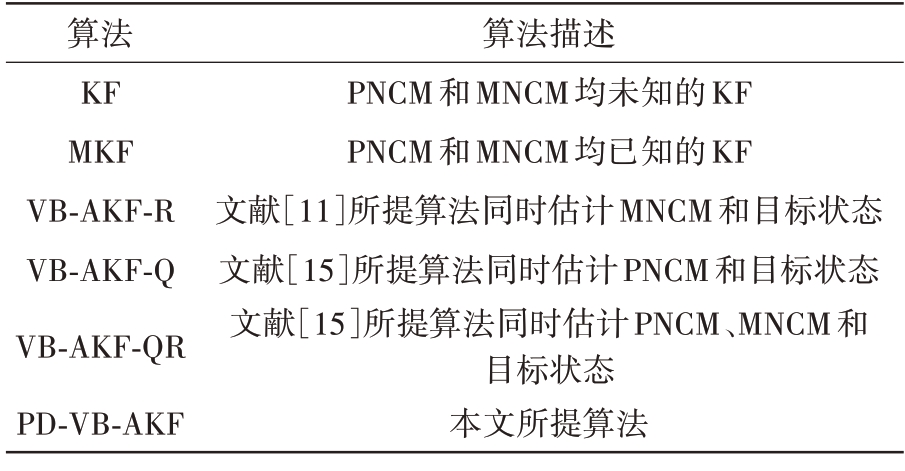
式中
分别表示过程噪声和量测噪声在一维上的方差，Ts 表示传感器的观测时间间隔，取值为Ts=2 s。目标的初始状态设置为x0=[10 km 50 m/s 10 km 50 m/s]T，状态估计误差的协方差矩阵初值设置为P0=diag(104,102,104,102)。收敛门限Tth=10-4。仿真实验采用模型匹配KF（Matched KF,MKF）作为状态估计算法的最优性能基准，同时采用均方根误差（Root Mean Square Error,RMSE）来衡量状态估计性能，蒙特卡洛仿真次数为500次。为了区分各类算法，本文将仿真实验涉及到的算法总结在表1中。
表1 仿真实验考虑到的算法
3.1 PNCM和MNCM时不变条件下的性能对比
图2（a）和（b）分别给出了各个时刻各算法的位置RMSE和速度RMSE。
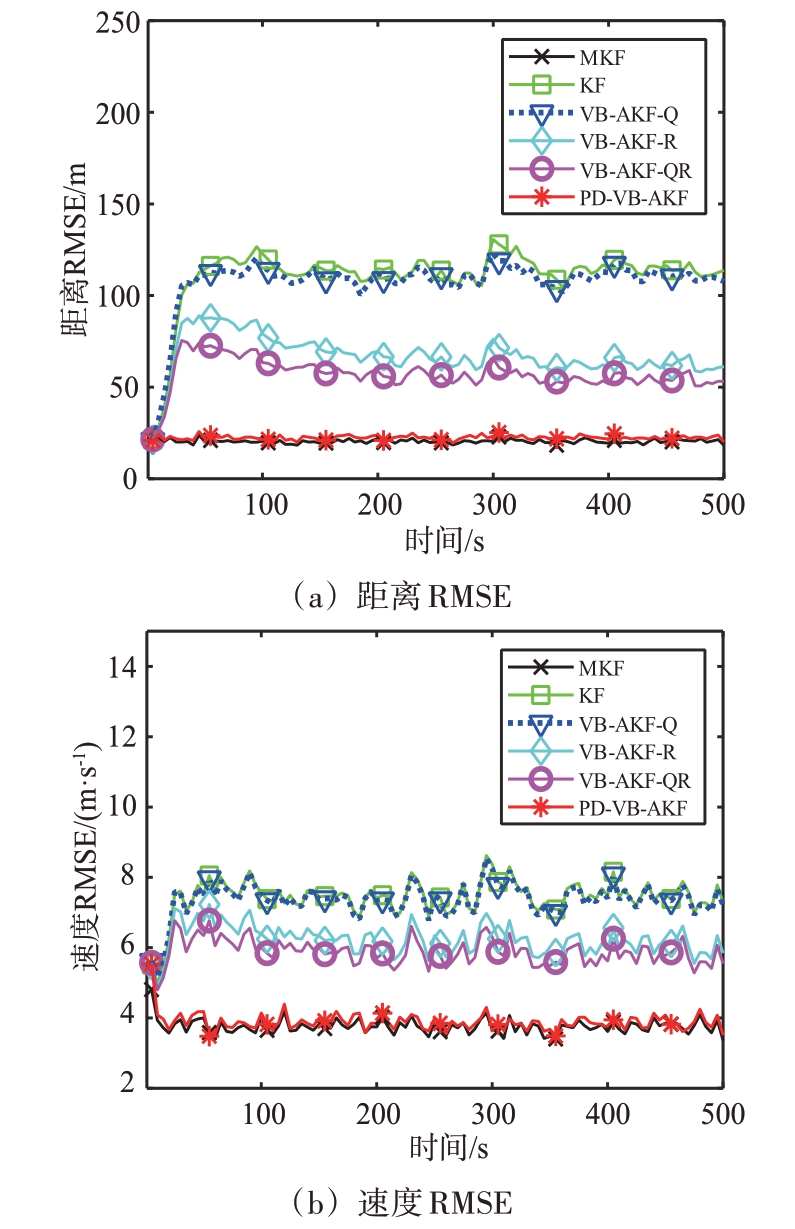
图2 PNCM和MNCM均处于未知时不变条件下各算法的RMSE
由图2 可知，与其余算法相比，本文所提PDVB-AKF 算法在各个时刻的均方根误差最小，对目标的滤波效果最佳，其效果基本接近于MKF。由于KF 算法是在模型失配条件下对目标做出的状态估计，因此其得到的RMSE最大，滤波效果最差。在PNCM 和MNCM 均未知条件下，VB-AKF-Q 算法只对PNCM 和目标状态作联合估计，而VB-AKF-R算法只对MNCM 和目标状态作联合估计，因此这两种算法的滤波效果都比VB-AKF-QR 和PD-VBAKF 差。VB-AKF-QR 和PD-VB-AKF 算法均可实现对PNCM、MNCM和目标状态的联合估计，但VBAKF-QR算法的滤波性能明显劣于PD-VB-AKF，这是因为VB-AKF-QR 算法在每一时刻均根据经验初始化PNCM，因此导致了初始化PECM 含有误差，导致RMSE 的误差较大。PD-VB-AKF 由于构造了PECM 的马尔可夫演化模型，可利用历史信息对PECM 进行初始化，进而提升了算法的估计性能，图中仿真结果也验证了引入历史信息可提升状态估计性能。
为进一步验证本文所提算法在不同失配度下的状态估计效果，令
，其中s和r分别为PNCM 和MNCM 的不匹配度系数。图3 给出了不同s 条件下各算法的RMSE。由图3（a）和（b）可以看出，以MKF为参考，随着s增大，PD-VB-AKF算法的RMSE 前期保持稳定，后期出现略微抬升，其滤波效果接近于MKF，整体呈现出优良稳定的滤波性能。在其余算法中，随着s 增大，它们的RMSE 呈现明显下降后逐渐上升的滤波效果，滤波效果性能较差，但在不匹配度s 处于特定值时，KF算法的滤波效果与MKF 接近。针对此问题，文献［20］证明了KF 的状态估计性能依赖于跟踪指标参数，定义为
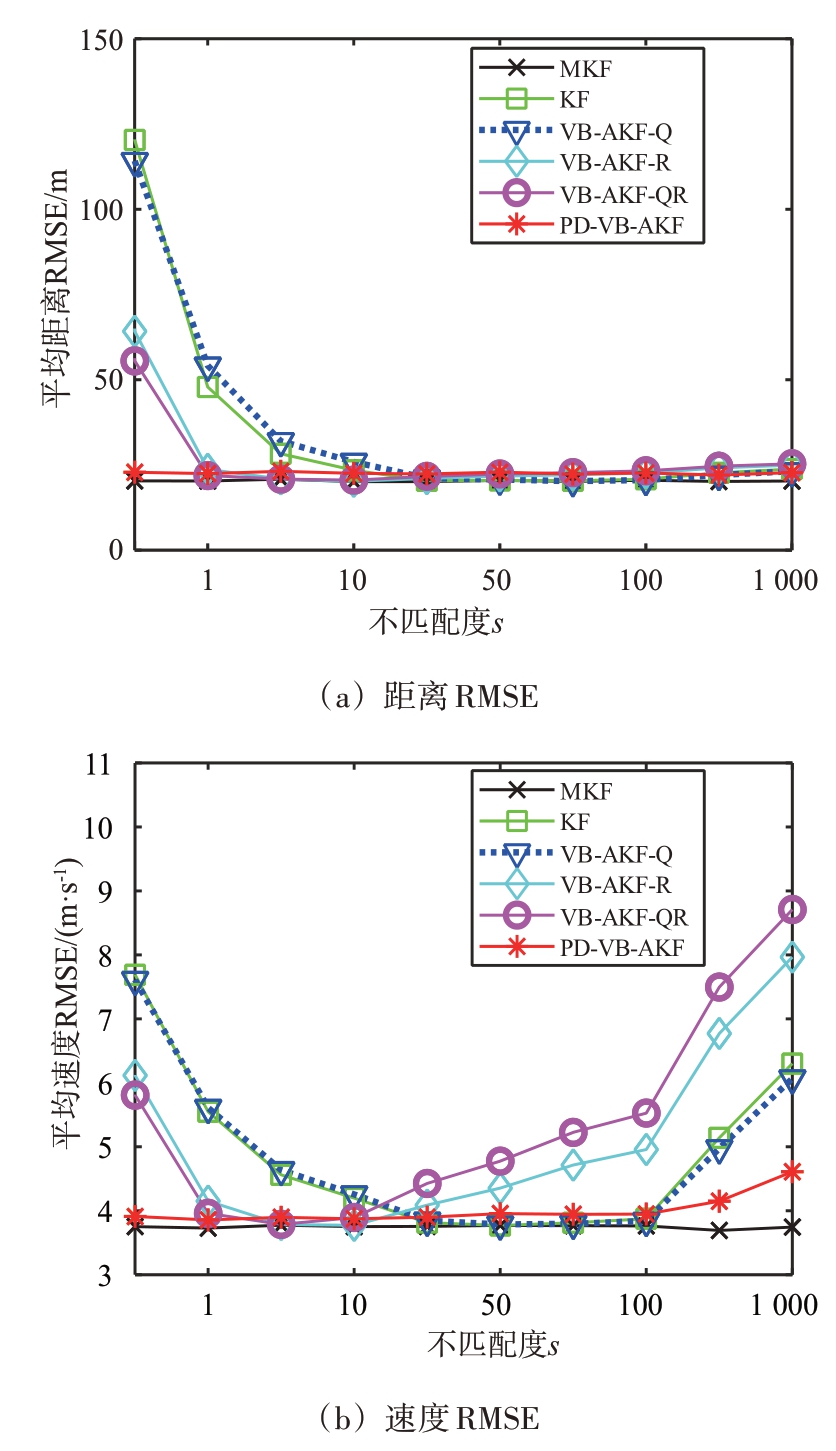
图3 PNCM和MNCM均处于未知时不变条件下各算法随s变化时的RMSE（r=50,s ∈[0.1,1,5,10,30,50,80,100,500,1 000]）
实际应用中，KF 参数设置越接近于理想的跟踪指标参数，状态估计性能越好。由式（28）可得，在给定的模型参数条件下，可给出相应的跟踪指标参数。在某些不匹配度s 和r 组合的条件下，也可能得到最佳的跟踪指标参数，此时的滤波效果接近于MKF 算法，例如图3 中，在KF 算法下，在s=50、r=50 条件下可得到最佳的跟踪指标参数，此时KF 算法的RMSE 接近于MKF；另外，VB-AKF-Q、VB-AKF-R 和VB-AKF-QR 算法也存在与KF 算法类似的情况。
图4 给出了不同r 条件下各算法的RMSE。由图4（a）和（b）可知，随着r 增大，PD-VB-AKF 算法的RMSE 初期略微偏离MKF 的RMSE，后期与MKF 算法下的RMSE 基本相同，体现了PD-VBAKF 在所有算法的优势。在KF、VB-AKF-Q、VBAKF-R 和VB-AKF-QR 算法中，随着r 的增大，算法的RMSE 整体都呈现出明显增大的发展趋势，滤波效果都在变差，但在不匹配度处于特定值时，KF、VB-AKF-Q、VB-AKF-R 和VB-AKF-QR 算法的滤波效果与MKF 接近，例如在图4 中，KF 算法在s=0.1、r=0.1 条件下的滤波效果与MKF 算法接近，这是因为该条件下，根据模型参数求得的跟踪指标参数与最佳指标接近。同理在VB-AKFQ、VB-AKF-R 和VB-AKF-QR 算法也存在与KF 算法类似的情况。
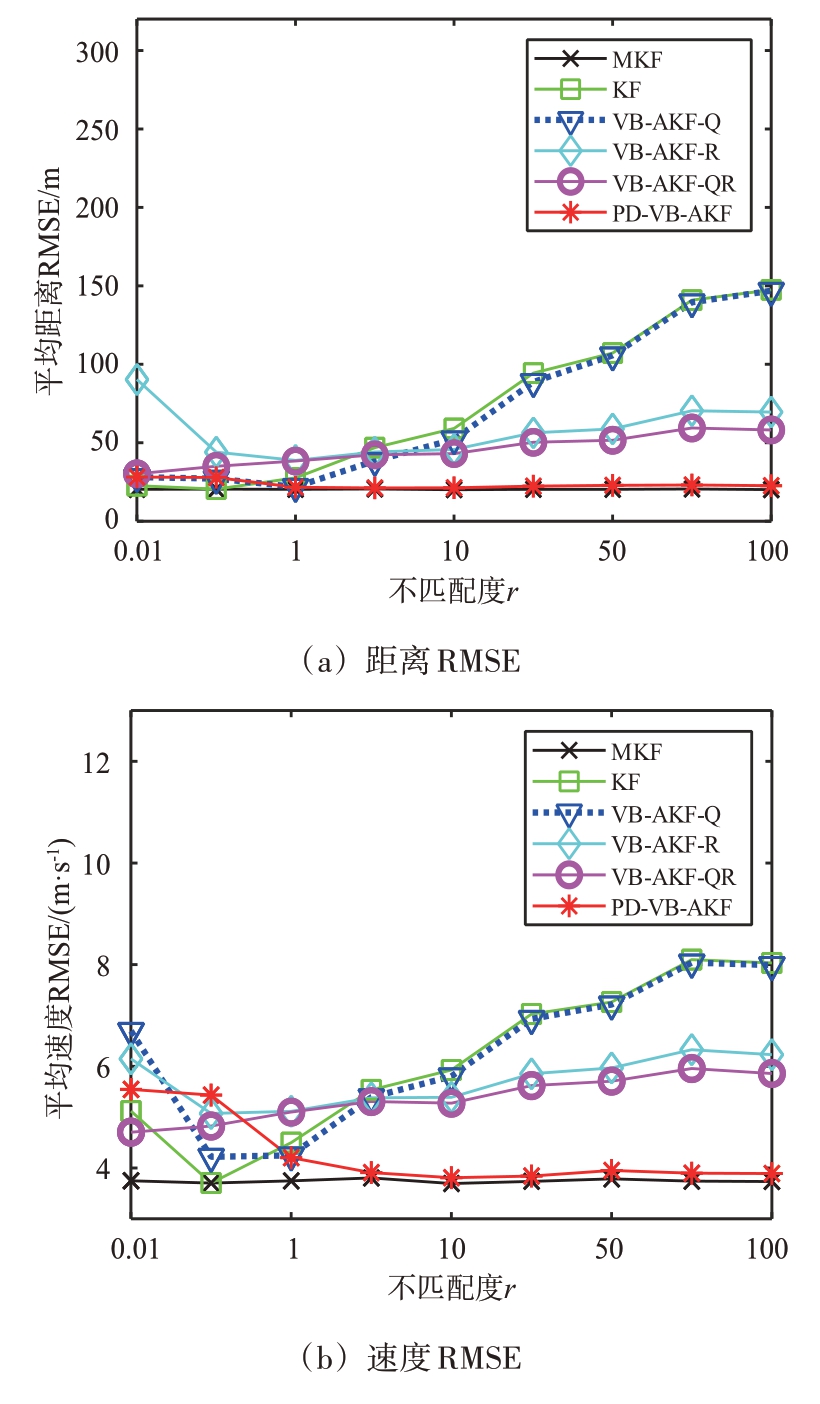
图4 PNCM和MNCM均处于未知时不变条件下各算法随r变化时的RMSE（s=0.1,r ∈[0.01,0.1,1,5,10,20,100,200,500,1 000]）
3.2 PNCM和MNCM缓变条件下的性能对比
本试验进一步考虑PNCM 和MNCM 均处于缓变条件下各算法的估计性能。令过程噪声和量测噪声方差分别为
因子λ=0.98，其余参数与时不变条件一致。图5 给出了PNCM和MNCM 均失配条件下各个时刻各算法对目标的跟踪结果，采用500 次蒙特卡洛仿真实验，图5（a）和（b）分别给出了各个时刻各算法的位置RMSE和速度RMSE，PD-VB-AKF算法在所有算法中依旧表现最优，而KF 算法表现最差，所得结论与时不变条件保持一致。仿真成功验证了本文所提算法的优越性。
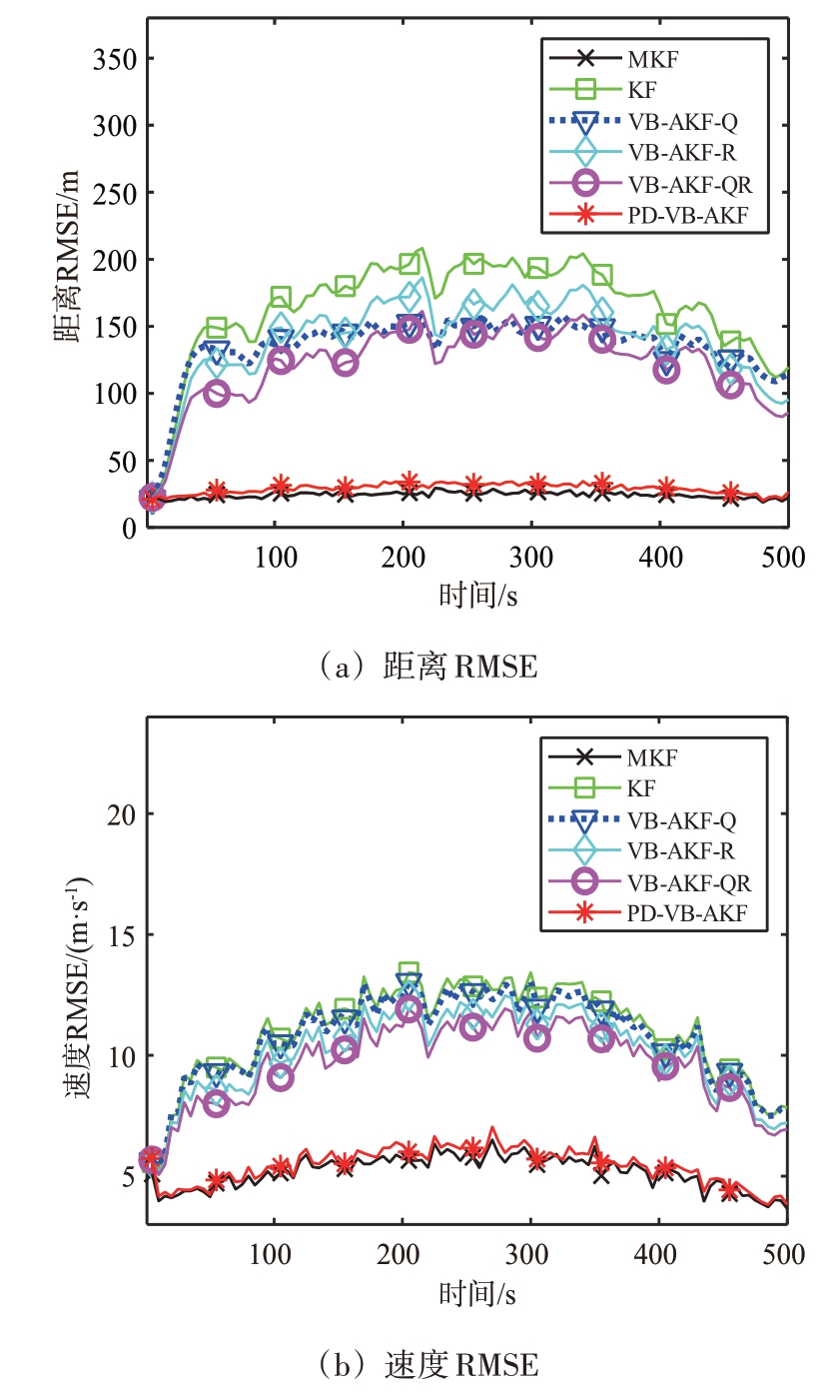
图5 PNCM和MNCM均处于未知缓变条件下各算法的RMSE
同理，为进一步验证本文所提算法在
时变时处于不同匹配度下目标的跟踪效果。图6给出了不同s条件下各算法的RMSE。通过仿真结果得出，图6 所得结论与时不变条件保持一致，验证了本文所提PD-VB-AKF 算法在缓变不匹配PNCM 的条件下具有稳定优良的滤波性能。图7给出了不同r 条件下的RMSE。固定s=0.1，仿真给出了各算法在不同r条件下的位置RMSE和速度RMSE，其结论依旧与时不变条件下保持一致。根据PNCM 和MNCM 均处于未知时不变和缓变两种条件下的仿真结果可得，首先，在不同失配度s 和r条件下，本文所提的PD-VB-AKF 算法优于KF和现有基于VB-AKF 类算法，并且其滤波效果与MKF接近；其次，由KF、VB-AKF-Q、VB-AKF-R 和VBAKF-QR 算法的RMSE 可知，尽管在特定的组合下，滤波效果会出现改善，但在工程应用中，很难提前获知哪些组合的滤波效果较好；最后，在实际应用中，为获得最佳的滤波效果，使用本文所提PDVB-AKF 算法时建议将初始的PNCM 和MNCM 设置大一些。
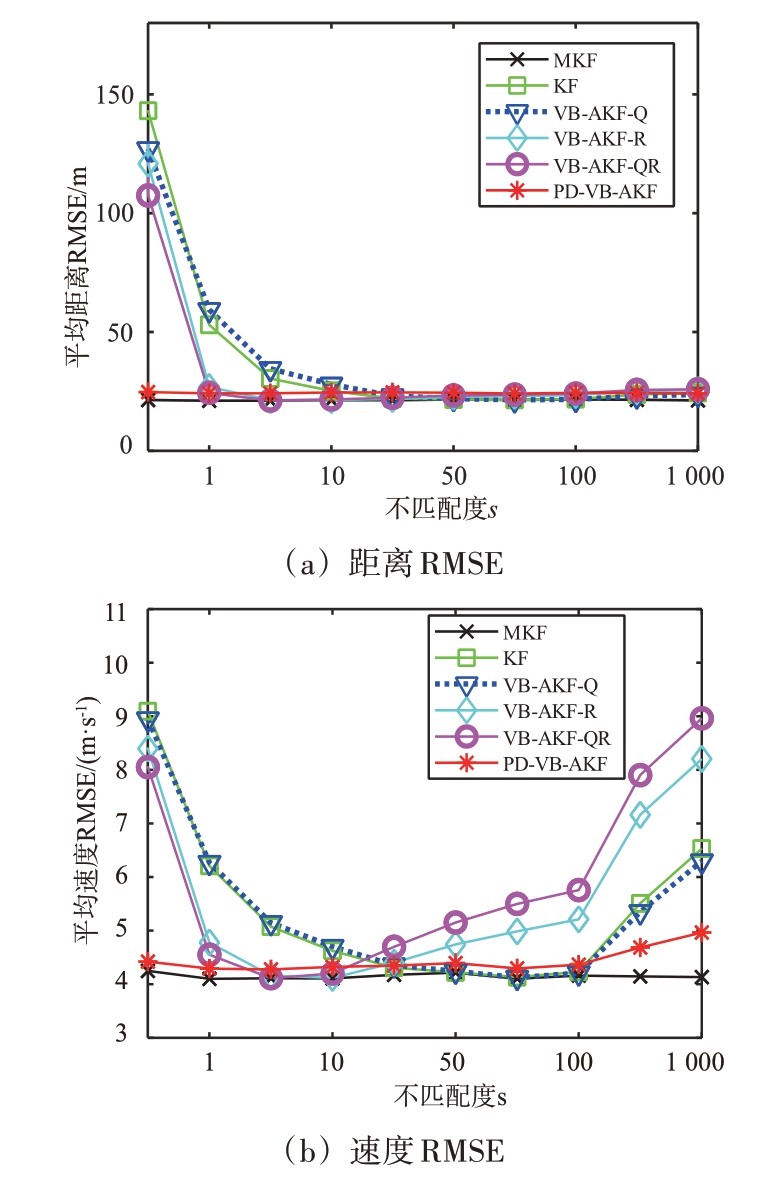
图6 PNCM和MNCM均处于未知缓变条件下各算法随s变化时的RMSE（r=50,s ∈[0.1,1,5,10,30,50,80,100,500]）
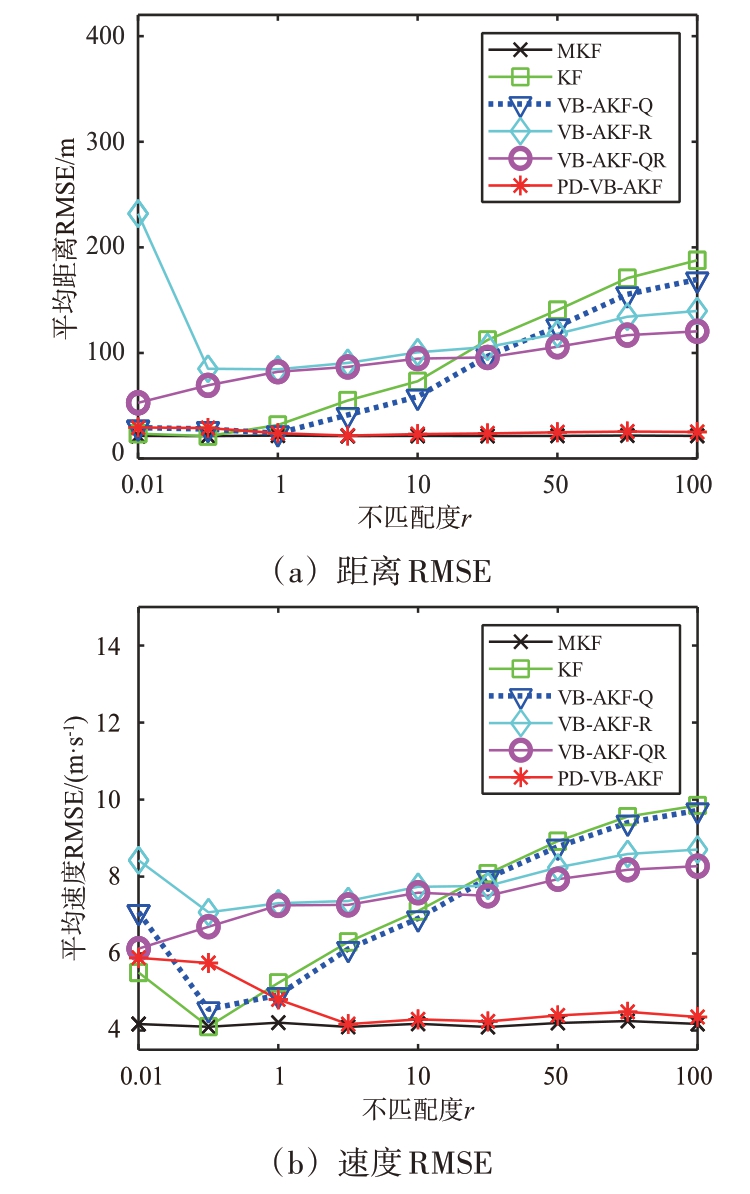
图7 PNCM和MNCM均处于未知缓变条件下各算法随r变化时的RMSE（s=0.1,r ∈[0.05,0.1,0.5,1,5,10,50,100,200,500]）
4 结束语
本文针对现有的变分贝叶斯卡尔曼滤波算法在PNCM 和MNCM 均未知的条件下，并未充分利用历史估计信息的缺陷，提出了一种基于参数解耦的变分贝叶斯自适应卡尔曼滤波算法，该算法通过采用间接变分推断方式并引入了PECM 的马尔可夫演化模型，构造了参数解耦的变分推断模型，可以解决PNCM 和MNCM 均未知条件下的自适应状态估计问题。仿真结果表明，相比于现有的VB-AKF 算法，所提算法由于充分利用了历史估计信息，状态估计精度更优。此外，该算法并未显著增加计算复杂度，计算复杂度较蒙特卡罗类方法明显更低。因此，PD-VB-AKF 算法更适用于PNCM和MNCM均未知条件下的自适应滤波问题。
［1］KALMAN R E.A New Approach to Linear Filtering and Prediction Problems［J］.Journal of Fluids Engineering,1960,82（1）:35-45.
［2］赵研，陶海红，畅鑫，等.基于差分模型的近场无源定位算法［J］.雷达科学与技术，2023，21（4）:405-410.
［3］GE Quanbo,SHAO Teng,DUAN Zhansheng,et al.Performance Analysis of the Kalman Filter with Mismatched Noise Covariances［J］.IEEE Trans on Automatic Control,2016,61（12）:4014-4019.
［4］MOHAMED A H,SCHWARZ K P.Adaptive Kalman Filtering for INS/GPS［J］.Journal of Geodesy,1999,73（4）:193-203.
［5］方青，任清安.机载有源无源传感器稳健融合方法［J］.雷达科学与技术，2011，9（1）:34-38.
［6］ZHU Hao,ZHANG Guorui,LI Yongfu,et al.An Adaptive Kalman Filter with Inaccurate Noise Covariances in the Presence of Outliers［J］.IEEE Trans on Automatic Control,2022,67（1）:374-381.
［7］ODELSON B J,RAJAMANI M R,RAWLINGS J B.A New Autocovariance Least-Squares Method for Estimating Noise Covariances［J］.Automatica,2006,42（2）:303-308.
［8］MYERS K A,TAPLEY B D.Adaptive Sequential Estimation with Unknown Noise Statistics［J］.IEEE Trans on Automatic Control,1976,21（4）:520-532.
［9］SARKKA S,NUMMENMAA A.Recursive Noise Adaptive Kalman Filtering by Variational Bayesian Approximations［J］.IEEE Trans on Automatic Control,2009,54（3）:596-600.
［10］ZHANG Cheng,BÜTEPAGE J,KJELLSTRÖM H,et al.Advances in Variational Inference［J］.IEEE Trans on Pattern Analysis and Machine Intelligence,2019,41（8）:2008-2026.
［11］AGAMENNONI G,NIETO J I,NEBOT E M.Approximate Inference in State-Space Models with Heavy-Tailed Noise［J］.IEEE Trans on Signal Processing,2012,60（10）:5024-5036.
［12］LI Hui,YAN Liping,XIA Yuanqing.Distributed Multiple Model Filtering for Markov Jump Systems with Measurement Outliers［J］.IEEE Trans on Aerospace and Electronic Systems,2023,59（3）:2823-2837.
［13］CHUGHTAI A H,MAJAL A,TAHIR M,et al.Variational-Based Nonlinear Bayesian Filtering with Biased Observations［J］.IEEE Trans on Signal Processing,2022,70（10）:5295-5307.
［14］DONG Peng,JING Zhongliang,LEUNG H,et al.The Labeled Multi-Bernoulli Filter for Multitarget Tracking with Glint Noise［J］.IEEE Trans on Aerospace and Electronic Systems,2019,55（5）:2253-2268.
［15］HUANG Yulong,ZHANG Yonggang,WU Zhemin,et al.A Novel Adaptive Kalman Filter with Inaccurate Process and Measurement Noise Covariance Matrices［J］.IEEE Trans on Automatic Control,2018,63（2）:594-601.
［16］WANG Jiaolong,WANG Jihe,ZHANG Dexin,et al.Kalman Filtering Through the Feedback Adaption of Prior Error Covariance［J］.Signal Processing,2018,152:47-53.
［17］XU Hong,DUAN Keqing,YUAN Huadong,et al.Black Box Variational Inference to Adaptive Kalman Filter with Unknown Process Noise Covariance Matrix［J］.Signal Processing,2020,169:107413.
［18］TZIKAS D G,LIKAS A C,GALATSANOS N P.The Variational Approximation for Bayesian Inference［J］.IEEE Signal Processing Magazine,2008,25（6）:131-146.
［19］LI X R,JILKOV V P.Survey of Maneuvering Target Tracking.Part I.Dynamic Models［J］.IEEE Trans on Aerospace and Electronic Systems,2003,39（4）:1333-1364.
［20］KALATA P R.The Tracking Index: A Generalized Parameter for α-β and α-β-γ Target Trackers［J］.IEEE Trans on Aerospace and Electronic Systems,1984,20（2）:174-182.