0 引言
为了更好地对抗集群无人机目标[1],反无人机系统要求无人机探测雷达必须尽可能地实现对于集群的规模(个数)、轮廓等信息进行准确估计。通常,集群无人机具有高密度的特点和相似的运动特性,受雷达的带宽、孔径、脉冲个数等因素限制,必然存在多架无人机回波落在一个角度-距离-多普勒回波单元中,造成目标混叠,无法分辨。为了提升对集群目标的分辨能力[2],可以通过增大雷达的带宽来提高雷达的距离分辨率,可以通过增大雷达的脉冲重复间隔和脉冲数量来提高目标的多普勒分辨率,增加雷达的孔径来提升目标的方位分辨率。受阵列规模的限制,雷达的波束宽度不可能做到无限窄,因此必须要寻求超分辨算法来解决测角分辨率不够的问题。
相比于常规的数字波束形成(Digital Beamforming,DBF)技术,Capon 算法和MUSIC(Multiple Signal Classification)算法等传统的DOA(Direction Of Arrival)估计方法虽然能够提供超分辨率,但是需要很多的快拍数(快拍数至少大于两倍阵元数时,才能保证估计协方差时的损失小于3 dB),并且当信号相干和存在阵列误差时效果急速下降。
为了实现抑制杂波、提高目标的能量积累得益以及获得精确的目标速度信息等目的,一般雷达各接收通道对应的回波信号需要先经过DBF、脉冲压缩及MTD 滤波处理,然后在距离-多普勒域上经过CFAR、测角处理[3]。这种处理流程不仅可以让不同距离、速度、波束(角度)维上的目标充分分离,使得在单个波束-距离-多普勒单元上的需要进行DOA 估计的信源个数大为降低,同时该流程下目标的信噪比得到有效的提升,估计得到的目标信息(距离、速度、角度)相互关联。虽然增加脉冲数可以提高信噪比和速度分辨率,然而每次相干积累只对应着距离-多普勒域的一次快拍,实际上可获得的快拍数很少,甚至只有单个快拍,而且同一个距离-多普勒单元上的回波信号为相干信号[4]。这就要求测角方法不仅能够在信号相干条件下,而且在少快拍数甚至单快拍数情况下依然有效。
与传统的子空间类DOA 估计方法相比,基于稀疏表示理论得到的DOA 估计方法在少快拍数(包含单快拍)、低信噪比、入射信号空间角度间隔较小等非理想条件下有着更为优异的估计性能。现有的稀疏表示类的测角方法,如基于LASSO[5-6](Least Absolute Shrinkage and Selection Operator)方法、以OMP(Orthogonal Matching Pursuit)算法为代表的BP[7-8](Basis Pursuit)方法等衍生出的算法虽然能够提供一个很高的分辨率,然而这些算法需要很多次迭代才能达到收敛,计算速度很慢,不能够满足实时处理的要求。同时,该类算法的效果依赖于超参数(或者正则化参数)的选取,超参数选取不合适可能会导致结果很差。并且在实际中,每更换一个场景就需要重新选择合适的超参数,难以满足实际应用需求。相比于以上几种方法,一种利用加权最小二乘理论推导出的迭代自适应方法(Iterative Adaptive Approach,IAA)[9]利用目标分布在空域上的稀疏性,结合正则化理论,同样能够突破现有阵列孔径的物理限制,实现对目标方位维超分辨处理,且具有无超参数的优点。文献[10]对IAA、MUSIC、OMP、DBF 等方法进行对比,只有IAA 法同时兼具高分辨率、高稳健性、可以单快拍数工作等优点。因此IAA 法在雷达回波经过距离-多普勒域处理后(单快拍数)、相干信号以及存在阵列误差的非理性条件下更具优势。
常规的IAA 算法适用于阵元域场景,要求雷达接收信号单元级的数字化,不仅会造成计算处理压力巨大,而且与当前相控阵雷达波束化的处理流程不适配。针对基于“宽发窄收”同时多波束的相控阵雷达系统,文中提出一种波束域的IAA算法。它可以与现有的基于多波束处理的系统融合在一起,首先利用多波束系统完成目标方位的粗估计,然后再使用波束域IAA 算法进行细估。研究结果表明,此方法不仅可以有效地提升现有系统对于集群无人机目标的分辨能力,无需超参数选择,而且具备在单快拍下工作能力,具有很强的应用价值。
1 阵元域IAA算法
假设存在一个L元均匀线阵,各个阵元全向同性且阵元间距为d,远场处有K 个窄带信号入射到该线阵上,则在t 时刻,整个阵列接收的信号模型可以表示为
式中,N为快拍数,A(θ)=[a(θ1),…,a(θK)]为L×K导向矢量矩阵,s(t)=[s1(t),…,sK(t)]T 为参考天线单元接收到的K 个信号组成的列向量,n(t)=[n1(t),…,nL(t)]T 代表每个阵元对应的接收机内部产生的高斯白噪声向量。对于均匀线阵,导向矢量a(θk)可定义为
式中:λ 为信号波长;θk 为第k 个入射信号的角度,定义为该信号入射方向与阵列法向之间的夹角。
由于一般情况下天线阵列接收到的目标信号个数远小于阵列通道数量,而目标信号DOA 与整个角度空间相比是稀疏的,因此可将传统的阵列接收信号模型进行稀疏化表示,得到稀疏表示的阵列接收信号模型。首先将可能存在目标的角度空间划分为G 个小网格:θ=[θ1,…,θG],假设网格划分得足够精细,目标真实入射的角度θk 必然可以与其中的某一网格重合或者与之相邻。因此,可将式(1)用稀疏表示模型描述为
式中:A(θ)=[a(θ1),…,a(θG)]为L×G 维稀疏基矩阵,一般有L ≪G;s(t)=[s1(t),…,sG(t)]为G×1维的稀疏信号矢量,其中s(t)只包含有K 个非零元素,即为信号![]()
定义一个除了期望信号s(g对应信号角度θg处)之外的由干扰和噪声构造的协方差矩阵
式中,R= APAH,P=diag[p1,…,pG]为G×G 维对角矩阵,其对角线对应着G个角度扫描网格上的接收信号功率p(gg=1,…,G)。在网格点θg 处接收信号功率pg可以表示为

其中,
最小化上式可得
根据矩阵求逆引理,上式可进一步写为
综上所述,算法的步骤如表1所示。
表1 阵元域IAA算法步骤

通过大量计算机仿真测试,可以发现:经过10~15 次迭代之后,IAA 算法性能不再有显著变化,意味着此时算法已达到收敛状态。此时,得到的列向量[p1,…,pG]对应的即是基于角度网格的稀疏功率谱,其中K个尖锐谱峰对应的网格就是估计出的目标角度![]()
2 波束域IAA算法
相控阵雷达通过“宽波束发射、同时多波束接收”可以提高发射能量利用效率,减少全空域的搜索时间,降低雷达波束的跨越损耗,提升雷达的平均探测距离。通过波束形成不仅可以抑制干扰和杂波,提升信噪比,还可以将几十个至上百个阵元的阵元域数据变换合成一个或多个波束,通过降维处理,可以极大地减少系统复杂度以及降低后续信号处理压力。工程上,同时多波束系统通常采用比幅测角[11]的方法,这种方法具有实现简单、鲁棒性强等优点,然而当两个相邻目标落入同一波束宽度内时,它不具备将两目标细分开的能力。阵元域的IAA 算法虽然具有精度高、超分辨能力强等优点,然而它要求接收信号单元级的数字化,不仅会造成计算处理压力巨大,而且与当前相控阵雷达波束化的处理流程不适配。因此,后文将研究波束域的IAA 方法,使之适配于相控阵多波束形成系统。
相控阵多波束形成系统在空域扫描时,针对期望方位的空域,形成覆盖空间区域[θleft,…,θright]的B个连续的波束,将天线阵阵元输出的数据经过多波束形成器,得到波束输出数据。
这B个波束形成处理器的输出为
式中,矩阵W=[w(θleft),w(θleft+Δθ),…,w(θright)],由B个间隔Δθ 的相邻波束形成器组成,Δθ 可以写为Δθ=(θright- θleft)/(B-1) 。
对于波束域IAA 算法,波束空间的导向矢量可以写为
将空间区域[θleft,…,θright]分为H 个网格:θ=[θ1,…,θH]。定义新的波束域信号协方差矩阵![]() 为
为

进一步地,整个波束域IAA 算法的迭代如表2所示。
表2 波束域IAA步骤

3 计算量分析
以MDN(Multiplication and Division Number)来表示算法计算过程中使用复数乘除法的次数[12]。
首先分析阵元域IAA 算法的计算量。在算法的初始化阶段,aH(θg)x(t)需要L次MDN,则计算G个网格点对应的信号功率谱![]() 计算量为LG 次MDN。算法迭代过程,R 的计算量为L2G 次MDN,R-1 计算量为
计算量为LG 次MDN。算法迭代过程,R 的计算量为L2G 次MDN,R-1 计算量为![]() 次MDN,计算aH(θg)R-1(θg)需要L2 次MDN,计算
次MDN,计算aH(θg)R-1(θg)需要L2 次MDN,计算![]() 所需要的计算量为L 次MDN,也即aH(θg)R-1(θg)x(t)总的计算量为L2+L次MDN,同理,计算aH(θg)R-1(θg)a(θg)需要L2+L次M D N。因此,计算G个网格点对应的sg(t)对应的计算量为2(L2+L)G。假设IAA 算法需要niter 次迭代实现收敛,则迭代过程计算量为(3L2G+2LG+2G3/3)niter 次MDN。加上初始阶段的计算量,阵元域IAA 方法总的计算量为(3L2G +2LG+2G3/3)niter+LG。
所需要的计算量为L 次MDN,也即aH(θg)R-1(θg)x(t)总的计算量为L2+L次MDN,同理,计算aH(θg)R-1(θg)a(θg)需要L2+L次M D N。因此,计算G个网格点对应的sg(t)对应的计算量为2(L2+L)G。假设IAA 算法需要niter 次迭代实现收敛,则迭代过程计算量为(3L2G+2LG+2G3/3)niter 次MDN。加上初始阶段的计算量,阵元域IAA 方法总的计算量为(3L2G +2LG+2G3/3)niter+LG。
假设波束域算法迭代的次数为![]() 类似的过程可以推导出波束域IAA 方法总的计算量为
类似的过程可以推导出波束域IAA 方法总的计算量为![]()
由波束域算法的过程可知,由于波束域IAA可以粗估目标方位,因此对应的网格点数H 远小于阵元域的网格点数G。此外,通过波束形成,将阵元域通道从数十上百个下降到几个。可见,波束域的IAA 方法比阵元域IAA 方法算法复杂度大为降低,具有更好的实时性。
4 仿真试验
在以下仿真实验中,由于仅考虑雷达在方位维对集群无人机目标进行超分辨。因此将雷达的模型简化为一个由32个接收阵元构成的均匀直线阵,阵元间距为半个波长。实验中均假设接收信号数据为单快拍采样。结合实际项目背景,该雷达“宽波束发射、同时多波束接收”,发射波束宽度为6°,接收波束以3°一个间隔,同时形成5个接收波束覆盖一个发射波束,接收波束采用Taylor加权,加权的幅度为-35 dB,经过加权后的波束宽度展宽为4.2°。
1)算法对相邻信号DOA 估计的分辨能力
假设两个相邻信号入射角度分别为-1°、1°,信号的信噪比为10 dB。
由于传统的超分辨算法如MUSIC 算法在单快拍数条件下不能使用,因此仿真中采用常规数字波束形成(Digital Beamforming,DBF)、阵元域IAA方法和波束域IAA 算法进行对比。其中,波束域IAA 算法在[-3°,…,3°]的空间区域内同时形成5个接收波束。
从图1的仿真曲线可见,当两个目标信号的角度间隔较小(角度间隔2°,小于展宽后的半个波束宽度)时,阵元域IAA 算法和波束域IAA 算法均可以在目标真实的方位附近产生尖锐的谱峰,实现对两邻近信号DOA 的精细分辨,而DBF 算法无法将两个信号分辨开。与阵元域IAA 算法需要全空域扫描,波束域IAA 算法依托于雷达波束化处理,需要扫描的范围更少,具有更好的实时性。
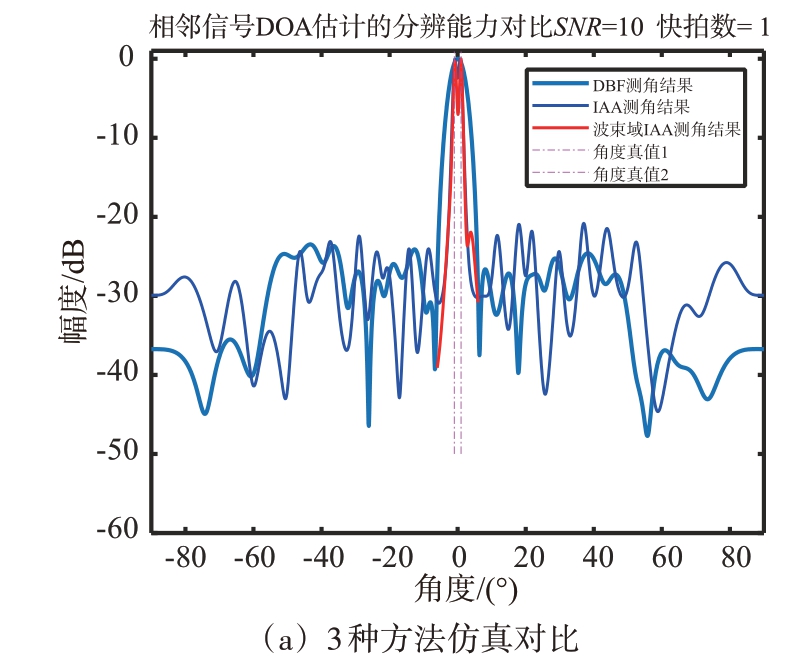
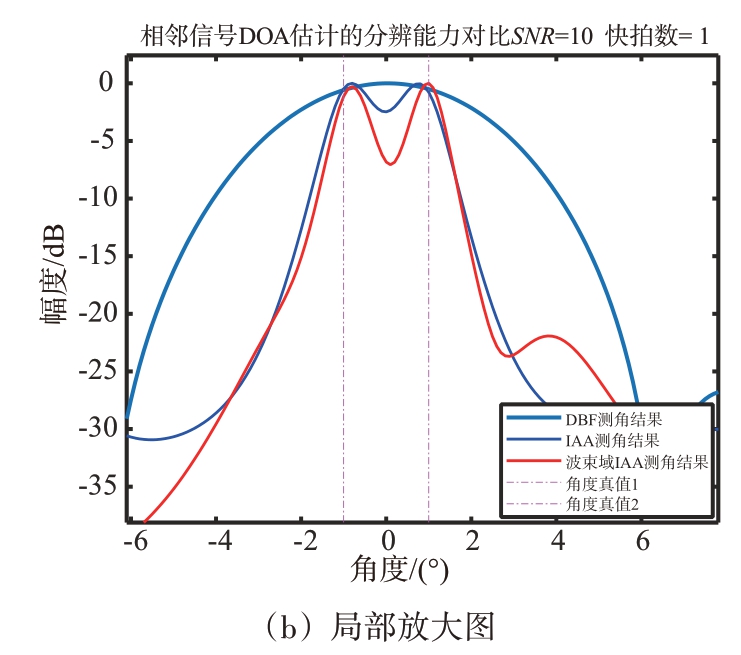
图1 3种算法仿真对比图
2)算法收敛特性
针对1)的仿真场景,图2给出了波束域IAA 算法分别在初始化阶段、迭代2 次、迭代5 次、迭代10次等算法中间过程得到的归一化功率谱图。
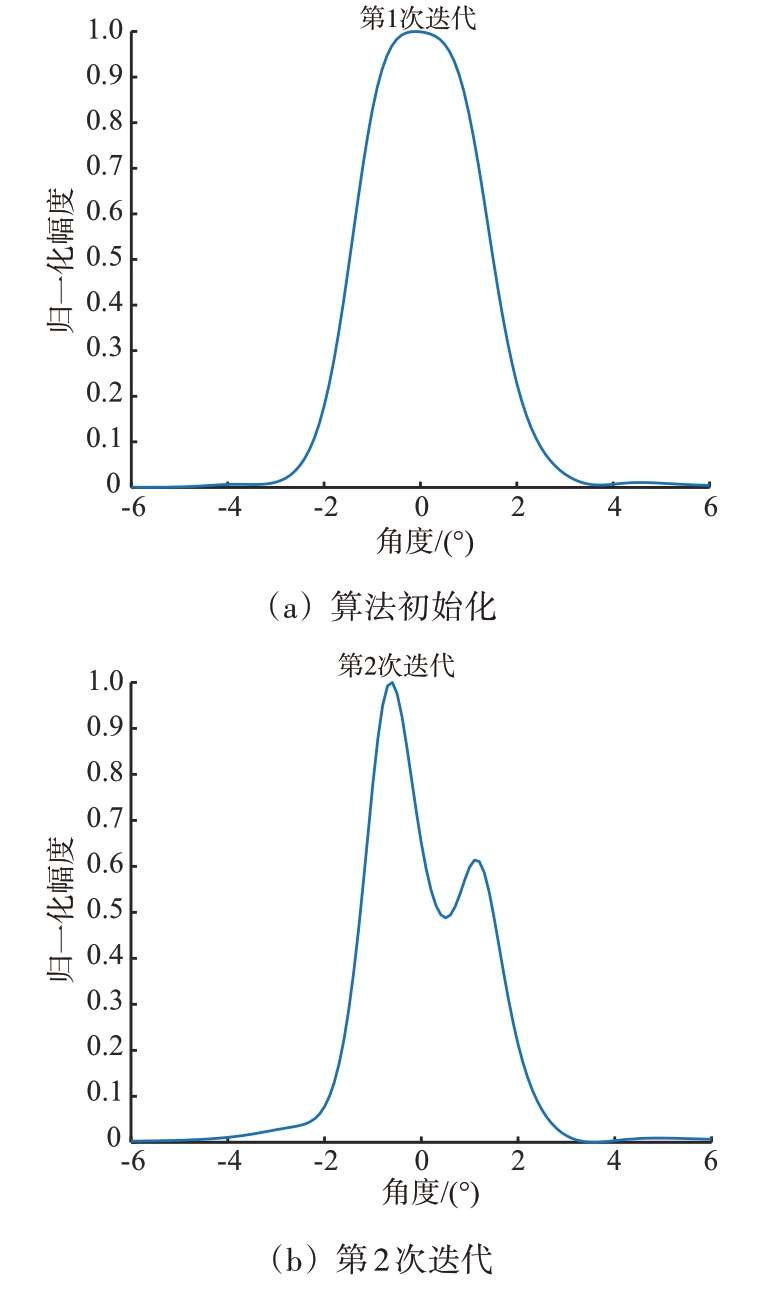
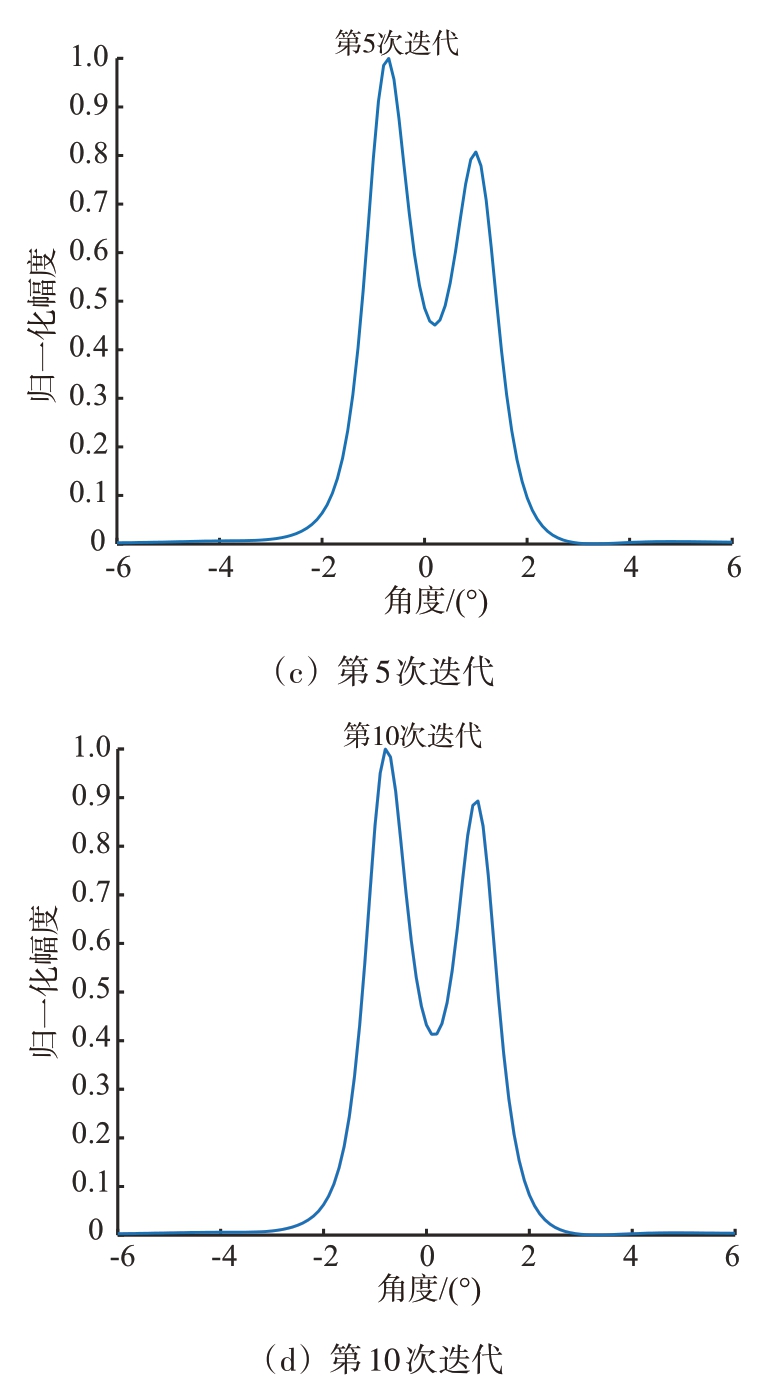
图2 波束域IAA算法不同迭代次数仿真结果
由图2 的4 组仿真曲线可以发现,随着迭代次数的逐渐增加,波束域IAA 算法在目标真实的方位附近形成的谱峰越来越尖锐,迭代到5 次之后,归一化功率谱的谱峰形状变化就不再明显,通过大量的仿真实验,一般波束域IAA 算法不超过10次迭代即可实现收敛,说明本文提出的算法收敛速度较快,可应用于实际工程。
3)相邻信号DOA分辨概率仿真
为进一步验证算法性能,下面通过蒙特卡洛仿真实验考察两个相邻信号的角度间隔对算法“超分辨”性能的影响,每一个实验结果都进行1 000次重复实验。分辨概率指的是算法能将两个相邻的信号有效区分开,定义两个到达角分别为θ1、θ2 的信源,如果得到的两个谱峰均值高于两信源角度均值处对应的谱峰,且两谱峰对应的估计出的目标方位![]() 满足:
满足:![]()
![]() 时,则称两相邻目标能够成功地被分辨。
时,则称两相邻目标能够成功地被分辨。
为了简化仿真场景,以两个并排飞行的无人机(横向间隔100 m)来替代集群无人机目标,两个无人机(假设信噪比为10 dB)从距离雷达5 km 的地方开始,向着雷达飞行,此时两架无人机之间的角度间隔从1.15°不断增大,一直增大到4.2°(对应着常规波束形成的3 dB 波束宽度,此时无人机距离雷达1.35 km)。对于雷达测量而言,如果需要在尽可能远的地方将两个无人机分开,要求雷达的方位分辨能力必须很高,否则两个落入同一个接收波束的目标无法分辨开。从图3可知,当两个目标角度间隔大于2.084°(对应着无人机距离2.75 km)时,波束域IAA 方法就有高于85%的概率将两个无人机分开。可见,波束域IAA 方法具有优于常规波束形成方法1倍的分辨能力,帮助雷达提前将密集目标分辨开。
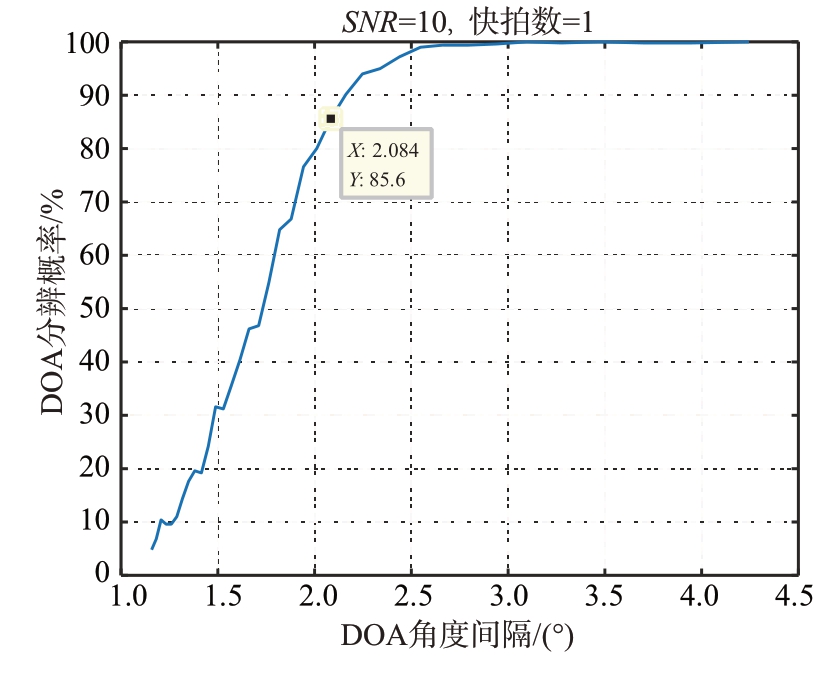
图3 不同目标角度间隔对应的分辨概率
图4 仿真了两个目标角度间隔2.08°时,DOA分辨概率随信噪比变化的情况。由图4可见,随着信噪比的提高,算法对于相邻信号的分辨概率也迅速提高。
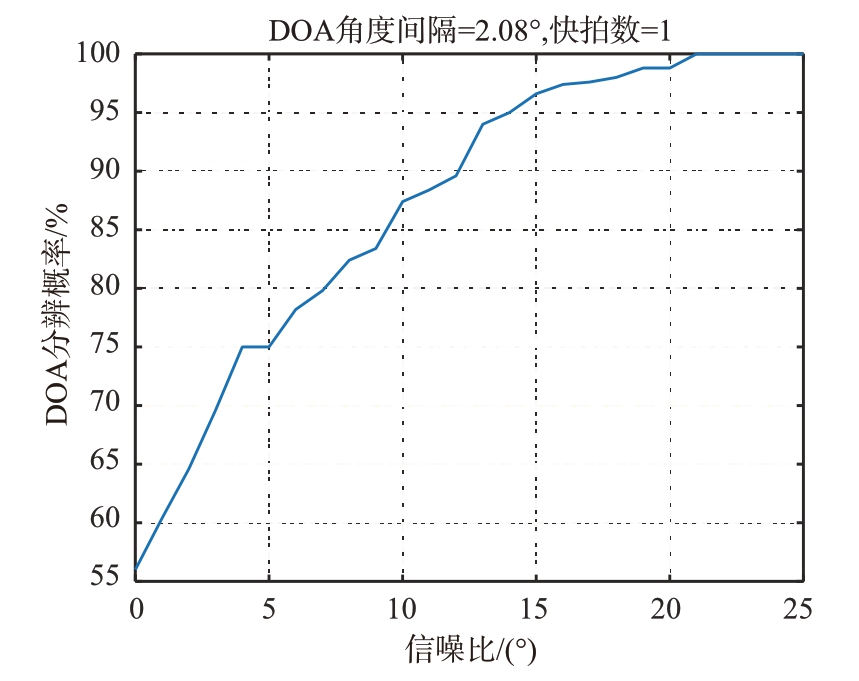
图4 DOA分辨概率随信噪比变化的情况
5 结束语
为了提升现有系统对于集群无人机目标的分辨能力,基于“宽发窄收”同时多波束的相控阵雷达系统,提出了一种波束域IAA 算法,不仅可以避免传统的稀疏表示类测角方法的计算复杂度高和需要选取超参数问题,而且在单快拍数、入射信号空间角度间隔较小等非理想情况下都具备很好的分辨能力。通过仿真试验,可以说明:该方法可以帮助雷达提前将密集目标分辨开,进而实现对于集群的规模(个数)、轮廓等信息进行准确估计,具有很强的应用价值。虽然本文旨在提供一种适配于相控阵雷达波束化、距离-多普勒域处理流程的超分辨方法,但该方法并不局限于此类系统,对于其他快变信号[13](单快拍或少快拍数)场景下的DOA估计依然适用。
[1]刘雷,刘大卫,王晓光,等.无人机集群与反无人机集群发展现状及展望[J].航空学报,2022,43(S1):4-20.
[2]YANG Tianyuan,DE MAIO A,ZHENG Jibin,et al.An Adaptive Radar Signal Processor for UAVs Detection with Super-Resolution Capabilities[J].IEEE Sensors Journal,2021,21(18):20778-20787.
[3]杨雪亚,沈显照,王贤翔.低空反无雷达的高精度测速方法及波形设计[J].火控雷达技术,2022,51(3):36-39.
[4]赵春雷,王亚梁,毛兴鹏,等.基于压缩感知的高频地波雷达二维DOA 估计[J].系统工程与电子技术,2017,39(4):733-741.
[5]YANG Jie,YANG Yixin.Sparse Bayesian DOA Estimation Using Hierarchical Synthesis Lasso Priors for Off-Grid Signals[J].IEEE Trans on Signal Processing,2010,68:872-884.
[6]BAI Longxin,ZHANG Jingchao,FAN Meiyu,et al.The Trimmed LASSO for Direction of Arrival Estimation by the Generalized Soft-Min Penalty[C]// 2023 IEEE 16th International Conference on Signal Processing and Communication System,Bydgoszcz,Poland:IEEE,2023:1-6.
[7]GUO Yiran,SHEN Qiang,DENG Zilong,et al.Research on a Super-Resolution and Low-Complexity Positioning Algorithm Using FMCW Radar Based on OMP and FFT in 2D Driving Scene[J].Sensors,2023,23(9):4531.
[8]ZHENG Baifu,ZENG Cao,LI Shidong,et al.The MMV Tail Null Space Property and DOA Estimations by Tail-ℓ 2,1 Minimization[J].Signal Processing,2022,194:108450.
[9]YARDIBI T,LI Jian,STOICA P,et al.Source Localization and Sensing: A Nonparametric Iterative Adaptive Approach Based on Weighted Least Squares[J].IEEE Trans on Aerospace and Electronic Systems,2010,46(1):425-443.
[10]SUN Shunqiao,PETROPULU A P,POOR H V.MIMO Radar for Advanced Driver-Assistance Systems and Autonomous Driving: Advantages and Challenges[J].IEEE Signal Processing Magazine,2020,37(4):98-117.
[11]王磊,邹佳龙,贾文渊.低数据量的相控阵雷达多波束鉴角曲线生成方法[J].空天预警研究学报,2022,36(1):19-22.
[12]LIU Changzan,ZHOU Yan,DANG Bo.A Low-Computational-Cost Alternating Switches Algorithm for Real-Valued Spatial Covariance Matrix Reconstruction[J].Electronics Letters,2022,58(14):557-559.
[13]舒月,傅东宁,陈展野,等.基于RD-ANM 的毫米波雷达动目标超分辨DOA 估计方法[J].雷达学报,2023,12(5):986-999.