0 引言
基于无源全球导航卫星系统的双基合成孔径雷达（GNSS-SAR），是一种无源SAR 体制，它使用来自GNSS 的信号，如GPS、Galileo、GLONASS 或北斗系统作为照射源［1］。由于不需要发射机，GNSSSAR 在各种应用中比传统SAR 具有更高灵活性和更低功耗。1988年，Hall等［2］首次提出应用GNSS-R进行海洋表面遥感后，国内外学者开展了大量关于GNSS-R 技术的研究，包括海面测风［3］、海面测高［4］、海冰探测［5］、海面溢油探测［6］、海洋盐度探测［7］、土壤湿度探测［8］等方面。应用GNSS-R 信号，利用SAR 的信号处理方法，实现目标成像，是GNSS-R技术的新研究方向［9］。
近年来，国内外学者对于GNSS-SAR 成像算法已经有一些研究，例如：后向投影（BP）算法、距离多普勒（RD）算法、距离徙动（RM）算法和一些改进算法。2007 年，Cherniakov 等［10］利用GLONASS 卫星作为外辐射源，应用机载接收机，采用RD 算法成功获得首张GNSS-SAR 图像，此次试验的成功证明了GNSS-SAR 体制的可行性。在此之后，GNSSSAR 体制成为了世界各国科研单位的研究热点。2015年，曾涛等［11］提出改进RM算法来处理多普勒参数的二维空间方差。2017 年，Zeng 等［12］以GPS L5 信号作为信号源，在RD 算法的基础上，提出了五阶二维点目标频谱的改进距离徙动校正。
相对于其他成像算法，由于BP 算法成像精度高，不受限于运动几何构型和平台轨迹，被广泛应用于GNSS-SAR 成像。2013 年，Antoniou 等［13］利用Galileo 卫星作为外辐射源，接收站采用地面移动的小车进行了成像试验，并运用BP 算法得到成像结果。2019 年，张元迪等［14］提出了一种基于高频散射理论的GNSS-R海面目标成像模型，并应用BP算法进行仿真成像。2020 年，杨东凯等［15］应用GPS和地面固定接收机提出基于BP算法的多周期成像算法，实现单颗卫星的不同时间不同角度下成像。GNSS-SAR 成像大部分研究都是直接应用BP 算法，但其逐点精确聚焦，运算量大，故需进行改进来降低其时间复杂度，进行快速成像。
到目前为止，快速BP 算法主要分为快速后向投影算法（FBP）［16］和快速分解后向投影算法（FFBP）［17］。FBP 算法在子孔径内获得极坐标下的低分辨率图像后，通过子孔径相干叠加得到高分辨率图像，计算复杂度达到O（N2.5）。FFBP 算法与FBP 算法最主要的区别为应用多级迭代法进一步地节省了计算量，每次迭代的结果都作为下一次迭代的输入值，计算复杂度达到O（N2log2N）。但与此同时，也需要大量的内存来存储回波以及中间变量。
基于此，本文提出了一种分割数据块和构造相位补偿核的改进BP 算法。首先建立了GNSSSAR 的信号模型，并定量分析了改进BP 算法运算量以及内存占用情况。其次应用改进BP 算法对点目标进行成像处理，与传统BP 算法、FFBP 算法的运算时间及成像结果进行对比，仿真结果表明，本文所提算法可在保证成像精度的情况下极大地提高成像运算速度。
1 信号模型
GNSS-SAR 以运行在太空中的GNSS 卫星作为发射机，以地面固定站或者飞机作为接收机，包含直射天线、反射天线和GNSS 信号采集器。直射天线用于接收GNSS 发射的直射信号，采用右旋极化天线。反射天线用于接收由GNSS 发射经过探测区域反射的反射信号，衰减较大且极化方式从右旋极化转变为左旋极化，故采用高增益、窄波束的左旋极化天线。利用GNSS 卫星反射信号产生的相位延迟、功率、频率等变化，提取目标反射面特征，实现目标表面成像的应用。GNSS-R 信号示意图如图1所示。
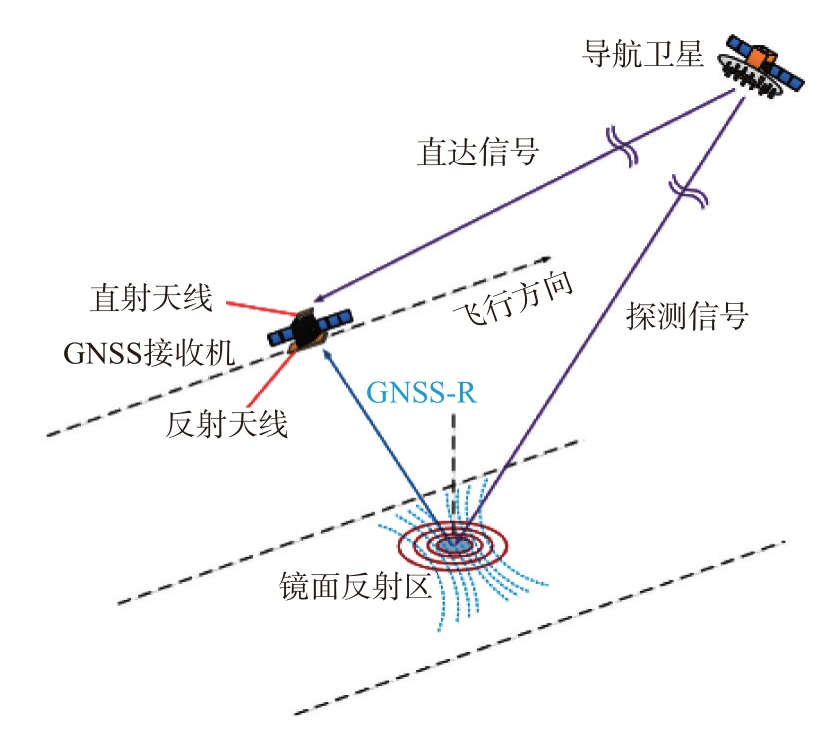
图1 GNSS-R信号示意图
本文以GPS L1 信号作为信号源展开研究，不考虑信号中的数据码影响，L1 信号由PRN 码和载波两部分组成，C/A码的直射信号形式为
式中，sCA 为C/A 码序列，fL1=1 575.42 MHz 为L1 信号的载波频率，τd为直射信号的时间延迟。
回波信号可视为经过衰减和延迟的发射信号，其信号形式为
式中，τr为回波信号的时间延迟。
2 改进BP算法
2.1 改进算法原理
BP 算法是一种时域成像算法，其主要原理是信号在时域的相干累加。传统BP 算法的具体过程为：对回波信号进行距离向脉冲压缩后，根据发射机、目标点和接收机之间的几何关系来计算信号传播时延，然后将回波信号中该时延处的值投影到目标点处，作为该点的成像值。对于该目标点，将不同方位向采样时刻的成像值进行相干累加，得到其在最终图像上的像素值。由于需要对探测区域中的每个点进行计算，因此计算量较大。FFBP 算法已经在传统BP 算法的基础上提升了成像效率，但需要占用大量的内存，为了实现高效率、低占用，本文在FFBP 算法的基础上进行改进，改进算法流程如图2所示。
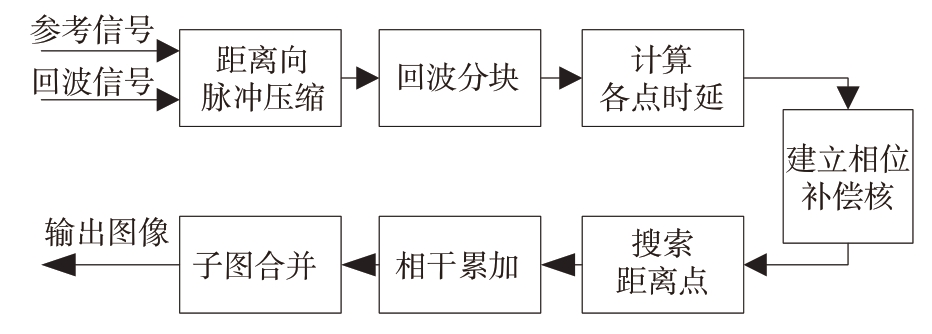
图2 改进BP算法流程图
首先对回波信号进行匹配滤波处理，使用频域处理的方法来加快运算速度，得到距离向脉冲压缩结果。
式中，F 和F-1分别表示傅里叶变换和逆变换，src(t)表示距离向脉冲压缩信号，sr(t)表示目标回波信号，sref(t)表示参考信号，*表示共轭。
假设最终图像矩阵为
在距离向上将区域目标划分为N 个子条带目标，并依次对其进行成像，对距离向脉冲压缩数据矩阵src(m,n)进行数据块分割，其中m 表示距离向采样点个数，n 表示方位向采样点个数，根据具体情况确定数据块分解因子q 和迭代级数s，计算子数据矩阵ssub(m′,n′)和每个子矩阵对应的发射机位置
和接收机位置
，表达式如下：
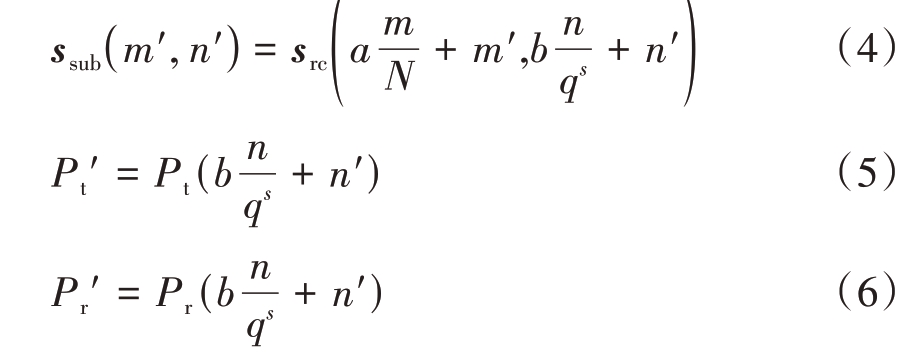
式中，a=0:N-1，b=0:qs-1，m′=1:m/qs，n′=1:n/qs。
经过数据块划分运算，可以得到Nqs 个子数据矩阵，并根据定位解算可以确定子矩阵中的发射机、目标成像子区域、接收机的几何关系，以接收机为参考点，计算成像子区域内各反射点的延迟距离和时延。为方便计算，信号的处理通常下变频到零中频进行，经变频后的直射和反射信号分别为
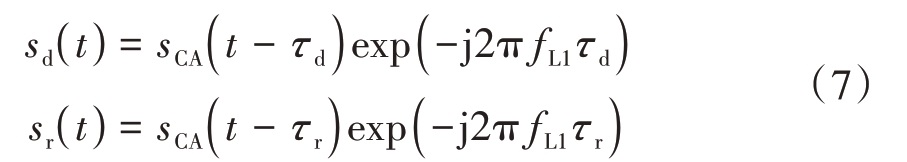
反射信号相对于直射信号的相位差为
因此，以接收机为参考点即以直射信号为基准，进行相位补偿时，补偿的相位为
式中：RSD 表示GPS 卫星到目标的距离；RDR 表示目标到接收机的距离；RSR 表示GPS 卫星到接收机的距离，RSD+RDR- RSR为延迟距离。
将最大延迟距离和最小延迟距离等间隔的划分成若干个距离刻度，可以表示为
式中，r 为延迟距离数组，Δr 为距离间隔，M为延迟距离数组r中包含的距离刻度数。建立相位补偿核：
式中，i的取值范围为1:M。
设网格点P(xp,yp,zp)的延迟距离为Rp，计算
，得到网格点P 对应延迟距离数组r 中的元素序号i，从而完成距离刻度搜索操作，得到该网格点的相位补偿值ki。对不同方位采样点得到的图像进行相干累加，完成后向投影操作，并对生成的粗分辨率子图像在距离向进行累加，得到新的粗分辨率子图像
，其中
在子图像合并过程中，将相邻的qs个子图像合并生成新的图像，然后对新生成的相邻子图像进行相同的操作，以此类推，直到最后只剩下一张图像。需要指出的是，由原子图像组合得到的新子图像所包含的网格点在方位向上是原子图像网格点的两倍。由于SAR 图像是一种复图像，因此子图像的插值需要同时对相位和幅值进行插值。本文采用“最近邻域插值”和“B 样条插值”两种插值方法对相位和幅值进行插值。子图像组合运算得到子条带图像的表达式为
将所有可能的相位补偿值进行离散化后备选，当需要时可以快速地选出相应的相位补偿值而无需对相位补偿值进行计算。由于相位补偿值的计算是耗时长的复数运算，而距离向搜索操作的运算量较小，因此可以明显提高计算效率。而对分块数据进行依次独立处理可以达到节省内存的效果。但由于延迟距离数组r 为非连续的，因此，网格点P(xp,yp,zp)的成像结果存在延迟距离误差ΔR=|Rp- ri|，则相位补偿误差为exp(j2πΔR/λ)，误差的大小取决于M 的取值。显然，M 取值越大，误差越小，成像效果越好，但与此同时成像效率也会降低，所以选取合适的M非常关键。
2.2 计算效率提升分析
下面对改进算法相比于传统BP算法、FFBP算法在计算效率和内存消耗方面的提升进行分析。假设方位向采样点为Na=4 000，距离向采样点数为Nr=10 000，划分的二维成像区域网格点数为Nx×Ny=512×512，数据块分解因子q=2，迭代级数s=3，分块数目为N，延迟距离数组r 中包含的距离刻度数M=100 000，进行1 次相位补偿时间为t1，构造延迟距离数组r 时间为t2，搜索距离点时间为t3。
则传统BP算法占用内存为Na×Nr，运算量为
FFBP算法占用内存为s×Na×Nr，运算量为
改进BP 算法占用内存为s×Na×Nr/N，运算量为
由于M ≪Nx×Ny，因此算法的耗时比主要与t3/t1 有关。由于t3 的值一般明显小于t1 的值，所以改进算法的计算效率将得到提升。在回波块数N=1的条件下，以t3/t1为变量进行估算，可得如图3 所示的耗时比曲线。从图中可以看出，改进算法的用时明显短于FFBP 算法的用时。通过多次实验验证，M/(Nx×Ny)为0.4～0.6 时，在提高速度的同时可以获得较好的成像结果。
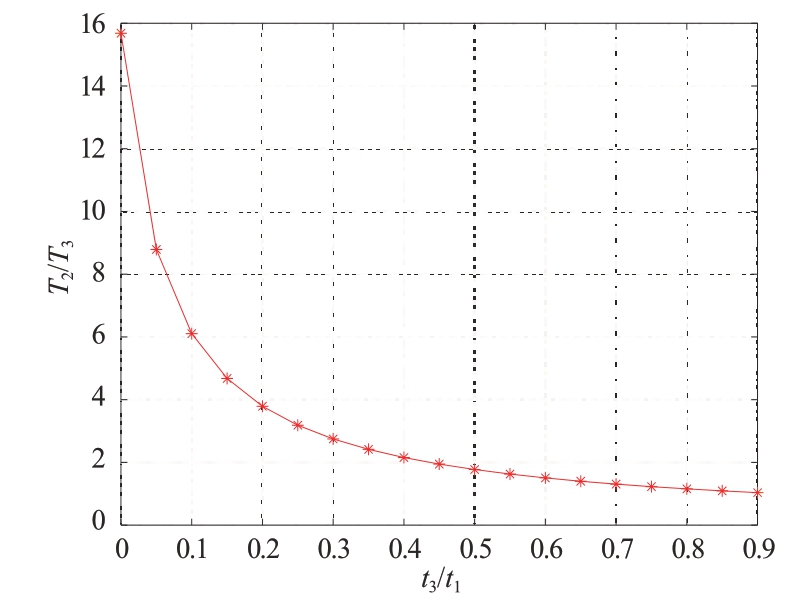
图3 FFBP与改进算法耗时比变化曲线
以分块数目N 为变量，其中内存与分块数目的关系曲线如图4 所示，与FFBP 算法相比，改进BP算法随着分块数目的增加，所占用的内存减少。
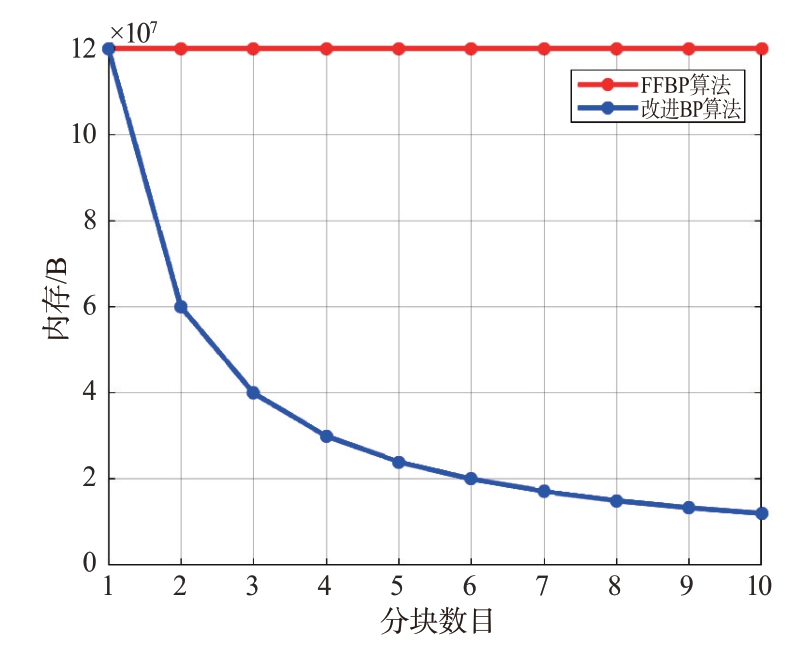
图4 内存与分块数目关系曲线
3 仿真实验与结果
为了验证改进算法的有效性，构建仿真场景如图5所示。
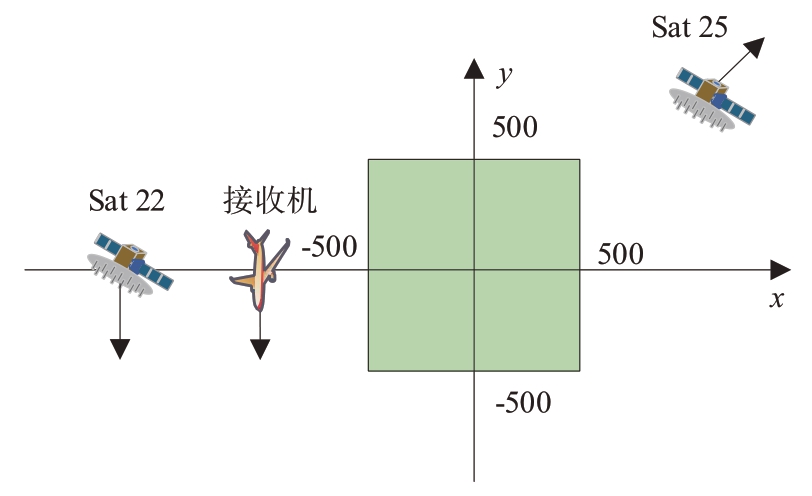
图5 GNSS-SAR成像仿真场景
以（0,0,0）、（-250,0,0）、（250,0,0）、（0,-250,0）、（0,250,0）为5个目标点坐标，以坐标系原点为中心的1 000 m×1 000 m 为探测范围，接收机为机载模式和地面固定接收机模式，GNSS-SAR 成像仿真参数如表1所示。
表1 GNSS-SAR成像仿真参数
通过解算历书得到卫星位置、卫星速度、高度角和方位角，获取的卫星天空图如图6 所示，针对后向散射模式和前向散射模式决定选取PRN 22和PRN 25两颗卫星进行成像。
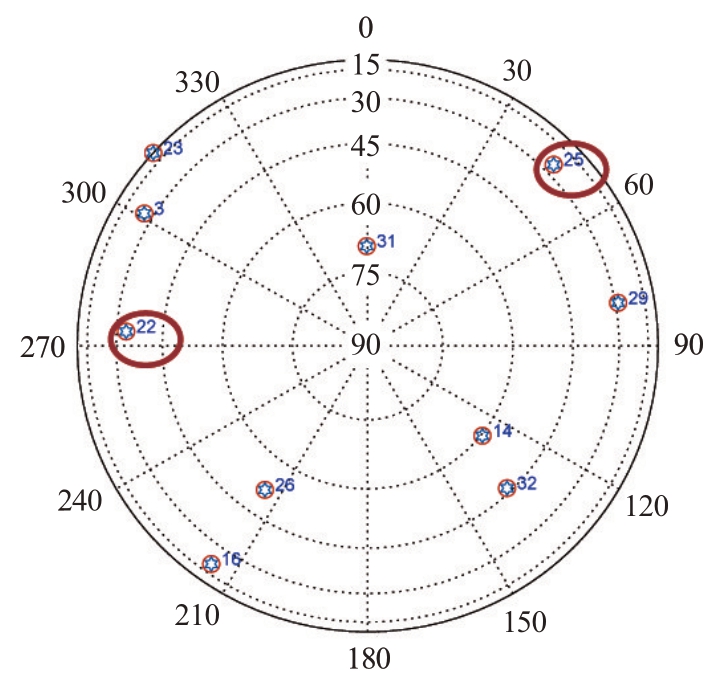
图6 卫星天空图
结合接收机类型，可以组合为4 种模式，分别为机载后向模式、机载前向模式、地面后向模式和地面前向模式。以下分别对这4 种模式采用传统BP算法进行仿真，仿真结果如图7所示。
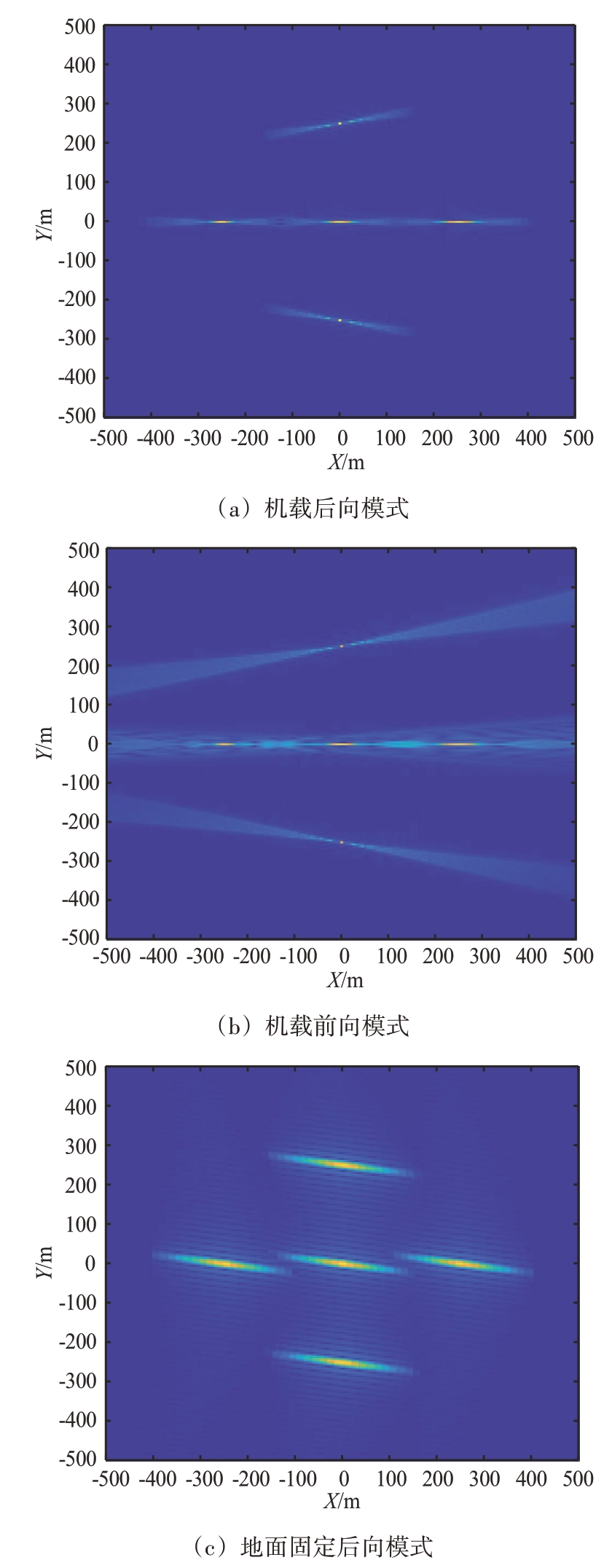
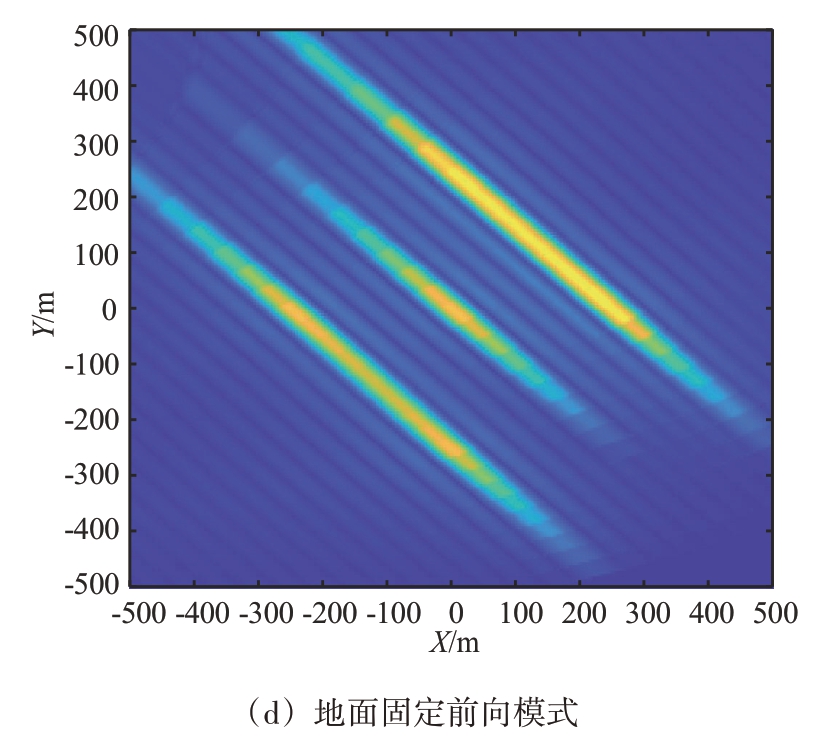
图7 C/A码成像仿真结果图
由于C/A 码带宽小，因此距离向分辨率低，在图像上表现为距离向出现“拉长”现象。方位向分辨率与信号带宽没有关系，只和相对运动有关系，因此方位向分辨率较好。为检验改进算法的有效性，在同一硬件条件下，对坐标为（0,0,0）的点目标进行成像，区域网格点数为512×512，M=10 000，数据块分解因子q=2，迭代级数s=3，分块数目N=4，针对机载后向模式使用GPS C/A 码分别应用传统BP 算法、FFBP 算法和改进BP 算法进行仿真成像。图8 给出了算法的成像结果以及其对应的处理时间和方位向切片。
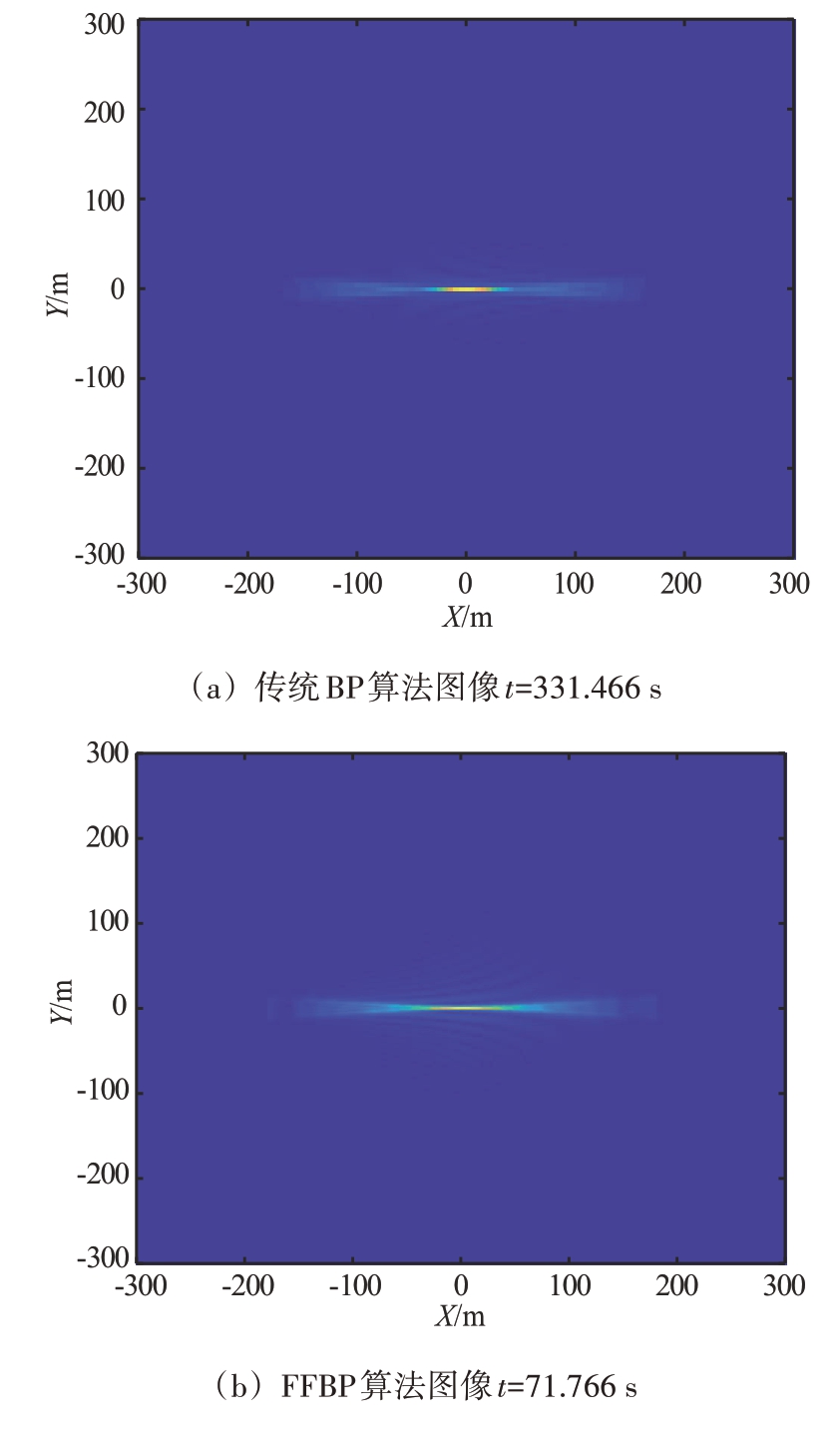
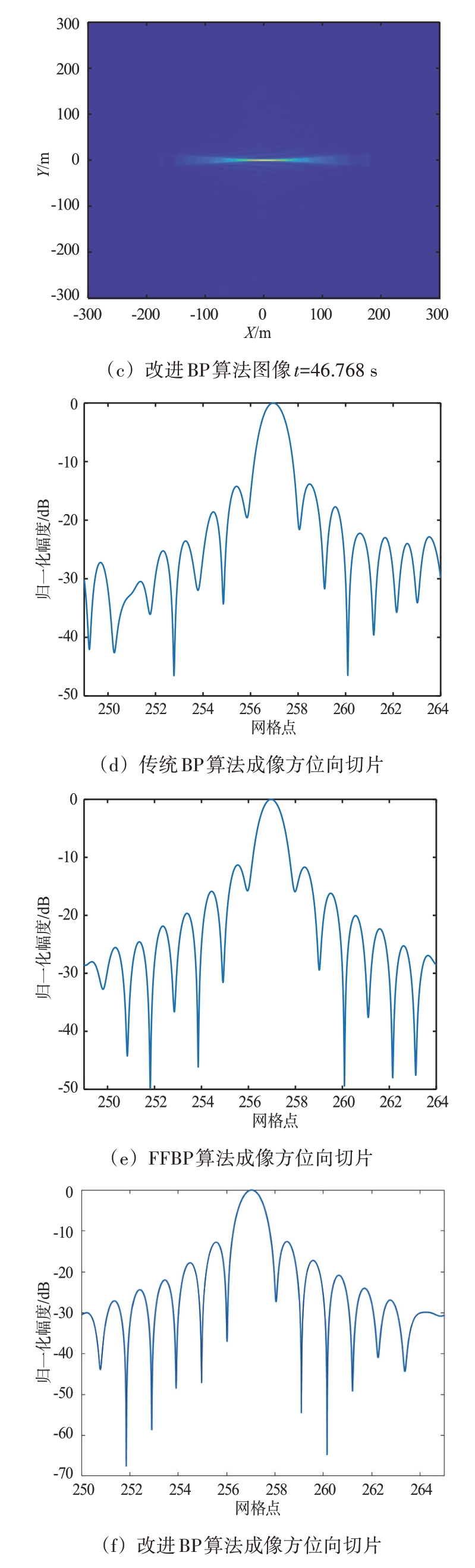
图8 改进算法与传统算法、FFBP算法成像对比结果
从图8（a）、图8（b）、图8（c）中可以看出，改进后BP 算法的成像效果相比于传统BP 算法近似一致，改进后BP算法的运算时间相对于传统BP提升了近90%，相对于FFBP 算法提升了近40%，而成像过程中只需要FFBP 算法的1/4 内存。当成像场景进一步增大，改进BP算法的优势将更明显。
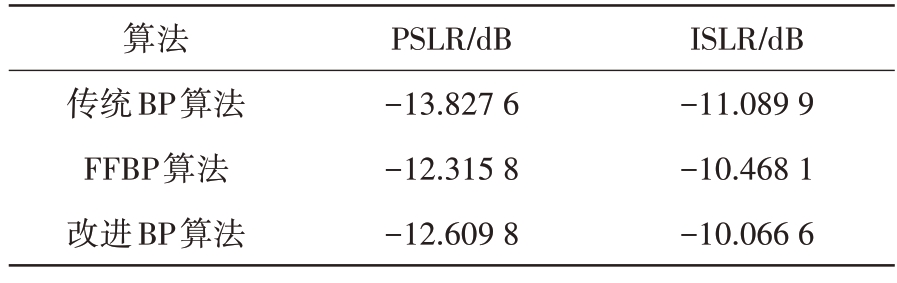
表2 给出了传统算法、FFBP 改进算法和改进BP 算法点目标成像结果的方位向峰值旁瓣比（PSLR）以及积分旁瓣比（ISLR），FFBP 算法和改进BP 算法成像结果的方位向PSLR 和ISLR 近似一致，且相对于传统BP 算法略有降低，但仍具有较好的成像质量。
表2 改进算法与传统算法、FFBP算法成像对比结果
为了进一步验证算法的有效性，针对不同信噪比（SNR=10，5，-10 dB）的情况分别进行了点目标成像，成像对比结果如图9所示。从图中可以看出，低信噪比的情况下，改进算法仍具有较好的成像性能。表3 给出了不同信噪比下运用改进算法进行点目标成像结果的PSLR 以及ISLR，随着信噪比的降低，PSLR和ISLR略有降低。
表3 不同信噪比下改进算法成像对比结果 dB
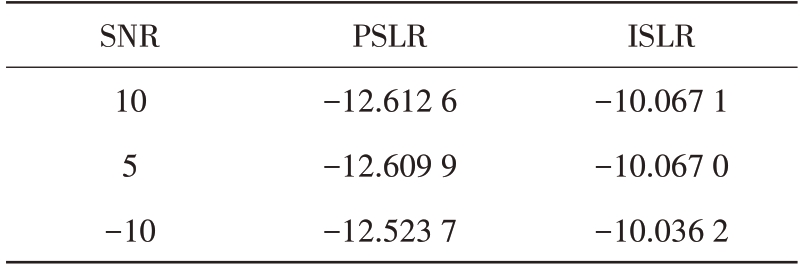
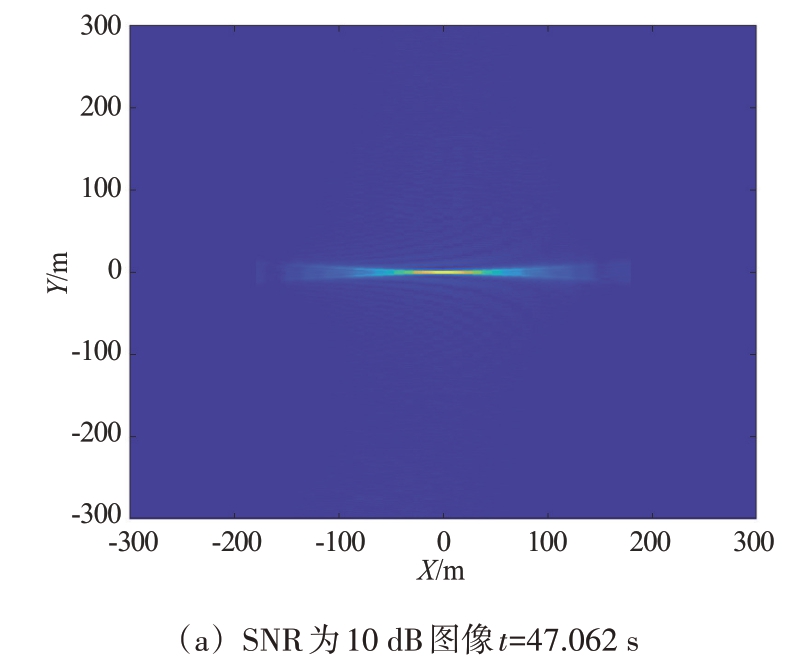
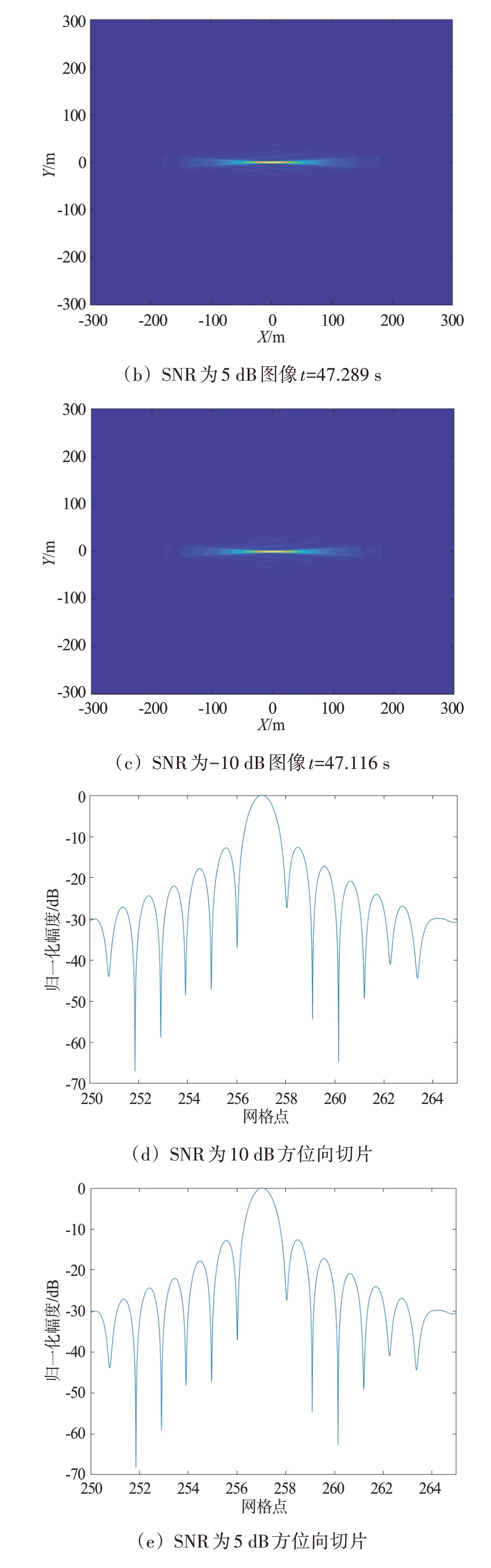
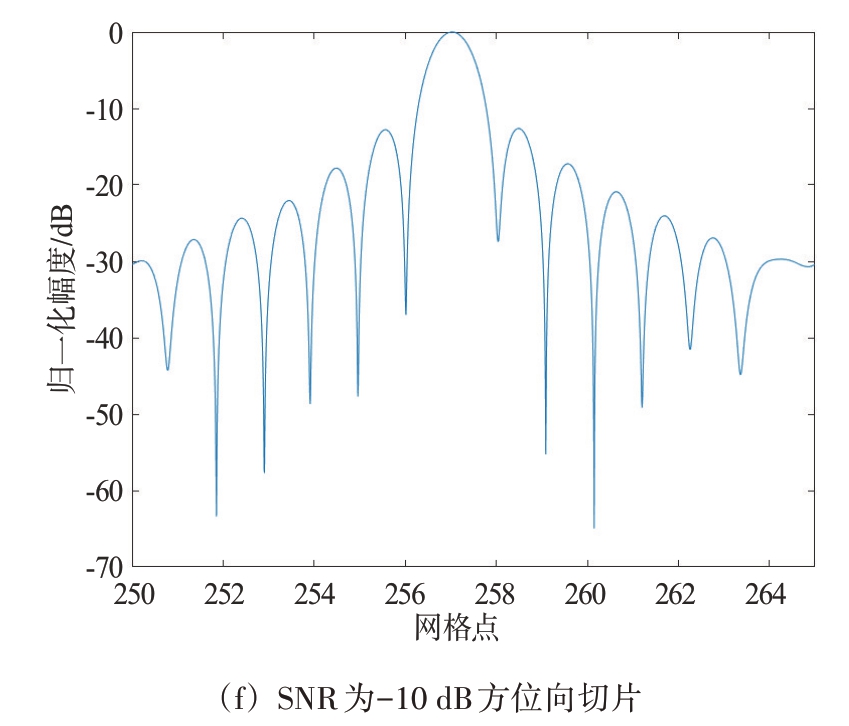
图9 不同信噪比下改进算法成像对比结果
4 结束语
针对应用于GNSS-SAR 的现有BP 算法时间复杂度高的问题，本文提出一种数据分块和构造相位补偿核的改进BP 算法，通过相位补偿核构造和距离向搜索操作降低了算法的运算量，通过回波数据分块并依次、独立进行处理减少了内存的占用。定量分析表明，改进后算法相比于传统BP 算法和FFBP 算法提升了成像效率，并相对于FFBP算法节省了内存。通过机载后向模式下的点目标仿真结果验证了改进BP算法的有效性。未来将针对C/A 码带宽小而导致距离向分辨率低的问题进行研究，在快速成像的基础上实现高分辨率成像。
［1］李中余，黄川，武俊杰，等.基于GNSS 的无源雷达海面目标检测技术综述［J］.雷达科学与技术，2020，18（4）:404-416.
［2］HALL C D,CORDEY R A.Multistatic Scatterometry［C］//IEEE International Geoscience and Remote Sensing Symposium,Edinburgh:IEEE,1988:561-562.
［3］XIE Heng,CHENG Xing,HE Shaobao,et al.MF-ANN:A Novel Artificial Neural Network-Based Method for Ocean Wind Speed Retrieval on Spaceborne GNSS-R Signal［J］.IEEE Trans on Geoscience and Remote Sensing,2023,61:1-17.
［4］胡媛，陈行杨，顾旺旺，等.GNSS-R 海面测高现状及其常用方法研究进展［J］.全球定位系统，2020，45（3）:96-103.
［5］刘奇，张双成，刘宁，等.GPS 反射信号用于海冰识别与海面测高［J］.测绘科学，2021，46（9）:43-48.
［6］王腾飞，张波.GNSS-R 溢油厚度探测方法研究［C］//第十四届全国信号和智能信息处理与应用学术会议论文集，北京：［出版者不详］，2021:275-278.
［7］LV Yanfang,ZHANG Yifan,LIU Jingyi,et al.Coastal Surface Salinity Retrieval Analysis from SMAP Mission Using Machine Learning［C］//2023 IEEE International Geoscience and Remote Sensing Symposium，Pasadena,CA,USA:IEEE,2023:3981-3983.
［8］汉牟田，许志超，常青，等.利用北斗GEO卫星干涉信号功率反演土壤湿度［J］.北京航空航天大学学报，2023，49（7）:1661-1670.
［9］何振宇，杨扬，陈武，等.基于GPS-R 的双基地SAR 移动目标成像方法研究［J］.遥感学报，2022，26（12）:2555-2567.
［10］CHERNIAKOV M,SAINI R,ZUO R,et al.Space-Surface Bistatic Synthetic Aperture Radar with Global Navigation Satellite System Transmitter of Opportunity-Experimental Results［J］.IET Radar Sonar &Navigation,2007,1（6）:447-458.
［11］ZENG Tao,LIU Feifeng,ANTONIOU M,et al.GNSSBased BiSAR Imaging Using Modified Range Migration Algorithm［J］.Science China Information Sciences,2015,58（8）:144-156.
［12］ZENG Hongcheng,CHEN Jie,ZHANG Haojie,et al.A Modified Imaging Formation Algorithm for Bistatic SAR Based on GPS-L5 Signal［C］//2017 IEEE International Geoscience and Remote Sensing Symposium,Fort Worth,TX,USA:IEEE,2017:4129-4132.
［13］ANTONIOU M,ZHOU Hong,ZENG Zhangfan,et al.Passive Bistatic Synthetic Aperture Radar Imaging with Galileo Transmitters and a Moving Receiver: Experimental Demonstration［J］.IET Radar Sonar &Navigation,2013,7（9）:985-993.
［14］张元迪，焦瑞莉，朱云龙，等.GNSS-R 海面目标成像仿真方法研究［J］.测绘通报，2019（2）:86-90.
［15］WANG Shu,ZHU Yunlong,YANG Dongkai,et al.GNSSR Multi-Period SAR Imaging Experimental Study［C］//2020 IEEE International Geoscience and Remote Sensing Symposium,Waikoloa,HI,USA:IEEE,2020:920-923.
［16］YEGULAIP A F.Fast Back Projection Algorithm for Synthetic Aperture Radar［C］//1999 IEEE Radar Conference,Waltham,MA,USA:IEEE,1999:60-65.
［17］ULANDER L M H,HELLSTEN H,STENSTROM G.Synthetic-Aperture Radar Processing Using Fast Factorized Back-Projection［J］.IEEE Trans on Aerospace and Electronic Systems,2003,39（3）:760-776.