0 引言
波达方向（Direction of Arrival,DOA）估计作为阵列信号处理领域中一个重要分支，在雷达、通信和电子对抗等领域有着广泛的应用。大部分算法都是在均匀阵列的基础上提出的，其中子空间类算法因其高分辨性能在DOA 估计中受到了广泛的关注，比较经典的有多重信号分类（Multiple Signal Classification Algorithm,MUSIC）算法、信号参数旋转不变（Estimation of Signal Parameters via Rotational Invariance Techniques,ESPRIT）算法等。但是均匀阵列的DOA 估计分辨率和阵列系统复杂性之间存在着矛盾［1］，且无法解决DOA估计的欠定问题。
稀疏阵列［2-3］相比于均匀阵列，阵元间距能够突破半波长限制，在不增加阵列系统复杂性的前提下，可以获得更大的孔径［4］，从而具有更高的分辨率。且由于稀疏阵列可以形成更高空间自由度的虚拟阵列，所以能够分辨出远多于阵元数目的信号源。主流的稀疏阵列DOA 估计算法可分为两类：一是子空间类［5-6］算法。该类算法利用连续的虚拟阵元构建满秩的协方差矩阵，并基于此进行特征值分解，通过构造信号子空间和噪声子空间来进行DOA 估计。如文献［5］通过空间平滑算法构建满秩的协方差矩阵，并通过MUSIC 算法完成DOA 估计。文献［6］从互质阵列中提取一对移位不变的均匀线性子阵列，利用ESPRIT 算法进行DOA 估计。这类算法仅能够利用虚拟阵列中的连续虚拟阵元部分进行DOA 估计，会损失一定的估计精度，且在小快拍、低信噪比下性能表现较差。二是稀疏重构类［7-9］算法。这类算法利用信号在空域的稀疏性，通过构造包含所有入射方向的过完备冗余字典，将DOA 估计问题转换成稀疏向量的恢复问题，能够有效提高估计准确率。如文献［7］将梯度下降算法引入到正交匹配追踪算法中，通过稀疏重构来进行DOA 估计。但是该算法对初始值较为敏感，一个不恰当的初始值可能会导致算法的错误收敛。文献［8］引入压缩感知算法，通过基于凸优化的稀疏恢复对输出数据进行优化，提高了信源估计的精度。但是该算法的估计精度依赖于正则化参数的取值，需要对正则化参数进行额外求解。文献［9］利用平移嵌套阵列等效的差分共阵接收矢量，建立了贝叶斯角度估计模型，通过迭代求解获取角度估计值。但是该算法对参数的选择和调整较为敏感，且计算复杂度较高。
本文研究了一种基于TOEPLITZ 重构的压缩感知嵌套阵列DOA 估计方法，该方法将虚拟阵列输出向量重构成满秩TOEPLITZ 协方差矩阵，利用信号在空间域的稀疏性，将阵列协方差矩阵进行稀疏表示，并对稀疏向量进行加权约束，通过压缩感知的信号重构算法求解入射信源的DOA 估计。本文方法与传统的稀疏阵列DOA 估计算法相比，在低信噪比、小快拍数和多信源数下具有更好的DOA估计性能。
1 嵌套阵列模型
二级嵌套阵列模型如图1所示，该嵌套阵列由两级均匀阵列构成。
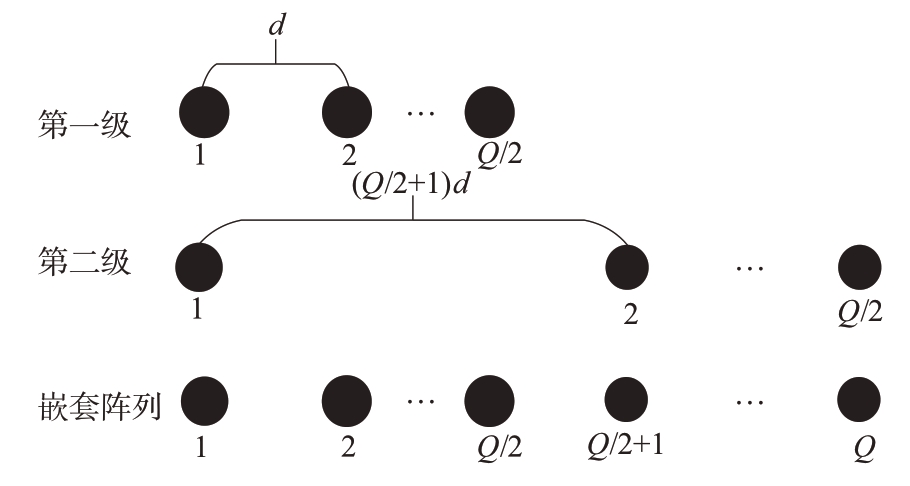
图1 二级嵌套阵列模型
二级嵌套阵列的阵元总数为Q（Q 为偶数），且每级阵元数为
，λ为信号波长。当两级嵌套阵列每一级阵元数满足N1= N2= N/2 时，通过差分形成的虚拟阵列的自由度可以取得最大值［10-11］。
假设空域中有K 个互相独立的远场窄带信号入射到如图1 所示的二级嵌套阵列模型中。第k个信号的入射角记为θk,k=1,2,…,K，快拍数为J，则阵列的接收信号可以表示为
式中，X 为阵列输出矩阵，S 为信源矩阵，N 为噪声矩阵，A为增广互质阵列的方向矢量，有
2 算法原理
2.1 TOEPLITZ重构
为了充分发挥嵌套阵列扩展孔径的优势，通过构建差分虚拟阵列进行DOA 估计。首先对R 进行向量化处理［12］：
式（4）中B 可被看作是该差分虚拟阵列的一个Q2×K 的阵列流型矩阵，但是这些数据存在冗余。从阵列流型矩阵B= A*⊙A 中建立一个维度是((Q2-2)/2+Q)×K 的矩阵B1，即从阵列流型矩阵中对具有相同数据的行进行加权平均，并按照相位进行排序，以便使其第i 行对应差分虚拟阵列的第(-Q2/4- Q/2+i)个阵元的位置。这等同与从观测向量Rv 中移除冗余数据，并按照阵元相位进行排序，可得到差分虚拟阵列的输出向量z：
式中
表示z的第一行的数据对应差分虚拟阵列的第-Q2/4- Q/2+1 个位置的阵元的输出信息。
式（4）中p可以看作是入射到差分虚拟阵列的单快拍信号向量。由此形成的虚拟阵列输出向量z 构建的协方差矩阵是一个单秩矩阵。对此，可以采用TOEPLITZ 重构方法，将向量z 重构成一个大小为(Q2/4+Q/2) ×(Q2/4+Q/2)的满秩协方差矩阵RT：
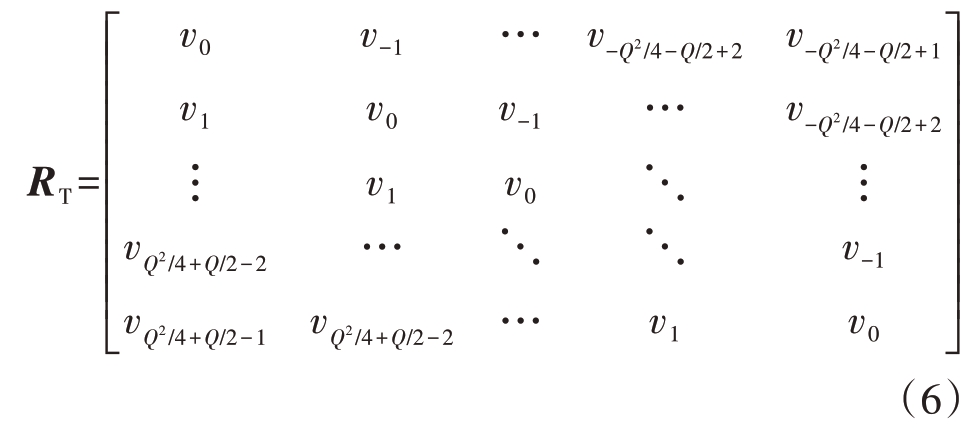
对RT 中的元素，有
。通过TOEPLITZ 重构得到的矩阵RT 是一个厄米特矩阵，即其主对角线元素是实数，其余元素关于主对角线呈共轭对称。所以该协方差矩阵与一个拥有Q2/4+Q/2 个天线阵元的均匀线阵阵列接收信号的协方差矩阵具有相同的结构，实现了仅使用Q 个物理阵元，却得到了O(Q2)的空间自由度。
2.2 构建压缩感知模型
在稀疏阵列DOA 估计中，子空间类的算法因其实现简单、分辨性能较高而备受瞩目，如基于空间平滑的SSMUSIC 算法、SSESPRIT 算法等，但是这类算法在小快拍数、低信噪比的条件下估计精度不高。
为了解决上述问题，本文引入压缩感知的思想，利用信号在空间域的稀疏性，将阵列协方差矩阵进行稀疏表示（Sparse Representation of Array Covariance Vectors,SRACV）［13］，将DOA 估计问题转换成稀疏向量的恢复问题，在一定程度上提高了DOA估计性能。
首先构建包含所有可能的入射角方向的过完备冗余字典Θ={θ1,θ2,…,θP}(P ≫K)，并据此构建扩展方向矢量AΘ：
式中，dv为差分虚拟阵列的虚拟阵元的阵列矢量，λ为信号波长，AΘ 为一个大小为(Q2/4+Q/2)×P 的矩阵。
利用扩展方向矢量AΘ 将协方差矩阵RT 稀疏表示，写成如下的矩阵形式：
稀疏表示完成后，将DOA 估计问题转换成稀疏向量的恢复问题，构建基于L1 范数的压缩感知模型：
使用数据协方差矩阵的估计值
来代替R 经过稀疏表示后存在估计误差，则将式（10）的问题写成［14］
式中：||·||F 表示矩阵的Frobenius 范数；ς 表示正则化参数，它用来衡量估计误差的上界。对误差矩阵
进行向量化处理，并将其转化为标准正态分布，有
ς 作为置信度上界，利用卡方的概率密度函数计算可得
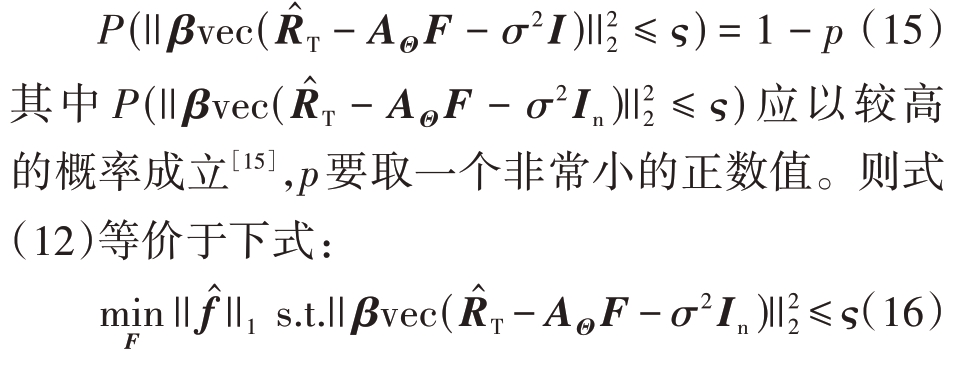
2.3 构建权值向量
为了确保在恢复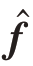
的过程中得到更好的稀疏解，避免DOA 估计中伪峰的出现，需要构造一个加权向量，对
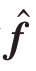中的每一个元素进行加权约束，这相当于给每个元素增加了惩罚因子。由于向量
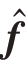与过完备冗余字典Θ 的一一对应关系，所以
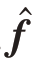中与入射信源方位角相对应的元素应该施加较小的约束，而其他元素则应施加较大的约束。
利用噪声子空间和信号子空间的正交关系，构造权值向量，便可以实现这一目标。对协方差矩阵RT 进行特征值分解，得信号子空间US 和噪声子空间UN。噪声子空间UN 与信源方向的阵列流型矩阵A的关系如下:
扩展方向矢量AΘ可以用如下方式来表示：
所以，引入加权向量后，最终的DOA 估计求解模型如下：
2.4 算法步骤总结
综上所述，基于TOEPLITZ 重构的压缩感知嵌套阵列DOA估计算法的实现步骤如下：
步骤1 构建二级嵌套阵列模型，利用阵列的输出信号矩阵，获取协方差矩阵，并对其进行向量化处理，得到向量Rv。
步骤2 对向量Rv 中的冗余数据进行加权平均，并按照相位信息重新进行排序，得到如式（5）所示的向量z。
步骤3 利用TOEPLITZ重构方法，将向量z重构成如式（6）所示的满秩协方差矩阵。
步骤4 构建过完备冗余字典Θ={θ1,θ2,…,θP}(P ≫K)，并据此构建如式（7）所示的扩展方向矢量AΘ。
步骤5 将协方差矩阵
特征值分解，获取噪声子空间
并通过式（19）和式（20）计算得到加权向量w。
步骤6 利用式（14）和式（15）计算得到参数ς和β的值，构建式（21）所示的DOA估计求解模型。
步骤7 求解式（21），得到稀疏向量
根据过完备冗余字典Θ 和向量
的对应关系，获取入射信源的DOA估计值。
3 仿真实验和结果分析
通过仿真实验对本文所提算法的性能进行分析，并与SSMUSIC 算法、SSESPRIT 算法进行比较。仿真选用如图1 所示的二级嵌套阵列作为接收阵列，其中第一级阵元数为3，阵元间距d= λ/2，第二级阵元数也为3，由此构建的二级嵌套阵列总阵元数为6。对比实验均采用100 次蒙特卡罗仿真，用均方根误差（Root Mean Square Errors,RMSE）来衡量算法的DOA估计性能，定义如下：
式中，C 为独立实验的次数，K 为信源数目
表示第c次独立实验下对θk的估计值。
仿真实验1 假设远场入射窄带非相干信源入射到二级嵌套阵列，入射信源个数为11，入射角度为-50°～50°，角度间隔为10°，快拍数J=128，信噪比SNR=10 dB。使用本文算法和传统的SSMUSIC 算法进行DOA 估计对比仿真，仿真的DOA估计空间谱对比如图2所示。
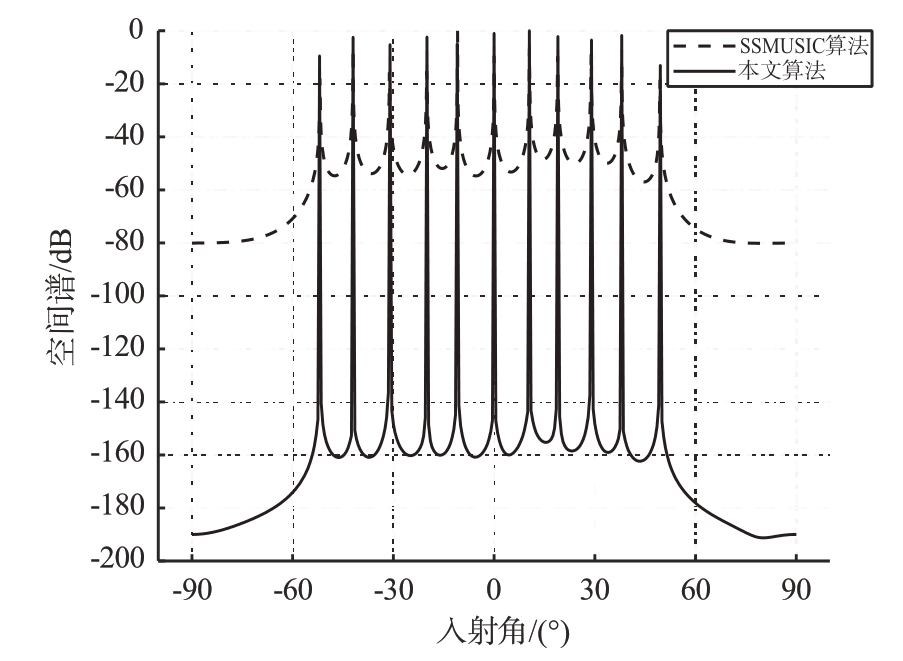
图2 DOA估计空间谱对比图
从图2可以看出，在给定快拍数和信噪比的仿真环境下，本文算法和传统的SSMUSIC 算法都能够得到准确的估计空间谱。但是本文算法的DOA估计空间谱的谱峰更尖锐，说明本文算法有着更高的测向精度和分辨率。
仿真实验2 假设远场入射窄带非相干信源入射到二级嵌套阵列，入射信源个数为3，入射方位角为[-10°,0°,10°]，快拍数J=128，信噪比从-10 dB 增加到10 dB，步进为2 dB。分别使用本文算法、SSMUISC 算法以及SSESPRIT 算法进行对比仿真，DOA 估计均方根误差与信噪比的关系曲线如图3所示。
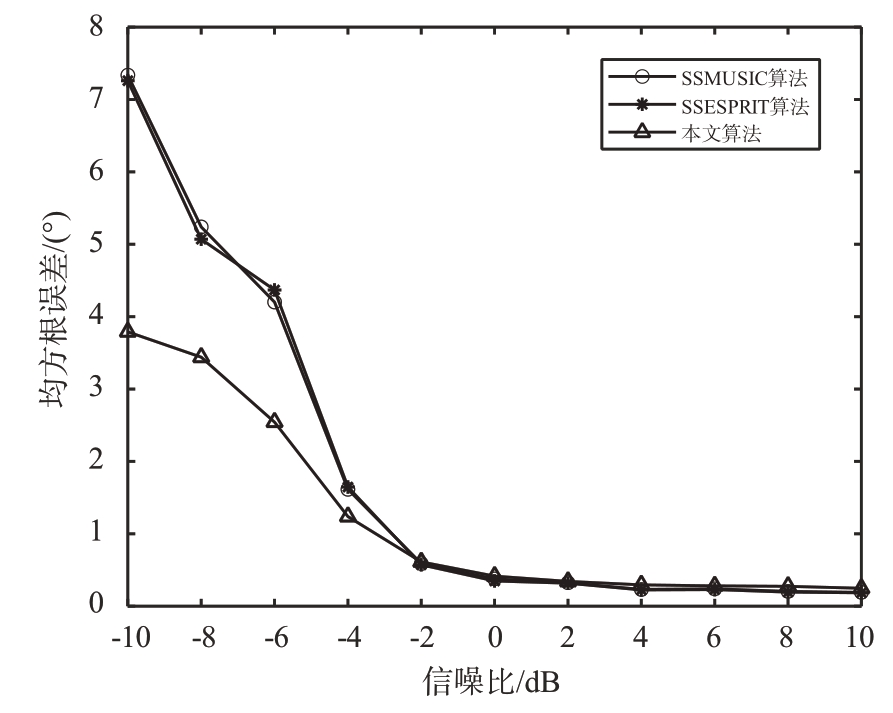
图3 RMSE与信噪比的关系曲线图
从图3可以看出，在当前仿真条件下，3种算法的角度估计均方根误差均随着信噪比的升高而降低。在低信噪比情况下，本文算法的估计均方根误差显著低于另外两种算法，所提算法具有明显的性能优势。在高信噪比时，3 种算法的估计均方根误差较为接近，估计性能相差不多。
仿真实验3 假设远场入射窄带非相干信源入射到二级嵌套阵列，入射信源个数从1 增加到11，信源角度间隔为10°，快拍数J=128，信噪比SNR=5 dB。分别使用本文算法、SSMUISC算法以及SSESPRIT 算法进行对比仿真，DOA 估计均方根误差与入射信源个数的关系曲线如图4所示。
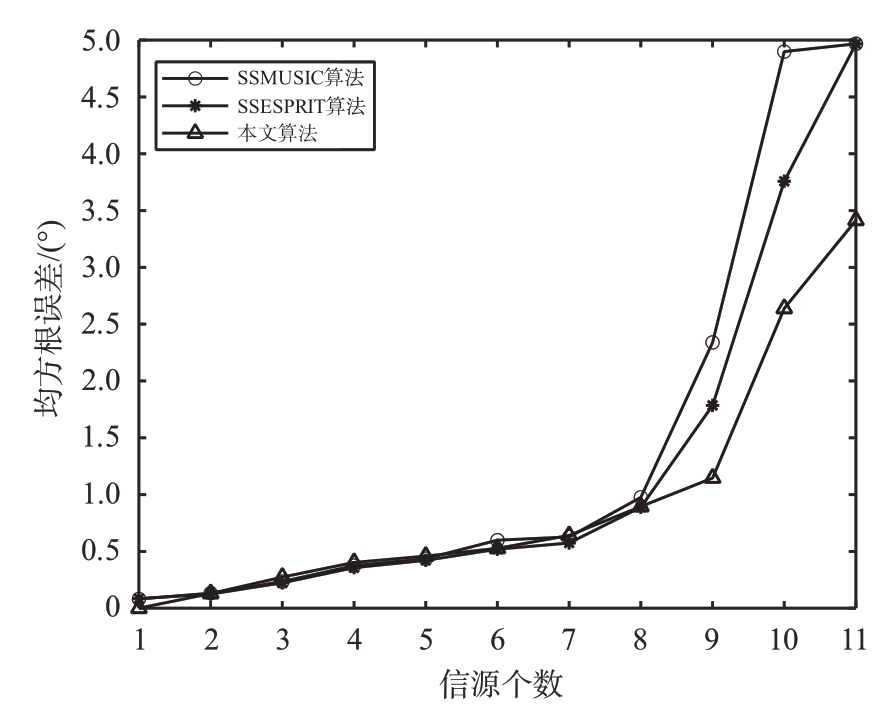
图4 RMSE与入射信源个数的关系曲线图
从图4可以看出，在当前仿真条件下，3种算法的DOA 估计均方根误差都随着入射信源个数的增加而增大。在入射信源个数较少时，3 种算法的DOA 估计均方根误差都比较接近，均趋向于0°。但是随着入射信源个数的增加，本文所提算法的估计均方根误差逐渐小于其他两种算法。由此可见，本文算法在入射信源数较多的时候，DOA 估计性能更好，更能适用于复杂的电磁环境。
仿真实验4 假设远场入射窄带非相干信源入射到二级嵌套阵列，入射信源个数为2，入射方位角为0°和0°+α，α 从1°增加到10°，快拍数J=128，信噪比SNR=5 dB。分别使用本文算法、SSMUISC 算法以及SSESPRIT 算法进行对比仿真，DOA 估计均方根误差与入射信源角度间隔的关系曲线如图5所示。
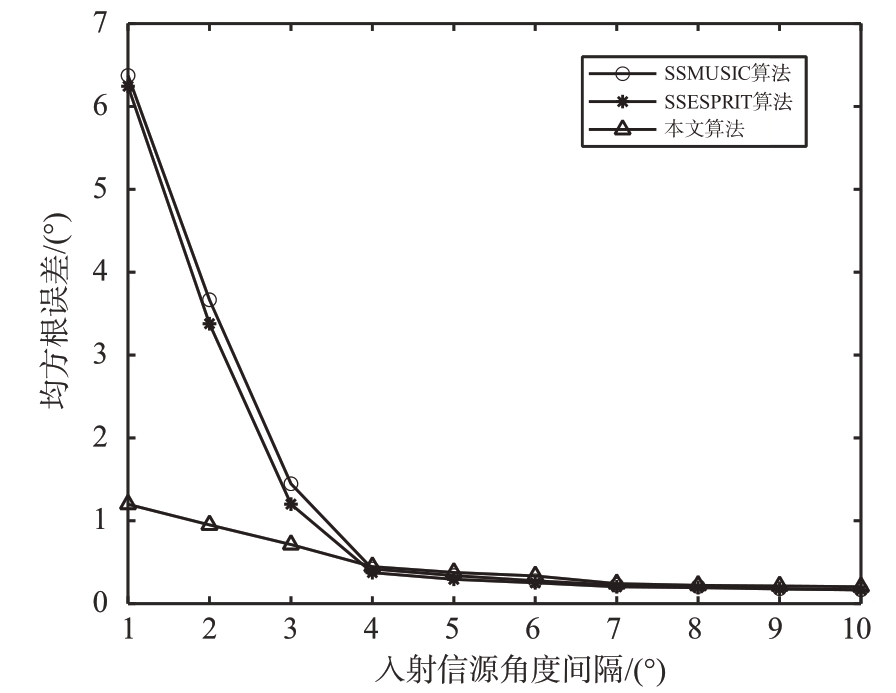
图5 RMSE与入射信源角度间隔的关系曲线图
从图5 可以看出，3 种算法的DOA 估计均方根误差都随着入射信源角度间隔的增大而减小。在入射信源角度间隔较小时，本文算法的DOA 估计均方根误差远远小于其他两种算法。由此可见，在当前仿真条件下，当入射信源的方位角较为接近时，其他两种算法的估计分辨率不高，无法准确地识别出入射信源。而本文算法则有着较高的DOA 估计分辨率，能够以较小的估计均方根误差分辨出入射信源。
仿真实验5 假设远场入射窄带非相干信源入射到二级嵌套阵列，入射信源个数为4，入射方位角为[-20°,-10°,10°,20°]，信噪比SNR=0 dB，快拍数从16 增加到128，步进大小为16。分别使用本文算法、SSMUISC 算法以及SSESPRIT 算法进行对比仿真，DOA 估计均方根误差与快拍数的关系曲线如图6所示。
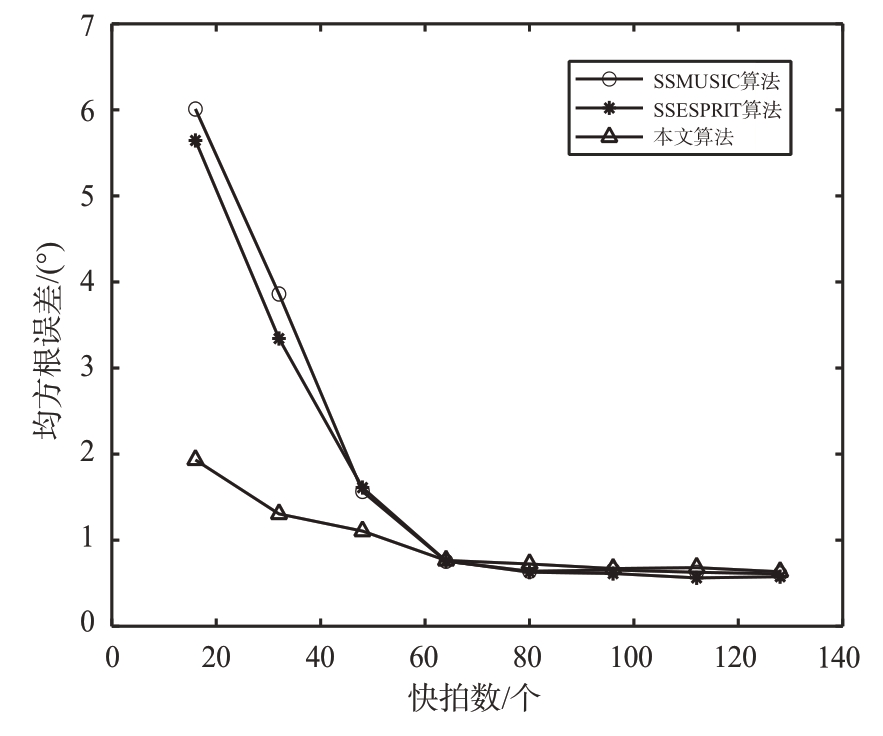
图6 RMSE与快拍数的关系曲线图
从图6 可以看出，3 种算法的DOA 估计均方根误差都随着快拍数的增大而减小。当快拍数较小的时候，本节所提算法的DOA 估计均方根误差远小于另外两种算法；当快拍数较大时，3 种算法的DOA 估计均方根误差趋于平缓，十分接近。这说明在当前仿真条件下，本文算法在低快怕数下有着明显优于其他两种算法的信源分辨准确率，在高快拍数下也有着不错的DOA估计性能。
4 结束语
本文研究了一种基于TOEPLITZ 重构的压缩感知嵌套阵列DOA 估计方法，该方法利用TOEPLITZ重构方法将入射到虚拟阵列的单快拍信号向量构建成满秩协方差矩阵，然后利用信号在空间域的稀疏性，将DOA 估计问题转换成稀疏向量的恢复问题，将DOA 估计问题转换成稀疏向量的恢复问题。本文方法与传统的稀疏阵列DOA 估计算法相比，在低信噪比、小快拍数和多信源数下具有更好的DOA估计性能。
［1］张燕，程先宬，陈伯孝,等.大孔径超稀疏阵列综合算法研究与应用［J］.雷达科学与技术，2020，18（4）:452-456.
［2］ZHENG Wang,ZHANG Xiaofei,LI Jianfeng,et al.Extensions of Co-Prime Array for Improved DOA Estimation with Hole Filling Strategy［J］.IEEE Sensors Journal,2021,21（5）:6724-6732.
［3］PENG Zhe,DING Yingtao,REN Shiwei,et al.Coprime Nested Arrays for DOA Estimation: Exploiting the Nesting Property of Coprime Array［J］.IEEE Signal Processing Letters,2022,29（1）:444-448.
［4］何劲，唐莽，舒汀，等.阵元位置互质的线性阵列：互耦分析和角度估计［J］.电子与信息学报，2022，44（8）：2852-2858.
［5］LIU Chunlin,VAIDYANATHAN P P.Remarks on the Spatial Smoothing Step in Coarray MUSIC［J］.IEEE Signal Processing Letters,2015,22（9）:1438-1442.
［6］ZHOU Chengwei,ZHOU Jinfang.Direction-of-Arrival Estimation with Coarray ESPRIT for Coprime Array［J］.Sensors,2017,17（8）:1779-1783.
［7］ARDAH K,HAARDT M.Compressed Sensing Constant Modulus Constrained Projection Matrix Design and High-Resolution DOA Estimation Methods［C］//25th International ITG Workshop on Smart Antennas,French Riviera,France:VDE,2021:1-5.
［8］PAIK J W,HONG W,LEE J H.Direction-of-Departure and Direction-of-Arrival Estimation Algorithm Based on Compressive Sensing: Data Fitting［J］.Remote Sensing,2020,12（17）:2773-2796.
［9］陈璐，毕大平，潘继飞.平移嵌套阵列稀疏贝叶斯学习角度估计算法［J］.电子与信息学报，2018，40（5）:1173-1180.
［10］LI Mingyang,ZHANG Chunjie.Improved Nested Array DOA Estimation Based on Sum Difference Virtual Array［C］//2023 8th International Conference on Intelligent Computing and Signal Processing,Xi’an,China:IEEE,2023:2133-2137.
［11］PATRA R K,DHAR A S.A Novel Nested Array for Real-Valued Sources Exploiting Array Motion［J］.IEEE Signal Processing Letters,2021,28（1）:1375-1379.
［12］胡斌.基于压缩感知的稀疏阵列DOA 估计关键技术研究［D］.哈尔滨:哈尔滨工业大学，2022.
［13］王书豪，阮怀林.基于加权稳健l1-SRACV 算法的宽带信号DOA估计［J］.计算机仿真，2020，37（2）:299-302.
［14］刘福来.阵列信号参数估计算法与优化［M］.北京:清华大学出版社，2021.
［15］韩树楠,李东生,雍爱霞,等.基于加权l1-SRACV算法的稀疏DOA估计［J］.现代雷达，2015，37（7）:22-25.
［16］马腾，杜江.基于加权子空间投影的改进空间平滑DOA估计算法［J］.电子设计工程，2022，30（18）:46-51.