0 引言
阵列信号处理是信号处理领域的重要组成部分，其中，方位角估计（Direction of Arrival，DOA）作为阵列信号处理中重要一环，已经广泛应用于雷达、声呐、导航、无线通信以及其他军用和民用领域［1］。均匀线性阵列（Uniform Linear Array，ULA）作为一种广泛应用于DOA 估计的天线阵列模型，具有阵列结构简单和算法成熟的特点［2］。根据奈奎斯特原理，对于一个具有P 个天线阵元，且阵元间距为波长的一半的均匀线性阵列，使用诸如MUSIC 和ESPRIT 等经典的子空间类的DOA 估计算法，能够分辨最多P-1个信号源［3］。因此，如果要估计更多的源信号，就需要更多的天线阵元，这会导致硬件成本和计算复杂度增加。此外，大量阵列的紧密排布也会导致天线耦合度上升，影响算法性能。
针对以上问题，许多学者致力于在限制天线数量的同时增加阵列自由度。一种可行方法是采用稀疏阵列［4］，如最小冗余阵列（Minimum Redundancy Array，MRA）、最小孔洞阵列（Minimum Hole Array，MHA）、嵌套阵列（Nested Array，NA）和互质阵列（Coprime Array，CA）。与均匀阵列不同，稀疏阵列通过阵列之间差分操作，虚拟出比阵元数更多的阵元，增加了稀疏阵列的自由度。这意味着使用稀疏阵列进行DOA 估计时可以分辨更多的信号源。
MRA 和MHA 对任意数量的传感器阵列并没有闭式解，通过穷举搜索获得阵列排布结构又限制了大规模使用。嵌套阵列具有完整的阵列表达式，它可以克服上述问题，通常由2 个子阵列经过系统嵌套构成，产生的差分阵列没有孔洞，在阵元总数为N 的情况下能够得到O(N2)的自由度［5］。但是嵌套阵列存在均匀线性子阵列，使得阵列耦合较高，导致测角性能下降［6］。Liu 等［7］提出了一种超级嵌套阵列（Super Nested Array，SNA），该阵列进行多层嵌套，减少了小阵元间距的阵元对，减少了阵元耦合。Yang 等［8］则通过移动首个阵元到特定位置，提出一种改进嵌套阵列（Improved Nested Array，INA），该阵列降低阵列耦合，同时也增加阵列自由度。与嵌套阵列类似，互质阵列同样具有阵列闭式解，但是阵列耦合相对较小。阵列由2个同向的均匀子阵列构成，并且共用第一个阵元。文献［9］表明，使用M+N-1 个阵元的互质阵列，可以达到O(NM)的自由度。虽然互质阵列的阵列耦合相对嵌套阵列小，但是虚拟阵列中存在大量的孔洞降低了算法的性能。因此，文献［10］提出了一种改进方法，称为增广互质阵列（Augmented CA，ACA）。将其中一个子阵列数量加倍，其余保持不变，填充了虚拟阵列孔洞，进而提升虚拟阵列中最大连续部分的数量。文献［11］则去除了ACA冗余的部分，不仅不影响最大连续部分和阵列自由度，而且减少了阵列数量。另一方面，将ACA 子阵列间进行平移和阵列间距压缩操作［12］，分别产生了压缩间距阵列（Coprime Array with Compressed Inter-element Spacing，CACIS）和移动子阵阵列（Coprime Array with Displaced Subarrays，CADiS），两种阵列产生的差分阵列连续部分和自由度均有一定程度增加。在CADiS 的基础上，通过增加两个额外的子阵列，Zheng 等［13］提出了一种新型互质阵列，称为填充差分共阵的互质阵列（Coprime Array with a Filled Difference Coarray，CAFDC）。此外，将互质阵列其中一个互质参数固定为3，同时引入两个子阵列，MA 在文献［14］中提出一种质数3 互质阵列（Coprime Array with Prime integer 3，CAP-3），由于该阵列的小阵元间距阵元对数量少，因此，阵列耦合程度较低。
上述方法的目的都是增加差分阵列最大连续部分的数量和减少阵列耦合程度，但是依旧存在大量的孔洞，因此，如何改进阵列结构，增加差分阵列最大连续部分的数量和差分阵列自由度，是一个亟待解决的问题。本文对差分阵列进行分析，提出了两种基于差分孔洞填充的互质阵列优化方法，增加了阵列最大连续部分的数量，增大了阵列的自由度、提高了DOA 的估计性能。本文的主要贡献为：优化了阵列排布结构。移动阵元到特定位置，实现阵元数不变情况下，填充原始差分阵列孔洞，增加了DOA 估计的性能；推导得到了两种物理阵列的数学表达式，虚拟阵列的最大连续部分和虚拟阵列自由度。
1 互质阵列信号模型
1.1 差分阵列分析
假设存在一个标准互质阵列，如图1所示，由2个子阵构成，其中子阵1 为均匀阵列，具有M 个阵元，阵元间距为Nd，子阵2 为均匀阵列，具有N 个阵元，阵元间距为Md。其中，N＞M，并且N 和M互质，d= λ/2 表示一个半波长，λ 为信号载波波长。由于两个子阵共用第一个子阵元，即参考阵元，并且同向分布，所以阵列阵元总数为M+N-1。该标准互质阵列可以表示为
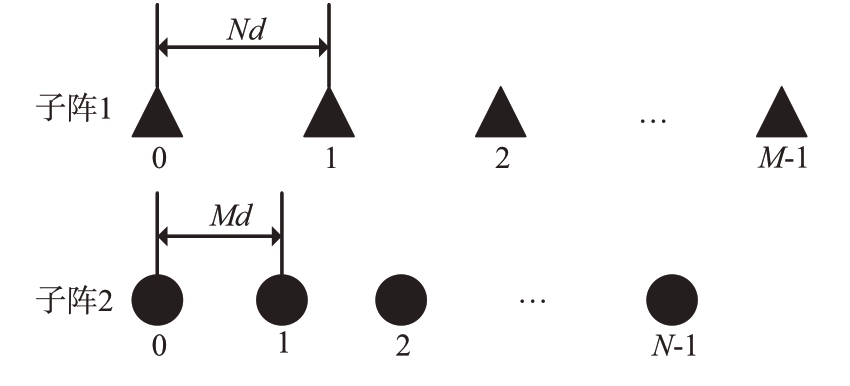
图1 标准互质阵列排布结构
忽略单位d，标准互质阵列S的差分阵列集合Ddiff可以表示为
根据式（2），Ddiff 可以表示为阵列自身产生的自差分阵列集合DS和阵列之间产生的互差分阵列集合DC：
式中：
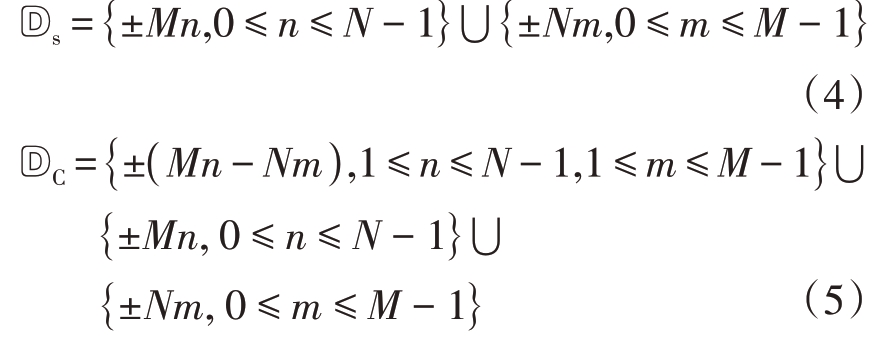
根据式（5），互差分阵列集合包括自差分阵列集合，令
表示互差分集合：
因此，差分阵列集合Ddiff可以表示为
由于集合相对于原点对称，因此可以只考虑正半轴部分，表示为
由于m 和n分别表示子阵列1和子阵列2的阵元索引，所以当m=0或n=0时，即0位置阵元，与其他阵元产生差分时，不会影响互差分集合
只有自差分集合
受到影响。
1.2 移除0阵元阵列分析
显然，移除0位置阵元使得差分阵列集合减少了4个元素，即
文献［15］表明，对于一个由M 和N 构成的标准互质阵列，当N＞2，M＞3时，移除0位置阵元产生的虚拟阵列的最大连续部分不会发生改变，只减少了虚拟阵列4 个自由度。利用该阵列进行DOA 估计时，不会影响算法性能。基于此，本文提出了两种新型的天线结构，称为移动阵元孔洞填充互质阵列（Filling Holes in Coprime Arrays with Moving Array Elements），能够有效提高算法性能和DOA估计精度。
2 孔洞填充互质阵列
2.1 提出的阵列1
假设标准互质阵列S的互质参数分别为M 和N，M＞3，N＞4，N＞M。现在将共用的0 位置阵元移动到N- M 位置上，虚线框为原始位置，如图2所示，则新的阵列S1可以表示为
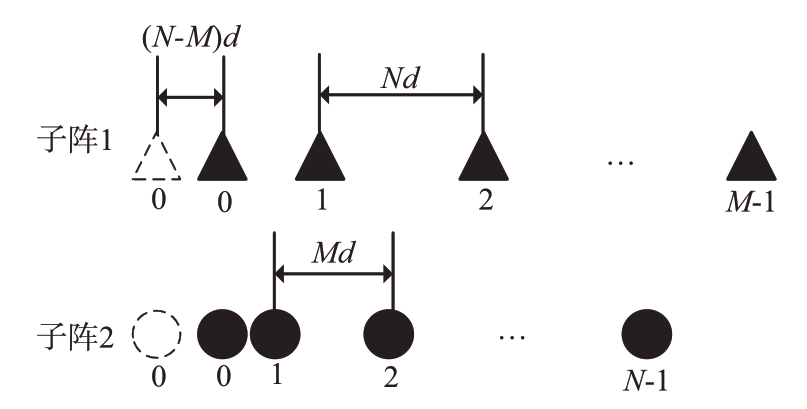
图2 提出的阵列1
文献［16］表明，标准互质阵列差分阵列最大连续部分为[-M- N+1,M+N-1]，孔洞位置集合为{±(aM+bN),a＞0,b＞0}，差分阵列集合的元素为MN+M+N-2个。因此
中的孔洞位置为
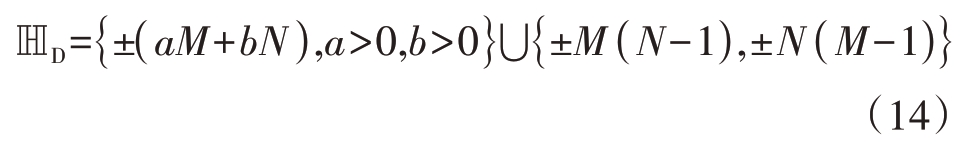
由于{±(Nm+M),0≤m≤M-2} 填充了2(M-2)个孔洞，包括{±(M+N)}位置的孔洞，但是下一对孔洞{±(2M+N)}没有出现在该集合中。
移动0 位置阵元使得差分阵列集合
减少部分元素D′，需要考虑减少的部分是否对D1 产生影响。应用反证法，假设D′存在部分元素在区间[-2M- N+1,2M+N-1] 中，因为{±(Mn- N),2≤n≤N}填充了{±N(M-1)}位置孔洞，不产生影响。
另一方面，假设满足该不等式
满足该不等式的解为
上述结果不满足条件，因此移动0阵元导致缺失的差分阵列元素不会对最大连续部分产生影响。所提出的阵列S1的差分阵列集合最大连续部分可以表示为[-2M- N+1,2M+N-1]。所提出的阵列S1一共填充2(M-1) 个孔洞。差分阵列集合的自由度为MN+3M+N-8，相对于标准互质阵列增加了2(M-3)的自由度。
2.2 提出的阵列2
假设标准互质阵列S的互质参数分别为M 和N，M＞3，kM ＜N ＜(k+1) M，k为任意正整数。现在将共用的0 位置阵元移动到M- N 位置上，虚线框为原始位置，如图3 所示，则新的阵列S2 可以表示为
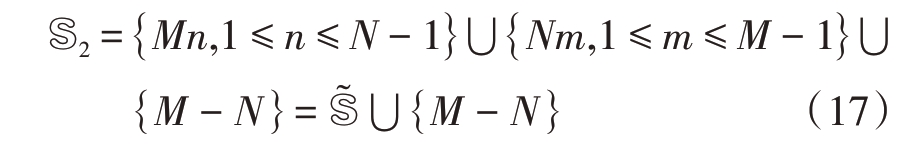
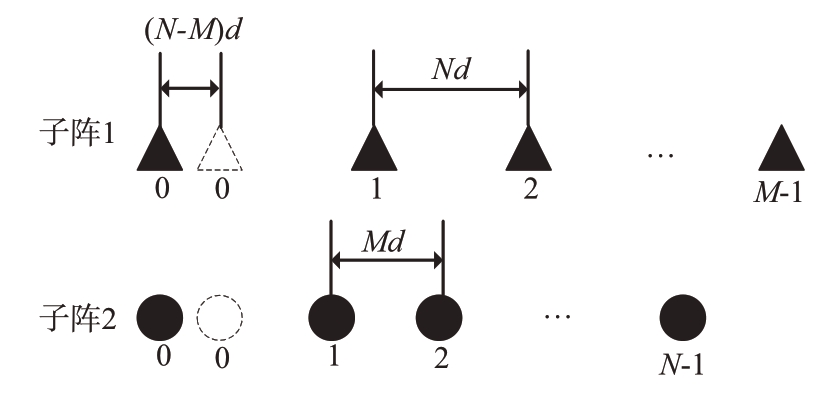
图3 提出的阵列2
同理，需要考虑减少的部分元素D′是否对D2产生影响。应用反证法，假设D′存在部分元素在区间[-2M- N+1,2M+N-1]中，因为{±(Nm- M),2≤m≤M}填充了{±M(N-1)}位置的孔洞，不产生影响。
另一方面，假设满足不等式
满足该不等式的解为
上述结果均与已知条件矛盾，因此移动0阵元缺失的差分元素不会对新阵列最大连续部分产生影响。所提出的阵列S2的差分阵列集合最大连续部分可以表示为[-2M- N+1,2M+N-1]。所提出的阵列S2一共填充2(N-1) 个孔洞。差分阵列集合的自由度为MN+M+3N-8，相对于标准互质阵列增加了2(N-3)的自由度。
3 阵列模型和互耦模型
3.1 DOA估计模型
假设有K 个窄带远场不相干信号源入射到提出的移动阵元孔洞填充互质阵列，阵元排布集合表示为L={did,1≤i≤P}，P 为阵元个数，di 为第i个天线到参考点的距离，d 为单位阵元间距。信源方向设置为θ={θk,k=1,2,…,K}，则t 时刻阵列接收的回波信号为
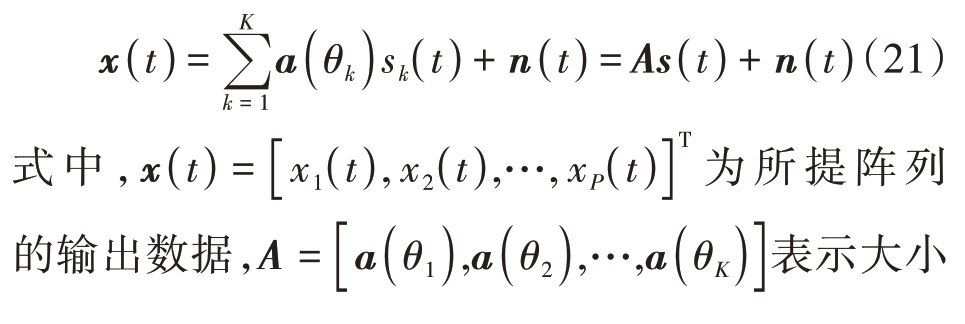
实际情况下，接收数据矩阵是有限长的，即快拍数有限，无法计算数学期望获取理想协方差矩阵，通常采用采样协方差矩阵近似替代：
3.2 阵列耦合模型
对于实际的阵列，每个阵元受到其邻近阵元的影响，降低了天线阵列的性能，称为互耦效应［18］。本文采用基于Toeplitz性质的B带互耦模型进行分析，根据文献［19］可以使用耦合泄漏量L来量化耦合效应带来的影响，L 是阵列元素之间相互耦合矩阵C 的函数。该模型下的互耦矩阵C 可以表示为
耦合泄漏量L可以表示为
4 仿真处理与分析
为了验证所提出阵列的性能，利用MATLAB进行实验仿真分析。本文采用标准互质阵列、提出的阵列1、提出的阵列2 和文献［20］的重构互质阵列（Redesigned CLA）进行算法性能分析。所比较的阵列互质参数M=4，N=7，总的阵元数都为10个。
4.1 天线阵列排布、阵列耦合和天线方向图
图4 显示了上述不同阵列的物理阵列对应的虚拟阵列排布，并根据式（26）计算耦合泄漏量，整理如表1所示。
表1 4种不同天线阵列属性
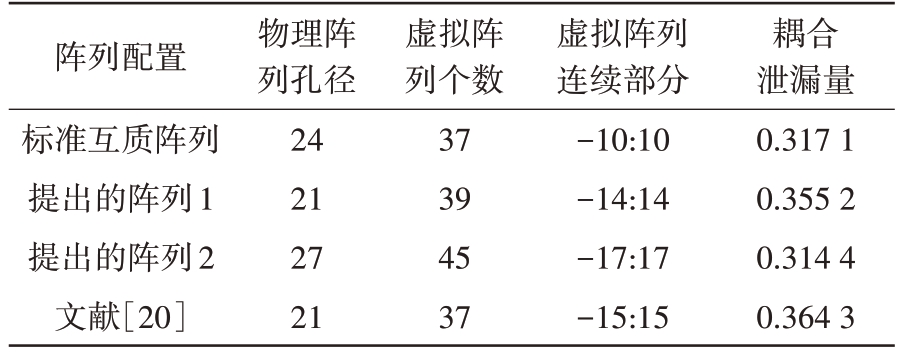
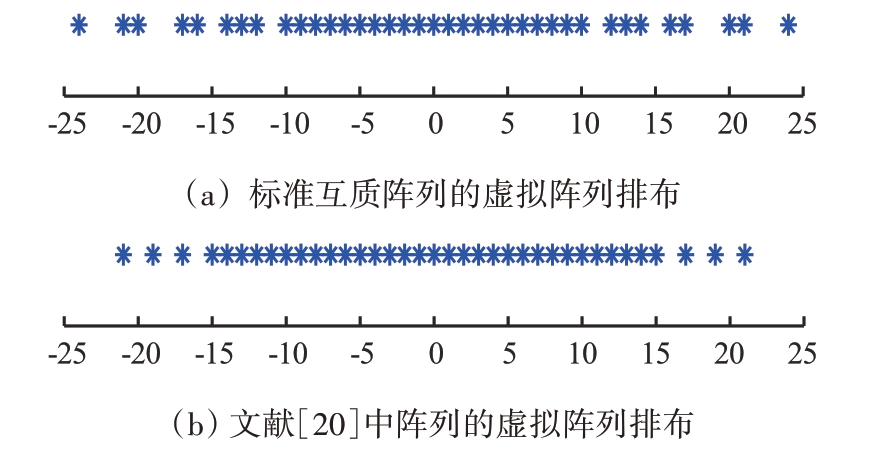
图4 4种阵列的虚拟阵列排布
根据表1的结果，我们可以明显观察到提出的阵列1和阵列2的连续部分个数分别为29和35，而标准互质阵列和文献［20］中的阵列则分别包含21和31 个连续部分。图4 中提出的阵列1 填充了第一个孔洞，提出的阵列2填充了第一个和第二个孔洞。在虚拟阵列数量方面，阵列1 和阵列2 分别具有39 和45 个虚拟阵元，明显优于标准互质阵列和文献［20］中的阵列，它们只包含37个虚拟阵元，增加的数量均符合上述的理论推导。
此外，提出的阵列1 和阵列2 的耦合泄漏量分别为L1=0.355 2 和L2=0.314 4，而标准互质阵列的耦合泄漏量为L3=0.317 1。这表明阵列1 的耦合泄漏量稍高于标准互质阵列，而阵列2的耦合泄漏量明显更低。这个差异是因为阵列2 中的0 位置天线移动到负半轴，导致了相对较大的天线距离，而另一个移动到正半轴，导致了较小的天线距离。相比之下，文献［20］中的阵列具有更高的耦合泄漏量L4=0.355 2，表明其耦合效应较强。综上所述，阵列1 和阵列2 具有更多的连续部分和自由度，同时具有较低的耦合效应，从而提高了目标分辨性。
4.2 不同阵列的DOA估计性能
设定仿真的信号源为9个，来波方向在［-40°，40°］均匀分布，源信号与噪声互不相关。信噪比（SNR）设置为0 dB，快拍数（snap）设置为1 000。图5显示了4种不同阵列的DOA 估计性能，根据图中的数据，明显可见提出的阵列在估计信号角度信息方面表现出色，能够实现高度精确的DOA 估计。相比之下，标准互质阵列在角度估计时误差较大，并且存在虚峰响应的问题，因此无法正确获取DOA 角度信息。文献［20］中的阵列性能介于两种提出的阵列之间，而在提出的两种阵列中，阵列2 相对于其他阵列来说，其谱峰更为尖锐，因此表现更为出色。
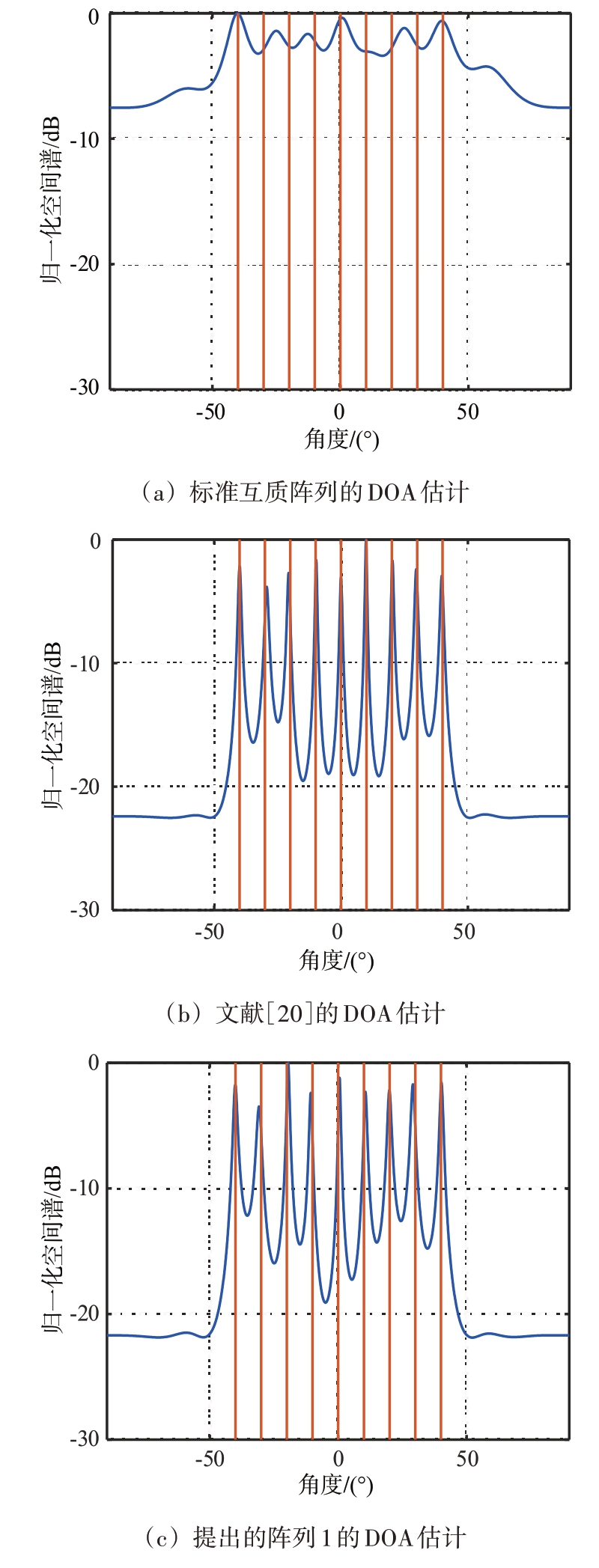
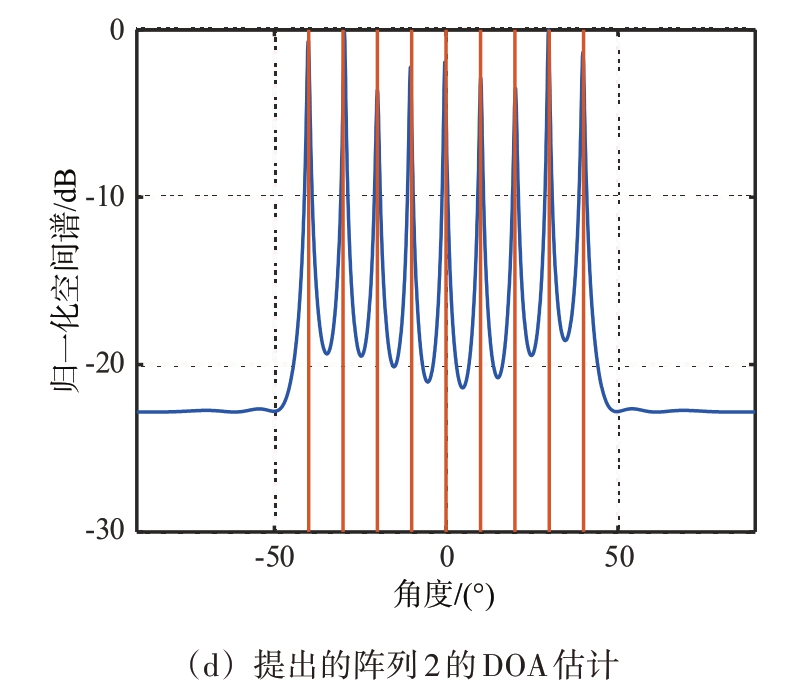
图5 4种阵列的DOA估计结果
4.3 蒙特卡洛条件下的DOA估计性能
为了验证所提出阵列的估计精度，本文分别从信噪比和快拍数两个方面进行蒙特卡洛仿真。定义角度均方根误差（RMSE）如下：
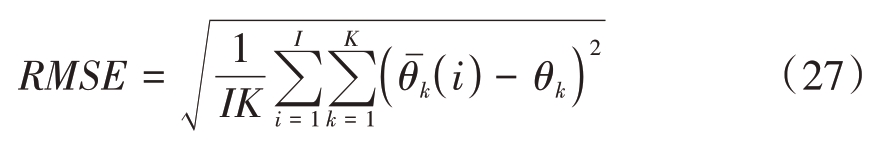
式中：I=1 000表示蒙特卡洛次数，K=9表示信源个数，来波方向在[-60°,60°] 均匀分布
表示第i 次蒙特卡洛仿真时，第k 个信号源的DOA 估计值，θk 表示对应的DOA 理论值。在信噪比SNR=5 dB，快拍数从200到1 000变化，步进为50的条件下和在快拍数为1 000，信噪比从-5 dB 到20 dB 变化，步进为1的条件下，分别进行1 000次蒙特卡洛仿真，实验结果如图6和图7所示。
图6 4种阵列RMSE随快拍数变化情况
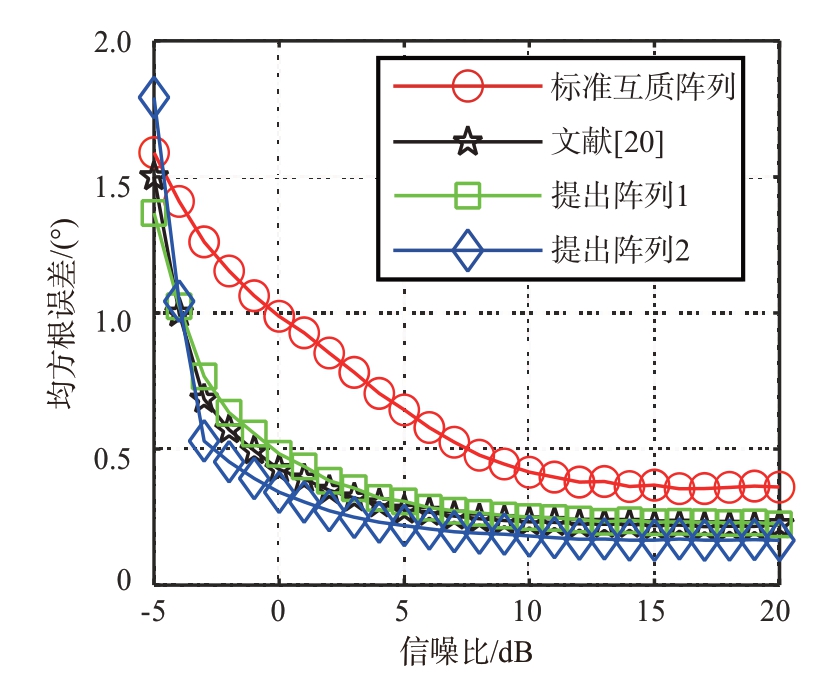
图7 4种阵列RMSE随信噪比变化情况
图6 表明，随着快拍数的增加，采样协方差矩阵更加接近真实协方差矩阵，我们可以观察到4种阵列得到的均方根误差都逐渐减小，从而提高了估计的精确度。图7则表明，均方根误差随着信噪比的增加而降低，其原因是协方差矩阵噪声分量随着信噪比增加而降低，从而提高了算法的性能。另一方面，由于文献［20］中阵列连续部分数量介于提出的阵列1 和阵列2 之间，这也反映在均方根误差上，即在图6 和图7 中，文献［20］中的阵列性能略优于提出的阵列1，但不及提出的阵列2。此外，提出的阵列1 和阵列2 的均方根误差都比标准互质阵列的误差小，这个现象可以解释为移动阵元导致了虚拟阵列的连续部分增加，从而提高了可以估计的信源数量，进而提升了算法的性能。而阵列2 相比阵列1 增加的连续部分更多，因此性能更加好。
5 结束语
本文通过分析互质阵列的虚拟阵列排布，从减少虚拟阵列孔洞的角度出发，提出了两种稀疏互质阵列优化方法。首先，本文对标准互质阵列进行分析，证明了标准互质阵列中移除0位置阵元不会对虚拟阵列的中间连续部分产生影响。然后，本文将0位置阵元分别移动到正半轴和负半轴互质数差分的位置，从而创造了一种全新的阵列结构。这些新阵列的虚拟排列填补了互质阵列中的部分孔洞，增加了虚拟排列中连续部分的数量，进而提高可分辨信源的数量以及DOA 估计的性能。最后通过多个角度的仿真验证了所提出的阵列相较于已有阵列的优越性能。下一步的研究中，需要在更复杂的稀疏阵列类型中推广应用这种算法。
［1］刘佳宁，司伟建.基于互质阵列的信号波达方向估计算法［J］.航空兵器，2023，30（2）:131-136.
［2］盘敏容，蒋留兵，车俐，等.基于协方差矩阵重构的互质阵列DOA估计［J］.雷达科学与技术，2020，18（1）:1-6.
［3］ZHANG Fei,ZHANG Zijing,JIN Aisuo,et al.2-D DOA Estimation Method Based on Coprime Array MIMO Radar［J］.EURASIP Journal on Advances in Signal Processing,2021（1）:1-18.
［4］张宇乐，胡国平，周豪，等.自由度和互耦联合优化的三阶嵌套阵［J］.信号处理，2021，37（2）:234-241.
［5］曾耀平，刘洋.基于移位内插互质阵列高分辨DOA 估计［J］.传感器与微系统，2022，41（1）:24-27.
［6］SUN Lu.Improved Coprime Array Designs Based on Moving Platform for Direction of Arrival Estimation［J］.IEEE Sensors Journal,2023,23（5）:5288-5298.
［7］LIU Chunlin,VAIDYANATHAN P P.Super Nested Arrays:Linear Sparse Arrays with Reduced Mutual Coupling-Part II: High-Order Extensions［J］.IEEE Trans on Signal Processing,2016,64（16）:4203-4217.
［8］YANG Minglei,SUN Lei,YUAN Xin,et al.Improved Nested Array with Hole-Free DCA and More Degrees of Freedom［J］.Electronics Letters,2016,52（25）:2068-2070.
［9］LIU Shengheng,MAO Zihuan,ZHANG Yimin,et al.Rank Minimization-Based Toeplitz Reconstruction for DOA Estimation Using Coprime Array［J］.IEEE Communications Letters,2021,25（7）:2265-2269.
［10］VAIDYANATHAN P P,PAL P.Sparse Sensing with Co-Prime Samplers and Arrays［J］.IEEE Trans on Signal Processing,2011,59（2）:573-586.
［11］RAZA A,LIU Wei,SHEN Qing.Thinned Coprime Array for Second-Order Difference Co-Array Generation with Reduced Mutual Coupling［J］.IEEE Trans on Signal Processing,2019,67（8）:2052-2065.
［12］QIN Si,ZHANG Yimin,AMIN Moeness G.Generalized Coprime Array Configurations for Direction-of-Arrival Estimation［J］.IEEE Trans on Signal Processing,2015,63（6）:1377-1390.
［13］ZHENG Wang,ZHANG Xiaofei,LI Jianfeng,et al.Extensions of Co-Prime Array for Improved DOA Estimation with Hole Filling Strategy［J］.IEEE Sensors Journal,2021,21（5）:6724-6732.
［14］MA Penghui,LI Jianfeng,ZHAO Gaofeng,et al.CAP-3 Coprime Array for DOA Estimation with Enhanced Uniform Degrees of Freedom and Reduced Mutual Coupling［J］.IEEE Communications Letters,2021,25（6）:1872-1875.
［15］刘可，朱泽政，于军，等.基于互质阵列孔洞分析的稀疏阵列设计方法［J］.电子与信息学报，2022，44（1）：372-379.
［16］WANG Xiaomeng,WANG Xin,LIN Xuehong.Co-Prime Array Processing with Sum and Difference Co-Arrays［C］// 49th Asilomar Conference on Signals,Systems and Computers,Pacific Grove,CA,USA: IEEE,2015:380-384.
［17］蓝东平.稀疏阵列波达方向估计算法研究［D］.哈尔滨:哈尔滨工业大学，2022.
［18］罗雪.基于未知互耦模型的波达方向估计［J］.北京理工大学学报，2021，41（12）:1286-1292.
［19］LIU Jianyan,ZHANG Yanmei,LU Yilong,et al.Augmented Nested Arrays with Enhanced DOF and Reduced Mutual Coupling［J］.IEEE Trans on Signal Processing,2017,65（21）:5549-5563.
［20］ YANG Xiao,WANG Yide,CHARGE P.Improved Coprime Linear Array Configuration for Moving Platform in DOA Estimation［J］.IEEE Communications Letters,2021,25（2）:470-473.