0 引言
二相码信号是雷达系统中广为采用的脉冲压缩信号[1],其优点是测距分辨率高,缺点是对多普勒频移敏感。因高速目标产生的高动态大偏差的多普勒频移,导致脉冲压缩体制雷达的脉冲压缩峰值降低。在航天测控系统中由于地面接收机与航天器之间相对高速运动引起的多普勒频移,带来载波频率捕获及跟踪同步难题,较大的多普勒频移导致扩频接收机无法完成解扩。这些问题的核心是如何准确估计载波频率[2-8],当前解决该问题的方法有频率扫描捕获及锁相环跟踪结合法[9-14]、最大似然估计法[15]以及自适应最小二乘法[16],这些方法需要预先补偿或搜索载波频率,其缺点有:搜索时间长,需要多个发射周期达成载波频率的捕获;处理方法复杂且占用硬件资源多,为了换取搜索时间的缩短。
本文提出自适应多普勒频移的二相码信号处理方法,不需要预先补偿或搜索载波频率,不需要估计载波频率,不采用鉴频器的方式,不需要采用锁相环执行载波频率捕获及跟踪,可以自适应二相码信号的多普勒频移大偏差高动态变化,在每个发射周期、在单脉冲的脉内,实时去除多普勒频移,恢复基带信号,进行脉冲压缩,其处理方法简捷新颖、计算量小、处理延时低、实时性好、搜索时间短、占用硬件资源少。该方法能在高动态大偏差多普勒频移场景中实现脉冲压缩雷达的脉冲压缩,以及航天测控通信接收机的解扩,广泛应用于导航、遥控、跟踪等技术领域。
1 信号模型
脉冲雷达发射的载波射频信号为二相码调制信号,其归一化的数学形式为
式中:f0为载波频率;t为时间;θ表示二进制相位调制,θ 取值0 或π,当θ=0 则ST(t)是正数,当θ=π 则ST(t)是负数,分别代表基带信号0、1。
雷达接收到的信号的数学形式为
式中:fΔ 为多普勒频移,其值可正可负;φ 为接收信号与发射信号之间的初相差。
把接收的信号下变频降为中频信号,中频信号的数学形式为
式中,fI 为中频信号频率。可见,多普勒频移fΔ 对基带信号实施了频率调制,收发信号之间的相位差为2π fΔt+φ,相位差2π fΔt+φ 处于0~2π 内,在4 个象限(①象限、②象限、③象限、④象限)其一,若相位差2π fΔt+φ 处于①象限,S(It)的符号位等于ST(t)的符号位,基带信号能正确恢复;多普勒频移等因素导致相位差随时间不断变化,当相位差处于其他象限,S(It)的符号位不一定等于ST(t)的符号位,码元被反相,基带信号恢复出错。
2 自适应多普勒频移的二相码信号处理方法
自适应多普勒频移的二相码处理方法的技术原理及实现步骤如下:
1)实时检测并提取多普勒频移的同相信号波形及多普勒频移的正交信号波形。
将二相码射频信号降至中频,A/D 采样正交变换生成一对信号I、Q:I 路信号I=sin(x+θ),Q路信号Q=cos(x+θ)。其中,θ 是调相信息,x 是收发信号之间的相位差,x=2π fΔt+φ,x 处于0~2π 4 个象限其一,而x 的频率值是多普勒频移。

2)实时四路并行计算,得到4个片段信号。
因为,将同相信号sin x 及正交信号cos x 进行四路并行运算,如下:I+Q=sin x+cos x=sin(x+0.25π),记为片段信号F1,等同于将sin x移相0.25π;I- Q=sin x-cos x=sin(x-0.25π),记为片段信号F2,等同于将sin x 移相-0.25π;-I-Q=-sin x-cos x=sin(x-0.75π),记为片段信号F3,等同于将sin x 移相-0.75π;Q- I=cos x-sin x=sin(x-1.25π),记为片段信号F4,等同于将sin x移相-1.25π。
片段信号F1、F2、F3、F4 依次间隔0.5π,片段信号F1、F2、F3、F4的单个周期波形图如图1所示。
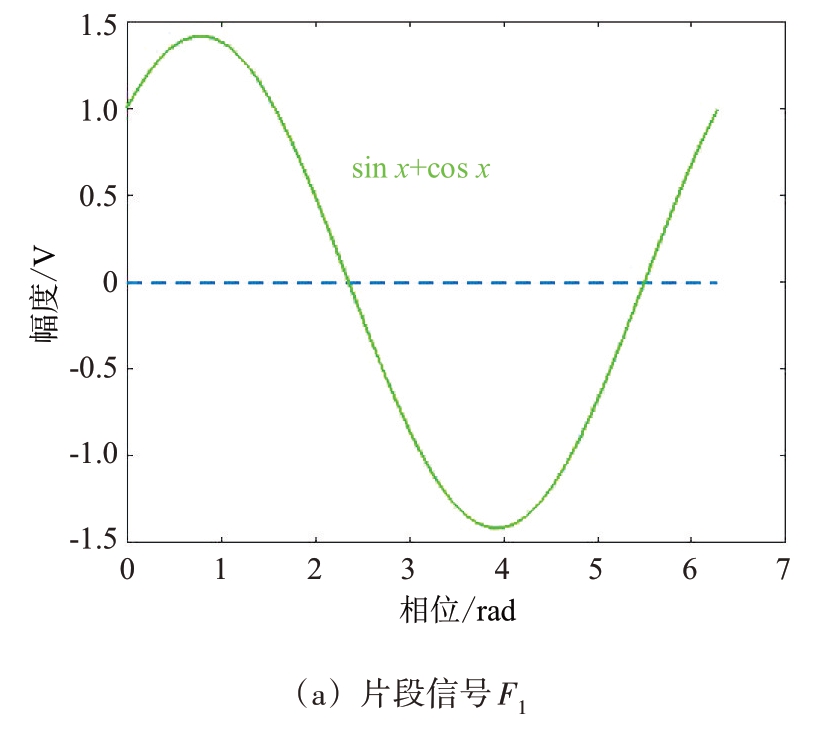
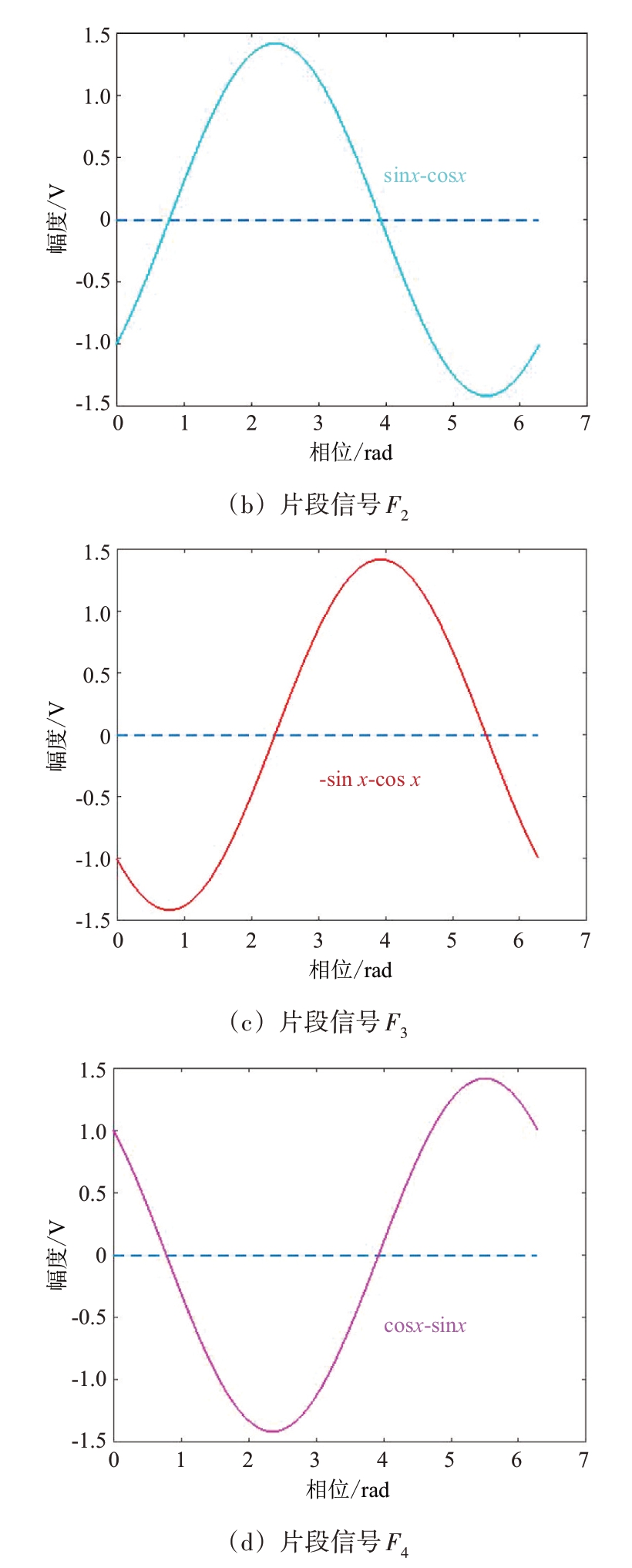
图1 片段信号F1、F2、F3、F4的单个周期波形图
因为基带信号的相位被多普勒频移波形进行了调制,即基带信号的相位在多普勒频移处于③象限、④象限里被翻转反相。在第i 个象限里,i=1~4,第i 个片段信号的波峰(范围0.5π)与二相码的基带信号同相,4 个片段信号覆盖了多普勒频移的4个象限,某一片段信号的波峰始终保持与基带信号同相,4 个片段信号与同相信号sin x、正交信号cos x的相位关系图如图2所示。
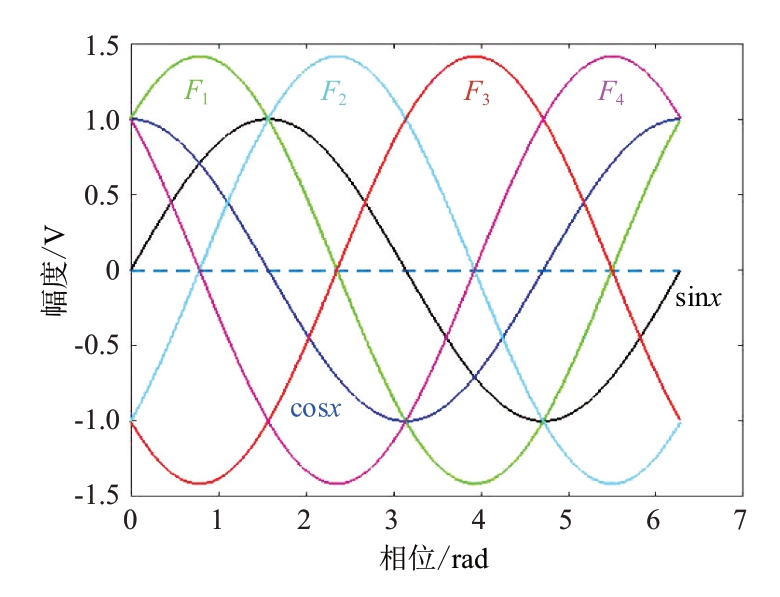
图2 4个片段信号与同相信号sin x和正交信号cos x的相位关系图
3)根据对应关系,预先设置一个查找表。
根据同相信号波形及正交信号波形的极性(正负值),可得知相位差x 处于的象限序号,相位差、象限序号、片段信号、基带信号之间有对应的相位关系如下:当相位差在①象限时,片段信号F1的波峰与基带信号同相;当相位差在②象限时,片段信号F2 的波峰与基带信号同相;当相位差在③象限时,片段信号F3的波峰与基带信号同相;当相位差在④象限时,片段信号F4 的波峰与基带信号同相。相位差x 处于的象限序号、片段信号、同相信号、正交信号的对应关系如图3所示。
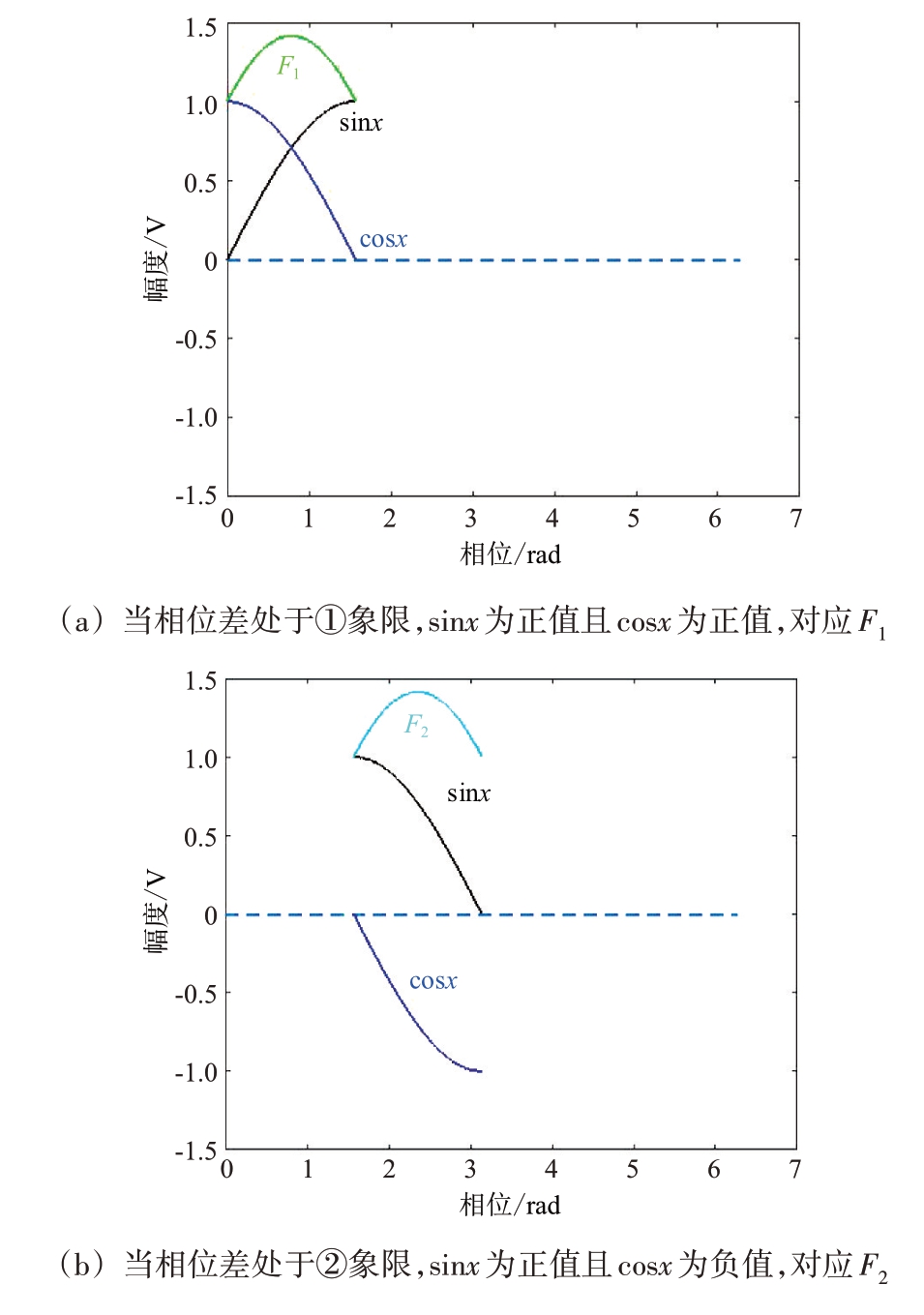
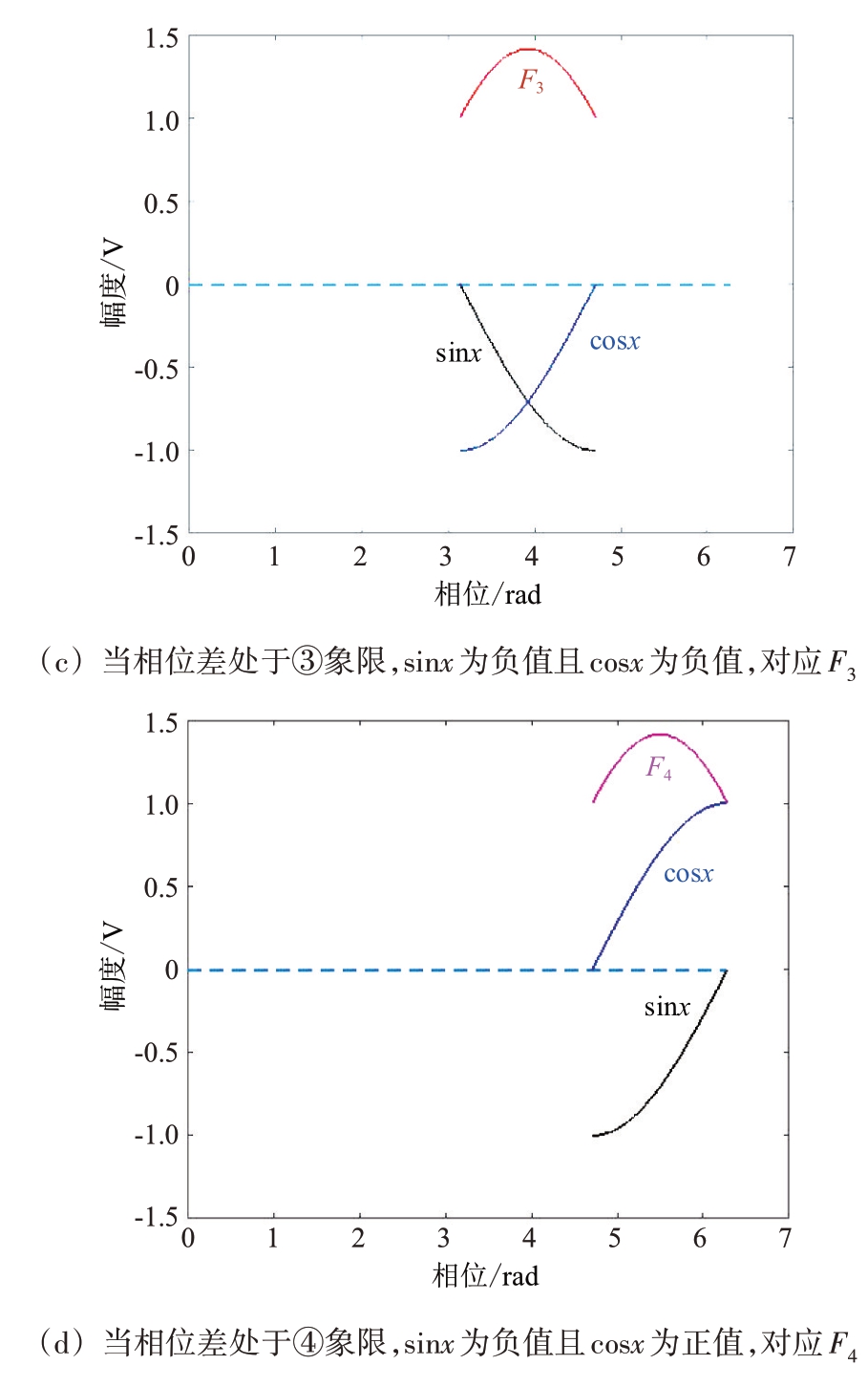
图3 相位差x处于的象限序号与正弦信号、余弦信号及片段信号的对应关系图
象限序号、同相信号、正交信号、片段信号及基带信号之间存在对应关系,如表1所示。
表1 象限序号、同相信号、正交信号、片段信号及基带信号的关系表

4 个象限、多普勒频移的同相信号及正交信号的极性、4 个片段信号,与基带信号之间存在固定的时序对应关系,据此预先设置一个查找表。
4)以查找表映射的方式,拼接恢复二相码的基带信号。
以查找表映射的方式,按时序从4个片段信号里选择其一,该片段信号始终与基带信号同相,将各片段信号串行拼接而成连续完整的二相码基带信号。选择片段信号F1~F4 拼接基带信号如图4所示。恢复基带信号实现原理如图5所示。
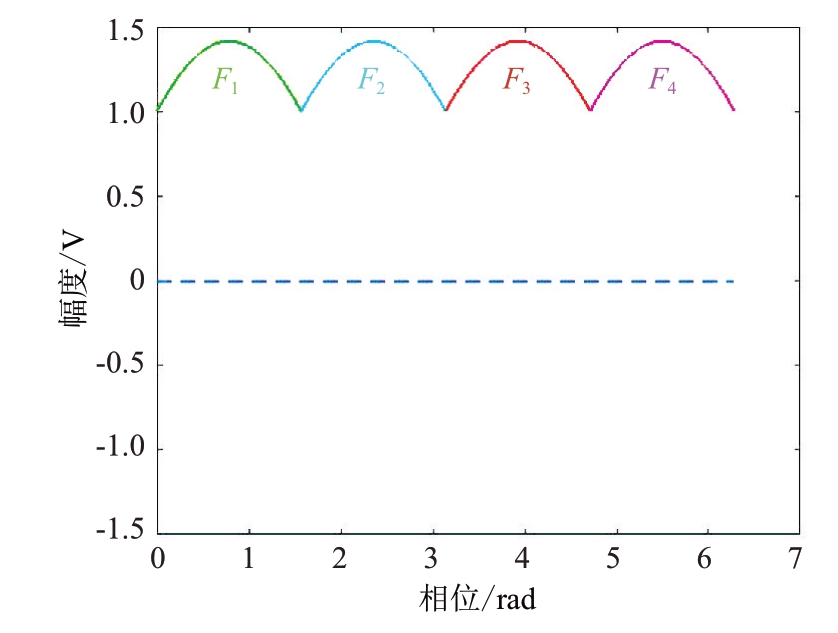
图4 选择片段信号F1~F4拼接基带信号图
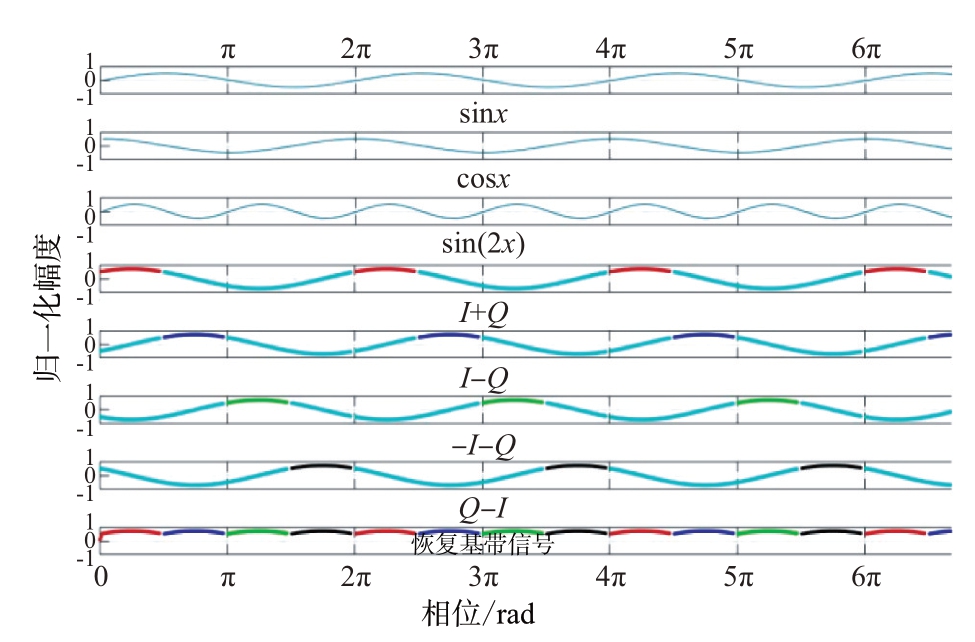
图5 恢复基带信号实现原理图
3 仿真验证
3.1 常规方法无多普勒频移的脉冲压缩
设雷达发射波长为0.03 m,二相码的码元宽度为1 μs,采用码长127 bit 的m 序列伪随机码,4 个目标的距离分别位于30,60,90,120 km。当4个目标静止,无多普勒频移,4 个目标分别得到各自的脉冲压缩峰,共计4 个。常规方法无多普勒频移4个目标脉压如图6所示。
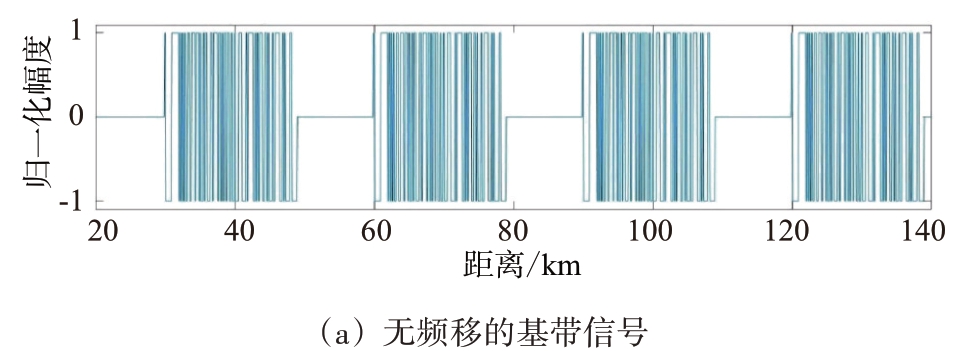
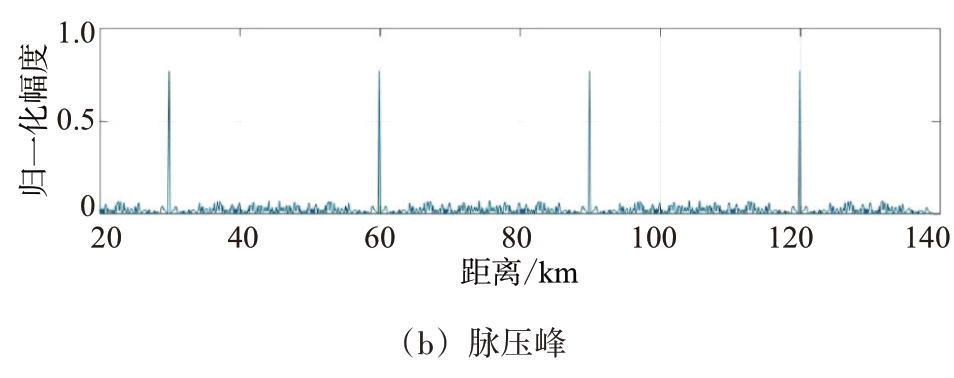
图6 常规方法无多普勒频移4个目标脉压处理图
3.2 常规方法有多普勒频移的脉冲压缩
当4 个目标的速度分别是30,300,600 和900 m/s,产生了多普勒频移。采用常规方法进行4 个目标脉冲压缩,常规方法有多普勒频移4 个目标脉压如图7 所示。目标1 的速度较慢,其多普勒频移较小,基带信号没有发生码元的翻转反相,目标1 得到1 个脉冲压缩峰,红色波形示意码元同相。目标2、目标3、目标4 的速度越来越大,多普勒频移也相应变大,超过多普勒容限,导致基带信号的码元翻转反相,3 个目标均没有得到脉冲压缩峰则脉压失败,蓝色波形示意码元反相。
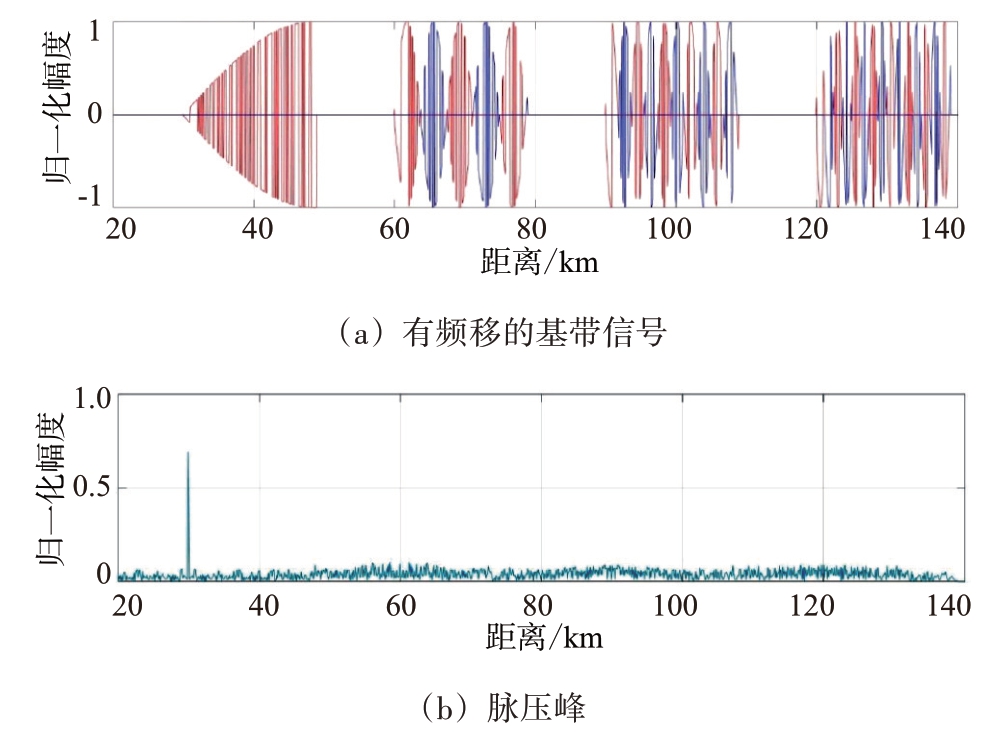
图7 常规方法有多普勒频移4个目标脉压处理图
3.3 新方法有多普勒频移的脉冲压缩
自适应多普勒频移的二相码信号处理过程如图8所示。图8(a)为信号I,因为存在多普勒频移,导致高速的目标2、目标3、目标4的基带信号码元发生翻转反相,低速目标1的基带信号码元没有反相。图8(b)~8(e)为四路并行运算得到4个片段信号。图8(f)~8(h)为多普勒频移同相信号、正交信号、二倍频信号。图8(i)拼接恢复了4个目标的基带信号。

图8 自适应多普勒频移的二相码信号处理过程
采用自适应多普勒频移的二相码信号处理方法,去除了多普勒频移,恢复了基带信号,在4个目标距离位置分别出现脉冲压缩峰,共计4个,与预期一致。新方法有多普勒频移的脉冲压缩如图9所示。
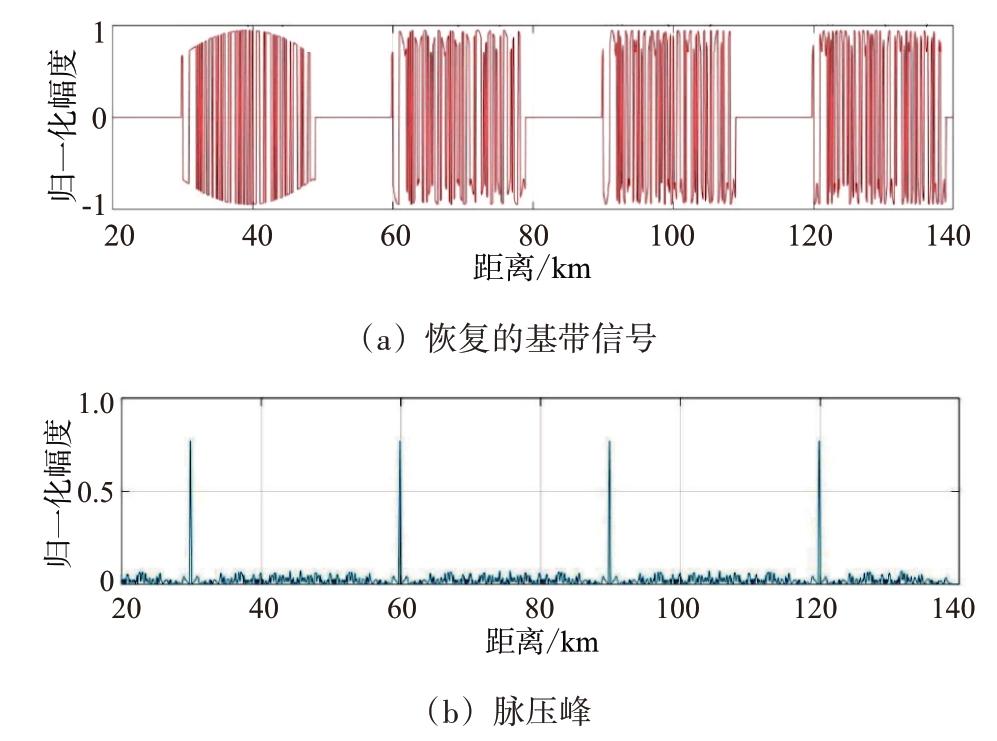
图9 新方法有多普勒频移4个目标脉压处理图
4 结束语
在国内外公开的文献中,二相信号的多普勒容限为90°,二相信号仅用于探测慢速或速度基本已知的运动目标,本文所述的自适应多普勒频移的二相码信号处理方法,突破了二相信号的技术局限,多普勒容限为360°,即无多普勒容限限制,克服了二进制调相信号“多普勒敏感性”缺陷,可实时去除多普勒频移对基带信号的乘性调制,自适应收发频率的高动态、大偏差、快变化,在频率维度快速搜索、捕获及跟踪,不需要预先速度补偿,不需要载波频率搜索,能实时捕获、实时跟踪,从而实现高速目标的快速探测,适用探测静止、慢速及高速,尤其超高速目标。该方法解决了在高动态大频偏场景,脉冲压缩雷达的脉压处理、扩频接收机的解扩处理、实时性较差等技术问题。仿真实验及工程应用表明,该方法计算量小、实时性好、硬件资源少,具有可行性和有效性,能很好解决相关信号处理的工程技术问题。
[1]徐景明,朱灿焰.一种复合调制信号的脉冲压缩及DSP实现[J].雷达科学与技术,2010,8(5):448-451.
[2]马晓岩.现代雷达信号处理[M].北京:国防工业出版社,2012.
[3]张艳艳.雷达相位编码信号的研究和应用[D].西安:西安电子科技大学,2009.
[4]SKOLNIK M I.雷达手册[M].北京:电子工业出版社,2010.
[5]朱晓华.雷达信号分析与处理[M].北京:国防工业出版社,2011.
[6]关键,裴家正,黄勇,等.杂波背景下的时距联合检测前聚焦方法研究[J].雷达学报,2022,11(5):753-764.
[7]周成,马丛珊,应涛,等.存在载频误差下的多普勒频移定位算法[J].电子科技大学学报,2022,51(4):529-534.
[8]裴家正,黄勇,陈宝欣,等.基于线性约束最小方差原则的稳健快速自适应脉冲压缩方法[J].系统工程与电子技术,2022,44(12):3621-3630.
[9]马罗文,刘宁,胡心语,等.FFT 幅相联合的快速高精度频率估计方法[J].计测技术,2022,42(6):34-39.
[10]王博业,耿虎军,王西夺,等.基于并行架构的宽带扩频信号捕获技术研究[J].计算机测量与控制,2023,31(2):284-289.
[11]马瑞,耿虎军,王西夺,等.基于多普勒变化率估计的载波跟踪算法[J].计算机测量与控制,2023,31(3):262-267.
[12]孙后印,贾方秀.大多普勒环境下扩频信号快速捕获算法研究[J].测试技术学报,2023,37(3):271-276.
[13]孙婷.面向高速移动通信系统的载波同步技术[J].信息技术,2021(1):142-146.
[14]方竹,张天骐,汪锐,等.高动态环境二进制偏移载波调制信号的捕获[J].信号处理,2022,38(10):2164-2172.
[15]郇浩,陶选如,陶然,等.多普勒频率变化率快速最大似然估计辅助的高动态载波跟踪环路[J].电子与信息学报,2014,36(3):577-582.
[16]KUMAR R.Differential Sampling for Fast Frequency Acquisition via Adaptive Extended Least Squares Algorithm[C]//International Telemetering Conference Proceedings,San Diego,CA,USA:International Foundation for Telemetering,1987:134-138.