0 引 言
二维稀疏阵列在信号处理领域具有广泛的应用，尤其在到达角估计（Direction of Arrival, DOA）中尤为重要。其广泛用于雷达系统［1-2］、声源估计［3］和多天线无线通信系统［4］等领域。稀疏阵相较于均匀阵能减少所需阵元，降低系统成本，提供更大的虚拟孔径，实现精确DOA 估计［5-7］。目前二维DOA 估计主要集中于特定结构中，如L 形阵列［8-9］和双平行阵列［10-11］，最小冗余阵列［12］等。L型阵列和双平行阵列虽减少阵元使用，但不适用于任意稀疏面阵，且会引起“角度兼并”。二维平面阵提高两个维度的角度分辨率，减少测量盲区，适用于复杂环境［13］。因此针对任意稀疏面阵精确估计方位角和俯仰角十分重要。
过去的几十年里，DOA 估计被广泛应用并学习，多重信号分类（Multiple Signal Classification,MUSIC）算法［14］、旋转不变技术（Estimation of Signal Parameters via Rotational Invariance Techniques,ESPRIT）算法［15］、二维离散傅里叶变换方法［16］等都可以实现二维DOA 估计。随着压缩感知（Compressive Sensing, CS）技术的兴起，信号稀疏性求解DOA 逐渐广泛。算法［17-19］依赖于ℓ1 范数正则化模型，针对网格结构划分角度间隔。由于更加密集的网格划分会违反受限等距特性［20］。因此基于无网格的原子范数算法被提出，文献［21］用于解决单快拍稀疏MIMO 阵列的角度估计。文献［22］在此基础上提出了多测量矢量联合稀疏的概念，利用二维范数求解。
矩阵填充［23-24］（Matrix Completion, MC）是压缩感知在高维度上的一个推广，矩阵填充在阵列设计中采用稀疏位置布局，有助于在实际应用中实现更灵活的阵列几何结构。传统的矩阵填充算法包括基于核范数最小化的奇异值阈值算法［25］、加速近端梯度下降算法［26］、交替迭代乘子法［27］、迭代最小二乘、拉格朗日乘子法［28］等。文献［29］利用核范数和平滑裁剪绝对偏差惩罚求解阵元故障的MIMO 雷达角度估计，文献［30］和［31］利用基于矩阵填充的ESPRIT 技术实现稀疏平面阵角度估计。上述算法虽能合理地实现角度估计，但是对大型稀疏平面模型，阵元分布复杂，计算缓慢，精度易受噪声影响。
受文献［32］利用截断核范数的启发，针对稀疏面阵计算复杂，对噪声敏感、角度估计困难的问题，本文提出了一种多快拍阵列信号角度估计算法（PM operator based on Truncated nuclear and Lpnorm, TP-PM），以截断核范数和ℓp 范数为函数模型，通过子阵划分利用基于最小二乘的PM 算法进行角度估计。通过截断核范数模型降低较小的奇异值贡献来减少噪声对信号恢复的影响，利用ℓp范数优化信号稀疏性。算法采取了迭代双步策略分解出独立的问题项，进而通过ADMM 算法对问题项分离成子问题求解，减少计算复杂度，适用于大规模面阵信号的处理。划分子阵并引入基于噪声的PM 传播算子模型，提取并优化计算的二维角度信息，提高了角度估计的准确性和效率。
1 稀疏面阵理论
1.1 稀疏面阵信号构造
构造均匀平面阵，阵列有N 行M 列，阵元间隔为d，目标的俯仰角和方位角分别为θi 和φi。θi 表示第i 个信号的俯仰角，φi表示第i 个信号的方位角。设空间中有K 个独立的窄带信号源si（t）, t=1,…,K 入射，快拍数为C。X 轴上N 个阵元的信号模型可以表示为
式中:Ax 为阵列流形矩阵，
,…,
，Ax=［ax（u1）,ax（u2）,…,ax（uk）］；s（t）为信号源矩阵，uk = sin θk cos φk, k = 1,…, K，nx（t）为独立的高斯白噪声，C 为快拍数。同理Y 轴的M 个阵元信号模型可以表示为
发现沿Y 轴平移的X 轴上的阵元满足以下关系:
其中，vk = sin θk sin φk
则沿X轴的阵面接收信号可以表示为
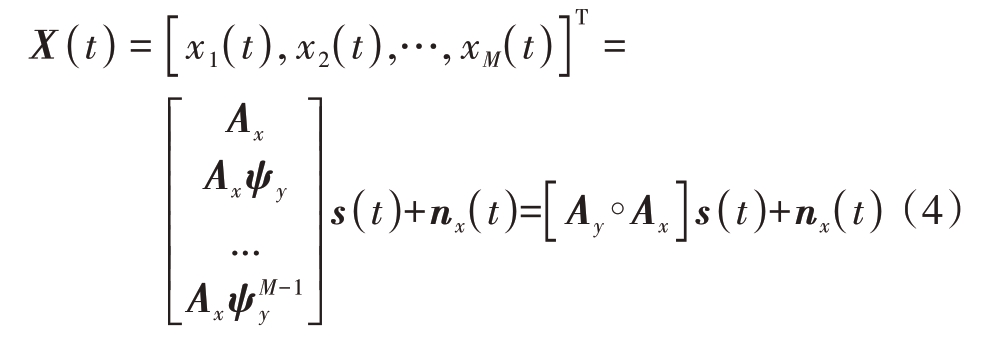
式中[Ay ∘Ax]表示Ay和Ax的Khatri-Rao 乘积。已知均匀阵列的接收信号模型，随机选取阵元，稀疏信号的接收矢量XS(t)中部分元素为0，协方差矩阵会出现行为0 或列为0 的情况，式（5）给出了稀疏阵列信号的阵列构造，其中Ω 表示阵元所在的位置空间集合，稀疏面阵模型如图1所示。
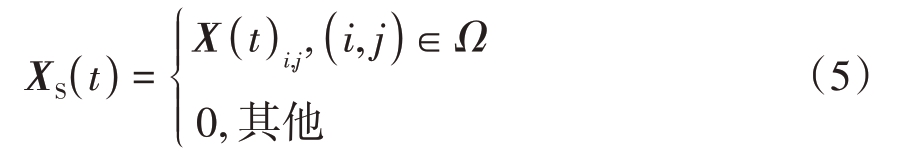
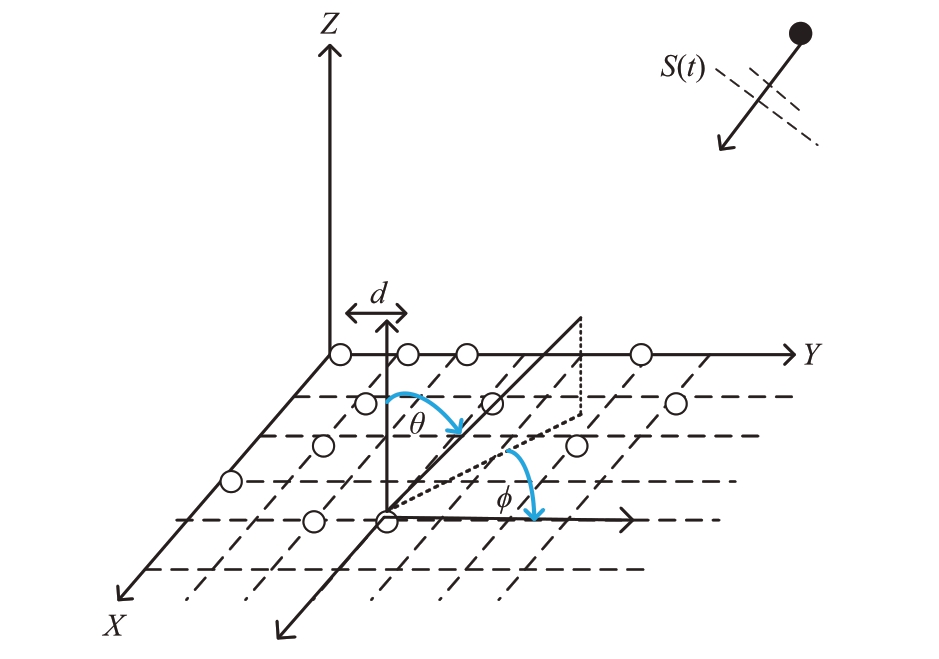
图1 稀疏面阵模型
1.2 阵列信号矩阵填充
首先需要将阵列的稀疏信号模型恢复为完整的阵列信号模型，恢复缺失数据，基于面阵信号的矩阵恢复原理如图2所示。
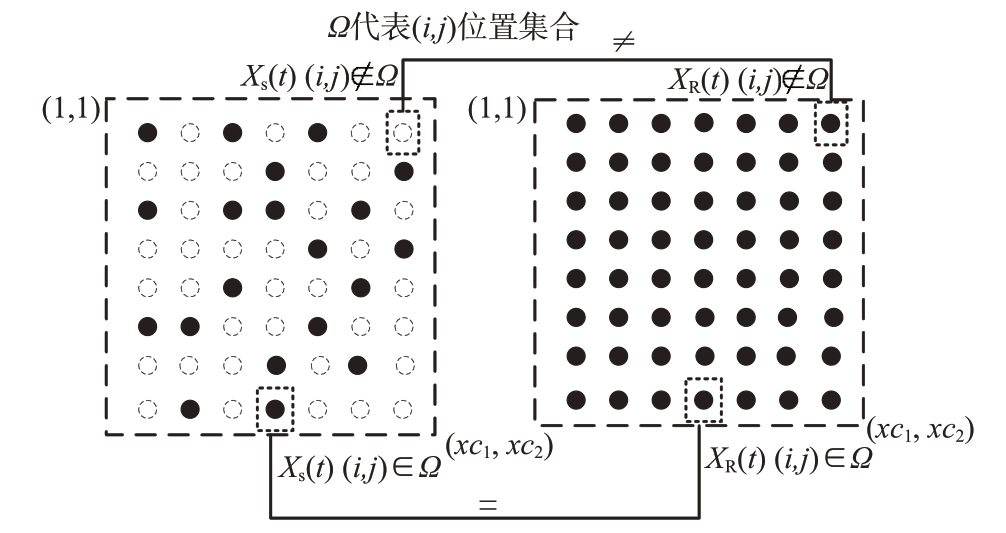
图2 完整阵列信号恢复原理
其关键思想利用矩阵的低秩性，如果事先知道观测矩阵A 是低秩的，那么矩阵补全问题可以表示为如下优化问题:
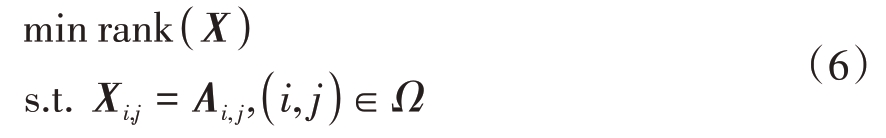
矩阵A 为真实存在的矩阵，X 为待填充的矩阵，构造投影函数PΩ。
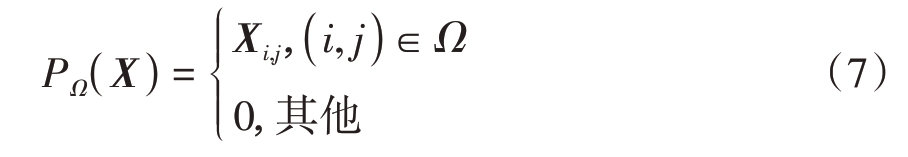
上述问题是一个NP-hard 问题，求解过程会随着矩阵累积而复杂度增加，因此实际中通常采用矩阵的核范数作为秩的凸松弛来近似求解，转化为凸优化过程如下:
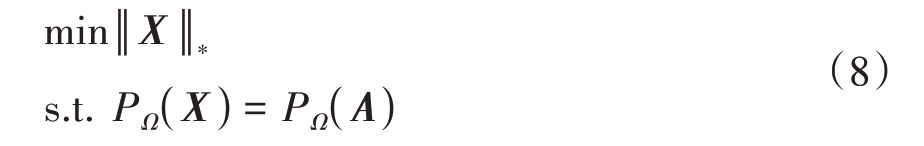
即
如果观测矩阵A ∈Rn × n 的秩为r，且r 的值远小于n，此时矩阵A 是低秩的。对于阵列天线的接收信号来说，其噪声N( t )的功率会远小于实际信号X( t )，信号的部分成分是零或接近零，只有少数成分包含重要的远场入射源信息。这种稀疏性可以与矩阵填充理论中的低秩性质相对应，即只需少数元素或向量就能重建整个矩阵或信号。信号的稀疏性意味着信号可以被看作是由少数几个基础信号的叠加构成，这些基础信号可以通过较低的维度来表示，因此可以通过矩阵填充使得接收信号被完整恢复。
2 问题求解—TP-PM算法
2.1 基于截断核范数和ℓp范数的模型
由矩阵填充的相关原理得到完整阵面信号恢复模型为
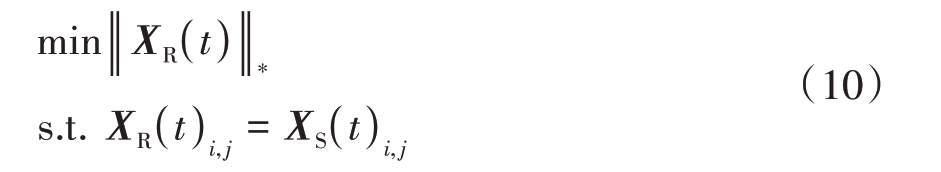
式中，XR(t)为待恢复的重构完整信号，XS(t)为矩阵已知的稀疏的信号模型，(i, j)为稀疏阵列所在位置的索引。式（10）变换为
其中ξ=1/2 代表惩罚参数，一般算法都是通过寻找式（11）的最优解获得重构信号。本文引入ℓp 范数的定义:
将式子进行变形，ℓp 范数是ℓ2 范数的扩展形式，由文献［33］得知，ℓp 范数( )0 < p ≤1 对于ℓ2 来说有着更好的数据鲁棒性，在这种情况下，异常值对误差项的贡献也会变得相对较小。因此，使用0<p≤1 的ℓp 范数可以减小异常值对误差函数的影响，会相比ℓ2 范数在处理异常值时更加稳定，因此式（11）可以改写为
由矩阵填充的理论知rank（min（X））的解在满足强非相干性条件下，几乎等价于核范数的解。同时，对矩阵进行奇异值分解时，假设矩阵有r 个非零奇异值，那么对角线上有r 个非零元素。如果只考虑最大的r 个非零奇异值，对于矩阵的秩，它等于非零奇异值的个数，即r。因此，只考虑最大的r个非零奇异值，而将其余的奇异值设为0，并不会影响矩阵的秩。因此，将考虑奇异值的个数代替考虑矩阵秩的问题，即
由于
是非凸函数，需要对式（14）进行变形。由文献［34］得知
可变成截断核范数的构成形式，即
，其中A 和B均满足正交矩阵的性质，将式（14）改写为
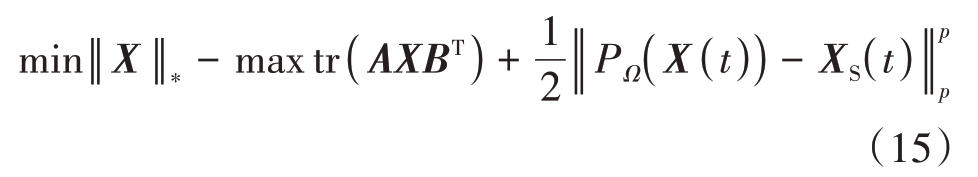
因此对于重构的完整信号求解由式（11）变成了式（15），问题重新写成
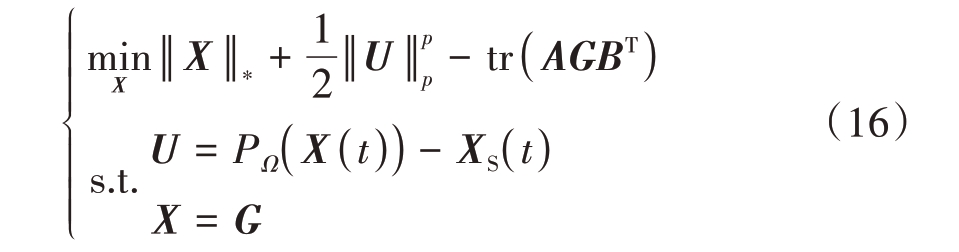
2.1.1 迭代双步策略
为解决上述问题，采用迭代双步策略来求解，确定好初始值输入X0 = XS( )t , μ0,η0,r0，迭 代 次数k。
第一步通过奇异值分解和截断奇异值的个数r确定A(k)和B(k):
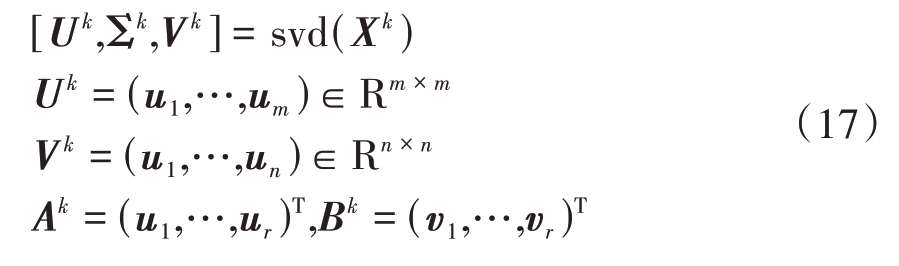
第二步解决如下问题更新X:
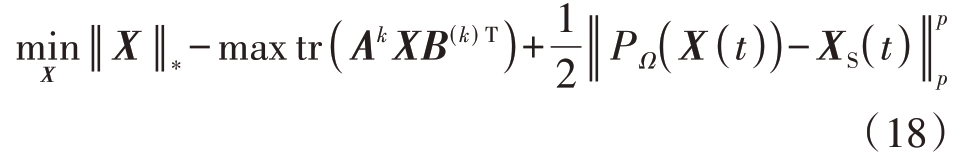
将每一次迭代更新产生的A(k)和B(k)当成已知量，引入拉格朗日函数法得到增广拉格朗日函数:
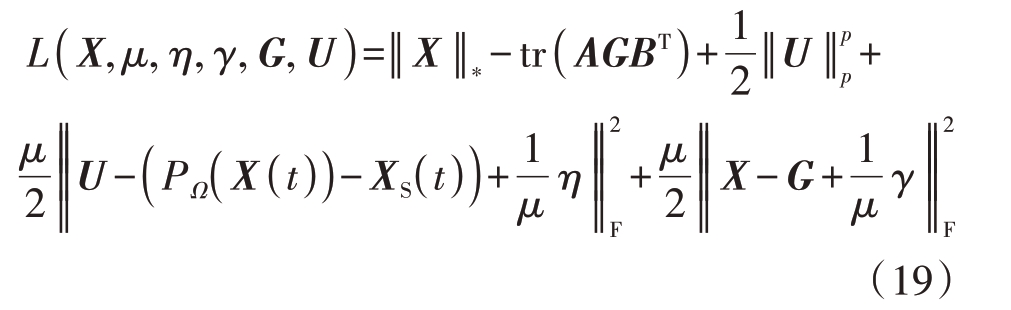
其中η, γ 为增广拉格朗日函数的缩放对偶变量。下面给出算法步骤。
算法1: 迭代双步策略
第一步: 对Xk进行SVD奇异值分解
[Uk, Sk, Vk]= svd( Xk)
其中，U(k) =(u1,…,um) ∈Rm×m
V(k) =(u1,…,un) ∈Rn×n
第二步: 依据截断奇异值数目r更新
A(k) =(u1,…,ur)T,B(k) =(v1,…,vr)T
根据目标函数更新X:
2.1.2 ADMM划分子问题
重新将式（19）中参数写成
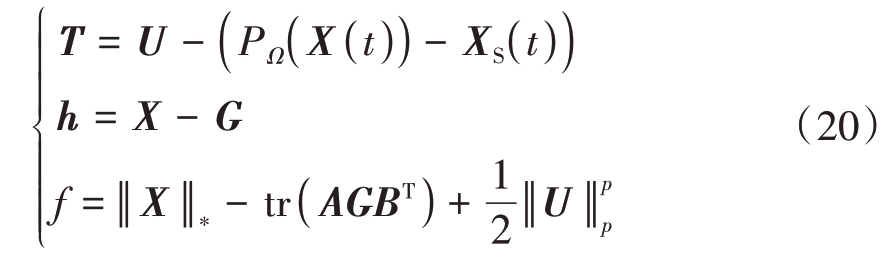
对上式求解问题，涉及到参数X, μ, η, r 的更新，其中μ, η, r的更新可以表示为
X的更新涉及到对拉格朗日函数循环迭代，可以通过ADMM算法解决:
① 固定U，G，优化X，问题被表述为
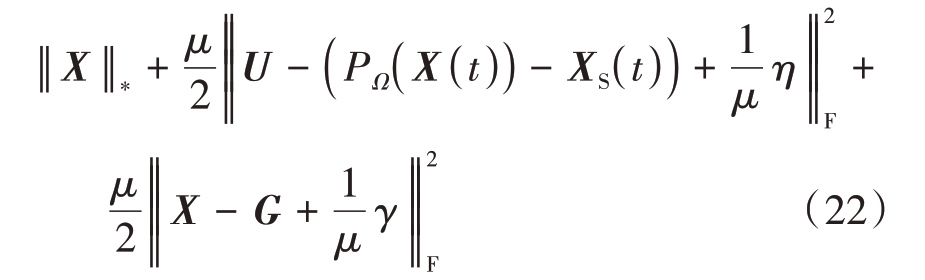
根据式（22）改写成
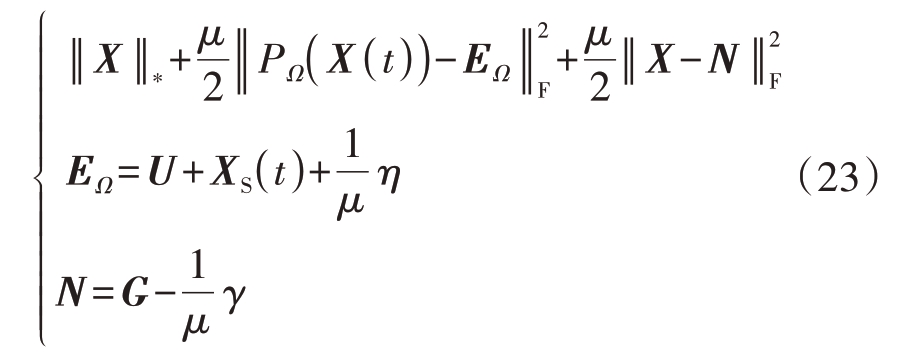
已知式（23）是一个最小核范数的问题，文献［25］证明了其可以通过SVD 进行处理。受软阈值迭代法启发，式子可以通过奇异值软阈值和梯度下降法求解。
1）针对式中的F 范数问题，通过解决关于X的线性系统来逼近F范数。
通常转换为
转化为
。当( i, j )∈Ω 时，构造线性方程:
将 F 范数整合到线性系统中得
，使用梯度下降法求解Xk。
时，
，更新后的Xk 为
。
2）针对式中的核范数问题:
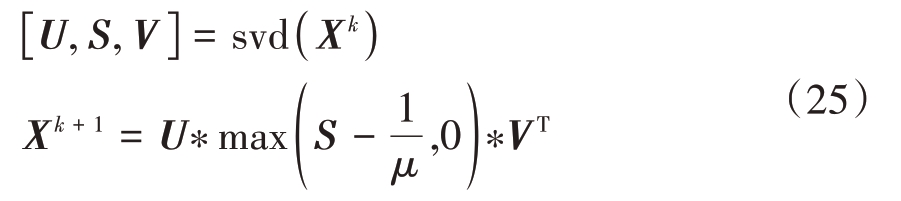
具体算法流程如下。
算法2: 奇异值软阈值化+梯度下降
1）Input:初始值X0，选择步长参数α，迭代计数器k0，初始值EΩ 0，初始值N0，ζ为最低限度。
2）计算X 在Xk 的梯度∇f( )Xk ，其中梯度信息由F范数获得。
3）Xk +1 = Xk -
4）对Xk进行奇异值求解
[U, S, V]= svd(Xk +1)
5）软阈值处理，构造新的Xk +1, Xk +1 = US′VT
6）检查收敛性，
7）Output:Xk +1
② 固定X，G，优化U，问题被表述为
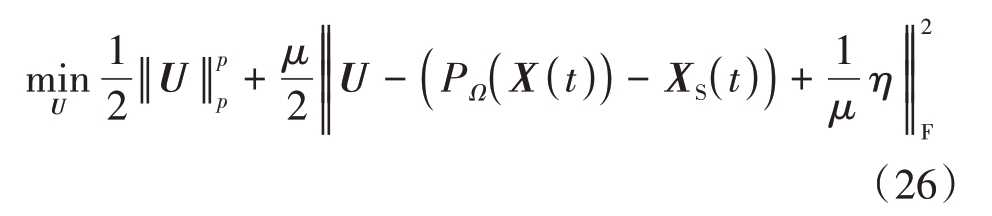
将式（26）变形为
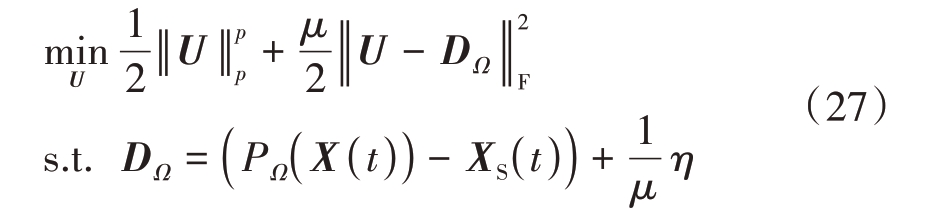
依据ℓp 范数和F 范数的定义，对于U 和D 中
均有
将其用函数公式写成
文献［35］证明中得知
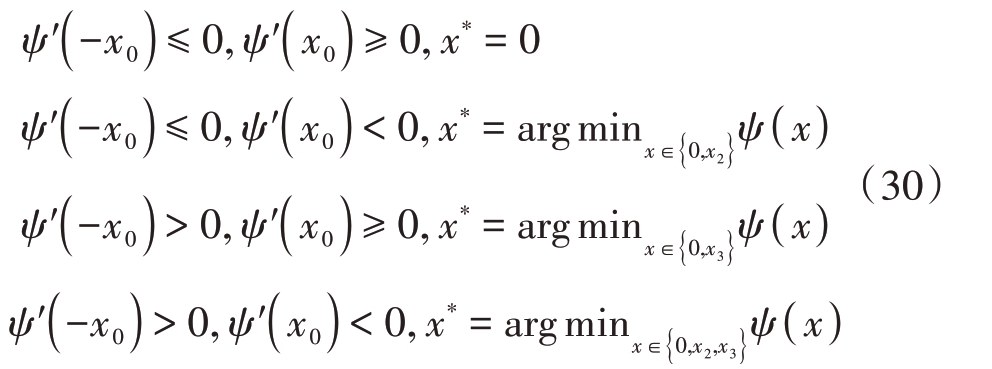
其中
，由函数的ψ( x )的二阶导数为零得来。x1,x2为函数的一阶导数大于0 的根，0 < x1 < x2，x3，x4 为函数的一阶导数小于0 的根，x3 < x4 < 0。
③ 固定U，X，优化G，问题被表述为
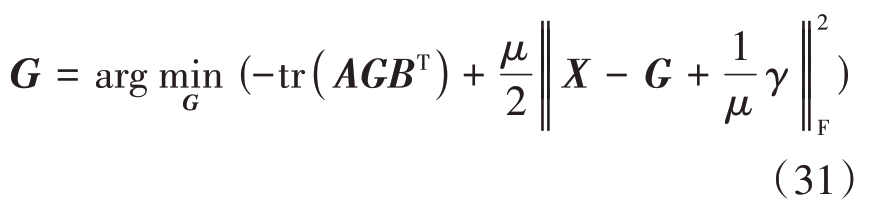
由矩阵迹的性质得
，矩阵的迹就等于两个矩阵的内积。由迹和F 范数的关系可以将内积看作G 与ATB 之间F范数的差的一部分［34］。为将迹与F 范数融合在一起，引入
，此时有
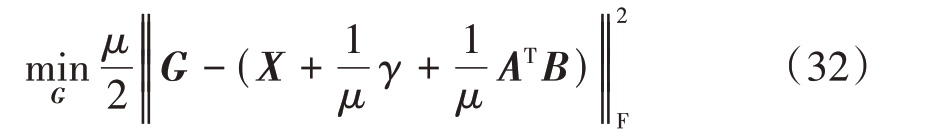
对式子求梯度并令其为0得
根据确定的A(k)和B(k)，G即满足
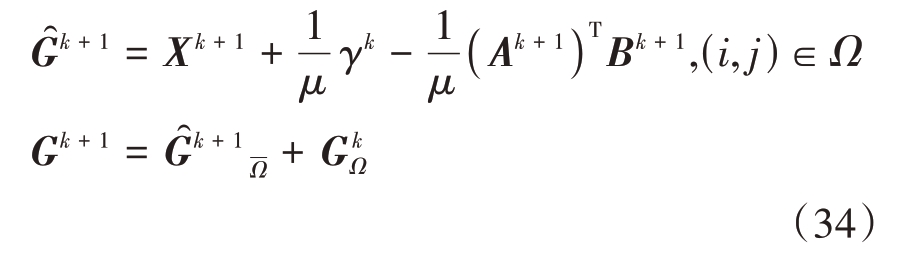
2.2 基于PM广播算子划分子阵求解
经过迭代后重构的完整阵面信号模型为XR(t)，对信号进行子阵划分，如图3所示。
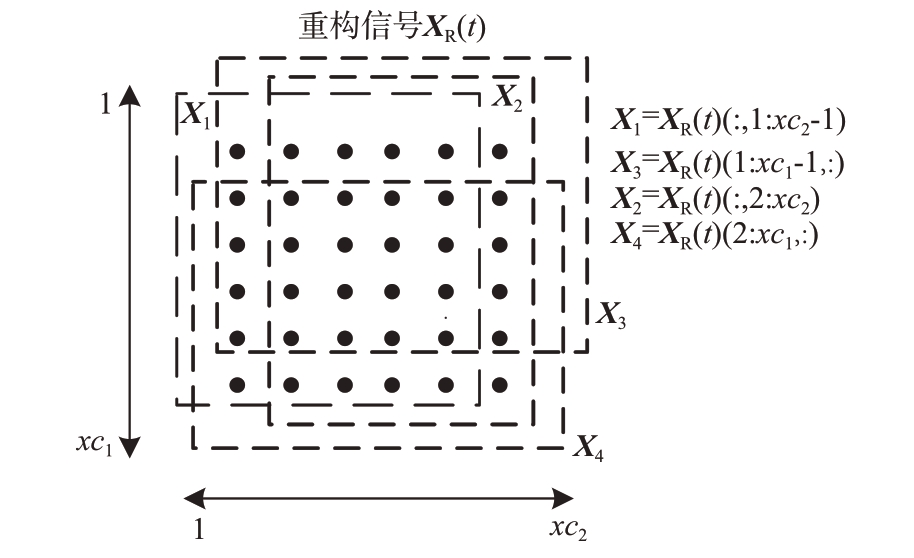
图3 重构信号子阵划分
由图3 可知，X1与X2之间的阵列信号有沿Y 轴包含的两个维度的角度信息，X3与X4之间有沿着X轴包含的两个维度的角度信息。
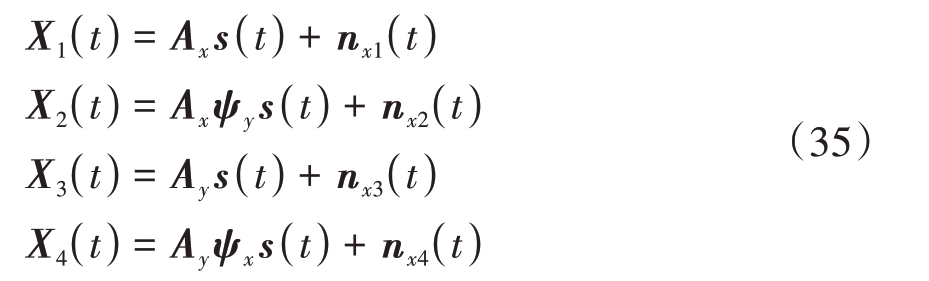
划分子阵的协方差矩阵，对子阵进行互相关矩阵
求解:
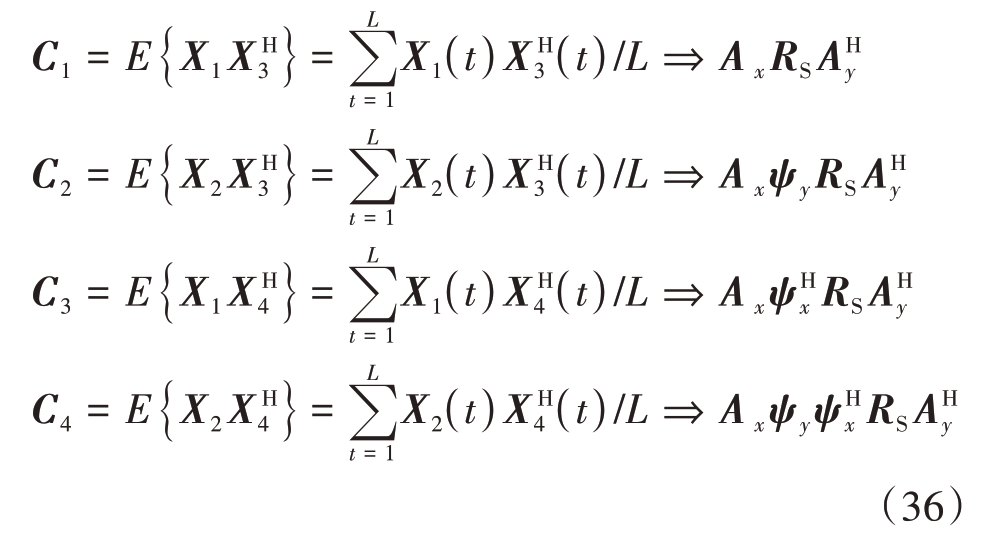
其中C2中包含与ψy 有关的项，C3中包含与
有关的项，C4中包含与
有关的项，接下来构造关于互相关矩阵的传播算子算法模型。
首先，合并互相关矩阵:
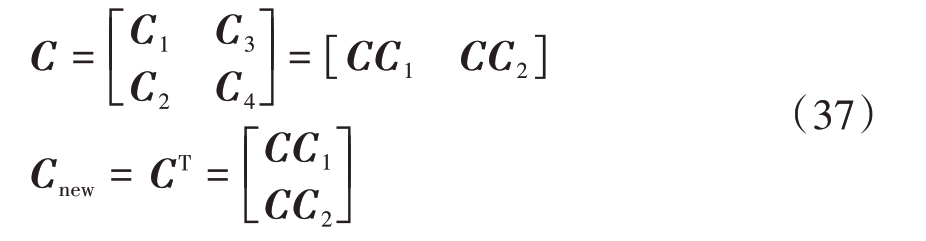
引入传播算子PM 的概念，假设存在矩阵J，对矩阵J进行分块:
J1是非奇异矩阵，将分块后的矩阵利用传播算子［36］进行矩阵计算可得
其中，P 代表关于矩阵J2 的传播算子，可由J1 的线性变换所得，该线性变换唯一。J1的矩阵维度为K×K，P 的维度为K×（4xc1×xc2-4xc1-K），其满足
= 0。
因此，将Cnew矩阵变换如下:
其中U 的维度是K×（4xc1×xc2-4xc1），Cnew的维度为（4xc1×xc2-4xc1-K）×（xc1×xc2-xc2）。当信号不包含噪声的情况下，可以直接用PM 算法求解，构造F =PHU,当信号中存在噪声时，由于重构信号满足矩阵填充理论，矩阵具有低秩性，噪声信号NR（t）的值远远小于信号X（t）值，即
可以通过构造最小二乘方程估计P͂来近似逼近P值
求出P͂后根据式子J的定义关系矩阵
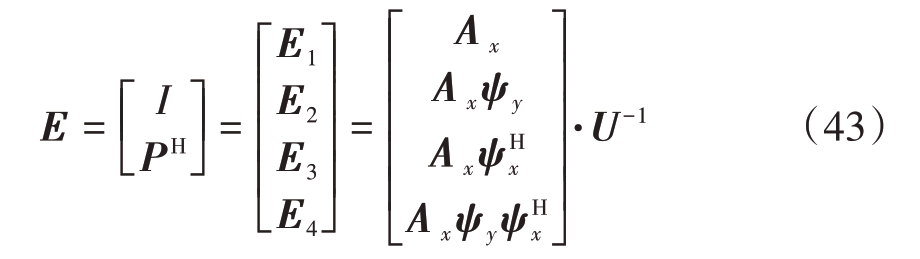
上式的［E1 E2］与［E3 E4］满足一定的关系，将E 进行分块，得
式中
。
对上式进行最小二乘法求解后进行特征值分解，所得的λk，uk值由特征值求得:uk=
同理对于ψy也是:
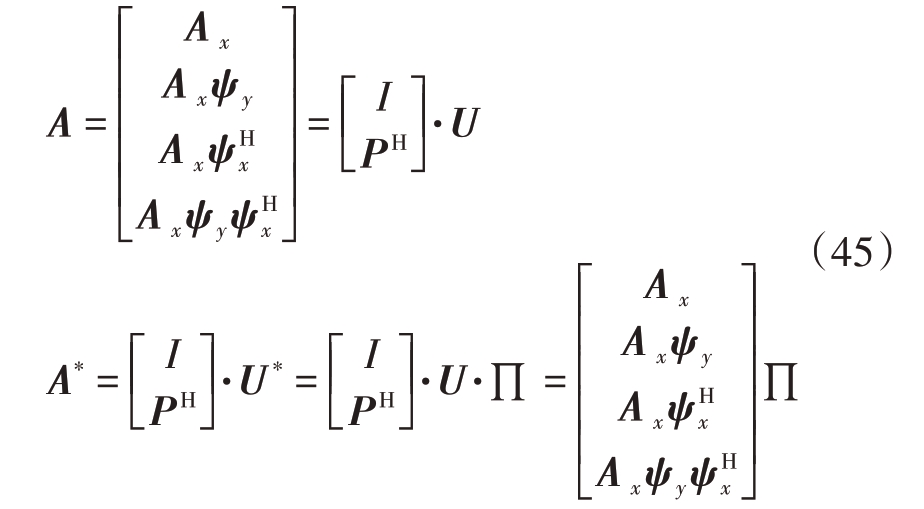
式中U*为特征值所对应的特征向量，其满足U* =U∏，∏为矩阵U进行行列交换时的转换矩阵。
对上式进行最小二乘法求解后进行特征值分解，所得的γk，vk值由特征值求得:
求角度
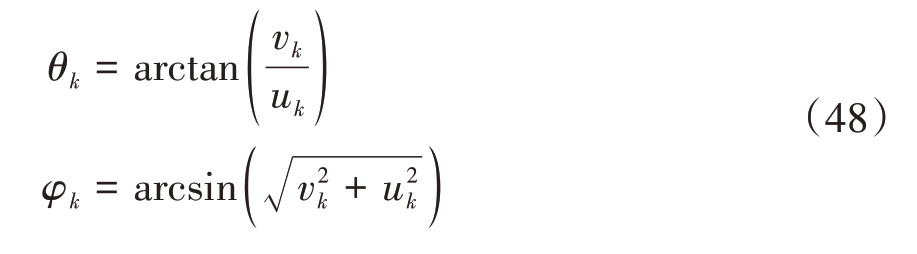
3 仿真与结果分析
本文通过仿真实验验证算法性能。从均匀平面阵xc1×xc2中随机生成稀疏平面阵列，对稀疏平面阵列进行矩阵填充恢复成完整阵列信号，将重构后的信号进行角度估计，通过均方根误差、时间复杂度等方面的对比算法性能。二个维度的角度估计的均方根误差（Root Mean Square Error, RMSE）为
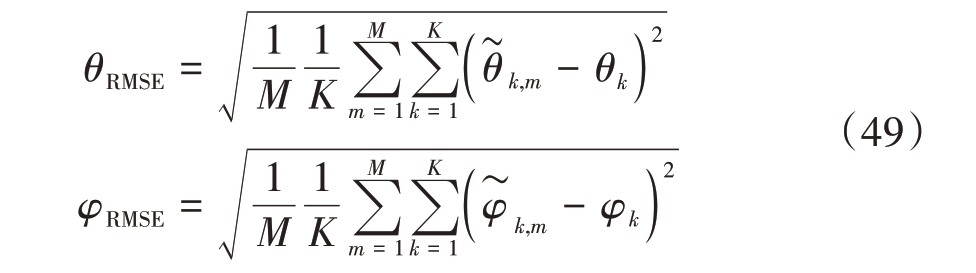
式中，M 代表蒙特卡洛实验次数，
代表第k 个信号源第m 次实验的方位角估计值，
代表第k 个信号源第m次实验的俯仰角估计值。
阵列信号矩阵填充的填充误差定义为
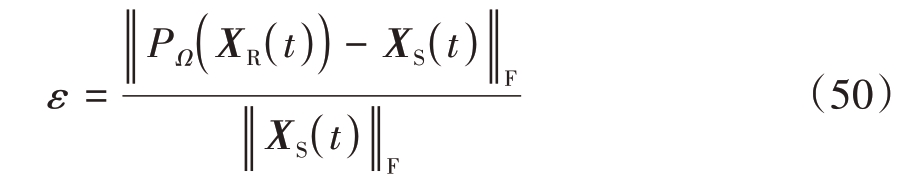
3.1 稀疏信号恢复性能分析
仿真考虑从64×64 的平面阵列中随机选择1 400 个阵元。在模拟过程中，采用50 个快拍，并在信号中加入了15 dB 的高斯白噪声，得到维度4 096×50 的数据矩阵。通过迭代计算评估了算法在稀疏信号恢复方面的性能。本文选取了常规的矩阵填充算法进行对比，仿真参数设置见表1。
表1 仿真参数设置
矩阵填充算法SVT参数项设置惩罚项系数:τ =APG xc1·xc2梯度迭代步长:δ = 2惩罚项系数:μ = 0.9‖ ‖Xs( )t 2 2 TNNR-ADMM MMV-ANM TP-PM算法梯度迭代步长:δ = 2惩罚项系数:β = 5秩rank r=1惩罚项系数:α = 2 p范数=0.2惩罚项系数mu=5
通过实验，填充误差结果如表2所示。本文算法（TP-PM算法）对稀疏信号恢复效果最好，通过截断核范数降低了噪声对信号重构的影响，划分为子问题求解减少迭代过程。SVT 算法、MMV-ANM算法、APG 算法、TNNR-ADMM 算法误差依次降低，但都低于本文算法。
表2 稀疏信号恢复算法误差结果
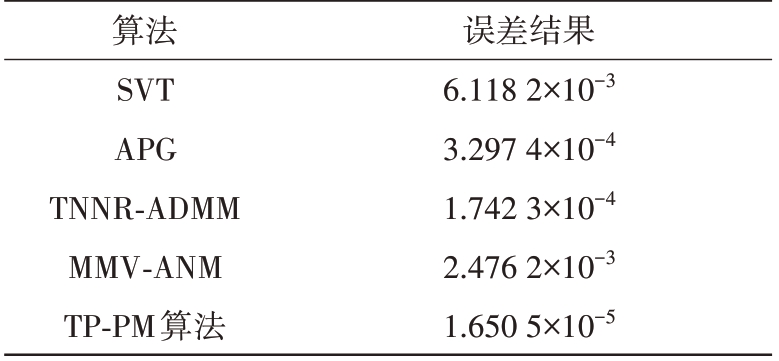
算法SVT APG TNNR-ADMM MMV-ANM TP-PM算法误差结果6.118 2×10-3 3.297 4×10-4 1.742 3×10-4 2.476 2×10-3 1.650 5×10-5
3.2 角度估计结果分析
从均匀平面（具有64 行64 列）中随机抽取1 000 个阵元，构建稀疏阵面。该阵列用于捕捉两个远场信号源的入射角度信息。这两个信号源的角度分别是（40°，50°）和（45°，30°），在15 dB 的信噪比下，收集了200个快拍。为了验证算法的有效性和鲁棒性，本实验进行了400次蒙特卡洛实验进行角度估计，结果如图4所示。
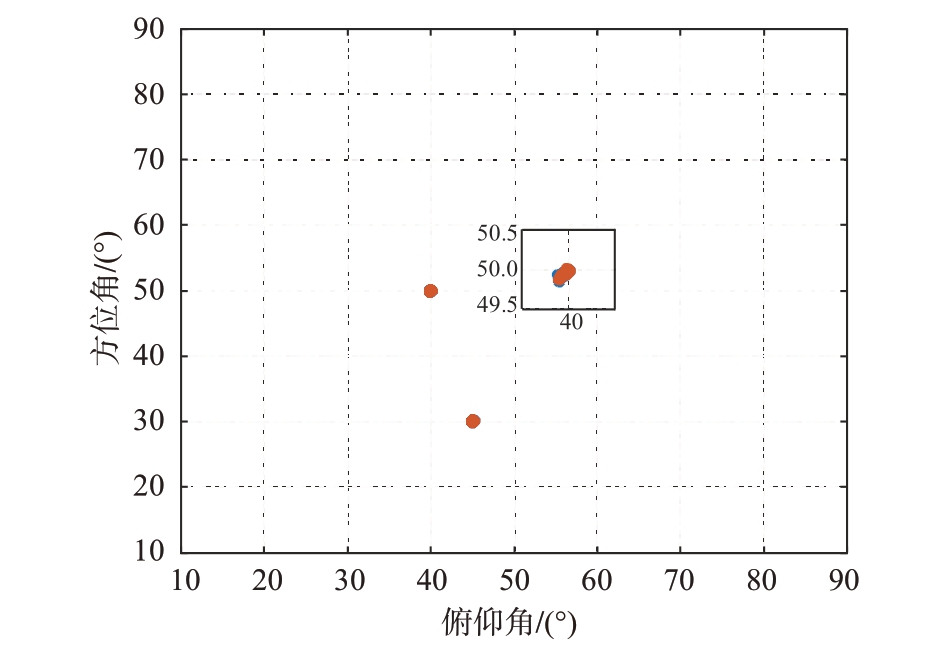
图4 本文算法二维角度估计图
实验结果表明，TP-PM算法计算结果较好，400次蒙特卡洛实验后的角度估计值分布较为集中且都集中于设定的理想的入射源角度附近。
3.3 算法性能与信噪比和快拍数的关系
通过RMSE 评价不同算法性能。在仿真实验中，通过与2D-MUSIC 算法、文献［22］算法、文献［30］算法对比分析了信噪比和快拍数对稀疏阵面接收信号角度估计精度的影响。仿真所用稀疏阵面阵元数为1 000。图5 显示RMSE 与信噪比的关系，其中阵列快拍数C 为50，图6 显示RMSE 与快拍数的关系，其中噪声设为15 dB。
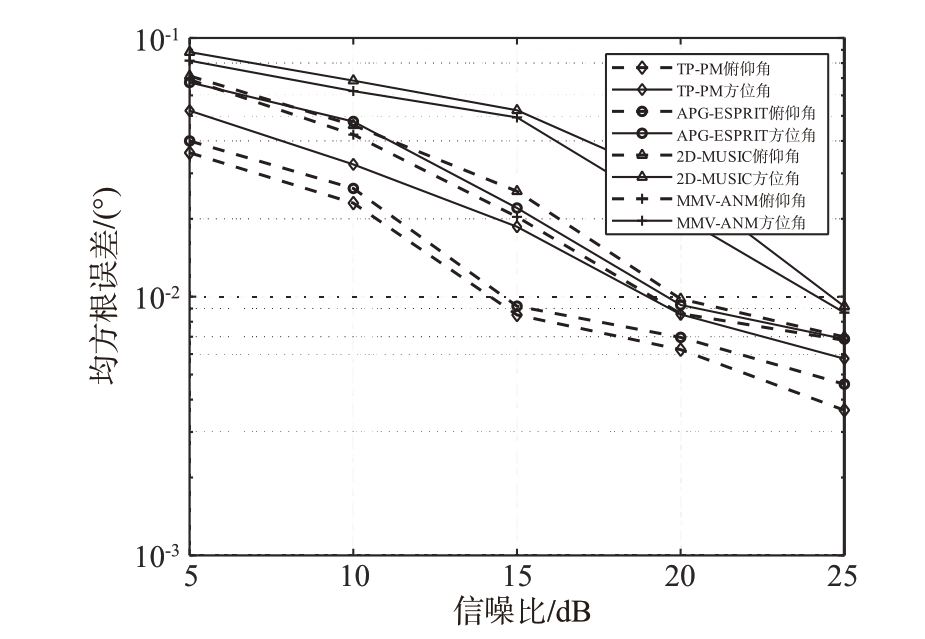
图5 RMSE与信噪比关系图
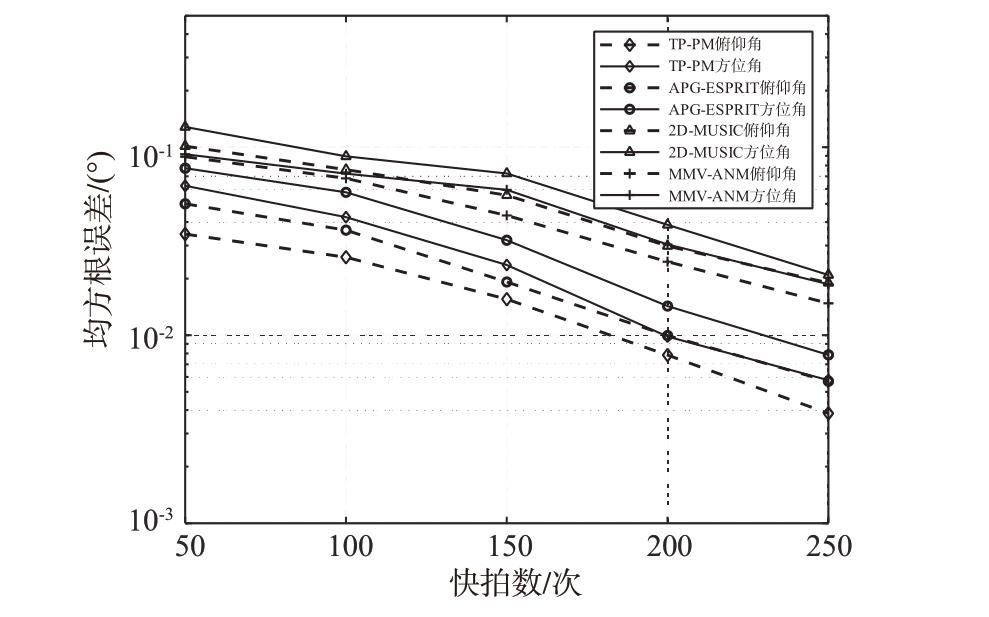
图6 RMSE与快拍数关系图
结果显示随着快拍数增加，增加了样本估计量，接近真实协方差矩阵，算法角度估计误差都逐渐下降，但本文算法效果更加显著。信噪比增加时2D-MUSIC 算法在进行角度估计时表现最为不佳，这部分原因在于其对阵列空间结构的高度依赖性。MMV-ANM 算法处理多快拍信号时矩阵构造更为复杂，且使用CVX 工具箱进行凸优化处理，计算复杂。APG-ESPRIT 算法角度估计效果较好，但使用核范数处理有噪声的信号，效果不如本文算法。
3.4 算法性能与面阵稀疏程度的关系
实验从64×64 的阵面中选取稀疏阵元数为900，1 500，2 400，3 200，3 900，对应稀疏率约为21%，36%，58%，78%，95%，快拍数设置为100，蒙特卡罗次数为500次，阵列稀疏性和角度估计之间的关系如图7所示。
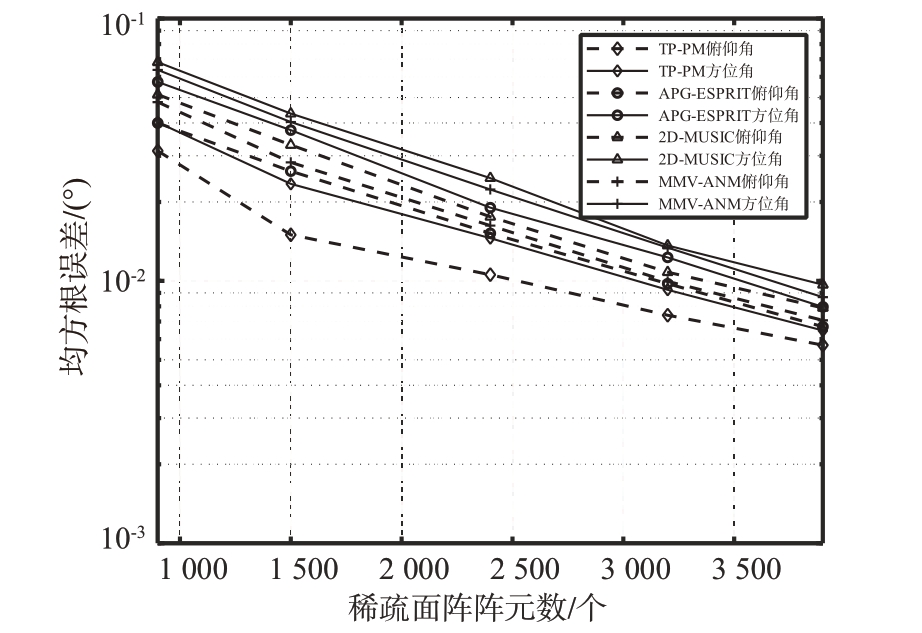
图7 算法与面阵稀疏程度的关系
本文算法（TP-PM 算法）在角度估计精度方面随着阵元利用率的提高而提升。2D-MUSIC 算法更依赖空间谱完成阵面角度估计，越稀疏的阵面阵元间隔越大，影响空间谱生成，效果最差。MMVANM 算法由于不规则的托普利兹矩阵结构也会影响角度估计。虽然APG-ESPRIT 算法性能较好，但它依赖于核范数模型，噪声影响较为敏感，矩阵恢复效果不如本文算法。综上所述，TP-PM算法优化了角度估计的流程，在稀疏阵列应用中展现了较好的性能。
3.5 算法的复杂度
本文从时间维度出发对比算法。从阵元数和快拍数着手，针对可能会影响算法求解速度的因素进行讨论，结果如表3、表4所示。本文算法求解速度较快，MMV-ANM 算法求解速度最慢。MMVANM 基于原子范数最小化的函数模型，将单个测量矢量拓展到多个测量矢量中进行半正定规划求解，其计算复杂度为o（（xc1*xc2+C）3.5log（1/ε）。本文算法无需进行半正定规划，且根据矩阵的运算法则，本文算法只需要划分子阵进行协方差矩阵求解，根据旋转不变关系进行两次最小二乘解运算提取特征值求解，比传统的使用ESPRIT 和MUSIC 算法的计算量减少，计算速度提升，计算复杂度 为o（
+4K3+16K2（xc1×xc2-xc1）+K2（xc1×xc2-xc2）+4K（xc1×xc2-xc1）（xc1×xc2-xc2）。
表3 阵元数与时间复杂度的关系
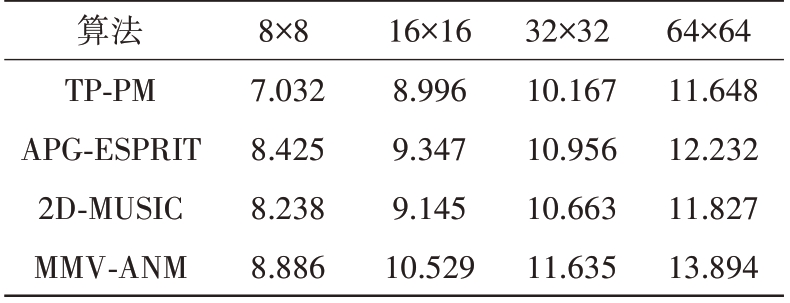
算法TP-PM APG-ESPRIT 2D-MUSIC MMV-ANM 64×64 11.648 12.232 11.827 13.894 8×8 7.032 8.425 8.238 8.886 16×16 8.996 9.347 9.145 10.529 32×32 10.167 10.956 10.663 11.635
表4 快拍数与时间复杂度的关系
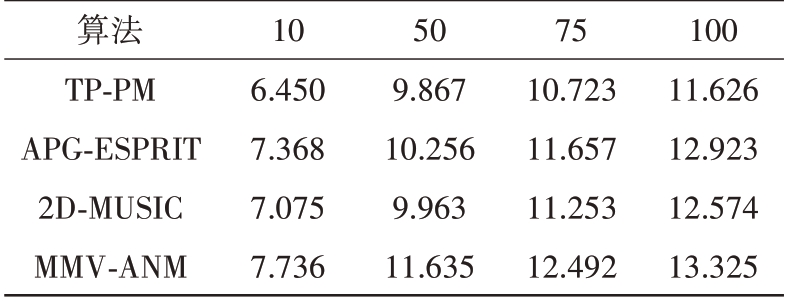
算法TP-PM APG-ESPRIT 2D-MUSIC MMV-ANM 10 6.450 7.368 7.075 7.736 50 9.867 10.256 9.963 11.635 75 10.723 11.657 11.253 12.492 100 11.626 12.923 12.574 13.325
1）与阵元数之间的关系，快拍数为50。
2）与快拍数的关系，阵元数为16×16。
4 结束语
本文提出的算法针对稀疏面阵的不规则结构带来角度估计困难和计算复杂，对噪声敏感等难题，从构建目标函数入手，基于ℓp 范数和截断核范数求解问题，减少噪声影响，保持矩阵重构过程的稳定性。通过ADMM算法划分为3个子问题，从而减少了计算量，并提升了算法的鲁棒性。此外，本文算法采用子阵划分的PM 算法进行求解，避免了ESPRIT 算法中手动匹配运算的需求，降低了误差发生的可能性，从而提供了更为可靠和高效的角度估计。实验证明本文算法相较于其他算法能减少均方根误差的同时减少计算时间，对任意稀疏的阵列具有普适性。
［1］陈金立，张程，陈宣，等.阵元失效下基于矩阵重构的MIMO 雷达DOA 估计［J］.雷达科学与技术，2022，20（5）:524-530.
［2］陈金立，蒋志军，朱熙铖，等.基于矩阵因子重构的MIMO 雷达角度估计方法［J］.雷达科学与技术，2023，21（6）:653-660.
［3］李超，刘志红，马鸣，等.扩展声源全变分规则化二维稀疏DOA 估计方法［J］.山东科技大学学报（自然科学版），2023，42（3）:111-119.
［4］李铭，侯艳丽，苏佳.OFDM系统中一种低复杂度的TOA和DOA 联合估计算法［J］.电子测量技术，2023，46（10）:155-163.
［5］QIN Guodong, AMIN M G, ZHANG Yimin.DOA Estimation Exploiting Sparse Array Motions［J］.IEEE Trans on Signal Processing, 2019, 67（11）:3013-3027.
［6］ZHANG Xue, ZHENG Zhi, WANG Wenqin, et al.DOA Estimation of Mixed Circular and Noncircular Sources Using Nonuniform Linear Array［J］.IEEE Trans on Aerospace and Electronic Systems, 2022, 58（6）:5703-5710.
［7］MAO Zihuan, LIU Shengheng, ZHANG Yimin, et al.Joint DOA-Range Estimation Using Space-Frequency Virtual Difference Coarray［J］.IEEE Trans on Signal Processing,2022, 70:2576-2592.
［8］秦雨萱，马越，缪晨，等.基于时间调制L 型阵列的无人机探测系统［J］.微波学报，2023，39（S1）:297-300.
［9］赵雪成，黄翔东，马金英.基于L 型级联互素阵列的多目标源载频和到达角联合估计［J］.系统工程与电子技术，2023，45（2）:336-342.
［10］王嘉伟，杨赟秀，陈文东，等.一种基于平行稀疏阵列虚拟孔洞填充的二维DOA 估计算法［J］.电讯技术，2023，63（10）:1531-1537.
［11］王宏，何培宇，喻伟闯，等.基于广义互质双平行阵列的二维DOA估计方法［J］.信号处理，2022，38（2）:223-231.
［12］HOCTOR R T, KASSAM S A.Array Redundancy for Active Line Arrays ［J］.IEEE Trans on Image Processing,1996, 5（7）:1179-1183.
［13］HEIDENRRICH P，ZOUBIR A M，RUBSAMEN M.Joint 2-D DOA Estimation and Phase Calibration for Uniform Rectangular Arrays［J］.IEEE Trans on Signal Processing，2012，60（9）:4683-4693.
［14］张蓝方，韦峻峰，廖灿杰，等.基于改进野狗优化算法的二维MUSIC 声源定位研究［J］.现代计算机，2023，29（13）:45-49.
［15］李佳楠，张骄.基于改进多重Toeplitz 矩阵重构算法的二维DOA 估计［J］.山西大学学报（自然科学版），2023，46（5）:1103-1110.
［16］沈超，郭雅娟，俞家融，等.超宽带系统中基于DFT 的TOA/DOA 联合估计方法［J］.数据采集与处理，2022，37（5）:1157-1168.
［17］HE Zhenqing, LIU Qinghua, JIN Liangnian, et al.Low Complexity Method for DOA Estimation Using Array Covariance Matrix Sparse Representation［J］.Electronics Letters, 2013, 49（3）:228-229.
［18］MALIOUTOV D, CETIN M, WILLSKY A S.A Sparse Signal Reconstruction Perspective for Source Localization with Sensor Arrays［J］.IEEE Trans on Signal Processing, 2005, 53（8）:3010-3022.
［19］YIN Jihao, CHEN Tianqi.Direction-of-Arrival Estimation Using a Sparse Representation of Array Covariance Vectors［J］.IEEE Trans on Signal Processing, 2011, 59（9）:4489-4493.
［20］CANDES E J.The Restricted Isometry Property and Its Implications for Compressed Sensing［J］.Comptes Rendus Mathematique, 2008（9-10）:589-592.
［21］CHI Yuejie, CHEN Yuxin.Compressive Two-Dimensional Harmonic Retrieval via Atomic Norm Minimization［J］.IEEE Trans on Signal Processing, 2015, 63（4）:1030-1042.
［22］卢爱红，郭艳，李宁，等.基于原子范数最小化的二维稀疏阵列波达角估计算法［J］.计算机科学，2020，47（5）:271-276.
［23］CANDES E J, ELDAR Y C, STROHMER T, et al.Phase Retrieval via Matrix Completion ［J］.SIAM Review,2015, 57（2）:225-251.
［24］ARAVKIN A, KUMAR R, MANSOUR H, et al.Fast Methods for Denoising Matrix Completion Formulations,with Applications to Robust Seismic Data Interpolation［J］.SIAM Journal on Scientific Computing, 2014, 36（5）:237-266.
［25］CAI Jianfeng, CANDES E J, SHEN Zuowei.A Singular Value Thresholding Algorithm for Matrix Completion［J］.SIAM Journal on Optimization, 2010, 20（4）:1956-1982.
［26］HUANG Minhui, MA Shiqian, LAI Lifeng.Robust Low-Rank Matrix Completion via an Alternating Manifold Proximal Gradient Continuation Method［J］.IEEE Trans on Signal Processing, 2021, 69:2639-2652.
［27］ZHANG Yanliang, LI Xingwang, ZHAO Guoying, et al.Signal Reconstruction of Compressed Sensing Based on Alternating Direction Method of Multipliers［J］.Circuits,Systems, and Signal Processing, 2020, 39（1）:307-323.
［28］ROCKAFELLAR R T.Augmented Lagrange Multiplier Functions and Duality in Nonconvex Programming［J］.SIAM Journal on Control, 1974, 12（2）:268-285.
［29］陈金立，付善腾，朱熙铖，等.阵元失效下基于核范数和SCAD 惩罚的MIMO 雷达DOA 估计［J］.电讯技术，2023，63（1）:39-46.
［30］曾文浩，朱晓华，李洪涛，等.基于矩阵填充的子阵重构二维波达方向估计算法［J］.南京理工大学学报，2017，41（3）:337-343.
［31］ZENG Wenhao, LI Hongtao, ZHU Xiaohua, et al.A FPCROOT Algorithm for 2D-DOA Estimation in Sparse Array［J］.International Journal of Antennas and Propagation,2016（4）:1-6.
［32］FAN Qing, LIU Yu, YANG Tao, et al.Fast and Accurate Spectrum Estimation via Virtual Coarray Interpolation Based on Truncated Nuclear Norm Regularization［J］.IEEE Signal Processing Letters, 2021, 29:169-173.
［33］NIE Feiping, HUANG Heng, CAI Xiao, et al.Efficient and Robust Feature Selection via Joint ℓ2, 1-Norms Minimization［J］.Advances in Neural Information Processing Systems, 2010, 23:1-9.
［34］HU Yao, ZHANG Deping, YE Jieping, et al.Fast and Accurate Matrix Completion via Truncated Nuclear Norm Regularization［J］.IEEE Trans on Pattern Analysis and Machine Intelligence, 2012, 35（9）:2117-2130.
［35］NIE Feiping, WANG Hua, HUANG Heng, et al.Joint Schatten p-Norm and ℓp-Norm Robust Matrix Completion for Missing Value Recovery［J］.Knowledge and Information Systems, 2015, 42（3）:525-544.
［36］周争光，廖桂生，王洪洋，等.基于PM的波达方向、频率的快速估计方法［J］.电波科学学报，2006（3）:428-431.