0 引 言
机载脉冲多普勒雷达广泛应用于多种关键军事和民用领域，如预警、搜索、火控和气象监测。在对空下视场景中，需要基于距离多普勒二维处理从强地海杂波中提取运动目标，当威力要求较远时，通常在L波段以上波段需要采用中重频来实现。由于平台和目标的快速移动，通常出现距离和多普勒二维模糊，需要基于多重频组来进行解模糊，检测并测量空中运动目标［1］。在中重频设计中，需考虑如发射频率、脉宽、极化和调制方式等多种参数，以确保目标检测的准确性和系统的可靠性［2-3］。然而设计过程中存在高维参数空间导致的组合爆炸和优化周期长等问题。
近年来，机载PD 多重频组设计在理论和工具开发方面取得了部分进展，尤其是遗传算法等智能计算技术，这些技术能在广阔的搜索空间中有效寻找最优解，为解决这些问题提供了可能［4-7］。
现有的多重频组设计文献与研究，存在以下几方面待改进的问题:
1）通常只以距离-速度二维解模糊空间的全程清晰区占比大小作为唯一优化目标［8-9］。而全程优化相对困难，难以达到较高的清晰区占比；其次清晰区占比高的重频组，可能在某些关注的距离-速度位置上存在难以接受的盲区，导致选择困难，需要保留多组结果，再进行人工逐一判断，拉长了优化周期，降低了优化效率。
2）遗传算法应用较为简单，未设置足够约束，对解空间进行有效压缩，寻优效率有待提高［10］。
3）在重频组筛选时未充分考虑解模糊多值虚警问题［11］。
本文的创新之处在于提出了多参数、多目标综合优化方法，在全程清晰区占比基础上，将重点关注区间清晰区占比也作为优化目标；考虑了解模糊多值问题，通过筛选重频组合进行优化。此外，将重频组筛选作为遗传算法迭代过程的条件，大幅降低了需全程清晰区计算的组合数，提高优化效率。
1 机载中重频设计流程
对于脉冲多普勒雷达来说，脉冲重复频率（PRF）的选择最为重要，它不仅直接决定了雷达的最大不模糊距离和最大不模糊速度，同时还影响了解距离、速度模糊时“虚影”出现的概率。机载中重频设计中需要考虑的因素众多，且多个参数相互制约，基于工程实践，可以基于如图1 所示流程进行设计。
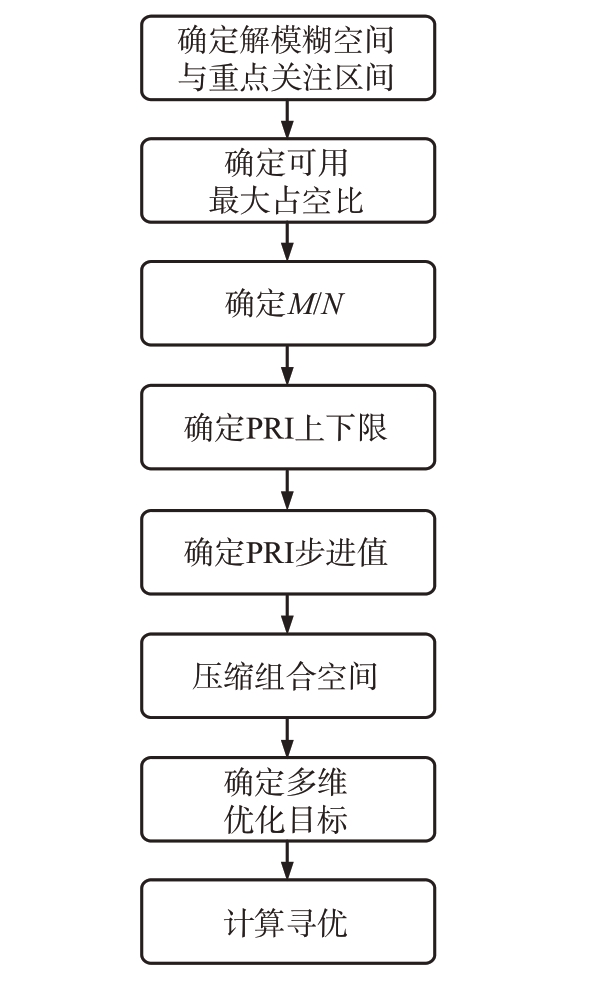
图1 重频设计流程图
1.1 确定解模糊空间和重点关注区间
根据机载雷达系统的任务需求，明确需要探测跟踪的全部目标的距离和速度分布，得到最大解模糊距离和最大解模糊速度，从而确定解模糊空间的大小。
脉冲多普勒雷达最大不模糊距离Ru，其计算公式为
式中c 为光速。距离模糊只与PRF 有关，与波长无关。
脉冲多普勒雷达的速度模糊Vu 与PRF 及雷达波长λ有关，其计算公式为
两者的乘积为Ru*Vu =
。可知当频率f 一定时，不模糊速度和不模糊距离乘积是固定的，也就是两者是相互制约的。
假设某机载雷达需要对中高空飞行民航进行探测，主要关注速度范围50～300 m/s，兼顾对速度为600 m/s 内目标观测，最大探测距离为600 km，主要关注距离段为300～500 km。
图2 为不同频率对应的不模糊速度与不模糊距离曲线，其中PRF的范围为100～50 000 Hz。
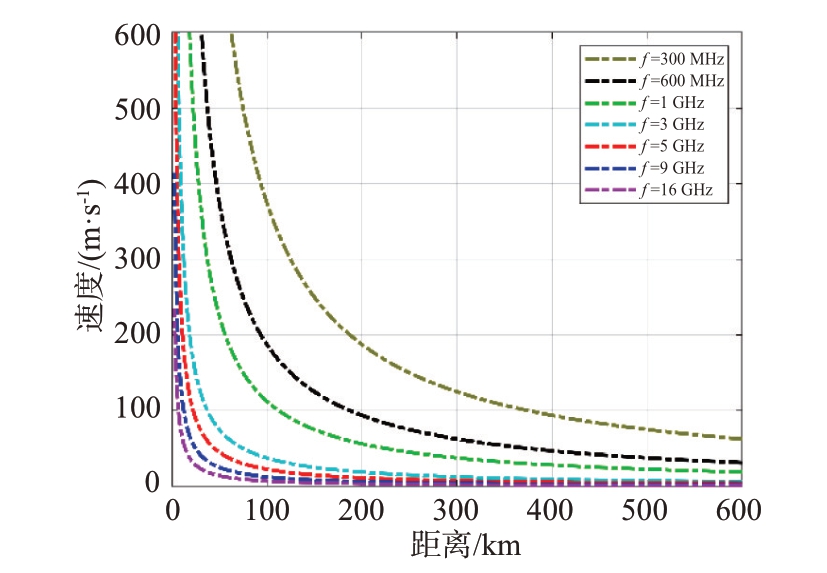
图2 不同频率对应的不模糊速度-不模糊距离曲线
从图中可知，最大目标速度和最远探测距离构成了所需要的解模糊空间。图中各频率对应曲线的左下方为单重频不模糊空间，曲线右上方为模糊空间。
由图2可知，波长越大不模糊空间越大。没有某一频率能够依靠单重频覆盖上述整个解模糊空间，因此需要采用多个重频。重频过高或过低将使速度或距离某一维模糊次数过多，对解模糊计算和剔除虚警不利。因此，在微波段通常采用中重频组进行距离和速度两维解模糊。下文以X 波段为例进行后续分析。
目标在空间中的分布并不是完全均匀的，并且目标处在不同的距离-速度组合时，其威胁程度和重要性也是不同的。因此在距离-速度空间中可以划分出特别关注的重点区域，作为需要重点优化的目标。图3中阴影区域边界为最小可检测速度，红色框图区域（距离300～500 km、速度50～300 m/s）为任务的重点关注区间。在N 重PRF 中，若某个距离-速度组合单元中目标在不少于M个重频中均可见，则此单元属于
距离-速度二维清晰区，即目标在二维清晰区能被检测和正确测量。
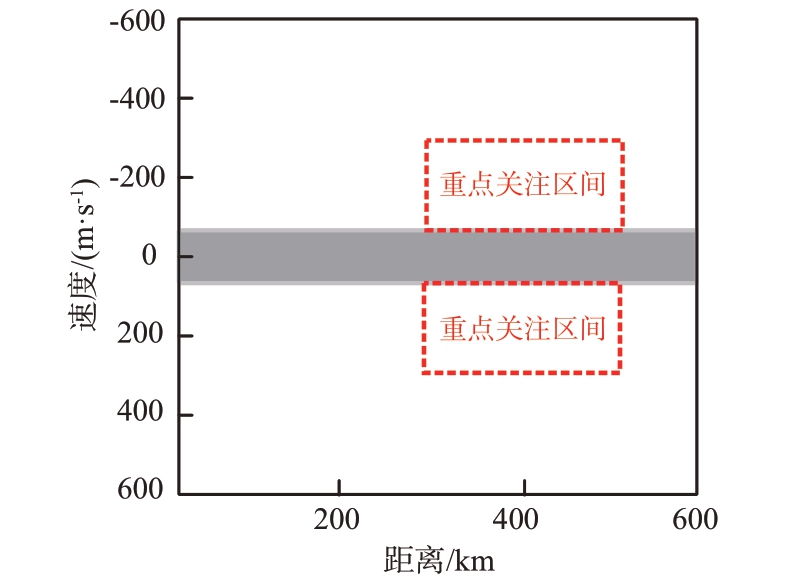
图3 解模糊空间与重点关注区间
1.2 确定可用最大占空比
基于脉冲多普勒雷达系统的功耗限制，确定系统可以承受的最大占空比。增加占空比可以提高能量，增加探测距离，但同时也会导致发射脉宽遮挡带来的距离盲区问题，占空比与清晰区占比成反比。当雷达的重频组个数确定时，较高的占空比意味着清晰区占比减少，影响雷达对接近目标的探测能力。
占空比对清晰区占比的影响还与系统的工作频段和重频高低有关。在相同的占空比下，较低的频段或较低的重频通常能够提供更大的清晰区。
从能量积累的角度考虑，使用单个长脉冲通常比多个短脉冲的能量积累效率更高，较高的占空比能有效提高雷达的能量积累效率，从而增强其探测和识别能力。因此，在条件允许下优选使用系统可支持的最大占空比。
1.3 确定M/N
中重频组设计的首要问题是能够解距离模糊和速度模糊，有两个基础的约束:
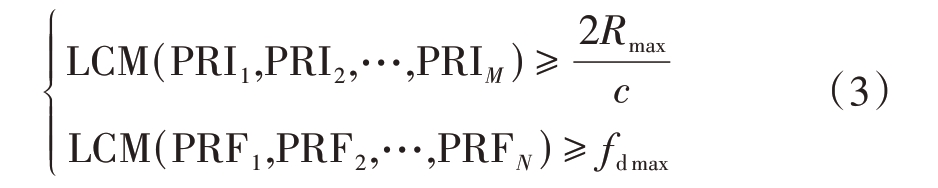
式中:LCM 为求最小公倍数运算；PRI（pulse repetition interval）为脉冲重复间隔，为PRF 的倒数；Rmax为最大探测距离；fd max 为最大多普勒偏移频率；M为解模糊所需最少PRF数目；N为重频组中PRF总数目。
1）确定总重频个数N
首先考虑清晰区占比，即系统在目标检测和跟踪时所能提供的有效信息占总观测时间的比例。清晰区占比与N 成正比，但随着N 的增加，脉冲间的时间间隔减小，连续脉冲积累的能量降低，从而影响雷达最大作用距离，同时增加N 会使单位时间内发射更多的脉冲，脉冲间的时间间隔减少，导致每个回波的驻留时间变短，从而影响到每个脉冲的信号处理能力。
2）确定非相参积累重频个数M
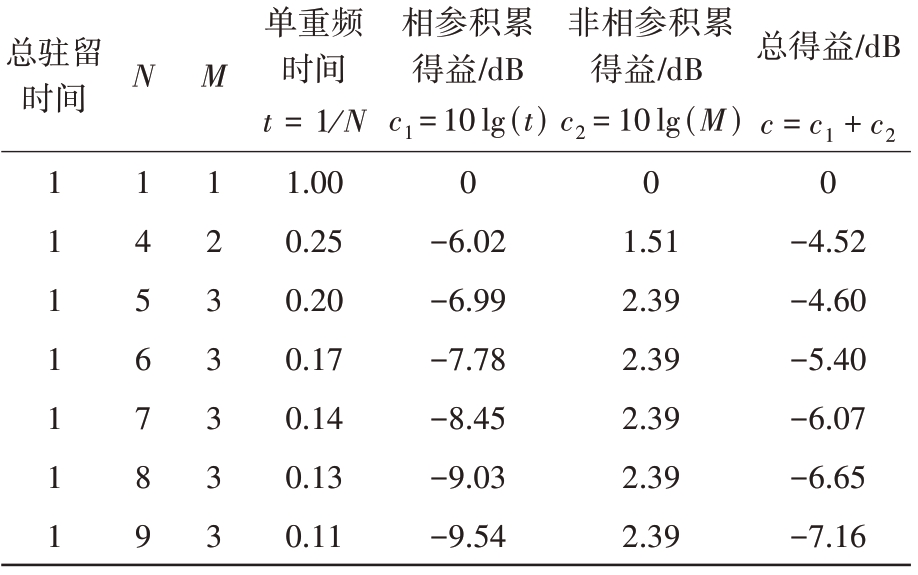
通常可以取
为最优，如2/4、3/5、3/6、3/7、3/8、3/9 等。表1 为在相同PRF 和占空比条件下，不同N 及对应最优M 值与单重频相比，近似的相参积累得益、非相参积累得益以及总得益情况。
表1 不同M/N对应结果
总驻留时间单重频相参积累 非相参积累得益/dB N 1 4 5 6 7 8 9 M 1 2 3 3 3 3 3时间得益/dB t =1 1 1 1 1 1 1 1 N 1.00 0.25 0.20 0.17 0.14 0.13 0.11 c1=10 lg(t)0-6.02-6.99-7.78-8.45-9.03-9.54 c2=10 lg(M)0 1.51 2.39 2.39 2.39 2.39 2.39总得益/dB c=c1+c2 0-4.52-4.60-5.40-6.07-6.65-7.16
由表1 可知，重频数N 越大损失会越大，当
为2/4、3/5 时损失较小，并且两者较为接近。由于2重频解模糊存在虚影问题，因此在占空比不大时，采用3/5是较好的选择。
占空比一定时，N 越大，重频组可达到的清晰区占比上限越高。当占空比大于10%时，3/5 通常难以获得较大的清晰区。如果系统可以将占空比提高到15%及以上，可以考虑采用3/8或更高的N。
1.4 确定PRI上限和下限
1）重频下限
重频下限的确定主要考虑主杂波的宽度，以及平台运动对杂波分布的影响。
从使待检测距离-速度单元内副瓣杂波强度尽可能小的角度出发，理想的最小PRF为
式中，fmc 为主瓣杂波抑制宽度（对应速度遮挡区），脉宽τ对应距离遮挡区。
由于平台的运动，副瓣杂波在频谱上扩展，其支撑区间宽度依赖于载机的平台运动速度以及阵面与运动方向的夹角。杂波支撑区间内，杂波分布与地物、入射角度、天线副瓣等因素有关，呈现出较大的非均匀性。因此需要重频范围可以使杂波支撑区间不折叠，降低处理的复杂度，对于非正侧视探测尤为重要。
对于远距离探测，通常距离会模糊。在较低频段，可以考虑选择重频仅距离模糊，对目标速度不模糊；在较高频段，可以考虑对目标速度模糊，但杂波支撑区间不模糊，以减少回波非均匀性；对于无法满足杂波支撑区间不模糊的情况，则在可能的范围内尽量选择较低的重频。
2）重频上限
重频上限主要受系统响应能力的限制，较高的重频要求整个系统从发射到接收全链路各环节的响应时间都必须足够短，通常由系统内各类开关的切换响应时间决定。
重频的上下限差距越大，越容易获得合适的组合，但计算量也随之大幅增加。在工程上，重频上限可以设定为重频下限的2倍，便于寻找既能满足系统响应需求，又能在距离-多普勒平面中保持较高清晰区占比的重频组合。
1.5 确定PRI步进值
PRI 步进值直接影响重频组优化的分辨率和计算复杂程度。系统采样频率通常是与信号带宽匹配，其倒数采样间隔决定了系统能够解析的最小时间单位，从而直接限定了PRI 的最小变化量。从最优化的角度，可以选择采样间隔作为PRI 步进值。
基于PRI 的上下限和步进值，可以确定PRI 遍历的具体数值范围，并与N 和M 取值共同确定了解空间的大小。从减少解空间考虑，可以将PRI步进值适当放大。
1.6 压缩组合空间
在确定总重频个数N 后，基于PRI 的遍历范围，可以预先获取所有可能的重频组合。然而这样的组合数量通常是非常庞大的，需要进行筛选以预先剔除不符合要求的组合，从而降低计算量。
例如当M=3 时，从所选的N 个重频中任意选择3 个重频进行组合。为了确保在整个解空间内不出现距离上的多值问题，可以通过计算这些组合中的重频最小公倍数所对应的最大不模糊距离来对组合进行筛选。这个距离应大于整个解空间的距离，从而保证在解空间内不出现距离上的多值情况。对于速度维度也可以进行类似的分析。
同时可以对不同PRI 对应的距离单元数间隔进行约束，比如限制相邻3 个PRI 对应的距离单元数相差不能都为1，减少目标跨距离单元时引起的解模糊虚警。
基于以上计算，可以剔除不符合需求的重频组合，从而降低需要进行清晰区计算的组合数量。压缩组合空间可以有效地提高优化效率，减少计算资源的消耗，同时加快设计迭代的速度。
1.7 确定多维优化目标
在机载PD 雷达系统设计中，全局优化与局部优化的结合至关重要。全局优化旨在寻找整体系统性能的最优解，而局部优化则针对特定区域或目标进行细致调整，以进一步提升系统性能。除了全局优化的考量之外，本文提出了将重点关注区域清晰区占比作为优化目标的方法，可以根据任务需求和系统性能要求，确定重点关注的距离-速度区间。可将重点关注区间的清晰区占比与全程清晰区占比加权求和作为综合优化目标。通过将这些重点区域的清晰区占比作为优化目标，能够更加精确地调节雷达系统的性能，以满足特定场景下的需求。
2 重频组遗传算法多维度优化
最优化是遗传算法的经典应用领域，可以比穷举法更快获得可用解，但如果不对解空间进行有效压缩，遗传算法寻优时间依然会比较长，难以匹配方案论证快速收敛的需求。本文将重频组解模糊多值约束作为遗传算法的非线性约束条件，提前筛选组合，节省计算迭代时间。同时在目标函数设置上综合考虑了全程和重点关注区的清晰区占比，更好地满足实际工程设计需求。
Matlab 包含了遗传算法工具箱（Genetic Algorithm Optimization Toolbox，以下简称GA），提供了最优化问题的一种解决方案，使用简单方便、快捷高效。基于GA 的参数与重频组优化映射关系图如图4所示。
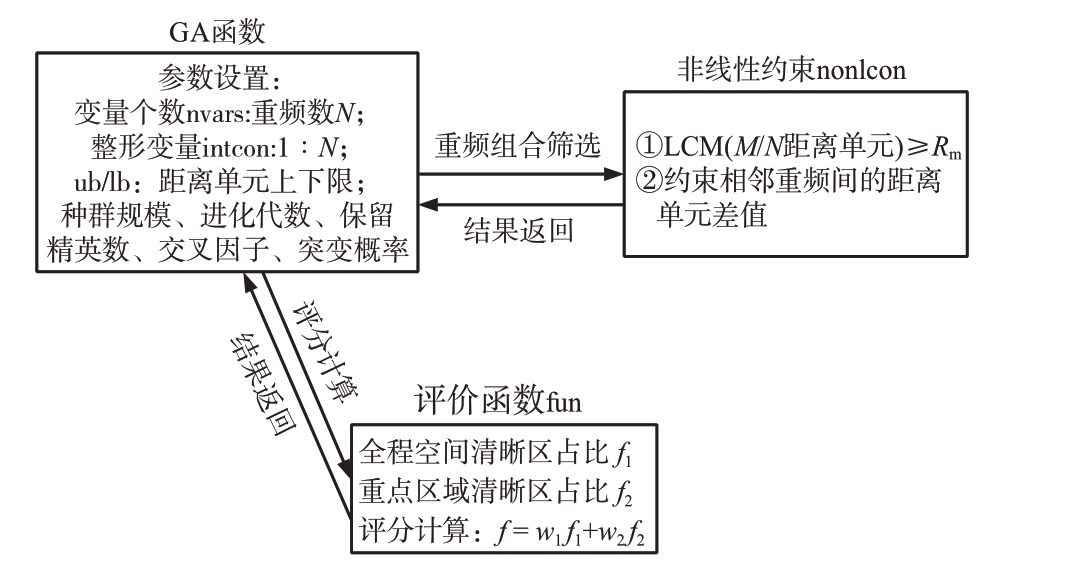
图4 基于GA的重频组优化设计模型与参数映射关系图
2.1 参数设置
仿真假设条件为机载飞行平台，安装对空探测雷达，假设平台飞行速度小于250 km/h，飞行高度6 000 m以上，雷达参数设置如下:
1）工作频段:X波段；
2）工作带宽:2.5 MHz；
3）占空比:小于15%；
4）重频组
；
5）重频下限6 000 Hz，上限40 000 Hz；
6）最大距离量程600 km；
7）目标最大速度600 m/s；
8）重点关注区域的距离区间为300～500 km、速度区间为50～300 m/s。
GA计算参数设置如下:
1）种群规模:100个；
2）精英数量:种群规模5%；
3）最大进化代数:200代；
4）相同结果最大代数:50代；
5）交叉因子:0.85；
6）突变概率:10%。
2.2 映射关系
在使用GA 进行多重频优化时，需要设置一系列参数以控制优化过程的行为。在多重频优化中，参数映射是将优化问题中的变量映射到遗传算法中的变量。在GA 中，参数映射关系的实现如下:
1）将重频的个数N 作为遗传算法中的变量个数nvars；
2）使用整形变量intcon 将变量范围设置为1至N，以确保遗传算法只生成整数解，对应于具体的重频选择；
3）将ub/lb 设置为距离单元的上下限，约束具体重频对应的距离单元范围，以确保优化结果符合距离约束条件。
2.3 评价函数
评价函数是遗传算法引导搜索的主要依据，改变种群内部结构的遗传操作均要通过评价函数加以控制。将全程及重点关注区间二维清晰区占比加权求和构建为评价函数。在优化过程中，GA根据评价函数分值来评估个体的适应性，并选择适应性较好的个体进行进化。对二维清晰区的计算可以叠加具体阵面构型、天线方向图副瓣、飞行航线地形等影响，本文主要面向项目论证，快速获得可用重频组以支持后续论证，计算中考虑了主瓣影响，对于副瓣主要考虑了杂波支撑区间范围，可在项目实施过程中针对具体波位开展进一步优化。
2.4 约束条件
在GA中设置非线性约束函数nonlcon，使该函数用于计算当前重频组的N 个重频中任意M 个重频组合，其距离单元最小公倍数大于解模糊空间距离最大值，以确保在整个距离量程内不出现多值。同时约束相邻重频间的距离单元个数差值，减少解模糊虚警，保证重频组合的可行性和有效性。非线性约束函数计算结果如果不满足约束条件，则不会调用评价函数中对二维清晰区的计算，可以节省大量的计算时间。
3 GA优化计算结果
基于Intel i7 CPU，运行内存16 GB，14 核并行计算，GA 优化运行时间在30 min 以内。图5 为经过迭代优化后重频组对应的二维清晰区。
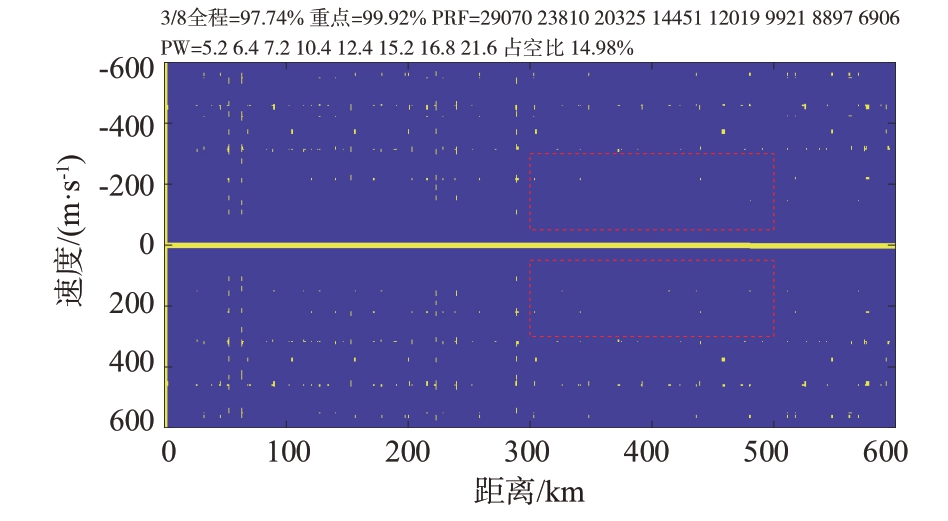
图5 重频组距离-速度二维清晰区
本文方法可以有效地寻出全部解空间以及重点关注区域的清晰区占比都较高的重频组。利用GA搜索得到的重频组为PRF=［29 070，23 810，20 325，14 451，12 019，9 921，8 897，6 906］，对应的脉宽为PW=［5.2，6.4，7.2，10.4，12.4，15.2，16.8，21.6］，平均占空比为14.98%。全程的清晰区占比为97.74%，重点关注区域的清晰区占比为99.92%，图中红色虚线区域即为距离-速度重点关注区域。可以看出在全部解空间内，遮挡区域分布较为均匀，无连片遮挡，对于空中目标探测较为有利。
4 结束语
本文详细阐述了机载中重频设计流程，既考虑了全解模糊空间内不产生多值虚假目标，又考虑了不同任务需求的重点关注区间，全局优化与局部按需优化结合，可以在多重约束条件下，获得与应用场景最优或次优匹配的结果。基于Matlab优化算法工具箱，快速实现遗传算法的部署，强化条件约束，降低计算复杂度，实现快速寻优，极大提升了设计迭代速度，提升了设计效率，并通过仿真实例验证了所提方法的有效性。
［1］文鸣.中重频雷达的检测前跟踪技术研究［D］.成都:电子科技大学，2019.
［2］马杰，王永良，谢文冲.机载预警雷达MPRF 优化方法研究［J］.空军预警学院学报，2018，32（5）:331-336.
［3］刘扬，郭锋，顾宗山，等.基于方向图的机载PD 雷达中重频设计［J］.雷达科学与技术，2020，18（1）:39-43.
［4］周仕霖.基于离散度多目标粒子群重频组优化算法［J］.兵器装备工程学报，2021，42（7）:127-133.
［5］王美凤.机载雷达目标检测及航迹规划方法研究［D］.西安:西安电子科技大学，2021.
［6］华瑶，孙晓闻.遗传算法搜索雷达脉冲重复周期［J］.现代雷达，2016，38（8）:17-19.
［7］周仕霖.基于改进粒子群的重频组多目标优化算法［J］.探测与控制学报，2021，43（3）:92-97.
［8］程琛.机载认知雷达PRF 参数优化及杂波抑制方法研究［D］.西安:西安电子科技大学，2017.
［9］连晓锋，汤子跃，朱振波，等.机载相控阵PD 雷达的MPRF设计与选择［J］.现代防御技术，2016，44（4）:129-135.
［10］王立坤，周琳，郭琰.基于多组重频相参积累的多普勒解模糊方法［J］.现代雷达，2020，42（3）:35-39.
［11］高飞，谢文冲，段克清,等.相控阵机载PD 雷达波形参数系统化设计方法研究［J］.空军预警学院学报，2017，31（1）:23-27.