0 引 言
频率步进探地雷达（Stepped Frequency Ground Penetrating Radar，SFGPR）具有高动态范围和低制造成本等特点，是探地雷达主要工作体制之一。随着探地雷达领域不断追求更高精度的成像，使得SFGPR 数据获取过于繁琐的缺点愈发突出。为了解决这一问题，研究者们将压缩感知（Compressive Sensing，CS）理论结合到SFGPR 系统构建和成像等领域［1］，实现通过采集少量的数据进行成像。目前SFGPR 压缩感知成像用到的重建方法主要分为三种:1）凸优化方法［2］，将NP 难的l0 范数优化问题转化为求解最小l1范数的凸优化问题；2）贪婪迭代方法［3］，在迭代过程中寻找并计算局部最优原子，逐步近似初始信号；3）基于贝叶斯框架方法［4］，通过初始信号的先验知识，将信号重建问题转化为概率估计问题。这三类重建方法的优点是数学模型成熟，有完整的理论证明。缺点是需要人工进行多次参数选择和调整，才能得到最佳的重建效果，且重建精度较低。
随着深度学习技术的飞速发展，基于深度学习的探地雷达成像方法被不断提出［5-7］。在训练数据集中，利用深度神经网络良好的特征学习能力，进而求解雷达成像问题。但是基于数据驱动的深度神经网络通常需要大量的训练数据，且网络结构的可解释性和对于不同应用场景的普适性较差。为了解决这些问题，一种可靠的想法是选择合适的迭代优化算法将其映射成深度网络。其中利用传统CS迭代算法展开成深度网络被认为是一种极具潜力的方法［8］。它既具备传统方法优秀的可解释性，又有深度学习的高效性和准确性。与传统的神经网络相比，深度展开网络有良好的学习效率，且需要较少的训练数据。目前，深度展开网络在图像重建、合成孔径雷达成像和无线通信等领域中均有较好的表现［9-11］。例如，文献［12］提出了经典的迭代收缩阈值算法展开成深度网络用于图像CS重建，相比于其他基于网络的CS重建方法，该方法在重建质量和重建速度上均有优势。文献［13］提出了近似消息传递算法展开成混合通道的深度网络用于合成孔径雷达成像，该方法具有较少的网络参数和较低的计算复杂度，且实现了高质量的成像。
因此，本文提出用于SFGPR 成像的深度展开网络，解决SFGPR 传统CS 成像中参数选取敏感、成像精度较低的问题。该方法将快速迭代收缩阈值算法（Fast Iterative Shrinkage Thresholding Algorithm，FISTA）的每一次迭代映射成深度网络结构的一层，加入卷积神经网络（Convolutional Neural Network，CNN）模块作为成像区域的稀疏表示及其逆过程，需要手动调整的参数设为可学习的网络参数，最后将SFGPR 降采样数据进行杂波抑制处理后输入网络。仿真和实测数据处理结果验证了该方法能够在无需人工进行参数选择和调整的情况下，提高地下目标的成像质量。
1 SFGPR压缩感知成像
1.1 SFGPR信号模型
在SFGPR 系统中，假设数据采集过程中存在M 个天线位置，在每一个天线位置都发射频率从f1到fn 共N 个工作频点，则系统在第m = 1, …, M 个天线位置的第n = 1, …, N 个工作频点接收到的地下目标信号表示为
式中，T 表示地下目标的个数，et 表示第t 个目标对应的反射系数，τt,m 表示在第m 个采集位置收发天线到第t个目标的双程传输时间。
图1为探地雷达成像示意图，假设收发天线和成像区域位于同一垂直截面内。成像区域沿深度方向和水平方向划分为P × Q 个大小一致的像素点。
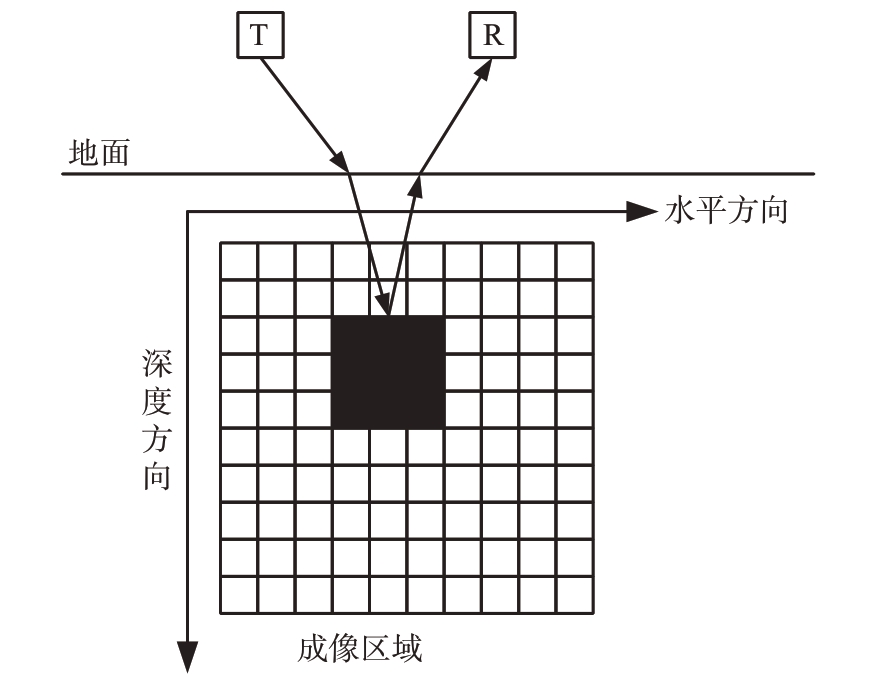
图1 探地雷达成像示意图
为了能够通过CS理论求解成像区域的二维反射率矩阵X(p, q)，其中p = 1, …, P；q = 1, …, Q，将X 列堆叠成PQ × 1 维的成像区域向量x，这样式（1）可表示为
式中，Sm =[Sm( )1 ,…, Sm(N)]T 为 第M 个 天 线 位 置的N × 1维的频域回波数据向量，Bm为第M个天线位置对应的N × PQ维的字典矩阵，其第j列表示为
根据M 个天线位置，得到MN × 1 维的全部回波数据向S =
和MN × PQ 维的字典矩阵B =
，因此全部回波数据向量S 和成像区域向量x之间的关系可表示为
通常，地下目标所占的像素点个数往往远少于成像区域的像素点总数，因此成像区域向量x具有较强的稀疏性。根据CS 理论，可以使用较少的频域回波数据重建稀疏向量x。在探地雷达的测量过程中，强地面杂波对成像质量有极大的干扰，因此在成像之前，需要对降采样数据进行杂波抑制处理，而大部分传统杂波抑制方法都是作用在均匀的采样数据，因此如图2 所示，构建一种均匀的回波数据采样方式。
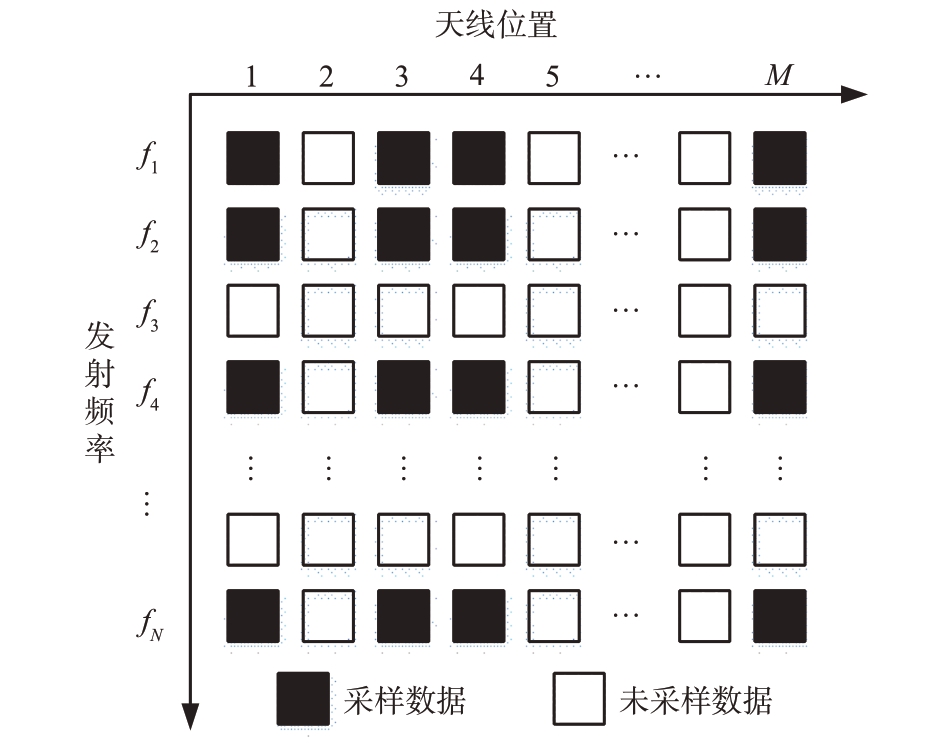
图2 回波数据采样示意图
首先从M 个天线位置随机选取L1 个位置，再从L1 个天线处选取L2 个相同频点位置的频域回波数据，构成L1L2 × MN维的降采样矩阵D:
式中:Ds为L1 × M维的空域采样矩阵，通过在M × M维单位矩阵中抽取L1 行得到；⊗为Kronecker 积；I为L2 × L2 维单位矩阵；Dm(m = 1, …, M)为L2 × N维的频域采样矩阵，通过在N × N维单位矩阵抽取L2行得到。
将降采样矩阵D 作用到全部回波数据向量S上，得到降采样回波数据向量s:
式中，A为L1L2 × PQ 维的测量矩阵。
对于成像区域向量x的重建，需要引入先验信息来构造解的约束条件，一般情况下x的稀疏性由l0 范数约束，但是l0 范数的优化问题是一个NP 难问题。因此在CS 中，通常是将l0 范数优化问题转化为求解最小l1 范数的凸优化问题，此时成像区域向量x的重建可以写成如下形式:
式中，λ为正则化系数。
1.2 FISTA方法
采用FISTA 重建方法按以下迭代步骤求解上述优化问题。FISTA 是迭代收缩阈值算法的快速版本，通过引入历史优化估计值提升方法的收敛性能。在第k次迭代中，首先使用先前的两次迭代结果xk - 1和xk - 2设计的线性组合更新额外估计zk:
式中:z1 = x0 = 0；(tk - 1 - 1)/tk 为收缩项，需满足非负和单调递增两个约束条件；tk 为收缩伪系数且t0 = 1。通过以下过程更新:
之后使用额外估计zk计算初始估计rk:
式中，μ 为迭代步长。基于初始估计rk，则式（7）对x的估计转化为如下LASSO问题:
最后采用软阈值收缩方法对式（11）进行快速求解，得到第k次迭代的重建结果xk:
式中，λ表示收缩阈值，sgn表示符号函数。
经过上述公式的迭代，使用FISTA方法可以重建成像区域向量x，但是方法中的参数（如迭代步长μ和收缩阈值λ）需要通过多次运行重建方法，人工调整到最优，这导致很难精准且快速地获得最佳的重建结果。
2 基于深度网络的SFGPR成像
本节基于FISTA迭代方法，在深度学习的框架下提出相应的深度展开网络模型。如图3所示，展开网络共有K 层，每一层网络都对应FISTA 的一次迭代，网络训练的过程可以视为是所有网络参数优化的过程。此外考虑到如果地下目标在成像区域所占像素点个数过多，那么其在成像区域就不能很好地满足稀疏条件，因此为了进一步提高网络的重建性能，在每层网络都加入CNN 模块作为成像区域的稀疏表示及其逆过程。
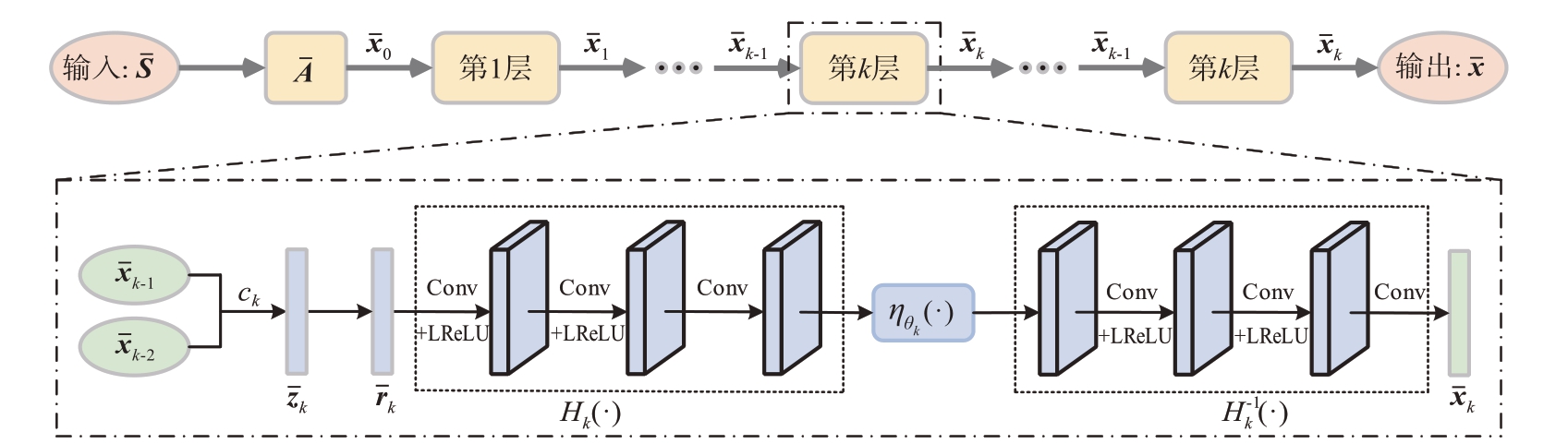
图3 FISTA展开网络示意图
在网络训练前，由于降采样回波数据向量s和测量矩阵A 中的元素均为复数值，而一般的深度网络只能处理实数。因此根据复数运算法则，将复数值数据的实部和虚部拆开，拼接成实数矩阵的形式输入网络，用上标
表示实部和虚部的拼接形式，生成网络输出后再重新组合得到重建结果x。因此式（6）中矩阵或向量可表示为
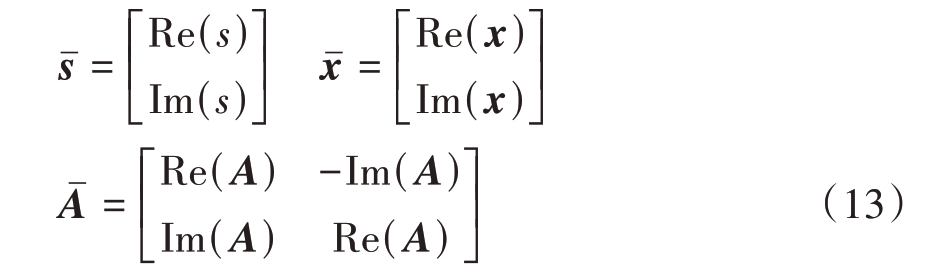
式中，Re(∙)和Im(∙)为复数值的实部和虚部。
在展开网络中，FISTA 的迭代过程被一一映射到网络的一层。以第k层为例，首先根据历史迭代估计值
和
更新额外估计
，初始化
= 0。
其中，收缩项为ck =(tk - 1 - 1)/tk，收缩伪系数tk 通过式（9）更新。
之后计算初始估计
，将μ 设为可学习的网络参数，μk 表示第k 层网络的迭代步长，因此每层网络第二步表示为
接下来引入基于CNN 模块设计的稀疏变换函数H(∙)，得到稀疏表示后的成像区域
:
式中:a1、a2、a3为3个卷积操作，卷积核的大小设置为3 × 3，卷积核通道数为64；LReLU 为激活函数，表示为
其中，ρ为LReLU的系数，默认设为0.01。
因此基于初始估计结果
，在展开网络中，式（11）可以重写为以下形式:
正如文献［12］所证明的，在合理的假设下，若
服从独立的正态分布，且有共同的均值和方差，则以下关系成立:
式中，α 为标量，
为第k 层稀疏表示后的初始估计。将该关系代入式（18）得到
式中，θ = αλ为网络的收缩阈值。之后采用软阈值收缩方法对式（20）求解得到
式中
为第k 层稀疏表示后的重建结果。为了还原第k 层的重建结果
，引入逆稀疏变换函数H-1(∙)作为稀疏表示的逆过程。如图3所示，H-1(∙)设计为与H(∙)对称的结构，使得H-1∙H = E，E为单位矩阵。因此
的最终求解形式为
其中，将θ、H(∙)和H-1(∙)均设置为可学习的网络参数，在迭代中更新，θk、Hk(∙)和
分别表示第k层网络的收缩阈值、稀疏变换函数和逆稀疏变换函数。
损失函数 根据重建信号的归一化均方误差和约束条件H-1∙H = E构建函数如下:
式中:W 为训练数据的总数目；
为第i 个训练数据在第K 层迭代后的重建结果；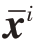
为第i 个训练数据对应的标签数据，使用Matlab 模拟地下目标在成像区域的真实位置分布并二值化后得到；γ为损失权重，默认设为0.01。
本网络是基于Pytorch神经网络框架实现，使用自适应矩估计优化器进行训练，学习率为0.000 1，整个网络设置为10层。
3 实验结果分析
3.1 仿真数据处理结果分析
为了验证所提成像方法的有效性，使用gprMax 电磁仿真软件进行探地雷达场景的仿真。共生成550组不同地下场景的雷达回波数据，其中500组用于训练网络，50组用于测试。仿真场景参数设置如下:激励信号设中心频率为1.5 GHz 的雷克子波，工作时窗为50 ns，收发天线位置间隔为12 cm，距离地面高度为27.8 cm，移动步长为2 cm，共有61个天线位置。地下介质的相对介电常数为4 ～ 8 之间随机整数。地下目标截面形状为圆形，直径范围为7～14 cm，在成像区域的随机位置生成1～2个目标。地下目标材质为铝或塑料，铝的相对介电常数和电导率分别为3.1 和2.3×107，塑料的相对介电常数和电导率分别为3.0和0.01。地面粗糙度设为±1 cm。由于成像方法在频域进行，将gprMax生成的时域散射场数据通过傅里叶变换技术转换为频域散射场数据，选择工作的频率段为0.06～3.06 GHz，频率步长为时窗的倒数20 MHz，每处天线位置有151个频点。
得到的全部频域数据首先加入信噪比为3 dB的加性高斯白噪声，然后通过降采样矩阵D，在61个天线位置随机抽取40 个，并在抽取的天线位置选取101 个相同频点位置的频域数据，即从9 211个数据中选取4 040 个用于成像，最后采用背景对消技术去除降采样数据中较强的地面杂波后输入网络。在图4仿真场景中，地下介质为相对介电常数4 的土壤，地下目标为两个直径9 cm 的铝制圆球，成像区域设为61 × 61 个像素点，每个像素点尺寸为1 cm × 1 cm，圆球中心分别位于成像区域的（-13 cm，12 cm）和（13 cm，24 cm）。
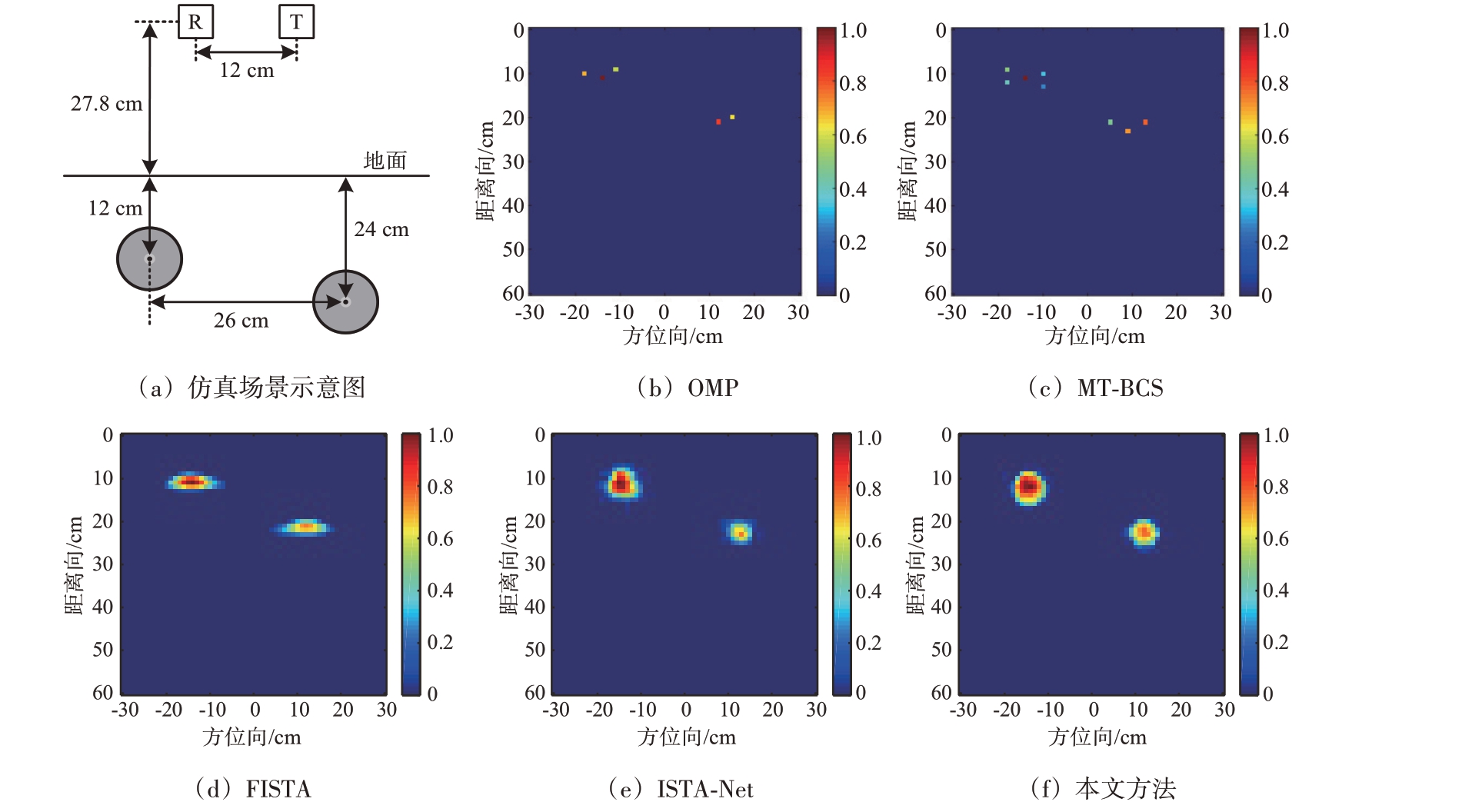
图4 仿真数据成像结果
为了验证本文方法的性能，采用正交匹配追踪（Orthogonal Matching Pursuit，OMP）、多任务贝叶斯压缩感知（Multitask Bayesian Compressive Sensing，MT-BCS）、FISTA、一种命名为迭代收缩阈值算法网络（Iterative Shrinkage Thresholding Algorithm Network，ISTA-Net）［9］的深度学习重建方法与本文方法进行成像结果对比，如图4（b）～（f）所示。可以看出，5 种方法均能较为准确地实现地下目标的定位。但OMP、MT-BCS 和FISTA 的重建结果难以反映地下目标真实形状；ISTA-Net和本文方法的重建结果都接近于圆形，但是本文方法更好地显示了地下目标的轮廓，成像效果好于前述方法。
采用目标杂波比（Target-to-Clutter Ratio，TCR）和重建时间作为评价标准来比较5 种方法的成像性能，TCR定义为
式中，Nt 和Nc 分别为目标区域和杂波区域的像素点个数，Pt 为目标区域所有像素点绝对值平方的和，Pc 为杂波区域所有像素点绝对值平方的和。实验共进行50 次独立测试，记录每次测试结果的TCR 和重建时间，最后取平均得到平均TCR 和平均重建时间。实验的计算环境为Intel Core i9-10980XE CPU。
表1 为5 种方法的仿真成像性能对比，从TCR值上看，本文方法高于传统CS 重建方法和ISTANet，说明成像质量最好。从重建时间上看，本文方法的耗时要长于OMP、FISTA 和ISTA-Net，原因是CNN 模块在提高成像精度的同时增加了网络的计算复杂度。但是相比于传统CS 重建方法，本文方法无需人工进行参数选择和调整，运行一次即可得到最佳的重建结果。
表1 仿真成像性能对比
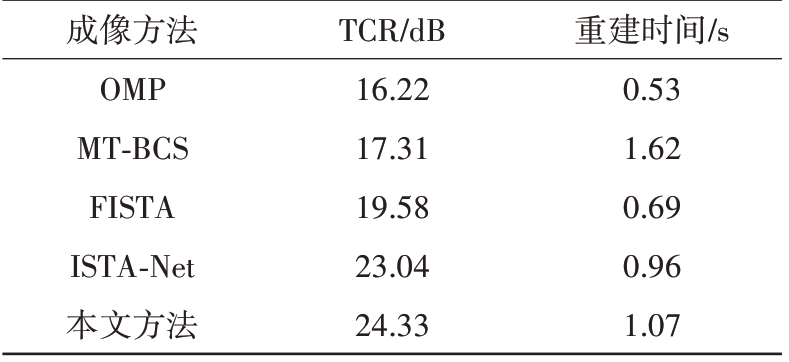
成像方法OMP MT-BCS FISTA ISTA-Net本文方法TCR/dB 16.22 17.31 19.58 23.04 24.33重建时间/s 0.53 1.62 0.69 0.96 1.07
3.2 实测数据处理结果分析
采用佐治亚理工大学公布的探地雷达实验数据［14］在训练好的网络上进行处理，网络使用3.1 节的仿真数据作为训练数据。在图5实测场景中，天线距离地面的高度为27.8 cm，收发天线间隔12 cm，移动步长2 cm，选取水平方向从-60 cm 到60 cm 之间的61 处天线位置，每处天线位置选取工作频率为0.06～3.06 GHz 的数据，频率步长为20 MHz，每处天线位置有151个频点。地下介质为沙地，地下目标为两个直径12.7 cm 的铝制圆球，成像区域设为61×61个像素点，每个像素点尺寸为1 cm×1 cm，圆球顶点在成像区域（-11 cm，12 cm）和（11 cm，12 cm）处。全部频域数据首先通过降采样矩阵D，在61 个天线位置随机抽取40 个，并在抽取的天线位置选取101 个相同频点位置的频域数据，即从9 211个数据中选取4 040个用于成像，然后采用低秩稀疏分解技术去除降采样数据中较强的地面杂波后输入网络。
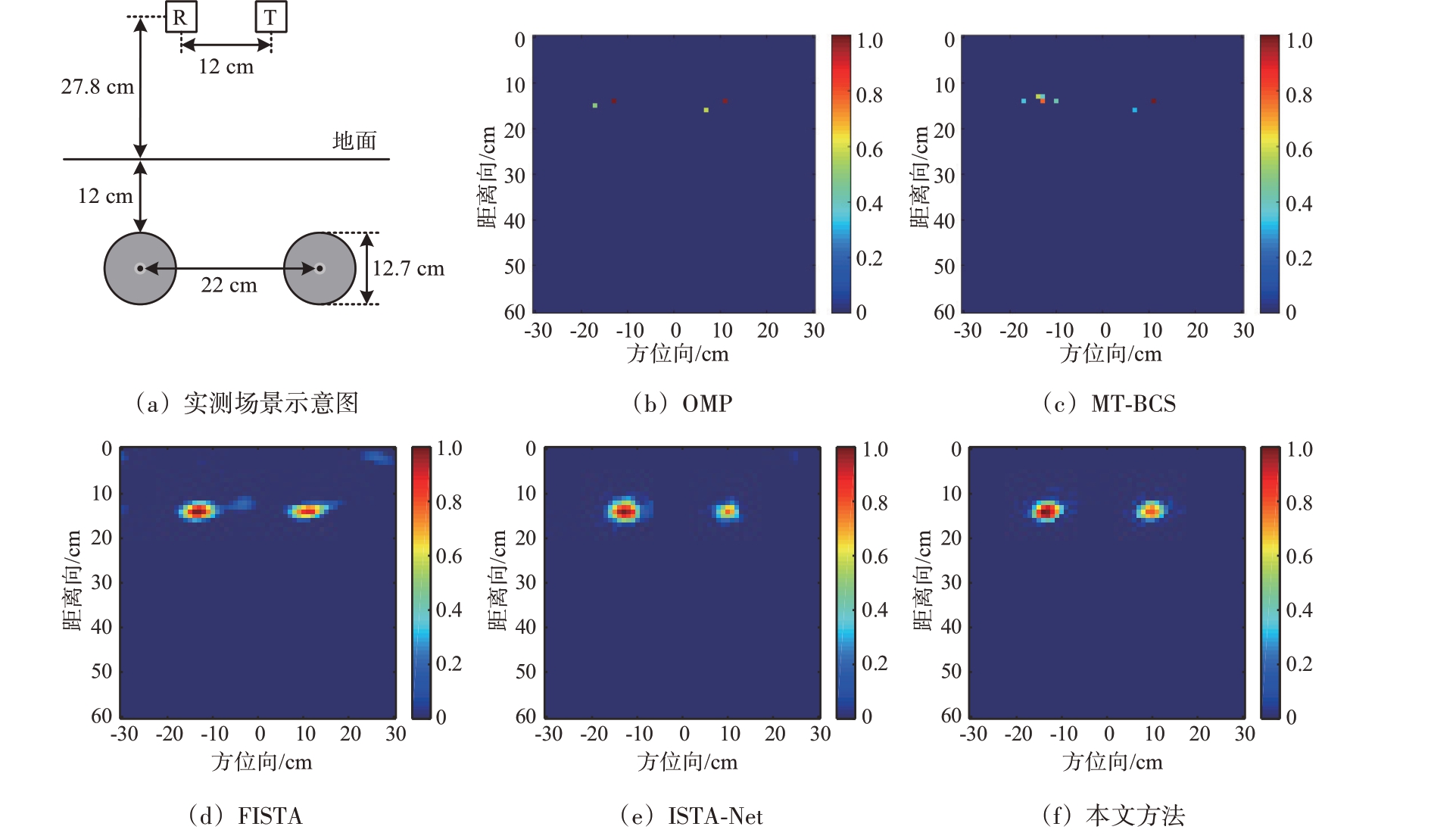
图5 实测数据成像结果
图5（b）～（f）为实测数据成像结果对比。可以看出，5 种方法均能较为准确地实现地下目标的定位。OMP 和MT-BCS 的成像结果由散点组成；FISTA 的成像结果存在少量伪影；ISTA-Net 和本文方法的成像结果视觉对比则较为接近。但是这两种基于深度学习的重建方法在实测数据中的表现并未有仿真数据测试集那样良好，原因是虽然在仿真数据制作过程中加入了3 dB 高斯白噪声，但生成的仿真数据仍然与实测数据的复杂情况存在一定差距。
表2 为5 种方法的实测成像性能对比。可以看出，本文方法的TCR 值最高，说明成像质量最好；虽然重建时间仅优于MT-BCS，但是相比于传统CS 重建方法，本文方法不需要通过多次运行程序，人工调优参数，进一步验证了本文方法优点。
表2 实测成像性能对比
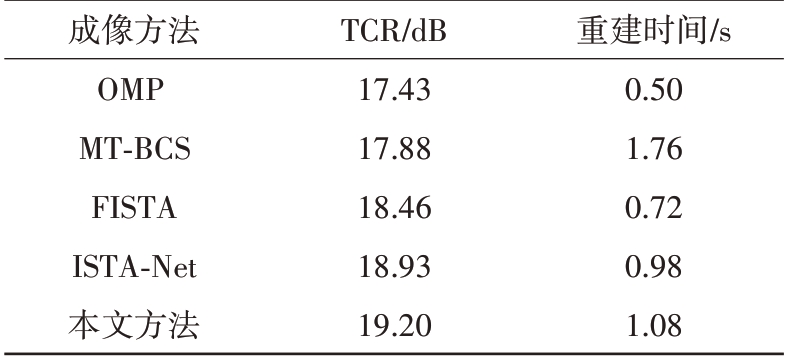
成像方法OMP MT-BCS FISTA ISTA-Net本文方法TCR/dB 17.43 17.88 18.46 18.93 19.20重建时间/s 0.50 1.76 0.72 0.98 1.08
4 结束语
本文提出了一种基于深度展开网络的SFGPR压缩感知成像方法。将FISTA 迭代方法展开成深度网络，CNN 模块作为成像区域的稀疏表示及其逆过程，需要手动调整的参数设置为可学习的网络参数。从实验结果来看，该方法能够在不需要人工调优参数的情况下，提高地下目标的成像精度。但是本文方法所需的重建时间较长，且在实际情况下的成像效果有待提升。因此在后续中，将继续探究更加轻量化的深度展开网络，使其在真实的场景中得到更好的应用。
［1］YANG Jungang, JIN Tian, HUANG Xiaotao, et al.Sparse MIMO Array Forward-Looking GPR Imaging Based on Compressed Sensing in Clutter Environment ［J］.IEEE Trans on Geoscience and Remote Sensing, 2014, 52（7）: 4480-4494.
［2］ZIBETTI M V W, HELOU E S, REGATTE R R, et al.Monotone FISTA with Variable Acceleration for Compressed Sensing Magnetic Resonance Imaging［J］.IEEE Trans on Computational Imaging, 2018, 5（1）:109-119.
［3］PAL D K, MENGSHOEL O J.Stochastic CoSaMP: Randomizing Greedy Pursuit for Sparse Signal Recovery［C］//Joint European Conference on Machine Learning and Knowledge Discovery in Databases, Cham:Springer International Publishing, 2016:761-776.
［4］SALUCCI M, ANSELMI N.Multi-Frequency GPR Microwave Imaging of Sparse Targets Through a Multi-Task Bayesian Compressive Sensing Approach［J］.Journal of Imaging, 2021, 7（11）:247-257.
［5］CHUN P J, SUZUKI M, KATO Y.Iterative Application of Generative Adversarial Networks for Improved Buried Pipe Detection from Images Obtained by Ground-Penetrating Radar［J］.Computer Aided Civil and Infrastructure Engineering, 2023, 38（17）:2472-2490.
［6］LIU Bin, REN Yuxiao, LIU Hanchi, et al.GPRInvNet:Deep Learning-Based Ground-Penetrating Radar Data Inversion for Tunnel Linings ［J］.IEEE Trans on Geoscience and Remote Sensing, 2021, 59（10）:8305-8325.
［7］ZHANG Xin, HAN Liangxiu, ROBINSON M, et al.Deep Learning-Based Nondestructive Evaluation of Reinforcement Bars Using Ground Penetrating Radar and Electromagnetic Induction Data ［J］.Computer Aided Civil and Infrastructure Engineering, 2022, 37（14）:1834-1853.
［8］曾春艳，余琰，王志锋，等.面向可解释压缩感知的算法展开综述［J］.华中科技大学学报，2022，50（11）:35-43.
［9］XIANG Jinxi, DONG Yonggui, YANG Yunjie.FISTA-Net:Learning a Fast Iterative Shrinkage Thresholding Network for Inverse Problems in Imaging［J］.IEEE Trans on Medical Imaging, 2021, 40（5）:1329-1339.
［10］ZHANG Hongwei, NI Jiacheng, XIONG Shichao, et al.SR-ISTA-Net: Sparse Representation-Based Deep Learning Approach for SAR Imaging［J］.IEEE Geoscience and Remote Sensing Letters, 2022, 19（8）:1-5.
［11］GUO Jianhua, WANG Lei, LI Feng, et al.CSI Feedback with Model-Driven Deep Learning of Massive MIMO Systems ［J］.IEEE Communications Letters, 2021, 26（3）:547-551.
［12］ZHANG Jian, GHANEM B.ISTA-Net: Interpretable Optimization-Inspired Deep Network for Image Compressive Sensing［C］//2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition,Salt Lake City, UT, USA:IEEE, 2018:1828-1837.
［13］LIANG Jiadian, WEI Shunjun, WANG Mou, et al.Sparsity-Driven ISAR Imaging via Hierarchical Channel-Mixed Framework［J］.IEEE Sensors Journal, 2021, 21（17）:19222-19235.
［14］COUNTS T, GURBUZ A C, SCOTT W R, et al.Multistatic Ground-Penetrating Radar Experiments ［J］.IEEE Trans on Geoscience and Remote Sensing, 2007, 45（8）:2544-2553.